| МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РСФСР
Горьковский политехнический институт им. А.А. Жданова Заочный факультет
Кафедра радиотехники
Г.В. Глебович
ПЕРЕХОДНЫЕ ПРОЦЕССЫ И ОСНОВЫ СИНТЕЗА ЛИНЕЙНЫХ РАДИОТЕХНИЧЕСКИХ ЦЕПЕЙ
Лекции по курсу "Основы теории цепей"
Горький - 1968
ПРЕДИСЛОВИЕ
В учебные планы радиотехнических факультетов для студентов специальности "Радиотехника" введен курс "Основы теории цепей" В него включен материал, ранее изучавшийся в курсах "Теоретические основы электротехники" и "Теоретические основы радиотехники".
Потребовался коренной пересмотр ряда разделов этих курсов, а также в соответствии с программой были включены новые разделы, в изучении которых появилась настоятельная необходимость.
Содержанием пособия являются два крупных раздела курса "Основы теории цепей" - анализ переходных процессов и основы синтеза линейных радиотехнических цепей. Последний раздел ранее практически не изучался в упомянутых курсах.
Первый раздел изложен кратко и по существу соответствует объему читаемых автором лекций. Второй раздел изложен более полно, несколько выходя за объем лекций.
Автор весьма признателен доценту, к.т.н. К.П. Полову за ценные замечания, сделанные им при рецензировании рукописи пособия, а также благодарен сотрудникам кафедры радиотехники за советы и замечания, высказанные ими при обсуждении рукописи.
Автор
1. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ
Введение
Современные радиотехнические системы часто включают в себя комплекс достаточно сложных электрических цепей, среди которых разнообразные линейные цепи.
В зависимости от характера воздействующих э.д.с. и назначения линейных цепей в них могут протекать самые различные процессы. Поэтому необходимо иметь ясное представление о таких процессах и уметь рассчитывать их для определенной цепи при заданном воздействии. Это относится к задачам анализа процессов в цепях. Среди них все больший интерес вызывают задачи, связанные с процессами в различных импульсных системах.
В этих задачах кроме анализа установившихся или стационарных процессов важное значение имеет анализ переходных процессов, возникающих при включении или выключении э.д.с. и при воздействии импульсных сигналов.
Переходные процессы, протекающие в линейных цепях, также, как и стационарные, подчиняются законам Кирхгофа, которые позволяют установить связь между э.д.с., действующей в некоторой ветви цепи и током в любой ветви.
Записанные для цепи уравнения Кирхгофа обычно приводятся к линейному дифференциальному уравнению, порядок которого зависит от числа реактивных элементов и сложности цепи.
Изучить процесс, возникающий в цепи под действием э.д.с., означает найти решение уравнения и исследовать его поведение вдоль всей временной оси.
Если по истечении некоторого времени с момента начала действия э.д.с. на цепь в ней устанавливается стационарный режим, отличный от стационарного режима, имевшегося до начала действия э.д.с., то это время, определяющее длительность переходного процесса, называют временем установления. Характер переходного процесса и величина времени установления часто являются главными факторами, от которых зависит правильность функционирования радиотехнического устройства.
Как уже говорилось, связь между током в любой ветви цепи и действующей э.д.с. устанавливается дифференциальным уравнением, которое в общем случае выглядит так:
 (0.1) (0.1)
где  (
K
= 0, 1, 2,...n
) - постоянные коэффициенты, зависящие от величины элементов цепи, i
-
ток в цепи, e
(
t
)-
внешняя э.д.с. произвольного вида. (
K
= 0, 1, 2,...n
) - постоянные коэффициенты, зависящие от величины элементов цепи, i
-
ток в цепи, e
(
t
)-
внешняя э.д.с. произвольного вида.
Известно, что решение уравнения (0.l) может быть представлено в форме суммы
 (0.2) (0.2)
Здесь i
2
(
t
) -
частное решение уравнения с правой частью, в качестве которого обычно принимается стационарное (вынужденное) решение, определяющее связь между i
(
t
)
и e
(
t
)
в установившемся режиме; i
1
(t
) -
решение однородного уравнения (правая часть равна нулю) , определяющее переходной процесс в цепи.
Если цепь такова, что, то можно указать времен ной интервал  конечной величины, по истечению которого с момента начала действия э.д.с. в цепи практически установится стационарный режим. конечной величины, по истечению которого с момента начала действия э.д.с. в цепи практически установится стационарный режим.
Поскольку i
1
(
t
)
есть решение уравнения без правой части, то длительность переходного процесса не зависит от интенсивности и характера входного воздействия, а определяется свойствами цепи. Характер переходного процесса также существенно зависит от свойств цепи.
Возможность представления решения уравнения (0.l) в виде (0.2) опирается на основное свойство линейных цепей, выражающееся в принципе суперпозиции.
Найти решение (0.2) можно и с помощью других способов, основанных на принципе суперпозиции. Так, э.д.с. сложной формы удобно рассматривать как образованную в результате сложения элементарных э.д.с. некоторой основной формы. Находя переходный процесс, вызванный действием всех элементарных э.д.с., образующих данную сложную э.д.с., и затем суммируя полученные результаты, оказывается возможным нахождение всего переходного процесса.
В зависимости от вида элементарных э.д.с. и особенностей вычисления результирующего переходного процесса различают ряд методов анализа. Основные из них - спектральный метод, основанный на преобразовании Фурье, операторный, использующий преобразование Лапласа и временной метод, основанный на интеграле Дюамеля.
Перечисленные методы во многих случаях существенно упрощают нахождение решения уравнения (0.l). Развитие этих методов привело к тому, что каждый из них позволяет на своем языке характеризовать существенные для практики свойства цепей без обращения к их дифференциальным уравнениям. Это придало большую самостоятельность этим методам и позволяет говорить о них, как об основных методах анализа процессов в линейных цепях. Их особенности и примеры применения будут рассмотрены в последующих главах.
Глава 1
АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДОМ РЕШЕНИЯ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1.1. Введение
Метод решения линейных дифференциальных уравнений, или так называемый классический метод, основан на отыскании решения вида (0.2) для уравнения (0.l).
Так, при подключении э.д.с, e
(
t
)
к последовательно соединенным индуктивности L
,
емкости С
и активному сопротивлению R
, на основании второго закона Кирхгофа получаем уравнение

которое приводится к линейному дифференциальному уравнению второго порядка
 (1.1) (1.1)
Согласно выражению (0.2) решение этого уравнения записывается в виде
 (1.2) (1.2)
То есть, процесс, происходящий в цепи, рассматривается условно состоящим из двух процессов — вынужденного, который наступил как бы сразу (ток i
2
), и свободного, наблюдающегося только во время переходного процесса (ток i
1
). Уместно отметить, что в рассматриваемой цепи физически существует только один ток i
, а его представление в виде суммы токов i
1
и i
2
является удобным приемом, облегчающим расчеты при данном методе анализа.
Известно, что в результате интегрирования уравнения (1.1),или в общем случае уравнения (0.l),eгo решение включает в себя постоянные интегрирования, которые должны быть определены по начальным значениям основных физических величин, т.е. необходимо знать начальные (при t
=
0) токи в индуктивностях и заряды на емкостях, иначе говоря, надо знать начальные условия задачи.
В общем случае уравнения (0.l) для n
постоянных интегрирования  c учетом n
начальных условии составляют дополнительно n
уравнений, из которых находятся постоянные интегрирования. После этого окончательно может быть найден вид решения (0.2) или, в данном случае, решения (l.2). c учетом n
начальных условии составляют дополнительно n
уравнений, из которых находятся постоянные интегрирования. После этого окончательно может быть найден вид решения (0.2) или, в данном случае, решения (l.2).
Если анализируемая цепь содержит несколько взаимосвязанных контуров, то при составлении дифференциального уравнения удобно пользоваться методом контурных токов. Сначала образуется система из m
уравнений относительно m
неизвестных контурных токов. Порядок каждого уравнения не выше второго. Если в контуре сложной цепи имеется несколько индуктивностей и емкостей, то они могут быть сведены (например, заменой двух емкостей одной эквивалентной) к одной независимой емкости и одной индуктивности.
Затем путем исключения всех токов, кроме одного интересующего, получают одно дифференциальное уравнение порядка  относительно выбранного тока. Порядок уравнения равен числу независимых реактивных элементов (накопителей энергии) в цепи. относительно выбранного тока. Порядок уравнения равен числу независимых реактивных элементов (накопителей энергии) в цепи.
Хотя процесс анализа переходных явлений методом решения дифференциальных уравнений достаточно наглядно вскрывает физические процессы в цепи, этот метод оказывается громоздким для случая сложных разветвленных цепей, когда определение постоянных интегрирования связано с составлением и решением системы из n
уравнений. Нахождение же этим методом переходных процессов в простейших цепях не вызывает трудностей и способствует пониманию физических явлений. Убедимся в этом на ряде примеров, часто встречающихся на практике.
1.2. Включение цепи
R,
C
на постоянное напряжение
 Пусть в момент t
=0
цепь, состоящая из последовательно соединенных активного сопротивления R
и не заряженной емкости C
, подключается к источнику постоянного напряжения E
(рис.1.1). Наличие переходного процесса в данной цепи связано с тем, что при весьма кратковременном ("мгновенном") изменении внешнего воздействия энергия поля конденсатора не может измениться мгновенно. Действительно, при скачкообразном изменении запаса энергии в цепи мощность, потребляемая цепью, принимала бы бесконечно большое значение, что не имеет физического смысла. Энергия электрического поля емкости Пусть в момент t
=0
цепь, состоящая из последовательно соединенных активного сопротивления R
и не заряженной емкости C
, подключается к источнику постоянного напряжения E
(рис.1.1). Наличие переходного процесса в данной цепи связано с тем, что при весьма кратковременном ("мгновенном") изменении внешнего воздействия энергия поля конденсатора не может измениться мгновенно. Действительно, при скачкообразном изменении запаса энергии в цепи мощность, потребляемая цепью, принимала бы бесконечно большое значение, что не имеет физического смысла. Энергия электрического поля емкости

Поэтому условие отсутствия скачкообразного изменения энергии означает, что в цепи R
,C
напряжение на емкости  скачком изменяться не может. скачком изменяться не может.
Выясним законы изменения напряжения на элементах схемы во времени, т.е. найдем характер переходного процесса. На основании второго закона Кирхгофа для данной цепи при t
= 0
имеем
 (1.3) (1.3)
где  и и  - соответственно падение напряжения на сопротивлении и напряжение на емкости C
. С момента включения цепи начинается заряд конденсатора через активное сопротивление. Ток в цепи - соответственно падение напряжения на сопротивлении и напряжение на емкости C
. С момента включения цепи начинается заряд конденсатора через активное сопротивление. Ток в цепи  , a напряжение на сопротивлении , a напряжение на сопротивлении  . .
Тогда выражение (l.3) принимает вид
 (1.4) (1.4)
Общее решение полученного линейного дифференциального уравнения первого порядка (l.4) представим аналогично выражению (l.2) в виде суммы напряжений на емкости  - для свободного процесса и - для свободного процесса и  - для вынужденного процесса в цепи - для вынужденного процесса в цепи
 (1.5) (1.5)
Напряжение  должно быть равно напряжению источника E
к концу переходного процесса, так как конденсатор зарядится до напряжения E
при должно быть равно напряжению источника E
к концу переходного процесса, так как конденсатор зарядится до напряжения E
при 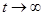 . Напряжение . Напряжение  есть решение однородного уравнения есть решение однородного уравнения

т.е. имеет вид

где A
– постоянная интегрирования, а  - постоянная времени цепи заряда конденсатора, т.е. время, за которое напряжение - постоянная времени цепи заряда конденсатора, т.е. время, за которое напряжение  уменьшается в уменьшается в  раз. Зная выражение для раз. Зная выражение для  , подставим его в равенство (1.5) и получи решение уравнения (1.4). , подставим его в равенство (1.5) и получи решение уравнения (1.4).
 (1.6)
(1.6)
Постоянная A
определяется из начальных условий для данной цепи, заключающихся в том, что при t
=0
,  = 0
, так как в момент включения цепи напряжение на конденсаторе скачком измениться не может в силу непрерывного характера изменения энергии электрического поля конденсатора. Таким образом, при t
=0
из (l.6) имеем 0=
A
+
E
т.е. A
=-
E
и = 0
, так как в момент включения цепи напряжение на конденсаторе скачком измениться не может в силу непрерывного характера изменения энергии электрического поля конденсатора. Таким образом, при t
=0
из (l.6) имеем 0=
A
+
E
т.е. A
=-
E
и

Напряжение на конденсаторе в процессе его заряда возрастает no экспоненциальному закону, приближаясь к величине E
тем быстрее, чем меньше постоянная времени цепи  . Теоретически . Теоретически  при при  . Однако на практики вводят понятие времени установления стационарного процесса . Однако на практики вводят понятие времени установления стационарного процесса  , определяемое из условия, что за это время напряжение на емкости достигает величины 0,95 E
, т.е. , определяемое из условия, что за это время напряжение на емкости достигает величины 0,95 E
, т.е.

откуда получаем

или

Время установления также часто определяется как разность моментов времени  и и  , т.e.
, т.e.  . Здесь в моменты . Здесь в моменты  и
и  напряжение на емкости достигает соответственно значений 0,lE
и 0,8E
, т.е. имеют место равенства
напряжение на емкости достигает соответственно значений 0,lE
и 0,8E
, т.е. имеют место равенства

откуда определяется время установления

Для тока в цепи находим выражение
 (1.8) (1.8)
т.е. ток убывает по экспоненциальному закону, а следовательно, и напряжение на сопротивлении  также убывает по этому закону, ибо также убывает по этому закону, ибо
 (1.9) (1.9)
Как видно из (1.8),при t
=0  , т.е. он изменяется скачком от нуля до
, т.е. он изменяется скачком от нуля до  . В цепи R
,C
скачок тока допустим. . В цепи R
,C
скачок тока допустим.
Графики изменения напряжений в цепи приведены на рис.1.2.

В процессе заряда емкости половина энергии, отдаваемой источником, переходит в энергию, запасаемую емкостью, а вторая половина расходуется в активном сопротивлении, переходя в тепло. Энергия, расходуемая на сопротивлении

где  - энергия, накопленная в емкости. - энергия, накопленная в емкости.
1.3. Разряд конденсатора на активное сопротивление
Если конденсатор  ,
предварительно заряженный до напряжения ,
предварительно заряженный до напряжения  замкнуть в момент замкнуть в момент  на сопротивление
на сопротивление  (рис.1.3), то будет происходить его разряд. В данном случае внешнего воздействия нет и следует рассматривать лишь свободный процесс в цепи, т.е. уравнение (l.4) будет (рис.1.3), то будет происходить его разряд. В данном случае внешнего воздействия нет и следует рассматривать лишь свободный процесс в цепи, т.е. уравнение (l.4) будет
 , ,
решением которого является выражение
 . .
Для определения константы интегрирования  воспользуемся начальным условием задачи: при
воспользуемся начальным условием задачи: при   .
Поэтому .
Поэтому  и тогда решение принимает вид и тогда решение принимает вид
 . .
Ток разряда
 (1.10) (1.10)
Сравнивая выражения (1.8) н (1.10),видим, что, как и следовало ожидать, направление тока разряда противоположно направлению тока заряда емкости для этой же цепи. Графики изменения напряжения и тока приведены на рнс.1.4. В процессе разряда емкости вся энергия, запасенная в ней, расходуется в активном сопротивлении в виде тепловых потерь.

1.4. Включение цепи
R,
L
на постоянное напряжение
Рассматриваемая цепь приведена на рис.1.5.Так как энергия магнитного поля катушки индуктивности равна
 , ,
и она не может изменяться скачком при мгновенном изменении внешнего воздействия, то отсюда заключаем, что в цепи R
,
L
ток скачком изменяться не может. Требуется конечное время переходного процесса, пока ток в цепи не достигнет стационарного значения. Рассмотрим этот процесс. Уравнение Кирхгофа для такой цепи
| Рис. 1.5
|
 (1.11) (1.11)
Общее решение этого уравнения  , где , где  -
свободный ток, являющийся решением однородного уравнения -
свободный ток, являющийся решением однородного уравнения

т.е.  .Ток .Ток  - вынужденный, который при - вынужденный, который при  достигает постоянной величины, равной достигает постоянной величины, равной  , ибо э.д.с, самоиндукции при , ибо э.д.с, самоиндукции при становится равной нулю. Таким образом, становится равной нулю. Таким образом,
 , ,
здесь  - постоянная времени, - постоянная времени,  - постоянная интегрирования, определяемая начальным условием задачи, т.е. количеством энергии, имеющимся в магнитном поле катушки в момент
- постоянная интегрирования, определяемая начальным условием задачи, т.е. количеством энергии, имеющимся в магнитном поле катушки в момент  . По условию при . По условию при  ток ток  , энергия в катушке не запасена. Следовательно, из выражения для тока находим , энергия в катушке не запасена. Следовательно, из выражения для тока находим  . Общее решение уравнения (1.11) будет . Общее решение уравнения (1.11) будет
 (1.12) (1.12)
Из этого выражения видно, что ток нарастает по экспоненциальному закону, достигая установившейся величины  тем быстрее, чем меньше постоянная времени тем быстрее, чем меньше постоянная времени  . Как и при заряде емкости, можно за время установления . Как и при заряде емкости, можно за время установления  принять время, равное принять время, равное  . .
По известному току  находится напряжение на активном сопротивлении находится напряжение на активном сопротивлении  и на индуктивности и на индуктивности  . .
 (1.13) (1.13)
 (1.14) (1.14)

Графики тока  и напряжения и напряжения  приведены на рис.1.6. Так как до включения цепи напряжение на индуктивности было равно нулю, а в момент включения приведены на рис.1.6. Так как до включения цепи напряжение на индуктивности было равно нулю, а в момент включения  , то напряжение на индуктивности изменяется скачком, а ток изменяется непрерывно, ибо с его величиной связана энергия, запасаемая в магнитном поле катушки. , то напряжение на индуктивности изменяется скачком, а ток изменяется непрерывно, ибо с его величиной связана энергия, запасаемая в магнитном поле катушки.
Необходимо отметить аналогию в характере изменения тока в данной цепи и напряжения на емкости  в цепи в цепи  при включении их на постоянное напряжения (см. рис. 1.4 и 1.6). Такая же аналогия имеет место относительно величин при включении их на постоянное напряжения (см. рис. 1.4 и 1.6). Такая же аналогия имеет место относительно величин  и и  в этих же цепях. в этих же цепях.
1.5. Разряд конденсатора в цепи  . .
 Пусть предварительно заряженный до напряжения Пусть предварительно заряженный до напряжения  конденсатор емкостью конденсатор емкостью  в исходный момент времени замыкается на последовательно соединенные активное сопротивление
в исходный момент времени замыкается на последовательно соединенные активное сопротивление  и катушку индуктивности и катушку индуктивности  (рис.1.7). Рассматриваемая цепь содержит, в отличие от предыдущих примеров, два энергоемких параметра - емкость и индуктивность. Поэтому составленное на основании второго закона Кирхгофа уравнение приводится к дифференциальному уравнению второго порядка. (рис.1.7). Рассматриваемая цепь содержит, в отличие от предыдущих примеров, два энергоемких параметра - емкость и индуктивность. Поэтому составленное на основании второго закона Кирхгофа уравнение приводится к дифференциальному уравнению второго порядка.
Действительно, имеем для суммы напряжений на элементах цепи
 , (1.15) , (1.15)
или, так как
 , ,
уравнение приводится к виду
 . (1.16) . (1.16)
Аналогичное уравнение записывается и для тока в цепи
 . (1.17) . (1.17)
Решением однородного уравнения (1.17) является
 , ,
Где  - корни характеристического уравнения - корни характеристического уравнения
 , ,
т.е.
 , ,
где
 , ,  , ,  . .
Тогда решение уравнения (1.17)
 . (1.18) . (1.18)
Постоянные интегрирования  и и  находятся из начальных условий задачи. Так как в момент замыкания цепи конденсатор заряжен до напряжения находятся из начальных условий задачи. Так как в момент замыкания цепи конденсатор заряжен до напряжения  , а в индуктивности энергия не запасена, то при , а в индуктивности энергия не запасена, то при  , ,  , ,  . Поэтому из (l.l8) находим . Поэтому из (l.l8) находим  , т.е. , т.е.  , а из (1.15) имеем при , а из (1.15) имеем при   или или  . Находя из (1.18) . Находя из (1.18)  и учтя предыдущее равенство, получаем и учтя предыдущее равенство, получаем
 . .
Подставив значения констант  и и  в выражение (1.18), находим ток в выражение (1.18), находим ток
 . (1.19) . (1.19)
Аналогично получается решение уравнения (1.18) для напряжения на емкости
 . (1.20) . (1.20)
В зависимости от того, будет ли  величиной мнимой или действительной, т.е. если величиной мнимой или действительной, т.е. если  или или  в цепи наблюдаются различные по характеру переходные процессы. в цепи наблюдаются различные по характеру переходные процессы.
В случае  или иначе или иначе  , величина , величина  - действительная. Пользуясь выражением (1.19) имеем - действительная. Пользуясь выражением (1.19) имеем
 . (1.21) . (1.21)
Согласно выражению (l.21) на рис.1.8 построен график тока  ,
а также приведен график напряжения на емкости ,
а также приведен график напряжения на емкости  . В рассматриваемом случае характер процесса в цепи носит название апериодического разряда конденсатора. Граничным случаем апериодического процесса является случай, когда . В рассматриваемом случае характер процесса в цепи носит название апериодического разряда конденсатора. Граничным случаем апериодического процесса является случай, когда  . T.e. . T.e.  . Величина тока для этого случая находится, если раскрыть неопределенность, получающуюся в выражении (1.19). Закон изменения тока во времени здесь таков: . Величина тока для этого случая находится, если раскрыть неопределенность, получающуюся в выражении (1.19). Закон изменения тока во времени здесь таков:
 . .
Как видно из рис.1.8, при апериодическом разряде емкости ток в цепи вначале равен нулю, что объясняется противодействием э.д.с, самоиндукции катушки. Затем по мере убывания этой э.д.с. ток по абсолютной величине растет. Однако в процессе разряда емкости напряжение  убывает, и ток с некоторого момента также начинает убывать. убывает, и ток с некоторого момента также начинает убывать.
В случае  , т.е. , т.е.  , величина , величина  - мнимая, а корни характеристического уравнения - мнимая, а корни характеристического уравнения
 , ,
где  . Тогда по формулам (1.19) и (1.20) находим . Тогда по формулам (1.19) и (1.20) находим
 (1.22) (1.22)
 (1.23) (1.23)
где  . .
Для контура с высокой добротностью, т.е. если  , то , то  и и  , a напряжение на емкости , a напряжение на емкости
 . .
 Графики тока и напряжения для этого случая приведены на рис.1.9. Такой процесс называется колебательным разрядом конденсатора. В течение этого процесса через каждые четверть периода колебаний происходит обмен энергией, запасенной в конденсаторе и катушке индуктивности. При этом часть энергии теряется в активном сопротивлении, что является причиной убывания амплитуды колебаний напряжения и тока с ростом времени, т.е. колебания затухают. Коэффициент Графики тока и напряжения для этого случая приведены на рис.1.9. Такой процесс называется колебательным разрядом конденсатора. В течение этого процесса через каждые четверть периода колебаний происходит обмен энергией, запасенной в конденсаторе и катушке индуктивности. При этом часть энергии теряется в активном сопротивлении, что является причиной убывания амплитуды колебаний напряжения и тока с ростом времени, т.е. колебания затухают. Коэффициент  , носящий название коэффициента затухания, определяет скорость убывания амплитуды во времени. Частота , носящий название коэффициента затухания, определяет скорость убывания амплитуды во времени. Частота
 (1.24) (1.24)
называется частотой собственных колебаний (или свободных колебаний) контура. Как видно, она зависит не только от реактивных параметров контура, но и от активного сопротивления, в отличие от резонансной частоты контура  , введенной при рассмотрении стационарных колебательных процессов в контуре. , введенной при рассмотрении стационарных колебательных процессов в контуре.
Затухание колебаний иногда характеризуют логарифмическим декрементом затухания  , являющимся натуральным логарифмом отношения амплитуд тока или напряжения, определяемых в моменты времени , являющимся натуральным логарифмом отношения амплитуд тока или напряжения, определяемых в моменты времени  и и  , т.е. , т.е.
 . (1.25) . (1.25)
Время, за которое амплитуда колебаний убывает в  раз, .иногда принимают за постоянную времени раз, .иногда принимают за постоянную времени  контура контура
 . (1.28) . (1.28)
 Интересно обратить внимание на то, что при последовательном соединении сопротивления Интересно обратить внимание на то, что при последовательном соединении сопротивления  коэффициент затухания коэффициент затухания  не зависит от емкости не зависит от емкости  . Но можно рассмотреть случай контура, в котором коэффициент затухания зависит от емкости . Но можно рассмотреть случай контура, в котором коэффициент затухания зависит от емкости  и не зависит от индуктивности и не зависит от индуктивности  .
Такой контур, где потери отнесены к емкости, изображен на рис. 1.10. Уравнение Кирхгофа для этой цепи приводится к дифференциальному уравнению, имеющему вид .
Такой контур, где потери отнесены к емкости, изображен на рис. 1.10. Уравнение Кирхгофа для этой цепи приводится к дифференциальному уравнению, имеющему вид
 , ,
или, так как  , имеем: , имеем:
 . .
Решение этого уравнения
 , ,
где  - коэффициент затухания. - коэффициент затухания.
1.6. Воздействие постоянного напряжения на L,
C,
R
цепь
Пусть постоянное напряжение  подключается в момент подключается в момент  к последовательному к последовательному  контуру (рис.1.11).Уравнение Кирхгофа для рассматриваемой цепи имеет вид контуру (рис.1.11).Уравнение Кирхгофа для рассматриваемой цепи имеет вид
  , (1.27) , (1.27)
и его общее решение  , где , где  - вынужденный ток, в данном случае равный нулю, так как переходный процесс заканчивается, как только конденсатор зарядится до напряжения - вынужденный ток, в данном случае равный нулю, так как переходный процесс заканчивается, как только конденсатор зарядится до напряжения  , а ток заряда прекратится. Ток , а ток заряда прекратится. Ток  - свободный ток, являющийся решением однородного уравнения - свободный ток, являющийся решением однородного уравнения
 , ,
рассмотренного в предыдущем примере. Однако начальные условия данной задачи несколько отличаются от условий предыдущей задачи. Здесь при  имеем имеем  , ,  , а напряжение на индуктивности , а напряжение на индуктивности  . Поэтому в выражении для решения этого однородного уравнения . Поэтому в выражении для решения этого однородного уравнения

постоянные интегрирования  и и  равны равны

и тогда ток  описывается выражением описывается выражением
 , (1.28) , (1.28)
напряжение на индуктивности выражается зависимостью
 , (1.29) , (1.29)
а для напряжения на емкости в соответствии с (1.27) получаем
 . (1.30) . (1.30)
 Если корни характеристического уравнения Если корни характеристического уравнения  - действительные, т.е. если - действительные, т.е. если  , то цепь апериодическая и на основании выражений (1.28), (1.29) и (l.30) можно построить графики для , то цепь апериодическая и на основании выражений (1.28), (1.29) и (l.30) можно построить графики для , ,  и и  (рис.1.12). Как видно из рисунка, напряжение на конденсаторе в процессе его заряда монотонно возрастает, приближаясь при
(рис.1.12). Как видно из рисунка, напряжение на конденсаторе в процессе его заряда монотонно возрастает, приближаясь при  к величине к величине  .
Ток .
Ток  вначале возрастает по мере уменьшения э.д.с. самоиндукции. Однако, с увеличением напряжения на емкости ток ее заряда должен уменьшаться. Поэтому достигнув в момент вначале возрастает по мере уменьшения э.д.с. самоиндукции. Однако, с увеличением напряжения на емкости ток ее заряда должен уменьшаться. Поэтому достигнув в момент  максимума, ток спадает, а напряжение на индуктивности меняет знак. максимума, ток спадает, а напряжение на индуктивности меняет знак.
Если корни  - комплексные, т.е. если - комплексные, т.е. если  , то контур становится колебательным и на основании выражений (l.28), (l.30) и полученных ранее выражений (l.22), (l.23) получаем для тока и напряжения на емкости выражения , то контур становится колебательным и на основании выражений (l.28), (l.30) и полученных ранее выражений (l.22), (l.23) получаем для тока и напряжения на емкости выражения
 , (1.31) , (1.31)
 (1.32) (1.32)
где, как и раньше,  
Если контур имеет высокую добротность, что обычно справедливо для радиотехнических контуров, то  , ,  и для напряжения на емкости получаем приближенное выражение и для напряжения на емкости получаем приближенное выражение
 . (1.33) . (1.33)
 На рис.1.13 приведены осциллограммы напряжения на емкости (на выходе контура) и тока в контуре при подаче на его вход постоянного напряжения На рис.1.13 приведены осциллограммы напряжения на емкости (на выходе контура) и тока в контуре при подаче на его вход постоянного напряжения  . Во время переходного процесса напряжение на емкости достигает максимальной величины, когда . Во время переходного процесса напряжение на емкости достигает максимальной величины, когда  , т.е. через половину периода колебаний от момента подачи напряжения на вход цепи. К этому времени напряжение , т.е. через половину периода колебаний от момента подачи напряжения на вход цепи. К этому времени напряжение  превышает величину превышает величину  за счет дополнительного поступления к емкости и энергии, запасенной ранее в катушке индуктивности. Из выражения (l.33) имеем за счет дополнительного поступления к емкости и энергии, запасенной ранее в катушке индуктивности. Из выражения (l.33) имеем
 , ,
т.е. в контуре с большой добротностью напряжение  близко к удвоенному напряжению источника близко к удвоенному напряжению источника  . .
Как видно из рис.1.13, напряжение на емкости осциллирует, приближаясь при  к величине к величине  . Практически можно считать, что переходной процесс заканчивается, когда амплитуда осцилляции убывает до 5% своего максимального значения . Практически можно считать, что переходной процесс заканчивается, когда амплитуда осцилляции убывает до 5% своего максимального значения  . Требующееся для этого время называется временем установления стационарного режима . Требующееся для этого время называется временем установления стационарного режима  . Оно может быть определено из равенства . Оно может быть определено из равенства

или
 (1.34) (1.34)
Чем меньше добротность контура и, следовательно, шире полоса пропускания  ,
тем быстрее затухают собственные колебания в контуре и тем меньше время установления. ,
тем быстрее затухают собственные колебания в контуре и тем меньше время установления.
1.7. Воздействие гармонической э.д.с, на колебательный контур
В начальный момент  к последовательному к последовательному  контуру подключается гармоническая э.д.с. Дифференциальное уравнение для данной цепи, составленное на основании уравнения Кирхгофа, имеет вид: контуру подключается гармоническая э.д.с. Дифференциальное уравнение для данной цепи, составленное на основании уравнения Кирхгофа, имеет вид:
 , (1.35) , (1.35)
а его решение  . Здесь . Здесь  -
ток свободных колебаний, а -
ток свободных колебаний, а  -
вынужденный ток. -
вынужденный ток.
Аналогичное уравнение записывается для напряжения на емкости 
 , (1.36) , (1.36)
решение которого  .Здесь .Здесь  - напряжение на емкости, соответствующее свободным колебаниям в контуре. Выражение для этого напряжения можно записать, пользуясь полученным ранее выражением (l.23) при рассмотрении свободных колебаний в контуре. Запишем выражение для напряжения - напряжение на емкости, соответствующее свободным колебаниям в контуре. Выражение для этого напряжения можно записать, пользуясь полученным ранее выражением (l.23) при рассмотрении свободных колебаний в контуре. Запишем выражение для напряжения  в виде в виде
 . .
Тогда для тока свободных колебаний  получим выражение получим выражение
 . .
Для контуров с достаточной добротностью ( )
можно считать )
можно считать  , ,  и поэтому и поэтому

При воздействии гармонической э.д.с, установившийся ток в контуре имеет вид
 , ,
где  и и  . Установившееся напряжение на емкости принимает вид . Установившееся напряжение на емкости принимает вид
 , ,
Тогда общее решение уравнения (l.35)
 . .
Для напряжения на емкости в переходном режиме получаем выражение
 . .
Для определения констант  и и  воспользуемся начальными условиями задачи. Если до включения э.д.с, в контуре не была запасена энергия, то при воспользуемся начальными условиями задачи. Если до включения э.д.с, в контуре не была запасена энергия, то при  , ,  и и  . Отсюда находим: . Отсюда находим:
 , ,
 . .
Заменяя здесь  на на  и деля второе уравнение на и деля второе уравнение на  , из получающихся уравнений находим , из получающихся уравнений находим  и и  : :
 и и 
При этом для тока и напряжения получаем обратные решения:
 (1.37) (1.37)
 (1.38) (1.38)
В случае, когда частота э.д.с. совпадает с частотой контура, т.е.  имеем имеем  , ,  и выражения для тока и напряжения упрощаются и выражения для тока и напряжения упрощаются
 , (1.39) , (1.39)
 . (1.40) . (1.40)
На рис.1.14 приведена осциллограмма напряжения  как сумма напряжения свободных колебаний как сумма напряжения свободных колебаний  и напряжения вынужденных колебаний и напряжения вынужденных колебаний  .
По мере затухания свободных колебаний растет амплитуда результирующего колебания. Огибающая амплитуды напряжения .
По мере затухания свободных колебаний растет амплитуда результирующего колебания. Огибающая амплитуды напряжения  изменяется по экспоненциальному закону изменяется по экспоненциальному закону
  . .
Величина амплитуды установившегося колебания зависит от добротности контура. Процесс установления колебаний заключается в постепенном заряде емкости и накоплении энергии в ней. Так как частота э.д.с.  и собственная частота контура и собственная частота контура  равны, то при смене знака э.д.с. ток в контуре также меняет направление, что приводит к увеличению заряда на емкости. Напряжение на емкости растет до того момента времени, пока энергия потерь в активном сопротивлении равны, то при смене знака э.д.с. ток в контуре также меняет направление, что приводит к увеличению заряда на емкости. Напряжение на емкости растет до того момента времени, пока энергия потерь в активном сопротивлении  ,
возрастая с ростом тока в контуре, не сравняется с энергией, поступающей в контур за счет источника э.д.с. ,
возрастая с ростом тока в контуре, не сравняется с энергией, поступающей в контур за счет источника э.д.с.
Процесс установления колебаний практически считается законченным, когда амплитуда напряжения на емкости (или ток в контуре) достигает 95% своего стационарного значения, т.е. можно записать
 , ,
или время установления
 . .

На рис.1.15 показана огибающая амплитуд напряжения на емкости для различных значений добротности контура. С ростом добротности  увеличивается время установления увеличивается время установления  , но и растет амплитуда установившихся колебаний. , но и растет амплитуда установившихся колебаний.
Если частота э.д.с, не совпадает с собственной частотой контура  , то, как показывает анализ выражения (1.37), закон нарастания колебаний более сложен (см.рис.1.16). Здесь огибающая тока в контуре (или напряжения на емкости) изменяется по колебательному закону. Вначале ток , то, как показывает анализ выражения (1.37), закон нарастания колебаний более сложен (см.рис.1.16). Здесь огибающая тока в контуре (или напряжения на емкости) изменяется по колебательному закону. Вначале ток  растет до величины, превышающей его стационарное значение, а затем, осциллируя, уменьшается по амплитуде и при растет до величины, превышающей его стационарное значение, а затем, осциллируя, уменьшается по амплитуде и при  его амплитуда приближается к стационарному значению его амплитуда приближается к стационарному значению  , где , где  -
модуль импеданса контура. Частота осцилляции огибающей амплитуды этого сложного колебания равна разности частот -
модуль импеданса контура. Частота осцилляции огибающей амплитуды этого сложного колебания равна разности частот  . .

|