|  ВЯТСКИЙ ВЯТСКИЙ
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
Кафедра математики
Вычислительная математика
Методические указания
по самостоятельной работе студентов
Киров
2010
Печатается по решению кафедры математики, протокол № 8 от 09 апреля 2010 г.
Вычислительная математика:
Методические указания по самостоятельной работе студентов / Сост. Ковязина Е.М. – Киров: ВСЭИ, 2010. – 16 с. – (кафедра математики)
Методические указания разработаны в соответствии с учебной программой дисциплины «Вычислительная математика» основной образовательной программы направления «Информатика и вычислительная техника». Методические указания содержат задания к контрольной работе, список основной и дополнительной литературы.
© Вятский социально-экономический
институт (ВСЭИ), 2010
Пояснительная записка
Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса по рекомендованным учебным пособиям. Если студент испытывает затруднения в освоении теоретического или практического материала, то он может получить консультацию у ведущего дисциплину преподавателя (см. часы консультаций на кафедре математики ВСЭИ).
Контрольная работа представляется на листах формата А4, титульный лист оформляется по стандартному образцу.
Решения задач необходимо приводить в той же последовательности, что и в предложенных вариантах. При этом условие задачи должно быть полностью переписано перед её решением. Решение задания выполняется на любом, известном вам, языке программирования. Программные коды должны быть приложены к контрольной работе.
В прорецензированной зачтенной работе студент должен исправить отмеченные рецензентом ошибки и учесть его рекомендации и советы. Если же работа не зачтена, то ее выполняют еще раз и сдают на повторную рецензию. Зачтенные контрольные работы предъявляются студентом при сдаче экзамена.
Контрольная работа состоит из 10 вариантов, по 5 заданий в каждом варианте. Номер варианта выбирается в зависимости от последней цифры зачетной книжки студента:
1 – 1 вариант
2 – 2 вариант
3 – 3 вариант
4 – 4 вариант
5 – 5 вариант
6 – 6 вариант
7 – 7 вариант
8 – 8 вариант
9 – 9 вариант
0 – 10 вариант
Задания контрольной работы
Вариант 1
1. Решить методом простой итерации и методом Зейделя систему уравнений (решение найти с точностью 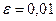 ): ): 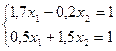
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
. Вычислить значение у
для х
=3.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (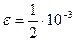 ): ): 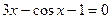 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: 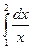 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:  найти найти  . .
Вариант 2
1. Решить методом простой итерации и методом Зейделя систему уравнений (решение найти с точностью 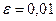 ): ): 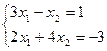 . .
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
. Вычислить значение у для х=9.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (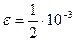 ): ): 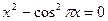 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: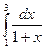 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
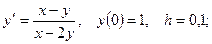 найти найти 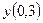 . .
Вариант 3
1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 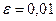 ): ): 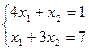
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
| х
|
10
|
12
|
14
|
16
|
| у
|
3
|
7
|
11
|
17
|
.Вычислить значение у для х=15.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (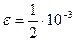 ): ): 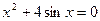 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: 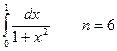 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
 найти найти 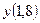
Вариант 4
1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 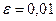 ) )
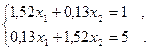
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
| х
|
-2
|
-1
|
0
|
1
|
2
|
| у
|
6
|
0
|
2
|
0
|
6
|
.Вычислить значение у для х=0,5.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (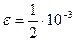 ): ):  . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: 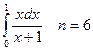 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
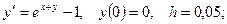 найти найти 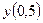 . .
Вариант 5
1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 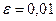 ) )
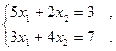
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
.Вычислить значение у для х=2,5.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (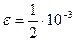 ): ):  . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: 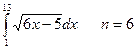 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
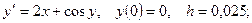 найти найти 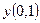 . .
Вариант 6
1. Исследовать сходимость и решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 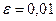 ) )

2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
.Вычислить значение у для х=0,5.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (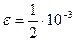 ): ): 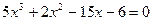 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: 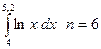 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
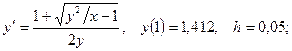 найти найти 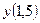 . .
Вариант 7
1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 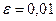 ) )
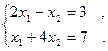
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
.Вычислить значение у для х=0,5.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (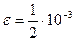 ): ): 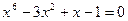 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: 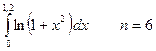 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках: 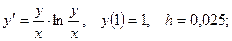 найти найти 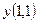 . .
Вариант 8
1. Исследовать сходимость и решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 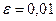 ) )
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
.Вычислить значение у для х=5.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (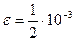 ): ): 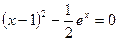 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона:  . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
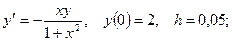 найти найти  . .
Вариант 9
1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 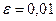 ) )
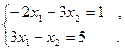
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
.Вычислить значение у для х=2,5 .
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (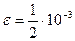 ): ): 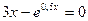 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: 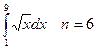 . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
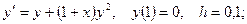 найти найти 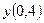 . .
Вариант 10
1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью 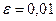 ) )
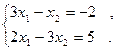
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции
.Вычислить значение у для х=1,5.
3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (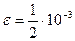 ): ): 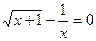 . .
4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона:  . .
5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:
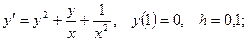 найти найти 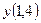 . .
Теоретические основы для выполнения контрольной работы
О приближенных вычислениях
Реальное проведение любых вычислений проводится над числами, которые задаются не только точно, но и приближенно. Например, запись 7/3 обозначает число, но записать его в виде десятичной дроби можно только приближенно. Если же вычисления проводятся на компьютере, то приближенно записывать приходится не только числа типа 7/3, но многие другие. В результате возникают ошибки, которые постепенно накапливаются и искажают результат.
К настоящему времени все программные средства, благодаря которым на компьютерах проводятся вычисления, устроены так, что точность проводимых расчетов можно регулировать программно. Можно, например, «поручить» компьютеру вести вычисления с точностью до трех знаков после десятичной запятой; определение точности результата в этом случае может оказаться сложнейшей математической задачей. В некоторых случаях полученный результат можно запросить заново с большей точностью или оставить без изменения.
Алгоритм, по которому ведутся вычисления, может быть устойчивым к приближенным числам и может не быть таковым. Слова «устойчивый алгоритм» означают, что чем точнее задаются числа для обработки, тем точнее получается результат, причем для любой точности результата можно указать такую точность обрабатываемых чисел, что алгоритм приведет к результату именно с этой заданной точностью. В последующем мы столкнемся именно с такой ситуацией при изучении метода итераций для решения систем линейных алгебраических уравнений. Примером метода, который не является устойчивым к приближенным числам, является метод последовательного исключения неизвестных для решения тех же систем. Одну из его реализаций мы рассмотрим в ближайшее время.
Алгоритм, реализующий те или иные вычисления, может требовать различное время для своей работы. Чем большего времени требует алгоритм, тем более высокую сложность по времени
он имеет. Точно так же, чем больше компьютерной памяти требуется для реализации алгоритма, тем более высокую сложность по памяти
он имеет.
Метод деления отрезка пополам для решения уравнений
Речь по-прежнему идет об отыскании корней уравнения
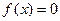 , ,
т.е. таких чисел  , что при подстановке в уравнение вместо символа , что при подстановке в уравнение вместо символа 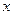 числа числа 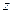 получается тождество. Само собой разумеется, что здесь, как и всюду в этом курсе, речь идет только о вещественных числах. получается тождество. Само собой разумеется, что здесь, как и всюду в этом курсе, речь идет только о вещественных числах.
О функции 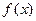 в приводимых ниже рассуждениях по-прежнему предполагается, что она обладает непрерывными производными тех порядков, которые упоминаются по ходу изложения. в приводимых ниже рассуждениях по-прежнему предполагается, что она обладает непрерывными производными тех порядков, которые упоминаются по ходу изложения.
Напоминаем, отделить корень
уравнения - это значит найти такой интервал (a,b
), который, во-первых, содержит корень уравнения и, во-вторых, содержит только один корень этого уравнения. Доказывается, что если на концах некоторого интервала (a,b) функция 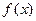 имеет разные знаки, а внутри этого интервала производная имеет разные знаки, а внутри этого интервала производная 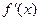 знак не меняет, то в интервале (a,b) корень уравнения есть и, притом, только один. знак не меняет, то в интервале (a,b) корень уравнения есть и, притом, только один.
Отсюда возникает простая методика приближенного поиска корня, отделенного в интервале (a,b
): надо построить последовательность точек 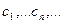 по следующему правилу: по следующему правилу: 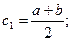 затем из двух интервалов (a,c1
) и (c1
,b
) выбирается тот, на концах которого затем из двух интервалов (a,c1
) и (c1
,b
) выбирается тот, на концах которого 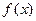 имеет разные знаки и его середина принимается за имеет разные знаки и его середина принимается за 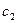 ; обозначим концы этого интервала (у которого ; обозначим концы этого интервала (у которого 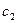 - середина) через (a2
,b2
), а затем выберем ту из его половин, на концах которой - середина) через (a2
,b2
), а затем выберем ту из его половин, на концах которой 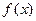 имеет разные знаки. Пусть (a3
,b3
) - эта половина и
имеет разные знаки. Пусть (a3
,b3
) - эта половина и 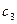 - середина этого отрезка и т.д. Доказывается, что построенная последовательность - середина этого отрезка и т.д. Доказывается, что построенная последовательность 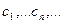 сходится к корню уравнения. сходится к корню уравнения.
Если с самого начала задается некоторая точность вычислений, то на практике построение последовательности 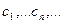 прерывается тогда, когда два раза подряд получаются одинаковые с заданной точностью числа. Это последнее перед прерыванием построения последовательности число и принимается за приближенное с заданной степенью точности значение корня. прерывается тогда, когда два раза подряд получаются одинаковые с заданной точностью числа. Это последнее перед прерыванием построения последовательности число и принимается за приближенное с заданной степенью точности значение корня.
Описанный метод уточнения корня называется методом деления отрезка пополам.
Метод хорд для решения уравнений
Предположим теперь на отрезке 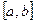 уже отделен корень уравнения. Схематически это можно изобразить так: уже отделен корень уравнения. Схематически это можно изобразить так:
При описании метода деления отрезка пополам строилась последовательность отрезков  и точек и точек 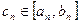 ., сходящихся к корню уравнения. В методе хорд тоже строится некоторая последовательность отрезков ., сходящихся к корню уравнения. В методе хорд тоже строится некоторая последовательность отрезков 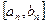 и точек и точек 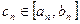 , сходящихся к корню. , сходящихся к корню.
В качестве отрезка 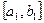 берется отрезок берется отрезок 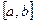 . Точка с
1
берется как точка пересечения с осью абсцисс прямой, проходящей через точки . Точка с
1
берется как точка пересечения с осью абсцисс прямой, проходящей через точки 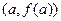 и и  . Укажем значение для c
1
в явной форме: . Укажем значение для c
1
в явной форме:  . .
Из двух отрезков  и и  выберем тот, на концах которого функция выберем тот, на концах которого функция  имеет разные знаки и этот отрезок примем за
имеет разные знаки и этот отрезок примем за  . Затем найдем точку . Затем найдем точку 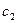 по отрезку по отрезку  точно так же, как нашли точку точно так же, как нашли точку  по отрезку по отрезку  : это будет точка пересечения с осью абсцисс прямой, проходящей через точки : это будет точка пересечения с осью абсцисс прямой, проходящей через точки  и и  : :  . .
Затем в качестве отрезка  берется тот из отрезков берется тот из отрезков  и и  , на концах которого , на концах которого 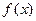 имеет разные знаки и т.д. Через последовательность точек
имеет разные знаки и т.д. Через последовательность точек  приближенное значение корня находится так же, как в п.1
. Название метода происходит из того, что конструируемые по ходу дела прямые являются хордами по отношению к графику функции. приближенное значение корня находится так же, как в п.1
. Название метода происходит из того, что конструируемые по ходу дела прямые являются хордами по отношению к графику функции.
Метод касательных для решения уравнений
Вновь рассмотрим ситуацию отделенного на отрезке 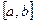 корня уравнения. Будем предполагать, что функция корня уравнения. Будем предполагать, что функция 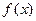 имеет разные знаки на концах этого отрезка, а ее первые две
производные на этом отрезке знака не меняют. На нижеприведенной схеме первая и вторая производные функции
имеет разные знаки на концах этого отрезка, а ее первые две
производные на этом отрезке знака не меняют. На нижеприведенной схеме первая и вторая производные функции 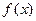 положительны. В случае метода касательных уточнения корня также строится последовательность отрезков
положительны. В случае метода касательных уточнения корня также строится последовательность отрезков 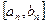 и точек и точек 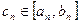 , сходящихся к корню. , сходящихся к корню.
Пусть 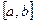 = =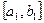 . Выберем тот край отрезка . Выберем тот край отрезка 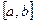 , на котором функция имеет тот же знак, что и ее вторая производная. В нашем примере на приведенной выше схеме - это точка b
. Проведем через точку , на котором функция имеет тот же знак, что и ее вторая производная. В нашем примере на приведенной выше схеме - это точка b
. Проведем через точку  касательную к графику функции касательную к графику функции 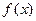 . Точку пересечения этой касательной с осью абсцисс и примем за точку c
1
. Вот соответствующая формула для рассматриваемого случая:
. Точку пересечения этой касательной с осью абсцисс и примем за точку c
1
. Вот соответствующая формула для рассматриваемого случая: 
Нетрудно получить аналогичные формулы для случаев, когда знаки упомянутых выше значений иные. Важен принцип: касательная проводится к графику в той точке, где знак значения функции совпадает со знаком ее второй производной. После этого из двух отрезков  и и  выберем тот, на концах которого функция выберем тот, на концах которого функция 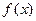 имеет разные знаки и этот отрезок примем за
имеет разные знаки и этот отрезок примем за  . Затем найдем точку . Затем найдем точку  по отрезку по отрезку  точно так же, как нашли точку точно так же, как нашли точку  по отрезку по отрезку  и т.д. Через последовательность точек и т.д. Через последовательность точек  приближенное значение корня находится так же, как в п.1. приближенное значение корня находится так же, как в п.1.
Методика решения алгебраического уравнения
Мы остановимся здесь подробнее на методике решения алгебраического уравнения, т.е. уравнения вида:  , левую часть которого будем обозначать также через , левую часть которого будем обозначать также через 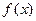 ; напомним, что речь идет только о вещественных корнях. ; напомним, что речь идет только о вещественных корнях.
При работе той или иной процедуры часто возникает необходимость вычислить значение  при некотором при некотором  ; организацию вычисления значения ; организацию вычисления значения  удобно проводить по схеме Горнера
: строится рекурсия удобно проводить по схеме Горнера
: строится рекурсия  где где  , ,  , так что , так что  . .
Далее заметим, что из алгебры известно следующее: существует простая формула, по которой устанавливается интервал (-R,R
) такой, что если уравнение  имеет какой-либо (напоминаем: вещественный!) корень, то он оказывается внутри этого интервала, а именно: имеет какой-либо (напоминаем: вещественный!) корень, то он оказывается внутри этого интервала, а именно:
 , где , где  . .
Предположим теперь, что относительно производной  многочлена многочлена  известны интервалы ее знакопостоянства, т.е. такие точки известны интервалы ее знакопостоянства, т.е. такие точки  , что на участках , что на участках   функция функция  знак не меняет, а проходя через каждую из точек знак не меняет, а проходя через каждую из точек  меняет знак. Нетрудно обосновать в этой ситуации следующие выводы: 1) если внутри интервала (-R,R
) точек меняет знак. Нетрудно обосновать в этой ситуации следующие выводы: 1) если внутри интервала (-R,R
) точек  нет вообще и нет вообще и  , то корней (напоминаем: вещественных!) у уравнения , то корней (напоминаем: вещественных!) у уравнения  нет; если нет; если  , то корень в интервале , то корень в интервале  есть и его надо уточнить с заданной точностью; 2) если в интервале (-R,R
) точки есть и его надо уточнить с заданной точностью; 2) если в интервале (-R,R
) точки  оказались, то надо просчитать оказались, то надо просчитать  в этих точках и в точках в этих точках и в точках  ; если среди этих значений нуля нет и все они имеют один и тот же знак, то корней (напоминаем: вещественных!) уравнение ; если среди этих значений нуля нет и все они имеют один и тот же знак, то корней (напоминаем: вещественных!) уравнение  не имеет; если же среди этих значений будут числа с разными знаками, то это позволит выделить все участки, на концах которых не имеет; если же среди этих значений будут числа с разными знаками, то это позволит выделить все участки, на концах которых  имеет разные знаки, а внутри которых имеет разные знаки, а внутри которых  знак не меняет. К каждому такому участку применима процедура уточнения корня (деление отрезка пополам, методы хорд и касательных). знак не меняет. К каждому такому участку применима процедура уточнения корня (деление отрезка пополам, методы хорд и касательных).
И еще одно замечание. Если вещественные корни (все) уравнения  известны, то по ним полностью восстанавливаются участки знакопостоянства функции известны, то по ним полностью восстанавливаются участки знакопостоянства функции  : надо просчитать : надо просчитать  между любыми двумя соседними корнями и по совокупности знаков полученных чисел сделать вывод. между любыми двумя соседними корнями и по совокупности знаков полученных чисел сделать вывод.
Процедуру выяснения участков знакопостоянства производной  можно организовать так. Вычислим производные многочлена можно организовать так. Вычислим производные многочлена  : :  ; заметим, что производная ; заметим, что производная  - линейная функция. Поэтому участки ее знакопостоянства вычислимы. Если - линейная функция. Поэтому участки ее знакопостоянства вычислимы. Если  , то уже возможны формальные действия по описанной выше схеме по уточнению корней исходного уравнения. Если же , то уже возможны формальные действия по описанной выше схеме по уточнению корней исходного уравнения. Если же  , то решим по описанной выше схеме уравнение , то решим по описанной выше схеме уравнение  и по его корням установим участки знакопостоянства функции и по его корням установим участки знакопостоянства функции  ; затем решим по описанной выше схеме уравнение ; затем решим по описанной выше схеме уравнение  и по его корням определим участки знакопостоянства функции и по его корням определим участки знакопостоянства функции  и так далее, пока не окажется решенным исходное уравнение и так далее, пока не окажется решенным исходное уравнение  . .
Полученная в процессе решения информация позволяет установить также и кратность каждого корня уравнения  ; напомним, что корень ; напомним, что корень  уравнения уравнения
 считается имеющим кратность считается имеющим кратность
 , если , если
 , но , но
 . В этом случае, как известно из алгебры, имеет место представление . В этом случае, как известно из алгебры, имеет место представление  , где , где  - многочлен степени - многочлен степени  . .
Основная литература
1. Бахвалов Н., Жидков Н., Кобельков Г. Численные методы. – М. – СПб.: Физматлит, 2008.
2. Пирумов У.Г. Численные методы. – М.: Дрофа, 2009.
3. Поршнев С.В. Вычислительная математика. – СПб.: БХВ - Петербург, 2004.
Дополнительная литература
1. Бакушинский А.Б., Власов В.К. Элементы высшей математики и численных методов. – М.: Просвещение, 1968
2. Бутузов и др. Математический анализ в вопросах и задачах: Уч. пособие для вузов. – М.: Высшая школа, 2007.
3. Гусак А.А., Гусак Г.М. Справочник по высшей математике. - Минск, 2009.
4. Колесников А.И. Краткий курс математики для экономистов. - М.: ИНФА-М, 20009.
5. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 2004.
6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. - М.: Наука 1999.
Ковязина Елена Михайловна
Вычислительная математика
Методические указания
Ответственный за выпуск: Глушкова А.И.
Технический редактор: Кочуров М.Г.
Корректор: Журавлева О.Н.
Издательский орган ВСЭИ
610000 Киров, Большевиков, 91А
тел./факс 67-02-35
Подписано в печать «____» ____________ 20__ г.
Тираж ____ экз.
Отпечатано на ризографе ВСЭИ
|