| Федеральное агентство по образованию
Ангарская государственная техническая академия
Кафедра «Машины и аппараты химических производств»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
ЛАБОРАТОРНЫХ РАБОТ ПО КУРСУ
ПРОЦЕССЫ И АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
ЧАСТЬ I «ГИДРОМЕХАНИЧЕСКИЕ ПРОЦЕССЫ»
Ангарск 2008
Методические указания по выполнению лабораторных работ по курсу «Процессы и аппараты химических производств». Часть I «Гидромеханические процессы».
Составили: Л. И. Рыбалко, В. В. Набока, В. М. Соломонова.
Ангарская государственная техническая академия - Ангарск, АГТА 2008 – 52с.
Методические указания предназначены для студентов химико-технологических и механических специальностей.
Рецензент к. т. н., доцент Фереферов М.Ю.
Рекомендовано к изданию учебно-методическим советом АГТА.
ЛАБОРАТОРНАЯ РАБОТА 1
ИЗУЧЕНИЕ ГИДРОДИНАМИКИ ТАРЕЛЬЧАТЫХ И НАСАДОЧНЫХ КОЛОНН
Цель работы:
практическое ознакомление с работой тарельчатых и насадочных колонн, определение гидравлических сопротивлений и изучение влияния скорости газа на сопротивление тарелок и насадок.
Приборы и принадлежности:
тарельчатая и насадочная колонны, ротаметры РС-7 и РС-5, микроманометр с наклонной трубкой.
Установка для изучения гидродинамики состоит из тарельчатой и насадочной колонн (рис. 1).

Рис.1. Схема установки для изучения гидродинамики тарельчатых и насадочных колонн
Тарельчатая колонна 1 состоит из цилиндрического корпуса, выполненного из органического стекла. Внутри колонны имеются две колпачковые 5 и две ситчатые тарелки 2. Каждая ситчатая тарелка имеет различное число и различный диаметр отверстий. Каждая колпачковая тарелка имеет по два капсульных колпачка 3. В нижней части колпачка имеются прорези в виде равнобедренного треугольника.
Вода в колонну подается сверху через ороситель 7 и перетекает вниз с тарелки на тарелку по сегментным переливным каналам 4. Концы переливных каналов находятся в сливных карманах 6, создавая гидравлический затвор на тарелках, что предотвращает проскок воздуха по сливным каналам. Сливные каналы выступают над тарелками, образуя сливной порог, что обеспечивает определенный уровень жидкости на тарелках. Подача воды в колонну регулируется вентилем 16, а ее расход измеряется ротаметром 8. Для подачи воды в тарельчатую колонну необходимо, чтобы рукоятка трехходового крана 18 находилась в положении Т
(тарелка). Вода, сливаясь в нижнюю часть колонны, отводится через гидрозатвор и вентиль 21 в канализацию.
Воздух от компрессора подается через ротаметр 12, которым измеряется его расход, и поступает в нижнюю часть колонны выше точки слива воды по гидрозатвору. Расход воздуха регулируется вентилем 17. При подаче воздуха в тарельчатую колонну необходимо, чтобы вентиль 20 был открыт, а вентиль 19 закрыт.
Для измерения гидравлического сопротивления тарелок колонна снабжена пробоотборниками I-V.
Насадочная колонна 9 имеет два слоя насадки из керамических колец Рашига размером 15*15*2 мм, расположенных на опорных решетках 10. Для перераспределения жидкости по сечению колонны и отвода ее от стенок под верхним слоем насадки установлен направляющий конус 11. Вода на орошение поступает в верхнюю царгу через ороситель. Расход воды измеряется ротаметром 8 и регулируется вентилем 16. При этом регулятор 18 должен находиться в положении Н
(насадка). Слив воды идет в нижнюю часть колонны, а затем через гидрозатвор и вентиль 22 в канализацию.
Подача воздуха от компрессора регулируется вентилем 17 и измеряется ротаметром 12. При этом вентиль 19 должен быть открыт, а вентиль 20 закрыт.
Гидравлическое сопротивление насадки измеряется через пробоотборники VI-VIII.
Тарельчатая и насадочная колонны могут работать только раздельно. Переключение осуществляется регулятором 18 и вентилями 19, 20. Регулирование слива из колонн производится вентилями 21 и 22 для предотвращения переполнения колонн жидкостью и возможного прорыва воздуха через слив.
Измерения гидравлических сопротивлений (перепада давлений) осуществляется микроманометром с наклонной трубкой 13 типа ММН, который подключен через многоходовые переключатели 14 (вход) и 15 (выход) с пробоотборниками. Для измерения перепада давления, например, верхней колпачковой тарелки необходимо переключатель 14 установить в положение II (т.е. отбор воздуха пойдет через пробоотборник II), а переключатель 15 в положение III (отбор сверху тарелки), и по микроманометру снять показания гидравлического сопротивления в мм. вод. ст. Аналогично производятся измерения для других тарелок и насадки или группы тарелок и колонн в целом.
В барботажных аппаратах, к которым относится тарельчатая колонна, контакт фаз осуществляется путем барботажа (пробулькивания) газа через слой жидкости. На колпачковой тарелке газ проходит по патрубкам под колпачками и барботирует через жидкость, выходя через прорези колпачков. На ситчатой тарелке газ проходит через небольшие отверстия в плоской тарелке и барботирует через жидкость, находящуюся на ней.
В насадочной колонне кольца Рашига, беспорядочно засыпанные в аппарат, увеличивают поверхность соприкосновения газа и жидкости. Жидкость стекает по поверхности насадки тонкой пленкой и одновременно распределяется в слое в виде капель и брызг.
Характеристика тарельчатой колонны:
Внутренний диаметр колонны – 150 мм
Количество колпачков на тарелке – 2 шт
Внутренний диаметр колпачка – 40 мм
Число прорезей в колпачке – 8 шт
Форма прорези – равнобедренный треугольник
Размер зуба у основания – 15 мм
Высота зуба – 10 мм
Высота перелива (сливного порога) – 20 мм
Периметр перелива – 150 мм
Площадь перелива – 8.0*10-4 м2
Ситчатая тарелка (нижняя) имеет 216 отверстий диаметром
4 мм
Ситчатая тарелка (верхняя) имеет 238 отверстий диаметром
3 мм
Характеристика насадочной колонны:
Диаметр колонны – 125 мм
Высота насадки (общая) - 600 мм
Высота насадки в одной царге – 300 мм
ОСНОВНЫЕ ПОНЯТИЯ
Общие сведения
В химической технологии широко распространены процессы, основанные на взаимодействии газа и жидкости. К ним относятся, в первую очередь, массообменные процессы, связанные с переходом вещества из фазы в фазу. К массообменным процессам относятся абсорбция, ректификация, экстракция, сушка и другие. Эти процессы в промышленных установках проводятся в аппаратах колонного типа.
Скорость перехода вещества из фазы в фазу пропорциональна поверхности соприкосновения фаз (поверхности контакта фаз). А саму скорость определяют как количество вещества, переходящего из фазы в фазу в единицу времени. Увеличение поверхности контакта фаз способствует более интенсивному течению процесса перехода вещества из одной фазы в другую. Поэтому одним из главных требований, предъявляемых к массообменному аппарату, является создание развитой поверхности контакта фаз между газом и жидкостью. Однако создание необходимой поверхности в этих аппаратах требует затраты энергии на преодоление сопротивлений движению газа (гидравлических сопротивлений).
Современные масштабы производства требует создания мощных аппаратов. Достаточно сказать, что в настоящее время имеются тарельчатые колонны диаметром 12 м и высотой 100 м. Гидравлическое сопротивление таких аппаратов, вызванное потерей напора на трение и местные сопротивления, велико и требует достаточно точной оценки при проектировании. Поэтому необходимо знать влияние различных факторов на гидравлическое сопротивление. Знание этих факторов позволяет получить необходимые расчетные уравнения.
Тарельчатые колонны
Тарельчатые колонны бывают с колпачковыми, ситчатыми, клапанными, провальными и другими типами контактных устройств – тарелками. Они относятся к барботажным аппаратам, в которых поверхность соприкосновения фаз создается потоками газа, распределяющегося в жидкости в виде пузырьков и струй. Особенностью тарельчатых колонн является то, что газ и жидкость последовательно соприкасаются на отдельных ступенях (тарелках) аппарата. В колоннах с колпачковыми тарелками газ проходит по патрубкам в пространстве под колпачком и барботирует через жидкость на тарелке, выходя из прорезей колпачков. В ситчатых аппаратах газ проходит через жидкость, находящуюся на тарелках.
При барботаже часть газа вследствие трения диспергируется в жидкость, образуя пену, а часть жидкости увлекается газом в виде брызг, что и создает развитую поверхность соприкосновения фаз (жидкости и газа).
Скорость газа оказывает непосредственное влияние на интенсивность пено- и брызгообразования. В зависимости от скорости газа различают три режима работы барботажных тарелок:
- режим непрерывной работы – наблюдается при скорости газа в свободном сечении колонны (между тарелками) 0,5-0,6 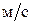 . При такой скорости прорези колпачков закрыты жидкостью не полностью. Газ барботирует по всей поверхности тарелки, и в отдельных местах остается небарботируемая жидкость; . При такой скорости прорези колпачков закрыты жидкостью не полностью. Газ барботирует по всей поверхности тарелки, и в отдельных местах остается небарботируемая жидкость;
- режим равномерной работы – наступает при увеличении скорости газа свыше 0,6-0,7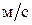 . При этом прорези колпачков полностью открыты. На тарелке образуется пена; . При этом прорези колпачков полностью открыты. На тарелке образуется пена;
- режим газовых струй – наблюдается при скорости газа 0,9-1,1 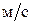 . В этом случае газ движется через жидкость в виде струй, которые выходят на поверхность пены, разрушая ее. При дальнейшем увеличении скорости газа начинается унос жидкости на вышележащую тарелку, что приводит к захлебыванию тарелки. Это сопровождается увеличением перепада давлений газа. . В этом случае газ движется через жидкость в виде струй, которые выходят на поверхность пены, разрушая ее. При дальнейшем увеличении скорости газа начинается унос жидкости на вышележащую тарелку, что приводит к захлебыванию тарелки. Это сопровождается увеличением перепада давлений газа.
Гидравлическое сопротивление тарельчатого аппарата зависит от его конструктивных особенностей, определяемых типом тарелки. Гидравлическое сопротивление различных типов тарелок будет неодинаково.
Общее гидравлическое сопротивление любой тарелки
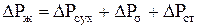 , (1) , (1)
где 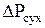 - сопротивление сухой тарелки, Па; - сопротивление сухой тарелки, Па;
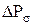 - сопротивление, вызываемое силами поверхностного натяжения, Па; - сопротивление, вызываемое силами поверхностного натяжения, Па;
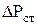 - статическое сопротивление слоя жидкости на тарелке, Па. - статическое сопротивление слоя жидкости на тарелке, Па.
Гидравлическое сопротивление сухой колпачковой и ситчатой тарелок для случая равномерного режима, т.е. при полном открытии прорезей и отверстий
 , (2) , (2)
где 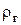 - плотность газа при рабочих условиях (плотность воздуха при - плотность газа при рабочих условиях (плотность воздуха при 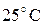  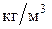 ); );
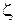 - коэффициент сопротивления. Для колпачковых тарелок со свободным сечением отверстий 7-10% он равен 4,5-5,0, для ситчатых - 1,82; - коэффициент сопротивления. Для колпачковых тарелок со свободным сечением отверстий 7-10% он равен 4,5-5,0, для ситчатых - 1,82;
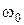 - скорость газа в прорезях колпачка или в отверстиях тарелки, - скорость газа в прорезях колпачка или в отверстиях тарелки, 
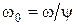 , (3) , (3)
где 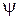 - живое сечение прорезей или отверстий тарелки, равное отношению суммарной площади прорезей или отверстий к площади поперечного сечения колонны; - живое сечение прорезей или отверстий тарелки, равное отношению суммарной площади прорезей или отверстий к площади поперечного сечения колонны;
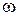 - скорость газа в свободном сечении колонны, - скорость газа в свободном сечении колонны, 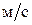 . .
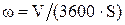 , (4) , (4)
где 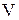 - объемный расход газа, - объемный расход газа, 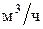 ; ;
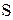 - площадь поперечного сечения колонны, - площадь поперечного сечения колонны, 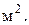
Сопротивление, вызываемое силами поверхностного натяжения:
 , ,  (5) (5)
где 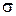 - поверхностное натяжение жидкости (воды). При - поверхностное натяжение жидкости (воды). При  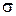 =0,072 =0,072 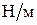 ; ;
 - эквивалентный диаметр отверстия, м; - эквивалентный диаметр отверстия, м;
Для колпачковых тарелок:
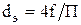 , ,  (6) (6)
где  - площадь свободного сечения прорези, - площадь свободного сечения прорези,  ; ;
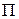 - периметр прорези, м; - периметр прорези, м;
Для ситчатых тарелок  равен диаметру отверстия. равен диаметру отверстия.
Сопротивление столба жидкости на колпачковой тарелке (при полном открытии прорезей)
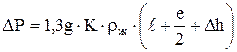 , ,  (7) (7)
где 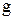 - ускорение силы тяжести, - ускорение силы тяжести, 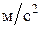 ; ;
K - отношение плотности газожидкостного слоя (пены) к плотности чистой жидкости (при расчетах принимается  ); );
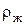 - плотность воды при температуре - плотность воды при температуре  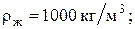
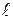 - расстояние от верхнего края прорезей до сливного порога (рис.2), м. Для исследуемой тарелки - расстояние от верхнего края прорезей до сливного порога (рис.2), м. Для исследуемой тарелки 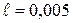 м; м;
 - высота прорези, м; - высота прорези, м;
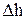 - высота уровня жидкости над сливным порогом, м. - высота уровня жидкости над сливным порогом, м.
Величина 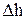 определяется по формуле определяется по формуле
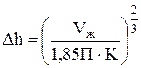 , (8) , (8)
где  - объемный расход жидкости, - объемный расход жидкости,  ; ;
П – периметр сливного устройства м;
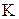 - коэффициент, учитывающий плотность пены, - коэффициент, учитывающий плотность пены,  . .
Сопротивление столба жидкости на ситчатой тарелке
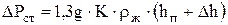 , (9) , (9)
где  - высота сливного порога, м (рис 3). - высота сливного порога, м (рис 3).
Все остальные величины, входящие в эту формулу, определяются так же, как и для колпачковой тарелки. Если в колонне имеется несколько однотипных тарелок, то общее их сопротивление
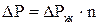 , (10) , (10)
где n – число тарелок в колонне.
 представляет ту энергию, которую необходимо сообщить газу для движения его по колонне с заданной скоростью. представляет ту энергию, которую необходимо сообщить газу для движения его по колонне с заданной скоростью.
 
а) б)
Рис. 2. Эскиз колпачка
а) колпачковая тарелка; б) ситчатая тарелка.
Насадочные колонны
Основным элементом этого типа колонн является насадка – твердые тела различной формы, предназначенные для увеличения поверхности соприкосновения газа и жидкости.
Существует три гидродинамических режима работы насадочных колонн: пленочный, подвисания (турбулентный) и эмульгирования.
Пленочный режим наблюдается при низких скоростях газа, когда жидкость стекает по насадке в виде пленки, и газ контактирует с жидкостью по поверхности этой пленки.
При увеличении скорости возникает турбулизация жидкости. При этом движение жидкости по насадке начинает тормозиться потоком газа. Такой режим называется режимом подвисания.
В режиме эмульгирования насадка начинает затопляться жидкостью. В этих условиях газ барботирует через жидкость с образованием газожидкостной системы (пены). Поверхность соприкосновения фаз значительно возрастает. Одновременно увеличивается гидравлическое сопротивление.
Скорость, соответствующая началу режима эмульгирования, называется скоростью инверсии. Дальнейшее увеличение скорости газа приводит к тому, что силы трения газа о жидкость становятся больше сил тяжести жидкости и начинается движение жидкости снизу вверх. Критическая скорость, соответствующая началу уноса жидкости газом, называется скоростью захлебывания.
Преимущество насадочных колонн – это низкое гидравлическое сопротивление, особенно в пленочном режиме, простота конструкции, малая металлоемкость. В то же время величина удельной поверхности контакта фаз в насадочных аппаратах несколько ниже, чем в тарельчатых.
Сопротивление сухой (неорошаемой) насадки определяется по уравнению:
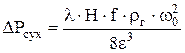 , (11) , (11)
где  - коэффициент сопротивления при прохождении газа через слой насадки, безразмерный; - коэффициент сопротивления при прохождении газа через слой насадки, безразмерный;
Н - высота слоя насадки, м;
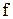 - удельная поверхность насадки, - удельная поверхность насадки, 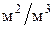 . Для колец Рашига размером 15*15*2 мм . Для колец Рашига размером 15*15*2 мм 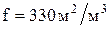 ; ;
 - плотность газа (воздуха). При - плотность газа (воздуха). При 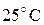 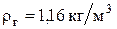 ; ;
 - фиктивная скорость газа, - фиктивная скорость газа, 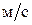 ; ;
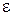 - свободный объем насадки, - свободный объем насадки,  . .
Фиктивная скорость газа, т. е. скорость, отнесенная к полному поперечному сечению аппарата, находится как
 , (12) , (12)
где 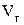 - расход газа, - расход газа,  ; ;
S - площадь поперечного сечения колонны, 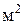 . .
Коэффициент сопротивления  зависит от режима движения газа и имеет следующие значения для беспорядочно засыпанной насадки: зависит от режима движения газа и имеет следующие значения для беспорядочно засыпанной насадки:
при ламинарном движении 
 (13) (13)
при турбулентном движении 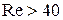
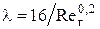 (14) (14)
Критерий Рейнольдса определяется из выражения
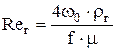 , (15) , (15)
где  - динамическая вязкость газа (воздуха), - динамическая вязкость газа (воздуха), 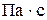 . При . При  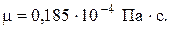
Гидравлическое сопротивление орошаемой насадки больше сопротивления сухой насадки. Это объясняется тем, что некоторое количество жидкости задерживается в насадке вследствие смачивания ее поверхности и скопления в узких криволинейных каналах, образуемых соприкасающимися насадочными телами. При этом уменьшается свободное сечение каналов и свободный объем насадки и, соответственно, увеличивается действительная скорость газа 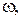 в результате чего возрастает сопротивление насадки в результате чего возрастает сопротивление насадки 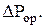
Точный расчет 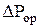 затруднителен. Для приближенного расчета величины затруднителен. Для приближенного расчета величины 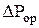 , при работе в режимах ниже точки инверсии, можно использовать уравнение , при работе в режимах ниже точки инверсии, можно использовать уравнение
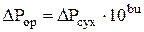 , (16) , (16)
где  - коэффициент, для колец Рашига 15*15*3 мм - коэффициент, для колец Рашига 15*15*3 мм 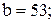
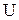 - плотность орошения, - плотность орошения, 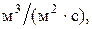
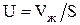 , (17) , (17)
где  - объемный расход жидкости на орошение колонны, - объемный расход жидкости на орошение колонны, 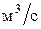 . .
При малых плотностях орошения (менее 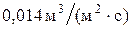 ) можно воспользоваться формулой ) можно воспользоваться формулой
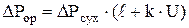 , (18) , (18)
где k– опытный коэффициент; для уложенной «навалом» насадки 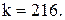
 - расстояние от верхнего края прорезей до сливного порога (рис.2), м. Для исследуемой тарелки - расстояние от верхнего края прорезей до сливного порога (рис.2), м. Для исследуемой тарелки 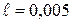 м; м;
Фиктивная скорость газа в точке захлебывания (инверсии) рассчитывается по уравнению
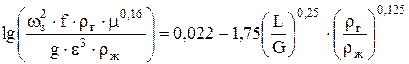 . (19) . (19)
Здесь 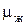 - динамическая вязкость жидкости (воды), при - динамическая вязкость жидкости (воды), при  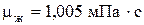 ; ;
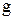 - ускорение свободного падения, - ускорение свободного падения, 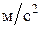 ; ;
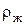 - плотность жидкости (воды), при - плотность жидкости (воды), при  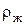 = 1000 кг/м3
; = 1000 кг/м3
;
 и и 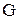 - массовые расходы жидкости и газа соответственно, - массовые расходы жидкости и газа соответственно, 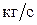 , определяемые по выражениям: , определяемые по выражениям:
 , , 
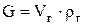 . .
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Перед началом работы продуть соединительные шланги от пробоотборников к микроманометру сжатым воздухом от компрессора. Проверить горизонтальность установки микроманометра и установить его показания на нулевую отметку или заметить его исходное положение и коэффициент наклона.
Для определения сопротивления сухой насадки необходимо подать воздух в колонну. Для этого включить компрессор и заполнить ресивер до установленного давления. Установить рукоятку трехходового крана 18 в положение Т
или Н
в зависимости от использования тарельчатой или насадочной колонн и, соответственно, закрыть вентиль 19 или 20. Используя вентиль 17, установить по ротаметру 12 заданный расход воздуха. С помощью переключателей 14 и 15 установить необходимые позиции точек отбора для исследуемого объекта (тарелки, группы тарелок, насадки). Снять показания микроманометра и умножить их на коэффициент наклона. При другом расходе воздуха установить по ротаметру новый расход и снять показания. При смене объекта исследования рукоятки 14 и 15 установить на обозначения исследуемых пробоотборников. Аналогично определяется гидравлическое сопротивление сухой насадки.
Для определения сопротивления орошаемых тарелок и насадки при том же расходе воздуха, при котором исследовалось гидравлическое сопротивление сухих тарелок и насадки, установить (по заданию преподавателя) расход воды. Для этого открыть вентиль 16 и по ротаметру 8 установить заданный расход воды. Поставить рукоятки 14 и 15 на исследуемые позиции и по микроманометру 13 определить перепад давления исследуемой тарелки или насадки. Если перепад давления большой и не хватает шкалы микроманометра, необходимо поднять его трубку на больший угол, зафиксировав новый коэффициент наклона.
Задание 1
Изучение гидродинамики колонны с колпачковой тарелкой.
1. Исследовать влияние скорости газа на сопротивление сухой тарелки. Для этого измерить сопротивление сухой тарелки при четырех расходах газа.
2. Исследовать влияние скорости газа на сопротивление орошаемой тарелки. Для того измерить сопротивление тарелки при том же расходе газа, что и для сухой. но при постоянном орошении тарелки. Расход жидкости задается преподавателем.
3. По формуле (2) рассчитать сопротивление сухой тарелки при исследуемых скоростях газа.
4. По формулам (1-10) рассчитать сопротивление орошаемой тарелки.
5. Сравнить результаты измерений и расчетов, для чего построить графики зависимости гидравлического сопротивления от скорости газа для сухой и орошаемой тарелок в координатах 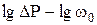 . .
6. Начертить схему установки и разрез колпачковой тарелки. Все измеренные и расчетные величины занести в таблицу 1.
Таблица 1
| Расход
возду-ха, 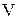 
|
Плот-ность
ороше-ния 
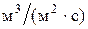
|
Скорость газа,
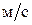
|
Гидравлическое сопротивление,

|
| В сво-
бодном сечении колонны 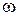
|
В про-
резях (отвер-стиях)

|
Опытное
|
Расчетное
|
| 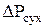
|
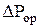
|
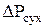
|

|
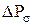
|
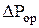
|
Задание 2
Изучение гидродинамики колонны с ситчатой тарелкой
Это задание выполняют так же, как и предыдущее. только работают с ситчатой тарелкой.
Задание 3
Определение гидродинамического сопротивления группы тарелок или колонны в целом.
По указанию преподавателя выбирается исследуемая группа тарелок или в целом тарельчатая колонна. Задание выполняется аналогично заданию 1.
Задание 4
Изучение гидродинамики насадочной колонны.
1. Исследовать влияние скорости газа на сопротивление сухой насадки. Для этого измерить перепад давления на сухой насадке при четырех расходах воздуха (по заданию преподавателя).
2. Исследовать влияние скорости газа на сопротивление орошаемой насадки при постоянной плотности орошения (задается преподавателем) для тех же скоростей газа, что и для сухой насадки.
3. Рассчитать по уравнениям (11-18) сопротивление сухой и орошаемой насадок.
4. Сравнить опытные и расчетные данные, для чего построить графики зависимости гидравлического сопротивления сухой и орошаемой насадок от скорости газа в координатах 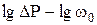 . .
5. Начертить схему установки. Измеренные и расчетные величины занести в таблицу 2.
Таблица 2
| Расход
воздуха,
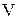 , ,
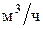
|
Плотность орошения,  , ,
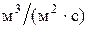
|
Скорость
газа в
свободном
сечении
колонны
 , , 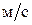
|
Гидравлическое сопротивление, Па
|
| Опытное
|
Расчетное
|
| 
|
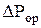
|

|
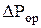
|
Задание 5
Изучение гидродинамики орошаемой насадки.
1. Исследовать влияние плотности орошения на сопротивление насадки. Для этого при постоянной скорости газа четыре раза измерить плотность орошения (расход воды) до режима захлебывания и каждый раз замерять сопротивление.
2. Рассчитать по формулам (11-18) гидравлическое сопротивление при заданных плотностях орошения.
3. Сравнить опытные и расчетные значения сопротивлений в виде графика в координатах 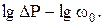
4. Рассчитать скорость газа, соответствующую точке инверсии, по уравнению 19.
5. Начертить схему установки. Измеренные и рассчитанные величины занести в таблицу 2.
Контрольные вопросы
1. Устройство тарельчатых и насадочных колонн.
2. Гидродинамические режимы работы тарельчатых и насадочных колонн.
3. Из чего складывается гидравлическое сопротивление тарелок?
4. Как рассчитывается гидравлическое сопротивление сухой насадки?
5. У каких тарелок больше гидравлическое сопротивление?
6. Что такое плотность орошения?
7. Как определяется сопротивление орошаемой насадки?
ЛАБОРАТОРНАЯ РАБОТА 2
ИЗУЧЕНИЕ КИНЕТИКИ
ГРАВИТАЦИОННОГО ОСАЖДЕНИЯ
Цель работы
:
экспериментальное изучение зависимости скорости осаждения твердых частиц от физических свойств твердого вещества и жидкости под действием силы тяжести и сопоставление полученных данных с теорией.
Приборы, принадлежности и материалы:
стеклянные цилиндры, секундомер, пинцет, твердые частицы силикагеля, свинца и алюминия, жидкости: вода, глицерин и трансформаторное масло.
Установка состоит из трех стеклянных цилиндров, заполненных разными жидкостями: водой. глицерином и трансформаторным маслом. На цилиндры нанесена градуировочная шкала, фиксирующая расстояние, которое частицы проходят в процессе осаждения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ОСАЖДЕНИЯ
Неоднородными называются системы, состоящие из двух и более фаз. В химической технологии часто возникает необходимость разделения неоднородных систем на составляющие фазы. Примером таких неоднородных систем являются пыли – взвеси твердых частиц в газе, туманы – взвеси мелких капель жидкости в газе, эмульсии – взвеси капель жидкости в других жидкостях, суспензии – взвеси частиц твердого вещества в жидкости.
Разделение неоднородных систем путем осаждения, может быть осуществлено несколькими методами:
-  путем гравитационного осаждения, т.е. под действием сил тяжести твердых частиц; путем гравитационного осаждения, т.е. под действием сил тяжести твердых частиц;
- под действием центробежных сил;
- под действием сил электрического притяжения в электрическом поле.
Гравитационное осаждение является простейшим методом разделения неоднородных смесей. На практике его осуществляют в аппаратах, называемых отстойниками. Для расчета последних необходимо знать скорость осаждения частиц.
Рассмотрим процесс осаждения твердой шарообразной частицы диаметром 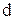 , плотность которой , плотность которой  в жидкости с плотно в жидкости с плотно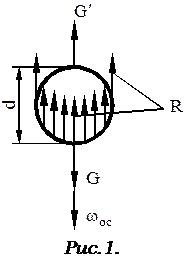 стью стью  (рис. 1). Если (рис. 1). Если 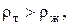 твердая частица будет осаждаться, если твердая частица будет осаждаться, если  частица будет всплывать. В остальном, кроме изменения направления движения частицы, принципиального различия между этими случаями нет. частица будет всплывать. В остальном, кроме изменения направления движения частицы, принципиального различия между этими случаями нет.
При движении частицы на нее действуют сила тяжести, равная весу частицы 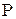 , выталкивающая (архимедова сила) , выталкивающая (архимедова сила) 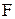 и сила сопротивления среды и сила сопротивления среды 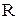 . Под действием силы . Под действием силы  равной разности сил равной разности сил  частица будет перемещаться. частица будет перемещаться.
Сила тяжести
 . (1) . (1)
Сила сопротивления среды
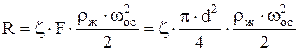 . (2) . (2)
Выталкивающая (архимедова) сила равна весу жидкости в объеме тела:
 . (3) . (3)
Здесь 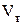 - объем твердой частицы, - объем твердой частицы, 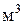 ; ;
 - коэффициент сопротивления; - коэффициент сопротивления;
 - ускорение силы тяжести, - ускорение силы тяжести, 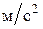 ; ;
 – диаметр частицы, – диаметр частицы, 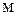 ; ;
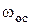 - скорость осаждения. - скорость осаждения.  ; ;
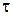 - время осаждения, - время осаждения,  ; ;
 - масса частицы, - масса частицы, 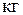 ; ;
  - плотности твердой частицы и жидкости соответственно, - плотности твердой частицы и жидкости соответственно,  . .
В начальный момент времени частица движется ускоренно под действием силы 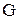 . По мере нарастания скорости частицы увеличивается сопротивление среды . По мере нарастания скорости частицы увеличивается сопротивление среды 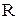 и уменьшается ускорение частицы. Наступает такой момент, когда и уменьшается ускорение частицы. Наступает такой момент, когда  , и частица начинает двигаться с постоянной скоростью, которая называется скоростью осаждения. , и частица начинает двигаться с постоянной скоростью, которая называется скоростью осаждения.
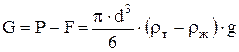 . .
Приравниваем силы 
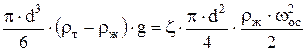 , ,
откуда скорость осаждения
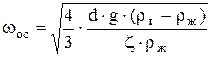 . (4) . (4)
Однако расчет 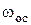 по уравнению (4) затруднен, так как уравнение (4) включает коэффициент сопротивления по уравнению (4) затруднен, так как уравнение (4) включает коэффициент сопротивления  , зависящий от критерия Рейнольдса (режима осаждения), в который входит искомая скорость осаждения. В связи с этим необходимо рассмотреть гидравлические режимы осаждения. , зависящий от критерия Рейнольдса (режима осаждения), в который входит искомая скорость осаждения. В связи с этим необходимо рассмотреть гидравлические режимы осаждения.
Исследования показывают, что наблюдается три режима осаждения: ламинарный, переходный и турбулентный. В пределах каждого режима характер обтекания частиц жидкостью различный.
При ламинарном режиме осаждения жидкость плавно обтекает частицу без образования вихрей. Переходный режим является промежуточным между ламинарным и турбулентным. Изменение характера обтекания при переходе от одного режима к другому как раз и обуславливает изменение характера зависимости коэффициента 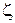 . .
Область существования режимов осаждения определяется величиной критерия Рейнольдса
 , (5) , (5)
где 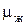 - динамический коэффициент вязкости жидкости, - динамический коэффициент вязкости жидкости, 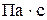 . .
При 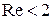 наблюдается ламинарный режим осаждения, при наблюдается ламинарный режим осаждения, при 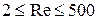 - переходный, при - переходный, при  - турбулентный. - турбулентный.
Коэффициент сопротивления 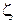 зависит от зависит от  , причем в ламинарном режиме , причем в ламинарном режиме 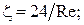 (6) (6)
в переходном 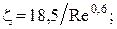 (7) (7)
в турбулентном 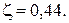 (8) (8)
Подстановка значений 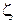 из уравнений (6 - 8) в уравнение (4) приводит к расчетным зависимостям скорости осаждения. Однако пользоваться ими неудобно, так как неизвестен режим осаждения. Целесообразнее переходить к критериальным уравнениям. Решив уравнение (4) относительно из уравнений (6 - 8) в уравнение (4) приводит к расчетным зависимостям скорости осаждения. Однако пользоваться ими неудобно, так как неизвестен режим осаждения. Целесообразнее переходить к критериальным уравнениям. Решив уравнение (4) относительно 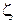 . получим . получим
 . .
Умножив левую и правую части на 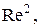 после сокращения приходим к выражению: после сокращения приходим к выражению:
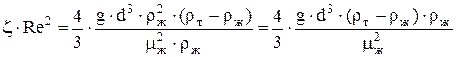 . .
Дробь в правой части уравнения (9) представляет собой безразмерный комплекс величин, носящий название критерия Архимеда
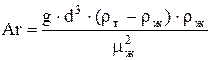 ; (10) ; (10)
 . (11) . (11)
Тогда уравнение (11), решенное относительно 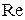 , запишется следующим образом: , запишется следующим образом:
 . (12) . (12)
В общем случае осаждающие частицы не шарообразны, а форма частиц влияет на величину скорости осаждения. С целью учета этого фактора в уравнение (12) вводится коэффициент формы 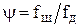 , представляющий собой отношение поверхности частицы шарообразной формы к поверхности частицы данной формы. , представляющий собой отношение поверхности частицы шарообразной формы к поверхности частицы данной формы.
Для шарообразных частиц 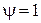 , а для любой иной формы , а для любой иной формы  С учетом коэффициента формы уравнение (12) примет вид С учетом коэффициента формы уравнение (12) примет вид
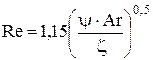 . (13) . (13)
Совместное решение уравнения (13) с уравнениями (6 - 8) дает критериальные уравнения, описывающее гравитационное осаждение.
В ламинарном режиме при  или при или при 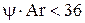
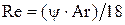 . (14) . (14)
В переходном режиме, при 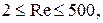 или при или при 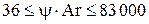
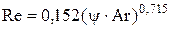 . (15) . (15)
В турбулентном режиме, при 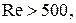 или при или при 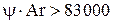
 . (16) . (16)
Критериальные зависимости (14–16) могут быть представлены в общем виде:
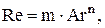 (17) (17)
откуда
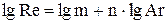 . (18) . (18)
Удобство уравнений (14–18) заключается в том, что искомая величина 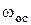 входит только в критерий Рейнольдса. В критерий Архимеда входят известные по условиям задачи величины входит только в критерий Рейнольдса. В критерий Архимеда входят известные по условиям задачи величины 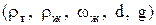 . Поэтому по величине критерия Архимеда можно судить о режиме осаждения и, используя соответствующую зависимость между . Поэтому по величине критерия Архимеда можно судить о режиме осаждения и, используя соответствующую зависимость между  и и 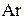 (уравнения 14 -16) для данного режима осаждения, рассчитать критерий, (уравнения 14 -16) для данного режима осаждения, рассчитать критерий,  а из него скорость осаждения а из него скорость осаждения
 . (19) . (19)
В практике осаждения наиболее распространен случай, когда режим осаждения ламинарный. Решая уравнение (14) относительно 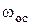 (при (при  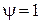 ), получим уравнение ), получим уравнение
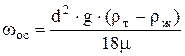 , ,
известное под названием формулы Стокса.
Обратим внимание на физический смысл критериев подобия Рейнольдса и Архимеда.
Критерий Рейнольдса является мерой отношения инерционных сил в потоке и сил трения (вязкости). При малых значениях критерия Рейнольдса поток жидкости формируется в условиях преобладания вязкостных сил над силами инерции и при обтекании частицы не происходит образование вихрей. При больших значениях критерия Рейнольдса уже преобладают инерционные силы, поэтому возникают возмущения жидкостного потока, которые вязкостные силы погасить не могут, и за частицей возникает цепочка вихрей.
Критерий Архимеда является мерой отношения подъемной силы (разности силы тяжести и Архимедовой силы) к вязкостным силам.
Таким образом, критериальные уравнения (14–16) в специфической форме учитывают не только действующие на частицу в процессе осаждения силы, но и характерные особенности обтекания частицы жидкостью.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Твердые частицы, у которых предварительно замеряют диаметр, берут пинцетом, вводят на уровень поверхности жидкости и отпускают. Секундомером засекают время прохождения частицы между метками. Чтобы исключить влияние ускоренного движения частиц в жидкости на начальном участке, верхняя метка расположена на 30-40 мм ниже уровня жидкости. Каждый замер дублируют (не менее трех раз). Частицу опускают точно по центру цилиндра. Если частица коснулась стенки сосуда или к частице прилип пузырек воздуха, то такой замер не засчитывается и опыт повторяется. Результаты замеров диаметра частиц и время осаждения заносят в протокол испытаний. При вычислении критериев используют усредненные значения диаметра частиц. За опытную скорость осаждения принимают среднюю из проведенных замеров.
В данной работе необходимо определить опытную и расчетную скорости осаждения, сравнить теоретический и истинный процесс осаждения путем построения в логарифмических координатах 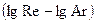 линий теоретического и истинного процессов осаждения. По истинной линии определить значение коэффициента линий теоретического и истинного процессов осаждения. По истинной линии определить значение коэффициента 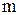 и показателя степени и показателя степени 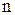 в уравнении (17) для полученных режимов осаждения. Для этого необходимо: в уравнении (17) для полученных режимов осаждения. Для этого необходимо:
1. Определить опытную скорость осаждения по уравнению
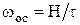 , ,
где 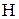 - расстояние между метками, - расстояние между метками, 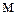 ; ;
 - время осаждения, - время осаждения, . .
Зная эту скорость, по формуле (5) можно рассчитать 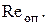
2. По формуле (10) рассчитать критерий 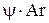 , определить режим осаждения и по формулам (14–16) рассчитать критерий , определить режим осаждения и по формулам (14–16) рассчитать критерий 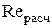 . .
3. По формуле (19) определить расчетную скорость осаждения на основе 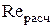 . .
4. Найти значения 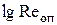 и и  для каждого усредненного замера и по ним в координатах для каждого усредненного замера и по ним в координатах 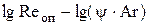 нанести точки, которые соединяют прямыми, в пределах соответствующего режима, наилучшим образом приближающихся к теоретическим линиям. Теоретические линии предварительно построить по уравнениям (14–16) исходя из критических значений нанести точки, которые соединяют прямыми, в пределах соответствующего режима, наилучшим образом приближающихся к теоретическим линиям. Теоретические линии предварительно построить по уравнениям (14–16) исходя из критических значений  и и 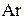 : :  , и , и 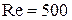 , , 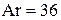 и и 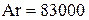 , как показано на рисунке 2. , как показано на рисунке 2.
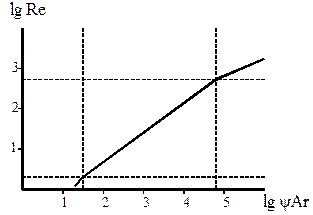
Рис. 2. Линия теоретического процесса осаждения
5. Тангенс угла наклона линий истинного процесса к оси абсцисс 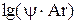 даст значения угловых коэффициентов даст значения угловых коэффициентов 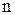 , а отрезок, отсекаемый этими линиями (или их продолжением) на оси ординат , а отрезок, отсекаемый этими линиями (или их продолжением) на оси ординат 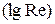 , значения , значения 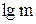 , из которого определить , из которого определить  . .
6. Провести анализ причин, приводящих к отклонению эксперимента от теории.
7. Опытные и расчетные величины занести в протокол испытаний (таблица 1).
Таблица 1.
| Частицы
|
Жидкость
|
Время осаждения
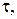
|
Скорость осаждения
|
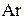
|

|
| Материал
|
rT
,
|
d,
|
Наименование
|
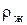 , ,
|
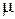 , ,
|
Опытн.
 
|
Расчетн.

|
| 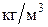
|
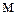
|
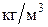
|
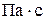
|
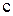
|

|
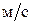
|
| Керамика
|
Вода
|
| 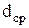
|
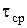
|
| Глицерин
|
| 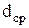
|

|
| Масло
|
| 
|
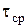
|
| Свинец
|
| Алюминий
|
Контрольные вопросы
1. Что называется скоростью осаждения?
2. От чего зависит скорость осаждения?
3. Какие бывают режимы осаждения и критические значения критериев Рейнольдса и Архимеда для этих режимов?
4. Как рассчитывается скорость гравитационного осаждения твердых частиц?
5. Какие силы действуют на осаждающуюся частицу?
6. Какими критериальными зависимостями описывается процесс осаждения?
7. Что характеризуют критерии Рейнольдса и Архимеда?
8. В каких случаях используется формула Стокса?
ЛАБОРАТОРНАЯ РАБОТА 3
ИССЛЕДОВАНИЕ РЕЖИМОВ ДВИЖЕНИЯ
ЖИДКОСТИ
Цель работы
: изучение изменений, происходящих в потоке при различных режимах течения.
Приборы и принадлежности
: установка для определения режима потока (рис 1), бюретка с подкрашенной жидкостью, термометр, секундомер.
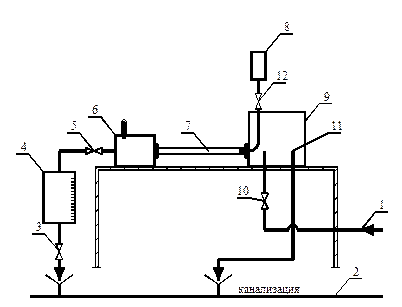
Рис. 1. Схема установки для определения режимов потока
Вода по трубопроводу 1 поступает в расходный бак 9. Подача воды регулируется вентилем 10. Для предупреждения переполнения бака 9 и поддержания постоянного уровня в баке установлена переливная труба 11, которая соединена с канализацией 2.
Из расходного бака 9 вода по стеклянной трубке 7 поступает в промежуточную емкость 6 и сливается из нее через регулировочный вентиль 5 в мерный бак 4.
Из бака 4 вода через кран 3 сливается в линию канализации 2.
Из емкости с краской 8 через кран 12 подкрашенная струйка воды по тонкой трубке поступает в стеклянную трубку 7.
Температуру воды (для определения вязкости) определяют по термометру, который установлен в емкости 6.
ПОНЯТИЕ ТЕОРИИ ПОДОБИЯ
Чтобы изучить любой технологический процесс, мы должны получить и решить математические зависимости, чаще всего дифференциальные уравнения, которые устанавливают связь между важнейшими параметрами процесса. Одним из примеров расчетных зависимостей, важным для практики, является уравнение Бернулли для движущейся жидкости, которое получается решением соответствующего дифференциального уравнения. В большинстве случаев процессы химической технологии сложны и характеризуются большим числом параметров, а уравнения, описывающие процесс, часто являются настолько сложными, что не могут быть решены известными математическими методами. Иллюстрацией этому является уравнение Навье - Стокса, решение которого оказывается невозможным для большинства важнейших практических случаев. Более того, для очень сложных процессов даже нельзя составить уравнения, которые бы исчерпывающе описывали данный процесс. В таких случаях, когда чисто теоретически процесс изучить невозможно, прибегают к экспериментальному исследованию, то есть к проведению опытов. Для этого можно на опыте осуществить процесс и измерить нужный параметр, а чтобы установить влияние на данный процесс каждого из многочисленных параметров, необходимо провести огромное число опытов. Но проведение опытов на промышленных аппаратах, которые порой достигают больших размеров, очень затруднительно и связано с большими затратами времени и средств. Поэтому целесообразно провести процесс на маленьком аппарате – модели
, а результаты опытов перенести на большой аппарат – натуру
, или выполнить измерения на нейтральной среде (воде или воздухе), и результаты измерений распространить на дорогие и агрессивные жидкости. В каких случаях мы можем переносить результаты опытов с одного аппарата на другой или с одной среды на другую можно узнать с помощью теории подобия.
Перенос результатов опытов с модели на натуру возможен только в том случае, когда процессы в модели протекают подобно процессам в большом аппарате (натуре). Теория подобия является учением о методах научного обобщения эксперимента и указывает, как надо ставить опыты, обрабатывать данные и обобщать их результаты для получения единых уравнений подобных явлений (процессов).
Простейшим видом подобия является геометрическое.
При подобии геометрических плоских фигур (треугольники, многоугольники) сходные стороны модели и натуры параллельны, а отношение этих сторон постоянно. Подобные фигуры отличаются друг от друга только масштабом. Следует сказать, что в геометрически подобных системах всегда можно найти сходственные точки, которые пропорционально удалены от каких-то фиксированных точек. Например, точки 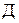 и и 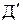 в подобных треугольниках в подобных треугольниках 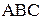 и и 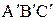 являются сходственными (рис.2). являются сходственными (рис.2).
Кроме геометрического подобия, существуют и более сложные виды подобия, такие как гидродинамическое (два потока текут подобно друг другу), тепловое (в двух аппаратах подобно осуществляется переход тепла от горячего теплоносителя к холодному).
Рис. 2.
Что же является признаком подобия? Когда мы можем считать, что явления протекают подобно? Рассмотрим этот вопрос на примере гидродинамического подобия, знакомство с которым и является целью данной работы. Как доказывается в теории подобия, движение жидкостей в двух трубопроводах разных диаметров (натуре и модели) будет подобно, если отношение всех сил, действующих в них, в сходственных точках будут постоянны. В потоке жидкости каждая частица находится под действием сил давления, тяжести и трения. Кроме этого, возникает сила инерции, равная по величине, но обратная по знаку равнодействующей этих сил. Рассмотрим действие лишь двух сил – силы инерции и силы внутреннего трения (силы вязкости). Ясно, что сила инерции будет тем больше, чем больше скорость потока 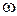 , плотность жидкости , плотность жидкости 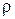 и участок и участок  , на котором она действует. Сила внутреннего трения будет тем больше, чем больше вязкость жидкости , на котором она действует. Сила внутреннего трения будет тем больше, чем больше вязкость жидкости 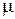 . Наиболее полно вопрос влияния этих сил на движение потока был изучен в 1883г. ученым Рейнольдсом. Поэтому безразмерный комплекс величин . Наиболее полно вопрос влияния этих сил на движение потока был изучен в 1883г. ученым Рейнольдсом. Поэтому безразмерный комплекс величин 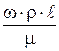 , являющийся мерой отношения сил инерции к силам вязкости получил название критерия Рейнольдса и обозначается , являющийся мерой отношения сил инерции к силам вязкости получил название критерия Рейнольдса и обозначается 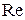 . .
Таким образом, если мы имеем одинаковое отношение сил в двух сходных точках, то и мера их отношения тоже должна быть одинаковой, то есть критерии Рейнольдса в сходных точках должны быть равны в натуре и модели:
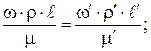
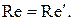
Итак, делаем вывод, что в подобных явлениях критерии подобия должны быть равны между собой ( I теорема подобия).
РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ
Остановимся подробнее на физической сущности критерия Рейнольдса. Критерий 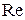 является мерой соотношения между силами инерции и вязкости в движущемся потоке. Эти силы в потоке играют противоположные роли. Любое нарушение упорядоченной формы течения потока (поворот, препятствие, выступы на стенках) вызывают появление инерционных сил, которые, в свою очередь, действуют на поток возмущающим образом, поддерживая и усиливая неупорядоченность движения. Наоборот, силы вязкости оказывают на течение потока упорядочивающее действие, стремясь привести его в возможно большее соответствие с руслом потока. является мерой соотношения между силами инерции и вязкости в движущемся потоке. Эти силы в потоке играют противоположные роли. Любое нарушение упорядоченной формы течения потока (поворот, препятствие, выступы на стенках) вызывают появление инерционных сил, которые, в свою очередь, действуют на поток возмущающим образом, поддерживая и усиливая неупорядоченность движения. Наоборот, силы вязкости оказывают на течение потока упорядочивающее действие, стремясь привести его в возможно большее соответствие с руслом потока.
Если силы инерции будут преобладать над силами вязкости, то течение жидкости будет беспорядочным, завихренным. Такое неупорядоченное движение, при котором отдельные частицы жидкости движутся по запутанным, хаотическим траекториям, в то время как вся масса перемещается в целом в одном направлении, называется турбулентным.
Если преобладают силы вязкости, то случайные возмущения будут гаситься, и течение жидкости, в целом, будет плавным. Такое движение, при котором все частицы движутся по параллельным траекториям, называется ламинарным.
Опыт показывает, что переход от ламинарного режима к турбулентному происходит тем легче, чем больше массовая скорость жидкости (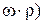 , диаметр трубы , диаметр трубы 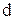 и меньше вязкость жидкости и меньше вязкость жидкости 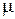 . Значение комплекса этих величин . Значение комплекса этих величин 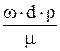 позволяет судить о режиме движения жидкости. позволяет судить о режиме движения жидкости.
Переход от ламинарного к турбулентному движению характеризуется критическим значением  , причем для прямых труб (гладких) , причем для прямых труб (гладких) 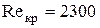 . Необходимо отметить, что движение жидкости при . Необходимо отметить, что движение жидкости при 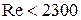 является устойчиво ламинарным
. Приведенное критическое значение является условным, так как трудно обнаружить резкий переход от ламинарного режима к турбулентному. В действительности обычно наблюдается так называемая «переходная» область исчезновения ламинарного режима и установления турбулентного состояния потока. Если является устойчиво ламинарным
. Приведенное критическое значение является условным, так как трудно обнаружить резкий переход от ламинарного режима к турбулентному. В действительности обычно наблюдается так называемая «переходная» область исчезновения ламинарного режима и установления турбулентного состояния потока. Если 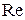 находится от 2300 до 10000, то турбулентное движение является
неустойчивым (переходный режим)
. При значении находится от 2300 до 10000, то турбулентное движение является
неустойчивым (переходный режим)
. При значении 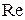 >10000 режим становится устойчивым (развитым) турбулентным
, т.к. силы инерции преобладают над силами вязкости. >10000 режим становится устойчивым (развитым) турбулентным
, т.к. силы инерции преобладают над силами вязкости.
Таким образом, критерий Рейнольдса характеризует режим движения потока, то есть степень перемешивания среды.
Рассматривая отношение других сил в сходственных случаях, получим другие критерии подобия, которые подробно рассмотриваются в лекционном курсе.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Работу начинают с установления ламинарного режима. Если движение ламинарное, то струйка краски вытягивается в виде волоска вдоль потока в трубке 7 (рис.1), не смешиваясь с основной жидкостью.
Постепенно увеличивая скорость течения и регулируя подачу красителя, можно наблюдать, как при некоторых условиях струйка красителя сначала начнет колебаться, принимая причудливые очертания. Это означает, что силы инерции начинают преобладать над силами вязкости. Этот режим соответствует начальной фазе развития турбулентности.
Для успешного проведения опытов весьма важным условием являются стабилизация потока в стеклянной трубке и согласование скорости истечения краски со скоростью самого потока.
При минимально возможном открытии вентиля 10 и при открытых вентилях 5 и 3 регулируются подача воды в расходный бак 9 так, чтобы непрерывно работал слив 11. В этом случае уровень воды в баке будет постоянным. Краном 12 устанавливается подача краски в трубку 7 в виде тонкой струйки.
Убедившись, что режим движения ламинарный, закрываем сливной вентиль 3 и засекаем время  , в течение которого накопится некоторый объем воды , в течение которого накопится некоторый объем воды  в мерном баке 4. Это позволит вычислить расход жидкости V, т.е. то количество воды, которое прошло через трубку в единицу времени. После этого вода из бака сливается в канализацию. Измерение в мерном баке 4. Это позволит вычислить расход жидкости V, т.е. то количество воды, которое прошло через трубку в единицу времени. После этого вода из бака сливается в канализацию. Измерение  и и 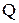 при одном режиме проводиться не менее трех раз. при одном режиме проводиться не менее трех раз.
Путем осторожного открывания вентилей 10 и 5 увеличивается расход жидкости до тех пор, пока не будет размываться струйка краски в трубке 7. При этом опять не менее трех раз определяется время, в течение которого накопиться объем жидкости  . .
Дальнейшим открыванием вентилей 10 и 5 расход воды увеличивается до получения однотонного цвета в трубке и также три раза определяется время 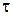 и объем и объем  . Результаты расчетов заносятся в таблицу 1. . Результаты расчетов заносятся в таблицу 1.
Таблица 1
| Расход
воды
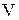 , ,

|
Температура
воды
 , ,
|
Вязкость
воды
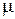 , ,

|
Скорость
движения
воды
 , ,
|
Критерий Рейнольдса
Re
|
Состояние
подкра-
шенной
струйки
|
Режим
потока
|
Задание 1
Установить соответствие рассчитанного критерия Рейнольдса с визуальными наблюдениями.
Для каждого замера определяется секундный расход жидкости:
 , ,
где 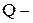 объем воды в баке; объем воды в баке; 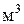 . .
 , ,
где 0,145 и 0,15 – размеры мерного бака,  ; ;
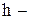 уровень воды в мерном баке, уровень воды в мерном баке,  . .
Для каждого испытываемого режима вычисляется среднее значение расхода из трех измерений:
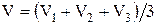 . .
Из уравнения расхода определяется скорость движения потока
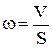 , ,
где 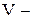 расход воды, расход воды, 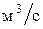 ; ;
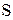 - площадь сечения стеклянной трубки, - площадь сечения стеклянной трубки,  . .
Для каждого режима вычисляется значение критерия Рейнольдса:
 , ,
где 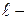 характерный линейный размер, характерный линейный размер, 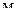 (диаметр стеклянной трубки, равный 15 мм); (диаметр стеклянной трубки, равный 15 мм);
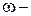 скорость потока, скорость потока, 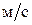 ; ;
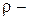 плотность воды, плотность воды, 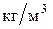 ; ;
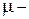 вязкость воды, вязкость воды, 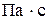 . .
Плотность и вязкость воды определяют по ее температуре из таблицы 2.
Все величины подставлять в системе СИ, тогда в результате расчетов критерий Рейнольдса получиться безразмерным.
Таблица 2.
Физические свойства воды
|  
|
0
|
10
|
20
|
30
|
40
|
50
|
| 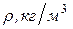
|
1000
|
1000
|
998
|
996
|
992
|
988
|
| 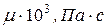
|
1,79
|
1,31
|
1,0
|
0,80
|
0,66
|
0,55
|
Контрольные вопросы
1. Понятие теории подобия.
2. Режимы движения жидкости.
3. Какие величины характеризуют режим течения потока?
4. Что такое критерий Рейнольдса? Каков его физический смысл?
5. Критические значения критерия Рейнольдса для прямых труб?
ЛАБОРАТОРНАЯ РАБОТА 4
ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ НАСАДКОВ
Цель работы
: практическое ознакомление с применением уравнения Бернулли для расчета коэффициентов расхода жидкости из насадков, определение времени опорожнения резервуаров через отверстие.
Приборы и принадлежности
: установка для истечения жидкости из насадков, секундомер, насадки.
Установка (рис.1) состоит из напорного резервуара А-1, питающего трубопровода с вентилем В-1, сливного трубопровода с краном В-2, водомерного стекла 1, насадков 2, укрепленных на кране В-4 в отверстии на боковой стенке резервуара А-1, расходомерного бака А-2 со сливным краном В-3.

Рис.1. Схема установки
ОСНОВНЫЕ ПОНЯТИЯ
При движении жидкости по трубопроводу без дополнительного подвода энергии или ее отвода энергия жидкости не изменяется согласно закону сохранения энергии, который читается так: «Энергия не исчезает и не появляется вновь, она лишь переходит из одного вида в другой». Частным случаем выражения закона сохранения энергии является уравнение Бернулли – одно из наиболее важных и широко используемых на практике уравнений гидродинамики. В гидравлике вводят понятие идеальной жидкости
. Идеальная жидкость абсолютно несжимаема, не изменяет плотности с изменением температуры и не обладает силами внутреннего трения (вязкостью).
Для идеальной жидкости уравнение Бернулли формулируется так: «При установившемся движении идеальной жидкости сумма потенциальной  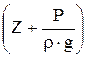 и кинетической и кинетической  энергий жидкости во всех сечениях потока есть величина постоянная». энергий жидкости во всех сечениях потока есть величина постоянная».
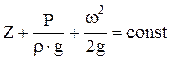 , ,
где 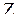 - нивелирная высота или геометрический напор, характеризующий положение (высоту) данной точки (сечения) жидкости относительно произвольно выбранной горизонтальной плоскости сравнения (см. рис. 2). Выражается - нивелирная высота или геометрический напор, характеризующий положение (высоту) данной точки (сечения) жидкости относительно произвольно выбранной горизонтальной плоскости сравнения (см. рис. 2). Выражается 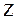 в единицах длины, м. По физическому смыслу в единицах длины, м. По физическому смыслу 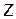 характеризует удельную потенциальную энергию положения данной точки (сечения), т.е. энергию характеризует удельную потенциальную энергию положения данной точки (сечения), т.е. энергию 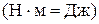 , приходящуюся на единицу веса , приходящуюся на единицу веса 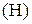 жидкости. жидкости.
Действительно,
 , ,
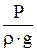 - гидростатический или пьезометрический, или напор, равный давлению столба жидкости в данном сечении (точке) потока, имеет размерность длины, - гидростатический или пьезометрический, или напор, равный давлению столба жидкости в данном сечении (точке) потока, имеет размерность длины, 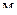 . По физическому смыслу величина . По физическому смыслу величина 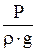 характеризует удельную потенциальную энергию давления жидкости в данном сечении (точке), характеризует удельную потенциальную энергию давления жидкости в данном сечении (точке), 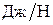 . .
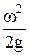 - скоростной или динамический напор, имеет размерность длины, - скоростной или динамический напор, имеет размерность длины,  . Характеризует удельную кинетическую энергию движущейся жидкости в данном сечении (точке), . Характеризует удельную кинетическую энергию движущейся жидкости в данном сечении (точке),  . .
Так как все напоры имеют размерность длины, то уравнение Бернулли можно наглядно представить графически на примере потока идеальной жидкости, движущейся через произвольно расположенный в пространстве трубопровод (рис.2).
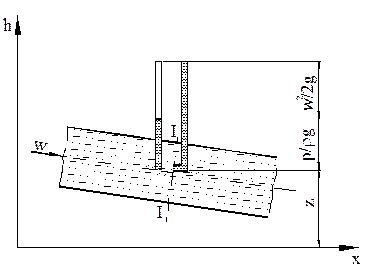
Рис.2. Графическая интерпретация уравнения Бернулли
Пьезометрический напор может быть измерен при помощи прямой вертикальной трубки (пьезометр), в которой под действием давления жидкость поднимается на высоту 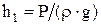 . .  В трубке с изогнутым под углом 90 В трубке с изогнутым под углом 90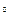 концом (гидрометрическая трубка), направленным навстречу потоку жидкости, жидкость поднимается на высоту концом (гидрометрическая трубка), направленным навстречу потоку жидкости, жидкость поднимается на высоту 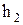 , равную сумме пьезометрического и скоростного напоров. Уровень жидкости в этой трубке будет выше уровня в пьезометре на высоту, равную скоростному напору. , равную сумме пьезометрического и скоростного напоров. Уровень жидкости в этой трубке будет выше уровня в пьезометре на высоту, равную скоростному напору.
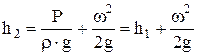 . .
Измерив, таким образом,  и и  , можно рассчитать из последнего уравнения скорость движения жидкости: , можно рассчитать из последнего уравнения скорость движения жидкости:
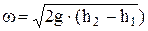 . .
На практике обе трубки конструктивно объединены в одном корпусе (трубки Пито-Прандтля) (рис. 3). Для измерения расхода жидкости или газа применяют и другие специальные приборы, такие как расходомер Вентури, диафрагма, ротаметр. Для измерения расхода жидкости или газа применяют и другие специальные приборы, такие как расходомер Вентури, диафрагма, ротаметр.

Рис. 3. Трубка Пито-Прандтля
Таким образом, можно рассчитать скорость движения жидкости:
  . .
Следует иметь в виду, что мы измеряем не среднюю скорость жидкости, а максимальную вдоль оси трубопровода, т.к. скорость движения жидкости по сечению трубопровода распределена неравномерно: равна нулю у стенок и достигает максимума вдоль оси трубы (рис.4).
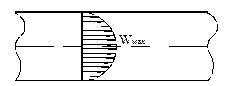
Рис.4. Распределение скоростей вдоль оси трубопровода
Для двух сечений потока уравнение Бернулли для идеальной жидкости примет вид:
  . (1) . (1)
С помощью этого уравнения решается ряд практически важных задач. Можно определить один из параметров для какого-либо сечения потока, зная два других параметра для этого сечения и все параметры для второго сечения.
Уравнение (1) справедливо для идеальной жидкости, в которой нет потери напора на преодоление сил трения. При движении реальной (вязкой) жидкости начинают действовать силы внутреннего трения, обусловленные вязкостью жидкости, и силы трения о стенки трубы, вызванные шероховатостью стенок.
Эти силы оказывают сопротивление движению жидкости. На преодоление сопротивления расходуется некоторая часть энергии потока. Потерянная при этом энергия превращается в тепло, которое безвозвратно теряется в окружающую среду. Для соблюдения баланса энергии при движении реальной жидкости в правую часть уравнения (1) вводится член 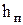 , выражающий потерянный напор. Тогда получим уравнение Бернулли для реальной жидкости: , выражающий потерянный напор. Тогда получим уравнение Бернулли для реальной жидкости:
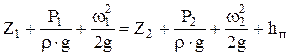 . . 
Потерянный напор 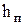 также имеет размерность длины также имеет размерность длины 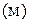 и характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении и характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении  реальной жидкости. Для реальной жидкости уравнение Бернулли формулируется так: в каждом сечении потока при установившемся движении вязкой жидкости сумма статического и динамического напоров, нивелирной высоты и потерянного напора есть величина постоянная и равная общему гидродинамическому напору Н. реальной жидкости. Для реальной жидкости уравнение Бернулли формулируется так: в каждом сечении потока при установившемся движении вязкой жидкости сумма статического и динамического напоров, нивелирной высоты и потерянного напора есть величина постоянная и равная общему гидродинамическому напору Н.

Рис.5. Графическая интерпретация уравнения Бернулли для реальной жидкости.
Уравнение Бернулли используется для расчета скорости, времени истечения и расхода жидкости из отверстий и насадков при расчетах диафрагм, дырчатых смесителей, наполнении и опорожнении резервуаров, бассейнов, водохранилищ, шлюзовых камер и других емкостей. Насадок – это короткая труба (штуцер, патрубок), приставленная к отверстию в стене или в днище сосуда, и ее длина в несколько раз больше внутреннего диаметра. Наиболее распространенные типы насадков приведены на рис.6.

Рис. 6. Типы насадков
а - цилиндрический внешний; б - цилиндрический внутренний; в - конический расходящийся; г - конический сходящийся; д - коноидально - расходящийся; е - коноидальный.
Цилиндрические насадки встречаются в виде деталей гидравлических систем машин и сооружений, дренажных труб резервуаров, емкостей и технологических аппаратов.
Конические сходящиеся и коноидальные насадки применяют для увеличения скорости и дальности полета струи воды (пожарные брандспойты, стволы гидромониторов, форсунки, сопла и т.п.).
Конические расходящиеся насадки применяют для уменьшения скорости и увеличения расхода жидкости и давления на выходе во всасывающих трубах турбин, центробежных насосов и др. В эжекторах и инжекторах также имеются конические насадки, как основной рабочий орган.
На практике часто встает вопрос о времени опорожнения резервуаров через отверстие или о величине отверстия, которое обеспечивало бы необходимое время опорожнения.
Определим расход жидкости при ее истечении из отверстия резервуара, в котором поддерживается постоянный уровень жидкости (рис.7).
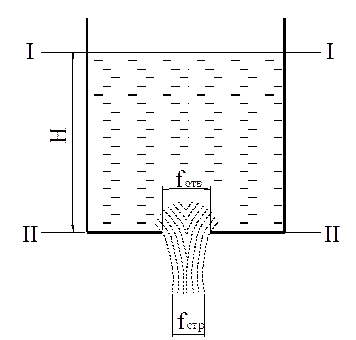
Рис. 7. Истечение жидкости из донного отверстия
Предположим, что истечение происходит из среды с атмосферным давлением в среду с таким же давлением.
Объемный расход жидкости равен произведению ее скорости на площадь сечения потока:
 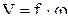 , , 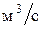 . .
Чтобы найти расход, необходимо определить скорость жидкости в отверстии резервуара.
Составим уравнение Бернулли для идеальной жидкости относительно сечения I-I, проходящего через верхний уровень жидкости в резервуаре, и сечения II-II, проходящего через отверстие в резервуаре, причем сечение II-II примем за плоскость сравнения (плоскость отсчета) (рис. 5.)
 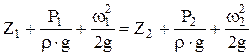 . (2) . (2)
Для сечения I-I геометрический напор 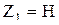 , а для сечения II-II напор , а для сечения II-II напор 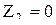 . При открытом резервуаре истечение происходит через отверстие в пространство с атмосферным давлением, следовательно . При открытом резервуаре истечение происходит через отверстие в пространство с атмосферным давлением, следовательно 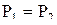 . При постоянном уровне жидкости скорость ее в сечении I-I . При постоянном уровне жидкости скорость ее в сечении I-I 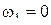 . Сделав соответствующие преобразования и сокращения в уравнении (2), получим: . Сделав соответствующие преобразования и сокращения в уравнении (2), получим:
 . .  (3) (3)
Таким образом, теоретическая скорость истечения 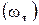 для идеальной жидкости для идеальной жидкости 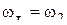 зависит только от высоты столба жидкости в резервуаре. Весь напор Н расходуется на создание скорости. Для реальной жидкости вводится ряд дополнительных поправок. Так при входе жидкости в отверстие происходит изменение ее скорости, а следовательно, изменяется и напор. Потеря напора вследствие изменения скорости потока по величине или по направлению происходит в местных сопротивлениях, к числу которых относятся вход и выход потока из трубы, напорные и регулирующие устройства (краны, вентили, задвижки и т.п.), внезапные расширения и сужения труб и другие. Потерю напора учитывает коэффициент местного сопротивления зависит только от высоты столба жидкости в резервуаре. Весь напор Н расходуется на создание скорости. Для реальной жидкости вводится ряд дополнительных поправок. Так при входе жидкости в отверстие происходит изменение ее скорости, а следовательно, изменяется и напор. Потеря напора вследствие изменения скорости потока по величине или по направлению происходит в местных сопротивлениях, к числу которых относятся вход и выход потока из трубы, напорные и регулирующие устройства (краны, вентили, задвижки и т.п.), внезапные расширения и сужения труб и другие. Потерю напора учитывает коэффициент местного сопротивления 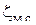 , который определяется опытным путем и для некоторых случаев приводится в приложении 1. , который определяется опытным путем и для некоторых случаев приводится в приложении 1.
Влияние коэффициента 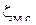 на величину скорости учитывает коэффициент скорости на величину скорости учитывает коэффициент скорости  : :
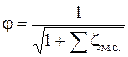 . (4) . (4)
Сумма местных сопротивлений равна:
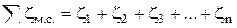 . .
Таким образом, скорость истечения реальной жидкости:
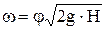 . .
Вследствие вязкости жидкости струя окажется сжатой при выходе из отверстия и ее сечение 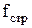 будет меньше сечения отверстия будет меньше сечения отверстия 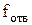 . Сжатие струи учитывает коэффициент сжатия . Сжатие струи учитывает коэффициент сжатия 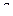 , который определяется опытным путем: , который определяется опытным путем:
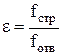 . .
Средние значения 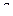 для некоторых случаев приводятся в приложении 2. Зная скорость истечения, можно определить расход жидкости через отверстие: для некоторых случаев приводятся в приложении 2. Зная скорость истечения, можно определить расход жидкости через отверстие:
 . .
Так как  , а , а  , то уравнение действительного расхода примет вид: , то уравнение действительного расхода примет вид:
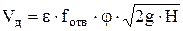 . .
Произведение 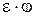 называется коэффициентом расхода и обозначается через называется коэффициентом расхода и обозначается через 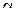 . .
Таким образом, расчетный коэффициент расхода:
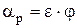 . (5) . (5)
Коэффициент расхода 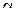 зависит от режима течения и от формы насадков, применяемых при опорожнении сосудов (мерников, цистерн и т.п.). Для некоторых случаев истечения его опытные значения приведены в приложении 2. зависит от режима течения и от формы насадков, применяемых при опорожнении сосудов (мерников, цистерн и т.п.). Для некоторых случаев истечения его опытные значения приведены в приложении 2.
Уравнение расхода реальной жидкости через отверстие получает окончательный вид:
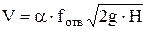 . (6) . (6)
Из уравнения (6) видно, что расход не зависит от формы сосуда. Опытные значения 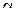 можно найти через отношение действительного расхода можно найти через отношение действительного расхода 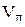 и теоретического и теоретического 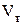 , т.е. , т.е.
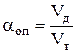 . (7) . (7)
При истечении жидкости через отверстие при переменном уровне, уровень H в сосуде снижается со временем. Согласно уравнению (3) уменьшается также и скорость истечения. Время истечения в этом случае оказывается больше времени истечения такого же объема жидкости при  . .
Время, за которое уровень жидкости в резервуаре опустится от первоначального уровня  до уровня до уровня 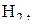 определяется из уравнения: определяется из уравнения:
 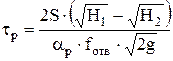 ; (8) ; (8)
где 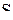 - площадь поперечного сечения резервуара, м2
: - площадь поперечного сечения резервуара, м2
:
 . .
Здесь 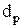 - диаметр резервуара А-1, м. - диаметр резервуара А-1, м.
При полном опорожнении сосуда формула упрощается, т. к. 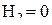 . .
Задание 1
Работа состоит из двух опытов: определение времени истечения жидкости из насадка при постоянном напоре (опыт 1) и изменяющемся напоре (опыт 2).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Опыт 1
Установить за краном В-4 насадок и измерить сечение (диаметр) его отверстия с помощью линейки или штангенциркуля. Заполнить резервуар А-1 водой, открыв питающий вентиль В-1. Открыть запорный кран В-4 и кран В-3. С помощью вентиля В-1 установить постоянный напор (по заданию преподавателя). По водомерному стеклу 4 определить величину напора Н1
. Закрыть кран В-3 на сливе воды из расходомерного бака А-2 и, одновременно отметив имеющейся уровень воды h0
в баке А-2, включить секундомер. Определить время 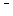 наполнения бака А-2 до какого-то уровня h (но не менее 10-15 см.). Полученные данные занести в таблицу 1. На время заполнения таблицы открыть кран В-3, при этом не изменять напор в резервуаре А-1 (краны В-1 и В-4 должны оставаться в прежнем положении). наполнения бака А-2 до какого-то уровня h (но не менее 10-15 см.). Полученные данные занести в таблицу 1. На время заполнения таблицы открыть кран В-3, при этом не изменять напор в резервуаре А-1 (краны В-1 и В-4 должны оставаться в прежнем положении).
Таблица 1.
| 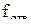 , ,
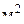
|
Н,

|
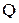 , ,

|
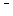 , ,

|
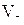 , ,

|
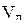 , ,

|
Коэф. расхода 
|
| Опытн.
|
Расчетн.
|

Опыт 2
Далее определяем время истечения жидкости при изменяющемся напоре в резервуаре А-1. Закрываем воду на сливе из резервуара А-2 с помощью крана В-3. Закрываем кран В-1 и сливаем воду в бак А-2 в том же количестве Q, что и в первом опыте. По секундомеру замеряем время истечения 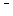 , за которое это количество воды вытечет из резервуара А-1 от уровня Н1
до уровня Н2
. , за которое это количество воды вытечет из резервуара А-1 от уровня Н1
до уровня Н2
.
Полученные данные занести в таблицу 2. По окончании опытов слить воду из бака А-2.
Таблица 2.
Алгоритм расчета
Опыт 1
Зная напор воды в резервуаре А-1, вычислить теоретический расход воды по формуле:
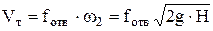 , ,
где  площадь поперечного сечения насадки, м2
; площадь поперечного сечения насадки, м2
; 
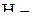 установленный напор воды в резервуаре, м; установленный напор воды в резервуаре, м;
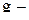 ускорение свободного падения. ускорение свободного падения.
Действительный расход жидкости определяется по формуле:
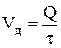 , ,
где  объем воды в резервуаре А-2 объем воды в резервуаре А-2 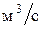 . Длина резервуара 1,25 м, ширина 0,4 м. . Длина резервуара 1,25 м, ширина 0,4 м.
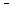 время наполнения расходомерного резервуара А-2 водой в количестве время наполнения расходомерного резервуара А-2 водой в количестве 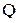 , с. , с.
Опытный коэффициент расхода находится по формуле:
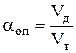 . .
Расчетный коэффициент расхода 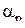 определяется из уравнения определяется из уравнения  с учетом реальных местных сопротивлений. При этом коэффициент скорости с учетом реальных местных сопротивлений. При этом коэффициент скорости  рассчитывается по уравнению: рассчитывается по уравнению:
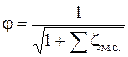 . .
Коэффициент сжатия струи  взять из приложения 2. взять из приложения 2.
Коэффициенты местных сопротивлений приведены в таблице приложении 1.
При определении местных сопротивлений для внезапных сужений и расширений используется критерий Рейнольдса. Для расчета 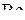 использовать опытную скорость истечения, которую определить из уравнения: использовать опытную скорость истечения, которую определить из уравнения:
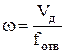 . .
Опыт 2
Рассчитать время истечения  жидкости из насадка при изменяющемся напоре и сравнить его с опытным значением жидкости из насадка при изменяющемся напоре и сравнить его с опытным значением 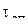 . .
Рассчитать уровень Н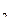 по уравнению: по уравнению:
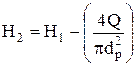 . .
Полученный результат сравнить с опытным Н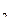 (по водомерному стеклу). (по водомерному стеклу).
  . .
Сравнить результаты первого и второго опытов и сделать выводы.
Задание 2
Задание 2 выполняется так же как и задание 1(опыт 1 с постоянным напором), но при этом меняют насадки. Полученные данные занести в таблицу 3 и сделать выводы.
Таблица 3.
| Тип
насадка
|
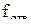 , ,
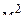
|
Н,

|
 , ,
|
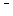 , ,

|
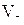 , ,

|
 , ,
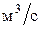
|
Коэф. расхода 
|
| Опытн.
|
Расчетн.
|

Контрольные вопросы
1. Уравнение Бернулли для идеальной жидкости.
2. Графическая интерпретация уравнения Бернулли.
3. Уравнения Бернулли дли реальной жидкости.
4. Практическое приложение уравнения Бернулли.
5. Поправочные коэффициенты, учитывающие реальность жидкости.
6. Назначение насадков, их типы, применение.
7. Местные сопротивления, виды местных сопротивлений.
8. Потери напора при движении реальной жидкости.
Приложение 1.
Коэффициенты местных сопротивлений
| Вид
сопротивления
|
Значение коэффициента местного сопротивления
|
| Вход в трубу

|
С острыми краями:  = 0,5 = 0,5
С закругленными краями:  = 0,2 = 0,2
|
| Выход из трубы

|
 = 1 = 1
|
| Внезапное
расширение

|
| 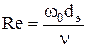
|

|
| 0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
| 10
|
3,10
|
3,10
|
3,1
|
3,1
|
3,1
|
3,1
|
| 100
|
1,70
|
1,40
|
1,20
|
1,10
|
0,90
|
0,80
|
| 1000
|
2,00
|
1,60
|
1,30
|
1,05
|
0,90
|
0,60
|
| 3000
|
1,00
|
0,70
|
0,60
|
0,40
|
0,30
|
0,20
|
| 3500
|
0,81
|
0,64
|
0,50
|
0,36
|
0,25
|
0,16
|
| и более
|
F0
- площадь меньшего поперечного сечения, м2
;
w0
- скорость потока в меньшем сечении, м/с;
F1
- площадь большего поперечного сечения, м2
;
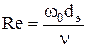 ; ; 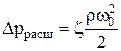
|
| Внезапное
сужение

|
| 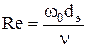
|
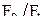
|
| 0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
0,6
|
| 10
|
5,00
|
5,00
|
5,00
|
5,00
|
5,0
|
5,0
|
| 100
|
1,30
|
1,20
|
1,10
|
1,00
|
0,90
|
0,80
|
| 1000
|
0,64
|
0,50
|
0,44
|
0,35
|
0,30
|
0,24
|
| 10000
|
0,50
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
| >10000
|
0,45
|
0,40
|
0,35
|
0,30
|
0,25
|
0,20
|
F0
- площадь меньшего поперечного сечения, м2
;
w0
- скорость потока в меньшем сечении, м/с;
F1
- площадь большего поперечного сечения, м2
;
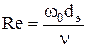 ; ; 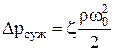
|
| Вентиль
прямоточный
|
При 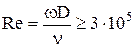 значение значение  определяется по таблице: определяется по таблице:
|  , мм , мм
|
25
|
38
|
50
|
65
|
76
|
100
|
150
|
200
|
250
|
| 
|
1,04
|
0,85
|
0,79
|
0,65
|
0,60
|
0,50
|
0,42
|
0,36
|
0,32
|
При  коэффициент сопротивления коэффициент сопротивления 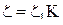 . Значение . Значение  определяется так же, как и при определяется так же, как и при 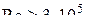 , а значение , а значение 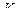 приведено в таблице: приведено в таблице:
| 
|
5000
|
10000
|
20000
|
50000
|
100000
|
200000
|
300000
|
| 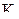
|
1,40
|
1,07
|
0,94
|
0,88
|
0,91
|
0,93
|
1
|
|
Приложение 2.
Гидродинамические характеристики наиболее
распространенных типов насадков
| Форма отверстия для истечения
|
ε
|
φ
|
|
| Цилиндрический:
|
| внешний
|
1,0
|
0,82
|
0,82
|
| внутренний
|
1,0
|
0,71
|
0,71
|
| короткий с закругленными краями
|
1,0
|
0,97
|
0,97
|
| Конический:
|
| сходящийся (с углом 12°)
|
0,99
|
0,96
|
0,95
|
| расходящийся (с углом 8°)
|
1,0
|
0,45
|
0,45
|
| коноидальный
|
1,0
|
0,98
|
0,98
|
| Отверстие круглое в тонкой стенке
|
0,64
|
0,97
|
0,62
|
| Примечание. Коэффициенты φ и m зависят от угла конусности.
|
Список литературы
1. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. – Изд. 10-е.- Л.: Химия, 1987. – 552 с.
2. Цыбин Л.А., Шанаев И.Ф. Гидравлика и насосы. Учебное пособие для техникумов. -М.: Высшая школа, 1976. -256 с.
3. Молоканов Ю.А. Процессы и аппараты нефтегазопереработки. Учебник для техникумов. М.: Химия, 1980. - 408 с.
4. Дытнерский Ю.И. Процессы и аппараты химической технологии. Учебник для вузов. Изд. 2-е. В 2-х кн.: Часть 1. Теоретические основы процессов химической технологии. М.: Химия, 1995.- 400 с.

Оглавление
| Лабораторная работа 1
|
| Изучение гидродинамики тарельчатых и насадочных колонн
|
3
|
| Лабораторная работа 2
|
| Изучение кинетики гравитационного осаждения
|
20
|
| Лабораторная работа 3
|
| Исследование режимов движения жидкости
|
31
|
| Лабораторная работа 4
|
| Истечение жидкости из насадков
|
41
|
| Приложения
|
56
|
| Список литературы
|
58
|
| |
|