| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТУРИЗМА И СЕРВИСА»
(ФГОУВПО «РГУТиС»)
Факультет сервиса
Кафедра Информационные системы
УТВЕРЖДАЮ
Проректор по учебной работе,
д.э.н., профессор
____________________Новикова Н.Г.
«____»______________________20__г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Дисциплина СД.06 «Надежность информационных систем»
Специальность 230201 «Информационные системы и технологии»
Специализация 230201.27 «Информационные системы в сфере сервиса»
230201.28 «Информационные системы и технологии в компьютерных сетях»
Москва 2009 г.
Методические указания по выполнению курсового проекта составлены на основании рабочей программы дисциплины СД.06 «Надежность информационных систем»
Методические указания рассмотрены и утверждены на заседании кафедры
«Информационные системы»
Протокол № 2
«26» октября 2009 г.
Зав кафедрой д.т.н., проф. Артюшенко В.М.
Методические указания рекомендованы Научно-методической секцией
факультета сервиса
Протокол №12
«9» ноября 2009 г.
Председатель
Научно-методической секции к.т.н., доц. Сумзина Л.В.
Методические указания одобрены Научно-методическим советом ФГОУВПО «РГУТиС»
Протокол №_______ «_____»______________________20__г.
Ученый секретарь
Научно-методического совета
к.и.н., доцент Юрчикова Е.В.
Методические указания разработал:
Преподаватель кафедры
«Информационные системы»
Мухлынин П.П.
На современном этапе экономического развития страны одной из важнейших, наиболее острых и неотложных проблем является качество и надежность продукции и работ (услуг). Немаловажное место в этой проблеме занимает повышение качества и надежности разработок в области создания информационных систем (ИС), используемых в различных сферах деятельности: обработки данных, проектирования, научных исследований и т.п., поскольку от прогрессивности создаваемых проектов ИС в значительной мере зависит научно-технических прогресс.
Повышение качества и надежности разработок в области создания ИС - многогранная проблема. Она имеет социальный, экономический, научно-технический, организационно-технический и другие аспекты.
Социальный аспект проблемы заключается в необходимости своевременного приведения качества и надежности разработок в соответствие с постоянно ужесточающимися во всем мире требованиями, предъявляемыми потребителем к качеству продукции, которое в первую очередь определяется такими социальными факторами, как профессиональное мастерство и качество труда.
Научно-технический аспект проблемы обусловливается тем, что, с одной стороны, уровень качества разработок ИС зависит от достижений науки и техники, а также темпов внедрения достижений в различных сферах производственной и непроизводственной деятельности, а с другой - тем, что уровень качества и надежности разработок ИС определяющим образом влияет на темпы научно-технического прогресса.
Организационно-технический аспект проблемы повышения качества и надежности проектных разработок ИС определяется зависимостью ее решения от уровня организации общественного производства в целом, а также от конкретных организаций, выполняющих разработки проектов ИС.
Информационная система является уникальной системой для каждого отдельного объекта автоматизации и требует особого подхода к процессу разработки и внедрения. Сложность разработки, связанная с невозможностью экспериментальной проверки проектных решений до момента внедрения написанных и отлаженных компьютерных программ, а также полной отработки операций, выполняемых персоналом, требует тщательной проработки основных принципиальных решений. Это объясняется тем, что все ошибки проектирования подобных систем проявляются практически только при вводе системы в эксплуатацию. Учитывая, что система предназначена для осуществления сложных по структуре процессов, следует предусмотреть возможность ее адаптации. В процессе создания необходимо включать в ИС современные формы организации и методы проектирования, средства вычислительной и организационной техники таким образом, чтобы не нарушалась непрерывность развития объекта автоматизации и создаваемые системы в дальнейшем модифицировались (расширялись, развивались), но не создавались заново. Опыт подсказывает, что это может быть достигнуто за счет интеграции в одну целостную систему процессов управления разработкой и внедрением ИС, за счет повышения качества и надежности этих процессов, а также процесса функционирования ЭИС.
Задания на контрольные работы
Контрольная работа № 1
Задача 1. В течение некоторого времени проводилось наблюдение за работой
N0 экземпляров восстанавливаемых изделий. Каждый из образцов проработал ti
часов и имел пi отказов. Требуется определить среднюю наработку на отказ по
данным наблюдения за работой всех изделий. Исходные данные для расчёта
Таблица 1
| Номер
|
Исходные данные
|
| |
|
|
|
|
|
|
|
|
|
| варианта
|
|
час
|
|
час
|
|
час
|
|
час
|
|
час
|
| 0
1
2
3
4
5
6
7
8
9
|
1
3
12
6
6
10
18
3
1
3
|
300
90
960
144
144
1020
2700
720
300
1650
|
3
6
15
5
5
26
32
4
3
2
|
600
270
1112
125
125
3120
4000
1040
600
1200
|
2
4
8
3
3
24
24
2
6
4
|
400
140
808
80
80
3480
3480
500
2300
2300
|
–
5
7
8
–
18
16
6
7
–
|
–
230
1490
176
–
2700
2080
1800
2450
–
|
–
3
–
5
–
–
24
–
–
–
|
–
180
–
150
–
–
3480
–
–
–
|
|
|
п1 t1,
п2 t2,
n3 t3,
n4 t4,
п5 t5,
Задача 2. В течение времени ∆t проводилось наблюдение за восстанавливае-
мым изделием и было зафиксировано п(∆t) отказов. До начала наблюдения изделие проработало t1 часов, общее время наработки к концу наблюдения составило t2 часов. Требуется найти среднюю наработку на отказ. Исходные данные для расчёта и ответы приведены в табл. 3.
Таблица 3
| Номер
варианта
|
Исходные данные
|
Ответы
tср , час
|
| t1,час
|
t2,час
|
п(∆t)
|
| 0
1
2
3
4
5
6
7
8
9
|
350
400
1000
770
1200
300
540
300
12
570
|
1280
1600
6400
4800
5558
540
1200
3200
184
2000
|
15
3
9
7
2
12
5
8
16
27
|
62
400
600
575
2179
20
132
362,5
10,75
53
|
Задача 3. Система состоит из N приборов, имеющих разную надёжность. Известно, что каждый из приборов, проработав вне системы ti часов, имел пi отказов. Для каждого из приборов справедлив экспоненциальный закон распре- деления отказов. Найти среднюю наработку на отказ всей системы. Исходные данные для расчёта и ответы приведены в табл. 4.
 Таблица 4 Таблица 4
 Вари- Вари-
Исходные данные Ответы
| ант
|
N
|
t1, час
|
п1
|
t2, час
|
n2
|
t3, час
|
n3
|
t4, час
|
n4
|
t5, час
|
п5
|
tср , час
|
| 0
|
3
|
4800
|
9
|
5500
|
3
|
1200
|
3
|
–
|
–
|
–
|
–
|
203
|
| 1
|
5
|
256
|
6
|
540
|
8
|
780
|
10
|
250
|
4
|
900
|
12
|
12,5
|
| 2
|
3
|
2000
|
6
|
1860
|
4
|
2160
|
3
|
–
|
–
|
–
|
–
|
153
|
| 3
|
4
|
960
|
12
|
1112
|
15
|
808
|
8
|
1490
|
7
|
–
|
–
|
24,6
|
| 4
|
5
|
90
|
3
|
270
|
6
|
140
|
4
|
230
|
5
|
180
|
3
|
8,2
|
| 5
|
5
|
600
|
45
|
600
|
2
|
200
|
4
|
200
|
6
|
200
|
2
|
7,25
|
| 6
|
3
|
144
|
6
|
125
|
5
|
80
|
3
|
–
|
–
|
–
|
–
|
8,4
|
| 7
|
4
|
720
|
3
|
1040
|
4
|
500
|
2
|
1800
|
6
|
–
|
–
|
65,4
|
| 8
|
3
|
1650
|
3
|
150
|
5
|
176
|
10
|
–
|
–
|
–
|
–
|
10,9
|
| 9
|
4
|
120
|
1
|
120
|
2
|
90
|
8
|
700
|
1
|
–
|
–
|
8,7
|
Задача 4 (для вариантов 0 – 4). Система состоит из k групп элементов. В
процессе эксплуатации зафиксировано п отказов. Количество отказов в j–й группе равно nj; среднее время восстановления элементов j–й группы равно tj. Требуется вычислить среднее время восстановления системы. Исходные данные для расчёта и ответы приведены в табл. 5. Изделие имеет среднюю
 наработку на отказ tср наработку на отказ tср
и среднее время восстановления tв
задача 4 (для
вариантов 5 – 9). Требуется определить коэффициент готовности изделия.
Исходные данные для расчёта и ответы приведены в табл. 6.
 Таблица 5 Таблица 5
| Вари-
|
Исходные данные
|
Ответы
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| ант
|
k
|
n
|
n
1
|
мин
|
n
2
|
мин
|
n
3
|
мин
|
n
4
|
мин
|
п
5
|
мин
|
t
в , мин
|
| 0
1
2
3
4
|
5
5
4
5
5
|
12
40
9
18
68
|
1
5
2
3
14
|
20
15
37
72
18
|
4
8
1
5
8
|
30
25
480
40
40
|
3
12
2
4
27
|
16
60
60
36
20
|
2
6
4
2
6
|
36
40
25
120
30
|
2
9
–
4
13
|
40
20
–
60
15
|
28,3
35,4
86
57,8
21,9
|
|
|
t1,
t2,
t3,
t4,
t5,
Таблица 6
| Варианты
|
Исходные данные
|
Ответы
|
| tср , час
|
tв , час
|
Kг
|
| 5
6
7
8
9
|
230
556
556
430
143
|
12
23
2,5
8
1,7
|
0,95
0,96
0,995
0,98
0,988
|
Контрольная работа № 2
Задача 1. Изделие состоит из N элементов, средняя интенсивность отказов которых λср. Требуется вычислить вероятность безотказной работы в течение t и среднюю наработку до первого отказа. Исходные данные для расчёта и ответы приведены в табл. 7.
Таблица 7
| Варианты
|
Исходные данные
|
Ответы
|
| N
|
λср, 1/час
|
t, час
|
P(t)
|
Tср, час
|
| 0
1
2
3
4
5
6
7
8
9
|
5200
3600
2500
2500
1000
750
500
250
20500
1000
|
0,16·10-5
0,2·10-5
0,35·10-6
0,5·10-5
0,5·10-5
0,5·10-5
0,5·10-5
0,5·10-5
2·10-5
0,5·10-3
|
200
50
100
100
100
100
100
100
2
0,5
|
0,19
0,698
0,916
0,2865
0,6065
0,6873
0,7788
0,8825
0,44
0,7788
|
120
139
1143
80
200
266
400
800
2,44
2
|
Задача 2 (для вариантов 0 – 4). Изделие состоит из N групп узлов. Отказы
узлов первой группы подчинены экспоненциальному закону с интенсивностью отказов λ, отказы узлов второй группы – нормальному закону с параметрами Т1
и σ, отказы узлов третьей группы – закону Вейбулла с параметрами λ0 и k. Требуется определить вероятность безотказной работы изделия в течение времени t. Исходные данные для расчёта и ответы приведены в табл. 8.
Задача 2 (для вариантов 5 – 9). Изделие состоит из N групп узлов. Отказы узлов первой группы подчинены экспоненциальному закону с интенсивностью отказов λ, отказы узлов второй группы – закону Релея с параметром σ и отказы узлов третьей группы – закону Вейбулла с параметрами λ0 и k. Требуется определить вероятность безотказной работы изделия в течение времени t. Исходные данные для расчёта и ответы приведены в табл. 9.
Таблица 8
Варианты N
λ·10-4,
Исходные данные Ответы
 λ0·10-5, λ0·10-5,
групп
1/час Т1, час σ, час
1/час k t P(t)
| 0
|
3
|
1
|
7200
|
2000
|
0,1
|
1,5
|
100
|
0,89
|
| 1
|
2
|
–
|
6000
|
4000
|
0,3
|
1,5
|
1000
|
0,87
|
| 2
|
2
|
3,2
|
–
|
–
|
0,2
|
1,3
|
500
|
0,45
|
| 3
|
2
|
0,93
|
8000
|
3000
|
–
|
–
|
2000
|
0,82
|
| 4
|
3
|
0,6
|
4000
|
4000
|
0,16
|
1,4
|
2400
|
0,67
|
 Таблица 9 Таблица 9
| |
|
|
|
|
|
|
|
| |
N групп
|
λ·10-3, 1/час
|
σ, час
|
λ0·10-3, 1/час
|
k
|
t, час
|
P(t)
|
| 5
6
7
8
9
|
3
3
2
2
2
|
0,2
0,1
–
0,09
0,06
|
1000
1200
1000
–
800
|
0,1
0,03
1,6
1,3
–
|
1,5
1,5
1,3
1,3
–
|
500
1000
500
120
200
|
0,7
0,54
0,53
0,93
0,96
|
Задача 3. В результате обработки данных по испытаниям и эксплуатации,
получен вариационный ряд значений времени безотказной работы изделия в часах. Требуется определить закон распределения времени безотказной работы.
Исходные данные для расчёта и ответы приведены в табл. 10.
Таблица 10
| Варианты
|
Исходные данные
|
Ответы
|
| ti
|
| 1
|
2
|
3
|
| 0
|
2; 2; 3; 3; 5; 6; 7; 8; 9; 9; 13; 15; 16; 17; 18; 20;
21; 25; 27; 35; 38; 53; 56; 69; 77; 86; 98; 120
|
Экспоненциальный
|
| 1
|
60; 100; 150; 170; 240; 300; 430; 650; 1100
|
Экспоненциальный
|
| 2
|
22; 31; 35; 50; 67; 74; 80; 84; 91; 93; 138; 152;
166; 171
|
Экспоненциальный
|
| 3
|
82; 89; 116; 124; 132; 197; 431; 1027
|
Экспоненциальный
|
| 4
|
3; 4; 5; 5; 6; 6; 7; 7; 7; 7; 7; 8; 9; 10; 10; 11; 12;
12; 12; 12; 12; 14; 14; 15; 15; 15; 16; 17; 18; 20;
20; 20; 21; 21; 22; 22; 23; 29; 30; 32; 33; 37; 38;
40; 40; 40; 42; 45; 46; 48; 49; 50; 53; 55; 55; 73;
86; 90; 110; 129
|
Экспоненциальный
|
Продолжение таблицы10
| 1
|
2
|
3
|
| 5
|
19; 28; 28; 32; 36; 36; 50; 51; 71; 124; 126; 138; 163; 231;
246; 260; 300; 302; 320; 341; 380; 384; 468; 477; 603;
807; 895; 920; 937
|
Экспоненциальный
|
| 6
|
17; 18; 57; 134; 160; 160; 174; 198; 200; 225; 279; 370;
420
|
Нормальный
|
| 7
|
61; 64; 92; 149; 150; 150; 178; 179; 200; 200; 250; 252;
255; 255; 312; 340; 341; 359; 362; 378; 600; 600
|
Нормальный
|
| 8
|
699; 724; 794; 799; 810; 935; 997; 1115; 1120; 1174;
1190; 1300; 1353; 1500; 1534; 1573; 1800; 1800; 1900;
2000; 2166; 2278; 2301; 2400; 2444; 2447; 2500; 2700;
2850; 2950
|
Экспоненциальный
|
| 9
|
200; 232; 328; 368; 393; 404; 421; 457; 483; 511; 527;
540; 544; 572; 598; 605; 619; 633; 660; 681; 736; 791; 942
|
Вейбулла
|
Задача 4. По данным задачи 3 и вариационному ряду исследуемого времени
безотказной работы построить полигон и гистограмму распределения, по виду которых ориентировочно подтвердить закон распределения
4.1. Методические указания к выполнению первой контрольной работы
Средней наработкой на отказ
восстанавливаемого изделия называется среднее значение времени между соседними отказами.
Для одного изделия статистическая оценка
средней наработки на отказ будет равна

где t
ì
- время исправной работы изделия между (ì - 1)-м и ì-м отказами; п -
число отказов за время t
.
Для N
наблюдаемых в течение времени t
изделий статистическая оценка
средней наработки на отказ определяется по формуле

где tij
-
время исправной работы j-го изделия между (i - 1)-м и i-м отказами; п
j
-число отказов j-го изделия за время t
.
Пример 4.1.1.
В течение некоторого периода времени проводилось наблюдение за работой одного восстанавливаемого изделия. За весь период наблюдения было зарегистрировано 15 отказов. До начала наблюдения изделие проработало 258 час, к концу наблюдения наработка изделия составила 1233 час. Требуется определить среднюю наработку на отказ tcp
.
Решение
:
Наработка изделия за наблюдаемый период равна
t = t2
- t1
=1233-258 = 975 час.
находим среднюю наработку на отказ:

Пример 4.1.2.
Проводилось наблюдение за работой трёх одинаковых восстанавливаемых изделий. За период наблюдения было зафиксировано по первому изделию 6 отказов, по второму - 11 отказов и по третьему - 8 отказов.
Наработка первого изделия составила 181 час, второго - 329 часов и третьего -245 часов. Требуется определить среднюю наработку изделий на отказ.
Решение
:
Суммарная наработка трёх изделий
| Суммарное количество отказов
|
Средняя наработка на отказ по формуле (2) будет равна
Пример 4.1.3.
Система состоит из 5 изделий, причём отказ любого одного из них ведёт к отказу системы. Известно, что первое изделие отказало 34 раза в течение 952 часов работы, второе — 24 раза в течение 960 часов работы, а остальные изделия в течение 210 часов работы отказали 4, 6 и 5 раз соответственно. Требуется определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надёжности для каждого из пяти изделий.
Решение
:
Для решения этой задачи воспользуемся соотношениями:

Интенсивность отказов для каждого изделия:

Интенсивность отказов системы:
Средняя наработка на отказ системы:

Пример 4.1.4.
При эксплуатации системы было зарегистрировано п
= 40 отказам. Распределение отказов по группам элементов и время, затраченное на восстановление, приведено в табл. 11. Найти величину среднего времени восстановления системы.
Таблица 11
| Группа элементов
|
Количество отказов по группе ni
|
Вес
отказов по группе
mi
=

|
Время восстановления
ti
, мин
|
Суммарное время восстановления по группе tв
,
мин
|
| 1
|
2
|
3
|
4
|
5
|
| ппп
|
8
|
0,2
|
80 59 110 91 45 43 99 73
|
600
|
| Резисторы и конденсаторы
|
10
|
0,25
|
61 73 91 58 44 112 82 54 91 94
|
760
|
| Реле, трансформаторы, дроссели
|
4
|
од
|
102 98 124 128
|
452
|
| ЭВП
|
14
|
0.35
|
60 64 56 36 65 44 42 33 32 23
|
700
|
Продолжение таблицы 11
| 1
|
2
|
3
|
4
|
5
|
| Прочие элементы
|
4
|
0,1
|
125 133 115 107
|
480
|
Решение
:
Определяем среднее время восстановления аппаратуры по группам элементов.
Для полупроводниковых приборов

Аналогично находим:
- для резисторов и конденсаторов 76 мин;
- для реле, трансформаторов, дросселей 113 мин;
- для ЭВП 50 мин;
- для прочих элементов 120 мин.
Рассчитываем среднее время восстановления системы по формуле

где tB
i
-
среднее время восстановления элементов i-й группы; mi
-
вес отказов по группам элементов.
Подставляя значения данных в формулу, получим
t
вс
= 0,2*75 + 0,25*76 + 0,1*113 + 0,35*50 + 0,1*120 = 75 мин.
Пример 4.1.5.
Изделие имело среднюю наработку на отказ t
ср
-
65 часов и среднее время восстановления tB
= 1,25 часа. Требуется определить коэффициент готовности изделия после отказа и восстановления.
Решение
:
По определению коэффициент готовности изделия будет равен

4.2. Методические указания к выполнению второй контрольной работы
Если отказ технического устройства наступает при отказе одного из его элементов, то говорят, что такое устройство имеет основное соединение
элементов. При расчёте надёжности таких устройств предполагают, что отказ элемента является событием случайным и независимым. Тогда вероятность безотказной работы изделия в течение времени t
равна произведению вероятностей безотказной работы его элементов в течение времени t
с учётом законов распределения отказов. Основные соотношения для количественных характеристик надёжности при различных законах распределения времени до отказа восстанавливаемых изделий приведены в табл. 12.
Таблица 12
Пример 4.2.1.
Система состоит из 12600 элементов, средняя интенсивность отказов которых 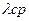 = 0,32*10-6
1/час. Определить вероятность безотказной работы и среднюю наработку до первого отказа в течение t
=
50 часов. = 0,32*10-6
1/час. Определить вероятность безотказной работы и среднюю наработку до первого отказа в течение t
=
50 часов.
Решение
:
В этом случае все элементы данного типа равнонадёжны и интенсивность отказов системы будет равна
тогда вероятность безотказной работы системы в течение 50 часов

а средняя наработка системы до первого отказа равна

Пример 4.2.2.
Время работы элемента до отказа подчинено экспоненциальному закону распределения с параметром  = 2,5 10-5
1/час. Требуется вычислить характеристики надёжности элемента P
(
t
),
a
(
t
)
и Тср
, если t
= 500 часов. = 2,5 10-5
1/час. Требуется вычислить характеристики надёжности элемента P
(
t
),
a
(
t
)
и Тср
, если t
= 500 часов.
Решение
:
Используя формулы для P
(
t
),
a
(
t
)
и Тср
, приведённые в табл. 12, вычисляем: вероятность безотказной работы

частота отказов
a
(
t
)
= (
t
)
*
Р(t), (
t
)
*
Р(t),
а(500) = 2,5*10-5
ехр(-2,5*10-5
*500) = 2,5-10-5
*0,9875 = 2,469*10-5
1/час; средняя наработка до первого отказа

Пример 4.2.3.
Время работы изделия до отказа подчинено закону распределения Релея. Требуется вычислить количественные характеристики надёжности изделия P
(
t
),
a
(
t
),
X
(
t
),
Гср
для t
= 500 часов, если параметр распределения а =
1000 часов.
Решение
:
Используя формулы для P
(
t
),
a
(
t
),
 (
t
)
и Tср
, приведённые в табл. 12, вычисляем: вероятность безотказной работы (
t
)
и Tср
, приведённые в табл. 12, вычисляем: вероятность безотказной работы
Р(500) = ехр(-t2
/2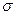 2
) = ехр(-5002
/2-10002
) = е-0125
= 0,88; частота отказов 2
) = ехр(-5002
/2-10002
) = е-0125
= 0,88; частота отказов
| средняя наработка до первого отказа
|
а(500) = (t/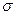 2
)ехр(-t2
/2 2
)ехр(-t2
/2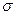 2
) = (500/10002
)ехр(-5002
/2*10002
) - 0,44-10-3
1/час; интенсивность отказов 2
) = (500/10002
)ехр(-5002
/2*10002
) - 0,44-10-3
1/час; интенсивность отказов
Пример 4.2.4.
Время безотказной работы изделия подчиняется закону Вейбулла с параметрами k=1,5и о=10-4
1/час, а время его работы 100 часов. Требуется вычислить количественные характеристики на, изделия. Решение
: о=10-4
1/час, а время его работы 100 часов. Требуется вычислить количественные характеристики на, изделия. Решение
:
Используя формулы для P
(
t
),
a
(
t
),
 (t), и Tср
, приведённые в табл. 12 (t), и Tср
, приведённые в табл. 12
вычисляем вероятность безотказной работы
P
(
t
)
= exp(- 0
*tk
), подставляя значения 0
*tk
), подставляя значения  0
, t
и к
из условия задачи, получим 0
, t
и к
из условия задачи, получим
Р(100) = 0,9.
Частота отказов определяется по формуле
а(t)= 0
ktk
-1
exp(- 0
ktk
-1
exp(- 0
tk
-1
). 0
tk
-1
).
Тогда
а(100)= 10-4
*l,5*1001,5-1
*0,9= 1,35*10-3
1/час,
 (100) = а(100)/Р(100) = 1,35*10-3
/0,9 =1,5*10-3
1/час. (100) = а(100)/Р(100) = 1,35*10-3
/0,9 =1,5*10-3
1/час.
Для вычисления средней наработки до первого отказа определяем гамма-функции из табл. [11], [12] для х = (1/к)
+ 1 = (1/1,5) + 1 = 1,67.
Подставляя в формулу для Тср
значение гамма-функцииГ(х)=
0,9033 и
параметры распределения  о и к,
получим о и к,
получим
|  1/
к
0
= 0,9033/(10-4
)1/1,5
=418 часов. 1/
к
0
= 0,9033/(10-4
)1/1,5
=418 часов.
|
Пример 4.2.5.
Время работы элемента до отказа подчинено нормальному закону с параметрами Т1
= 8000 часов, 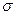 = 2000 часов. Требуется вычислить количественные характеристики надёжности P
(
t
),
a
(
t
), = 2000 часов. Требуется вычислить количественные характеристики надёжности P
(
t
),
a
(
t
),
 (t), Tср
для t
=
4000 часов. (t), Tср
для t
=
4000 часов.
Решение
;
Используя формулы, приведённые в табл. 12, вычисляем вероятность безотказной работы

Для вычисления Р(4000) по данным табл. П.7.16 находим F
{2)
= 0,97725 и F(4) = 1, тогда
Р(4000) = F[(8000 - 4000)/2000]/F(4) = F(2)/F(4)
= 0,97725/1 = 0,97725.
Частота отказов
Вычисления удобно производить,
используя табл. П.7.17 функции
В данном случае х
=
(t - T1
)/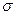 . Имея в виду, что F
(
T
1
/ . Имея в виду, что F
(
T
1
/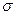 )
= F(8000/2000) = F(4)= 1, находим a
{
t
) = )
= F(8000/2000) = F(4)= 1, находим a
{
t
) =
 (x)/ (x)/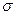 . Тогда: . Тогда:
a(4000) =  [(4000 - Т1
)/ [(4000 - Т1
)/
 /
/
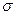 =
=  [(4000 - 8000)/2000]/2000 = [(4000 - 8000)/2000]/2000 =  (-2)/2000 = (-2)/2000 =
 (2)/2000 = 0,05399/2000 = 2,7*10-5
1/час. (2)/2000 = 0,05399/2000 = 2,7*10-5
1/час.
Подставляя найденные значения a
(
t
)
и P
(
t
)
в выражение 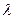 (t) = a
{
t
)/
P
{
t
),
рассчитываем интенсивность отказов (t) = a
{
t
)/
P
{
t
),
рассчитываем интенсивность отказов
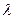 (4000) = а(4000)/P(4000) =2,7*10
-
5
/0,97725
= 2,76* 10-5
1/час. Вычисляем среднюю наработку до первого отказа (4000) = а(4000)/P(4000) =2,7*10
-
5
/0,97725
= 2,76* 10-5
1/час. Вычисляем среднюю наработку до первого отказа
Тср
= Т1
+ 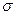 ехр(-T1
2
/2 ехр(-T1
2
/2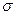 2
)/ 2
)/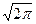 F(T1
/ F(T1
/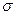 ) = 8000 + 2000*ехр(-0,5*42
)/ ) = 8000 + 2000*ехр(-0,5*42
)/ F4) = F4) =
=8000,26 часов.
Пример 4.2.6.
В результате опыта получен следующий вариационный ряд времени исправной работы в часах: 2;3;3;5;6;7;8;8;9;9;13;15;16;17;18;20,21,25,
28,35,37,53,56,69,77,86,98.119.
| Требуется установить закон распределения времени безотказной работы.
|
Решение
:
Проверка соответствия принятого закона распределения отказов осуществляется по критериям согласия, наиболее распространёнными из которых являются критерий Пирсона и критерий Колмогорова.
По критерию Пирсона вычисляют вероятность вида
где   - мера расхождения; - мера расхождения; 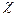 2
- функция плотности распределения 2
- функция плотности распределения

где п -
общее число наблюдаемых изделий; р
i
=
ni
/n частость i-го интервала статистического рада; к —
число интервалов статистического рада

где r= к-
1 -
число степеней свободы распределения.
Если вероятность Р(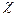 2 2
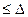 < 0,1) < 0,1)  0,1 , то экспериментальное распределение соответствует теоретическому. 0,1 , то экспериментальное распределение соответствует теоретическому.
По критерию Колмогорова соответствие теоретического и экспериментального распределений проверяется по выполнению условия
D  1, (8)
1, (8)
где D
- наибольшее отклонение теоретической кривой распределения от экспериментальной; к
- общее количество экспериментальных точек. Общее число отказов  i
= 28.
Заполняем табл. 13. i
= 28.
Заполняем табл. 13.
Таблица 13
Статистические данные об отказах
|  ti,
час ti,
час
|
0-20
|
20-40
|
40-60
|
60-80
|
80-100
|
100-120
|
| n(ti
)
|
16
|
5
|
2
|
2
|
2
|
1
|
| 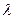 ( ( ti),
1/час ti),
1/час
|
0,0400
|
0,0263
|
0,0167
|
0,0250
|
0,0500
|
—
|
По
данным табл. 13 строится гистограмма требуемого показателя надёжности и аппроксимируется кривой, по виду которой ориентировочно устанавливается закон распределения отказов путём сравнения с соответствующими теоретическими кривыми (см. рис.).
Находим среднее значение 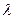 ср
и наибольшее отклонение D
: ср
и наибольшее отклонение D
:

D
=
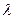 max
- max
- 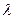 cp = 0,0500 - 0,0316 = 0,0184 1/час. cp = 0,0500 - 0,0316 = 0,0184 1/час.
Проверяем экспериментальное распределение на соответствие предполагаемому нормальному распределению по критерию согласия Колмогорова (8)
В соответствии с критерием считаем, что закон распределения отказов нормальный.
Список литературы
Основная
1. Леонтьев Е. А. Надежность экономических информационных систем. Учебное пособие. Тамбов: ТГТУ, 2006.
2. Матвеевский В.Р. Надежность технических систем. Учебное пособие.- М.: МГИЭИМ, 2006.
Дополнительная
1. Александров А.Е. Проектирование высоконадежных информационно-вычислительных систем. М.: Омега-Л, 2004.
ТИТУЛЬНЫЙ ЛИСТ КОНТРОЛЬНОЙ РАБОТЫ (бланк)
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТУРИЗМА И СЕРВИСА»
(ФГОУВПО «РГУТиС»)
____________________________________факультет
Кафедра______________________________________
КОНТРОЛЬНАЯ РАБОТА по
______________________________________________________
наименование дисциплины
____ -й семестр
Студента(ки) заочной формы обучения__________________________________________
Ф.И.О., полностью
_____________________________________________________________________________
№ зачетной книжки _________________________ группа__________________________
Специальность _______________________________________________________________
код и наименование специальности
_____________________________________________________________________________
№ варианта_________________ Выполнила _________________________
подпись студента(ки)
Работа предъявлена на проверку «____»_________200__г.__________________________
подпись преподавателя
Результаты проверки__________________________________________________________
Замечания, рекомендации______________________________________________________
_____________________________________________________________________________
Проверил преподаватель «___»__________200__г. ________________________________
Ф.И.О., подпись
Вторично
предъявлена на проверку «___»__________200__г. ______________________
подпись преподавателя
Результаты проверки_________________________________________________________
Замечания_________________________________________________________________________________________________________________________________________________
Проверил преподаватель «___»________200__г. __________________________________
Ф.И.О., подпись
Работа принята (проведено собеседование) «___»_______200__г____________________
подпись преподавателя
РЕЦЕНЗИЯ НА КОНТРОЛЬНУЮ РАБОТУ (бланк)
РЕЦЕНЗИЯ
на контрольную работу
студента (ки) заочной формы обучения __________________ ____________________________________________________
Ф.И.О
________________________группы _____________ курса
специальности_____________________________________
__________________________________________________
по дисциплине _____________________________________
__________________________________________________
тема: _____________________________________________
__________________________________________________
1. Соответствие контрольной работы заявленной теме, заданию: _________
__________________________________________________________________
2. Оценка качества выполнения контрольной работы:____________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
3. Оценка полноты разработки поставленных вопросов:__________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
4. Недостатки и замечания___________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
5. Оценка контрольной работы: ______________________________________
__________________________________________________________________
Преподаватель ____________________/______________
|