| 
|
“МАТИ” – Государственный технологический
Университет им. К.Э. Циолковского.
Кафедра “Системное моделирование и
Инженерная графика”
|

|
В.М. Лебедев, С.И. Лелюшенко
И Н Д И В И Д У А Л Ь Н Ы Е З А Д А Н И Я
П О Н А Ч Е Р Т А Т Е Л Ь Н О Й
Г Е О М Е Т Р И И
Методические указания
(Сокращенное переиздание пособия 1986 года выпуска)
Москва, 2006 г.
Методические указания содержат сведения по выполнению индивидуальных заданий по начертательной геометрии с элементами учебно-исследовательской работы студентов (УИРС). В пособии дается содержание и объем заданий, даются указания по их выполнению и оформлению.
Пособие предназначено для студентов дневного и вечернего отделений.
У К А З А Н И Я
К О Ф О Р М Л Е Н И Ю Ч Е Р Т Е Ж Е Й
Программой предусмотрено выполнение заданий по трем основным разделам курса начертательной геометрии:
1. Пересечение плоскостей.
2. Пересечение поверхностей и развертки.
3. Способы преобразования комплексного чертежа.
Задание выдается на дом по вариантам и выполняется на чертёжной бумаге. Четыре формата А3(297х420) на дневном и вечернем отделениях.
Общие правила оформления чертежей изучается в школе и повторяются в вузовском курсе «Машиностроительное черчение» [1,3]
О б щ и е т р е б о в а н и я
1. Все задания выполняются в карандаше в соответствии с требованиями стандартов Единой системы конструкторской документации (ЕСКД).
2. Особые точки следует выделять кружочками Æ 1...1,5 мм. Рекомендуется применять трафарет с отверстиями Æ 2 мм.
3. Надписи на чертежах выполняются шрифтом № 5.
4. Обозначения точек и линий должны иметь соответствующие индексы (например, А1
, A2
, А/
и т.д.).
5. Этапы работы при выполнении заданий:
- изучить теоретический материал,
- решить соответствующие задачи в рабочей тетради,
- выполнить чертеж в тонких линиях,
- консультация с преподавателем,
- обвести чертеж, предварительно удалив ненужные построения,
- представить чертеж на подпись преподавателю.
6. Необходимо обводить все линии чертежа без исключения.
7. В заданиях 1 и 2 видимые части плоскостей и поверхностей выделяются цветом. Каждая геометрическая фигура должна иметь свой цвет. Раскрашивание чертежа производится легким нажимом цветного карандаша с последующей растушевкой ватным тампоном. Эта работа выполняется перед обводкой чертежа после консультации с преподавателем.
Ф о р м а т
Выполнение чертежа начинается с оформления формата. Это внешняя и внутренняя рамки, основная надпись и дополнительная графа (рис.1). Порядок выполнения формата:
            1. Построить внешнюю рамку по стандартным размерам (линию обреза). 1. Построить внешнюю рамку по стандартным размерам (линию обреза).  
2. Построить внутреннюю рамку и обвести ее сплошной толстой основной линией. 
         3. Начертить основную надпись и дополнительную графу с необходимой обводкой. Заполнить тексты. 3. Начертить основную надпись и дополнительную графу с необходимой обводкой. Заполнить тексты.
К а р а н д а ш и
Качество чертежа во многом зависит от выбора и состояния карандаша. Некоторые рекомендации:
1. Твёрдость карандаша для тонких линий берётся в пределах от Т до ТМ (Н, НВ или F), для толстых линий - от М до 2М (от В до 2В). Твёрдость графита в циркуле должна быть меньше на один номер, по сравнению с твёрдостью карандаша для проведения однотипных линий при помощи линейки.
2. Заточка деревянной части карандаша показана на рис. 2. Для проведения тонких линий графитовый стержень затачивается на конус, для толстых линий стержень затачивается лопаточкой (рис.3). Расстояние между плоскими гранями "лопатки" определяется необходимой толщиной линии. Стержень для циркуля затачивают лопаткой или в виде одностороннего скоса (рис. 4).
Для заточки графитовых стержней рекомендуется использовать самодельный оселок (рис.5). Это полоска мелкозернистой наждачной бумаги, наклеенная на деревянную дощечку, фанерку, картон или чертёжную бумагу.
Последовательность заточки карандаша лопаткой показана на рис.6. Плоская грань "лопатки" прилегает к линейке (рис.7).
3. Карандаш, заточенный лопаткой, во время работы периодически поворачивается на 180°. Карандаш с коническим стержнем необходимо поворачивать вокруг оси, чтобы сохранить относительное постоянство толщины линии.
О п р я т н о с т ь ч е р т е ж а
Необходимо стараться не загрязнять чертёж во время работы.
1. Свободную часть чертежа следует прикрывать листами писчей бумаги (не газетой!). Это предохраняет бумагу от непосредственного контакта с чертёжными инструментами.
2. Мягкий ластик не приводит к "засаливанию" чертежа. Удаление ненужной линии следует начинать лёгким нажимом ластика до тех пор, пока на бумаге не образуются мелкие крошки. После этого нажим можно усилить и удалить линию окончательно.
3. Если линия не стирается, её надо поскоблить уголком лезвия безопасной бритвы, обработать ластиком и "сбрить" образовавшийся ворс той же бритвой, не бывшей в употреблении.
4. Перед обводкой чертежа необходимо удалить ненужные линии.
Задание I. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Цель задания - получить практические навыки самостоятельного решения задач по теме "Позиционные задачи для прямых и плоскостей" с элементами учебно-исследовательской работы (УИРС).
Номер варианта даётся студенту на весь семестр. Таблица исходных данных и список учебной литературы приведён в конце пособия.
Объём и содержание задания
Задание включает две задачи. Студенты-вечерники выполняют
задачу № 1.
Даны координаты точек: А, В, С, В, Е, F.
Задача
I.
Построить линию пересечения треугольника ABC и параллелограмма DEFG. Точку G определить графически. Записать алгоритм решения задачи в пространстве. Задачу решить на двухкартинном комплексном чертеже в масштабе 1:1. Видимые части плоскостей выделить цветом.
Задача 2
. Выбрать сторону параллелограмма, пересекающую треугольник ABC. Построить точку пересечения стороны параллелограмма с треугольником. Записать алгоритм решения. Задачу решить в стандартной приведённой диметрии. Видимые части посредника и треугольника выделить цветом.
Примерные композиции форматов показаны на рис. 8 и 9. Условные обозначения: КЧ – комплексный чертёж, Акс – аксонометрия, А – алгоритм, Т – таблица координат точек. Размеры и содержание таблицы даны на рис.10.
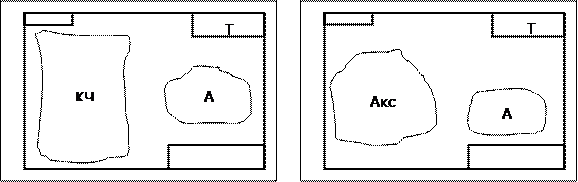 
Рис. 8 Рис. 9
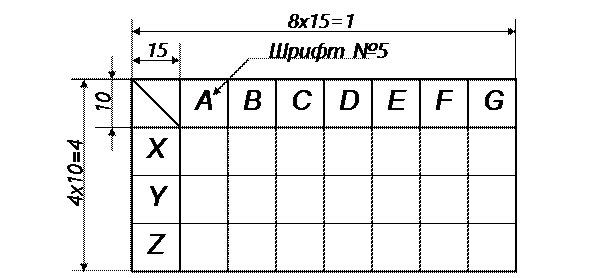 Материал для изучения
Для успешного выполнения задания необходимо решить соответствующие задачи в рабочей тетради, а также изучить теорию по одному из учебников.
[1] Глава 2: §§ 2.1–2.4.
[2] §§1–4.
[3] §31.
[4] §4.4a, примеры 1 и 3; §8.2.
Этапы выполнения задания
1-й этап
– подготовительный.
- Оформить формат.
- Начертить таблицу и вписать координаты заданных точек.
- Предъявить для проверки преподавателю.
2-й этап
– решение задачи I в тонких линиях.
- Построить треугольник ABC и параллелограмм DEFG. Определить координаты точки G и вписать их в таблицу.
- Построить искомую линию пересечения. Посредники должны быть заданы разомкнутой линией и обозначены. Обосновать выбор посредников (устно, по требованию преподавателя).
- Определить видимость с помощью конкурирующих точек. Конкурирующие точки должны быть заданы и обозначены.
- Записать алгоритм решения задачи в пространстве.
- Предъявить для проверки преподавателю.
3-й этап
– решение задачи 2 в тонких линиях.
- Построить треугольник и сторону параллелограмма.
- Построить искомую точку пресечения. Задать и обозначить посредник.
- Определить видимость прямой с помощью конкурирующих точек. Конкурирующие точки должны быть заданы и обозначены.
- Записать алгоритм решения задачи в пространстве.
- Предъявить для проверки преподавателю. Получить разрешение на обводку чертежа.
4-й этап
– заключительный.
- Удалить ненужные линии.
- Выделить цветом видимые части геометрических фигур.
- Обвести чертёж.
- Предъявить преподавателю на подпись.
Методические указания и примеры решения
З а д а ч а I
Напомним в общих чертах решение задачи на построение линии пересечения двух плоскостей. Искомая прямая строится по двум точкам. Эти точки определяются с помощью двух плоскостей-посредников. Каждый посредник пересекает заданные плоскости по двум прямым. Точка пересечения этих прямых принадлежит искомой линии. В общем случае для решения задачи требуется построить 8 вспомогательных точек и по ним провести 4 вспомогательные прямые. Однако в каждом конкретном случае следует искать возможность сократить число таких точек и линий за счет использования точек и линий, которые заданы по условию задачи. Точность построения прямых тем выше, чем больше расстояние между точками, задающими эти прямые.
Трудоёмкость и точность графических построений во многом определяется выбором посредников. Это исследовательская часть работы. Основные направления учебно-исследовательской работы (УИРС) в данной задаче:
1. Если посредники параллельны?
2. Если посредники проходят через прямые, которые задают плоскости?
3. Расстояние между проекциями точек, задающих вспомогательные прямые, должно быть не менее 20 мм (условное число).
Пункт I ведёт к сокращению вспомогательных точек с 8 до 6. Пункт 2 ведет к сокращению числа вспомогательных точек и линий в два раза. Пункт 3 обеспечивает достаточную точность графических построений. По какому пути пойти? По первому? По второму? Использовать то и другое? А требования пункта 3? Всё зависит от конкретных условий задачи. Думайте и решайте!
Пример решения
(рис.11):
1. По заданным точкам строим треугольник и параллелограмм. Для построения вершины G используем свойство параллелограмма.
2. Через стороны параллелограмма DE и FG проводим параллельные посредники:
Σ (Σ2
) и Σ/
( Σ/
2
). (Таким образом, мы выбрали сразу два направления УИРС: первое и второе).
3. Пресекаем посредник Σ с плоскостью ABC по прямой m. Прямая m строится по точкам I и 2, которые получаются путём пересечения посредника со сторонами треугольника АС и АВ. (Расстояние между проекциями точек соответствует требованию пункта 3). Прямые DE и m принадлежат посреднику и пересекаются в точке K искомой линии.
4. Пересекаем посредник Σ/
с плоскостью ABC по прямой m/
. Прямая m/
проводится через точку 3 параллельно прямой m. Точка 3 определяется пересечением прямой GF с посредником. Прямые GF и m/
пересекаются в точке L. Это вторая точка искомой линии.
5. Cтроим искомую прямую ℓ(K,L) и ограничиваем её отрезком [КМ], по которому пересекаются треугольник и параллелограмм.
6. Определяем видимость с помощью конкурирующих точек. На фронтальной проекции используем точки I и 4, у которых 12
=24
. Точка I принадлежат треугольнику, точка 4 - параллелограмму. Фронтальная проекция точки 4 видима, значит видима в этом месте и часть параллелограмма. Аналогично с помощью точек 5 и 6 определяется видимость на горизонтальной проекции.
7. Запишем алгоритм решения (рис.11).
Что дал нам выбор посредников?
1. Задача решена при помощи 2-х вспомогательных прямых и 3-х вспомогательных точек вместо 4-х прямых и 8-ми точек в общем случае. Это сокращение трудоёмкости.
2. Выдержаны требования пункта 3 УИРС. Этим обеспечена достаточная точность построения вспомогательных прямых.
      
| 1. Задать Σ(Σ2
)ÉDE.
2. 1=Σ∩AC,
2= Σ∩AB,
m(1,2)= Σ∩(ABC).
3. K=m∩DE.
4. Задать Σ/
(Σ/
2
)ÉFG,
Σ/
|| Σ.
5. 3= Σ/
∩AC,
m/
(3,DE)=Σ/
∩(ABC).
6. L=m/
∩FG.
7. ℓ(K,L) – линия пересечения.
8. [KM]Ìℓ
|
|
 |
З а д а ч а 2
Пример решения
(рис.11):
1. Зададим систему аксонометрических осей. С помощью координатных ломаных линий построим диметрию и вторичную проекцию треугольника и стороны параллелограмма. Укажем масштаб аксонометрического изображения.
2. Зададим горизонтально проецирующий посредник Г, проходящий через заданный отрезок DE. Вторичная проекция посредника Г/
1
определяется концами вторичной проекции отрезка DЕ.
3. Пересекаем посредник Г с плоскостью треугольника ABC по прямой m. Прямая m строится по точкам 1 и 2, которые получаются путем пересечения посредника сторонами треугольника АС и BC.
4. Прямые DE и m принадлежат посреднику и пересекаются в искомой точке К.
5. Запишем алгоритм решения (рис.12).
| 1. Задать ГÉDE, Г^П1
2. 1=Г∩AC,
2=Г∩BC,
m(1,2)=Г∩(ABC).
3. K=m∩DE –
|
|
 |
Задание 2. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Цель задания - получить практические навыки самостоятельного речения задач с элементами УИРС по теме задания.
Объём и содержание задания
Построить линию пересечения двух заданных поверхностей. Масштаб изображения 1:1. Для построения опорных точек можно использовать преобразование комплексного чертежа. Видимые части поверхностей выделить цветом.
Материал для изучения
[2] §§ 58, 61, 62.
[4] §§ 4.1, 4.4, 4.4a, 4.4б.
Этапы выполнения задания аналогичны этапам 1-го задания.
Методические указания и примеры решения
Искомая линия пересечения поверхностей строится по нескольким точкам. Точки определяются с помощью поверхностей-посредников. Каждый посредник пересекает заданные поверхности по двум линиям. Точки пересечения этих линий принадлежат искомой линии. Точность построения искомой линии тем выше, чем больше точек будет построено. Трудоёмкость и точность графических построений определяется выбором посредников. Посредники должны пересекаться с данными поверхностями по линиям, которые проецируются в прямые и окружности. Это исследовательская часть работы. Основные направления УИРС в данной работе:
1. Выбор способа решения задачи (т.е. поверхностей-посредников).
2. Выбор способа построения опорных точек.
3. Определение области построения посредников.
4. Выбор оптимального количества посредников.
Пункт I позволяет выбрать наименее трудоёмкий способ решения задачи. В пункте 2 возможны по крайней мере 3 варианта:
1. Опорные точки уже есть на чертеже. Их нужно только отметить.
2. Опорные точки строятся тем же способом, что и все точки искомой линии.
3. Для построения опорных точек используется преобразование комплексного чертежа.
Исследовав конкретные условия задачи, решайте, по какому пути пойти. Выполнение пунктов 3 и 4 позволяет использовать необходимое и достаточное количество построений.
Примеры решения
Задача 1.
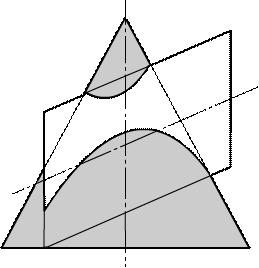
Построить линию пересечения прямого кругового конуса и сферы (рис.13)
Решение:
1. Строим проекции заданных поверхностей.
2. Выбирают в качестве поверхностей-посредников горизонтальные плоскости
Г, ∆, … Плоскости Г, ∆, … пересекаются с данными поверхностями по окружностям, лежащим в горизонтальных плоскостях.
3. Строят опорные точки. Самая верхняя точка А и самая нижняя - В располагаются в общей плоскости симметрии Σ.. Для построения точек А и В используется преобразование комплексного чертежа. Следует выбрать наиболее рациональный способ для данного случая (обосновать). На рис.13 использовано вращение плоскости Σ вокруг оси конуса до совмещения с фронтальной плоскостью Λ
. Этот способ позволил получить компактное решение задачи. Линии ℓ
и m
после поворота, займут положение ℓ/
и m/
.
Тогда A/
2
=ℓ
/
2
∩m
/
2
и B/
2
=ℓ
/
2
∩m
/
2
. Фронтальные проекции точек А и В получают обратным поворотом плоскости Λ
в положение Σ, т.e. A2
=ℓ
2
∩А2
А/
2
(А2
А/
2
||х12
); B2
=ℓ
2
∩B2
B/
2
(B2
B/
2
||х12
). Ai
и Вi
находятся с помощью вертикальных линий связи.
Опорные точки Е и F находятся на очерковой образующей конуса. Они расположены в плоскости Λ
, которая пересекает сферу по окружности n
. Тогда E2
=ℓ
/
2
∩n
2
; F2
=ℓ
/
2
∩n
2
. Строят Ei
и Fi
.
Опорные точки С и в лежат на экваторе сферы и строятся с помощью плоскости Г. Эти точки – граница видимости искомой линии на Пi
. Плоскость Г пересекает конус по окружности k
, а сферу – по окружности экватора. Точки пересечения этих двух окружностей есть точки С и в .
4. Ряд промежуточных точек строят с помощью горизонтальных плоскостей типа ∆. Плоскость ∆ рассекает конус и сферу по окружностям р
и t
, тогда I=
p
∩t
; 2=p
∩t.
Таких плоскостей нужно выбрать достаточное количество, чтобы выявить характер искомой линии. Необходимо учесть, что А и В – самая верхняя и нижняя точки линии пересечения, поэтому плоскости Г и ∆,… выбирают ниже точки А и выше точки В.
5. Опорные точки К и L (границы видимости линии пересечения на П2
) строят после обводки её на П1
. Точки Ki
и Li
просто отмечают. Затем строят K2
и L2
на очерке.
Задача 2.
Построить линию пересечения прямого кругового конуса и цилиндра (рис.14)
Решение:
1. Строят проекции заданных поверхностей.
2. Выбирают в качестве посредников концентрические сферы с центром в точке 0 пересечения осей данных поверхностей.
3. Строят опорные точки. Точки А, В и С уже есть на чертеже. Их нужно только обозначить. Другие опорные точки требуют для себя особых построений.
4. Минимальная сфера (вписанная в цилиндр) касается поверхности цилиндра по окружности т
и пересекает конус по окружностям ℓ
и п
.
В итоге – очередные опорные точки: K=m
∩ℓ
и F=m
∩n
. Симметричные точки, лежащие на невидимой стороне, не обозначены. Горизонтальные проекции точек строятся с использованием каркаса параллелей конуса.
Проанализируйте вопрос о максимальной сфере в этом примере.
5. Ряд промежуточных точек строят с помощью вспомогательных сфер типа ∆ . Сфера ∆ пересекает конус по окружностям k и k/
а цилиндр - по t и t/
. Тогда 1=k/
∩t; 2=k∩t; 3=k∩t/
.
6. Опорные точки Е, в и M получают после построения проекции искомой линии на П2
. Горизонтальные проекции точек E и в являются очерковыми.
  Задание 3. СПОСОБЫ ПРЕОБРАЗОВАНИЯ
КОМПЛЕКСНОГО ЧЕРТЕЖА
Цель задания – получить практические навыки самостоятельного решения задач с элементами УИРС по теме преобразования чертежа.
Объём и содержание задания
Задание состоит из пяти задач. Студенты-вечерники задачу № 2 не выполняют.
Даны координаты точек: А, В, С, D. Таблица та же.
Задача
I
. Построить трёхкартинный комплексный чертёж тетраэдра ABCD с учётом видимости рёбер. Задать профильно-проецирующую плоскость Т, пересекающую тетраэдр по четырёхугольнику. Построить проекции и натуральный вид сечения. Использовать способ замены плоскостей проекций.
Задача 2.
Построить треугольник ABC. Определить угол наклона треугольника к горизонтальной плоскости проекций. Использовать линию ската и способ вращения вокруг проецирующей прямой.
Задача 3
. Построить отрезки АВ и CD. Определить угол между отрезками. Способ замены плоскостей проекций.
Задача 4
. Построить треугольник ABC и точку D. Построить точку D/
, симметричную точке в относительно плоскости треугольника. Способ преобразования выбрать самостоятельно, преследуя цель: сократить трудоемкость, улучшить наглядность и т.д. Выбор способа обосновать (устно, по требованию преподавателя).
Примерная композиция формата показана на рис.15.

рис.15
Материал для изучения
Для успешного выполнения задания необходимо изучить способы преобразования комплексного чертежа и решить соответствующие задачи в рабочей тетради. Разделы курса для изучения:
[2] §§ 39, 40, 42.
[4] §§ 5.1, 5.2, 5.3.
Этапы выполнения задания
1-й этап
– оформить формат (обвести).
2-й этап
– решить задачу в тонких линиях, предъявить для проверки преподавателю, получить разрешение на обводку.
3-й этап
– удалить ненужные линии, обвести чертёж, предъявить преподавателю на подпись.
Чертежи сдаются в назначенные сроки по мере выполнения отдельных задач.
Методические указания и примеры решения
З а д а ч а 1
Пример решения
(рис. 16):
1. По заданным точкам строим трёхкартинный чертёж тетраэдра. Определяем видимость рёбер по конкурирующим точкам, выделенным на чертеже кружочками без обозначения. Для П1
использованы точки на рёбрах АС и BD, для П2
– на рёбрах АВ и CD, для П3
– на AD и ВС.
2. Задаём секущую плоскость Т и строим проекции сечения 1234. Видимость периметра сечения соответствует видимости граней тетраэдра.                                                                               3. Строим натуральный вид сеченая на новой плоскости проекций П4
, параллельной плоскости сечения. На комплексном чертеже новая ось проекций х34
параллельна профильной проекции сечения. 3. Строим натуральный вид сеченая на новой плоскости проекций П4
, параллельной плоскости сечения. На комплексном чертеже новая ось проекций х34
параллельна профильной проекции сечения.
             4. Выделим сечение штриховкой. 4. Выделим сечение штриховкой.
З а д а ч а 2
Угол наклона заданной плоскости к П1
равен углу наклона линии ската. Линия ската перпендикулярна к горизонтали плоскости. Это свойство используется для её задания. Угол наклона линии ската определяется после приведения её в положение фронтали.
Пример решения
(рис.17)
1. Строим треугольник ABC.   2. Строим горизонталь h(1,C) и линию ската (2,В). 2. Строим горизонталь h(1,C) и линию ската (2,В).
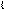            
3. Задаём горизонтально проецирующую ось вращения i
и производим поворот линии ската до положения линии уровня 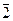 В. Угол наклона фронтальной проекции В. Угол наклона фронтальной проекции 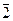 2
B2
равен искомому углу 2
B2
равен искомому углу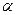 . .
З а д а ч а 3 Угол между скрещивающимися прямыми равен углу между пересекающимися прямыми, параллельными, соответственно, скрещивающимися прямыми. Выбор положения точки, через которую проводят пересекающиеся прямые, во многом определяет наглядность графических построений и их трудоёмкость. Это исследовательская часть работы. Основные направления УИРС в данной задаче:
| 1. Если точка задана на свободном поле чертежа?
2. Если проекция точки принадлежит проекции одной из скрещивающихся прямых?
3. Если точка принадлежит одной из скрещивающихся прямых?
|
Пункт 1 приводит к максимальной трудоёмкости решения, зато улучшает наглядность, даёт возможность избежать наложения проекций. Пункт 2, наоборот, ухудшает наглядность из-за наложения проекций, зато отпадает необходимость в построении одной проекции точки и одной проекции прямой. Взаимная принадлежность проекций может быть задана на П1
или П2
. Выбор плоскости проекции также оказывает влияние на наглядность чертежа и трудоёмкость решения задачи в целом. Пункт 3 приводит к минимальной трудоёмкости. Есть над чем подумать.
Результаты исследования представляются устно по требованию преподавателя.
Ниже приводятся примеры решения задач заведомо с максимальной трудоёмкостью(рис.18).
1. Отроим прямые АВ и CD.
2. Зададим точку К на свободном поле чертежа и проведём через нее вспомогательные прямые: ℓ||AB и m||CD.
3. Выполним первую замену плоскостей проекций для получения вырожденной проекции плоскости (ℓ||m). Зададим в этой плоскости горизонталь h(1,2) и спроецируем её на новую плоскость проекций П4
^h. На чертеже новая ось проекций x14
^ h1
.
4. Выполним вторую замену плоскостей проекций для получения натурального вида плоской фигуры (ℓ∩m) на новой плоскости проекций П5
, параллельной этой фигуре. На чертеже новая ось х45
параллельна вырожденной проекции ℓ4
=m4
. Угол между проекциями ℓ5
и m5
есть искомый угол φ.
З а д а ч а 4
Симметричные точки относительно плоскости находятся на одном перпендикуляре к плоскости по разные стороны от неё и на одинаковом расстоянии. Независимо от способа преобразования перпендикуляр должен быть спроецирован в натуральную величину. Он должен стать параллельным плоскости проекций. Для этого плоскость симметрии надо перевести в положение плоскости уровня.
Пример решения
способом замены плоскостей проекций (рис.19):
1. Строим треугольник ABC и точку D.
2. Задаём горизонталь h(1,C) в плоскости треугольника.
3. Проецируем заданную фигуру на новую плоскость проекций П4
^h. На чертеже новая ось проекций x14
^ h1
.
4. Строим искомую точку D/
, начиная с проекции D/
4
при условии: D/
4
К4
= К4
D4
, где К есть точка пересечения прямой и плоскости.
5. Строим отрезок D4
D/
4
.
6. Определяем видимость отрезка DD/
относительно треугольника.
Таблица координат
| №
вар.
|
А
|
В
|
С
|
D
|
E
|
F
|
| x
|
v
|
z
|
x
|
v
|
z
|
x
|
v
|
z
|
x
|
v
|
z
|
x
|
v
|
z
|
x
|
v
|
z
|
| 1
|
145
|
65
|
20
|
75
|
10
|
125
|
10
|
110
|
65
|
135
|
105
|
100
|
40
|
85
|
75
|
0
|
15
|
20
|
| 2
|
135
|
85
|
20
|
65
|
30
|
125
|
0
|
130
|
65
|
135
|
120
|
100
|
55
|
135
|
85
|
30
|
30
|
30
|
| 3
|
150
|
115
|
105
|
0
|
60
|
95
|
120
|
20
|
25
|
105
|
40
|
90
|
40
|
20
|
135
|
20
|
105
|
35
|
| 4
|
150
|
55
|
65
|
50
|
110
|
85
|
0
|
55
|
20
|
90
|
110
|
15
|
115
|
30
|
120
|
30
|
50
|
115
|
| 5
|
150
|
105
|
40
|
80
|
40
|
120
|
0
|
120
|
80
|
150
|
65
|
105
|
90
|
100
|
120
|
50
|
50
|
50
|
| 6
|
145
|
110
|
40
|
75
|
30
|
100
|
0
|
70
|
25
|
145
|
45
|
75
|
85
|
30
|
40
|
45
|
100
|
100
|
| 7
|
120
|
120
|
105
|
55
|
30
|
25
|
15
|
75
|
130
|
120
|
60
|
80
|
65
|
30
|
140
|
25
|
85
|
75
|
| 8
|
135
|
120
|
95
|
55
|
30
|
25
|
25
|
75
|
120
|
130
|
65
|
70
|
75
|
85
|
130
|
25
|
85
|
75
|
| 9
|
140
|
60
|
30
|
50
|
110
|
140
|
25
|
0
|
40
|
110
|
15
|
135
|
25
|
50
|
110
|
0
|
115
|
30
|
| 10
|
130
|
20
|
70
|
90
|
115
|
120
|
0
|
60
|
20
|
170
|
80
|
60
|
105
|
115
|
50
|
40
|
50
|
120
|
| 11
|
120
|
20
|
80
|
80
|
120
|
130
|
10
|
70
|
50
|
100
|
115
|
50
|
55
|
40
|
125
|
0
|
65
|
80
|
| 12
|
190
|
95
|
25
|
80
|
30
|
20
|
40
|
105
|
110
|
125
|
45
|
95
|
80
|
115
|
40
|
0
|
115
|
20
|
| 13
|
140
|
130
|
60
|
80
|
30
|
20
|
40
|
110
|
110
|
125
|
45
|
95
|
80
|
115
|
40
|
0
|
115
|
20
|
| 14
|
140
|
10
|
50
|
80
|
130
|
125
|
0
|
80
|
30
|
140
|
80
|
10
|
60
|
100
|
30
|
10
|
20
|
115
|
| 15
|
160
|
10
|
50
|
100
|
130
|
125
|
20
|
80
|
30
|
140
|
85
|
25
|
50
|
110
|
40
|
0
|
70
|
120
|
| 16
|
140
|
70
|
105
|
75
|
120
|
45
|
15
|
25
|
80
|
150
|
50
|
50
|
50
|
100
|
120
|
10
|
140
|
110
|
| 17
|
160
|
140
|
50
|
90
|
10
|
0
|
40
|
95
|
110
|
120
|
100
|
15
|
90
|
40
|
90
|
0
|
80
|
100
|
| 18
|
160
|
85
|
0
|
90
|
130
|
110
|
45
|
45
|
40
|
120
|
105
|
30
|
60
|
60
|
100
|
0
|
80
|
80
|
| 19
|
145
|
65
|
110
|
80
|
125
|
10
|
10
|
20
|
65
|
155
|
15
|
0
|
100
|
85
|
120
|
0
|
115
|
120
|
| 20
|
135
|
65
|
130
|
70
|
125
|
30
|
0
|
20
|
85
|
105
|
30
|
30
|
80
|
85
|
135
|
0
|
100
|
120
|
| 21
|
150
|
95
|
60
|
0
|
105
|
115
|
30
|
25
|
20
|
125
|
60
|
85
|
110
|
135
|
20
|
45
|
90
|
40
|
| 22
|
150
|
20
|
55
|
115
|
110
|
125
|
0
|
65
|
55
|
115
|
65
|
65
|
40
|
100
|
15
|
20
|
40
|
85
|
| 23
|
130
|
100
|
120
|
70
|
120
|
40
|
0
|
40
|
105
|
100
|
50
|
50
|
60
|
120
|
100
|
0
|
105
|
65
|
| 24
|
145
|
25
|
70
|
70
|
100
|
40
|
0
|
40
|
110
|
100
|
100
|
100
|
60
|
40
|
30
|
0
|
75
|
45
|
| 25
|
120
|
130
|
75
|
80
|
25
|
30
|
15
|
105
|
120
|
115
|
75
|
85
|
70
|
140
|
30
|
15
|
80
|
60
|
| 26
|
120
|
65
|
130
|
75
|
120
|
40
|
0
|
20
|
80
|
100
|
30
|
40
|
75
|
80
|
140
|
0
|
100
|
120
|
| 27
|
140
|
30
|
80
|
60
|
125
|
130
|
0
|
50
|
10
|
130
|
115
|
60
|
80
|
30
|
100
|
0
|
10
|
80
|
| 28
|
150
|
40
|
70
|
80
|
120
|
115
|
40
|
70
|
20
|
130
|
120
|
50
|
65
|
50
|
105
|
0
|
60
|
80
|
| 29
|
145
|
45
|
65
|
75
|
115
|
110
|
35
|
65
|
25
|
125
|
115
|
45
|
60
|
45
|
100
|
0
|
65
|
85
|
| 30
|
120
|
110
|
105
|
80
|
20
|
30
|
0
|
25
|
95
|
160
|
80
|
115
|
80
|
40
|
115
|
35
|
95
|
45
|
 Варианты задач на пересечение поверхностей Варианты задач на пересечение поверхностей
Л И Т Е Р А Т У Р А
1. Левицкий В.С. Машиностроительное черчение и автоматизация выполнения чертежей. М., Высшая школа, 2004г.
2. Лагерь А.И., Мата А.Н., Рушелюк К.С. Основы начертательной геометрии. М., Высшая школа, 2005г.
3. Лебедев В.М. Общие правила оформления чертежей и сопряжения. М., МАТИ, 2006г.
4. Лебедев В.М. Конспект лекций для 16 часового курса начертательной геометрии. М., МАТИ, 2006г.
С О Д Е Р Ж А Н И Е
Указания к оформлению чертежей………………………………………………3
Задание 1. Пересечение плоскостей……………………………………………..5
Задание 2. Пересечение поверхностей…………………………………………10
Задание 3. Способы преобразования комплексного чертежа………………...13
Таблица координат………………………………………………………………17
Варианты задач на пересечение поверхностей………………………………...18
 Литература…………………………………………………………………..…...19 Литература…………………………………………………………………..…...19
Компьютерная обработка – Михайлов П.Ю., Ключников А.С.
|