|
Федеральное агентство по образованию
ГОУ ВПО «Волжский государственный инженерно-педагогический университет»
Ж.В. Смирнова
Решение задач
при проектировании сварных конструкций
Методические указания к практическим занятиям по дисциплине «Производство сварных конструкций»
Н.Новгород 2010
ББК 34.641
С 50
Смирнова Ж.В. Решение задач при проектирование сварных конструкций: Методические указания к практическим занятиям по дисциплине «Производство сварных конструкций». – Н.Новгород: ВГИПУ, 2010.-32с.
Методические указания предназначены для оказания помощи студентам при решение задач проектирования сварных конструкций, приведены примеры по расчету, что позволяет студентам самостоятельно работать по расчетам сварных конструкций.
ББК 34.641
© Смирнова Ж.В., 2009
© ВГИПУ, 2009
ПРИНЦИПЫ РАСЧЕТА СВАРНЫХ КОНСТРУКЦИЙ
Известны два принципа сварных конструкций и соединений:
– по допускаемым напряжениям;
– по предельному состоянию, по расчетным сопротивлениям.
Принцип расчета по допускаемым напряжениям применяется при проектировании машиностроительных конструкций. В расчете по этому принципу конструкция рассматривается в рабочем состоянии под действием нагрузок, допускаемых при ее нормальной эксплуатации, нормативных нагрузок 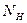 . .
Условие прочности конструкции или соединения заключается в том, чтобы напряжения от нормативных нагрузок не превышали некоторого допускаемого напряжения. Допускаемое напряжение при растяжении для основного материала сварной конструкции называют основным допускаемым напряжением  . Допускаемые напряжения от других видов нагрузок и для материала сварных швов определяются как производные от . Допускаемые напряжения от других видов нагрузок и для материала сварных швов определяются как производные от  : :
 , ,
где 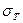 – предел текучести материала; – предел текучести материала;
 – коэффициент запаса прочности, принимаемый обычно равным 1,4…1,6. – коэффициент запаса прочности, принимаемый обычно равным 1,4…1,6.
Условия прочности по этому принципу записываются в следующем виде:
 , ,  . .
где  и и 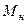 – нормативные продольная сила и изгибающий момент; – нормативные продольная сила и изгибающий момент;
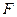 и и 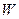 – площадь поперечного сечения рассчитываемого элемента конструкции и момент сопротивления. – площадь поперечного сечения рассчитываемого элемента конструкции и момент сопротивления.
Принцип расчета по предельному состоянию, по расчетным сопротивлениям, используется при проектировании строительных конструкций. При расчете на прочность по этому принципу конструкция рассматривается в своем предельном состоянии, т.е. в таком, при котором она перестает сопротивляться внешним силовым воздействиям и теряет свою несущую способность. Величину напряжений в конструкции определяют при некоторой расчетной нагрузке, которая представляет наибольшее возможное значение нагрузки на конструкцию в период ее эксплуатации, способной привести к нарушению нормальной работы конструкции:
 , ,  , ,  . .
где 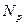 и и  – расчетные нагрузки; – расчетные нагрузки;
 – коэффициент надежности или коэффициент перегрузки, – коэффициент надежности или коэффициент перегрузки,
 = 1,1…1,3; = 1,1…1,3;
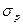 – расчетное напряжение. – расчетное напряжение.
Расчетом предусматривается, что наибольшее расчетное напряжение 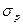 в конструкции должно быть не больше минимально возможного значения предельного напряжения, называемого расчетным сопротивлением R: в конструкции должно быть не больше минимально возможного значения предельного напряжения, называемого расчетным сопротивлением R:
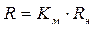 . .
где 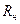 – нормативное сопротивление материала, которое для стали равно – нормативное сопротивление материала, которое для стали равно 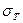 ; ;
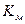 – коэффициент безопасности по материалу, коэффициент однородности материала. – коэффициент безопасности по материалу, коэффициент однородности материала.
Условия прочности по этому принципу записываются в следующем виде:
 , ,  . .
где m
– коэффициент условий работы.
Значения допускаемых напряжений, расчетных сопротивлений, коэф-фициентов  , ,  , m
определяются отраслевыми стандартами. , m
определяются отраслевыми стандартами.
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ
Задача 1.
Две пластины из алюминиевого сплава В92Т соединены встык косым швом, выполненным аргонодуговой сваркой с применением присадочного материала Св-АК5. Толщина пластин 10 мм. Определить угол наклона 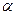 косого шва для обеспечения равнопрочности сварного шва и основного металла. Концы шва выведены на технологические планки. Расчет выполнить по предельному состоянию. косого шва для обеспечения равнопрочности сварного шва и основного металла. Концы шва выведены на технологические планки. Расчет выполнить по предельному состоянию.

Решение
По учебнику [2, с. 324-325. прил. 10 и 12] определяем расчетные сопротивления для шва и основного металла (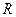 = 190 МПа, = 190 МПа,  = 150МПа и = 150МПа и
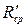 = 90 Мпа). = 90 Мпа).
Проверяем отношение расчетного сопротивления на срез для сварного шва к расчетному нормальному сопротивлению основного металла:
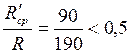 . .
Так как это отношение меньше 0,5, то проводим проверку прочности сварного шва на действие как касательных, так и нормальных напряжений.
Из условия равнопрочности по действию нормальных напряжений находим
 , , 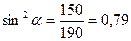 , ,  . .
Из условия равнопрочности по действию касательных напряжений определяем
 , , 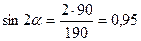 , ,  , ,  . .
Оптимальный угол наклона косого шва 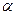 должен быть должен быть 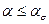 , в то же время , в то же время  и и  . Для наглядности определения оптимального угла . Для наглядности определения оптимального угла 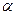 , удовлетворяющего всем этим условиям, изображаем числовую ось и находим область существования , удовлетворяющего всем этим условиям, изображаем числовую ось и находим область существования 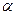 . .

Таким образом, для обеспечения условия равнопрочности сварного шва и основного металла угол наклона косого шва должен быть
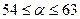 . .
Задача 2.
Сконструировать и рассчитать прикрепление к косынке фермы стержня фермы, состоящего из двух швеллеров № 10, исходя из условия равнопрочности швов и швеллеров. Узел выполнить из стали Ст. 3. Расчет выполнить по допускаемым напряжениям.

Решение.
Размеры швеллера № 10, необходимые для расчета: h = 100 мм, в = 4,5 мм, t = 7,6 мм, b = 46 мм. Площадь поперечного сечения швеллера  = 1090 мм2
. = 1090 мм2
.
В прил. 8 [2, с. 324.] находим, что 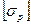 = 160 МПа. Предположим, что сварка произведена вручную электродами обыкновенного качества Э42, тогда = 160 МПа. Предположим, что сварка произведена вручную электродами обыкновенного качества Э42, тогда
 = 0,6 = 0,6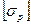 = 96 МПа. = 96 МПа.
Расчет выполняем для одного швеллера, при этом считая, что второй швеллер имеет такие же размеры соединительных сварных швов.
Определяем предельную допустимую нагрузку на один швеллер:
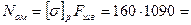 174 400 Н. 174 400 Н.
Предельно допустимая нагрузка на сварные швы
 . .
где 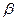 – коэффициент расчетной высоты сварного шва, определяется по – коэффициент расчетной высоты сварного шва, определяется по
[3, c. 27];
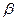 = 0,7 – для ручной и многопроходной автоматической и полуавтоматической сварки, = 0,7 – для ручной и многопроходной автоматической и полуавтоматической сварки,
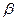 = 0,8 – для 2-х и 3-х проходной полуавтоматической сварки, = 0,8 – для 2-х и 3-х проходной полуавтоматической сварки,
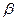 = 0,9 – для 2-х и 3-х проходной автоматической сварки или однопроходной полуавтоматической сварки, = 0,9 – для 2-х и 3-х проходной автоматической сварки или однопроходной полуавтоматической сварки,
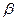 = 1,1 – для однопроходной автоматической сварки. = 1,1 – для однопроходной автоматической сварки.
Допустим, что сварные швы выполнены ручной дуговой сваркой, следовательно, 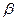 = 0,7. По условию равнопрочности = 0,7. По условию равнопрочности  . Так как в последнем уравнении три неизвестных, то оно имеет множество решений. Выделим из их числа только три. . Так как в последнем уравнении три неизвестных, то оно имеет множество решений. Выделим из их числа только три.
1. Произвольное решение.
Принимаем , что  мм, мм,  мм. мм.
 мм. мм.
2. Решение, обеспечивающее наименьшую массу наплавленного металла.
Для обеспечения этого условия необходимо, чтобы 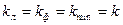 . При этом катет швов определяется из системы уравнений: . При этом катет швов определяется из системы уравнений:
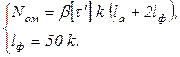
3. Решение, обеспечивающее наименьшие габариты по фланговым швам.
Для обеспечения этого условия необходимо, чтобы 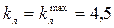 мм, мм,  мм. мм.
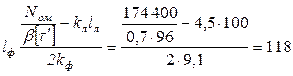 мм. мм.
Задача 3.
Сконструировать и рассчитать прикрепление к косынке фермы стержня фермы, состоящего из двух равнополочных уголков 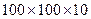 мм, из условия равнопрочности швов и уголков. Узел выполнен из стали 15ХСНД. мм, из условия равнопрочности швов и уголков. Узел выполнен из стали 15ХСНД.

Решение
Из прил. 2 [2, с. 306] выписываем необходимые для расчета характеристики уголка: 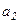 = 28,3 мм, = 28,3 мм,  = 71,7 мм, = 71,7 мм,  = 1920 мм2
. В прил. 8 [2] находим, что для стали 15ХСНД = 1920 мм2
. В прил. 8 [2] находим, что для стали 15ХСНД  = 225 МПа. = 225 МПа.
Полагаем, что присоединение уголка осуществляется лобовым и двумя фланговыми швами, сварка полуавтоматическая однопроходная. Тогда
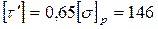 МПа. МПа.
Допустимое усилие на один уголок
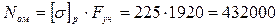 Н. Н.
Размеры швов можно определить из системы уравнений:
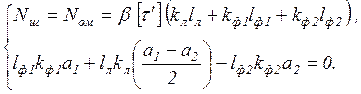
1. Решение, обеспечивающее наименьшую массу наплавленного металла.
Принимаем, что 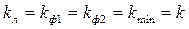 . .
Катет швов определяется из системы уравнений:

 /см. задачу 2/, /см. задачу 2/,  мм. мм.
Решая вышеприведенную систему уравнений, получаем 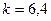 мм, мм,  мм, мм,  мм. мм.
2. Решение, обеспечивающее наименьшие габариты по фланговым швам.
Для обеспечения этого условия необходимо, чтобы 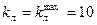 мм, мм,  мм, мм, 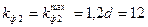 мм. мм.
Длины швов  и и  определяются из системы уравнений: определяются из системы уравнений:
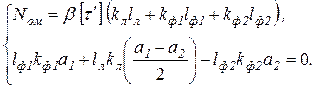
Подставив вышепринятые значения катетов в систему уравнений, получим  мм, мм,  мм. мм.
Задача 4.
Сконструировать и рассчитать присоединение втавр элемента таврого соединения из стали Ст. 3, растягиваемого усилием  кН, кН,  мм, мм,  мм, мм,  мм, мм,  МПа. МПа.

Решение
Полагаем, что прикрепление осуществляется по всему периметру сечения тавра угловыми швами. Сварка ручная дуговая электродами обыкновенного качества Э42. Следовательно, 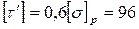 МПа. МПа.
1-й вариант решения. Согласно этому варианту, все усилие, приходящееся на поперечное сечение присоединяемого тавра сложной конфигурации, разбивается на усилия, приходящиеся на отдельные простые элементы. А затем, полагая, что усилие, приходящееся на каждый простой элемент сечения, воспринимают сварные швы, присоединяющие это сечение, определяют размеры сварных швов (чаще всего катет).
Определяем напряжения в основном материале присоединяемого узла:
 МПа. МПа.
Усилия, воспринимаемы стенкой и полкой тавра:
 Н, Н,
 Н. Н.
Катеты швов, присоединяющие полку и стенку, определяем из следующего выражения:
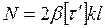 , ,
где  – усилие, воспринимаемое простым элементом разветвленного сечения; – усилие, воспринимаемое простым элементом разветвленного сечения; 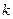 – катет шва; – катет шва;  – длина шва. – длина шва.
Так как сварка ручная дуговая, то 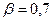 . .
 мм, мм,
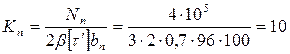 мм. мм.
2-й вариант решения. При решении данной задачи вторым способом считается, что размеры катетов швов, приваривающих отдельные простые элементы сложного разветвленного сечения, соотносятся между собой так же, как толщины этих элементов.
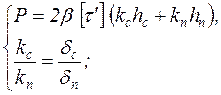
 , ,  , ,
 мм, мм,
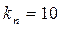 мм. мм.
Задача 5.
Кронштейн, сваренный из двух пластин стыковым швом № 1, присоединен к соседнему элементу конструкции в тавр угловыми швами № 2 и нагружен силой 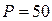 кН, направленной под углом кН, направленной под углом  к его оси. Конструкция изготовлена из стали Ст. 3. Провести проверочный расчет сварных швов № 1 и № 2: к его оси. Конструкция изготовлена из стали Ст. 3. Провести проверочный расчет сварных швов № 1 и № 2:  мм, мм, 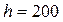 мм, мм, 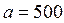 мм, мм,  мм, мм,
 мм: мм:  мм. мм.

Решение
Полагаем, что швы выполнены ручной дуговой сваркой, электродами обыкновенного качества Э42. Тогда допускаемые напряжения  МПа, МПа, 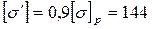 МПа, МПа,  . .
Производим проверочный расчет стыкового шва № 1. Сварной шов № 1 воспринимает следующие нагрузки:
– продольную силу 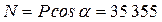 Н, Н,
– поперечную нагрузку  Н, Н,
– изгибающий момент 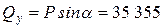 Н×мм. Н×мм.
Эпюры напряжений от перечисленных нагрузок в сечении шва № 1 будут иметь следующий вид:
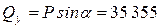 ; ; 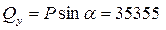 ; ;  . .

Наиболее опасными с точки зрения величины действующих напряжений в сечении шва № 1 будут точки 1 и 2.
Нормальные напряжения в т. 1 шва № 1:
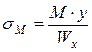 , ,
где  – момент сопротивления поперечного сечения шва; – момент сопротивления поперечного сечения шва;
 , ,
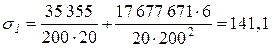 МПа. МПа.
По условию прочности это напряжение не должно превышать допускаемого нормального для сварного шва  МПа. Так как МПа. Так как 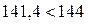 , то прочность в т. 1 сечения шва № 1 удовлетворительная. , то прочность в т. 1 сечения шва № 1 удовлетворительная.
В т. 2 шва № 1 действуют нормальные и касательные напряжения, поэтому для оценки прочности в этой точке необходимо определить эквивалентные напряжения:
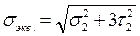 , , 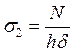 , ,  , ,
где – максимальный статический момент отсеченной части сечения шва; – максимальный статический момент отсеченной части сечения шва;
 – момент инерции сечения шва. – момент инерции сечения шва.
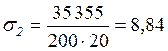 МПа, МПа,
 мм3
, мм3
,
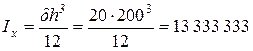 мм4
, мм4
,
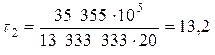 МПа, МПа,
 МПа МПа  . .
Таким образом, прочность шва № 1 удовлетворительная.
Производим проверочный расчет угловых швов № 2. Сварные швы № 2 воспринимают следующие нагрузки:
– продольную силу  Н, Н,
– поперечную нагрузку 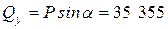 Н, Н,
– изгибающий момент  Н×мм. Н×мм.
Эпюры напряжений от перечисленных нагрузок в расчетном сечении швов №2 будут иметь следующий вид:
 , , 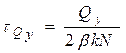 , , 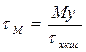 . .
где  – осевой момент инерции контура швов в сечении II – II. – осевой момент инерции контура швов в сечении II – II.

Направление действия касательных напряжений показано на рисунке:

Как видно из эпюр касательных напряжений, в угловых швах наиболее нагруженными точками являются периферийные т. 1. Напряжение в т. 1 от продольной нагрузки
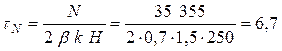 МПа, МПа,
от поперечной нагрузки –
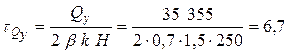 МПа, МПа,
от изгибающего момента –
 , ,  , ,
 МПа. МПа.
Определяем результирующее напряжение в т. 1 углового шва:
 МПа МПа . .
Следовательно, прочность сварных швов № 2 неудовлетворительная. Для снижения действующих в них расчетных напряжений и повышения несущей способности швов необходимо увеличить катет.
Задача 6.
Консоль двутаврового сечения приварена к колонне угловыми швами по всему контуру своего сечения и нагружена силой 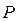 , как показано ниже на рисунке Конструкция изготовлена из стали Ст. 3, швы выполнены ручной дуговой сваркой электродами обыкновенного качества Э42. Определить катеты швов, приваривающих полку и стенку. , как показано ниже на рисунке Конструкция изготовлена из стали Ст. 3, швы выполнены ручной дуговой сваркой электродами обыкновенного качества Э42. Определить катеты швов, приваривающих полку и стенку.  МПа, МПа, 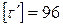 МПа, МПа,  кН, кН,  мм, мм,  мм, мм, 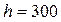 мм, мм,  мм, мм, 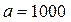 мм. мм.

Решение
Определяем действующие нагрузки на угловые швы. В плоскости присоединения действуют:
– поперечная нагрузка  кН, кН,
– изгибающий момент  Н×мм. Н×мм.
Катеты швов определяем из системы уравнений:
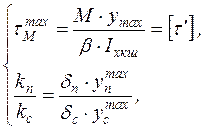
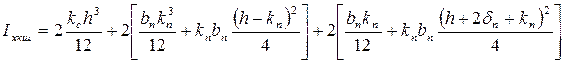 . .
Пренебрегая слагаемыми, содержащими 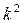 , ,  и т. д., получаем и т. д., получаем
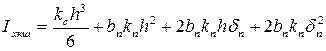 , ,
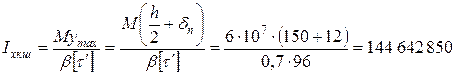 мм4
, мм4
,

Решая последнюю систему уравнений, находим 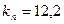 мм, мм, 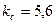 мм. мм.
Так как при расчете угловых швов не учитывалась поперечная нагрузка, которую по условной методике расчета воспринимают только вертикальные швы, производим проверку выбранных швов по расчетным напряжениям в т. 1 (см. рис. выше). В этой точке действуют касательные напряжения от момента 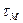 и от поперечной нагрузки и от поперечной нагрузки 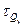 : :
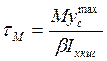 , ,

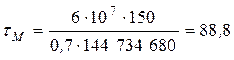 МПа, МПа,
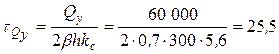 МПа. МПа.
Так как напряжения действуют во взаимно перпендикулярных направлениях, то результирующее напряжение
 МПа МПа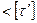 . .
Результирующее напряжение в т. 1 углового шва, приваривающего стенку, не превышает допускаемого 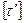 , следовательно, прочность выбранных швов удовлетворительная. , следовательно, прочность выбранных швов удовлетворительная.
Задача 7.
Решить предыдущую задачу из условия, обеспечивающего равнопрочность сварных швов и основного металла двутавра.
Решение
При решении этой задачи считаем, что нагрузка 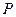 на консоль двутаврового сечения не известна. Величина этой нагрузки является предельно допустимой для основного металла двутавра с учетом схемы нагружения и допускаемых напряжений на консоль двутаврового сечения не известна. Величина этой нагрузки является предельно допустимой для основного металла двутавра с учетом схемы нагружения и допускаемых напряжений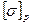 и и 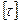 . .

Предельно допускаемую нагрузку определяем из условия прочности в опасных точка 1, 2 и 3 сечения двутавра.
В т. 1 действуют максимальные нормальные напряжения от изгибающего момента (см. эпюры напряжений).
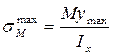 , ,  , , 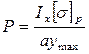 , ,
 , ,
 мм4
. мм4
.
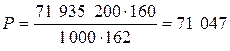 Н. Н.
В т. 2 действуют нормальные напряжения от изгибающего момента, величина которых несколько ниже, чем в т. 1, однако в т. 2 действуют еще касательные напряжения от поперечной нагрузки, определяемые по формуле Журавского. Прочность в т. 2 оцениваем по эквивалентным напряжениям:
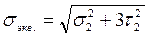 , ,  , ,
где 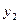 – ордината точки 2; – ордината точки 2;
 , ,
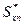 – статический момент отсеченной части сечения (в данном случае - полки), – статический момент отсеченной части сечения (в данном случае - полки),
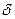 – толщина сечения двутавра в месте отсечения. – толщина сечения двутавра в месте отсечения.
Согласно схеме нагружения консоли 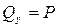 и и 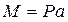 . .
 мм3
, мм3
,
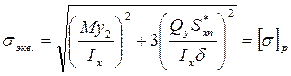 , ,
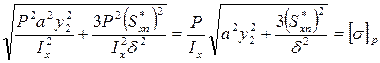 , ,
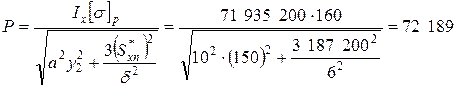 Н. Н.
В т. 3 действуют только касательные напряжения, однако величина их наибольшая (см. эпюры напряжений).
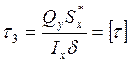 , ,
 мм3
, мм3
,
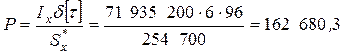 Н. Н.
Таким образом, наименьшую нагрузку P
по условию прочности допускает т. 1, следовательно, предельно допускаемую нагрузку на консоль определяем
из условия прочности в т. 1, т.е.  Н. Далее задача решается так же, как и задача 6. Пользуясь приведенной в этой задаче программой, находим Н. Далее задача решается так же, как и задача 6. Пользуясь приведенной в этой задаче программой, находим  мм, мм,  мм. мм.
Задача 8.
Определить величину предельной нагрузки  , приложенной к кронштейну (см. рис.) под углом , приложенной к кронштейну (см. рис.) под углом  к его оси. Кронштейн к соединяемому элементу конструкции приварен внахлестку угловым швом по всему контуру присоединения. Материал кронштейна – сталь Ст. 3, сварка произведена вручную электродами обыкновенного качества, к его оси. Кронштейн к соединяемому элементу конструкции приварен внахлестку угловым швом по всему контуру присоединения. Материал кронштейна – сталь Ст. 3, сварка произведена вручную электродами обыкновенного качества,  мм, мм, 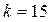 мм, мм,  , ,  мм, мм,  мм, мм, 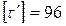 МПа. МПа.

Решение
Определяем координату центра тяжести контура швов 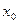 : :
 , ,
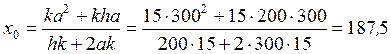 мм. мм.
Определяем действующие нагрузки в центре тяжести контура сварных швов:
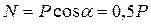 ; ;
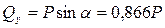 ; ;
 . .
Расчет сварных швов производим методом осевого момента инерции. Согласно этому методу, напряжения в отдельных точках угловых швов от момента, действующего в плоскости контура сварных швов, пропорциональны расстоянию до этих точек от оси 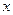 . Поэтому максимальные напряжения от момента определяются по следующей формуле: . Поэтому максимальные напряжения от момента определяются по следующей формуле:
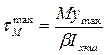 , ,

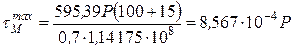 МПа. МПа.
Напряжения в швах от продольной силы
 МПа. МПа.
Напряжения в швах от поперечной нагрузки
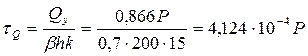 МПа. МПа.
Так как напряжения от продольной нагрузки и момента действуют в одном направлении, а напряжения от поперечной силы им перпендикулярны, то результирующее напряжение

Результирующее напряжение не должно превышать допускаемого напряжения на срез для сварного шва  . Определяем величину предельной нагрузки . Определяем величину предельной нагрузки  на сварные швы: на сварные швы:
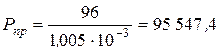 Н. Н.
Задача 9.
Две пластины из стали Ст. 3 сварены встык ручной дуговой сваркой электродом Э42. Определить допустимое усилие на сварное соединение при статической нагрузке; при переменной нагрузке, когда усилие 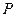 изменяется от изменяется от  до до 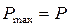 . .

Решение
Для стали Ст. 3 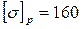 МПа, при ручной дуговой сварке электродами обыкновенного качества Э42 МПа, при ручной дуговой сварке электродами обыкновенного качества Э42  МПа. МПа.
При статической нагрузке допустимое усилие на сварной шов
 . .
При динамической нагрузке допустимое усилие на сварной шов определяется по следующей формуле:
 , ,
в околошовной зоне
 . .
Коэффициент уменьшения допускаемого напряжения при расчете на усталость
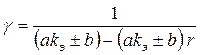 , ,
где 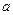 и и  – коэффициенты, устанавливаемые нормами проектирования; – коэффициенты, устанавливаемые нормами проектирования;
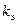 –эффективный коэффициент концентрации напряжений; –эффективный коэффициент концентрации напряжений;
 – характеристика цикла нагружения. – характеристика цикла нагружения.
 . .
По табл. 10.10 [1, с. 240] принимаем 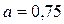 , , 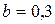 . Эффективный коэффициент концентрации напряжений . Эффективный коэффициент концентрации напряжений 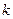 , определяем по табл. 1010.11 , определяем по табл. 1010.11
[1, с. 240–242]. Для шва  , для основного металла , для основного металла  . .
Так как по условию задачи  , а среднее напряжение /усилие/ цикла нагружения больше нуля, то коэффициенты , а среднее напряжение /усилие/ цикла нагружения больше нуля, то коэффициенты
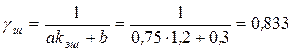 , ,
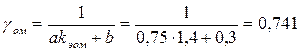 , ,
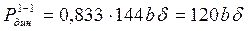 , ,
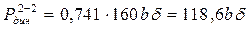 . .
Основной материал, прилегающий к сварному шву, оказался более чувствительной зоной к динамическим нагрузкам, поэтому допустимое усилие на сварное соединение  . .
Задача 10.
В раскосе фермы действует переменное усилие, изменяющееся от 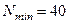 кН до кН до  кН. Раскос состоит из двух швеллеров, подобрать их сечение и рассчитать присоединение швеллера к косынке фермы одним лобовым и двумя фланговыми швами. Ферма изготовлена из стали 15ХСНД, швы сварены вручную электродами Э50. кН. Раскос состоит из двух швеллеров, подобрать их сечение и рассчитать присоединение швеллера к косынке фермы одним лобовым и двумя фланговыми швами. Ферма изготовлена из стали 15ХСНД, швы сварены вручную электродами Э50.

Решение
В прил. 8 [2, с. 324] находим  МПа. Так как сварка ручная электродом обыкновенного качества, то МПа. Так как сварка ручная электродом обыкновенного качества, то
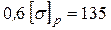 МПа МПа . .
Определяем характеристику цикла нагружения:
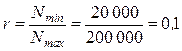 . .
По прил. 7 [2, с. 319–323] определяем, что 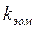 максимален в местах перехода от фланговых швов к основному металлу и равен максимален в местах перехода от фланговых швов к основному металлу и равен  , принимаем , принимаем 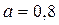 , , 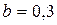 . .
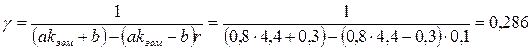
Так как на одни швеллер действует максимальная нагрузка 200 кН, требуемое сечение швеллера
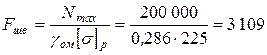 мм2
. мм2
.
По прил. 2 [2, с. 305–312] выбираем швеллер № 24а (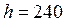 мм, мм,  мм, мм,  мм). мм).
Определяем размеры швов.
Эффективные коэффициенты концентрации напряжений по расчетным сечениям сварных швов.
для лобового шва  , ,
для фланговых швов  . .
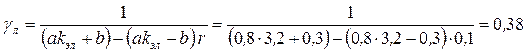 , ,
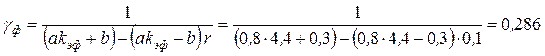
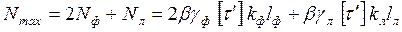 . .
Для ручной дуговой сварки 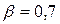 . Принимая, . Принимая, 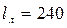 мм, мм,
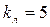 мм, мм,  мм, получаем: мм, получаем:
 мм. мм.
Задача 11.
С помощью линий влияния определить изгибающий момент и поперечную нагрузку в сечениях A, B и C балки.

Решение
1. Построение линий влияния  и и 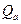 : :
 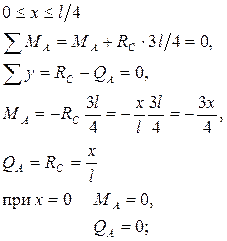
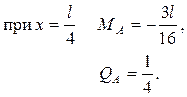


2. Построение линий влияния 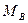 и и  : :

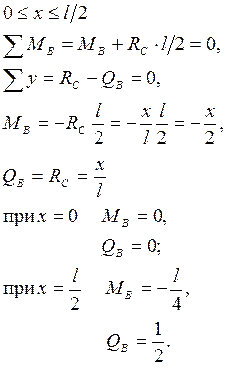

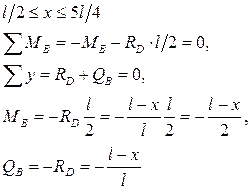
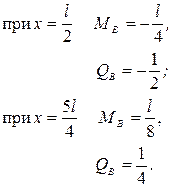
3. Построение линий влияния  и и 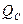 : :

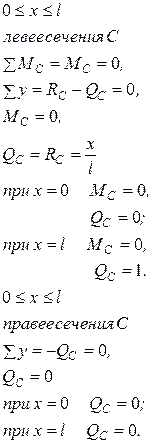 
 
 
4. Определение величины действующих нагрузок в сечениях A, B и C балки.
Величину действующих нагрузок по известным линиям влияния можно определить по формуле
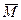 или или  , ,
где 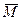 или или  – действующий в сечении момент или сила; – действующий в сечении момент или сила;
 – сосредоточенные силы; – сосредоточенные силы;
 – интенсивность распределения нагрузки; – интенсивность распределения нагрузки;
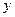 – ордината соответствующей линии влияния ( – ордината соответствующей линии влияния (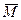 или или  ) под сосредоточенной нагрузкой; ) под сосредоточенной нагрузкой;
 – алгебраическая сумма площадей под соответствующей линией влияния на длине действия распределенной нагрузки. – алгебраическая сумма площадей под соответствующей линией влияния на длине действия распределенной нагрузки.
Определяем
 , ,
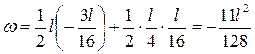 , ,
 . .
Определяем
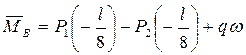 , ,
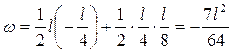 , ,
 . .
Определяем
 , ,
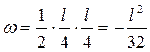 , ,
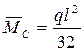 . .
Определяем  . Так как в сечении А приложена сосредоточенная сила, то величина действующей поперечной нагрузки в этом сечении неопределенна (изменяется скачком). Поэтому определенной является поперечная нагрузка левее сечения А и правее сечения А. Разность между этими поперечными нагрузками должна быть равна по величине сосредоточенной силе: . Так как в сечении А приложена сосредоточенная сила, то величина действующей поперечной нагрузки в этом сечении неопределенна (изменяется скачком). Поэтому определенной является поперечная нагрузка левее сечения А и правее сечения А. Разность между этими поперечными нагрузками должна быть равна по величине сосредоточенной силе:
 , ,
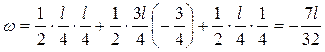 , ,
 . .
 , ,
 , ,
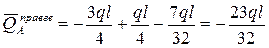 , ,
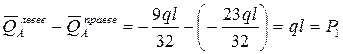 . .
Определяем
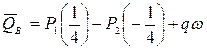 , ,
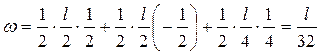 , ,
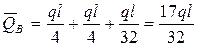 . .
Определяем 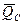 . В сечении С приложена сосредоточенная сила – реакция опоры С. Поэтому в сечении С так же, как и в сечении А, определяем два значения поперечной нагрузки: одно левее точки С, а другое правее. Разность между этими поперечными нагрузками должна быть равна реакции опоры: . В сечении С приложена сосредоточенная сила – реакция опоры С. Поэтому в сечении С так же, как и в сечении А, определяем два значения поперечной нагрузки: одно левее точки С, а другое правее. Разность между этими поперечными нагрузками должна быть равна реакции опоры:
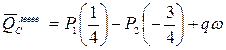 , ,
 , ,
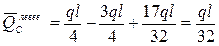 , ,
 , ,
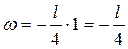 , ,
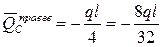 , ,
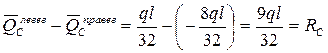 . .
Задача 12.
С помощью линий влияния определить экстремальные нагрузки в стержнях 1–2 и 1–3 фермы,  м, м,  мм, мм, 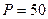 кН, кН, 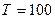 кН. кН.

Решение
Для определения экстремальных усилий в стержнях 1 – 2 и 1 – 3 фермы строим линии влияния продольных усилий в этих стержнях, единичную нагрузку при этом перемещаем по нижнему поясу фермы, т. е. по тому, где приложены реальные нагрузки  и и 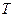 . .
Строим линию влиянии продольных усилий в стержне 1 – 2:
 

 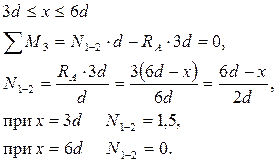
Строим линию влияния продольных усилий в стержне 1–3:

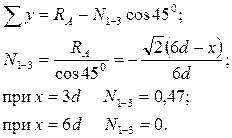
Располагаем подвижную нагрузку 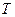 в наиболее невыгодное положение над соответствующей линией влияния и определяем экстремальные значения усилий в наиболее невыгодное положение над соответствующей линией влияния и определяем экстремальные значения усилий 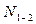 и и  : :
 ; ;
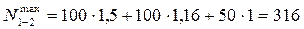 кН; кН;
 ; ;
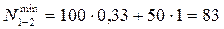 кН; кН;
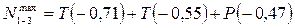 ; ;
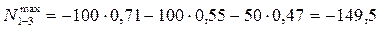 кН; кН;
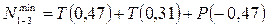 ; ;
 кН. кН.
Библиографический список
1. Николаев, Г.А. Расчёт, проектирование и изготовление сварных конструкций: учеб. пособие для студентов машиностроит. вузов и фак. /
Г.А. Николаев, С.А. Куркин, В.А. Винокуров, 1971. – 760 с.
2. Николаев, Г.А. Сварные конструкции. Технология изготовления. Автоматизация производства и проектирование сварных конструкций: учеб. пособие для вузов по специальности «Технология сварочного производства» / Г.А. Николаев, С.А. Куркин, В.А. Винокуров, 1983. – 344 с.
3. Лопаев, Б.Е. Линии влияния в расчетах сварных конструкций: учеб. пособие для вузов по направлению 651400 «Машиностроительные технологии и оборудование по специальности 120500 / Б.Е. Лопаев, Е.Н. Еремин, 2004. – 94 с.
|