| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ
технологический институт
ОРЛОВСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО
УНИВЕРСИТЕТА
Методические указания
для самостоятельной работы студентов
по дисциплине: «Математика»
I курс
для специальностей:
080501 – «Менеджмент (по отраслям)»
151001 – «Технология машиностроения»
230106 – «Техническое обслуживание средств
вычислительной техники и компьютерных сетей»
260202 – «Технология хлеба, кондитерских и макаронных изделий»
Составитель:
преподаватель факультета СПО ТИ ОрелГТУ
Сосова Т.В.
Утверждено:
на заседании кафедры естественнонаучных и
математических дисциплин
(протокол №____ от «____»_______200___г.)
Зав. кафедрой_________________Быкова В.Н.
| Наименование разделов и тем
|
Вид самостоятельной работы
|
Количество часов
|
| Тема 1. Приближенные вычисления и вычислительные средства.
|
- решение упражнений: [5] гл. I № 9, 10, 130, 131, 132, 133, 135, 36, 42, 69;
- подготовка к зачетным и практическим работам: [1] § 2, 3, 4, 5, 6, 10, 14;
- рефераты: «Математика и жизнь», «Математика в быту», «Математика и техника» (по желанию студентов).
|
4
|
| Тема 2. Функции, их свойства и графики.
|
- решение упражнений по теме: [5] гл. IV № 14, 30, 33, 38, 50-52, 77, 79, 74, 75;
- подготовка к зачетным и практическим работам: [1] § 16, 19 (1-4), 20, 14(4);
- домашняя зачетная работа «Построение графиков функций методом элементарных преобразований».
|
4
|
| Тема 3. Показательная, логарифмическая и степенная функции.
|
- решение упражнений по теме: [5] гл. V № 9, 24, 30, 32, 77, 103, 100, 102,
114, 178, 163, 175, 139, 145, 161.
- подготовка к зачетным и практическим работам: [1] § 21, 22, 23, 20.
- домашние зачетные работы «Элементарные преобразования графиков показательной и логарифмической функций»;
- подготовка и участие студентов в познавательной игре «Степень. Показатель. Логарифм».
|
6
|
| Тема 4.
Прямые и плоскости в пространстве.
|
- решение упражнений по теме: [5] гл. X № 89, 101, 8, гл. III № 51; [4] § 16 № 5(1, 2), 27, 29, 32, 8, 52, 7, 50, 10, 38, 46, 48, 45.
- подготовка к зачетным и практическим работам: [4] п. 130-133, 138-141, 142-149, 166-167, 163;
- изготовление стереометрических моделей к задачам (по желанию студентов).
|
6
|
| Тема 5. Тригонометрические функции.
|
- решение упражнений по теме: [5] гл. VI № 54, 98, 132, 161, 171, 164, 158, 168, 31, 189, 81,. 75;
- подготовка к зачетным и практическим работам: [1] § 24, 25, 27, 28;
- подготовка к контрольной работе;
- домашние зачетные работы: «Построение графиков функций y = cosx и y = сtgx»; «Построение графиков тригонометрических функций методом элементарных преобразований».
|
4
|
| Тема 6.
Векторы и координаты.
|
- решение упражнений по теме: [5] гл. II № 440, 43, 119, 122, 152, 140, 149, 159
- подготовка к зачетным и практическим работам: [3] § 1-6, 8-10, 11-12, 26-31, 32-33, 37, 38, 40, 42
- подготовка и участие студентов в познавательной игре «Линии и поверхности».
|
6
|
| Тема 7. Производная и ее приложения.
|
- решение упражнений по теме: [5] гл. VIII № 71, 86, 118, 27, 38, 52, 155, 141, 8, 14, 13, 9, 15, 17, 209, 216, 250, 255.
- подготовка к зачетным и практическим работам: [1] § 29-34, 36-37, 40, 35.
- подготовка к контрольной работе: [5]гл. VIII № 246, 227.
- подготовка и участие в познавательной игре «Производная и ее приложения»;
- домашняя зачетная работа «Исследование функции и построение ее графика».
|
10
|
| Тема 8. Интегралы и его приложения.
|
- решение упражнений по теме: [5] гл. IX № 58, 78, 89, 176, 181, 217, 219, 233,
- подготовка к зачетным и практическим работам: [1] § 41, 42, 43, 44, 45, 47, 48.
- подготовка и участие в познавательной игре «Интеграл и его приложения»;
- реферативная работа по теме «Технические приложения определенных и неопределенных интегралов» (по желанию студентов).
|
6
|
| Тема 9. Геометрические тела и поверхности.
Объемы и площади поверхностей геометрических тел.
|
- решение упражнений по теме: [5] гл. X № 33, 51, 74, 25, 90, 84, 93, 105,108, 131;
- решение упражнений по теме: [5] гл. № 31, 40, 18, 35, 58, 61, 141, 172, 182;
- подготовка к зачетным и практическим работам: [4] п. 194-201, 202-210.
- изготовление стереометрических моделей к задачам (по желанию студентов).
|
6
|
Тема: «Приближенные вычисления и вычислительные средства» (4 часа)
Требования к знаниям и умениям:
- выполнять с заданной точностью на ИМК арифметические действия;
- вычислять значения элементарных функций;
- решать линейные и квадратные уравнения и неравенства;
- решать простейшие уравнения и неравенства со знаком модуля.
Виды самостоятельной работы студентов:
1. решение упражнений: [5] гл. I № 9, 10, 130, 131, 132, 133, 135, 36, 42, 69;
- подготовка к зачетным и практическим работам: [1] § 2, 3, 4, 5, 6, 10, 14;
- рефераты «Математика и жизнь», «Математика в быту», «Математика и техника» (по желанию студентов).
Тема: «Функции, их свойства и графики» (4 часа)
Требования к знаниям и умениям:
- пользоваться различными способами задания функции;
- находить область определения функции;
- строить графики известных элементарных функций;
- применять геометрические преобразования (сдвиг и деформация) при построении графиков;
- устанавливать по графику функции ее важнейшие свойства (монотонность, нечетность, периодичность, непрерывность, знакопостоянство), находить значение функции, заданной аналитически, по значению аргумента и наоборот;
- вычислять простейшие пределы функций в точке и на бесконечности;
- решать рациональные неравенства методом интервалов.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. IV № 14, 30, 33, 38, 50-52, 77, 79, 74, 75;
2. подготовка к зачетным и практическим работам: [1] § 16, 19 (1-4), 20, 14(4);
3. домашняя зачетная работа «Построение графиков функций методом элементарных преобразований».
Тема: «Показательная, логарифмическая и степенная функции» (6 часов)
Требования к знаниям и умениям:
- строить графики степенных, показательных и логарифмических функций;
- решать несложные уравнения, приводимые к видам:
a f(x)
= a g(x)
; a f(x)
= b ; log a
f(x) = b ; log a
f(x) = log a
g(x);
- решать несложные неравенства, приводимые к видам:
a f(x)
< a g(x)
; log a
f(x) < log a
g(x);
- вычислять значения показательных и логарифмических выражений с
помощью основных тождеств и вычислительных средств.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. V № 9, 24, 30, 32, 77, 103, 100, 102, 114, 178, 163, 175, 139, 145, 161.
2. подготовка к зачетным и практическим работам [1] § 21, 22, 23, 20.
3. домашние зачетные работы «Элементарные преобразования графиков показательной и логарифмической функций»;
4. подготовка и участие студентов в познавательной игре «Степень. Показатель. Логарифм».
Тема: «Прямые и плоскости в пространстве» (6 часов)
Требования к знаниям и умениям:
- знать основные понятия стереометрии, аксиомы стереометрии следствия
из них;
- устанавливать в пространстве параллельность прямых, прямой и
плоскости, двух плоскостей, используя признаки и основные теоремы о
параллельности;
- применять признаки перпендикулярности прямых, прямой и плоскости,
двух плоскостей, теорему о трех перпендикулярах, признак
перпендикулярности для вычисления углов в пространстве;
- выполнять сечение многогранников и рассчитывать площадь сечения.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. X № 89, 101, 8, гл. III № 51; [4] § 16 № 5(1, 2), 27, 29, 32, 8, 52, 7, 50, 10, 38, 46, 48, 45.
2. подготовка к зачетным и практическим работам [4] п. 130-133, 138-141, 142-149, 166-167, 163;
3. изготовление стереометрических моделей к задачам (по желанию студентов).
Тема: «Тригонометрические функции» (4 часа)
Требования к знаниям и умениям:
- знать формулы перевода градусной меры угла в радианную и обратно;
- знать определения синуса, косинуса, тангенса и котангенса числа;
- вычислять значения тригонометрических функций с заданной степенью
точности;
- преобразовывать тригонометрические выражения, используя
тригонометрические формулы;
- строить графики тригонометрических функций и на них иллюстрировать
свойства функций;
- знать обратные тригонометрические функции;
- решать тригонометрические уравнения и неравенства.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. VI № 54, 98, 132, 161, 171, 164, 158, 168, 31, 189, 81,. 75;
2. подготовка к зачетным и практическим работам [1] § 24, 25, 27, 28;
3. подготовка к контрольной работе;
4. домашние зачетные работы «Построение графиков функций y = cos x и y = ctg x»; «Построение графиков тригонометрических функций методом элементарных преобразований».
Тема: «Векторы и координаты» (6 часов)
Требования к знаниям и умениям:
- выполнять действия над векторами;
- выполнять разложение вектора на составляющие;
- решать задачи, связанные со сложением сил, скоростей, вычисление длин
отрезков и углов;
- составлять уравнения прямой на плоскости;
- знать определения и уравнения линий второго порядка;
- определять координаты векторов, их длины, углы между векторами.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. II № 440, 43, 119, 122, 152, 140, 149, 159
2. подготовка к зачетным и практическим работам [3] § 1-6, 8-10, 11-12, 26-31, 32-33, 37, 38, 40, 42
3. подготовка и участие студентов в познавательной игре «Линии и поверхности».
Тема: «Производная и ее приложения» (10 часов)
Требования к знаниям и умениям:
- знать определения производной, дифференциала функции, их
геометрический и физический смысл;
- знать правила и формулы дифференцирования функций;
- знать условия монотонности функции;
- уметь дифференцировать функции, используя таблицу производных и
правила дифференцирования, находить производные сложных функций
вида f(ax + b);
- находить угловой коэффициент касательной, составлять уравнения
касательной и нормами к графику функции в данной точке;
- применять производную для исследования функции и для построения ее
графика;
- находить дифференциал функции и с его помощью вычислять
приближенные значения функции, погрешностей;
- решать несложные задачи на экстремум.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. VIII № 71, 86, 118, 27, 38, 52, 155, 141, 8, 14, 13, 9, 15, 17, 209, 216, 250, 255.
2. подготовка к зачетным и практическим работам [1] § 29-34, 36-37, 40, 35.
3. подготовка к контрольной работе [5]гл. VIII № 246, 227.
4. подготовка и участие в познавательной игре «Производная и ее приложения»;
5. домашняя зачетная работа «Исследование функции и построение ее графика».
Тема: «Интеграл и его приложения» (6 часов)
Требования к знаниям и умениям:
- находить неопределенные интегралы, сводящиеся к табличным, с
помощью основных свойств и простейших преобразований;
- выделять первообразную, восстанавливать закон движения по заданной
скорости, скорость по ускорению, работу по переменной силе и т.д.;
- вычислять определенный интеграл с помощью основных свойств и
формулы Ньютона-Лейбница;
- находить площади плоских фигур;
- решать простейшие прикладные задачи, сводящиеся к нахождению
интеграла.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. IX № 58, 78, 89, 176, 181, 217, 219, 233,
2. подготовка к зачетным и практическим работам [1] § 41, 42, 43, 44, 45, 47, 48.
3. подготовка и участие в познавательной игре «Интеграл и его приложения»;
4. реферативная работа по теме «Технические приложения определенных и неопределенных интегралов» (по желанию студентов).
Тема: «Геометрические тела и их поверхности» (6 часов)
Требования к знаниям и умениям:
- вычислять и изображать основные элементы прямых призм, пирамид, цилиндра, конуса и шара;
- знать определения многогранников, правильных многогранников;
- знать понятие тела вращения и поверхности вращения;
- знать свойства геометрических тел и их поверхностей.
- находить объемы прямой призмы, пирамиды, цилиндра, конуса, шара и его частей;
- находить площади поверхностей геометрических тел;
- знать понятия объема и поверхности геометрического тела;
- знать формулы для вычисления объемов и поверхностей геометрических тел.
Виды самостоятельной работы студентов:
1. решение упражнений по теме [5] гл. X № 33, 51, 74, 25, 90, 84, 93, 105,108, 131;
2. решение упражнений по теме [5] гл. № 31, 40, 18, 35, 58, 61, 141, 172, 182;
3. подготовка к зачетным и практическим работам [4] п. 194-201, 202-210.
4. изготовление стереометрических моделей к задачам (по желанию студентов).
Практические работы
Тема: «Приближенные вычисления и вычислительные средства»
1. Абсолютная и относительная погрешности.
2. Решение квадратных уравнений и неравенств, уравнений и неравенств с модулем.
3. Вычисления на ИМК.
Тема: «Функции, их свойства и графики»
4. Решение рациональных неравенств методом интервалов.
5. Вычисление пределов функций.
Тема: «Степенная, показательная и логарифмическая функции»
6. Степень и корень n-ой степени.
7. Иррациональные ур-ия и нер-ва.
8. Вычисление значений логарифмов и логарифмических выражений.
9. Степень. Показатель. Логарифм.
10. Уравнения и неравенства: иррациональные, показательные и логарифмические.
Тема: «Тригонометрические функции»
11. Тригонометрические функции числового аргумента
12. Решение тригонометрических ур-ий и нер-в разного вида.
Тема: «Прямые и плоскости в пространстве»
13. Аксиомы стереометрии и следствия из них.
Тема: «Векторы и координаты»
14. Действия над векторами в координатной форме.
15. Уравнения прямой.
16. Решение задач о линиях 1-го и 2-го порядка.
Тема: «Производная и ее приложения»
17.Вычисление производных.
18.Дифференциал и его приложения.
Тема: «Интеграл и его приложения»
19. Вычисление неопределенных интегралов.
20. Вычисление определенных интегралов.
Тема: «Геометрические тела и их поверхности»
21. Вычисление объемов и площадей поверхностей геометрических тел.
Задания
для проведения экзамена по математике
в форме тестирования (1 семестр).
1. Найдите относительную погрешность числа
x =
a ±
h с точностью до сотых.
1) х = 2,1 ± 0,01; 6) х = 7,1 ± 0,01;
2) х = 3,1 ± 0,01; 7) х = 8,1 ± 0,01;
3) х = 4,1 ± 0,01; 8) х = 9,1 ± 0,01;
4) х = 5,1 ± 0,01; 9) х = 10,1 ± 0,01;
5) х = 6,1 ± 0,01; 10) х = 11,1 ± 0,01.
2. Найдите область определения функции.
1)  ; 6) ; 6)  ; ;
2)  ; 7) ; 7)  ; ;
3)  ; 8) ; 8)  ; ;
4)  ; 9) ; 9)  ; ;
5)  ; 10) ; 10)  . .
3. Найдите значение выражения
.
а) 1) 2-2
; 2) 3-2
; 3) 4-2
; 4) 5-2
; 5) 2-3
;
6)  ; 7) ; 7)  ; 8) ; 8)  ; 9) ; 9)  ; 10) ; 10) 
б) 1)  ; 2) ; 2) 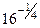 ; 3) ; 3) 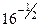 ; 4) ; 4) 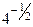 ; 5) ; 5) 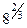 ; ;
6) 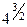 ; 7) ; 7)  ; 8) ; 8) 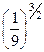 ; 9) ; 9) 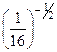 ; 10) ; 10) 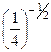
в) 1) log2
2; 2) log2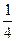 ;
3) log2
8; 4) log3 ;
3) log2
8; 4) log3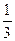 ;
5) log3 ;
5) log3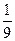 ; ;
6) log3
27; 7) lg0,1; 8) lg100; 9) lg0,001; 10) log5
25
г) 1) 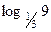 ; 2) ; 2) 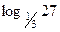 ; 3) log9
3; 4) log27
3; 5) log8
2; ; 3) log9
3; 4) log27
3; 5) log8
2;
6) log8
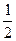 ;
7) ;
7) 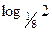 ; 8) log32
2; 9) log16 ; 8) log32
2; 9) log16
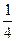 ;
10) log16 ;
10) log16
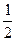
4. Решите уравнение.
а) 1) 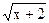 = 2; 2) = 2; 2) 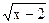 = 2; 3) = 2; 3) 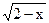 = 2; 4) = 2; 4) 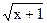 = 3; 5) = 3; 5) 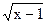 = 3; = 3;
6) 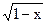 = 3; 7) = 3; 7) 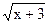 = 4; 8) = 4; 8) 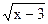 = 4; 9) = 4; 9) 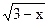 = 4; 10) = 4; 10) 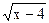 = 2 = 2
б) 1) 2х-4
= 8; 2) 8х+2
= 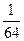 ; 3) ; 3) 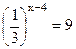 ; 4) ; 4) 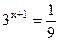 ; 5) ; 5) 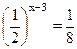 ; ;
6) 2х-3
= 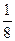 ; 7) ; 7) 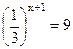 ; 8) 16х-1
= 4; 9) 8х-1
= 2; 10) 9х-1
= 3 ; 8) 16х-1
= 4; 9) 8х-1
= 2; 10) 9х-1
= 3
в) 1) log2
x = 3; 2) logx
8 = 3; 3) log3
x = –1; 4) logx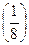 = –3; 5)
= –3; 5) 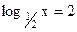 ; ;
6) logx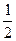 = –1;
7)
= –1;
7) 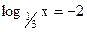 ; 8) logx ; 8) logx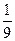 = –2; 9) log2
x = –3; 10) logx
= –2; 9) log2
x = –3; 10) logx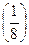 = 3
= 3
г) 1) sin x = 0,1; 2) cos x = 0,1; 3) tg x = 0,1; 4) ctg x = 0,1; 5) sin x = – 0,1;
6) cos x = – 0,1; 7) tg x = – 0,1; 8) ctg x = – 0,1; 9) sin x = 2; 10) cos x = – 2
5. Решите неравенство.
а) 1) 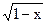 ≤ 3; 2) ≤ 3; 2) 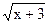 ≤ 4; 3) ≤ 4; 3) 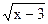 ≤ 4; 4) ≤ 4; 4) 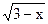 ≤ 4; 5) ≤ 4; 5) 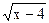 ≤ 2; ≤ 2;
6) 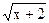 ≤ 2; 7) ≤ 2; 7) 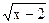 ≤ 2; 8) ≤ 2; 8) 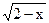 ≥ 2; 9) ≥ 2; 9) 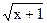 ≤ 3; 10) ≤ 3; 10) 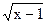 ≤ 3 ≤ 3
б) 1) 2х-3
≥ 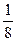 ; 2) ; 2) 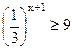 ; 3) 16х-1
≥ 4; 4) 8х-1
≥ 2; 5) 9х-1
≥ 3; ; 3) 16х-1
≥ 4; 4) 8х-1
≥ 2; 5) 9х-1
≥ 3;
6) 2х-4
≥ 8; 7) 8х+2
≥ 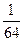 ; 8) ; 8) 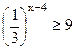 ; 9) ; 9) 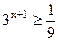 ; 10) ; 10) 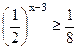
в) 1) log2
x ≥ 3; 2) log2
x ≥ 2; 3) log3
x ≥ 3; 4) log3
x ≥ 9; 5) 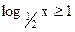 ; ;
6) 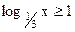 ; 7) ; 7) 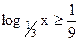 ; 8) ; 8) 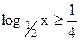 ; 9) log2
x ≥ 1; 10) log3
x ≥ 1 ; 9) log2
x ≥ 1; 10) log3
x ≥ 1
6. Вычислите предел функции.
а) 1) 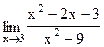 ; 6) ; 6) 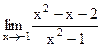 ; ;
2) 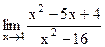 ; 7) ; 7) 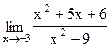 ; ;
3) 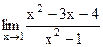 ; 8) ; 8) 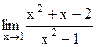 ; ;
4) 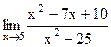 ; 9) ; 9) 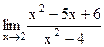 ; ;
5) 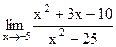 ; 10) ; 10) 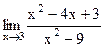
б) 1) 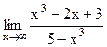 ; 6) ; 6) 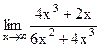 ; ;
2) 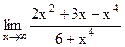 ; 7) ; 7) 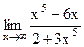 ; ;
3) 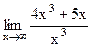 ; 8) ; 8) 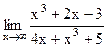 ; ;
4) 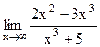 ; 9) ; 9) 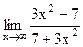 ; ;
5) 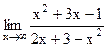 ; 10) ; 10) 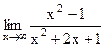
Задания
для проведения экзамена в форме тестирования
по дисциплине «Математика»
(2 семестр).
1. Найти значение производной данной функции в данной точке.
1) у = 2х2
– 3х + 5, х = 0; 16) y = (x – 3x2
+ 5)3
, x = 0;
2) у = 7х3
– 6 + 3х2
, х = 0; 17) y = (7x – 1 + 4x3
)5
, x = 0;
3) у = 12 – 3х3
+ 2х2
, х = 0; 18) y = (x3
+ 1)2
, x = 0;
4) у = х3
– 4х2
+ х, х = 0; 19) y = (1 – 2x)7
, x = 0;
5) у = 21х + 3х5
+ 7х2
– 5, х = 0; 20) y = (4x + 5x2
– 7)2
, x = 0;
6) у = х3
∙ 3х0,5
, х = 1; 21) y = 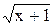 , x = 0; , x = 0;
7) у = (х + 1) ∙ 2х3
, х = 1; 22) y = 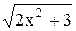 , x = 0; , x = 0;
8) у = 4х ∙ (7х2
+ 5), х = 1; 23) y = 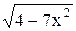 , x = 0; , x = 0;
9) y = (2x2
+ 3x) ∙ (x – 1), x = 1; 24) y = 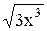 , x = 1; , x = 1;
10) y = (6x – 3x2
) ∙ (x2
+ 2), x = 1; 25) y = 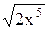 , x = 1; , x = 1;
11) y = 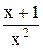 , x = 1; 26) y = , x = 1; 26) y = 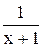 , x = 0; , x = 0;
12) y = 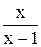 , x = 0; 27) y = , x = 0; 27) y = 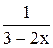 , x = 0; , x = 0;
13) y = 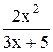 , x = 0; 28) y = , x = 0; 28) y = 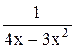 , x = 1; , x = 1;
14) y = 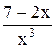 , x = 1; 29) y = , x = 1; 29) y = 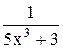 , x = 0; , x = 0;
15) y = 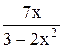 , x = 0; 30) y = , x = 0; 30) y = 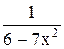 , x = 0. , x = 0.
2. Найдите значение дифференциала данной функции.
1) f(x) = x2
– 3x +5, x = 10, Δx = 0,01;
2) f(x) = x2
∙(x–1), x = 10, Δx = 0,01;
3) f(x) = 2x3
– 2x2
+ 1, x = 10, Δx = 0,01;
4) f(x) = (x – 5)∙3x2
, x = 10, Δx = 0,01;
5) f(x) = 7x – 3x2
+ 2, x = 10, Δx = 0,01.
3. Найдите точки экстремума функции.
1) f(x) = 2x3
– 3x2
– 12x + 1;
2) f(x) = 2x3
– 15x2
+ 24x +3;
3) f(x) = 2x3
+ 3x2
– 12x – 1;
4) f(x) = – x3
– 3x2
+ 9x – 2;
5) f(x) = 2x3
+ 3x2
+ 2.
4. Найдите интеграл непосредственно.
1) 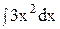 ; 6) ; 6) 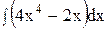 ; ;
2) 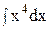 ; 7) ; 7) 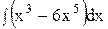 ; ;
3) 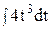 ; 8) ; 8) 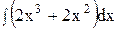 ; ;
4) 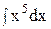 ; 9) ; 9) 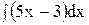 ; ;
5) 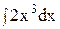 ; 10) ; 10) 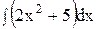 . .
5. Найдите интеграл способом подстановки.
1) 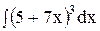 ; 6) ; 6) 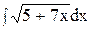 ; 11) ; 11) 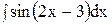 ; ;
2) 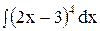 ; 7) ; 7) 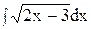 ; 12) ; 12) 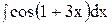 ; ;
3) 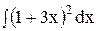 ; 8) ; 8) 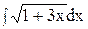 ; 13) ; 13) 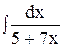 ; ;
4) 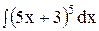 ; 9) ; 9) 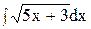 ; 14) ; 14) 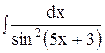 ; ;
5) 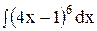 ; 10) ; 10)  ; 15) ; 15) 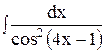 . .
6. Вычислите определенный интеграл.
1) 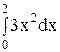 ; 6) ; 6) 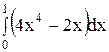 ; ;
2) 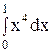 ; 7) ; 7) 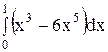 ; ;
3) 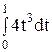 ; 8) ; 8) 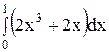 ; ;
4) 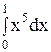 ; 9) ; 9) 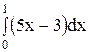 ; ;
5) 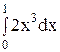 ; 10) ; 10) 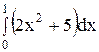 . .
Литература
Основная:
[1] «Алгебра и начала анализа» (под ред. Г.Н. Яковлева).
Ч. I, М. «Наука», 1987г.
[2] «Алгебра и начала анализа» (под ред. Г.Н. Яковлева).
Ч. II, М. «Наука», 1988г.
[3] «Геометрия» (под ред. Г.Н. Яковлева), М. «Наука», 1989г.
[4] «Геометрия 7-11 кл.», А.В. Погорелов, М. «Просвещение», 1990г.
[5] «Сборник задач по математике», П.Т. Апанасов, М. «Высшая школа»,
1987г.
[6] «Математика» Н. В. Богомолов, 2005 г.
[7] «Сборник задач по математике» Н. В. Богомолов, 2005 г.
[8] «Геометрия» Л. С. Атанасян, 2005 г.
Дополнительная:
[12] «Сборник задач по математике» О.Н. Афанасьева, Я.С. Бродский, А.Л. Павлов, М. «Наука», 1987г.
[13] «Сборник дидактических заданий по математике» Н.В. Богомолов, М. «Высшая школа», 1987г.
[11] «Математика для техникумов» И.И. Валуцэ, Г.Д. Дилигул, М. «Высшая школа», 1990г.
|