| Одесский национальный университет им. И. И. Мечникова
Институт математики, экономики и механики
линейная алгебра
( решение типовых задач)
Часть 2
Методические указания для студентов 1 курса
Одесса – 2008
Составители: д-р ф-м н., проф. Варбанец П.Д.,
к-т ф-м н., доц. Савастру О.В.
Рецензенты: д-р ф-м н., проф. Евтухов В.М.,
к-т ф-м н., доц. Белозеров Г.С.
Рекомендовано к печати
Ученым
советом ИМЭМ Одесского национального университета им. И. И. Мечникова
протокол № 1 от 5 февраля 2008 г.
.
СОДЕРЖАНИЕ
Обозначения…………………………………………………4
1.
Линейные пространства …………………………………...5
1.1. Линейные пространства и подпространства………….5
1.2. Базис пространства, его размерность…………………6
1.3. Координаты вектора в данном базисе…………….…11
1.4. Сумма и пересечение подпространств………………12
2.
Евклидовы и унитарные пространства ………….…........17
2.1. Процесс ортогонализации Шмидта………………….17
2.2.Ортогональные дополнения…………………………..19
2.3. Ортогональная проекция и перпендикуляр на подпространство……………………………………………………..20
3.
Операторы в линейных пространствах…………….........23
3.1. Образ, ядро линейного оператора……………………28
3.2. Матрица линейного оператора в данных базисах…..29
3.3. Собственные векторы и собственные значения..…...31
3.4. Канонический корневой базис и жорданова нормальная форма…………………………………………………….34
4.
Операторы в евклидовых и унитарных пространствах..40
5.
Приведение двух квадратичных форм к каноническому виду…………………………………………………………...45
Список литературы………………………………………….51
Линейные пространства и линейные операторы представляют собой начало абстрактной части математики, с которой студенту в дальнейшем неоднократно придется иметь дело.
Эти методические указания по самостоятельной работе студентов предполагают использование следующего задачника:
И.В.Проскуряков. Сборник задач по линейной алгебре.
М., Наука, 1974.
ОБОЗНАЧЕНИЯ
В дальнейшем мы будем придерживаться следующих обозначений (если в тексте нет специальной оговорки):
¾  - произвольные пространства над некоторым полем - произвольные пространства над некоторым полем  ; ;
¾  - пространство - пространство  - мерных строк (столбцов) с элементами из поля - мерных строк (столбцов) с элементами из поля  над полем над полем  (арифметическое пространство). (арифметическое пространство).
В частности
¾ 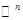 - действительное - действительное  - мерное арифметическое пространство; - мерное арифметическое пространство;
¾  - комплексное - комплексное  - мерное арифметическое пространство; - мерное арифметическое пространство;
¾ 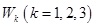 - пространства геометрических векторов (прямой, плоскости, пространства); - пространства геометрических векторов (прямой, плоскости, пространства);
¾  - евклидовы пространства (с указанием размерности или без него); - евклидовы пространства (с указанием размерности или без него);
¾ 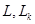 - подпространства данного пространства ( - подпространства данного пространства (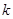 - индекс, не связанный с размерностью); - индекс, не связанный с размерностью);
¾  векторы рассматриваемого пространства; векторы рассматриваемого пространства;  - нулевой вектор; - нулевой вектор;
¾  скаляры из данного поля, скаляры из данного поля,  - нуль этого поля; - нуль этого поля;
¾  линейные операторы, в отдельных случаях – матрицы; линейные операторы, в отдельных случаях – матрицы;
¾ 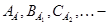 матрицы линейных операторов в базисах соответственно матрицы линейных операторов в базисах соответственно 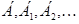 ; ;
¾  размерности пространств размерности пространств 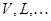 ; ;
¾  ранги операторов (матриц) ранги операторов (матриц)  ; ;
¾  скалярное произведение в данном пространстве; скалярное произведение в данном пространстве;
¾ 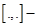 векторное произведение в данном пространстве векторное произведение в данном пространстве 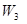 . .
- ЛИНЕЙНЫЕ ПРОСТРАНСТВА.
Основными типами задач этого параграфа являются следующие:
А) выяснение вопроса, будет ли данное множество с указанными операциями линейным пространством, подпространством;
В) выделение базиса пространства, определение его размерности;
С) вычисление координат вектора в данном базисе;
D) нахождение суммы, пересечения подпространств, их размерностей и базисов.
1.1.
Линейные пространства и подпространства.
Для решения задач первой группы необходимо знание аксиом линейного пространства (вообще, не следует приниматься за решение задач любого раздела, не ознакомившись предварительно с основными понятиями и теоремами данного раздела). Заметим, что в группе аксиом линейного пространства содержатся требования неограниченной применимости, однозначности и замкнутости линейных операций, которые не выделены под отдельными номерами. Распространенная ошибка: забывают проверить выполнение этих условий.
В тех условиях, когда данное множество состоит из векторов некоторого известного пространства, полезной является следующая теорема (критерий подпространства):
Теорема.
Подмножество  векторов пространства векторов пространства  над полем над полем  является подпространством тогда и только тогда, когда является подпространством тогда и только тогда, когда
1.  замкнуто относительно сложения, т.е. замкнуто относительно сложения, т.е. 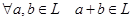 , ,
2.  замкнуто относительно умножения векторов на любые скаляры из основного поля замкнуто относительно умножения векторов на любые скаляры из основного поля  : : 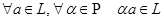 . .
Некоторые из задач требуют хорошего знания других разделов курса (элементарной теории матриц, квадратичных форм, систем линейных уравнений). Ниже мы подробнее остановимся на одной из этих задач.
1.2.
Базис пространства, его размерность.
Построение базиса пространства, подпространства несколько упрощается, если мы располагаем некоторыми представлениями о размерности пространства, подпространства. Одним из наводящих соображений здесь может быть следующее. Подмножество  векторов пространства векторов пространства  выделяется из выделяется из  с помощью дополнительных условий, накладываемых на векторы. При этом, чем больше таких условий, тем меньшей, вообще говоря, будет размерность подпространства с помощью дополнительных условий, накладываемых на векторы. При этом, чем больше таких условий, тем меньшей, вообще говоря, будет размерность подпространства  . Если . Если 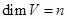 , а , а  выделено с помощью выделено с помощью 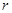 условий специального вида, то есть основания ожидать, что условий специального вида, то есть основания ожидать, что  . .
Задача 1.1. (№1297[4])
Доказать, что множество  п
-мерных векторов, у которых первая и последняя координаты равны между собой, образует линейное подпространство пространства п
-мерных векторов, у которых первая и последняя координаты равны между собой, образует линейное подпространство пространства 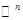 . .
Решение.
Множество  образует линейное подпространство пространства образует линейное подпространство пространства 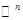 , так как удовлетворяет критерию подпространства. Действительно, , так как удовлетворяет критерию подпространства. Действительно,  выделяется из выделяется из 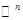 с помощью одного условия с помощью одного условия 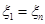 , поэтому , поэтому
1.
 , ,
2.
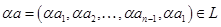 . .
Кроме того, нетрудно показать, что  . Для этого рассмотрим векторы стандартного базиса . Для этого рассмотрим векторы стандартного базиса 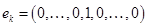 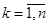 . Векторы . Векторы  не принадлежат не принадлежат  . Но построение базиса подпространства в ряде случаев удобно выполнить, исходя из стандартного базиса самого пространства, изменяя его векторы так, чтобы они «попали» в подпространство. Поэтому преобразуем векторы . Но построение базиса подпространства в ряде случаев удобно выполнить, исходя из стандартного базиса самого пространства, изменяя его векторы так, чтобы они «попали» в подпространство. Поэтому преобразуем векторы  так, чтобы у них первая и последняя координаты были равны. Например, пусть так, чтобы у них первая и последняя координаты были равны. Например, пусть   . Рассмотрим систему векторов . Рассмотрим систему векторов 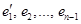 . Она образует базис . Она образует базис  , так как нетрудно проверить, что она является линейно независимой и каждый вектор из подпространства линейно выражается через вектора этой системы. А так как количество векторов системы равно , так как нетрудно проверить, что она является линейно независимой и каждый вектор из подпространства линейно выражается через вектора этой системы. А так как количество векторов системы равно  , то и , то и  . Итак, наше предположение оказалось верным. . Итак, наше предположение оказалось верным.
Линейные подпространства, размерности которых на 1 меньше размерности самого пространства называются гиперплоскостями
.
В следующей задаче условий больше.
Задача 1.2.
(№1298[4])
Доказать, что множество  п
-мерных векторов, у которых координаты с четными номерами равны нулю, образует линейное подпространство пространства п
-мерных векторов, у которых координаты с четными номерами равны нулю, образует линейное подпространство пространства 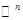 . .
Решение.
Для доказательства того, что  является подпространством, нужно также воспользоваться критерием подпространства. Так как является подпространством, нужно также воспользоваться критерием подпространства. Так как 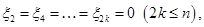 поэтому следует ожидать, что поэтому следует ожидать, что  , где , где 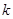 - наибольшее четное число, не превышающее - наибольшее четное число, не превышающее  ( (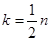 , если , если  - четное, и - четное, и  , если , если  - нечетное). Базисом - нечетное). Базисом  является подсистема стандартного базиса пространства является подсистема стандартного базиса пространства 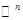 , содержащая векторы только с нечетными номерами. , содержащая векторы только с нечетными номерами.
Задача 1.3.
Проверить, является ли множество  многочленов степени 3 с вещественными коэффициентами подпространством пространства многочленов степени многочленов степени 3 с вещественными коэффициентами подпространством пространства многочленов степени  ( (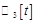 ). ).
Решение.
Воспользуемся критерием подпространства. Проверим условие 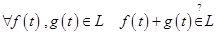 . .
Пусть  , тогда , тогда
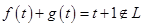 , ,
так как степень суммы этих двух многочленов равна двум. Итак, множество  не является подпространством. не является подпространством.
Задача 1.4.
(№№1291, 1308[4])
Найти какой-нибудь базис и размерность линейного подпространства  пространства пространства 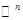 , если , если  составляют все векторы из составляют все векторы из 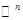 , у которых сумма координат , у которых сумма координат 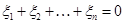 . .
Решение.
Очевидно векторы стандартного базиса
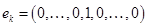 (1 на (1 на 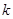 - ой позиции ) множеству - ой позиции ) множеству  не принадлежат ни при каком не принадлежат ни при каком  . Однако, замена на векторах . Однако, замена на векторах 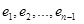 последнего нуля числом (-1) дает нам векторы из последнего нуля числом (-1) дает нам векторы из  . Таким образом мы получаем систему . Таким образом мы получаем систему  векторов векторов
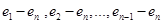
из  , которая линейно независима (почему?) и обязана быть базисом , которая линейно независима (почему?) и обязана быть базисом  , ибо из условия задачи явно следует, что из , ибо из условия задачи явно следует, что из 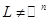 и, следовательно, и, следовательно, 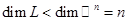 . .
Попутно решен вопрос (и подтвердилась гипотеза) о размерности  ( (  выделено из выделено из 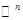 одним условием). одним условием).
Задача 1.4.
(№1306[4])
Пусть  - неотрицательная квадратичная форма от - неотрицательная квадратичная форма от  неизвестных ранга неизвестных ранга 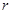 . Доказать, что все решения уравнения . Доказать, что все решения уравнения  =0 образуют =0 образуют  мерное линейное подпространство пространства мерное линейное подпространство пространства 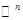 . .
Поиск решения.
Вспоминаем основные понятия теории квадратичных форм (матрица формы, ранг формы, определение формы). Очевидно, что более подробные записи данного уравнения в виде 
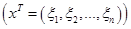 , никак не указывают на способ решения задачи. , никак не указывают на способ решения задачи.
В процессе дальнейших размышлений начинаем понимать, что мы должны исходить из неотрицательной определенности формы 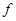 . Нормальный вид такой формы . Нормальный вид такой формы
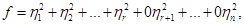 (1) (1)
а множество решений уравнения 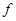 =0 в этом случае состоит из векторов вида =0 в этом случае состоит из векторов вида
 , (2) , (2)
Где  - произвольные числа из - произвольные числа из  . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть ( . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть ( )-мерное подпространство пространства )-мерное подпространство пространства  . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга 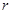 невырожденным линейным преобразованием приводится к виду (1). Создается план решения: преобразовать форму невырожденным линейным преобразованием приводится к виду (1). Создается план решения: преобразовать форму 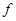 к виду (1) , найти решения (2) уравнения к виду (1) , найти решения (2) уравнения  =0 для преобразованной формы, а затем с помощью обратного преобразования построить решения уравнения =0 для преобразованной формы, а затем с помощью обратного преобразования построить решения уравнения  =0 для данной формы =0 для данной формы  . .
Решение.
По теореме о приведении квадратичной формы к нормальному виду существует невырожденное линейное преобразование
 , приводящее форму , приводящее форму  к виду к виду
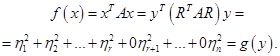
Множество решений уравнения 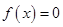 состоит из векторов состоит из векторов 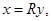 где где  , то есть из векторов , то есть из векторов
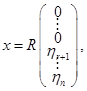  . .
Обозначим 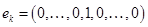 (1 на (1 на 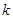 - ой позиции) и докажем, что множество - ой позиции) и докажем, что множество 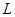 решений уравнения решений уравнения 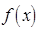 =0 есть линейная оболочка системы векторов =0 есть линейная оболочка системы векторов 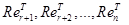
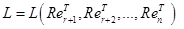 . .
Пусть 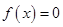 . Тогда . Тогда

Очевидно и другое:

Кроме того, система  линейно независима (проверяется непосредственно). Составляем линейную комбинацию линейно независима (проверяется непосредственно). Составляем линейную комбинацию  . Получаем . Получаем 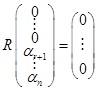 . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица  является невырожденной. является невырожденной.
 . .
Отсюда  . Тем самым мы показали, что система . Тем самым мы показали, что система  является линейно независимой. Следовательно, является линейно независимой. Следовательно, 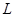 - линейное пространство (по построению) и его размерность - линейное пространство (по построению) и его размерность 
1.3.
Координаты вектора в данном базисе.
Решение вопроса о ранге системы векторов, заданных координатами в некотором базисе, выделение из системы ее максимальной линейно независимой подсистемы, выражение остальных векторов в виде линейных комбинаций векторов этой подсистемы сводится к решению этих же задач для системы строк (столбцов) координатной матрицы, которые подробно обсуждались в соответствующем параграфе первой части.
1.4.Сумма и пересечение подпространств.
Пусть 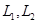 - данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление - данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление  не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств 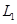 и и  . .  находится по формуле находится по формуле
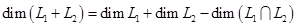 . (3) . (3)
Несколько сложнее обстоит дело с поиском базиса пересечения 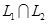 . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй - с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали). . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй - с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).
Задача 1.6.
Найти базис суммы и пересечения подпространств, натянутых на системы векторов
 и и 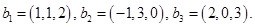
Решение.
Обозначим 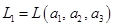 , ,  . Будем считать, что координаты векторов заданы в единичном базисе . Будем считать, что координаты векторов заданы в единичном базисе  . .
1 способ.
Как известно, базисом суммы служит любая база системы векторов  , , 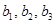 . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства. . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.
Итак,  . Базис . Базис 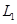 составляют составляют  . .
 . Базис . Базис  составляют составляют  . .
 . .
Базис 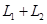 составляют составляют 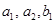 . По формуле (3) получаем . По формуле (3) получаем  . Базис пересечения будем искать из условия . Базис пересечения будем искать из условия  . Значит, . Значит, 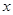 представим в виде представим в виде  и и 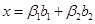 . Приравниваем правые части . Приравниваем правые части  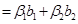 . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда 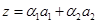 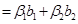 будет образовывать базис пересечения. будет образовывать базис пересечения.

Решив систему, строим ФСР.

Вектор  образует базис образует базис 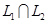 . .
2 способ.
1) Составим таблицу Штифеля для объединенной системы векторов  , , и перебрасываем наверх сначала векторы и перебрасываем наверх сначала векторы  , пока это возможно (квадратиками выделены разрешающие элементы). Векторы , пока это возможно (квадратиками выделены разрешающие элементы). Векторы  , переходящие налево, не пишем и их координаты не вычисляем. , переходящие налево, не пишем и их координаты не вычисляем.
| а)
|
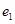
|
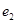
|
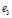
|
|
б)
|
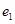
|
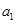
|
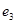
|
|
| 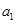
|
2
|
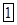
|
0
|
|

|
-3
|
2
|
3
|
|
| 
|
1
|
2
|
3
|
|

|
-1
|
-2
|
|
|
| 
|
-5
|
-2
|
1
|
|

|
-1
|
1
|
2
|
|
| 
|
1
|
1
|
2
|
|

|
-7
|
3
|
0
|
|
| 
|
-1
|
3
|
0
|

|
2
|
0
|
3
|
|
| 
|
2
|
0
|
3
|
|
|
|
|
|
| в)
|
|
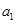
|

|
| 
|
0
|
8
|
3
|
| 
|
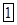
|
5
|
2
|
| 
|
-7
|
3
|
0
|
| 
|
5
|
6
|
3
|
Перебросить  наверх вместо наверх вместо 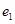 невозможно. Следовательно, невозможно. Следовательно,  =2, а базис =2, а базис 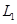 составляют составляют  , ,  . Исключаем из таблицы строку . Исключаем из таблицы строку  и перебрасываем наверх и перебрасываем наверх  вместо оставшихся вместо оставшихся 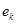 . .
Из таблицы г) получаем: 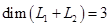 , то есть , то есть  и базис суммы образуют векторы и базис суммы образуют векторы  , ,  , ,  . .
2) Продолжаем работу с таблицей г), перебрасывая наверх  вместо находящихся наверху вместо находящихся наверху  , пока это возможно. Как и выше, векторы, уходящие налево, опускаем. , пока это возможно. Как и выше, векторы, уходящие налево, опускаем.
Вектор  перебросить наверх вместо перебросить наверх вместо 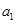 невозможно. Приходим к выводу, что невозможно. Приходим к выводу, что  , базис , базис  составляют составляют  , ,  . По (3) . По (3) 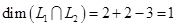 . .
3) Возвращаемся к таблице г). Вектор  , вошедший в базис , вошедший в базис  , представим через базис суммы , представим через базис суммы  в виде: в виде:

Отсюда находим 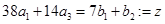 . .
Вектор  и и  , а так как , а так как  , то , то 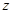 образует базис пересечения образует базис пересечения 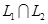 . Оба представления вектора . Оба представления вектора 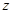 дают один результат дают один результат 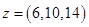 , что подтверждает правильность вычислений. Задача решена. , что подтверждает правильность вычислений. Задача решена.
Для более полного усвоения понятия суммы, прямой суммы подпространств полезно решить задачи №№1323-1329 [4].
Задача 1.7.
Для подпространства 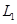 , натянутого на векторы , натянутого на векторы  , найти дополнительное подпространство. , найти дополнительное подпространство.
Решение.
Для любого подпространства 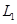 линейного пространства линейного пространства  всегда найдется дополнительное подпространство всегда найдется дополнительное подпространство  , то есть такое подпространство, что , то есть такое подпространство, что  . Причем, оно определяется неоднозначно. Найдем одно из таких подпространств. Для этого мы должны найти базис . Причем, оно определяется неоднозначно. Найдем одно из таких подпространств. Для этого мы должны найти базис  подпространства подпространства 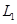 и дополнить его до базиса всего пространства и дополнить его до базиса всего пространства  . Пусть . Пусть  - базис - базис  . Тогда . Тогда  . .
Найдем базис и размерность  . .
 . .
Базис  - - 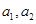 . Так как . Так как  - сумма прямая, то - сумма прямая, то  . Чтобы найти базис . Чтобы найти базис  дополним базис дополним базис 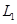 до базиса всего пространства до базиса всего пространства 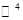 векторами векторами  , ,  . .
 . Итак, . Итак,  . .
2. ЕВКЛИДОВЫ И УНИТАРНЫЕ ПРОСТРАНСТВА.
Основные типы задач этого параграфа:
· проверка выполнения аксиом скалярного произведения и доказательство его различных свойств (№№1351-1354, 1384)
;
· ортогонализация данной системы векторов, построение ортогональных и ортонормированных базисов (№№1355-1363)
;
· построение ортогональных дополнений данных подпространств (№№1364-1368)
;
· нахождение ортогональных проекций и перпендикуляров на подпространство (№№1369-1372)
;
· вычисление длин, расстояний, углов (№№1373-1406)
.
2.1.
Процесс ортогонализации Шмидта.
Обычно метод ортогонализации Шмидта рассматривают и обосновывают в лекциях. Тем не менее, подчеркнем, что данная система векторов  и ортогональная, т.е. полученная из данной методом Шмидта и ортогональная, т.е. полученная из данной методом Шмидта 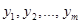 , являются эквивалентными системами - их линейные оболочки совпадают. Поэтому ортогонализация системы векторов, порождающей подпространство , являются эквивалентными системами - их линейные оболочки совпадают. Поэтому ортогонализация системы векторов, порождающей подпространство  , приводит к построению ортогонального базиса , приводит к построению ортогонального базиса  . Обратим внимание на некоторые частные случаи, встречающиеся в задачах: . Обратим внимание на некоторые частные случаи, встречающиеся в задачах:
1. если подлежащая ортогонализации система  распадается на две взаимно ортогональные подсистемы распадается на две взаимно ортогональные подсистемы 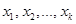 и и  , то для решения задачи достаточно ортогонализировать каждую из этих подсистем независимо от другой; , то для решения задачи достаточно ортогонализировать каждую из этих подсистем независимо от другой;
2. если выяснилось, что подсистема 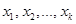 уже ортогональна, то ортогонализацию начинаем с вектора уже ортогональна, то ортогонализацию начинаем с вектора  , полагая , полагая

и дальше по стандартной схеме;
3. если в процессе ортогонализации, полученная система векторов 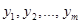 содержит нулевой вектор, то можно сразу сказать, что исходная система является линейно зависимой. содержит нулевой вектор, то можно сразу сказать, что исходная система является линейно зависимой.
Задача 2.1.
Применить процесс ортогонализации к следующей системе векторов из  : : 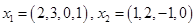 , ,  . .
Решение.
Можно сразу заметить, что система распадается на две взаимно ортогональные подсистемы  и и  . Поэтому ортогонализируем каждую из подсистем независимо друг от друга. . Поэтому ортогонализируем каждую из подсистем независимо друг от друга.
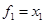 , ,  , ,
 , ,  . .
 , ,  . .
 , ,
 . .
2.2.Ортогональные дополнения.
Задачи этого раздела не вызовут трудностей, если разобраться в свойствах решений линейной однородной системы как векторов евклидова (унитарного) пространства.
Рассмотрим пространство 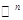 и систему линейных однородных уравнений над и систему линейных однородных уравнений над 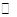 : :
 (4) (4)
Обозначив  и и  , перепишем систему (4) в виде , перепишем систему (4) в виде
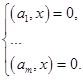 (5) (5)
Пусть  . Тогда уравнения (5) означают, что . Тогда уравнения (5) означают, что  и, следовательно, и, следовательно,  , а каждый вектор из , а каждый вектор из 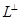 является решением системы (4). Итак, множество решений системы (4) и линейная оболочка ее строк коэффициентов являются ортогональными дополнениями друг для друга в пространстве является решением системы (4). Итак, множество решений системы (4) и линейная оболочка ее строк коэффициентов являются ортогональными дополнениями друг для друга в пространстве  . (Какие изменения надо внести в рассуждения в случае пространства . (Какие изменения надо внести в рассуждения в случае пространства  ?) ?)
Задача 2.2.
Найти базис ортогонального дополнения 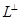 подпространства подпространства  , натянутого на векторы: , натянутого на векторы:
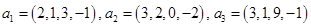 . .
Найти уравнения, задающие подпространство  . .
Решение.
Так как 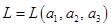 , то , то 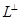 состоит из множества решений системы уравнений состоит из множества решений системы уравнений
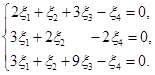
Находим фундаментальную систему ее решений (ранг системы 2)
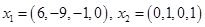 . .
Следовательно, 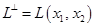 , а система уравнений со строками коэффициентов , а система уравнений со строками коэффициентов  и и 

задает подпространство  , как множество решений этой системы (убедитесь: системы векторов , как множество решений этой системы (убедитесь: системы векторов  и и 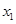 , ,  взаимно ортогональны, а объединение их базисов есть базис взаимно ортогональны, а объединение их базисов есть базис  ). ).
Аналогичные соображения используются при дополнении ортогональной системы до ортогонального базиса.
2.3.
Ортогональная проекция и перпендикуляр на подпространство.
Известно, что
 , ,
и потому каждый вектор  единственным способом представим в виде суммы единственным способом представим в виде суммы

где  Вектор Вектор  называют (ортогональной) проекцией вектора называют (ортогональной) проекцией вектора 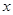 на подпространство на подпространство  и обозначают и обозначают 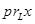 , а , а  - перпендикуляром (ортогональной составляющей) из вектора - перпендикуляром (ортогональной составляющей) из вектора 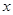 на подпространство на подпространство  : : 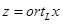 . Очевидно, что . Очевидно, что
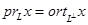 , ,  . (6) . (6)
Если 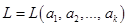 , то , то
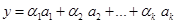 (7) (7)
и тогда
 . .
Умножаем последнее равенство скалярно на 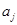 , ,  , с учетом , с учетом  , получаем , получаем
 (8) (8)
Эта система в силу существования представления (7) совместна. Определитель матрицы этой системы есть определитель Грама 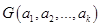 . Если . Если  - линейно независима, то - линейно независима, то 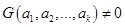 и система (8) имеет единственное решение. В противном случае у системы (8) решений бесконечно много. Но нам достаточно найти одно (все другие решения дадут нам те же векторы и система (8) имеет единственное решение. В противном случае у системы (8) решений бесконечно много. Но нам достаточно найти одно (все другие решения дадут нам те же векторы  и и  ). Если система (8) получилась несовместной, ищите ошибку. Вычисления сокращаются, если известны базисы ). Если система (8) получилась несовместной, ищите ошибку. Вычисления сокращаются, если известны базисы  и и 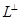 и если, опираясь на соотношения (6), выбрать то подпространство, размерность которого меньше. и если, опираясь на соотношения (6), выбрать то подпространство, размерность которого меньше.
Умение находить 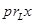 и и 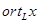 позволит успешно справиться с большинством задач на вычисление длин, расстояний и углов. позволит успешно справиться с большинством задач на вычисление длин, расстояний и углов.
Задача 2.3.
Вычислить расстояние от вектора  до плоскости до плоскости  , заданной системой уравнений , заданной системой уравнений
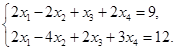 . .
Решение.
Напомним: плоскостью (линейным многообразием) называется множество векторов вида
 , ,
где  - вектор сдвига, - вектор сдвига,  - данное (направляющее) подпространство. Любая плоскость может быть задана как множество решений некоторой системы линейных уравнений. Частное решение этой системы дает координаты вектора сдвига. Общее решение приведенной системы - направляющее подпространство. Учитывая это, находим, что - данное (направляющее) подпространство. Любая плоскость может быть задана как множество решений некоторой системы линейных уравнений. Частное решение этой системы дает координаты вектора сдвига. Общее решение приведенной системы - направляющее подпространство. Учитывая это, находим, что  , где , где
  , ,
 . .
Расстояние от вектора  до плоскости до плоскости  определяется как определяется как  или как или как 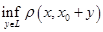 . .
Так как 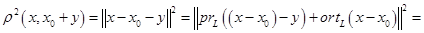
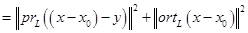
(применена теорема Пифагора), то
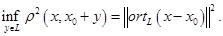
Мы получили формулу 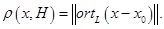
Остается вычислить 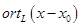 и его длину. и его длину.  . .

и тогда
 . .
Умножаем последнее равенство скалярно на 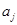 , , 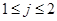 , с учетом , с учетом 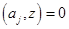 , получаем , получаем

Решая систему, находим 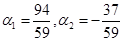 . .
Тогда
  . .
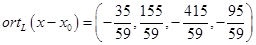 . .
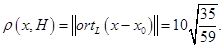
3. ОПЕРАТОРЫ В ЛИНЕЙНЫХ ПРОСТРАНСТВАХ.
Пусть  и и 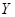 - два произвольных линейных пространства. Как известно, оператором, действующим из - два произвольных линейных пространства. Как известно, оператором, действующим из  в в 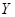 называется отображение пространства называется отображение пространства  в пространство в пространство  . Если отображение обозначить символом . Если отображение обозначить символом  , то это записывают так: , то это записывают так:
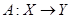 . .
Образ вектора  обозначают обозначают 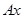 или или 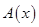 и называют значением оператора и называют значением оператора 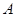 на векторе на векторе  . По определению . По определению 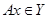 . .
Оператор 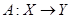 называют линейным оператором
, если называют линейным оператором
, если  и и  - пространства над одним и тем же полем - пространства над одним и тем же полем 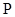 и при этом и при этом
1. 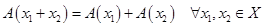
(аддитивность оператора);
2. 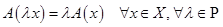
(однородность оператора).
Понятие линейного оператора является одним из важнейших в математике. Это подтверждается хотя бы тем, что основные операторы, изучаемые в математическом анализе и алгебре (предельный переход, дифференцирование, интегрирование, проектирование на подпространство, умножение на матрицу и др.) являются линейными.
Оператор  называют также преобразованием пространства называют также преобразованием пространства  . .
Основные типы задач по этой теме:
a) проверка линейности заданного оператора;
b) нахождение образа, ядра, ранга и дефекта линейного оператора;
c) построение матрицы линейного оператора в данных базисах (в данном базисе);
d) нахождение собственных значений и собственных векторов линейного оператора (№№1465-1484)
;
e) построение канонического базиса и жордановой нормальной формы линейного оператора (№№1529-1536)
.
Основная трудность задач первой группы состоит в том, что примеры операторов могут быть взяты из различных разделов математики и требуют от студента эрудиции и определенной математической культуры. Приведем несколько примеров.
Задача 3.1.
Проверьте линейность следующих операторов:
1. 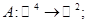 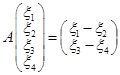 . .
2.  ( ( -пространство многочленов степени -пространство многочленов степени  над некоторым полем). над некоторым полем).
 . .
3.  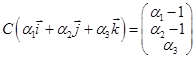 . .
4. 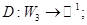  . .
5. 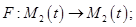  . .
6. 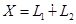 . Определим оператор . Определим оператор  так: если так: если  и и 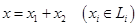 , то , то 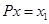 (оператор проектирования на (оператор проектирования на 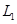 параллельно параллельно 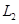 ). ).
7.  ( (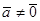 - фиксированный вектор). - фиксированный вектор).
Решение.
1.  является отображением. Проверим аддитивность и однородность. является отображением. Проверим аддитивность и однородность.
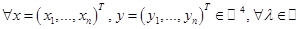

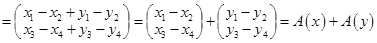 . .
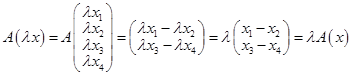 . .
Все условия выполнены, значит,  является линейным оператором. является линейным оператором.
5.  . .

 , ,
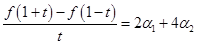 . .

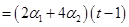 . .
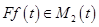 . Теперь проверяем аддитивность и однородность. Напомним: если . Теперь проверяем аддитивность и однородность. Напомним: если 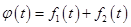 , то , то  и и  . .
Находим 

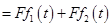 . .
Точно так же
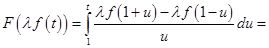
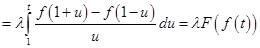 . .
Все условия определения линейного оператора выполнены.
 - линейный оператор. - линейный оператор.
Линейный оператор нулевой вектор отображает в нулевой ( ). Поэтому, если ). Поэтому, если 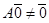 , то , то  нелинейный. Рекомендуем в подозрительных случаях прежде, чем начинать проверку аддитивности и однородности, вычислить значение оператора на нулевом векторе. Так в упражнении 2 нелинейный. Рекомендуем в подозрительных случаях прежде, чем начинать проверку аддитивности и однородности, вычислить значение оператора на нулевом векторе. Так в упражнении 2 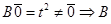 - нелинейный. В упражнении 3 - нелинейный. В упражнении 3  - нелинейный. - нелинейный.
Для доказательства нелинейности достаточно привести пример двух векторов, для которых нарушена аддитивность, или пример вектора или скаляра, для которых не выполнена однородность (равенство  может иметь место и для нелинейных операторов). Например: в упражнении 7 настораживает то, что текущий вектор может иметь место и для нелинейных операторов). Например: в упражнении 7 настораживает то, что текущий вектор  находится под знаком находится под знаком 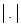 . Поэтому проверку ведем на конкретных векторах. . Поэтому проверку ведем на конкретных векторах.
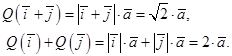
Очевидное неравенство  доказывает неаддитивность доказывает неаддитивность  и его нелинейность. и его нелинейность.
В этом же примере можно поступить и так:

Поэтому оператор  неоднороден, следовательно, и нелинеен. неоднороден, следовательно, и нелинеен.
Проверку линейности операторов из упражнений 4 и 6 предоставляем читателю.
Чтобы глубже понять определение линейного оператора, придумайте примеры:
1. оператора аддитивного, но не однородного;
2. оператора однородного, но не аддитивного.
3.1. Образ, ядро линейного оператора.
Образом
линейного оператора  называется множество всех векторов вида называется множество всех векторов вида  . Если . Если  , то образ , то образ  есть подмножество из есть подмножество из 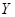 . Его обозначают . Его обозначают 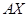 или или  . .
Если  - линейный оператор, то - линейный оператор, то  , где , где  - какой-либо базис пространства - какой-либо базис пространства 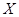 . .
Ядро
линейного оператора  - это множество тех - это множество тех  , для которых , для которых 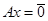 . Ядро линейного оператора (обозначается . Ядро линейного оператора (обозначается  ) – подпространство пространства ) – подпространство пространства  . Полезно уметь находить ядра и образы линейных операторов, их размерности (дефект и ранг). . Полезно уметь находить ядра и образы линейных операторов, их размерности (дефект и ранг).
Задача 3.2.
Найти образ, ядро, ранг и дефект оператора 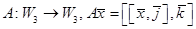 (оператор двойного векторного умножения). (оператор двойного векторного умножения).
Решение.
Будем считать, что мы уже убедились в линейности оператора 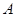 . .
Вычисление образа.
Возьмем стандартный базис пространства  : : 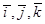 . Находим . Находим

(подпространство одномерное).
 . .
Вычисление ядра.
Пусть   . Это означает, что . Это означает, что  или или 
Отсюда  где где 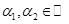 . Другими словами . Другими словами  , а дефект , а дефект 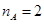 . .
(В нашем примере  , но это не общее правило). Можно было воспользоваться формулой для двойного векторного произведения. Но решение вряд ли упростилось бы от этого. , но это не общее правило). Можно было воспользоваться формулой для двойного векторного произведения. Но решение вряд ли упростилось бы от этого.
Как правило, нахождение ядра в конце концов сводится к решению системы линейных однородных уравнений относительно координат произвольного вектора ядра. В рассмотренном нами примере эта система оказалась очень простой
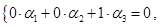
что позволило нам сразу записать общее решение  . .
3.2. Матрица линейного оператора в данных базисах.
Обязательно нужно научиться строить матрицу линейного оператора в данных базисах. Но кроме этого, еще раз обратим наше внимание на следующую теорему: каждый линейный оператор из 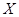 в в 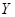 однозначно определяется своими значениями на каком-либо базисе пространства однозначно определяется своими значениями на каком-либо базисе пространства  . Эта теорема позволяет строить примеры различных операторов, удовлетворяющих наперед заданным свойствам. . Эта теорема позволяет строить примеры различных операторов, удовлетворяющих наперед заданным свойствам.
Задача 3.3.
Для каждого из нижеперечисленных условий постройте пример линейного оператора 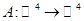 : :
 . .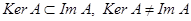 . . . . , где , где  . .- На
  действует как тождественный, но действует как тождественный, но 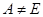 . .
- Каждое
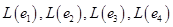 переводит в себя, но переводит в себя, но 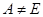 . .
Решение.
1. Возьмем какой-либо базис в  , например, стандартный , например, стандартный
 . .
Так как  , то из условия , то из условия  следует следует 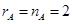 . Для определенности возьмем . Для определенности возьмем 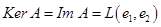 . Определим . Определим  на базисе так: на базисе так:

Этими условиями линейный оператор  полностью определен. полностью определен.
Если  то по нашему определению то по нашему определению

Легко убеждаемся, что  . .
Действительно, 
 - это множество тех - это множество тех  , для которых , для которых  , то есть , то есть  . .
6. Так как необходимо построить такой линейный оператор  , который каждое , который каждое 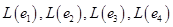 переводит в себя, но переводит в себя, но 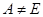 , то будем считать, что система , то будем считать, что система  является линейно независимой, а значит, является базисом является линейно независимой, а значит, является базисом  . Определим . Определим 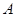 на базисе так: на базисе так:

Можно проверить, что таким образом введенный операторм является линейным и удовлетворяет всем необходимым условиям.
3.3. Собственные векторы и собственные значения.
Процедура вычисления собственных значений и собственных векторов (собственных подпространств) линейного оператора  вытекает из соответствующего теоретическоо материала. Продемонстрируем ее на конкретном примере. вытекает из соответствующего теоретическоо материала. Продемонстрируем ее на конкретном примере.
Задача 3.4.
Найдите собственные значения и собственные подпространства оператора  (необходимо самостоятельно проверить линейность) (необходимо самостоятельно проверить линейность)
 . .
Решение.
1) Строим матрицу оператора  в стандартном базисе в стандартном базисе 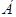 пространства пространства  (предполагаем, что линейность оператора проверена): (предполагаем, что линейность оператора проверена):
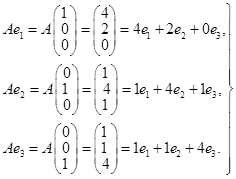 , ,  . .
2) Составляем характеристическую матрицу 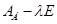 , вычисляем ее определитель и находим корни характеристического многочлена. , вычисляем ее определитель и находим корни характеристического многочлена.
 ; ;
 

 ; ;
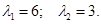
Оба корня принадлежат полю  и являются собственными значениями оператора; и являются собственными значениями оператора; 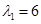 - кратности 1; - кратности 1; 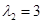 - кратности 2. - кратности 2.
3) Составляем систему линейных однородных уравнений с матрицей  и находим ее фундаментальную систему решений: и находим ее фундаментальную систему решений:

Система ранга 2. Множество ее решений - одномерное пространство, линейно независимых решений. Легко находим ее фундаментальную систему решений -  . Собственное подпространство, относящееся к . Собственное подпространство, относящееся к 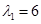

4) Составляем систему линейных однородных уравнений с матрицей  и находим ее фундаментальную систему решений: и находим ее фундаментальную систему решений:

Система ранга 2. Множество ее решений также является одномерным пространством. Легко находим ФСР - . Собственное подпространство, относящееся к . Собственное подпространство, относящееся к 
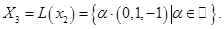
Задача решена.
Замечание 1.
Если оператор  задан своей матрицей, то пункт 1) не нужен. задан своей матрицей, то пункт 1) не нужен.
Замечание 2.
Если в процессе решения получилась несовместная система, то допущена ошибка (неверно вычислен характеристический многочлен, найденное  не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы). не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы).
Замечание 3.
Полезно помнить, что размерность собственного подпространства, относящегося к собственному значению  у любого линейного оператора не превышает (меньше или равна) кратности этого собственного значения, как корня характеристического многочлена (геометрическая кратность собственного значения его алгебраической кратности). Например, в задачах №№1465, 1466, 1481
есть собственные значения с алгебраической кратностью 3, а их геометрическая кратность соответственно равна 1,2 и 3. у любого линейного оператора не превышает (меньше или равна) кратности этого собственного значения, как корня характеристического многочлена (геометрическая кратность собственного значения его алгебраической кратности). Например, в задачах №№1465, 1466, 1481
есть собственные значения с алгебраической кратностью 3, а их геометрическая кратность соответственно равна 1,2 и 3.
Замечание 4.
В учебных примерах, как правило, корни характеристического многочлена вычисляются точно. На практике часто приходится довольствоваться их приближениями. Возникающие при этом проблемы достаточно сложны и здесь не обсуждаются.
3.4. Канонический корневой базис и жорданова нормальная форма.
Задачи построения канонического корневого базиса (ККБ
) и жордановой нормальной формы (ЖНФ
) матрицы линейного оператора наиболее сложные, так как 1)
большой объем вычислений и 2)
приходится опираться на обширный и серьезный теоретический материал.
Рассмотрим сначала задачу о построении ККБ
. Так как ККБ
линейного пространства есть объединение ККБ
корневых подпространств данного оператора, то можно предположить, что мы уже выделили корневые подпространства и имеем дело с одним из них - 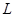 , относящимся к собственному значению , относящимся к собственному значению  , кратность которого совпадает с , кратность которого совпадает с 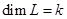 . .
В лекционном курсе ККБ
корневого подпространства был построен в виде системы башен убывающей этажности, нижний этаж которых состоял из линейно независимых собственных векторов, а в каждом столбце нижестоящий вектор получался из непосредственно вышестоящего в результате применения оператора  . .
Процедура практического построения ККБ
такова:
1. опираясь на какой-либо базис 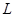 , строим систему башен, вообще говоря, линейно зависимую; , строим систему башен, вообще говоря, линейно зависимую;
2. элементарными преобразованиями, сохраняющими башенную структуру, преобразуем систему так, чтобы ее нижний этаж состоял из линейно независимых векторов (этим будет обеспечиваться ЛНЗ всей системы).
Для этого элементарные преобразования будем выполнять сразу над целым столбцом: его перемещение, прибавление к другому столбцу (с меньшей этажностью) и т.п.
Если  - некоторый базис пространства, то исходная система башен, упорядоченных по высоте, имеет вид: - некоторый базис пространства, то исходная система башен, упорядоченных по высоте, имеет вид:
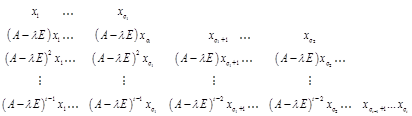
Преобразования выполняем слева направо, выбирая их по векторам нижней строки.
Рассмотрим конкретный пример.
Задача 3.5.
Постройте ККБ
оператора 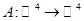
 . .
Решение.
1) Строим матрицу оператора  в стандартном базисе в стандартном базисе  пространства пространства  . Находим образы базисных векторов: . Находим образы базисных векторов:
 , , , ,
  . .
Тогда
 . .
2) Вычисляем характеристический многочлен оператора и собственные значения:

 кратности 4. кратности 4.
Пространство  является корневым пространством, относящимся к собственному значению является корневым пространством, относящимся к собственному значению 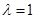 . .
3) Берем произвольный базис (например, стандартный) и к каждому его вектору применяем оператор 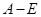 до получения нуля: до получения нуля:
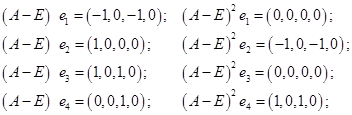

Можно сделать некоторые предварительные выводы: максимальная высота корневого вектора равна 3, поэтому в ЖНФ
матрицы оператора будет клетка порядка 3 и, следовательно (так как 4-3=1), одна клетка порядка 1. Хотя этого задача не требует, но мы можем написать ЖНФ
матрицы оператора:
 . .
4) Полагаем  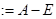 . Выписываем полученные в 3) векторы (кроме нулей, разумеется) в башню: . Выписываем полученные в 3) векторы (кроме нулей, разумеется) в башню:
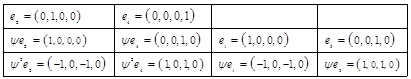
и рассматриваем нижнюю строку.
Замечаем:
а) третий столбец векторов пропорционален (равен) соответствующей части первого, а четвертый - соответствующей части второго. Выбрасываем без сожаления третий и четвертый столбцы.
в) нижний вектор второго столбца пропорционален своему соседу слева. Прибавляем ко второму столбцу первый, умноженный на 1, и получившийся нуль во втором столбце отбрасываем. Таблица примет вид:
 . .
Нижняя строка все еще линейно зависима. Ко второму столбцу прибавляем первый, умноженный на 1 (верхний вектор первого столбца, у которого нет соседа справа, в этой операции не участвует), отбрасываем получившийся нуль и приходим к таблице:
 . .
Нижняя строка этой таблицы линейно независима, поэтому и вся система векторов линейно независима. Она, занумерованная снизу вверх и слева направо, образует ккб:
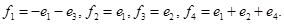
Упражнение.
Постройте матрицу оператора  в базисе в базисе  . Сравните ее с ЖНФ
из 3). . Сравните ее с ЖНФ
из 3).
ЖНФ
матрицы оператора можно отыскать, не выполняя построения ККБ
. Число жордановых клеток каждого порядка и максимальный порядок жордановых клеток для каждого собственного значения  могут быть вычислены, если известны ранги матриц могут быть вычислены, если известны ранги матриц   , где , где  - показатель степени такой, что - показатель степени такой, что

(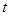 - «момент» стабилизации ранга). - «момент» стабилизации ранга).
В нашем примере


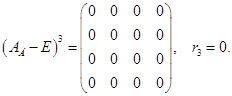
«Момент» стабилизации ранга  , так как , так как  невозможно по определению ранга. невозможно по определению ранга.
Есть клетка третьего порядка (и только одна) и, очевидно, еще одна клетка первого порядка (результат, полученный нами в 3)).
Напомним, что в общем случае (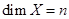 , , 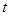 - «момент» стабилизации рангов матриц - «момент» стабилизации рангов матриц  ) число клеток, относящихся к собственному значению ) число клеток, относящихся к собственному значению  определяется формулами: определяется формулами:
клеток порядка  : :  , ,
клеток порядка  : :  , ,
клеток порядка 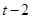 : :  , ,
…………………………………………
клеток порядка 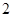 : :  , ,
клеток порядка 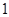 : :  . .
Следует помнить, что хотя жнф матрицы определена однозначно с точностью до порядка клеток вдоль главной диагонали, ККБ
существует бесконечно много. Поэтому не удивительно, если найденный вами ККБ
не совпадает с ответом в сборнике задач (но проверить свое решение полезно).
Замечание.
Если 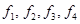 - ККБ
оператора - ККБ
оператора  и и 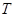 - матрица перехода от базиса - матрица перехода от базиса 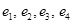 к ККБ
, то имеет место равенство: к ККБ
, то имеет место равенство:
 . .
Таким образом нами «попутно» найдена преобразующая матрица Е, приводящая данную матрицу 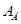 к ЖНФ
. к ЖНФ
.
4. ОПЕРАТОРЫ В ЕВКЛИДОВЫХ И УНИТАРНЫХ ПРОСТРАНСТВАХ
Пусть  и и 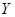 - два произвольных пространства, оба евклидовых или оба унитарных. Рассмотрим линейный оператор - два произвольных пространства, оба евклидовых или оба унитарных. Рассмотрим линейный оператор 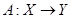 . Напомним, что оператор . Напомним, что оператор  называется сопряженным
по отношению к оператору называется сопряженным
по отношению к оператору  , если , если  и и  выполняется равенство выполняется равенство
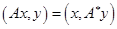 . .
Для всякого оператора  сопряженный оператор сопряженный оператор 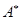 существует и единственный. Причем существует и единственный. Причем
 , (9) , (9)
где  - какой-либо ортонормированный базис (ОНБ) - какой-либо ортонормированный базис (ОНБ)  . .
Равенство (9) можно применять за определение сопряженного оператора.
Матрица 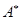 размерности размерности  с элементами с элементами  называется сопряженной по отношению к матрице называется сопряженной по отношению к матрице  размерности размерности  с элементами с элементами 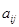 , если , если  . .
Заметим, что в любых ОНБ унитарных пространств  и и 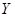 сопряженному оператору соответствует соряженная матрица, справедливо и обратное. сопряженному оператору соответствует соряженная матрица, справедливо и обратное.
Если мы рассматриваем евклидовы пространства  и и 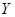 , то таким же образом устанавливается соответствие между сопряженными операторами и транспонированными матрицами. , то таким же образом устанавливается соответствие между сопряженными операторами и транспонированными матрицами.
Задача 4.1.
Найти сопряженный оператор для оператора 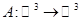
 . .
В  введено естественное скалярное произведение введено естественное скалярное произведение
 . .
Решение.
В заданном унитарном пространстве 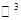 стандартный базис стандартный базис  является ОНБ. Для построения сопряженного оператора воспользуемся равенством (9). является ОНБ. Для построения сопряженного оператора воспользуемся равенством (9).
 , ,
 , ,
 , ,

 . .
Итак, искомый сопряженный оператор имеет вид
 . .
Задача решена.
Задача 4.2.
В пространстве  введено скалярное произведение введено скалярное произведение 
и задана матрица  линейного оператора линейного оператора  в базисе в базисе  . .
Построить матрицу  сопряженного оператора сопряженного оператора 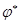 в базисе в базисе  . .
Решение.
Проверим, является ли базис  ортонормированным в заданном евклидовом пространстве. ортонормированным в заданном евклидовом пространстве.
  , , 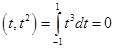 , ,
 , ,  , ,  . .
Ортогонализируем систему 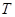 . .
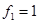 , ,
 , ,
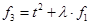 , ,  , ,
 . .
Осталось нормировать полученную систему
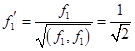 , ,
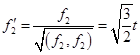 , ,
 . .
Мы построили ОНБ  . Теперь мы должны, используя матрицу перехода от одного базиса к другому, перейти к матрице оператора в ОНБ. Зная, как связаны матрицы сопряженных операторов в ОНБ, можно построить матрицу сопряженного оператора . Теперь мы должны, используя матрицу перехода от одного базиса к другому, перейти к матрице оператора в ОНБ. Зная, как связаны матрицы сопряженных операторов в ОНБ, можно построить матрицу сопряженного оператора 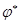 в базисе в базисе  , а затем вернуться опять к исходному базису. , а затем вернуться опять к исходному базису.
Матрица перехода от базиса 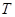 к базису к базису 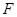 имеет вид имеет вид
 , , 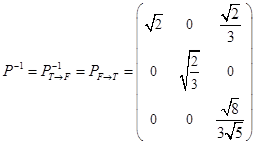 . .
 . .
Мы знаем, как связаны матрицы сопряженных операторов в ОНБ
 , ,
поэтому
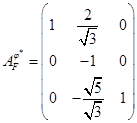 . .
Используя матрицу перехода 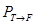 , возвращаемся к исходному базису , возвращаемся к исходному базису 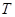
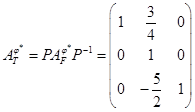 . .
Задача решена.
5. ПРИВЕДЕНИЕ ДВУХ КВАДРАТИЧНЫХ ФОРМ К КАНОНИЧЕСКОМУ ВИДУ
Рассмотрим две вещественные квадратичные формы 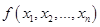 и и  . Можно ли заданные формы единым преобразованием привести к каноническому виду? Эту задачу помогают решить результаты, относящиеся к линейным операторам. Мы рассмотрим случай, когда одна из этих квадратичных форм, например . Можно ли заданные формы единым преобразованием привести к каноническому виду? Эту задачу помогают решить результаты, относящиеся к линейным операторам. Мы рассмотрим случай, когда одна из этих квадратичных форм, например , является положительно определенной. Тогда выполняем сначала преобразование , является положительно определенной. Тогда выполняем сначала преобразование 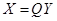 , которое приводит форму , которое приводит форму  к нормальному виду (сумме квадратов переменных). При этом форма к нормальному виду (сумме квадратов переменных). При этом форма  перейдет в новую форму от переменных перейдет в новую форму от переменных 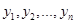 . На следующем шаге выполняется ортогональное преобразование . На следующем шаге выполняется ортогональное преобразование  , которое приводит форму , которое приводит форму 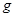 к каноническому виду. Квадратичная форма к каноническому виду. Квадратичная форма  при этом не изменится, так как ее матрица является единичной, а при этом не изменится, так как ее матрица является единичной, а 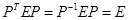 . .
Итак, результирующим преобразованием, которое приведет обе квадратичные формы к каноническому виду, причем положительно определенную представит в виде суммы квадратов, будет 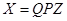 . .
Задача 5.1.
Для заданной пары квадратичных форм найти невырожденное линейное преобразование, которое приводит эти формы к каноническому виду.
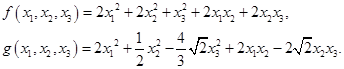
Решение.
Перепишем формы  и и  в виде в виде 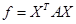 и и  , где , где 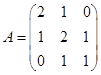 , ,  - матрицы соответствующих квадратичных форм. - матрицы соответствующих квадратичных форм.
Так как   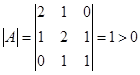 , то согласно критерию Сильвестра, форма , то согласно критерию Сильвестра, форма  является положительно определенной. Поэтому по ней можно восстановить соответствующую билинейную форму и ввести в является положительно определенной. Поэтому по ней можно восстановить соответствующую билинейную форму и ввести в 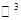 скалярное произведение скалярное произведение  . .
Оно удовлетворяет всем аксиомам скалярного произведения (положительная определенность формы необходима для выполнения аксиомы 4 , а именно 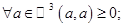 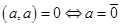 ). ).
Рассмотрим стандартный базис в  : :  . .
Используя введенное скалярное произведение, ортогонализируем его:

Нормируем вектора  и получаем ОНБ в
и получаем ОНБ в  , в котором билинейная форма (следовательно, и квадратичная форма , в котором билинейная форма (следовательно, и квадратичная форма  ) будет иметь единичную матрицу. ) будет иметь единичную матрицу.
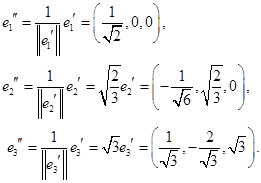
Матрица перехода от старого базиса к новому задает матрицу  невырожденного преобразования переменных невырожденного преобразования переменных 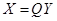 квадратичных форм квадратичных форм  и и 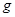 . .
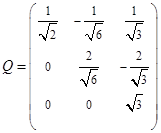 . .
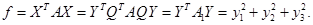
Действительно,
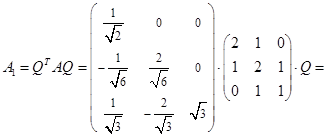

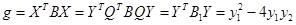 . .
Аналогично,

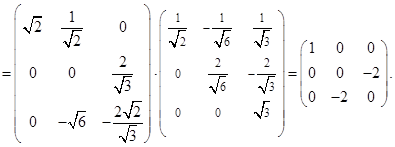
Далее используем метод приведения квадратичной формы к главным осям.
Характеристический многочлен
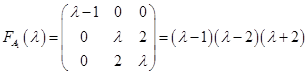 имеет три корня имеет три корня  , которым соответствуют следующие собственные вектора: , которым соответствуют следующие собственные вектора: 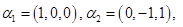  . Они являются попарно ортогональными, так как соответствуют разным собственным значениям, и образуют собственный ортогональный базис. Осталось его пронормировать: . Они являются попарно ортогональными, так как соответствуют разным собственным значениям, и образуют собственный ортогональный базис. Осталось его пронормировать:

 . .
Теперь составляем ортогональную матрицу, столбцами которой являются векторы 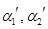 , , 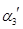 , ,
 . .
Тогда матрица 
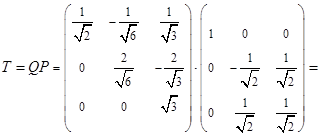

и будет искомой матрицей невырожденного линейного преобразования переменных

приводящего формы 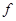 и и  к каноническому виду к каноническому виду
 , ,
 . .
Задача решена.
Список литературы
1.
Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел, ч.1. –
К.: Вища школа, 1980.
2.
Кострикин А. И. Введение в алгебру
. - М.: Наука, 1977 .
3.
Курош А.Г. Курс высшей алгебры
. – М.: Наука, 1975.
4.
Проскуряков. Сборник задач по линейной алгебре.
М., Наука, 1974.
|