|
МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ
Методические указания к выполнению лабораторной работы №1
«Изучение статистических методов обработки опытных данных»
«Аттестация контрольно-измерительных приспособлений»
Приборы и принадлежности
:
измерительный прибор, набор резисторов одного номинала.
Цель работы
:
изучение статистических методов обработки опытных данных; вычисление числовых характеристик статистического распределения; графическое представление распределения; изучение нормального закона распределения случайной величины.
Элементы теории погрешностей.
Результат измерения какой-либо величины зависит от многих факторов, влияние которых заранее учесть невозможно. Знания, полученные в результате прямых измерений какого-либо параметра, являются случайными. Если число измерений одного и того же параметра велико, то в распределении его значений обнаруживаются некоторые закономерности. Использование методов математической статистики для обработки результатов измерений позволяет установить эти закономерности.
Статистической совокупностью
называется совокупность объектов, характеризующаяся наличием некоторого общего признака. Наиболее полная совокупность, которая включает все объекты, обладающие данным признаком, называется генеральной совокупностью
.
Обычно провести изучение всей генеральной совокупности не представляется возможным, поэтому для исследования берут часть ее объектов, которые образуют выборочную совокупность
, или выборку
. В зависимости от числа объектов (объема выборки
) n различают большую
(n³30) и малую
(n<30) выборки.
Наблюдаемые значения членов выборки называют вариантами
. Обычно, особенно при проведении большого числа измерений, значения измеряемой величины повторяются. Поэтому число вариант k£n. Число mi
наблюдений варианты xi
называют частотой
данной варианты. Относительной частотой
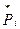 называется величина, равная отношению частоты mi
данной варианты к общему числу n значений измеряемой величины: называется величина, равная отношению частоты mi
данной варианты к общему числу n значений измеряемой величины:
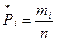 . (1.1) . (1.1)
Данные, получаемые при проведении экспериментов, представляют в виде статистических рядов
. Значения величины X в выборке, записанные в последовательности измерений, составляют простой статистический ряд. Располагая полученные значения в последовательности их возрастания, получают ранжированный ряд
:
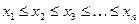 . .
Точечное
(дискретное) статистическое распределение (вариационный ряд) – это статистическое распределение, состоящее из вариант и соответствующих им частот и относительных частот.
Для составления интервального
(непрерывного) статистического распределения весь диапазон значений величины X делят на равные по величине интервалы 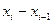 и указывают mi
– сумму частот вариант, попавших в каждый интервал, и и указывают mi
– сумму частот вариант, попавших в каждый интервал, и 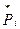 - сумму относительных частот. - сумму относительных частот.
Ширина интервала 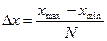 , где xmax
и xmin
– соответственно наибольшее и наименьшее значения измеряемой величины; N – число интервалов определяемое по формуле , где xmax
и xmin
– соответственно наибольшее и наименьшее значения измеряемой величины; N – число интервалов определяемое по формуле
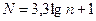 . (1.2) . (1.2)
Графически статистическое распределение изображают в виде полигона частот и гистограммы.
Для построения полигона частот
по оси абсцисс откладывают варианты x, а по оси ординат – значения частот или относительных частот, полученные точки соединяют ломаной линией.
Гистограмму
строят по данным интервального статистического распределения, и она представляет собой совокупность смежных прямоугольников, основанием которых является отрезок оси абсцисс, равный ширине интервала, а высота равна отношению 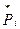 для каждого интервала к для каждого интервала к  . .
Числовыми характеристиками распределения для выборки являются выборочная средняя, медиана, мода, выборочная дисперсия, выборочное среднее квадратическое отклонение.
Выборочная средняя 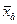 - величина, равная среднему арифметическому значению вариант статистического ряда: - величина, равная среднему арифметическому значению вариант статистического ряда:
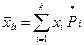 . (1.3) . (1.3)
Медиана равна такому значению случайной величины, которое делит ранжированный статистический ряд пополам (по числу членов).
Мода равна варианте, которой соответствует наибольшая частота.
Выборочная дисперсия характеризует рассеяние вариант вокруг выборочной средней:
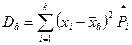 . (1.4) . (1.4)
Выборочное среднее квадратическое отклонение sв
равно корню квадратному из выборочной дисперсии:
 . (1.5) . (1.5)
Плотность вероятности – f(x) равна отношению вероятности того, что значение случайной величины находится в интервале от x до x+dx, к величине этого интервала:
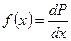 . .
Вероятность попадания значения случайной величины в некоторый интервал (ab):
 . .
Функция распределения F(x) равна вероятности того, что случайная величина X принимает значения, меньшие x:
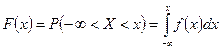 . .
Существует много законов распределения случайной величины. Наиболее распространенным является нормальный закон распределения:
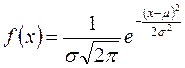 . .
Порядок выполнения работы
Накопление и обработка статистических данных
1. Измерьте сопротивления xi
100 резисторов.
2. Результаты измерений представьте в виде простого статистического ряда.
3. Составьте вариационный ряд.
4. Составьте интервальный ряд:
а) разбейте диапазон значений x на N равных интервалов с границами xi
min
и xi
max
. Число интервалов определите по формуле 1.2;
б) рассчитайте 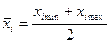 для каждого интервала; для каждого интервала;
в) подсчитайте частоту mi
для каждого интервала;
г) по формуле 1.1 определите относительные частоты, соответствующие каждому интервалу;
д) найдите значения 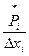 для каждого интервала. для каждого интервала.
5. По данным точечного вариационного ряда постройте полигон частот.
6. По данным интервального ряда постройте гистограмму.
7. Определите:
а) выборочную среднюю;
б) медиану;
в) моду;
г) выборочную дисперсию;
д) выборочное среднее квадратическое отклонение.
8. Найдите значения функции 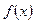 , для чего проделайте следующие вычисления: , для чего проделайте следующие вычисления:
а) вычислите значения zi
для каждого интервала 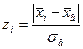 ; ;
б) найдите по таблице значения функции 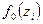 ; ;
в) вычислите значения функции  . .
9. Постройте график плотности вероятности f(x). Максимум кривой соответствует  . Для нахождения ординаты этой точки следует определить по таблице значение функции . Для нахождения ординаты этой точки следует определить по таблице значение функции 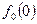 , и вычислить , и вычислить 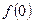 . .
10. Найдите значения функции  . Для этого вычислите значения . Для этого вычислите значения 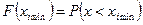 . .
11. Постройте график функции распределения F(x).
Проверка соответствия эмпирического распределения нормальному закону распределения случайной величины.
I. Определение характера погрешности.
1. Постройте теоретическую и эмпирическую кривую и сопоставить.
Для этого необходимо:
а) построить гистограмму,
б) построить по гистограмме практическую кривую и сравнить с существующими законами распределения,
Практическая кривая похожая на кривую нормального закона распределения сравнивается с теоретической кривой. С этой целью их строят в одном масштабе. Для определения точности контрольно-измерительных приспособлений построение рекомендуется проводить по методу Апарина и Городецкого.
в) построить теоретическую кривую,
Масштаб по оси абсцисс выбирается таким образом, чтобы в поле чертежа уместилось не менее  . При этом
s
изображается отрезком 25 мм. . При этом
s
изображается отрезком 25 мм.
Масштаб по оси ординат выбирается таким, чтобы
ymax
(при
s
=0) изображался отрезком длиной 100 мм.
Соотношение
y
и
s
| s
|
0
|
0
,5
|
1
|
1,5
|
2
|
2,5
|
3
|
| y
|
100
|
88
|
60,5
|
32,5
|
13,5
|
4,4
|
1,1
|
г) нанести на теоретическую кривую эмпирическую, пересчитав ее по масштабу:
масштаб по оси абсцисс:  мм/Ом, мм/Ом,
масштаб по оси ординат: 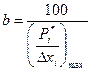 мм/на одно измерение, мм/на одно измерение,
д) выразить в масштабе а
выборочную среднюю «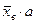 » которая будет являться центром рассеяния, и его следует отложить в точке s=0, » которая будет являться центром рассеяния, и его следует отложить в точке s=0,
е) положения точек  определяются относительно нулевой точки « определяются относительно нулевой точки «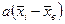 », по ординате откладывают соответствующие « », по ординате откладывают соответствующие «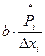 »; полученные точки соединить ломаной линией – это и есть практическая кривая, »; полученные точки соединить ломаной линией – это и есть практическая кривая,
ж) рассчитать значение эксцесса 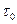 по формуле: по формуле: 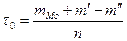 , где , где
 - частота моды, - частота моды, 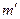 - частота соседнего интервала перед модой, - частота соседнего интервала перед модой,
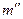 - частота соседнего интервала после моды; - частота соседнего интервала после моды;
чем меньше 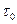 тем ближе эмпирическая кривая к кривой нормального распределения, допустимые значения: тем ближе эмпирическая кривая к кривой нормального распределения, допустимые значения:  ; ;
з) рассчитать меру асимметрии -  по формуле: по формуле:  , где значение моды определить по формуле: , где значение моды определить по формуле: 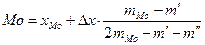 , где , где 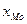 - нижняя граница интервала моды; - нижняя граница интервала моды;
допустимые значения: 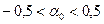 ; ;
и) если значения 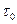 и и  укладываются в пределы то делается положительное заключение о совпадении эмпирической и теоретической кривой, иначе определяют причины доминирования не случайных погрешностей и следует сделать проверку критерия согласия по Колмогорову. укладываются в пределы то делается положительное заключение о совпадении эмпирической и теоретической кривой, иначе определяют причины доминирования не случайных погрешностей и следует сделать проверку критерия согласия по Колмогорову.
II. Определение критериев согласия по Колмогорову.
Методика определения критерия согласия.
1. Рассчитать накопленные частоты:
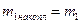 , , 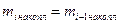 . .
2. Найти функцию  для каждого накопленного интервала. для каждого накопленного интервала.
3. Определить интегральную функцию предполагаемого теоретического распределения: 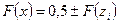 , где , где  - функция Лапласа, а знак «+» берется если ( - функция Лапласа, а знак «+» берется если (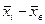 ) положительно, иначе берется знак «-». Значение функции Лапласа берут из таблицы. ) положительно, иначе берется знак «-». Значение функции Лапласа берут из таблицы.
4. Определить разности 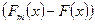 для каждого интервала и найти максимальное значение из них для каждого интервала и найти максимальное значение из них  . .
5. Найти критерий значимости Колмогорова: 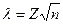 . .
6. По таблице найти значение вероятности 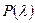 . .
7. Если вероятность 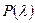 наблюдаемого расхождения наблюдаемого расхождения 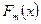 и и 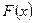 больше 0,01, то можно заключить, что эмпирическое распределение соответствует предполагаемому теоретическому. Считают, что совпадение эмпирической кривой с кривой нормального распределения удовлетворительно, при значениях: больше 0,01, то можно заключить, что эмпирическое распределение соответствует предполагаемому теоретическому. Считают, что совпадение эмпирической кривой с кривой нормального распределения удовлетворительно, при значениях: 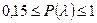 и и 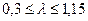 . .
8. Сделайте выводы.
Форма отчета по лабораторной работе
ОТЧЕТ
по лабораторной работе № .
Аттестация типовых приборов и контрольно измерительных приспособлений
Выполнил студент .
Группа .
Принял преподаватель .
Отметка о зачете .
Цель работы:
Тип элемента применяемого для аттестации:
Наименование прибора (КИП):
Величина, по которой аттестуется прибор:
Заводской номер:
Протокол испытаний
| № отсчета
|
1
|
2
|
…
|
100
|
| Отсчет (варианта): xi
, Ом
|
|
|
|
|
Ранжированный ряд .
Вариационный ряд
Медиана:
Математическое ожидание:
Дисперсия:
Среднее квадратическое отклонение:
Определение погрешности объекта
| № интервала
|
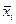 , Ом
, Ом
|
mi
|
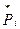
|
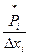 , Ом-1 , Ом-1
|
| |
|
|
|
|
Полигон частот:
Гистограмма:
Метрологическая карта
| Наименование прибора
|
Пределы измерения прибора
|
Диапазон показаний шкалы
|
Длина деления шкалы
|
Цена деления прибора
|
Чувствительность прибора
|
Погрешность измерения
|
| |
|
|
|
|
|
|
Данные для расчета 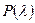
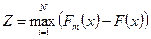 =… =…
 =… =…
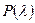 =… =…
Выводы:
Паспорт аттестации
Прибор (КИП)№: Наименование .
Эталон, применяемый для аттестации:
Параметры, по которым аттестуется прибор:
Дата « » 2005 г.
Исполнители:
Характеристики выборки
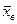 =… =…
s=…
Масштабы: а
=…, b
=….
Ширина интервала:  =… =…
Мера асимметрии: 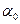 =… =…
Эксцесс: 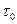 =… =…
Размер выборки: n=…
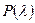 =… =…
Заключение .
Дать описание эмпирической кривой:
Представить все графические материалы:
|