| Федеральное агентство по образованию
ГОУ ВПО
Уральский государственный горный университет
 Институт геологии и геофизики Кафедра геоинформатики Институт геологии и геофизики Кафедра геоинформатики
620144 , г. Екатеринбург, ул. Куйбышева, 30
Тел. (343) – 2576661. E-mail: Pisetski@hotmail.com
РЕФЕРАТ
Преобразование Хартли
Краткое содержание работы Р. Брейсуэлла
«Преобразование Хартли. Теория и приложения», М: Мир, 1990.
Курс: Теория цифровой обработки данных
Выполнила: Балаева Л.А.
E-mail:
balaeva-lydmila@yandex.ru
Руководитель
:
проф
.
Давыдов А.В.
E-mail:
prodav@yandex.ru
Содержание
.
1. Введение.
2. Преобразование Хартли.
2.1. Четная и нечетная составляющие.
2.2. Формулы связи.
2.3. Энергетический и фазовый спектры.
3. Теоремы.
3.1. Соответствие операций.
3.2. Свертка.
4. Дискретное преобразование Хартли.
4.1. Физический смысл величин τ и ν.
4.2. Чётная и нечётная составляющие.
4.3. Степени свободы.
4.4. Другие вещественные ядра.
4.5. Теоремы, связанные с ДПХ.
4.6. Выводы по ДПХ.
5. Заключение.
Без сохранения форматирования исходного документа
Екатеринбург
2005
Введение.
Преобразование Хартли, как и преобразование Фурье, может применяться для спектрального анализа и различных видов обработки сигналов. Данный вид преобразования назван в честь Р. Хартли, опубликовавшего в 1942 г. статью о паре интегральных преобразований - прямом и обратном, использующих введенную им функцию 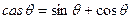 . До начала 1980-х годов эти результаты оставались в забвении, пока к ним не привлек внимание исследователей Р. Брейсуэлл, разработавший основы теории как непрерывного, так и дискретного преобразования Хартли, а также один из вариантов его быстрого преобразования. . До начала 1980-х годов эти результаты оставались в забвении, пока к ним не привлек внимание исследователей Р. Брейсуэлл, разработавший основы теории как непрерывного, так и дискретного преобразования Хартли, а также один из вариантов его быстрого преобразования.
Непрерывный прогресс в области обработки информации связан с задачами всевозрастающей сложности. Обращение к преобразованию Хартли обусловлено ситуацией, сложившейся в ряде методов обработки информации, в частности использующих вещественные последовательности данных (одномерных и двумерных). Обработку таких данных желательно осуществлять в области вещественных чисел с помощью взаимно симметричных прямого и обратного преобразований. В отличие от преобразования Фурье, отображающего вещественные функции в комплексную область и несимметричного по i
(происходит изменение знака при переходе от прямого к обратному преобразованию), преобразование Хартли осуществляет прямое и обратное преобразования только в вещественной области и обладает указанной симметрией.
В своём реферате я постараюсь изложить на основе теории и практических примеров некоторые основные аспекты преобразования Хартли.
Эта тема является актуальной, так как в настоящее время преобразование Хартли находит широкое применение при разработке двумерных и трехмерных быстрых преобразований, быстрых алгоритмов интерполяции и т.д.
Хартли ввел пару формул.
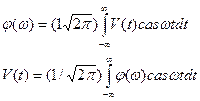 . .
В этих соотношениях для функции cas мы будем следовать определению автора, в соответствии с которым эта функция представляет собой сумму косинуса и синуса одного и того же аргумента cas t =
cos t + sin t.
2. Преобразование Хартли.
В определение Хартли для преобразования y (w) в явном виде был включен коэффициент 1/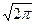 для получения симметричного выражения. Если опустить этот коэффициент, то оба интеграла одновременно не могут быть корректными. Однако следует признать нецелесообразным сохранение пары таких специфических коэффициентов, особенно при выполнении численных расчетов. Многие авторы отреагировали на подобную ситуацию применительно к преобразованию Фурье рассмотрением функции для получения симметричного выражения. Если опустить этот коэффициент, то оба интеграла одновременно не могут быть корректными. Однако следует признать нецелесообразным сохранение пары таких специфических коэффициентов, особенно при выполнении численных расчетов. Многие авторы отреагировали на подобную ситуацию применительно к преобразованию Фурье рассмотрением функции 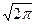 S(w) вместо S(w).В результате коэффициент 1/ S(w) вместо S(w).В результате коэффициент 1/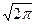 исчезает в определении прямого преобразования Фурье, однако в формуле обратного преобразования Фурье появляется коэффициент 1/2p. Таким образом, эти авторы намеренно жертвуют симметрией формул. Справедливо замечание, что это дополнительная нагрузка для памяти, так как приходится запоминать, какая из формул содержит величину 2p .Один способ запоминания состоит в том, что коэффициент 1/2p стоит перед интегралом, в котором фигурирует дифференциал d
w
,
что означает наличие величины вида w/2p , т. е. циклической частоты f
. Отсюда естественно возникает вопрос: почему непосредственно не иметь дело с частотой? Именно к этому выводу в течение многих лет склонялось мнение разных исследователей. Приверженцев использования коэффициента 1/ исчезает в определении прямого преобразования Фурье, однако в формуле обратного преобразования Фурье появляется коэффициент 1/2p. Таким образом, эти авторы намеренно жертвуют симметрией формул. Справедливо замечание, что это дополнительная нагрузка для памяти, так как приходится запоминать, какая из формул содержит величину 2p .Один способ запоминания состоит в том, что коэффициент 1/2p стоит перед интегралом, в котором фигурирует дифференциал d
w
,
что означает наличие величины вида w/2p , т. е. циклической частоты f
. Отсюда естественно возникает вопрос: почему непосредственно не иметь дело с частотой? Именно к этому выводу в течение многих лет склонялось мнение разных исследователей. Приверженцев использования коэффициента 1/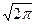 в настоящее время практически уже нет, тогда как имеется достаточное количество сторонников правомерности записи d
w
/
2p;
но общепринятой практикой является применение множителя 2
p
под знаком экспоненты в интегралах для прямого и обратного преобразований. Данная процедура реализуется автоматически при использовании частоты в настоящее время практически уже нет, тогда как имеется достаточное количество сторонников правомерности записи d
w
/
2p;
но общепринятой практикой является применение множителя 2
p
под знаком экспоненты в интегралах для прямого и обратного преобразований. Данная процедура реализуется автоматически при использовании частоты 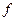 вместо угловой частоты w. При этом имеем вместо угловой частоты w. При этом имеем
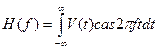
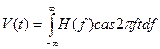
2.1.Четная и нечетная составляющие.
Взаимосвязь преобразований Фурье и Хартли базируется на анализе свойства симметрии. Для пояснения этого представим 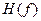 в виде четной и нечетной компонент в виде четной и нечетной компонент 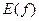 и и 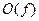 соответственно. Четная компонента определяется как полусумма функции соответственно. Четная компонента определяется как полусумма функции 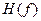 и ее зеркального изображения, т.е. функции и ее зеркального изображения, т.е. функции 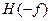 . Нечетная компонента определяется как полуразность этих функций и обладает свойством антисимметрии, а именно . Нечетная компонента определяется как полуразность этих функций и обладает свойством антисимметрии, а именно 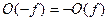 .
Любая функция может быть представлена однозначно в виде суммы четной и нечетной компонент, и, обратно, при заданных четной и нечетной компонентах однозначно может быть восстановлена исходная функция. Одним из интересных свойств четной и нечетной компонент является равенство суммы их энергий энергии самого процесса. .
Любая функция может быть представлена однозначно в виде суммы четной и нечетной компонент, и, обратно, при заданных четной и нечетной компонентах однозначно может быть восстановлена исходная функция. Одним из интересных свойств четной и нечетной компонент является равенство суммы их энергий энергии самого процесса.
Для установления связи преобразования 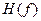 с преобразованием Фурье с преобразованием Фурье 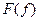 функции функции 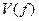 примем следующее определение. примем следующее определение.
Пусть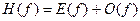 где где 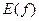 и и 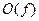 - соответственно четная и нечетная составляющие функции - соответственно четная и нечетная составляющие функции 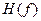 .
Тогда .
Тогда
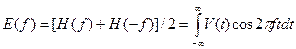
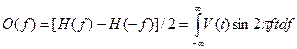
Эти два интеграла известны под названиями соответственно косинус- и синус-преобразование Фурье.
Для иллюстрации чётной и нечётной составляющей рассмотрим ряд примеров:
Пример №1.
Рассмотрим функцию вида  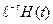 , которая в момент времени t = 0 имеет единичный скачок, а затем монотонно убывает по экспоненциальному закону. В данном выражении фигурирует единичная ступенчатая функция Хевисайда H
(
t
),
которая определяется следующим образом: , которая в момент времени t = 0 имеет единичный скачок, а затем монотонно убывает по экспоненциальному закону. В данном выражении фигурирует единичная ступенчатая функция Хевисайда H
(
t
),
которая определяется следующим образом:
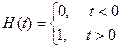

Заметим, что значение функции 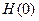 , т. е. , т. е. 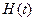 при t
= 0, не определено. Причина этого заключается в следующем. Рассмотрим две функции при t
= 0, не определено. Причина этого заключается в следующем. Рассмотрим две функции 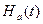 и и 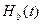 ,
которые совпадают с ,
которые совпадают с 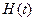 при при 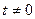 , но в отличие от , но в отличие от 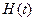 определены при t = 0. Пусть На
(0) = а
и Нь
(0) = b
.
Тогда разность определены при t = 0. Пусть На
(0) = а
и Нь
(0) = b
.
Тогда разность 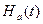 - -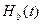 представляет собой нулевую функцию. Поскольку рассматриваются интегралы, на их величину не влияет выбор какого-либо определенного конечного значения Н(0). представляет собой нулевую функцию. Поскольку рассматриваются интегралы, на их величину не влияет выбор какого-либо определенного конечного значения Н(0).
Оцениваемый интеграл равен:
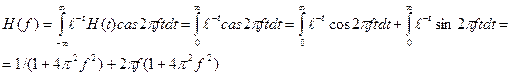
На данном примере №1 можно видеть симметрию чётной компоненты 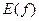 и её относительно быстрое убывание, и симметрию относительно начала координат нечётной составляющей и её относительно быстрое убывание, и симметрию относительно начала координат нечётной составляющей 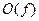 . .
Можно заметить, что H
(
f
)
не является ни четной, ни нечетной функцией. Минимум функции H
(
f
)
имеет место при 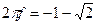 , максимум при , максимум при 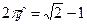 , и она обращается в нуль при , и она обращается в нуль при 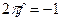 . При . При 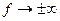 функция убывает как функция убывает как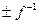 . .
Пример №2.
Рассмотрим сигнал 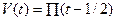 , где , где 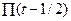 - смещенная единичная прямоугольная функция, имеющая свое начало при t = 0. Стандартная единичная прямоугольная функция, которая часто необходима для стробирования сегментов колебаний, определяется как - смещенная единичная прямоугольная функция, имеющая свое начало при t = 0. Стандартная единичная прямоугольная функция, которая часто необходима для стробирования сегментов колебаний, определяется как
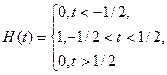

Для данного примера имеем преобразование Хартли
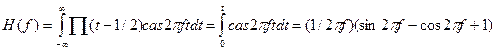 ,
,
2.2.Формулы связи.
При заданной функции 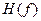 для получения преобразования Фурье для получения преобразования Фурье 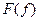 можно сформировать сумму можно сформировать сумму 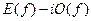 : :
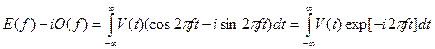
Таким образом, из 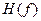 легко получить преобразование Фурье колебания V
(
t
)
путем формирования зеркального изображения вида легко получить преобразование Фурье колебания V
(
t
)
путем формирования зеркального изображения вида 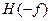 и операций суммирования функций. Вещественная часть F
(
f
)
равна E
(
f
),
а мнимая часть противоположна по знаку функции и операций суммирования функций. Вещественная часть F
(
f
)
равна E
(
f
),
а мнимая часть противоположна по знаку функции 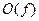 : :
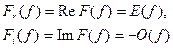
Наглядно связь преобразования Хартли с преобразованием Фурье можно представить на примере (в качестве примера возьмём стробирующую функцию)

И обратно, из заданного преобразования Фурье F
(
f
)
можно получить 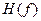 , заметив, что , заметив, что
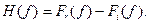 , ,
т.е., исходя из F
(
f
),
функция 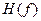 определяется как сумма вещественной части преобразования Фурье и ее мнимой части, взятой с обратным знаком. определяется как сумма вещественной части преобразования Фурье и ее мнимой части, взятой с обратным знаком.
Помня о том, что мнимая часть комплексной величины сама является вещественной, убеждаемся в том, что 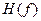 представляет собой вещественную функцию, как и должно быть при условии, что исходное колебание представляет собой вещественную функцию, как и должно быть при условии, что исходное колебание 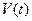 вещественно. Если бы вещественно. Если бы 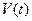 не было вещественной функцией (в этом случае не было вещественной функцией (в этом случае 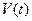 не могло бы представлять собой напряжение электрического колебания), то не могло бы представлять собой напряжение электрического колебания), то 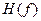 , а тем более , а тем более 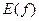 и и 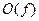 также не были бы вещественными. В результате можно резюмировать: также не были бы вещественными. В результате можно резюмировать:
Преобразование Фурье равно разности четной составляющей пре
образования Хартли и нечетной составляющей, умноженной на
i
; напротив, преобразование Хартли определяется как разность вещественной и мнимой составляющих преобразования Фурье.
2.3.Энергетический и фазовый спектры.
Не всегда легко понять характер изменения комплексной функции, имея графики ее вещественной и мнимой частей, однако в оптике и других областях физики более привычным является использование понятия квадрата модуля преобразования, или энергетического спектра:
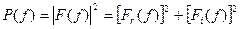
Энергетический спектр является четной функцией частоты и поэтому более прост для понимания. С другой стороны, энергетический спектр содержит в себе, по крайней мере, половину информации об исходном колебании, так как теряется информация о фазе. Тем не менее, для ряда приложений энергетический спектр может оказаться инструментом исследования, который необходим.
Энергетический спектр можно получить непосредственно из преобразования Хартли. Имеем
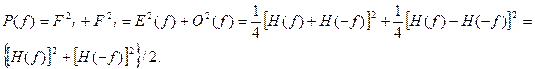
Рассмотрим энергетический спектр, полученный из преобразования Хартли на примере прямоугольного импульса.

Таким образом, вместо возведения в квадрат вещественной и мнимой частей и их суммирования при данном значении 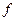 мы возводим в квадрат и суммируем два значения преобразования Хартли для частот + мы возводим в квадрат и суммируем два значения преобразования Хартли для частот +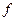 и — и —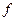 . При этом результат суммирования должен быть разделен на два, так как каждая из функций вида . При этом результат суммирования должен быть разделен на два, так как каждая из функций вида 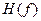 и и 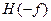 , возведенная в квадрат, равна полному энергетическому спектру, тогда как вещественная и мнимая части содержат по половине этой величины. , возведенная в квадрат, равна полному энергетическому спектру, тогда как вещественная и мнимая части содержат по половине этой величины.
В оптике представляет затруднение измерение фазы преобразования Фурье, однако в анализе сигналов рассмотрение фазовых функций (фазочастотных характеристик) является привычной процедурой, хотя их понимание и толкование требуют определенной подготовки и опыта. Фазовая функция может быть непосредственно вычислена из выражения
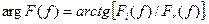
Фаза преобразования Фурье может быть также непосредственно получена из преобразования Хартли
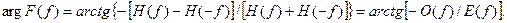
В объяснении характера изменения фазы при изменении частоты оказывается полезным опыт. При интерпретации фазы следует учитывать, что поведение фазы непосредственно связано с амплитудой, причем большие фазовые изменения происходят вблизи нуля амплитуды, и наоборот - незначительные изменения фазы при больших амплитудах.
Имеем следующую формулу для определения фазы преобразования Фурье через преобразование Хартли:
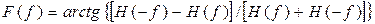
Наглядно это можно представить на следующем примере.

Полезной альтернативой одновременному представлению вещественной и мнимой частей является построение траектории на комплексной плоскости путем изображения 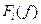 как функции как функции 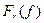 с обозначением на этой траектории значений частоты как параметра. Тогда для любой данной частоты амплитуда | с обозначением на этой траектории значений частоты как параметра. Тогда для любой данной частоты амплитуда | 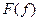 | определяет расстояние от начала координат до соответствующей точки параметрически заданной кривой, а фаза преобразования определяет угловую координату. Такая диаграмма для функции | определяет расстояние от начала координат до соответствующей точки параметрически заданной кривой, а фаза преобразования определяет угловую координату. Такая диаграмма для функции 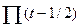 изображена на рис.1. Комплексная плоскость для данной диаграммы - это не плоскость из теории функции комплексной переменной, где независимая переменная оказывается комплексной величиной. Здесь независимая переменная изображена на рис.1. Комплексная плоскость для данной диаграммы - это не плоскость из теории функции комплексной переменной, где независимая переменная оказывается комплексной величиной. Здесь независимая переменная 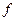 вещественна, однако зависимая переменная вещественна, однако зависимая переменная 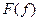 является комплексной, и можно рассматривать ее вещественную и мнимую части как декартовы координаты. является комплексной, и можно рассматривать ее вещественную и мнимую части как декартовы координаты.

Заслуживает внимания тот факт, что при движении по траектории к началу координат скорость «вычерчивания» траектории, измеряемая отношением длины дуги к частотному интервалу, уменьшается таким образом, что угловая скорость «бегущей» точки на траектории остается постоянной. Это свойство отражает линейную природу графа argF
(
f
)
; разрывы фазовой функции обусловлены прохождением траектории через начало координат.
Можно также рассматривать это преобразование в виде трехмерной винтовой траектории, для которой в данном случае можем представить только перспективную проекцию, но может быть сделана проволочная модель этой кривой. На рис.2 показана эта винтовая кривая, дополняющая наше представление еще одним измерением. Траекторию в полярных координатах можно представить в виде проекции винтовой кривой на плоскость 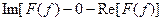 , а вещественную и мнимую части как проекции на горизонтальную и вертикальную плоскости прямоугольной системы координат соответственно. , а вещественную и мнимую части как проекции на горизонтальную и вертикальную плоскости прямоугольной системы координат соответственно.
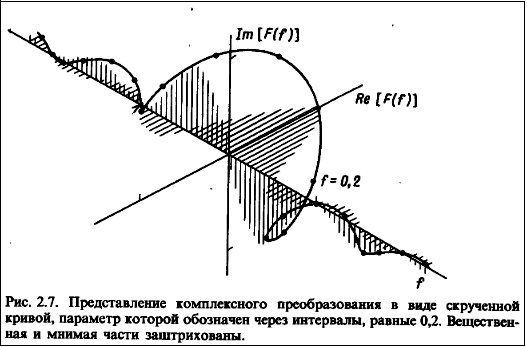
В определенном смысле преобразование Хартли может рассматриваться как гладкая форма представления вещественного колебания. Будучи чисто вещественным, преобразование Хартли не требует других способов представления, тогда как другие способы могут быть непосредственно получены из него.
3.Теоремы.
Теоремы преобразований полезны тем, что они позволяют избежать сложного математического анализа. Владея рядом теорем, можно получить новые преобразования, исходя из традиционных, свести данную задачу к известной и объединить функции в более сложные формы без необходимости все выполнять с самого начала. За счет этого упрощается интегрирование функций, имеющих аналитическое описание.
Численные методы расчетов также оказываются выгодными, когда применяются теоремы, позволяющие перейти к более простым или быстрым операциям. Наконец, это обеспечивает владение необходимым аппаратом логического мышления.
Рассматриваются два класса теорем. Первый из них связан с такими процедурами, как усечение, модуляция, свертка, и другими общепринятыми операциями, которые могут выполняться над функцией. Этот класс теорем дает ответ на вопрос: какой процедуре подвергается (как видоизменяется) преобразование исходной функции? Например, каким образом изменяется преобразование функции, являющейся зеркальным изображением исходной функции? Ответ заключается в следующем: преобразование также изменяется на зеркальное, что может показаться не столько простым, сколько очевидным выводом. Тем не менее, опыт показывает, что подобные знания оказываются полезными, особенно если могут быть применены соображения относительно симметрии, как в данном примере.
Второй класс теорем связан с соотношениями между функциями и их преобразованиями, что обычно может быть выражено в виде равенств. Например, интеграл от функции в бесконечных пределах равен главному значению ее преобразования. Здесь мы вновь имеем крайне простую теорему, которая, однако, избавляет от необходимости выполнять трудоемкое интегрирование, оказывается полезной при проверке численных расчетов и является сильным инструментом в случае, когда при решении какой-либо задачи возникает вопрос о выборе метода ее решения: аналитического или численного.
Значительная часть сведений об этих теоремах может быть сведена в таблицы, которые неизменны.
3.1.Соответствие операций.
Если колебание V
(
t
)
имеет преобразование Хартли H
(
f
),
то каким будет это преобразование для функции V
(
t
/
T
),
т. е. функции, получающейся из исходного колебания в результате растяжения шкалы времени в Т
раз? Непосредственное определение интеграла для положительных Т приводит к выражению
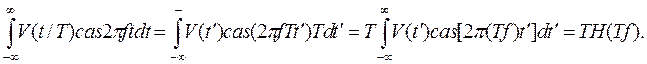
Если Т отрицательно, то для новой переменной 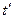 =
t
/
T
должно быть произведено изменение пределов интегрирования, вследствие чего результат равен -
TH
(
Tf
).
Чтобы учесть обе возможности (положительных и отрицательных Т), можно сформулировать вывод следующим образом: =
t
/
T
должно быть произведено изменение пределов интегрирования, вследствие чего результат равен -
TH
(
Tf
).
Чтобы учесть обе возможности (положительных и отрицательных Т), можно сформулировать вывод следующим образом:
Если V(t) имеет преобразование Хартли H (f), то V(t/T) имеет преобразование Хартли вида |T|H(Tf). Для сравнения приведем теорему подобия, или теорему изменения масштаба, применительно к преобразованию Фурье:

Если
V
(
t
) имеет преобразование Фурье
F
(
f
), то
V
(
t
/
T
) имеет преобразование Фурье вида |
T
|
F
(
Tf
).
Благодаря этой очень близкой аналогии удобно перечислить теоремы для обоих преобразований так, чтобы были наглядны и очевидны их различия. Ниже будут опущены выводы для простых соотношений, подобных рассмотренному примеру.
3.2.Свертка.
В таблице операции свертки и взаимной корреляции условно обозначены символами «звездочка» (*) и «пентаграмма» (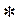 ). В соответствии с этими обозначениями имеем ). В соответствии с этими обозначениями имеем
V
1
(
t
)*
V
2
(
t
)=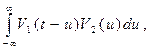
V
1
(
t
)
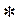 V
2
(
t
)= V
2
(
t
)=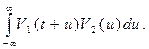
Важным свойством теоремы о свертке является следующее: если одна или обе функции, входящие в формулу свертки, являются либо четными, либо нечетными, то теоремы Хартли и Фурье (т. е. формулы прямых преобразований Хартли и Фурье для свертки) совпадают. Имеем теорему:
Если
V
1
(
t
) является четной функцией, то свертка
V
1
(
t
)
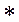 V
2
(
t
)
имеет преобразование Хартли вида Н1
(
f
)Н2
(
f
). V
2
(
t
)
имеет преобразование Хартли вида Н1
(
f
)Н2
(
f
).
Если одна из этих функций является нечетной, то формула упрощается.
Если
V
1
(
t
) -
нечетная функция, то свертка
V
1
(
t
)
*
V
2
(
t
) имеет преобразование Хартли вида Н1
(
f
)
H
2
(-
f
).
4. Дискретное преобразование Хартли
.
Хотя мы стремимся рассматривать время как непрерывную переменную, на практике необходимо использовать дискретную переменную для описания временных рядов, например, когда для вычисления требуется дискретизация этой переменной или в случае накапливания данных на регулярных интервалах. Поэтому введем дискретную переменную τ, которая будет соответствовать времени, но принимать только целочисленные значения от 0 до N - 1. Выбран именно этот интервал, а не [1, N] или [- (N/2) + 1,N/2] в соответствии с общепринятой практикой. Таким образом, прямое дискретное преобразование Фурье
(ДПФ) и обратное ему преобразование имеют стандартную форму
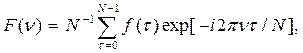
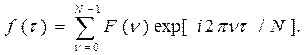
Функция f(τ) может быть дискретным представлением исходного непрерывного колебания или функцией переменной, дискретной по своей природе.
Дискретное преобразование Хартли (ДПХ) вещественной функции f(τ) и соответствующее обратное преобразование определяются соотношениями
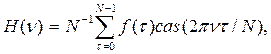
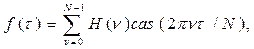
где, как и выше, используется обозначение cas θ= cos θ + sin θ, введенное Хартли.
Для получения обратного ДПХ воспользуемся свойством ортогональности
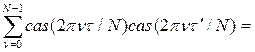 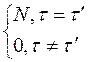
Подставляя величину 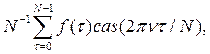 определяющую преобразование H
(
v
),
в выражение
определяющую преобразование H
(
v
),
в выражение 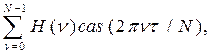 получим
получим
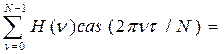
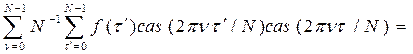
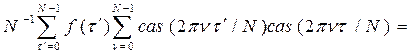
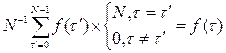 , ,
что подтверждает справедливость обратного преобразования.
Коэффициент 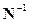 в ДПХ заимствуется из практики использования ДПФ, для которого величина F (0) равна постоянной составляющей функции
в ДПХ заимствуется из практики использования ДПФ, для которого величина F (0) равна постоянной составляющей функции 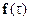 ; другими словами, ДПХ является симметричной процедурой. Кроме этого, ДПХ является вещественным преобразованием, так как вещественной является функция ; другими словами, ДПХ является симметричной процедурой. Кроме этого, ДПХ является вещественным преобразованием, так как вещественной является функция 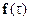 . .
Пример дискретного прямого и обратного преобразования Хартли:

4.1.Физический смысл величин τ и
ν
.
Переменная τ интерпретируется как время, а дискретная переменная ν - как частота; однако следует помнить две особенности. Если в качестве единицы времени t принята секунда, т. е. временной интервал между последовательными элементами временного ряда 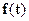 равен 1 с, то частота равна ν /N [Гц], а не ν, следовательно, частотный интервал между соседними элементами последовательности H(v) равен равен 1 с, то частота равна ν /N [Гц], а не ν, следовательно, частотный интервал между соседними элементами последовательности H(v) равен 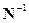 [Гц]. По мере увеличения ν возрастает соответствующая частота, но только до значения ν = N/2;
при дальнейшем росте величины ν соответствующая ей частота становится равной (N - ν)/N, обращаясь в нуль при ν = N. [Гц]. По мере увеличения ν возрастает соответствующая частота, но только до значения ν = N/2;
при дальнейшем росте величины ν соответствующая ей частота становится равной (N - ν)/N, обращаясь в нуль при ν = N.
4.2.Чётная и нечётная составляющие.
Как в случае непрерывного преобразования, ДПХ имеет чётную и нечетную компоненты
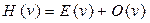 , ,
однако должны быть высказаны некоторые соображения в отношении определений в силу принятого ограничения диапазона изменения ν от 0 до N - 1. Общепринятый способ учета этого ограничения заключается в присвоении функции вне области ее определения таких значений, чтобы сформировать циклическую (периодическую) функцию с периодом N.
Таким образом, для ν = -1 мы присваиваем функции значение H(N - 1), так как ν = -1 и ν = N - 1 разделены периодом длины N. В общем случае будем присваивать функции Н(-ν), где -N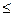 ν ν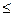 -1, значения H(N-ν) для которых независимая переменная заключена в основном диапазоне изменения ν. С помощью данной процедуры мы приходим к более простому соотношению между ν и частотой: можно сказать, что ν/N представляет собой не что иное, как частоту в герцах в диапазоне -N/2<ν<N/2.
Получим также соотношения для четной и нечетной составляющих, согласующиеся с равенствами, приведенными выше. Таким образом, имеем -1, значения H(N-ν) для которых независимая переменная заключена в основном диапазоне изменения ν. С помощью данной процедуры мы приходим к более простому соотношению между ν и частотой: можно сказать, что ν/N представляет собой не что иное, как частоту в герцах в диапазоне -N/2<ν<N/2.
Получим также соотношения для четной и нечетной составляющих, согласующиеся с равенствами, приведенными выше. Таким образом, имеем
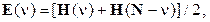
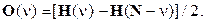
Рассмотрим чётную и нечётную составляющие ДПХ на примере биномиального импульса (см. ниже)
Из определения F(ν) для ДПФ очевидно, что F(ν) может быть получено с использованием четной и нечетной составляющих ДПХ: F(ν) = E(ν)-i
O(ν).
С другой стороны, если мы располагаем преобразованием F(ν), то можно сформировать H(ν): H(ν) = ReF(ν)-ImF(ν).
Эти выражения имеют сходство с соотношениями, полученными выше для непрерывного преобразования.

4.3.Степени свободы
.
Нами были установлены взаимно однозначные соотношения между дискретными преобразованиями Фурье и Хартли. При этом возникает вопрос из области теории информации. Как объяснить тот факт, что N вещественных значений ДПХ можно использовать вместо N комплексных значений ДПФ, которые содержат 2N вещественных чисел? Это можно понять, вспомнив о том, что эрмитово свойство ДПФ означает двойную избыточность. Таким образом, ДПФ имеет только N степеней свободы, несмотря на то, что имеется 2N вещественных коэффициентов. Так как для ДПХ вследствие его симметрии не характерно свойство вырожденности, N его вещественных коэффициентов эквивалентны N комплексным коэффициентам ДПФ.
4.4.Другие вещественные ядра.
Функция cas θ может рассматриваться как синусное колебание со сдвигом 45°, автоматически соответствующее косинусной и синусной компонентам. Если в качестве ядра преобразования использовать функцию 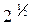 sin(θ+α), где α -произвольный сдвиг, то весовые множители косинусной и синусной компонент будут неодинаковы, однако при этом будут отсутствовать информационные потери, за исключением случаев, когда α = 0, π/2,… . sin(θ+α), где α -произвольный сдвиг, то весовые множители косинусной и синусной компонент будут неодинаковы, однако при этом будут отсутствовать информационные потери, за исключением случаев, когда α = 0, π/2,… .
Следовательно, можно предположить справедливость обратного преобразования; ядро обратного преобразования равно 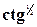 α sin θ + α sin θ + 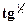 α cos θ. α cos θ.
4.5.Теоремы связанные с ДПХ.
 Каждой теореме дискретного преобразования Фурье соответствует подобная теорема для дискретного преобразования Хартли. Для полноты представления материала ниже даются все теоремы, в том числе теоремы о свертке и корреляции. Свертка функций непрерывного аргумента, обозначаемая символом Каждой теореме дискретного преобразования Фурье соответствует подобная теорема для дискретного преобразования Хартли. Для полноты представления материала ниже даются все теоремы, в том числе теоремы о свертке и корреляции. Свертка функций непрерывного аргумента, обозначаемая символом 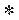 , отличается от процедуры циклической свертки дискретных последовательностей, для обозначения которой используется символ , отличается от процедуры циклической свертки дискретных последовательностей, для обозначения которой используется символ 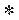 . .
Можно отметить, что среднее значение последовательности 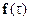 определяется величиной H(0), а значение ее среднего квадрата равно определяется величиной H(0), а значение ее среднего квадрата равно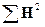 . .

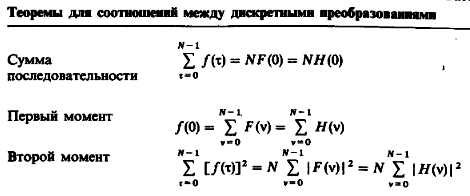
Некоторые теоремы для двух различных преобразований характеризуются точным соответствием, как, например 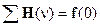 и и  , тогда как в других случаях имеют место различия. , тогда как в других случаях имеют место различия.
Теорема о зеркальном изображении.
Если из последовательности 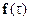 сформировать ее зеркальное изображение сформировать ее зеркальное изображение 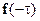 , то в результате ведущий (нулевой) элемент сохранит неизменное положение, а остальные элементы изменят порядок следования на обратный. Таким образом, вместо элемента f(1) исходной последовательности имеем f(-1), который интерпретируется как f(-1 mod N)
и равен f(N-1), т.е. является последним элементом новой последовательности. Следовательно, вместо последовательности {a b c в e f g h} имеем {a h g f e в c b},
что в области преобразования соответствует замене вида {ABCDEFGH} , то в результате ведущий (нулевой) элемент сохранит неизменное положение, а остальные элементы изменят порядок следования на обратный. Таким образом, вместо элемента f(1) исходной последовательности имеем f(-1), который интерпретируется как f(-1 mod N)
и равен f(N-1), т.е. является последним элементом новой последовательности. Следовательно, вместо последовательности {a b c в e f g h} имеем {a h g f e в c b},
что в области преобразования соответствует замене вида {ABCDEFGH}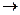 {AHGFEDСВ}. {AHGFEDСВ}.
Теорема сложения.
Свойство суперпозиции, иллюстрируемое теоремой сложения, просто отражает линейность оператора ДПХ.
Теорема о сдвиге.
Сначала рассмотрим пример, в котором реализуется единичный сдвиг последовательности {a0
a1
a2
... aN
-1
}, имеющей ДПХ вида {α0
α1
α2
... αN
-1
}. В соответствии с теоремой о сдвиге для Т=
1 имеем последовательность {a
N
-1
а0
а1
аг
…
a
N
-
2
}, для которой ДПХ равно
{ α 0
C1
α1
C2
a2
... C N-1
αN-1
} - { 0 S1
α N-1
S2
αN-2
... SN-1
α1
},
где Cν
= cos (2πν/N), Sν
= sin(2πν/N).
Для выполнения данной операция сдвига мы перемещаем каждый элемент исходной последовательности на одну позицию вправо. Последний элемент в соответствии с принятым свойством цикличности перемещается на первую позицию.
ДПХ состоит из двух последовательностей, одна из которых содержит косинусные, другая - синусные коэффициенты. ДПФ также представляет собой совокупность двух последовательностей с синусными и косинусными коэффициентами, однако для ДПХ в отличие от ДПФ для синусной компоненты характерно зеркальное отображение - это свойство именуется обратной индексацией. Для доказательства теоремы о сдвиге подставим f(t+T) в формулу, определяющую прямое ДПХ, и получим
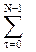 f(τ+T)cas(2πντ/N) = f(τ+T)cas(2πντ/N) = 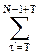 f( f(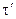 )cas[2πν( )cas[2πν(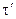 -T)/N] = -T)/N] =
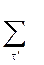 f( f(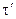 )[cas (2πν )[cas (2πν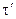 /N) cos (2πνT/N) + cas'(2πν /N) cos (2πνT/N) + cas'(2πν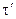 /N) sin(2 πνT/N)] = /N) sin(2 πνT/N)] =
cos (2πνT/N) 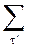 f( f(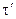 )cas(2πν )cas(2πν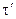 /N) + sin(2πνT/N) /N) + sin(2πνT/N) 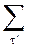 f( f(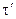 )cas'(2πνT/N) = )cas'(2πνT/N) =
cos (2πνT/N) H(ν) - sin(2πνT/N) 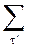 f( f(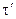 )cas(-2πν )cas(-2πν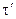 /N) = /N) =
cos(2πνT/N) H(ν) -sin(2πνT/N)H(-ν).
 Теорема о свертке.
В общем случае преобразование свертки Теорема о свертке.
В общем случае преобразование свертки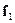 (τ) (τ) 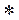 f2
(τ) содержит четыре компоненты. Основными величинами, которые должны быть вычислены, являются прямые произведения Ра
(ν)= H1
(ν)H2
(ν) и смешанные произведения Рb
(ν)=
H1
(ν)H2
(-ν). С использованием этих обозначений имеем H(ν)= f2
(τ) содержит четыре компоненты. Основными величинами, которые должны быть вычислены, являются прямые произведения Ра
(ν)= H1
(ν)H2
(ν) и смешанные произведения Рb
(ν)=
H1
(ν)H2
(-ν). С использованием этих обозначений имеем H(ν)= 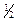 N[Pa
(ν)-Ра
(-ν)+Рb
(ν)+Рb
(-ν)]. N[Pa
(ν)-Ра
(-ν)+Рb
(ν)+Рb
(-ν)].
Таким образом, данная процедура включает два, а не четыре действия умножения. Теперь если Н2
(ν) - четная функция (т. е. Н2
(ν)= H2
(-ν)), то
H(ν) =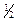 NHl
(ν)H2
(ν). NHl
(ν)H2
(ν).
Рассмотрим пример, когда H2
(ν) –чётная функция.

Точно так же простую формулу получим в случае, когда Н2
(ν) является нечетной функцией; при этом имеем H(ν)=NHl
(-ν)H2
(ν).
Вследствие коммутативности Н(ν)=NHl
(ν)H2
(ν), если либо H1
(ν), либо Н2
(ν) являются четными функциями. Часто одна либо другая функция обладает свойствами симметрии или антисимметрии, что приводит к более простым соотношениям. Ввиду важности операции свертки мы вернемся к ней в следующей главе.
Теорема о произведении.
В теореме о произведении четыре компоненты предполагают выполнение только двух операций свертки, так как две другие просто реализуются путем зеркального отображения двух сомножителей.
Теорема о растяжении.
Сходство этой теоремы с соответствующей теоремой для случая непрерывной независимой переменной относится к изменению масштаба по оси абсцисс, когда V(t) преобразуется в V(t/T). Так как величина T может быть либо больше, либо меньше единицы, операция может представлять собой либо растяжение, либо сжатие. В случае дискретной переменной изменения масштаба также имеют практическое значение, например, когда последовательность регулярных измерений должна быть повторена с большей или меньшей скоростью. Функция V(t/T) определена для любого Т при заданной V(t), но это утверждение несправедливо для f(τ/Т) при заданной функции f(τ), где τ=0,1, … ,N-1.
Следовательно, применительно к теореме подобия отсутствует строгая аналогия. Теорема о растяжении имеет отношение только к увеличению масштаба времени, что осуществляется добавлением нулей в исходную последовательность. Наиболее просто это можно проиллюстрировать на примере.
Пусть последовательность {abcd} имеет последовательность ДПХ {α β γ δ}. Тогда последовательности {а 0 b 0 с 0 в 0} соответствует последовательность ДПХ вида 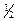 {α β γ δ α β γ δ }. {α β γ δ α β γ δ }.
В правомерности этого результата можно убедиться, анализируя выражение для прямого ДПХ:
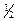 α+ α+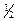 βcas τθ+ βcas τθ+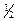 γcas 2τθ+ γcas 2τθ+
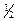 δcas 3τθ+ δcas 3τθ+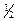 αcas 4τθ+ αcas 4τθ+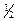 βcas 5τθ+ βcas 5τθ+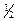 γcas 6τθ+ γcas 6τθ+ δcas7τθ. δcas7τθ.
Убеждаемся в том, что при τ = 0 имеем f(0) = а.
При нечетном τ сумма равна нулю, для четного τ эта сумма сводится к выражению: α+βcasτθ+γcas2τθ+δcas3τθ, для которого обратное преобразование Хартли имеет вид: {a b c d}.
Теорема о второй производной.
Рассмотрим данную теорему на примере экспоненциальной функции.

4.6.Выводы по ДПХ.
Свойства ДПХ свидетельствуют в пользу использования этого преобразования в численном анализе. Тот факт, что значения преобразования Хартли являются вещественными, создает удобства при выполнении расчетов. Кроме того, полезно свойство симметрии обращения преобразования, так как не требуется запоминать, к какой области представления относится данная последовательность. Более того, ряд теорем для преобразования Фурье имеет различную форму для разных областей представления (временной или частотной); этот недостаток отсутствует у ДПХ. Множитель N зависит от области представления, и от него можно было бы избавиться, однако на практике почти всегда существуют нормирующие или калибровочные факторы, которые должны быть учтены по окончании численных расчетов. Опыт показывает, что последний этап заключается в учете в совокупной форме коэффициентов пропорциональности, поэтому отклонение от точного соответствия между прямым и обратным преобразованиями, заключающееся в появлении коэффициента N, не имеет значения в практике вычислений.
5.Заключение.
Таким образом, в данном реферате были рассмотрены некоторые основы преобразования Хартли. В результате чего можно сделать следующие выводы.
Во-первых, хотя между интегралами преобразования Хартли
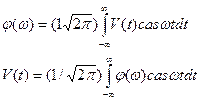
отсутствуют существенные отличия от обычных интегральных формул преобразования Фурье, однако на практике эти различия значительны.
Во-вторых, функция 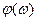 вещественна в отличие от функции преобразования Фурье. вещественна в отличие от функции преобразования Фурье.
В-третьих, обратное преобразование для его реализации требует точно такой же процедуры интегрирования, как и прямое преобразование.
Наконец, 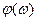 не является обычным преобразованием Фурье, и мы должны быть готовы к нетрадиционным характеру и свойствам этого преобразования. Значительная часть умозрительных построений относительно преобразования Фурье, а, именно спектра колебания, являющегося функцией времени, непосредственно неприменима к не является обычным преобразованием Фурье, и мы должны быть готовы к нетрадиционным характеру и свойствам этого преобразования. Значительная часть умозрительных построений относительно преобразования Фурье, а, именно спектра колебания, являющегося функцией времени, непосредственно неприменима к 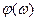 . .
|