| Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 20»
История развития математики на примере палеолита, средних веков и нашего времени
(реферат)
Автор-составитель
Хасанова Анастасия
6 «А» класс
Руководитель
С.А. Галимова, учитель математики
высшей квалификационной категории
Анжеро-Судженск 2010
СОДЕРЖАНИЕ
Введение………………………………………………………3
Глава 1. Первоначальное появление математики………… 4
Глава 2. Математика в средние века ……………..……….. 7
Глава 3. Начало современной математики………………. 12
Заключение…………………………………………………...15
Список литературы…………………………………………. 16
ВВЕДЕНИЕ
Что дала математика людям? Зачем её изучать? Когда она родилась и что явилось причиной её возникновения?
Часто можно прочесть, что математика возникла в глубокой древности из практических потребностей людей. По поводу древности математики никто спорить не будет, а вот о том, что побудило людей ею заниматься, существует и другое мнение. Согласно ему, математика, так же как поэзия, живопись, музыка, театр и вообще – искусство, была вызвана к жизни духовными потребностями человека.
Цель реферата: ознакомление с историей развития математики.
Задачи:
1. изучить литературу по истории развития математики (энциклопедии, словари, сайты из интернета и т.д.);
2. расширить свой кругозор по данному вопросу;
3. выявить пути развития математики.
Данная работа будет полезна тем, кто проявляет повышенный интерес к изучению математики и истории.
ГЛАВА 1. ПЕРВОНАЧАЛЬНОЕ ПОЯВЛЕНИЕ МАТЕМАТИКИ.
Наши первоначальные представления о числе и форме относятся к очень отдаленной эпохе древнего каменного века — палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях, мало отличавшихся от жизни животных, и их энергия уходила преимущественно на добывание пищи простейшим способом — собиранием ее, где только это было возможно. Люди изготовляли орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки.
Пока не произошел переход от простого собирания
пищи к активному ее производству,
от охоты и рыболовства к земледелию, люди мало продвинулись в понимании числовых величин и пространственных отношений. Лишь с наступлением этого фундаментального перелома, переворота, когда пассивное отношение человека к природе сменилось активным, мы вступаем в новый каменный век неолит.
Постепенно прекращались кочевые странствия в поисках пищи. Рыболовы и охотники все больше вытеснялись первобытными земледельцами. Такие земледельцы, оставаясь на одном месте, пока почва сохраняла плодородие, строили жилища, рассчитанные на долгие сроки.
Деревни вели между собой значительную торговлю, которая настолько развилась, что можно проследить наличие торговых связей между областями, удаленными на сотни километров друг от друга. Эту коммерческую деятельность сильно стимулировали открытие техники выплавки меди и бронзы и изготовление сначала медных, а затем бронзовых орудий и оружия. Это в свою очередь содействовало дальнейшему формированию языков. Слова этих языков выражали вполне конкретные вещи и весьма немногочисленные абстрактные понятия, но языки уже имели известный запас слов для простых числовых «терминов» и для некоторых пространственных образов.
Числовые термины, выражающие некоторые из «наиболее абстрактных понятий, какие в состоянии создать человеческий ум», как сказал Адам Смит, медленно входили в употребление. Впервые они появляются скорее как качественные, чем количественные термины, выражая различие лишь между одним (или, вернее, «каким-то»—«какой-то» скорее, чем «один человек») и двумя и многими. С понятия числа большие числа сначала образовывались с помощью сложения: 3 путем сложения 2 и 1, 4 путем сложения 2 и 2, 5 путем сложения 2 и 3.
Развитие ремесла и торговли содействовало кристаллизации понятия числа. Числа группировали и объединяли в большие единицы, обычно пользуясь пальцами одной руки или обеих рук—обычный в торговле прием.
Пальцевый счет, то есть счет пятками и десятками, возник только на известной ступени общественного развития. Но раз до этого дошли, появилась возможность выражать числа в системе счисления, что позволяло образовывать большие числа. Так возникла примитивная разновидность арифметики. Четырнадцать выражали как 10 + 4, иногда как 15 - 1. Умножение зародилось тогда, когда 20 выразили не как 10 + 10, а как 2 * 10. Подобные двоичные действия выполнялись в течение тысячелетий, представляя собой нечто среднее между сложением и умножением.
Возникла и необходимость измерять длину и емкость предметов. Единицы измерения были грубы, и при этом часто исходили из размеров человеческого тела. Об этом нам напоминают такие единицы, как палец, фут
(то есть ступня), локоть.
Когда начали строить дома такие, как у земледельцев Индии или обитателей свайных построек Центральной Европы, стали вырабатываться правила, как строить по прямым линиям и под прямым углом.
Человек неолита обладал так же острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин и тканей, позже — обработка металлов вырабатывали представление о плоскостных и пространственных соотношениях.
ГЛАВА 2. МАТЕМАТИКА В СРЕДНИЕ ВЕКА
Начиная с 3 века н.э., все крупные государства Античного мира вошли в эпоху кризисов. Многие из них - как Римская империя в Средиземноморье и китайская империя Хань на восточном краю Евразии - распались на мелкие княжества и вскоре стали добычей соседних варваров. Затем эпоха распада империй сменилась эпохой переселения народов. На просторах Евразии разноплеменные варвары вновь и вновь делили наследство древних государств. Большая часть античной культуры погибла в этом пожаре: города были разграблены и покинуты, библиотеки сгорели, университеты закрылись, а ученые вымерли, не оставив учеников. В новом мире невежества островки науки и просвещения сохранялись только в монастырях разных религий: христианских на западе, буддийских или индуистских на востоке и юге Евразии. Позднее (с 8 века н.э.) в новой империи - Арабском Халифате - возникли исламские монастыри.
Большинство богословов Средневековья не одобряло античную мудрость; об ученых-исследователях говорили, что они "ум свой ставят в Бога место". Но в монастырях сохранилось уважение к древним рукописям: монахи переписывали их дословно, не вникая в смысл того, что написано. Таким путем многие достижения ученых эллинов или римлян сохранились в течение веков и достигли новых мыслителей, пройдя сквозь множество невежд.
Любознательные представители каждого нового народа, включаясь в мировую культуру, были вынуждены осваивать древнюю мудрость самостоятельно - без помощи старших коллег. Эта работа занимала века и поглощала все силы новых ученых. Поэтому в большинстве стран нового мира дело не дошло до оригинальных открытий вроде тех, которые сделали эллины. В средневковом мире нехватало городов-республик, подобных полисам Эллады; пока они не появились, наука развивалась очень медленно.
Из всех ойкумен Земли Индия оказалась наименее затронута переселением народов. Не удивительно, что именно здесь в 6 веке н.э. расцвела самобытная математическая школа. Познакомившись с достижениями эллинов, индийцы были удивлены: какая совершенная у них геометрия, и какая неудобная арифметика! Хуже всего греческая система записи чисел: с помощью букв, без всякой связи с привычным счетом на пальцах. Надо связать обозначения чисел с процедурой счета! Индийские ученые сделали это, создав позиционную десятичную систему счисления.
Первый шаг к этой цели сделал около 500 года молодой математик Ариабхата из города Кусумапура. Он начал изображать каждый разряд в десятичной записи целого числа парой букв. Согласная обозначала цифру, а гласная - номер разряда, так что символ ВА означал В*10.. Эти пары букв записывались по возрастанию степеней числа 10. Но различить такое слово-число в обычном тексте было не просто; поэтому вскоре начертания букв-цифр были изменены, и появились первые десятичные цифры. Нуля среди них еще не было - но вскоре пришлось его ввести, для удобства чтения десятичной записи. Через сто лет после Ариабхаты его соотечественник Брахмагупта уже свободно оперировал с отрицательными числами и нулем и решал целочисленные уравнения с таким же искусством, как Диофант.
Оставалось разнести эту полезную новинку по всему свету. Тут важнейшую роль сыграл современник Брахмагупты - пророк Мухаммед из Мекки. Он сам и многие его сподвижники были в равной мере воинами и купцами. Поэтому как только арабы покорили Иран и вторглись в Индию (в 660-е годы), они сразу оценили индийскую систему счета и переняли ее. Вскоре позиционная система счисления распространилась во всем арабском Халифате - от Индии до Андалузии (будущей Испании), от Египта до Поволжья. С тех пор во всем мире (кроме Индии) десятичные цифры называют "арабскими". Но, конечно, скорость усвоения этой новинки разными народами зависела от их экономического развития.
В конце 8 века мировое научное первенство перешло из Индийского мира в Исламский мир, центром которого стал Багдад, расположенный на Тигре - вблизи развалин Вавилона. Основатель Багдада - халиф Мансур (707-775) - хотел, чтобы его столица превзошла великолепием и ученостью Александрию и Константинополь. Но ученых арабов в ту пору было еще мало; ведущую роль в новом "Доме Мудрости" в Багдаде играли сирийцы и персы, согдийцы и греки, принявшие ислам.
Наибольших успехов в математике достиг согдиец Мухаммед ибн Муса аль-Хорезми (то есть, родом из Хорезма - с берегов Сыр-Дарьи). Он работал в первой половине 9 века и был любимцем ученейшего из халифов - Маамуна (сына знаменитого Гаруна ар-Рашида). Главная книга Хорезми названа скромно: "Учение о переносах и сокращениях", то есть техника решения алгебраических уравнений. По арабски это звучит "Ильм аль-джебр ва"ль-мукабала"; отсюда произошло наше слово "алгебра". Другое известное слово - "алгоритм", то есть четкое правило решения задач определенного типа - произошло от прозвания "аль-Хорезми". Третий известный термин, введенный в математику знаменитым согдийцем - это "синус", хотя в этом деле не обошлось без курьеза.
Геометрический смысл синуса - это половина длины хорды, стягивающей данную дугу. Хорезми назвал эту вещь красиво и точно: "тетива лука"; по арабски это звучит "джейяб". Но в арабском алфавите есть только согласные буквы; гласные изображаются "огласовками" - черточками, вроде наших кавычек и запятых. Мало сведущий человек, читая арабский текст, нередко путает огласовки; так случилось с переводчиком книги Хорезми на латынь. Вместо "джейяб" - "тетива" - он прочел "джиба" - "бухта"; по латыни это пишется "sinus". С тех пор европейские математики используют это слово, не заботясь о его изначальном смысле.
Первое столетие крестовых походов расширило кругозор очень многих европейцев. Особенно отличились жители приморских городов Италии: Венеции, Генуи, Пизы. Здешние мореходы переправляли крестоносцев и паломников в Святую землю, а купцы наживались, продавая добычу крестоносцев и иные "восточные" товары по всей Европе. Постепенно многие города католической Италии превратились в торговые республики, похожие на полисы античной Эллады. С начала 13 века в этих республиках заметна научная самодеятельность не только церковников, но и мирян - прежде всего, купцов.
В 1202 году появился первый "самодельный" учебник арифметики для широкого читателя - "Книга Абака". Его составил Леонардо Фибоначчи из Пизы (1180-1240), с детства причастный к торговым делам своего отца. Арифметике он научился в Алжире у местных мусульман, а теперь сам обучал единоверцев новому десятичному счету. Позднее Фибоначчи написал учебник "Практическая геометрия" и "Книгу квадратов". В них впервые были изложены (на латыни) правила действий с нулем и отрицательными числами, а также появились знаменитые числа Фибоначчи.
Тем временем на папский престол взошел второй ученый человек: Лотарио ди Конти ди Сеньи (1160-1216), выпускник Парижского университета. Потомки запомнили его под грозным именем Иннокентия 3 - "Раба рабов Божьих", помыкавшего королями и свергавшего герцогов или князей по всей Европе. Только король Франции Филипп 2 Август порою осмеливался противоречить грозному папе - в тех случаях, когда он мог опереться на авторитет Парижского университета. Так первые католические университеты заявили о своей независимости от любой духовной или светской власти. Наряду с городами-республиками Италии, они сделались рассадником независимой учености в Европе. Процветающий Католический Интернационал начал походить на созвездие полисов Эллады.
Английские университеты заявили о себе в середине 13 века. Тогда англичане, опираясь на свою первую конституцию (Великую Хартию Вольностей), попытались взять под контроль легкомысленного короля Генри 3 и его алчных фаворитов. Духовным лидером этого движения стал ученейший богослов - Роберт Гросетест ("Головастый"), епископ Линкольна (1175-1253). Он увлекся оптикой и пришел к мысли, что весь мир возник из света - самой совершенной формы материи. Более грубые тела получились при застывании света. Таким образом, Гросетест представил мир как результат игры двух начал - света и порядка, или (в понятиях 20 века) энергии и симметрии. Ни один современный физик или математик не станет с этим спорить!
Подобно античным натурфилософам, Гросетест не мог рассчитать свою физическую модель. Зато другая таинственная вещь - бесконечность - поддавалась расчету, и Гросетест увлекся этим делом. Он начал суммировать бесконечные ряды чисел, и вскоре научился отличать сходящийся ряд от расходящегося. Но и расходиться ряд может с разной скоростью. Гросетест заметил, что сумма натуральных чисел растет гораздо медленнее, чем сумма их квадратов, а сумма квадратов - медленнее, чем сумма последовательных степеней двойки. Так первый из христиан проник в область бесконечно больших и бесконечно малых величин - вслед за Архимедом и на 4 столетия опережая Ньютона. Хорошая компания для богослова!
Однако решающий прорыв из Средневековья в Новое время европейцы совершили, когда изобрели печатный станок с подвижным металлическим шрифтом. В 1454 году Иоганн Гутенберг напечатал в Майнце первые 300 экземляров Библии и положил начало информационной революции - столь же важной, как появление алфавита в Элладе в 8 веке до н.э., или появление электронных компьютеров в середине 20 века. В 1482 году в Венеции была впрервые напечатана (по латыни) книга Евклида "НГачала". С этого момента для математиков кончилось Средневековье и началось Новое время.
ГЛАВА 3. НАЧАЛО СОВРЕМЕННОЙ МАТЕМАТИКИ
Наступление 16 в. в Западной Европе ознаменовалось важными достижениями в алгебре и арифметике. Были введены в обращение десятичные дроби и правила арифметических действий с ними. Настоящим триумфом стало изобретение в 1614 логарифмов Дж.Непером. К концу 17 в. окончательно сложилось понимание логарифмов как показателей степени с любым положительным числом, отличным от единицы, в качестве основания. С начала 16 в. более широко стали употребляться иррациональные числа. Б.Паскаль (1623–1662) и И.Барроу (1630–1677), учитель И.Ньютона в Кембриджском университете, утверждали, что такое число, как 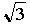 , можно трактовать лишь как геометрическую величину. Однако в те же годы Р.Декарт (1596–1650) и Дж.Валлис (1616–1703) считали, что иррациональные числа допустимы и сами по себе, без ссылок на геометрию. В 16 в. продолжались споры по поводу законности введения отрицательных чисел. Еще менее приемлемыми считались возникавшие при решении квадратных уравнений комплексные числа, такие как , можно трактовать лишь как геометрическую величину. Однако в те же годы Р.Декарт (1596–1650) и Дж.Валлис (1616–1703) считали, что иррациональные числа допустимы и сами по себе, без ссылок на геометрию. В 16 в. продолжались споры по поводу законности введения отрицательных чисел. Еще менее приемлемыми считались возникавшие при решении квадратных уравнений комплексные числа, такие как  , названные Декартом «мнимыми». Эти числа были под подозрением даже в 18 в., хотя Л.Эйлер (1707–1783) с успехом пользовался ими. Комплексные числа окончательно признали только в начале 19 в., когда математики освоились с их геометрическим представлением. , названные Декартом «мнимыми». Эти числа были под подозрением даже в 18 в., хотя Л.Эйлер (1707–1783) с успехом пользовался ими. Комплексные числа окончательно признали только в начале 19 в., когда математики освоились с их геометрическим представлением.
Достижения в алгебре. В 16 в. итальянские математики Н.Тарталья (1499–1577), С.Даль Ферро (1465–1526), Л.Феррари (1522–1565) и Д.Кардано (1501–1576) нашли общие решения уравнений третьей и четвертой степеней. Чтобы сделать алгебраические рассуждения и их запись более точными, было введено множество символов, в том числе +, –, ,  , =, > и <. Самым существенным новшеством стало систематическое использование французским математиком Ф.Виетом (1540–1603) букв для обозначения неизвестных и постоянных величин. Это нововведение позволило ему найти единый метод решения уравнений второй, третьей и четвертой степеней. Затем математики обратились к уравнениям, степени которых выше четвертой. Работая над этой проблемой, Кардано, Декарт и И.Ньютон (1643–1727) опубликовали (без доказательств) ряд результатов, касающихся числа и вида корней уравнения. Ньютон открыл соотношение между корнями и дискриминантом [b2
– 4ac] квадратного уравнения, а именно, что уравнение ax2
+ bx + c = 0 имеет равные действительные, разные действительные или комплексно сопряженные корни в зависимости оттого, будет ли дискриминант b2
– 4ac равен нулю, больше или меньше нуля. В 1799 К.Фридрих Гаусс (1777–1855) доказал т.н. основную теорему алгебры: каждый многочлен n-й степени имеет ровно n корней. , =, > и <. Самым существенным новшеством стало систематическое использование французским математиком Ф.Виетом (1540–1603) букв для обозначения неизвестных и постоянных величин. Это нововведение позволило ему найти единый метод решения уравнений второй, третьей и четвертой степеней. Затем математики обратились к уравнениям, степени которых выше четвертой. Работая над этой проблемой, Кардано, Декарт и И.Ньютон (1643–1727) опубликовали (без доказательств) ряд результатов, касающихся числа и вида корней уравнения. Ньютон открыл соотношение между корнями и дискриминантом [b2
– 4ac] квадратного уравнения, а именно, что уравнение ax2
+ bx + c = 0 имеет равные действительные, разные действительные или комплексно сопряженные корни в зависимости оттого, будет ли дискриминант b2
– 4ac равен нулю, больше или меньше нуля. В 1799 К.Фридрих Гаусс (1777–1855) доказал т.н. основную теорему алгебры: каждый многочлен n-й степени имеет ровно n корней.
Основная задача алгебры – поиск общего решения алгебраических уравнений – продолжала занимать математиков и в начале 19 в. Когда говорят об общем решении уравнения второй степени ax2
+ bx + c = 0, имеют в виду, что каждый из двух его корней может быть выражен с помощью конечного числа операций сложения, вычитания, умножения, деления и извлечения корней, производимых над коэффициентами a, b и с. Молодой норвежский математик Н.Абель (1802–1829) доказал, что невозможно получить общее решение уравнения степени выше 4 с помощью конечного числа алгебраических операций. Однако существует много уравнений специального вида степени выше 4, допускающих такое решение. Накануне своей гибели на дуэли юный французский математик Э.Галуа (1811–1832) дал решающий ответ на вопрос о том, какие уравнения разрешимы в радикалах, т.е. корни каких уравнений можно выразить через их коэффициенты в помощью конечного числа алгебраических операций. В теории Галуа использовались подстановки или перестановки корней и было введено понятие группы, которое нашло широкое применение во многих областях математики.
Если математику, известную до 1600, можно охарактеризовать как элементарную, то по сравнению с тем, что было создано позднее, эта элементарная математика бесконечно мала. Расширились старые области и появились новые, как чистые, так и прикладные отрасли математических знаний. Выходят около 500 математических журналов. Огромное количество публикуемых результатов не позволяет даже специалисту ознакомиться со всем, что происходит в той области, в которой он работает, не говоря уже о том, что многие результаты доступны пониманию только специалиста узкого профиля. Ни один математик сегодня не может надеяться знать больше того, что происходит в очень маленьком уголке науки.
ЗАКЛЮЧЕНИЕ
Мной была прочитана необходимая литература, которая помогла мне в изучении данного вопроса. После анализа всего прочитанного, я поняла, что мне ёще недостаточно знаний в освоении некоторых математических истин, не совсем понятны термины, используемые в литературных источниках. Я убедилась, насколько широки пути развития математики. Об этом можно говорить еще очень много.
«Тот, кто не знает математики, не может узнать никакой другой науки и даже не может обнаружить своего невежества» (Роджер Бэкон – английский философ, 18 в.)
СПИСОК ЛИТЕРАТУРЫ
1. Энциклопедия для детей. Т.11. Математика/ Глав. Ред. М.Д. Аксенова; метод. и отв. редактор В.А. Володин. – М.:Аванта+, 2003
2. http://www.5ballov.ru
|