Реферат: «Система mathematica 4»
|
Название: «Система mathematica 4» Раздел: Остальные рефераты Тип: реферат | |||||||||||||||
| Министерство образования и науки Российской Федерации Хабаровский государственный педагогический университет РЕФЕРАТ на тему: «Система MATHEMATICA 4» Выполнил: студент 233 гр. ИМФиИТ Лагойко Евгений Проверил преподаватель: Ершов Николай Егорович г. Хабаровск 2004 г.
Содержание.
I. Введение................................................................................................. 3 II. Основная часть 1. Система Mathematica 4..................................................................... 4 2. Строка меню и окно редактора документа..................................... 5 3. Палитры математических операций и функций.............................. 7 4. Особенности интерфейса Mathematica 4.......................................... 8 5. Работа с файлами.............................................................................. 9 6. Меню File.......................................................................................... 11 7. Основные классы данных................................................................. 13 8. Функции компьютерной алгебры.................................................... 14 9. Операции математического анализа................................................ 17 10. Двумерная графика.......................................................................... 20 11. Трехмерная графика............................................................................................. 23 12. Методы программирования........................................................................... 27 III. Заключение............................................................................................ 30 IV. Список использованной литературы.................................................... 32
I. Введение Зарождение и развитие систем компьютерной алгебры У истоков рождения систем компьютерной алгебры Эру создания компьютерной символьной математики принято отсчитывать с начала 60-х годов. Именно тогда в вычислительной технике возникла новая ветвь компьютерной математики, не совсем точно, но зато броско названная компьютерной алгеброй. Речь шла о возможности создания компьютерных систем, способных осуществлять типовые алгебраические преобразования: подстановки в выражениях, упрощение выражений, операции со степенными многочленами (полиномами), решение линейных и нелинейных уравнений и их систем, вычисление их корней и т. д. При этом предполагалась возможность получения аналитических (символьных) результатов везде, где это только возможно. К сожалению, книги по этому направлению были способны лишь отпугнуть обычного читателя и пользователя компьютера от изучения возможностей компьютерной алгебры в силу перенасыщенности их узкоспециальным теоретическим материалом и весьма специфического языка описания. Материал таких книг, возможно, интересен математикам, занимающимся разработкой систем компьютерной алгебры, но отнюдь не основной массе их пользователей. Большинство же пользователей заинтересовано в том, чтобы правильно выполнить конкретные аналитические преобразования, вычислить в символьном виде производную или первообразную заданной функции, разложить ее в ряд Тейлора или Фурье, провести аппроксимацию и т. д., а вовсе не в детальном и сложном математическом и логическом описании того, как это делается компьютером (или, точнее, его программистом). Здесь та же ситуация, что и с телевизором, радиоприемником или факсом: большинство из нас пользуются этими аппаратами, вовсе не интересуясь тем, как именно они выполняют свои довольно сложные функции. Это тем более важно в связи с тем, что предметные области, представляющие интерес для пользователя (будь он математик, физик, биолог или химик), перегружены своим собственным математическим аппаратом. Словом, большинству пользователей нужны системы компьютерной алгебры в качестве простого и удобного инструмента >для работы, а не в виде сборища головоломок и ребусов, требующих массы времени на разгадку их таинств. Поняв эту истину, многие западные фирмы приступили к созданию компьютерных систем символьной математики, ориентированных на широкие круги пользователей, не являющихся профессионалами в компьютерной алгебре. Учитывая невероятно большую сложность автоматизации решения задач в аналитическом виде (число математических преобразований и соотношений весьма велико, и некоторые из них неоднозначны в истолковании), первые подобные системы удалось создать лишь для больших ЭВМ. Но затем появились и системы, доступные для мини-ЭВМ. Заметное развитие получили языки программирования для символьных вычислений Reduce, система muMath для малых ЭВМ, а в дальнейшем — интегрированные системы символьной математики для персональных компьютеров: Derive, MathCAD, Mathematica, Maple V и др. В бывшем СССР большой вклад в развитие систем символьной математики внесла школа покойного академика Глушкова. В конце 70-х годов были созданы малые инженерные ЭВМ класса «Мир», способные выполнять аналитические вычисления даже на аппаратном уровне. Был разработан и успешно применялся язык символьных вычислений «Аналитик». Эти работы отчасти предвосхитили развитие систем символьной математики. К огромному сожалению, они появились слишком рано для своего времени и не соответствовали «генеральной линии» развития советской вычислительной техники в те годы. Уклон в сторону развития больших ЭВМ серии ЕС, навязанный в СССР компьютерными чиновниками, отодвинул компьютеры «Мир» на задний план, а затем этот класс компьютеров просто прекратил свое существование и развитие. К сожалению, в отрыве от мировой науки и серьезных источников финансирования наши работы (за исключением некоторых теоретических) в области компьютерной алгебры оказались малоэффективными — отечественных систем компьютерной алгебры для персональных компьютеров, доведенных до серийного производства и мировой известности, так и не было создано (впрочем, как и конкурентоспособных ПК на нашей элементной базе). Зато множество наших специалистов — как математиков, так и программистов — эмигрировали на Запад и приняли участие, порой весьма серьезное, в разработке западных систем символьной математики. В том числе и систем класса Mathematica. Стоимость серийных СКМ все еще чрезмерно велика для большинства наших пользователей. Поэтому не случайно, что (за редчайшим исключением) наши пользователи используют такие системы, распространяемые на CD-ROM сомнительного происхождения. Однако программные продукты на таких CD-ROM поступают без документации, а порой даже в неполном и неполноценном виде, что затрудняет их серьезное применение. II. Основная часть 1. Система Mathematica 4 Ожидалось, что, как и предшествующие реализации 1 и 2, система Mathematica 3 даст начало многолетнему марафону постепенного усовершенствования этой системы. Но вопреки этому фирма Wolfram совершила довольно неожиданный для нее шаг — не успели пользователи разобраться с многими новациями Mathematica 3, как в июне 1999 г. на рынок была выпущена новейшая реализация системы — Mathematica 4. При этом имеющиеся данные свидетельствуют о коренном пересмотре базовых концепций, заложенных в систему. Видимо, роль в этом сыграло приближение 2000 года. Новая система получила развитие прежде всего как система для быстрых и объемных численных вычислений при сохранении всего ее могущества в области символьной математики. Значительно повышена скорость основных численных вычислений и операций с произвольной разрядностью. Улучшена плотность упаковки массивов, введен ряд новых встроенных функций. Повышена скорость работы пользовательского интерфейса, он стал более удобным. Чего стоит, к примеру, такая мелочь, как изменение цвета элементов выражений в ходе их ввода — это облегчает устранение ошибок при вводе сложных выражений. Теперь уже окончательно ясно — разработчики системы продолжают интенсивно работать над ней и превратили Mathematica 4 в мощную универсальную СКМ. И первые данные о новой версии системы, которые читатель найдет в этой книге, ясно говорят о том, что разработчики систем этого класса отнюдь не намерены уступать первенство в создании наиболее сложных и продвинутых систем компьютерной алгебры. Возможности новой системы весьма впечатляют! Важно отметить, что весьма обширные новые возможности Mathematica 4 относятся почти исключительно к количественным показателям системы и никоим образом не влияют на статический вид интерфейса систем (в сравнении с Mathematica 3) и на вид готовящихся документов-блокнотов (notebooks). Поэтому в дальнейшем мы под системой Mathematica будем иметь в виду одновременно обе версии — ставшую у нас хорошо известной Mathematica 3 и новейшую Mathematica 4. Указание на конкретную версию будет делаться только в том случае, если описываются ее специфические возможности. Многочисленные внутренние отличия системы Mathematica 4 от Mathematica 3 будут рассмотрены по ходу дела. 2. Строка меню и окно редактирования документов До сих пор разработчики пользовательского интерфейса математических систем по существу копировали стандартный интерфейс программ из комплекса Microsoft Office 95/97, в частности, самого популярного текстового процессора Word 95/97. Разработчики интерфейса пользователя систем Mathematica 3/4 отошли от этой традиции. Нетрудно заметить, что пользовательский интерфейс систем Mathematica 3/4 реализует отдельный вывод своих элементов — окон (включая основное окно редактирования), панелей, палитр знаков и т. д. Это позволяет располагать их в любых местах экрана, что особенно удобно при работе с дисплеями, имеющими большой размер изображения — от 17 дюймов по диагонали и выше. При работе с дисплеями, имеющими небольшой экран (14 или 15 дюймов) и стандартном разрешении 640x480 пикселей раздельный вывод элементов интерфейса скорее неудобен, поскольку приходится тщательно располагать их в нужных местах и индивидуально подстраивать размеры отдельных окон и палитр. Однако после настройки элементы интерфейса выводятся в том виде, как это было задано. Главное окно системы имеет крайне невзрачный вид, поскольку не содержит ничего, кроме строки заголовка и строки меню. Справа и снизу большого окна редактирования находятся линейки прокрутки с характерными ползунками, управляемыми мышью. Они предназначены для скроллинга текстов больших документов, если последние не помещаются в видимой части окна. Положение ползунка приближенно указывает место в документе, которое в данный момент отображается на экране. В самом низу в начале линейки прокрутки имеется строка состояния (Status bar) с информацией о текущем режиме работы. Эта информация (если она есть в данный момент) полезна для оперативного контроля в ходе работы с системой.
Рис.1 Главное окно системы Mathematica 4. Главное меню системы содержит следующие позиции: Файл (File) — работа с файлами: создание нового файла, выбор файла из каталога, закрытие файла, запись текущего файла, запись файла с изменением имени, печать документа и завершение работы; Редактировать (Edit) — основные операции редактирования (отмена операции, копирование выделенных участков документа в буфер с их удалением и без удаления, перенос выделенных участков, их стирание); Ячейка (Cell) — работа с ячейками (объединение и разъединение ячеек, установка статуса ячейки, открытие и закрытие); Формат (Format) — управление форматом документов; Ввод (Input) — задание элементов ввода (графиков, матриц, гиперссылок и т. д.); Ядро (Kernel) — управление ядром системы; Найти (Find) — поиск заданных данных; Окно (Window) — операции с окнами и их расположением; Помощь (Help) — управление справочной системой. Часть команд может быть в данный момент невыполнима — например, нельзя вычислить значение выражения, если его самого нет в окне редактирования или если ячейка с ним не выделена. Названия таких команд выделяются характерным серым расплывчатым шрифтом. Четкий шрифт, напротив, характерен для тех команд, которые в данный момент могут исполняться. Управление главным меню самое обычное. 3. Палитры математических операторов и функций У многих программ интерфейс предусматривает вывод панелей с кнопками быстрого управления — уже привычными стали панели инструментов и панели форматирования. С одной стороны, эти панели упрощают работу, особенно для начинающих пользователей, но, с другой стороны, они загромождают экран. Тогда как большинство фирм-разработчиков программ компьютерной математики пошло по пути уменьшения числа таких кнопок, Wolfram Research сделала решительный шаг и вообще отказалась от вывода инструментальной панели с подобными кнопками. Причина такого шага вполне очевидна — запомнить назначение множества кнопок по рисункам на них оказалось ничуть не проще, чем иметь дело с множеством имен команд в обычном меню. Однако все же надо признать, что некоторое количество кнопок быстрого управления стоило бы оставить. Однако, сделав шаг назад, упомянутая фирма одновременно сделала два шага вперед — она ввела выбираемые пользователем и перемещаемые по экрану в любое место инструментальные палитры со множеством пиктограмм ввода математических символов, функций и команд управления системой. Они выводятся с помощью меню Файл | Палитры.
Рис. 2 Инструментальные палитры системы Mathematica 4 Палитры, предназначенные для ввода математических спецзнаков, намного упрощают работу по подготовке документов. Общее число специальных математических знаков (греческих и латинских букв, операторов, функций и команд), вводимых с помощью палитр, составляет около 700. Многие знаки имеют альтернативные варианты ввода с применением комбинаций клавиш — их можно найти в справочной базе данных системы. Рисунок 2, однако, наглядно показывает, что целесообразно пользоваться не более чем 2-3 панелями одновременно. Для удаления ненужных панелей в правом верхнем углу каждой из них расположены маленькие кнопки со знаком х. Все панели максимально компактны и могут перетаскиваться мышью в наиболее удобное место экрана. Если убрать все панели, то интерфейс системы на первый взгляд оказывается даже слишком простым — остается единственная панель с главным меню и висящее отдельно окно документа. Вокруг него можно разглядеть объекты рабочего стола операционной системы Windows 95/98 (при подготовке этой книги использовалась Windows 98). Если работа идет с несколькими документами, то можно увидеть несколько окон документов. 4. Особенности интерфейса Mathematica 4 Интерфейс системы Mathematica 4 в целом повторяет интерфейс третьей версии, кратко описанный выше. Однако ряд внешне незаметных, но существенных новинок все же введен: · улучшена плавная прокрутка больших документов; · введен экспорт табличных данных; · улучшены возможности создания документов в стиле Notebook; · добавлена панель ввода шаблонов ЗD-фигур; · расширена поддержка преобразований файлов в формат HTML; · введена дополнительная команда для вывода в формате ТеХ; · обеспечена поддержка дополнительных наборов символов, включая символы китайского и корейского языков; · переработаны редакторы программ с цветной раскраской листингов; · улучшены средства отладки программ; · улучшена связь программных модулей. Средства Mathematica 4 позволяют готовить документы в стиле Notebook на самом высоком полиграфическом уровне воспроизведения текстов, математических формул и графиков. Общий вид одного из таких документов, содержащего рисунок с высоким разрешением. Размеры блокнота практически не ограничены, и он может быть распечатан во всей красе с помощью цветного струйного или лазерного принтера. 5. Работа с файлами Файлы — важнейший компонент любой программной среды или любого приложения:. В этом разделе мы познакомимся с различными типами файлов, обычно называемыми их форматами. Основное внимание будет уделено файлам документов, которые создаются пользователями систем Mathematica. Основные виды файлов и пакеты расширения Файлы документов прежних версий системы Mathematica имели расширение .та (от слов Mathematical Applications — применения системы Mathematica), их можно загружать в окно редактирования для исполнения, дополнения или редактирования. При записи таких файлов система одновременно создает бинарные файлы с расширением .mb, хранящие битовый графический образ документа. Благодаря этому считывание файлов ранее подготовленных в системе документов происходит быстро, без включения в работу символьного процессора, так что текст с графиками сразу появляется на экране дисплея. Однако бинарные файлы, особенно для документов со сложными графическими объектами, имеют большие размеры и хранить их на диске не всегда разумно. Поэтому такие файлы можно с диска стереть, но в этом случае все построения повторяются при загрузке файлов с включением в работу символьного процессора. В версиях Mathematica 3/4 основным типом документов стали блокноты (notebooks). Им соответствуют файлы текстового формата с расширением .nb. Эти файлы могут редактироваться любым текстовым редактором, поддерживающим формат ASCII. Файлы содержат подробное описание документа с указаниями типов шрифтов, деталей оформления и местоположения различных объектов. Они завершаются довольно пространным описанием того, что собой представляет notebook. К сожалению, это ведет к значительному росту объема таких файлов — он значительно больше, чем у документов систем Mathcad. Зато файлы блокнотов весьма наглядны, и при необходимости в них может разобраться обычный пользователь. Кроме того, система имеет ряд стандартных пакетов расширения (в оригинале — Add-Ons), расположенных в каталоге ADDONS: Algebra — работа с полиномами, алгебраическими неравенствами, Гамильтоновой алгеброй и т. д. Calculus — символьные вычисления производных, интегралов и пределов функций, прямое и обратное преобразования Фурье и Лапласа, решение систем нелинейных уравнений, реализация инвариантных методов, решение дифференциальных уравнений в частных производных, нахождение полных интегралов и дифференциальных инвариантов нелинейных уравнений, аппроксимация Паде, вычисление эллиптических интегралов и работах векторами. DiscreteMath — вычисления из области дискретной математики, комбинаторики, вычислительной геометрии и теории графов, решение рекуррентных и разностных уравнений, операции с целыми числами и т. д. Geometry — функции для выполнения геометрических расчетов, создания правильных прямоугольников и многогранников, вращения геометрических фигур в плоскости и в пространстве. Graphics — построение графиков специального вида, геометрических фигур и поверхностей, графиков параметрически и неявно заданных функций, представления функций комплексного переменного, отображение ортогональных проекций трехмерных фигур, имитация теней, средства оформления графиков. LinearAlgebra — решение задач линейной алгебры, дополнительные векторные и матричные операции, задание ортогональных векторных базисов и т. д. Miscellaneuos — задание единиц измерения физических величин, данные о химических элементах, физические константы, географические данные и все прочее, не вошедшее в другие категории. NumberTheory — функции теории чисел. NumericalMath — реализация важнейших численных методов, аппроксимация данных и аналитических функций полиномами, сплайнами и тригонометрическими рядами, численное интегрирование и дифференцирование, решение дифференциальных уравнений, вычисление корней нелинейных уравнений, нахождение вычетов и разложений в комплексной плоскости и т. д. . Statistics — статистические функции для непрерывных и дискретных распределений, реализация линейной и нелинейной регрессии, вычисление параметров ряда распределений (особенно нормального), функции сглаживания и подгонки данных и т. д. Utilities — дополнительные утилиты для работы с бинарными файлами и памятью компьютера, поддержки языков, работы с системами класса AutoCAD и т.д. Пакеты расширения содержат множество (полторы сотни) библиотечных файлов с расширениями .m, в каждом из которых определен ряд новых функций системы. Число функций в одном пакете расширений лежит в пределах от нескольких функций до нескольких десятков, а общее число дополнительных функций и их вариантов достигает тысячи. С их помощью можно реализовывать новые алгоритмы решения математических задач и постоянно расширять возможности системы. Все библиотечные файлы подробно прокомментированы, что облегчает их использование пользователями, владеющими английским языком. В версии Mathematica 4 число файлов в пакетах расширения несколько сокращено по сравнению с версией Mathematica 3. Часть таких файлов вообще являются «пустышками» — они оставлены ради сохранения полной совместимости с предшествующими версиями системы. Перенос части имеющихся в пакетах расширений функций и команд в тщательно оптимизированное ядро системы позволил существенно повысить скорость выполнения соответствующих операций. 6. Меню File Для работы с файлами служит меню File.
Рис. 3 Меню File В этом меню содержатся следующие команды: Новый (New) (Ctrl+N) — вывод окна нового документа; Открыть (Open) (Ctrl+0) — загрузка существующего документа; Закрыть (Close) (Ctrl+F4) — закрытие текущего окна; Сохранить (Save) (Ctrl+S) — запись документа с текущим именем; Сохранить как… (Save As) (Shift+Ctrl+S) — запись документа с изменением имени; Сохранить как особо (Save As Special) — запись в специальных форматах; Вернуть (Open Special) — открытие файлов в специальных форматах; Импортировать (Import) — вставка содержимого файла в ячейку текущего документа; Послать к (Send To) — зарезервированная команда; Послать выделенные (Send Selection) — зарезервированная команда; Палитры (Palettes) — вывод палитр математических спецзнаков, операторов и функций; Notebook — вывод списка документов, которые загружались ранее; Generate Palette from Selection — преобразует выделенные ячейки документа в палитру; Generate Notebook from Palette — преобразует палитру в документ; Printing Settings — установка параметров печати; Print (Ctrl+P) — печать текущего документа; Print Selection — печать выделенных ячеек; Exit (Alt+F4) — завершение работы с системой. Следует отметить, что хотя библиотечные файлы расширений можно, как и файлы с расширением .mа, загружать в окно редактирования, как правило, это делается только при их подготовке и отладке. Указанные файлы обычно подгружаются в текущий документ без отображения их текстов с помощью специальных команд. Эти команды будут рассмотрены в дальнейшем. Открытие окна нового документа — команда New Команда New используется, когда нужно начать работу с новым документом. Эта команда полностью очищает экран, выводя запрос о том, нужно ли записать текущий документ, если он есть и модифицировался со времени последнего сохранения. Окно будущего документа получает имя Untitled-N (в версиях Mathematica 2.x имя было Newnb-N), где N — текущий номер документа. После исполнения этой команды можно начинать ввод документа с помощью клавиатуры и выполнять его редактирование. Важно отметить, что даже эта. команда не отменяет определений, сделанных в предшествующих исполненных документах и в ранее загруженных файлах пакетов расширений. Лишь полная перезагрузка системы отменяет эти определения. Загрузка ранее созданных документов — команда Open Загрузка файлов ранее созданных документов — одна из самых распространенных операций. Она реализуется командой Open, которая служит для загрузки ранее созданного документа с его поиском в файловой системе компьютера. Эта команда выводит диалоговое окно, типичное для Windows-приложений и предназначенное для удобного поиска файлов. Кроме команды Open, которая загружает документ, открывая его в новом окне, в меню File. имеется еще команда Import, вставляющая содержимое указанного файла в текущий документ. Обе команды позволяют загружать файлы как основного формата notebook с расширением .nb, так и файлы ряда других форматов. Запись документа с текущим именем — команда Save Если документ создан с помощью команды New или открыт с помощью команды Open, то он обычно подвергается модификации и редактированию. После отладки документа его измененный вариант бывает нужно записать на магнитный диск — гибкий или жесткий. Для этого служат команды Save и Save As. Команда Save выполняет запись текущего документа без изменения его имени. Поэтому она выполняется быстро и без каких-то дополнительных действий. Запись идет в формате notebook. Печать документов — команда Print После настройки параметров можно осуществить собственно печать с помощью команды Print для всего документа или Print Selection для печати только выделенных ячеек. Команда Print открывает окно печати. В этом окне имеется поле Принтер с переключателем выбора принтера и кнопкой вывода окна его свойств. Интересна опция Печать в файл, с помощью которой данные печати направляются вместо принтера на диск. Поле Печатать позволяет установить номера страниц, которые будут распечатаны, или задать печать только выделенных ячеек. Поле Копии служит для установки числа копий и задания (если это нужно) разборки копий. Нажатие кнопки Свойства в окне выводит окно настройки принтера. Вид этого окна зависит от применяемого для печати принтера и установленного для него драйвера. В связи с этим работа с данным окном подробно не рассматривается. Команда Print Selection служит для печати набора выделенных ячеек. Обычно она также выводит окно печати. В этом окне, как отмечалось, можно выбрать нужный принтер из нескольких, если их драйверы были инсталлированы. Завершение работы с системой — команда Exit Команда Exit используется для окончания работы с системой Mathematica. Если все документы, с которыми пользователь работал (их может быть много), были записаны на диск, то при исполнении этой команды можно наблюдать последовательное закрытие окон с текстами документов. Если какой-то из документов не был записан после модификации, то команда Exit выведет запрос о необходимости записи. В подменю Notebooks меню File содержится перечень файлов, с которыми в последнее время работал пользователь. Выбор любого из этих файлов ведет к его загрузке в новое окно редактирования. Это делает работу с системой более удобной, так как избавляет пользователя от поиска наиболее нужных файлов по дискам и директории 7. Основные классы данных Mathematica оперирует с тремя основными классами данных: численными данными, представляющими числа различного вида; символьными данными, представляющими символы, тексты и математические выражения (формулы); списками — данными в виде множества однотипных или разнотипных данных. Каждый из этих классов данных в свою очередь имеет ряд специальных, более частных типов данных. На них мы остановимся более подробно. Численные данные Двоичные числа, биты и байты Минимальной единицей информации в компьютерной технике является двоичная единица — бит. Она имеет представление в виде 0 или 1, удобное для реализации простейшими электронными схемами с двумя состояниями электрического равновесия (например, триггерами или иными ячейками памяти). Многоразрядные двоичные числа представляют собой набор цифр 0 и 1, например, 100110 или 111001. Каждый старший разряд относительно предыдущего имеет весовой коэффициент, равный 2. Именно с битами работает микропроцессор на нижнем уровне операций. Однако бит — слишком мелкая единица, не очень удобная в обращении. К тому же мы привыкли к куда более удобным и наглядным для нас элементам информации, таким как буквы, цифры, знаки арифметических операций, спецзнаки и символы псевдографики. В принципе, набор этих знаков, минимально необходимый для представления обычной текстовой и цифровой информации, содержит до 28 = 256 элементов. Каждый из них в компьютере представляется кодом от 0 до 255. Для задания таких кодов достаточно 8 бит (2^8=256), которые и образуют наиболее распространенную единицу представления информации — байт. 1024 байта образуют килобайт (Кбайт), 1024 Кбайт дают 1 Мбайт (мегабайт) и т. д. Широко применяется общеизвестный стандарт кодирования текстовой информации ASCII (American Standard Code for Information Interchange). Десятичные числа К наиболее известным типам данных в математике относятся привычные нам десятичные числа (DECIMAL). Каждый разряд таких чисел имеет представление, заданное одной из арабских цифр — 0, 1, 2,..., 9. Весовой коэффициент старшего разряда относительно предшествующего равен 10. Количество цифр, представляющих число, может быть, в принципе, любым. Десятичные числа относятся к следующим основным типам.
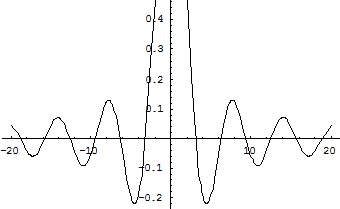
8. Функции компьютерной алгебры Системы компьютерной алгебры имеют несколько характерных для них функций, выполняющих достаточно сложные преобразования выражений. Эти функции имеют вполне установившиеся названия (Simplify, Expand, Collect, Factor и т. д.) и встречаются практически во всех системах символьной математики. Настало время детально познакомиться с ними, что и делается в данном разделе. Упрощение выражений — функция Simplify Упрощение математических выражений — одна из самых важных задач символьной математики. Частенько невероятно сложное математическое выражение, пугающее новичков своим грозным видом, является просто нулем или единицей либо сводится к простому выражению после ряда вполне заурядных (хотя, порою, и довольно сложных) преобразований. Качество выполнения операции упрощения во многом определяется мощью ядра математической системы, поскольку зависит от числа заложенных в него функций и правил преобразования выражений. С точки зрения простоты выражений они делятся на недостаточно простые и достаточно простые выражения. Недостаточно простые выражения таят в себе всевозможные «излишества»: сокращаемые общие члены, лишние переменные и функции, полиномы со степенями, допускающими понижение, и т. д. Это затрудняет качественный анализ выражений и может даже приводить к неоднозначным и даже неверным результатам. Mathematica всегда старается упростить то или иное выражение, если для этого не требуется каких-либо особых средств. Например, сложные выражения, содержащие элементарные или специальные функции, превращаются в более простые выражения — в том лишь смысле, что они состоят из более простых функций. Однако так бывает далеко не всегда, и для проведения необходимых преобразований используются различные функции, описанные ниже. Для упрощения выражений используется функция Simplify [ехрг]. Она исполняет последовательность алгебраических преобразований над выражением ехрг и возвращает простейшую из найденных форм (обычно это бывает нормальная форма выражения). Функция Simplify работает с самыми различными математическими выражениями: многочленами, рациональными выражениями (состоящими из полиномов и их отношений), расширенными рациональными выражениями (имеющими дробные степени переменных), элементарными и специальными функциями, алгебраическими и тригонометрическими выражениями и т. д. Обычно она приводит выражения к нормальному виду, что автоматически означает и приведение к виду достаточно простых выражений. Операция Simplify часто выполняется по умолчанию. Например, это обычно происходит при вычислении выражений, примеры чего приводились выше. Несомненно, это одна из наиболее важных и часто применяемых операций компьютерной алгебры. Вообще говоря, понятие упрощения математических выражений не является однозначным. К примеру, некоторые пакеты символьной математики упрощают sin(x)/cos(x) к единой математической функции tan(x), тогда как другие упрощают tan(x) к sin(.r)/cos(.r), считая, что функции sin(x) и cos(.r) более простые, чем функция tan(.r). Эта неоднозначность часто путает неопытных пользователей, пытающихся проверить символьные системы примерами из справочников, — вполне возможно, что авторы их придерживались несколько иного подхода к упрощению выражений, чем разработчики той или иной математической системы. Функции преобразования тригонометрических выражений Хотя представленные выше функции иногда применимы для тригонометрических выражений, для последних есть ряд специальных функций, дающих более надежные результаты в ходе преобразований тригонометрических функций. В названии этой группы функций имеется слово Trig. Начнем с функции Trig-Expand [expr ], которая обеспечивает расширение выражения ехрг, содержащего тригонометрические и гиперболические функции. Следующие две функции обеспечивают взаимные преобразования экспоненциальных и тригонометрических выражений: TrigToExp [expr] — преобразует тригонометрические выражения к экспоненциальному виду; ExpToTrig [expr] — преобразует экспоненциальные выражения в тригонометрические. Приведем еще две функции: TrigFactor [expr] — раскладывает на простые множители тригонометрическое выражение ехрr; TrigFactorList [expr] — раскладывает тригонометрическое выражение ехрг на списки с термами выражения. Применение рассмотренных функций расширяет круг задач, решаемых с применением символьных преобразований. Основные операции над полиномами Полиномом называют выражение, состоящее из нескольких частей одного вида. В западной математической литературе к ним часто относят степенной многочлен вида Р(х) = а0 + а1х + а2 х2 + а3 х3 + ... + аnхn. Хотя термин «полином» не очень прижился в отечественной математической литературе, мы оставляем его ввиду краткости и ради лучшего понимания синтаксиса функций системы, поскольку слова poly и Polynomial входят в параметры и имена многих функций. При этом полиномы мы будем кратко обозначать как poly или pi (здесь i — индекс или порядковый номер полинома). Над полиномами можно выполнять обычные арифметические операции: сложение, вычитание, умножение и деление. Это иллюстрируют следующие примеры (здесь р1 и р2 — полиномы от одной переменной х): р1 := х^3 + 2*х^2 + 3*х + 4 р2 := х^2 - 1 р1 + р2 3+3х+3х2+х3 р1 - p2 5+3х+х2+х3 Если ситуация со сложением и вычитанием полиномов достаточно очевидна, то с умножением и делением результат часто повторяет задание. Для получения результата умножения полиномов в обычной форме следует использовать функцию расширения символьных выражений Expand. Если один полином делится на другой (это бывает далеко не всегда), то для получения результата надо использовать функцию Simplify. В общем случае при делении полиномов может оставаться остаток. Функция, обеспечивающая деление полиномов и вычисляющая остаток, описана ниже. Функции для расширенных операций с выражениями Выше была описана сравнительно немногочисленная группа функций для работы с выражениями — их упрощения, расширения, выделения множителей и т. д. Эти функции способны решать большинство повседневных задач, связанных с аналитическими преобразованиями выражений. Однако система Mathematica имеет гораздо более полный набор функций для работы с выражениями. Они приведены в приложении. К сожалению, объем книги не позволяет привести примеры использования всех этих функций, да и вряд ли они будут интересны всем читателям. Поэтому приведем лишь отдельные примеры работы с некоторыми из этих функций: Apart [expr] — переписывает рациональное выражение expr в виде суммы членов с минимальными знаменателями; Apart [expr, var] — аналогична Apart [expr], но все переменные, кроме var, интерпретируются как константы. Следующие функции позволяют судить о размерности выражений: Depth [expr ] — возвращает значение, на единицу превышающее максимальное число индексов, требуемых для указания любой части выражения expr; Dimensions [expr] — возвращает список размерностей выражения expr; Dimensions [expr, n] — возвращает список размерностей expr до уровня n. 9. Операции математического анализа Вычисление сумм В числе операций математического анализа прежде всего надо отметить суммы Сумма от i=min до imax по fi В этих операциях индекс i принимает целочисленные значения от минимального (начального) imin до максимального (конечного) imax с шагом, равным +1. Суммы и произведения легко вычисляются численными математическими системами, такие вычисления просто описываются на всех языках программирования. Однако важным достоинством систем символьной математики, включая Ма-thematica, является вычисление сумм и произведений в аналитическом виде (если это возможно) и при большом числе членов — вплоть до стремящегося к бесконечности. Для вычисления сумм в системе Mathematica предусмотрена функция Sum, используемая в ряде форм: Sum [f, {i, imax}] — вычисляет сумму значений f при изменении индекса i от 1 до imax с шагом +1; Sum[f,{i, imin, imax}]—вычисляет сумму значений f при изменении индекса i от минимального значения i=imin до максимального i=imax с шагом +1; Sum[f, {i, imin, imax, di}]— вычисляет сумму значений f при изменении управляющей переменной вещественного типа от минимального значения i=imin до максимального i=imax с шагом di; Sum[f, {i, imin, imax}, {j, jmin, jmax},...] — вычисляет многократную сумму значений f при изменении индексов i от imin до imax с шагом +1, j от jmin до jmax с шагом +1 и т. д. (число индексов не ограничено). Вычисление производных К числу наиболее часто используемых математических операций принадлежит вычисление производных функций как в аналитической, так и в символьной форме. Для этого используются следующие функции: D [ f, х ] — возвращает частную производную функции f по переменной х; D [f, {х, n}]— возвращает частную производную n-го порядка по х; D[f, xl, х2,...] — возвращает смешанную производную; Dt[f, х] — возвращает обобщенную производную функции f по переменной х; Dt [ f ] — возвращает полный дифференциал f. Название функции из одной буквы — это явно исключение из правил. Оно выбрано осознанно, в силу массовости этой операции. Для функции в существует опция NonConstants, которая позволяет задать список объектов, находящихся в неявной зависимости от переменных дифференцирования. По умолчанию этот список пустой. Для функции Dt имеется опция Constants, которая, наоборот, указывает символы, которые являются константами (по умолчанию их список также пуст). На практике применять данные опции приходится редко. Существует еще одна функция, Derivative [nl, n2,...] [f ], — основная (общая) форма представления функции, полученной в результате nl-кратного дифференцирования функции f по первому аргументу, п2-кратного — по второму аргументу и т. д. К примеру, Derivative [2] [х*у] возвращает (ху)", a Derivative [2, 3] [х*у] — соответственно, (ху)(2.3) Следующие примеры показывают применение функции в для вычисления производной в аналитическом виде: Производная тригонометрической функции: D[x*Sin[x],x] xCos[x] + Sin[x] Производная логарифмической функции: D[Log[3*x/4],x] 1/x Производная степенного многочлена: D[а*х^2+b*х+с,х] b+ 2ах Пятая производная от хn: D[х^n,{х,5}] (-4 + n) (-3+n) (-2+n) (-1+n)nх-5+n Вычисление интегралов Одна из важнейших операций — вычисление первообразных и определенных интегралов в символьном виде. Первообразная — это функция F(x), удовлетворяющая уравнению f(x)dx = F(x) + C, где С — постоянная интегрирования. А вычисление определенного интеграла с пределами — верхним b и нижним а — производится по формуле f(X)dX = F(b)-F(a) Заметим, что определенный интеграл может быть представлен как аналитическим, так « численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов — от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x). Для интегрирования в системе Mathematica используются следующие функции: Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х; Integrate [f, {x, xmin, xmax}] — возвращает значение определенного интеграла с пределами от xmin до xmax; Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},...] —возвращает значение кратного интеграла с пределами от xmin до xmax по переменной х, от ymin до ymax по переменной у и т. д. (кратность реально не ограничена). Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции: Options[Integrate] {Assumptions -> {}, GenerateConditions->Automatic, PrincipalValue > False) Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком «минус». Пределы могут задаваться как константами, так и функциями. 10. Двумерная графика Графическая функция Plot Концептуально графики в системе Mathematica являются графическими объектами, которые создаются (возвращаются) соответствующими графическими функциями. Их немного, около десятка, и они охватывают построение практически всех типов математических графиков. Как уже отмечалось, достигается это за счет применения опций и директив. Поскольку графики являются объектами, то они могут быть значениями переменных. Поэтому Mathematica допускает следующие конструкции: · Plot[Sin[x],{x,0,20}] — построение графика синусоиды; · g:=Plot [Sin [x], {х, 0, 20} ] — задание объекта — графика синусоиды — с отложенным выводом; · g=Plot [Sin [x], {х, 0, 20} ] — задание объекта — графика синусоиды — с немедленным выводом. Начнем рассмотрение графических возможностей системы с построения простейших графиков функций одной переменной вида у =f(x) или просто f(x). График таких функций строится на плоскости, то есть в двумерном пространстве. При этом используется прямоугольная (декартова) система координат. График представляет собой геометрическое положение точек (х, у) при изменении независимой переменной (абсциссы) в заданных пределах, например от минимального значения xmin до максимального хтах с шагом dx. По умолчанию строятся и линии координатной системы. Для построения двумерных графиков функций вида f(x) используется встроенная в ядро функция Plot: · Plot [f, {x, xmin, xmax}] — возвращает объект, представляющий собой график функции f аргумента х в интервале от xmin до xmax; · Plot[{f1, f2,...}, {x, xmin, xmax}]— возвращает объект в виде графиков ряда функций fi. Функция Plot используется для построения одной или нескольких линий, дающих графическое представление для указанных функций f, f1, f2 и т. д. На рис. 4 показано построение графика функции sin(x)/x без использования каких-либо опций (точнее, с набором опций по умолчанию).
Рис. 4 Построение двумерного графика Тут виден как раз тот случай, когда масштаб графика по вертикали выбран системой неудачно — часть графика сверху просто отсекается. В большинстве же случаев применение функции Plot позволяет получить вполне «удобоваримый» график. Опции функции Plot По мере усложнения задач, решаемых пользователем, его рано или поздно перестанут устраивать графики, получаемые при автоматическом выборе их стиля и иных параметров. Для точной настройки графиков Mathematica использует специальные опции графических функций Для вывода их списка надо использовать команду Options [Plot]. Полный список опций дан в приложении. Опции внутри.графических функций задаются своим именем name и значением value в виде name -> value Наиболее распространённые символьные значения опций: Automatic — используется автоматический выбор; None — опция не используется; All — используется в любом случае; True — используется; False — не используется. Многие опции могут иметь числовые значения. В сомнительных случаях рекомендуется уточнять форму записи опций и их значений по оперативной справочной системе. Рассмотрим примеры применения опций двумерной графики. С помощью опции Axes со значением None можно убрать с графика отображение осей. Часто возникает необходимость построения на одном рисунке нескольких графиков одной и той же функции, но при разных значениях какого-либо параметра — например, порядка специальных математических функций. В этом случае они могут быть заданы в табличной форме.. Применение других опций позволяет задавать массу свойств графиков, например цвет линий и фона, вывод различных надписей и т. д. Помимо представленных примеров, полезно просмотреть и множество примеров построения двумерных графиков, приведенных в справочной системе Mathematica. Директивы двумерной графики Еще одним важным средством настройки графиков являются графические директивы. Синтаксис их подобен синтаксису функций. Однако директивы не возвращают объектов, а лишь влияют на их характеристики. Используются следующие основные директивы двумерной графики: AbsoluteDashing [ {dl, d2,...}]— задает построение последующих линией пунктиром со смежными (последовательными) сегментами, имеющими абсолютные длины dl, d2, ... (повторяемые циклически). Значения длины di задаются в пикселях; AbsolutePointSize [d] — задает построение последующих точек графика в виде кружков с диаметром в (в пикселях); AbsoluteThickness [d] — задает абсолютное значение толщины (в пикселях) для последующих рисуемых линий; Dashing [{rl, r2,...}] — задает построение последующих линий пунктиром с последовательными сегментами длиной rl, г2, ..., повторяемыми циклически, причем ri задается как доля полной ширины графика; PointSize [d] — задает вывод последующих точек графика в виде кружков с относительным диаметром d, заданным как доля общей ширины графика; Thickness [r] — устанавливает для всех последующих линий толщину г, заданную как доля полной ширины графика. Применение графических директив совместно с опциями позволяет создавать графики самого различного вида, вполне удовлетворяющие как строгим требованиям, так и различным «извращениям» в их оформлении. Построение графика по точкам — функция List Plot Часто возникает необходимость построения графика по точкам. Это обеспечивает встроенная в ядро графическая функция ListPlot: ListPlot [ {yl, у2,...}]— выводит график списка величин. Координаты х принимают значения 1, 2, ...; ListPlot [{{x1, y1}, {х2, у2 },...}]—выводит график списка величин с указанными х- иy-координатами. В простейшем случае эта функция сама задает значения координаты х= 0, 1, 2, 3, ... и строит на графике точки с координатами (х, у), выбирая у последовательно из списка координат.
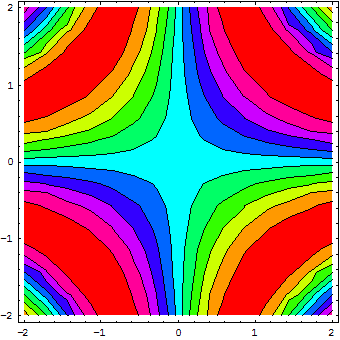
Рис. 5 Построение графика по точкам Можно заметить характерный недостаток построений — точки (особенно при небольшом размере) имеют вид, заметно отличающийся от идеального круга. Функция ListPlot, особенно в ее второй форме (с заданными координатами х и г/), удобна для вывода на график экспериментальных точек. 11. Трехмерная графика Трехмерная графика, называемая также ЗD-графикой, представляет в аксонометрической проекции объемное изображение поверхностей или фигур, которые описываются либо функциями двух переменных, либо параметрически заданными координатами объектов. В данном разделе описаны многие способы построения трехмерных графиков, начиная от простых контурных графиков и кончая графиками поверхностей и фигур с функциональной окраской. Построение контурных графиков Контурные графики, или графики линий равных высот, используются для отображения поверхностей на плоскости. Они удобны для выявления всех экстремумов функций в пределах области графика. Такие графики являются линиями пересечения поверхности с секущими горизонтальными плоскостями, расположенными параллельно друг под другом. Они часто используются в картографии. Основными функциями и директивами для построения контурных графиков являются следующие: ContourPlot[f,{x, xmin, xmax}, {у, ymin, ymax}] — порождает контурный график f как функции от х и у; ContourGraphics [array] — представляет контурный график массива array; ListContourPlot[array] — формирует контурный график из массива величин высот. Этих функций достаточно для построения практически любых монохромных графиков такого типа. Для управления возможностями графической функции ContourPlot используются опции, полный список которых выводит команда Options [ContourGraphics ]. Помимо уже рассмотренных ранее опций используются следующие: ColorFunction — задает окраску областей между линиями; Contours — задает число контурных линий; ContourLines — задает прорисовку явных (explicit) контурных линий; ContourShading — задает затенение областей между контурными линиями; ContourSmoothing — задает сглаживание контурных линий; ContourStyle — задает стиль рисуемых линий для контурных графиков; MeshRange — задает области изменения х- и y-координат. Рисунок 6 показывает построение контурного графика с окраской промежуточных областей между линиями. Окраска обеспечивается опцией ColorFunction-> Hue. Опция ContourSmoothing->True задает сглаживание контурных линий.
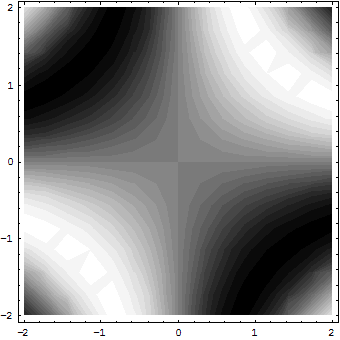
Рис. 6. Контурный график поверхности sin(x у) с закраской областей между линиями равного уровня оттенками серого цвета Иногда график оказывается более наглядным, если убрать построение контурных линий, но оставить закраску областей между линиями. Такой вариант графика более предпочтителен, если нужно наблюдать качественную картину. Для построения такого графика надо использовать опцию ContourLine->False (рис. 7).
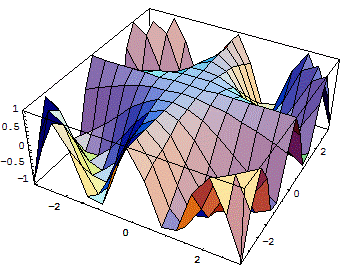
Рис. 7. Контурный график без линий равного уровня В данном случае используется вариант монохромной окраски областей между линиями (PostScript). Он может оказаться предпочтителен, например, если предполагается печать графика монохромным принтером. Построение графиков поверхностей — функция Plot 3D Функция двух переменных z = f(x, у) образует в пространстве некоторую трехмерную поверхность или фигуру. Для их построения приходится использовать координатную систему с тремя осями координат: х, у и z. Поскольку экран дисплея плоский, то на самом деле объемность фигур лишь имитируется — используется хорошо известный способ наглядного представления трехмерных фигур с помощью аксонометрической проекции. Вместо построения всех точек фигуры обычно строится ее каркасная модель, содержащая линии разреза фигуры по взаимно перпендикулярным плоскостям. В результате фигура представляется в виде совокупности множества криволинейных четырехугольников. Для придания фигуре большей естественности используются алгоритм удаления невидимых линий каркаса и функциональная закраска четырехугольников с целью имитации бокового освещения фигуры. Для построения графиков трехмерных поверхностей используется основная графическая функция Plot 3D: · Plot3D[f, {x, xmin, xmax), {у, ymin, ymax}] — строит трехмерный график функции f переменных х и у; · Plot3D[{f, s}, {x, xmin, xmax}, {y, ymin, ymax}] — строит трехмерный график, в котором высоту поверхности определяет параметр f, а затенение — параметр s. На рис. 8 показан пример построения поверхности, описываемой функцией двух переменных cos(x у) при х и у, меняющихся от -3 до 3. Поверхность строится в виде каркаса с прямоугольными ячейками с использованием функциональной окраски. Все опции заданы по умолчанию.
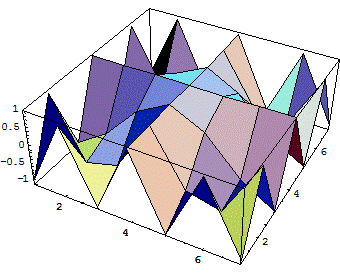
Рис. 8. Пример построения поверхности cos(xy) функцией Plot3D с опциями по умолчанию Э тот график будем считать исходным для демонстрации его модификаций, получаемых путем изменения опций. Графическая функция ListPlot3D Часто трехмерная поверхность задается массивом своих высот (аппликат). Для построения графика в этом случае используется графическая функция ListPlotSD: ListPlot3D [array] — строит трехмерный график поверхности, представленной массивом значений высот; ListPlot3D [array, shades] — строит график так, что каждый элемент поверхности штрихуется (затеняется) согласно спецификации shades. Plot Joined — дополнительная опция для ListPlot, указывающая, следует ли соединять линией точки, нанесенные на график. Пример применения функции ListPlotSD показан на рис. 9. График построен по данным таблицы tS, формирующей значения аппликат поверхности, которая описывается функцией cos(xy).
Рис. 9. Пример применения функции ListPlotSD 12. Методы программирования Такие мощные системы, как Mathematica, предназначены, в основном, для решения математических задач без их программирования большинством пользователей. Однако это вовсе не означает, что Mathematica не является языком (или системой) программирования и не позволяет при необходимости программировать решение простых или сложных задач, для которых имеющихся встроенных функций и даже пакетов расширений оказывается недостаточно или которые требуют для реализации своих алгоритмов применения типовых программных средств, присущих обычным языкам программирования. Все обстоит совсем иначе. Фактически, основой системы Mathematica является проблемно-ориентированный на математические расчеты язык программирования сверхвысокого уровня. По своим возможностям этот язык намного превосходит обычные универсальные языки программирования, такие как Фортран, Бейсик, Паскаль или С. Важно подчеркнуть, что здесь речь идет о языке программирования системы Mathematica, а не о языке реализации самой системы. Языком реализации является универсальный язык программирования C++, показавший свою высокую эффективность в качестве языка системного программирования. Как и всякий язык программирования, входной язык системы Mathematica содержит операторы, функции и управляющие стриктуры. Основные операторы и функции этого языка и относящиеся к ним опции мы фактически уже рассмотрели. Набор описанных ранее типовых операторов и функций характерен для большинства современных языков программирования. Мощь системы Mathematica как средства программирования решения математических задач обусловлена необычно большим (в сравнении с обычными языками программирования) набором функций, среди которых немало таких, которые реализуют сложные и практически полезные математические преобразования и современные вычислительные методы (как численные, так и аналитические). Число этих функций только в ядре и библиотеках приближается к тысяче. Среди них такие операции, как символьное и численное дифференцирование и интегрирование, вычисление пределов функций, вычисление специальных математических функций и т. д. — словом, реализации именно тех средств, для создания которых на обычных языках программирования приходится составлять отдельные, подчас довольно сложные программы. Почти столько же новых функций (или модернизированных старых) содержат пакеты расширения (Add-on Packages). Язык программирования системы Mathematica трудно отнести к какому-либо конкретному типу. Можно разве что сказать, что он является типичным интерпретатором и не предназначен для создания исполняемых файлов. Впрочем, для отдельных выражений этот язык может осуществлять компиляцию с помощью функции Compile, что полезно при необходимости увеличения скорости счета. Это язык вобрал в себя лучшие средства ряда поколений языков программирования, таких как Бейсик, Фортран, Паскаль и С. Благодаря этому он позволяет легко реализовывать все известные типы (концепции) программирования: функциональное, структурное, объектно-ориентированное, математическое, логическое, рекурсивное и т. д. К примеру, вычисление таких функций, как факториал, в Mathematica можно запрограммировать в виде функции пользователя целым рядом способов: f[n_] =n! f[n_] =Gamma[n-l] f [n_] =n*f [n-1] ;f [0]=l;f [1]=1; f[n_] =Product[i/i,n] f [n_] =Module[t=l,Do[t=t*i,i,n] ;t] f [n_] =Module [ { t=l } , For [ i=l , i<=n , i++ , t*=i ] ; t] f[n_] =Fold [Times,1, Range [n] ] Все их можно проверить с помощью следующего теста: {f[0],f[1],f[5],f[10]} {1, 1, 120, 3628800} Как отмечалось, внутреннее представление всех вычислений базируется на применении полных форм выражений, представленных функциями. И вообще, функциям в системе Mathematica принадлежит решающая роль. Таким образом, Mathematica. фактически, изначально реализует функциональный метод программирования — один из самых эффективных и надежных. А обилие логических операторов и функций позволяет полноценно реализовать и логический метод программирования. Множество операций преобразования выражений и функций позволяют осуществлять программирование на основе правил преобразования. Надо также отметить, что язык системы позволяет разбивать программы на отдельные модули (блоки) и хранить эти модули в тексте документа или на диске Возможно создание полностью самостоятельных блоков — именованных процедур и функций с локальными переменными. Все это наряду с типовыми управляющими структурами позволяет реализовать структурное и модульное программирование. Столь же естественно язык системы реализует объектно-ориентированное программирование. Оно базируется прежде всего на обобщенном понятии объекта и возможности создания множества связанных друг с другом объектов. В системе Mathematica каждая ячейка документа является объектом и порождается другими, предшествующими объектами. При этом содержанием объектов могут быть математические выражения, входные и выходные данные, графики и рисунки, звуки и т. д. С понятием объекта тесно связаны три основных свойства, перечисленные ниже: инкапсуляция — объединение в одном объекте как данных, так и методов их обработки; наследование — означает, что каждый объект, производный от других объектов, наследует их свойства; полиформизм — свойство, позволяющее передать ряду объектов сообщение, которое будет обрабатываться каждым объектом в соответствии с его индивидуальными особенностями. Приведенный ниже пример объектно-ориентированного программирования дает три определения, ассоциированные с объектом h: h/ : h [x_] +h [y_] : =hplus [х , у] h/:p[h[x_],x]:=hp[x] h/:f_[h[x_]] :=fh[f,x] В принципе, язык программирования системы Mathematica специально создан для реализации любого из перечисленных подходов к программированию, а также ряда других — например, рекуррентного программирования, при котором очередной шаг вычислений базируется на данных, полученных на предыдущих шагах. Наглядным примером этого может служить вычисление факториала рекуррентным методом. Возможно также создание рекурсивных функций (с обращением к самим себе) и, соответственно, использование рекурсивного программирования. Оно, кстати, играет большую роль в осуществлении символьных преобразований. Средства языка Mathematica позволяют осуществить и визуально-ориентированное программирование. Его смысл заключается в автоматической генерации программных модулей путем визуального выбора интуитивно понятного объекта — чаще всего путем щелчка на кнопке. Mathematica позволяет создавать палитры и панели с различными кнопками, позволяющими управлять программой или вводить новые программные объекты. Однако визуально-ориентированное программирование не является основным. В основном оно ориентировано на создание палитр пользователя с нужными ему функциями. Поскольку алфавит языка программирования системы и набор операторов и функций уже были рассмотрены ранее, в этой главе нам остается рассмотреть лишь специфические средства языка и его управляющие структуры. III. Заключение
Система Mathematica 4 относится к программным продуктам, которым крайне трудно найти достойного конкурента. Пожалуй, лишь система компьютерной математики Maple V R5 способна всерьез претендовать на эту роль. Эти две системы напоминают двух спортсменов, заметно оторвавшихся от своих соперников'и попеременно обгоняющих друг друга. Каждая из систем имеет свое лицо и может решать самые серьезные математические и научно-технические задачи. Высочайшая эффективность решения численных задач, превосходная графика и постоянно совершенствующиеся возможности символьной (аналитической) математики — это и есть лицо новейшей системы Mathematica 4. Да и одежка - пользовательский интерфейс под стать «Мисс Мира» — Mathematica. Оторвавшись от эпитетов, можно сказать, что Mathematica 4 (как и ее предшественница Mathematica 3, отставшая по скорости вычислений) действительно представляет собой самую современную систему искусственного интеллекта, ориентированную на выполнение разнообразных математических вычислений — от простейших до самых сложных, достойных ума и пера математиков-аналитиков. Одновременно эта система является уникальным по своей полноте «живым» справочником по различным математическим понятиям, алгоритмам и функциям. Она обеспечивает высочайшую степень визуализации вычислений, начиная от представления исходных данных и кончая выводом промежуточных и конечных результатов вычислений. Таким образом, главным для системы становится предоставление пользователю самых серьезных и, порой, новых знаний в столь почетной и древней области человеческого интеллекта, как математика. Более миллиона пользователей системы Mathematica (всех версий) и сотни опубликованных книг о ней (в том числе множество вышедших уже в 1999 г., лишь в середине которого четвертая версия системы появилась) говорят сами за себя. Mathematica 4 — это продукт широкого потребления, с которым можно достойно войти в третье тысячелетие новой эры в истории Человечества. Будучи по своей сути профессиональными инструментами для математиков, системы Mathematica 3/4 сделали решительный шаг в сторону массового пользователя. Не случайно на Западе эти системы используются не только в крупнейших научных центрах и ведущих университетах, но и в обычных вузах и даже школах. Примечательно, что сейчас Mathematica все чаще применяется представителями гуманитарных наук, а также специалистами в области экономики и финансов.
IV . Список использованной литературы 1. Дьяконов В.П. Mathematica 4: учебный курс – СПб: Питер, 2001. 2. Акритас А. Основы компьютерной алгебры/ Пер. с англ. – М.: Мир, 1994. 3. Капустина Т.В. Компьютерная система Mathematica 3.0 для пользователей – М.: Солон-Р, 1999. 4. Дьяконов В.П. Mathematica 3/4 с пакетами расширений – М.: Нолидж, 2000. |