|
Федеральное Агентство по образованию
ГОУ ВПО
Уральский государственный технический университет – УПИ
ТЕПЛОЭНЕРГЕТИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
КУРСОВАЯ РАБОТА
КОМПЬЮТЕРНАЯ ГРАФИКА
Преподаватель: Костоусов В. Б.
Студент: Ахмадинуров М.М.
Группа: Т-430
Екатеринбург, 200
6
СОДЕРЖАНИЕ
1. ПОСТАНОВКА ЗАДАЧИ 3
1.1. Классы
C
++: VECTOR и MATRIX
3
1.1.1. Тор 3
1.1.2. Куб 4
1.2.
OpenGL
5
1.2.1. Поверхность 5
1.2.2. Пружина 6
2. РЕШЕНИЕ 7
2.1. Классы
C
++: VECTOR и MATRIX
7
2.1.1. Тор 7
2.1.1.1. Введение 7
2.1.1.2. Решение 8
2.1.1.3. Текст программы 8
2.1.1.4. Результат работы программы 12
2.1.2. Куб 13
2.1.2.1. Введение 13
2.1.2.2. Решение 13
2.1.2.3. Текст программы 14
2.1.2.4. Результат работы программы 17
2.2.
OpenGL
18
2.2.1. Поверхность 18
2.2.1.1. Введение 18
2.2.1.2. Решение 18
2.2.1.3. Текст программы 18
2.2.1.4. Результат работы программы 20
2.2.2. Пружина 21
2.2.2.1. Введение 21
2.2.2.2. Решение 21
2.2.2.3. Текст программы 22
2.2.2.4. Результат работы программы 25
3. ЗАКЛЮЧЕНИЕ 26
1. ПОСТАНОВКА ЗАДАЧИ
1.1. Классы
C++: VECTOR и MATRIX
1.1.1. Тор
Построить трехмерную модель тора и визуализировать её используя классы C++ для работы с векторами и преобразованиями: VECTOR и MATRIX.
ТОР (от лат. torus - выпуклость) – геометрическое тело, образуемое вращением окружности вокруг непересекающей его и лежащей в одной с ним плоскости прямой (Рис. 1).
Приблизительную форму тора имеет спасательный круг, баранка.

Рис. 1
1.1.2. Куб
Построить трехмерную модель куба с нормалями к граням и визуализировать её используя классы C++ для работы с векторами и преобразованиями: VECTOR и MATRIX.
КУБ (лат. cubus, от греч. kybos) – один из пяти типов правильных многогранников, правильный прямоугольный параллелепипед; имеет 6 квадратных граней, 12 ребер, 8 вершин, в каждой сходится 3 ребра (Рис.2).

Рис. 2
1.2.
OpenGL
1.2.1. Поверхность
Поверхность задана формулой:
Z (x, y) = (sin x2
+ cos y2
) xy
Поверхность имеет такой вид (Рис. 3).

Рис. 3
1.2.2. Пружина
Пружина – модификация тора, получаемая из последнего путем распространения вдоль оси OZ, при этом большой радиус не меняется (Рис. 4).

Рис. 4
x = (R + r cos(f)) sin(k w),
y = (R + r cos(f)) cos(k w),
z = r sin(f) + k w,
где k – константа, определяющая шаг витков спирали по высоте. Углы f и w должны изменяться в полном круговом диапазоне, например от 0 до 360.
2. РЕШЕНИЕ
2.1. Классы
C++: VECTOR и MATRIX
2.1.1. Тор
Строить тор будем, опираясь на его определение. Тор
– геометрическое тело, образуемое вращением окружности вокруг непересекающей его и лежащей в одной с ним плоскости прямой.
То есть задача построения тора разбивается на две подзадачи:
1. Определение координат окружности;
2. Вращение окружности вокруг вектора w
, находящегося в центре тора, при этом сохраняя координаты вращающейся окружности (Рис. 5).

Рис. 5
Базовую окружность строим в плоскости YOZ. Координаты окружности определяем с помощью формул перехода из полярной системы координат в декартовую, то есть в нашем случае:
y = r*cos φ;
z = r*sin φ.
Угол φ задаем формулой 2π/n, где n – число, определяющее сглаженность окружности, чем больше, тем лучше.
Вращение вокруг вектора w (0, 1, 0) реализуется с помощью матрицы поворота и функции Rotate () из класса Matrix. Координаты повернутой окружности получаем путем умножения матрицы поворота на вершины базовой окружности.
Tor_form.cpp
#include <vcl.h>
#pragma hdrstop
#include "TOR.h"
#include "TOR_form.h"
//------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
//------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
disp=new Display(300,350,700,700,0.05,0.05,Form1->Canvas);
tor=new Tor();
}
//------------------------------------------------------
void __fastcall TForm1::Timer1Timer(TObject *Sender)
{
disp->Clear();
Vector v(1,1,2);
v=v/(!v);
Matrix A=Rotate(v,0.1);
tor->Transform(A);
tor->Show();
}
Tor
.
h
#define N 50 // количество окружностей в торе
#define n 20 // количество ребер в окружности
#define r 2 // радиус малого круга
#define R 7 // радиус тора
Display * disp;
class Tor
{
int i, j;
Vector Circle[n], Ver[N][n];
double fi;
public:
//--- Tor ---
Tor()
{
// определяем вершинки круга
fi = (2*M_PI)/n;
for (i=0; i<n; i++)
{
Circle[i] = Vector(0, r*cos(i*fi), r*sin(i*fi)+R);
}
// определяем вершины тора
fi = (2*M_PI)/N;
//вектор, вокруг которого происходит вращение окружности
Vector w(0, 1, 0);
w=w/(!w);
for (j=0; j<N; j++)
{
// поворачиваем окружность вокруг вектора w
Matrix B=Rotate(w, j*fi);
// записываем координаты вершин тора
for (i=0; i<n; i++)
{
Ver[j][i]=B*Circle[i];
}
}
}
//--- Show ---
void Show()
{
disp->MoveTo(Ver[0][0].x, Ver[0][0].y);
for (j=0; j<N; j++)
{
// рисуем кольца
for (i=0; i<n; i++)
{
disp->LineTo(Ver[j][i].x, Ver[j][i].y);
}
disp->LineTo(Ver[j][0].x, Ver[j][0].y);
// рисуем грани
if (j<N-1) {
for (i=0; i<n; i++)
{
disp->MoveTo(Ver[j][i].x, Ver[j][i].y);
disp->LineTo(Ver[j+1][i].x, Ver[j+1][i].y);
}
}
}
// рисуем окончательные грани
for (i=0; i<n; i++)
{
disp->MoveTo(Ver[N-1][i].x, Ver[N-1][i].y);
disp->LineTo(Ver[0][i].x, Ver[0][i].y);
}
}
//--- Transform ---
void Transform(Matrix & M)
{
for (j=0; j<N; j++)
for (i=0; i<n; i++)
{
Ver[j][i]=M*Ver[j][i];
}
Matrix M1=M;
M1.Invert();
M1.Transpose();
}
};
Disp.h
class Display
{
int x_org,y_org,W,H;
double dx,dy;
TCanvas * Canva;
public:
Display(int ax_org,
int ay_org,
int aW,
int aH,
double adx,
double ady,
TCanvas * aCanva)
{
x_org=ax_org;
y_org=ay_org;
W=aW;
H=aH;
dx=adx;
dy=ady;
Canva=aCanva;
};
int Convx2xs(double x)
{
int xs;
xs=x_org+x/dx;
return xs;
};
int Convy2ys(double y)
{
int ys;
ys=y_org+y/dy;
return ys;
};
void MoveTo(double x,double y)
{
Canva->MoveTo(Convx2xs(x),Convy2ys(y));
};
void LineTo(double x,double y)
{
Canva->LineTo(Convx2xs(x),Convy2ys(y));
};
void Clear()
{
Canva->Brush->Color=clWhite;
TRect rect;
rect.right=H;
rect.bottom=W;
rect.left=0;
rect.top=0;
Canva->FillRect(rect);
};
};
Результат работы программы рисования тора приведен на Рис. 6.


Рис.6
2.1.2. Куб
Строить куб будем, опираясь на его определение.
Куб
– правильный прямоугольный параллелепипед; имеет 6 квадратных граней, 8 вершин и 12 ребер. К тому же необходимо к каждой грани построить нормаль, итого будет 6 нормалей.
Куб задаем с помощью вершин, на основе которых считаем нормали к граням. Для отображения куба удобно использовать грани, поэтому определяем координаты всех граней.
Все 8 вершин задаем вручную.
Нормали определяем так:
1. Берем два вектора лежащих в одной плоскости грани и исходящих из одной точки  и и 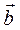 . .
Координаты этих векторов определяем так:
V1 (x1, y1, z1), V2(x2, y2, z2) – две вершины, тогда вектор, проходящий через эти точки равен
 = (x2-x1, y2-y1, z2-z1) = (x2-x1, y2-y1, z2-z1)
2. Находим  , векторное произведение векторов , векторное произведение векторов  и и 
 = =  x x 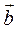 = ( (ay
bz
– az
by
), (ax
bz
– az
bx
), (ax
by
– ay
bx
) ) = ( (ay
bz
– az
by
), (ax
bz
– az
bx
), (ax
by
– ay
bx
) )
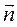 ┴ ┴  и и 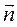 ┴ ┴ 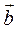 , значит , значит 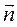 – нормаль к грани. – нормаль к грани.
При отображении куба прорисовываем только те ребра, которые видны наблюдателю. Определяется это с помощью направление нормали: если координата z нормали положительная, значит, отображаем ребра грани и нормаль, иначе нет.
2.1.
2.3. Текст программы
Kub
_
form
.
cpp
#include <vcl.h>
#pragma hdrstop
#include "Kub2.h"
#include "Kub_form_2.h"
//-------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
//-------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
disp=new Display(200,200,600,600,0.01,0.01,Form1->Canvas);
kub=new Kub();
}
//-------------------------------------------------------
void __fastcall TForm1::Timer1Timer(TObject *Sender)
{
disp->Clear();
Vector v(10,10,-3);
v=v/(!v);
Matrix A=Rotate(v,0.1);
kub->Transform(A);
kub->Show();
}
Kub.h
#include "Disp.h"
#include "Vector.h"
#include "Matrix.h"
Display * disp;
class Kub
{
Vector Ver[8],Norm[6],points[6];
int Gran[6][4];
public:
Kub()
{
Ver[0]=Vector(0,0,0);
Ver[1]=Vector(1,0,0);
Ver[2]=Vector(1,1,0);
Ver[3]=Vector(0,1,0);
Ver[4]=Vector(0,0,1);
Ver[5]=Vector(1,0,1);
Ver[6]=Vector(1,1,1);
Ver[7]=Vector(0,1,1);
Norm[0]=(Ver[1]-Ver[0])^(Ver[4]-Ver[0]);
Norm[1]=(Ver[2]-Ver[1])^(Ver[5]-Ver[1]);
Norm[2]=(Ver[7]-Ver[3])^(Ver[2]-Ver[3]);
Norm[3]=(Ver[4]-Ver[0])^(Ver[3]-Ver[0]);
Norm[4]=(Ver[5]-Ver[4])^(Ver[7]-Ver[4]);
Norm[5]=(Ver[3]-Ver[0])^(Ver[1]-Ver[0]);
for(int i=0;i<6;i++)
{
Norm[i]=Norm[i]/!Norm[i];
}
for(int i=0;i<4;i++)
{
Gran[4][i]=i+4;
}
Gran[5][0]=0;
Gran[5][1]=3;
Gran[5][2]=2;
Gran[5][3]=1;
Gran[0][0]=0;
Gran[0][1]=1;
Gran[0][2]=5;
Gran[0][3]=4;
Gran[1][0]=1;
Gran[1][1]=5;
Gran[1][2]=6;
Gran[1][3]=2;
Gran[2][0]=2;
Gran[2][1]=3;
Gran[2][2]=7;
Gran[2][3]=6;
Gran[3][0]=3;
Gran[3][1]=0;
Gran[3][2]=4;
Gran[3][3]=7;
Vector s=Vector(0,0,0);
for(int j=0;j<6;j++)
{
s=(0, 0, 0);
for(int i=0;i<4;i++)
{
s=s+Ver[Gran[j][i]];
}
s=s/4;
points[j]=s;
}
}
void Show()
{
for(int j=0;j<6;j++)
{
// отображаем только видимые ребра и нормали
if(Norm[j].z>0)
{
disp->MoveTo(Ver[Gran[j][0]].x,Ver[Gran[j][0]].y);
for(int i=1;i<4;i++)
{
disp->LineTo(Ver[Gran[j][i]].x,Ver[Gran[j][i]].y);
}
disp->LineTo(Ver[Gran[j][0]].x,Ver[Gran[j][0]].y);
disp->MoveTo(points[j].x,points[j].y);
disp->LineTo(Norm[j].x+points[j].x,Norm[j].y+points[j].y);
}//if
}
}
void Transform(Matrix & M)
{
for(int i=0;i<6;i++)
{
points[i]=M*points[i];
}
for(int i=0;i<8;i++)
{
Ver[i]=M*Ver[i];
}
Matrix M1=M;
M1.Invert();
M1.Transpose();
for(int i=0;i<6;i++)
{
Norm[i]=M1*Norm[i];
}
}
};
Результат работы программы рисования куба с нормалями приведен на Рис. 7.

Рис. 7
2.2.
OpenGL
2.2.1. Поверхность
Поверхность задана формулой:
Z (x, y) = (sin x2
+ cos y2
) xy
Функцию будем искать учитывая:
x  [– 0,8; 0,8] [– 0,8; 0,8]
y  [– 1,5; 1,5] [– 1,5; 1,5]
Шаг итерации равен 0,03.
Для правильного отображения освещения необходимо найти нормали в каждой точке поверхности.
F (x, y, z) = 0, z = f(x, y), т.е. F = f(x, y) – z = 0,
Следовательно, нормали вычислим так:

Найдем частные производные:
 = 2 x x y cos x2
+(sin x2
+ cos y2
) y = 2 x x y cos x2
+(sin x2
+ cos y2
) y
 = – 2 x y y sin y2
+x (sin x2
+ cos y2
) = – 2 x y y sin y2
+x (sin x2
+ cos y2
)
double Z(double x,double y)
{
double z=(sin(x*x)+cos(y*y))*x*y;
return z;
}
double dZx(double x,double y)
{
double pr=2*x*x*y*cos(x*x)+(sin(x*x)+cos(y*y))*y;
return pr;
}
//-------------------------------------------------------------------
double dZy(double x,double y)
{
double pr=(-2)*x*y*y*sin(y*y)+x*(sin(x*x)+cos(y*y));
return pr;
}
//-------------------------------------------------------------------
void Draw()
{
Vector Norm;
glPolygonMode(GL_FRONT_AND_BACK,GL_FILL);
for(double x=-0.8; x<0.8; x=x+0.03)
{
for(double y=-1.5; y<1.5; y=y+0.03)
{
glBegin (GL_QUADS);
glTexCoord2d(0, 0);
Norm=Vector(dZx(x,y),dZy(x,y),-1);
glNormal3d(Norm.x,Norm.y,Norm.z);
glVertex3d(x,y,Z(x,y));
glTexCoord2d(0, 1);
Norm=Vector(dZx(x+1,y),dZy(x+1,y),-1);
glNormal3d(Norm.x,Norm.y,Norm.z);
glVertex3d(x+1,y,Z(x+1,y));
glTexCoord2d(1,1);
Norm=Vector(dZx(x+1,y+1),dZy(x+1,y+1),-1);
glNormal3d(Norm.x,Norm.y,Norm.z);
glVertex3d(x+1,y+1,Z(x+1,y+1));
glTexCoord2d(1,0);
Norm=Vector(dZx(x,y+1),dZy(x,y+1),-1);
glNormal3d(Norm.x,Norm.y,Norm.z);
glVertex3d(x,y+1,Z(x,y+1));
glEnd();
}
}
}
//----------------------- Рисование сцены --------------------------
void __fastcall TFormMain::DrawObjects()
{
glBindTexture(GL_TEXTURE_2D,texture1);
Draw();
}
Результат работы программы рисования поверхности приведен на Рис. 8.

Рис. 8
2.2.2. Пружина
Пружина – модификация тора, получаемая из последнего путем распространения вдоль оси OZ, при этом большой радиус не меняется.
Формула пружины:
x = (R + r cos(f)) sin(k w),
y = (R + r cos(f)) cos(k w),
z = r sin(f) + k w,
где k – константа, определяющая шаг витков спирали по высоте. Углы f и w должны изменяться в полном круговом диапазоне, например от 0 до 360.
Поверхность пружины полностью определена формулами (см. пункт «2.2.2.1. Введение»).
Для правильного отображения освещения необходимо найти нормали в каждой точке поверхности пружины. Нормали вычислим, используя класс VECTOR, где нормали определяются в соответствии правилу:
1. Берем два вектора лежащих в одной плоскости полигона и исходящих из одной точки 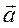 и и  . .
Координаты этих векторов определяются так:
V1 (x1, y1, z1), V2(x2, y2, z2) – две вершины, тогда вектор, проходящий через эти точки равен
 = (x2-x1, y2-y1, z2-z1) = (x2-x1, y2-y1, z2-z1)
2. Вычисляем 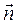 , векторное произведение векторов , векторное произведение векторов  и и 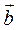
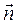 = = 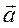 x x  = ( (ay
bz
– az
by
), (ax
bz
– az
bx
), (ax
by
– ay
bx
) ) = ( (ay
bz
– az
by
), (ax
bz
– az
bx
), (ax
by
– ay
bx
) )
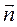 ┴ ┴ 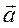 и и 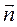 ┴ ┴  , значит , значит 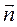 – нормаль к полигону. – нормаль к полигону.
Затем на поверхность пружины накладываем текстуру, которую берем из bmp-файла.
void DrawPruzina(double R,double r,double x,double y,double z)
{
const int N=50; // число хорд в окружности
const int M=200; // число окружностей в пружине
const int k=2; // константа, определяющая число витков пружины
Vector V[N][M];
Vector Norm[N][M];
Vector NormV[N][M];
glTranslatef(x,y,z);
glPolygonMode(GL_FRONT_AND_BACK,GL_LINE);
//вычисление вершин
for(int i=0;i<N;i++)
{
for(int j=0;j<M;j++)
{
V[i][j].x=(R+r*cos(i*2*3.14/N))*sin(j*k*2*3.14/M);
V[i][j].y=(R+r*cos(i*2*3.14/N))*cos(j*k*2*3.14/M);
V[i][j].z=r*sin(i*2*3.14/N)+k*j*3.14/M;
}
}
//вычисление нормалей к полигонам
for(int i=0;i<N-1;i++)
{
for(int j=0;j<M-1;j++)
{
Norm[i][j]=(V[i+1][j]-V[i][j])^(V[i][j+1]-V[i][j]);
Normalize( Norm[i][j]);
}
}
for(int i=0;i<N-1;i++)
{
Norm[i][M-1]=(V[i+1][M-1]-V[i][M-1])^(V[i][0]-V[i][M-1]);
Normalize(Norm[i][M-1]);
}
for(int j=0;j<M-1;j++)
{
Norm[N-1][j]=(V[0][j]-V[N-1][j])^(V[N-1][j+1]-V[N-1][j]);
Normalize(Norm[N-1][j]);
}
Norm[N-1][M-1]=(V[0][M-1]-V[N-1][M-1])^(V[N-1][0]-V[N-1][M-1]);
Normalize( Norm[N-1][M-1]);
//вычисление нормалей к вершинам
for(int i=1;i<N;i++)
{
for(int j=1;j<M;j++)
{
NormV[i][j]=(Norm[i][j]+Norm[i-1][j]+Norm[i][j-1]+Norm[i-1][j-1])/4;
Normalize(NormV[i][j]);
}
}
for(int i=1;i<N;i++)
{
NormV[i][0]=(Norm[i][0]+Norm[i-1][0]+Norm[i][M-1]+Norm[i-1][M-1])/4;
Normalize(NormV[i][0]);
}
for(int j=1;j<M;j++)
{
NormV[0][j]=(Norm[0][j]+Norm[N-1][j]+Norm[0][j-1]+Norm[N-1][j-1])/4;
Normalize(NormV[0][j]);
}
NormV[0][0]=(Norm[0][0]+Norm[N-1][0]+Norm[0][M-1]+Norm[N-1][M-1])/4;
Normalize(NormV[0][0]);
// рисуем пружину
glBegin(GL_QUADS);
for(int i=0;i<N-1;i++)
{
for(int j=0;j<M-1;j++)
{
glNormal3d(NormV[i][j].x,NormV[i][j].y,NormV[i][j].z);
glTexCoord2d((double)i/N,(double)j/M);
glVertex3d(V[i][j].x,V[i][j].y,V[i][j].z);
glNormal3d(NormV[i+1][j].x,NormV[i+1][j].y,NormV[i+1][j].z);
glTexCoord2d((double)(i+1)/N,(double)j/M);
glVertex3d(V[i+1][j].x,V[i+1][j].y,V[i+1][j].z);
glNormal3d(NormV[i+1][j+1].x,NormV[i+1][j+1].y,NormV[i+1][j+1].z);
glTexCoord2d((double)(i+1)/N,(double)(j+1)/M);
glVertex3d(V[i+1][j+1].x,V[i+1][j+1].y,V[i+1][j+1].z);
glNormal3d(NormV[i][j+1].x,NormV[i][j+1].y,NormV[i][j+1].z);
glTexCoord2d((double)i/N,(double)(j+1)/M);
glVertex3d(V[i][j+1].x,V[i][j+1].y,V[i][j+1].z);
}
}
glEnd();
}
//-------------------------- Рисование сцены ------------------------------
void __fastcall TFormMain::DrawObjects()
{
glBindTexture(GL_TEXTURE_2D,texture1);
DrawPruzina(3,1,0,0,0);
}
//------------------- Загружаем текстуру из файла -------------------------
void __fastcall TFormMain::SetupTextures()
{
bitmap = new Graphics::TBitmap;
bitmap->LoadFromFile("pic.bmp");
GLubyte bits1[64][64][4];
GLubyte bits2[64][64][4];
GLubyte bits3[64][64][4];
for(int i = 0; i < 64; i++)
{
for(int j = 0; j < 64; j++)
{
bits1[i][j][0]= (GLbyte)GetRValue(bitmap->Canvas->Pixels[i][j]);
bits1[i][j][1]= (GLbyte)GetGValue(bitmap->Canvas->Pixels[i][j]);
bits1[i][j][2]= (GLbyte)GetBValue(bitmap->Canvas->Pixels[i][j]);
bits1[i][j][3]= (GLbyte)255;
}
}
glPixelStorei(GL_UNPACK_ALIGNMENT, 4);
glGenTextures(1, &texture1);
glBindTexture(GL_TEXTURE_2D, texture1);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, 64, 64, 0, GL_RGBA, GL_UNSIGNED_BYTE, bits1);
glEnable(GL_TEXTURE_2D);
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_MODULATE);
}
//------------------------- Параметры освещения ---------------------------
void __fastcall TFormMain::SetupLighting()
{
GLfloat MaterialAmbient[] = {1.0, 1.0, 1.0, 1.0};
GLfloat MaterialDiffuse[] = {1.0, 1.0, 1.0, 1.0};
GLfloat MaterialSpecular[] = {1.0, 1.0, 1.0, 1.0};
GLfloat MaterialShininess[] = {100.0};
GLfloat AmbientLightPosition[] = {0.5, 1.0, 1.0, 0.0};
GLfloat LightAmbient[] = {0.5, 0.5, 0.5, 1.0};
glMaterialfv(GL_FRONT, GL_AMBIENT, MaterialAmbient);
glMaterialfv(GL_FRONT, GL_DIFFUSE, MaterialDiffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, MaterialSpecular);
glMaterialfv(GL_FRONT, GL_SHININESS, MaterialShininess);
glLightfv(GL_LIGHT0, GL_POSITION, AmbientLightPosition);
glLightModelfv(GL_LIGHT_MODEL_AMBIENT, LightAmbient);
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glEnable(GL_COLOR_MATERIAL);
glColorMaterial(GL_FRONT, GL_AMBIENT_AND_DIFFUSE);
glShadeModel(GL_SMOOTH);
}
Результат работы программы рисования пружины приведен на Рис. 9.

Рис. 9
3. ЗАКЛЮЧЕНИЕ
Разработанные программы на языке программирования Borland С++ с применением классов для работы с векторами и преобразованиями: VECTOR и MATRIX и библиотеки OpenGL, представляют собой яркий пример использования объектного языка программирования в области компьютерной графики. Еще раз объектно-ориентированное программирование показало свои высокие возможности.
|