| КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ ПО РЫБОЛОВСТВУ
фгоувпо «МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра высшей математики и
программного обеспечения ЭВМ
Математика
Часть
7
Задания контрольной работы по теме
«Специальные разделы высшей математики»
и методические указания к ее выполнению
для студентов 2 курса вечерне-заочного факультета
всех специальностей
Мурманск
2008 г.
УДК 51 (076.5)
ББК 22.1 я 73
3 15
Составители:
Хохлова Людмила Ивановна, к.ф.н., доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ,
Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой ВМ и ПО
13 февраля 2008 г., протокол № 5
Рецензент – Кацуба В.С
., канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ
ÓМурманский государственный технический университет, 2008
Оглавление
Стр.
Введение. 4
Задания на контрольную работу по теме «Специальные разделы высшей математики». 5
Содержание теоретического материала и ссылки на литературу.. 9
Справочный материал к выполнению контрольной работы 10
1. Алгебра логики. 10
1.1. Высказывания и операции над ними
. 10
1.2. Формулы алгебры логики
. 13
1.3. Приложение алгебры логики. Релейно-контактые схемы
.. 15
2. Булевы функции. 17
3. Графы.. 19
3.1. Основные определения
. 19
3.2. Матрицы графов
. 20
4. Элементы вариационного исчисления. 22
4.1. Функционалы в линейном нормированном пространстве
. 22
4.2. Экстремумы
функционала
. 24
5. Оптимальное управление. 27
5.1. Математическая модель системы управления
. 27
5.2. Оптимальное управление динамической системой
. 28
5.3. Принцип максимума Понтрягина
. 29
Решение примерного варианта контрольной работы.. 31
Рекомендуемая литература.. 39
Введение
Настоящее пособие предназначено для студентов 2 курса вечерне-заочного факультета, обучающихся по техническим специальностям. В пособии содержатся ссылки на теоретический материал по теме «Специальные разделы высшей математики», список рекомендуемой литературы и задания к выполнению контрольной работы. К специальным разделам высшей математики в данном пособии отнесены «Математическая логика», «Графы», «Элементы функционального анализа», «Вариационное исчисление и оптимальное управление». В результате изучения этих разделов студенты должны:
• знать, что такое высказывание, и уметь записывать формулы сложных высказываний при помощи логических операций;
• уметь упрощать логические формулы при помощи равносильных преобразований;
• иметь представление о булевых функциях одной и двух переменных;
• знать основные термины теории графов, иметь представление о способах задания ориентированных и неориентированных графов;
• знать, что такое функционал, вариация функционала, вариационная задача;
• уметь находить экстремали некоторых функционалов;
• иметь преставление о математических моделях систем управления;
• знать принцип максимума Понтрягина и уметь находить оптимальное управление для динамической системы.
Данные методические рекомендации включают справочный материал, необходимый для выполнения контрольной работы по теме «Специальные разделы высшей математики», и решение примерного варианта работы, в котором имеются ссылки на используемый справочный материал.
Задания на контрольную работу по теме
«Специальные разделы высшей математики»
Контрольная работа состоит из пяти задач. Задание для каждой задачи включает в себя ее формулировку и десять вариантов исходных данных.
Перед выполнением контрольной работы необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии со ссылками на литературу, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задача 1.
Дана формула алгебры логики. Требуется:
1) при помощи равносильных преобразований упростить формулу;
2) построить релейно-контактные схемы для исходной и упрощенной формул.
| Номер
варианта
|
Формула
|
| 1
|
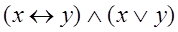
|
| 2
|
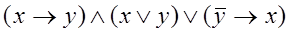
|
| 3
|
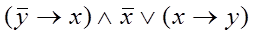
|
| 4
|
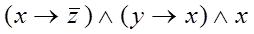
|
| 5
|
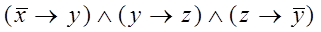
|
| 6
|

|
| 7
|
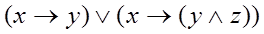
|
| 8
|

|
| 9
|

|
| 10
|
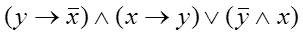
|
Задача 2.
Дана булева функция f
(x
, y
).
Составить таблицу значений функции и указать значение f
(1, 0).
| Номер варианта
|
Функция f
(x
, y
)
|
| 1
|
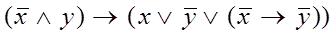
|
| 2
|

|
| 3
|
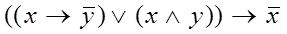
|
| 4
|

|
| 5
|
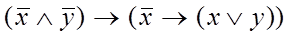
|
| 6
|

|
| 7
|
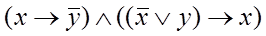
|
| 8
|

|
| 9
|

|
| 10
|

|
Задача 3.
Составить список дуг ориентированного графа, изображенного на рисунке. Сформировать матрицу инцидентности и матрицу смежности этого орграфа.
| Номер
варианта
|
Орграф
|
Номер
варианта
|
Орграф
|
| 1
|

|
6
|

|
| 2
|

|
7
|

|
| 3
|

|
8
|

|
| 4
|

|
9
|

|
| 5
|

|
10
|

|
Задача 4.
Даны функционал I
[y
(x
)] = 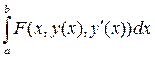 и граничные условия для функции y
(х
): y
(a
) = A
, y
(b
) = B
.
Требуется найти экстремали функционала, удовлетворяющие граничным условиям. и граничные условия для функции y
(х
): y
(a
) = A
, y
(b
) = B
.
Требуется найти экстремали функционала, удовлетворяющие граничным условиям.
| Номер
варианта
|
Функционал I
[y
(x
)]
|
Граничные условия
|
| 1
|
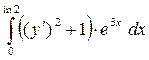
|
y
(0) = 3
|
y
(ln2) = 2
|
| 2
|

|
y
(0) = 0
|
y
(3) = 2
|
| 3
|

|
y
(0) = 1
|
y
(ln2) = –
1
|
| 4
|
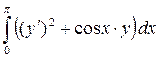
|
y
(0) = –
0,5
|
y
(π
) = 0,5
|
| 5
|

|
y
(0) = 0
|
y
(2) = e
|
| 6
|
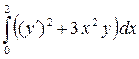
|
y
(0) = 1
|
y
(2) = 5
|
| 7
|
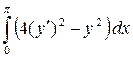
|
y
(0) = 2
|
y
(π
) = 0
|
| 8
|
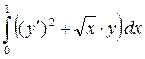
|
y
(0) = 0
|
y
(1) = –
2
|
| 9
|
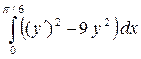
|
y
(0) = 0
|
 = 1
= 1
|
| 10
|
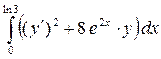
|
y
(0) = 2
|
y
(ln3) = 10
|
Задача 5.
Дана модель объекта управления, описываемая системой дифференциальных уравнений 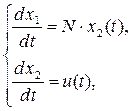 и граничными условиями и граничными условиями
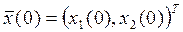 , , 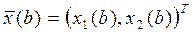 , ,
где N
–
номер варианта, t
–
время (t
 [0; b
]), [0; b
]),  –
фазовый вектор (траектория объекта), u
(t
) –
функция управления объектом. –
фазовый вектор (траектория объекта), u
(t
) –
функция управления объектом.
Требуется найти оптимальное управление объектом u
*(t
) и соответствующую ему оптимальную траекторию 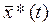 , если задан критерий качества управления: I
[u
(t
)] = , если задан критерий качества управления: I
[u
(t
)] = 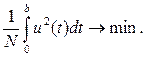
| Номер
варианта
|
[0; b
]
|
x
1
(0), x
2
(0)
|
x
1
(b
), x
2
(b
)
|
| 1
|
[0; 3]
|
x
1
(0) = 0, x
2
(0) = 1
|
x
1
(3) = –
1, x
2
(3) = 0
|
| 2
|
[0; 4]
|
x
1
(0) = 2, x
2
(0) = 0
|
x
1
(4) = 0, x
2
(4) = 1
|
| 3
|
[0; 2]
|
x
1
(0) = 1, x
2
(0) = 0
|
x
1
(2) = –
1, x
2
(2) = 3
|
| 4
|
[0; 3]
|
x
1
(0) = 0, x
2
(0) = –
1
|
x
1
(3) = 1, x
2
(3) = 0
|
| 5
|
[0; 4]
|
x
1
(0) = 0, x
2
(0) = –
2
|
x
1
(4) = 0, x
2
(4) = 1
|
| 6
|
[0; 2]
|
x
1
(0) = 0, x
2
(0) = 1
|
x
1
(2) = –
2, x
2
(2) = 0
|
| 7
|
[0; 1]
|
x
1
(0) = –
7, x
2
(0) = 0
|
x
1
(1) = 0, x
2
(1) = 3
|
| 8
|
[0; 2]
|
x
1
(0) = 0, x
2
(0) = 2
|
x
1
(2) = 0, x
2
(2) = 1
|
| 9
|
[0; 1]
|
x
1
(0) = –
3, x
2
(0) = 0
|
x
1
(1) = 6, x
2
(1) = 0
|
| 10
|
[0; 2]
|
x
1
(0) = 0, x
2
(0) = 1
|
x
1
(2) = –
10, x
2
(2) = 0
|
Содержание теоретического материала
и ссылки на литературу
| №
задачи
|
Содержание (темы)
|
Литература
|
| 1
|
Высказывания, их значения истинности. Операции над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Таблицы истинности. Свойства логических операций, порядок их выполнения. Равносильные логические формулы. Алгебра Буля
|
[1], часть 1, гл. 1, §1-6;
часть 2, гл. 1, §1,2, №1.1-1.22, 1.45, 1.46(1,2), 1.48(1-7), 1.50, 1.51;
[2], гл. 1, п.1.1.1-1.1.3, задачи 1-6;
[3], гл. 16.3
|
| 2
|
Функции алгебры логики (булевы функции) и их преставление при помощи логических формул. Приложение алгебры логики: упрощение релейно-контактных схем
|
[1], гл. 1, §7, 8, 13;
часть 2, гл. 1, §3,4, №1.49;
[2], гл. 1, п.1.2.1, 1.2.4, зад. 17;
[3], гл. 16.4
|
| 3
|
Графы. Основные определения: вершины, ребра, кратные ребра. Ориентированные и неориентированные графы. Задание графов. Матрица инцидентности и матрица смежности графа
|
[2], гл. 4, п.4.1.1, 4.1.4;
[6], гл.III, §1-5
|
| 4
|
Функционал. Приращение функционала. Вариация функционала. Экстремумы функционала, необходимое условие экстремума. Экстремали функционала. Уравнение Эйлера для функционала вида 
|
[4], гл. 7, §1-2;
[5], гл. II, §3.1, 3.3, 3.6, 4; №71, 72, 75-78;
[7], гл.X, № 1281-1285, 1289-1298;
[8], гл. 16, №3.1-3.8
|
| 5
|
Система управления и ее математическая модель. Оптимальное управление. Гамильтониан. Принцип максимума Понтрягина. Каноническая система уравнений задачи оптимального управления
|
[9], часть III, гл. 9.1.1-9.1.2, №9.1, 9.3, 9.4
|
Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке рекомендуемой литературы.
Справочный материал
к выполнению контрольной работы
1.1.
Высказывания и операции над ними
Математическая логика – разновидность формальной логики, т.е. науки, которая изучает умозаключения с точки зрения их формального строения.
Высказыванием
называется предложение, к которому можно применить понятия «истинно» или «ложно». Обозначаются высказывания малыми прописными буквами: a
, b
, х
,….
В математической логике не рассматривается смысл высказываний, определяется только их логическое значение – «истина» или «ложь», что принято обозначать соответственно «1» или «0».
Примеры.
1. «Волга впадает в Каспийское море» – высказывание (истинное).
2. «Число 16 кратно 3» – высказывание (ложное).
3. «Может быть, сегодня пойдет снег» – не высказывание.
4. «3х
– 5 = 0» – не высказывание.
Истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами «и», «или», связками «не», «следует» и др. Таким образом, операции над высказываниями можно описывать при помощи некоторого математического аппарата.
Основные логические операции над высказываниями.
Отрицанием
высказывания х
называется высказывание, которое истинно тогда и только тогда, когда высказывание х
ложно. Отрицание обозначается 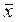 или Øх
(читается: «не х
»). или Øх
(читается: «не х
»).
Логические операции можно задавать при помощи таблиц истинности
, показывающих соответствие значений истинности высказываний. Для высказываний x
и 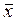 эта таблица имеет вид: эта таблица имеет вид:
| х
|

|
| 1
|
0
|
| 0
|
1
|
Конъюнкцией
двух высказываний х
и y
называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания х
и y
. Конъюнкция обозначается: х
Ù y
, или х
& y
(читается: «х
и y
»). Таблица истинности для х
Ù y
имеет вид:
| х
|
y
|
х
Ù y
|
| 1
|
1
|
1
|
| 1
|
0
|
0
|
| 0
|
1
|
0
|
| 0
|
0
|
0
|
Дизъюнкцией
двух высказываний х
и y
называется высказывание, ложное тогда и только тогда, когда оба высказывания х
и y
ложны. Дизъюнкция обозначается х
Ú y
(читается: «х
или y
»). Таблица истинности для х
Ú y
имеет вид:
| х
|
y
|
х
Ú y
|
| 1
|
1
|
1
|
| 1
|
0
|
1
|
| 0
|
1
|
1
|
| 0
|
0
|
0
|
Импликацией
двух высказываний х
и y
называется высказывание, ложное тогда и только тогда, когда высказывание х
истинно, а y
– ложно. Импликация обозначается: х
® y
(читается: «х
влечет y
» или «из х
следует y
»). Высказывание х
называется посылкой импликации
, а высказывание y
– следствием
. Таблица истинности для х
® y
имеет вид:
| х
|
y
|
х
® y
|
| 1
|
1
|
1
|
| 1
|
0
|
0
|
| 0
|
1
|
1
|
| 0
|
0
|
1
|
Эквиваленцией
(эквивалентностью) двух высказываний х
и y
называется высказывание, истинное тогда и только тогда, когда истинности высказываний х
и y
совпадают. Эквиваленция обозначается: х
« y
, или х
~ y
(читается: «х
эквивалентно y
» или «х
тогда и только тогда, когда y
»). Таблица истинности для х
« y
имеет вид:
| х
|
y
|
х
« y
|
| 1
|
1
|
1
|
| 1
|
0
|
0
|
| 0
|
1
|
0
|
| 0
|
0
|
1
|
Формулами алгебры логики
называются выражения, полученные из переменных x
, y
,… посредством применения логических операций: отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции, а также сами переменные, принимающие значения истинности высказываний x
, y
,….
Формулы алгебры логики будем обозначать большими буквами латинского алфавита: А
, В
,…..
Если в формулу алгебры логики вместо переменных x
, y
,… подставить конкретные высказывания, то получится высказывание, имеющее логическое значение «1» или «0».
Пример.
Высказывание x
: «Волга впадает в Каспийское море» – истинное (x
= 1),
высказывание y
: «Число 16 кратно 3» – ложное (y
= 0),
тогда формула А
= x
Ú y
будет иметь логическое значение «1»: А
= 1 (см. таблицу истинности для х
Ú y
).
На основе таблиц истинности основных логических операций можно составлять таблицы истинности для различных формул алгебры логики.
Две формулы алгебры логики называются равносильными
или эквивалентными
, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы переменных (элементарных высказываний). Равносильность формул А
и В
будем обозначать знаком «º»: А
º В
.
Равносильность логических формул можно установить при помощи их таблиц истинности.
Пример.
С помощью таблиц истинности проверить, являются ли равносильными формулы А
= 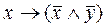 и В
= и В
= 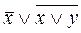 . .
Решение.
Составим таблицы истинности для каждой из формул А
и В
.
| x
|
y
|

|

|
 Ù Ù
|
А
= 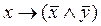
|
| 1
|
1
|
0
|
0
|
0
|
0
|
| 1
|
0
|
0
|
1
|
0
|
0
|
| 0
|
1
|
1
|
0
|
0
|
1
|
| 0
|
0
|
1
|
1
|
1
|
1
|
| x
|
y
|

|
x
Ú y
|
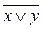
|
В
= 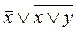
|
| 1
|
1
|
0
|
1
|
0
|
0
|
| 1
|
0
|
0
|
1
|
0
|
0
|
| 0
|
1
|
1
|
1
|
0
|
1
|
| 0
|
0
|
1
|
0
|
1
|
1
|
Ответ: данные формулы являются
равносильными.
Другой способ доказательства равносильности логических формул – их упрощение с использованием основных равносильностей
.
Основные равносильности.
Для любых элементарных высказываний x
, y
, z
справедливы следующие равносильности, которые можно разбить на 3 группы.
1. Основные законы:
1) x
Ù x
º x
; 2) x
Ú x
º x
; 3)  º x
; º x
;
4) x
Ù 0 º 0; 5) x
Ú 0 º x
; 6)  Ù x
º 0; Ù x
º 0;
7) x
Ù 1 º x
; 8) x
Ú 1 º 1; 9) 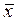 Ú x
º 1; Ú x
º 1;
законы поглощения:
10) x
Ù (y
Ú x
) º x
; 11) x
Ú (y
Ù x
) º x
.
2. Выражения одних логических операций через другие:
12) x
® y
º 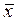 Ú y
; 13) Ú y
; 13) 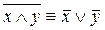 ; ;
14) x
« y
º (x
® y
) Ù (y
® x
); 15) 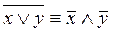 . .
3. Свойства логических операций:
16) x
Ù y
º y
Ù x
; 17) x
Ú y
º y
Ú x
;
18) x
Ù (y
Ù z
) º (x
Ù y
) Ù z
; 19) x
Ú (y
Ú z
) º (x
Ú y
) Ú z
;
20) x
Ù (y
Ú z
) º (x
Ù y
) Ú (x
Ù z
); 21) x
Ú (y
Ù z
) º (x
Ú y
) Ù (x
Ú z
).
Множество высказываний с введенными для них логическими операциями и основными равносильностями называется алгеброй Буля
.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквиваленция. Если над формулой стоит знак отрицания, то скобки тоже опускаются.
Пример.
Упростить логическую формулу:  . .
Решение
. Используем основные равносильности.
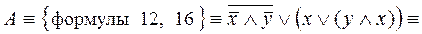

 . .
Ответ: А
º x
Ú y
.
Релейно-контактной схемой
(РКС
) или переключательной схемой
называется схематическое изображение устройства, состоящего из следующих элементов:
1) переключателей (контактов, реле, ламп и др.);
2) соединительных проводников;
3) входов-выходов (полюсов РКС).
Рассмотрим простейшую РКС, содержащую один переключатель Р
. Если переключателю Р
поставить в соответствие высказывание х
: «Переключатель Р
замкнут», то истинному значению х
(х
= 1) будет соответствовать замкнутое состояние переключателя, при котором РКС проводит ток, т.е. импульс, поступающий на вход, может быть снят на выходе. Значению х
= 0 будет соответствовать разомкнутое состояние РКС (ток не проводится).
Каждой РКС, состоящей из нескольких переключателей, можно поставить в соответствие высказывание, выраженное некоторой формулой А
, таким образом, что истинному значению формулы (А
= 1) будет соответствовать замкнутое состояние РКС, а значению А
= 0 – разомкнутое состояние. Примеры таких соответствий приведены в таблице.
Простейшие РКС и соответствующие им формулы логики.
| РКС
|
Формула
|
Значения
|
| Переключатель х
:

|
Простейшее высказывание: х
|
х
= 1, если переключатель замкнут;
х
= 0, если переключатель разомкнут
|
| Переключатель 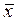

|
Отрицание простейшего высказывания: 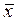
|
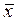 = 0, если переключатель замкнут; = 0, если переключатель замкнут;
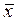 = 1, если переключатель разомкнут = 1, если переключатель разомкнут
|
| Последовательное соединение:

(схема замкнута, когда
оба переключателя замкнуты)
|
Конъюнкция высказываний:
x
Ù y
|

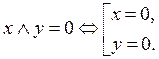
|
| Параллельное соединение:

(схема разомкнута, когда
оба переключателя разомкнуты)
|
Дизъюнкция высказываний:
x
Ú y
|
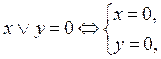
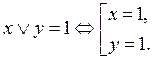
|
| Схема, которая всегда разомкнута

|
x
Ù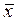
|
x
Ù º 0 º 0
|
| Схема, которая всегда замкнута

|
x
Ú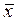
|
x
Ú º 1 º 1
|
Из простейших РКС путем их последовательного и параллельного соединения могут быть построены более сложные переключательные схемы.
Доказано, что любая формула алгебры логики может быть преобразована к виду, содержащему только операции отрицания, конъюнкции и дизъюнкции. Это позволяет изображать логические формулы при помощи РКС, а РКС задавать формулами.
Например, согласно формулам основных равносильностей
x
® y
º 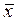 Ú y
и x
« y
º (x
® y
) Ù (y
® x
), Ú y
и x
« y
º (x
® y
) Ù (y
® x
),
следовательно, логическим операциям импликации и эквиваленции соответствуют РКС, изображенные рис. 1.
 Используя равносильные преобразования логической формулы, соответствующей некоторой РКС, можно упростить
РКС
, т.е. привести ее к виду, содержащему меньшее число переключателей. Используя равносильные преобразования логической формулы, соответствующей некоторой РКС, можно упростить
РКС
, т.е. привести ее к виду, содержащему меньшее число переключателей.
 Пример
. Упростить РКС, изображенную на рис. 2. Пример
. Упростить РКС, изображенную на рис. 2.
Решение.
Запишем соответствующую РКС формулу, используя таблицу простейших РКС и соответствующих им формул логики:
 . .
Упростим формулу, используя основные равносильности:
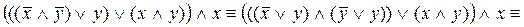
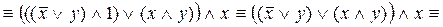  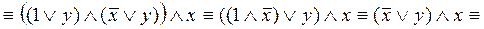
  . .
Таким образом,  . Построим РКС, соответствующую упрощенной формуле (рис. 3). . Построим РКС, соответствующую упрощенной формуле (рис. 3).
2.
Булевы функции
Будем рассматривать логические переменные x
1
, x
2
, …, xn
,
принимающие только два значения: «1» или «0».
Булевой функцией
f
(x
1
, x
2
, …, xn
) называется произвольная функция, аргументами которой являются логические переменные и принимающая только одно из двух значений: «1» или «0».
Количество булевых функций одного аргумента равно 22
= 4, это функции:
f
1
(x
) = 0, f
2
(x
) =1, f
3
(x
) = x
и f
4
(x
) = 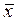 . .
Булевых функций двух аргументов всего 24
= 16, а количество булевых функций n
аргументов равно 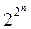 . .
Всякой формуле алгебры логики, составленной из элементарных высказываний x
1
, x
2
, …, xn
соответствует булева функция f
(x
1
, x
2
, …, xn
), аргументы которой принимают значения истинности соответствующих элементарных высказываний: «1» или «0». Две равносильные формулы алгебры логики определяют одну и ту же булеву функцию, т.к. значения истинности этих формул совпадают для одинаковых значений входящих в них переменных.
Для булевых функций можно составлять таблицы значений – всякую булеву функцию n
аргументов можно задать таблицей из 2n
строк.
Например, таблица значений некоторых функций 2-х аргументов, соответствующих основным логическим операциям (отрицание одного аргумента, конъюнкция, дизъюнкция, импликация и эквиваленция) выглядит так:
| x
1
|
x
2
|
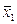
|
x
1
Ù x
2
|
x
1
Ú x
2
|
x
1
® x
2
|
x
1
« x
2
|
| 1
|
1
|
0
|
1
|
1
|
1
|
1
|
| 1
|
0
|
0
|
0
|
1
|
0
|
0
|
| 0
|
1
|
1
|
0
|
1
|
1
|
0
|
| 0
|
0
|
1
|
0
|
0
|
1
|
1
|
Значение булевой функции f
(x
1
, x
2
) при известных значениях аргументов устанавливается по строке таблицы, соответствующей заданным значениям x
1
и x
2
. Например, для функции f
(x
1
, x
2
) = x
1
® x
2
значение f
(1, 0) = 0, а значение f
(1, 1) = 1.
Каждой релейно-контактной схеме (РКС), составленной из переключателей x
1
, x
2
, …, xn
, можно поставить в соответствие булеву функцию, называемую ее функцией проводимости:

Функция проводимости РКС задается при помощи формулы логики, соответствующей этой РКС. Например, РКС, изображенная на рис. 2, имеет функцию проводимости 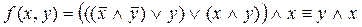 , таблица значений которой имеет вид: , таблица значений которой имеет вид:
| х
|
y
|
f
(x, y
)
|
| 1
|
1
|
1
|
| 1
|
0
|
0
|
| 0
|
1
|
0
|
| 0
|
0
|
0
|
3.1.
Основные определения
Рассмотрим некоторое конечное множество точек V
= {v
1
, v
2
,…,vn
} и конечное множество линий Х
, соединяющих некоторые пары из точек множества V
. Полученная совокупность точек и линий называется графом
и обозначается G
=
{V
, X
}.
Элементы множества V
называются вершинами
графа, а элементы множества Х
– ребрами
.
Граф можно изобразить при помощи геометрической конфигурации. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины (рис. 4). При этом несущественным является расположение вершин, форма и длина ребер графа, важно лишь, соединены две данные точки ребром, или нет.
 Ребра, соединяющие одну и ту же пару вершин, называются кратными
(или параллельными
) ребрами (ребра х
4
, х
5
графа G
1 на рис. 4). Ребра, соединяющие одну и ту же пару вершин, называются кратными
(или параллельными
) ребрами (ребра х
4
, х
5
графа G
1 на рис. 4).
Если х
– ребро графа, соединяющее вершины vi
, vj
, то вершины vi
и vj
называются концами ребра
х
.
Множество ребер графа Х
можно задать, как множество пар вершин из множества V
. Если пары в этом множестве Х
являются упорядоченными, то граф называется ориентированным или орграфом
. Ребра орграфа называют дугами
и на рисунках помечают стрелками (рис. 4).
Если х
= (vi
, vj
) – дуга орграфа, то вершина vi
называется началом дуги
х
, а вершина vj
– концом
дуги х
.
При помощи графов удобно изображать связь атомов в молекуле, кристаллические решетки, схемы дорог, маршруты движения, электрические цепи, экономические связи объектов, графики работ и др.
Для того, чтобы задать граф, необходимо задать множества его вершин и ребер (V
и X
).
Иногда граф задают списком ребер (дуг)
, например, орграф G2, изображенный на рис. 4, можно задать следующим списком дуг:
X
= {х
1
, х
2
, х
3
, х
4
, х
5
, х
6
} = {(v
1
, v
4
), (v
1
, v
4
), (v
4
, v
2
), (v
2
, v
4
), (v
2
, v
3
), (v
3
, v
4
)}.
В этом списке каждой из 6-ти дуг орграфа соответствует упорядоченная пара вершин (если граф неориентированный, то порядок записи вершин в каждой паре – произвольный).
Если граф содержит изолированные вершины
, т.е. не связанные ни с одной другой вершиной ребрами (дугами) графа (см. вершину v
5
в графе G1 на рис. 4), то список ребер не даст полного представления о графе. Кроме того, использовать список ребер (дуг) можно только при относительно небольшом количестве вершин графа. Для практического использования более удобен матричный способ задания графов
.
Пусть G
= {V
, X
} – граф, где V
= {v
1
, v
2
,…,vn
}, X
= {x
1
, … , xm
}.
Если вершины графа vi
, vj
являются концами ребра х
, то говорят, что вершины vi
, vj
и ребро х
инцидентны
.
Матрицей инцидентности графа
G
называется матрица размерности n
´m
B
(G
), элементы которой
bij
= 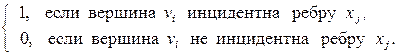
Строки матрицы инцидентности графа соответствуют его вершинам, а столбцы – ребрам.
Для орграфа вершина vi
и дуга х
j
инцидентны, если vi
является началом или концом дуги х
j
. Элементы матрицы инцидентности орграфа определяются по формулам:
bij
= 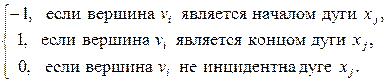 (1) (1)
Вершины vi
, vj
графа G
называются смежными
, если существует ребро х
= (vi
, vj
)ÎX
, инцидентное этим вершинам (соединяющее эти вершины).
Матрицей смежности
графа G
называется квадратная матрица A
(G
) порядка п
, каждый элемент которой aij
равен количеству ребер, инцидентных вершинам vi
и vj
.
Для орграфа G
= {V
, X
} элементы матрицы смежности определяются по формулам:
aij
=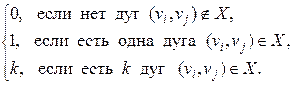 (2) (2)
Пример.
Записать матрицу инцидентности и матрицу смежности для орграфа G2, изображенного на рис. 4.
Решение.
Данный граф является ориентированным. Для построения матрицы инцидентности составим таблицу, используя формулы (1). Заполняем таблицу по столбцам, соответствующим дугам орграфа: в j
-
м столбце ставим в i
-й строке
«–1», если вершина vi
является началом дуги х
j
,
«1», если вершина vi
является концом дуги х
j
,
«0» в остальных случаях (вершина vi
и дуга х
j
не инцидентны).
| |
x
1
|
x
2
|
x
3
|
x
4
|
x
5
|
x
6
|
Получили матрицу инцидентности:
В
(G
2) = 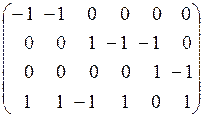 . .
|
| v
1
|
–1
|
–1
|
0
|
0
|
0
|
0
|
| v
2
|
0
|
0
|
1
|
–1
|
–1
|
0
|
| v
3
|
0
|
0
|
0
|
0
|
1
|
–1
|
| v
4
|
1
|
1
|
–1
|
1
|
0
|
1
|
Для построения матрицы смежности составим таблицу, используя формулы (2). Так как граф G
2 ориентированный, то элемент матрицы aij
равен количеству ребер с началом в i
-й вершине, а концом в j
-й вершине.
| |
v
1
|
v
2
|
v
3
|
v
4
|
Получили матрицу смежности
A
(G
2) = 
|
| v
1
|
0
|
0
|
0
|
2
|
| v
2
|
0
|
0
|
1
|
1
|
| v
3
|
0
|
0
|
0
|
1
|
| v
4
|
0
|
1
|
0
|
0
|
Матрица инцидентности более информативна, чем матрица смежности, т.к. по ней можно восстановить не только нумерацию вершин и связи между ними, но и нумерацию ребер. Однако, при помощи матрицы инцидентности задают только графы, не имеющие изолированных вершин (в матрице смежности изолированной вершине соответствуют нулевая строка и нулевой столбец).
Кроме матриц инцидентности и смежности существуют и другие формы матричного задания графов. Матричный метод задания графов удобен для обработки данных на ЭВМ.
4.
Элементы вариационного исчисления
Линейным пространством Е
называется множество элементов
{x
, y
, z
,….}, в котором определены операции сложения элементов и умножения элемента на число, удовлетворяющие 8 свойствам:
1. x
+ y
= y
+ x
 ; ;
2. (x
+ y
) + z
= x
+ (y
+ z
)  ; ;
3. λ
(m
x
) = (λ
m
) x
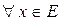 , где λ
, m
– числа; , где λ
, m
– числа;
4. (λ +
m
) x
= λ
x
+ m
x
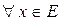 , где λ
, m
– числа; , где λ
, m
– числа;
5. λ
(x
+ y
) = λ
x
+ λу
 , где λ
– число; , где λ
– число;
6. 1·x
= x
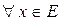 ; ;
7. существует нулевой элемент 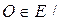 O
+
x
= x O
+
x
= x
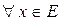 ; ;
8. для 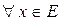 существует противоположный элемент существует противоположный элемент  . .
Примеры линейных пространств
:
• координатное пространство Rn
с элементами – n
-мерными векторами либо точками;
• пространство матриц размерности 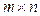 ; ;
• Cn
[a
; b
] – пространство функций, непрерывных на промежутке [a
; b
] вместе со своими производными 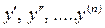 . .
В линейном пространстве вводится понятие нормы элемента.
Нормой элемента
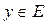 называется число, обозначаемое называется число, обозначаемое 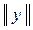 и удовлетворяющее трем условиям: и удовлетворяющее трем условиям:
1.  ³ 0 и ³ 0 и  = 0 тогда и только тогда, когда у
= О
; = 0 тогда и только тогда, когда у
= О
;
2. 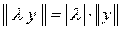  , где λ
– число; , где λ
– число;
3. 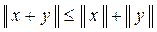  , где λ
– число. , где λ
– число.
Пример.
В пространстве C
[a
; b
] (пространство функций, непрерывных на промежутке [a
; b
]) норма элемента у
может быть введена следующим образом:
 . .
Если каждой функции из некоторого линейного нормированного пространства функций У
ставится в соответствие число, то говорят, что на множестве У
задан функционал
I
[y
(x
)].
Примеры функционалов.
• 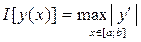 – функционал, заданный на пространстве функций, имеющих непрерывные производные на промежутке [a
; b
], т.е. на C
1
[a
; b
]; – функционал, заданный на пространстве функций, имеющих непрерывные производные на промежутке [a
; b
], т.е. на C
1
[a
; b
];
• – функционал, заданный на пространстве функций, интегрируемых на промежутке [0; 1]. – функционал, заданный на пространстве функций, интегрируемых на промежутке [0; 1].
Рассмотрим пространство C
[a
; b
] – множество функций (кривых), непрерывных на промежутке [a
; b
], и функционал I
[y
(x
)], определенный на этом пространстве.
ε
-окрестностью кривой
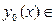 C
[a
; b
] называется совокупность кривых C
[a
; b
] называется совокупность кривых 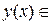 C
[a
; b
], таких что C
[a
; b
], таких что
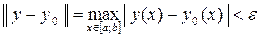 . .
Разность 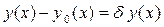 называется вариацией аргумента функционала
. Вариация d
y
(x
) есть функция от x
и тоже принадлежит функциональному пространству C
[a
; b
]. называется вариацией аргумента функционала
. Вариация d
y
(x
) есть функция от x
и тоже принадлежит функциональному пространству C
[a
; b
].
Приращением функционала
называется разность DI
= I
[y
(x
)] – I
[y
0
(x
)], где y
0
(x
) – фиксированная функция, а y
(x
) – произвольная функция из пространства C
[a
; b
].
Используя вариацию d
y
(x
), можно представить приращение функционала в виде  . .
Линейным функционалом
называется функционал I
[y
(x
)], удовлетворяющий следующим условиям:
1) I
[λ
y
(x
)] = λ
I
[y
(x
)], где λ
– число;
2) I
[y
1
(x
) + y
2
(x
)] = I
[y
1
(x
)] + I
[y
2
(x
)].
Вариацией функционала
называется главная часть его приращения, линейная относительно d
y
(x
).
Если приращение функционала можно представить в виде
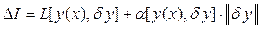 , ,
где 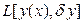 – линейный функционал относительно d
y
(x
), и функционал – линейный функционал относительно d
y
(x
), и функционал 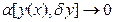 при при 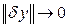 , то d
I
[y
] = , то d
I
[y
] =  – вариация функционала I
[y
(x
)]. – вариация функционала I
[y
(x
)].
Функционал I
[y
(x
)], определенный на некотором пространстве функций (кривых) достигает на кривой y
= y
0
(x
) экстремума
, если существует  -окрестность этой кривой, в которой приращение функционала сохраняет знак, причем, если DI
=
I
[y
] – I
[y
0
] > 0, то функционал I
[y
] достигает на кривой y
= y
0
(x
) минимума
, а если DI
< 0, то функционал I
[y
] достигает на кривой y
= y
0
(x
) максимума
. Функцию y
0
(x
) называют соответственно точкой минимума
или точкой максимума
. -окрестность этой кривой, в которой приращение функционала сохраняет знак, причем, если DI
=
I
[y
] – I
[y
0
] > 0, то функционал I
[y
] достигает на кривой y
= y
0
(x
) минимума
, а если DI
< 0, то функционал I
[y
] достигает на кривой y
= y
0
(x
) максимума
. Функцию y
0
(x
) называют соответственно точкой минимума
или точкой максимума
.
Теорема.
(Необходимое условие локального экстремума).
Если функционал I
[y
(x
)], имеющий вариацию, достигает минимума или максимума на кривой y
= y
0
(x
), где y
0
(x
) – внутренняя точка области определения функционала, то при y
(х
) = y
0
(x
) вариация функционала равна нулю:
d
I
[y
0
(x
)] = 0. (3)
Функции, удовлетворяющие условию (3), называются экстремалями функционала
.
Вариационная задача
: среди функций (кривых) y
(x
), принадлежащих некоторому множеству М
, требуется найти кривую y
= y
*(x
), на которой функционал I
[y
(x
)], определенный на множестве М
, достигает экстремума, т.е. 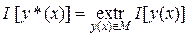 . .
Решение этой задачи заключается в поиске экстремалей, т.е. функций, «подозрительных на экстремум», и в последующей проверке выполнения достаточных условий существования экстремума. На практике, как правило, экстремалей немного, и установить наличие (или отсутствие) на них экстремума функционала удается, исходя из смысла задачи. Следует отметить, что вариационная задача не всегда имеет точное решение, а если решение существует, то оно не всегда единственно.
Рассмотрим пространство M
функций y
(x
), дифференцируемых на отрезке [a
; b
] и удовлетворяющих граничным условиям:
y
(a
) =
A
,
y
(b
) = B
, (4)
то есть все кривые проходят через две закрепленные граничные точки.
Пусть на этом пространстве M
определен функционал
I
[y
(x
)] = 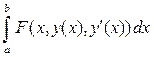 , (5) , (5)
где подынтегральная функция 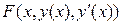 имеет непрерывные частные производные до второго порядка включительно по всем переменным. имеет непрерывные частные производные до второго порядка включительно по всем переменным.
Требуется найти экстремали функционала I
[y
(x
)].
Можно доказать, что, если для функционала (5) выполнено необходимое условие (3), то функция  удовлетворяет уравнению Эйлера: удовлетворяет уравнению Эйлера:
 (6) (6)
Так как 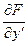 тоже является функцией от тоже является функцией от  , то это уравнение можно записать в развернутой форме: , то это уравнение можно записать в развернутой форме:
 . (7) . (7)
При  уравнение Эйлера представляет собой обыкновенное дифференциальное уравнение второго порядка относительно функции y
(x
). Его общее решение зависит от двух произвольных постоянных С
1
, С
2
, которые можно найти из граничных условий (4). уравнение Эйлера представляет собой обыкновенное дифференциальное уравнение второго порядка относительно функции y
(x
). Его общее решение зависит от двух произвольных постоянных С
1
, С
2
, которые можно найти из граничных условий (4).
Пример.
Найти экстремали функционала  , удовлетворяющие граничным условиям y
(0) = 0, y
(ln2) = 2. , удовлетворяющие граничным условиям y
(0) = 0, y
(ln2) = 2.
Решение
. Запишем уравнение Эйлера (7) для данного функционала. Для подынтегральной функции 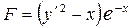 , получаем частные производные , получаем частные производные
 , ,  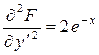 . .
Тогда уравнение Эйлера:  или или 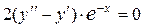 . Учитывая, что . Учитывая, что 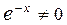 , получаем , получаем 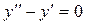 – однородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно функции y
(x
). – однородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно функции y
(x
).
Его характеристическое уравнение k
2
– k
= 0 имеет корни k
1
= 0, k
2
= 1.
Напомним, что общее решение однородного дифференциального уравнения второго порядка с постоянными коэффициентами в зависимости от корней характеристического уравнения имеет вид:
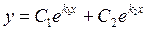 , если , если  (корни вещественные различные); (корни вещественные различные);
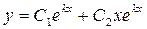 , если , если  (корни вещественные равные); (корни вещественные равные);
 , если , если 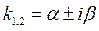 (корни комплексно-сопряженные). (корни комплексно-сопряженные).
В данном случае k
1
= 0, k
2
= 1,  и общее решение уравнения имеет вид и общее решение уравнения имеет вид  . .
Определим произвольные постоянные С
1
, С
2
из граничных условий
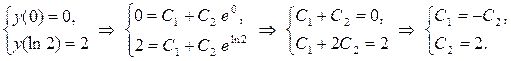
Отсюда получаем С
1
= –2, С
2
= 2, следовательно, экстремаль функционала  . .
Ответ. 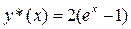 . .
Система управления
состоит из управляющего устройства
(УУ) и объекта управления
(ОУ). Примерами систем управления служат семейный бюджет, экономика отрасли, технологический процесс, научное исследование и т.д.
УУ передает в ОУ сигнал – управление
. Управление может быть механическим воздействием, электромагнитным импульсом, потоком инвестиций и др. Под воздействием сигнала u
(t
), где t
– время, u
(t
) – скалярная или векторная функция, система изменяет свое состояние (возможна обратная связь). Простейшая математическая модель системы управления без учета внешних воздействий включает:
• модель ОУ
– оператор, в соответствии с которым осуществляется преобразование входа – управления u
(t
) в реакцию системы;
• алгоритм управления
, который зависит от цели управления
и наличия обратной связи.
В общем случае состояние динамической системы управления характеризуется n
-мерным вектором (матрицей-столбцом)
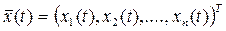 , ,
где xj
(t
) для j
= 1,2,…,n
называют фазовыми координатами
, а  – фазовым вектором
. – фазовым вектором
.
Например, положение самолета определяет 6-мерный вектор, в котором 3 координаты задают положение центра масс самолета в пространстве и 3 координаты – его вращение относительно центра масс. Курс самолета – это вектор-функция 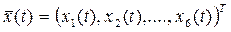 . .
Модель ОУ обычно описывается уравнениями состояний, отражающих законы физики, экономики и прочее. Довольно часто процесс управления без учета внешних воздействий может быть задан системой обыкновенных дифференциальных уравнений:
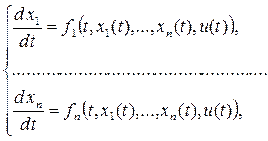 (8) (8)
или, в векторной форме: 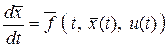 , где , где  – вектор-функция, характеризующая изменение состояния системы, u
(t
) – функция управления. В реальных условиях множество управлений ограничено: – вектор-функция, характеризующая изменение состояния системы, u
(t
) – функция управления. В реальных условиях множество управлений ограничено: 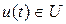 , где U
– класс допустимых управлений
. , где U
– класс допустимых управлений
.
Для того, чтобы процесс управления был определен на некотором промежутке 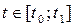 , необходимо задать начальное состояние системы – вектор , необходимо задать начальное состояние системы – вектор  . Тогда . Тогда  будет соответствовать траектория
– вектор-функция будет соответствовать траектория
– вектор-функция  , переводящая систему из состояния , переводящая систему из состояния 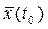 в в  – состояние
, достижимое
из состояния – состояние
, достижимое
из состояния
 на данном классе управлений U
. на данном классе управлений U
.
Рассмотрим некоторый процесс управления без учета внешних воздействий, заданный системой обыкновенных дифференциальных уравнений 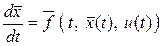 , где , где  – заданная вектор-функция, u
(t
) – функция управления из некоторого класса допустимых управлений U
, и – заданная вектор-функция, u
(t
) – функция управления из некоторого класса допустимых управлений U
, и  соответствует фазовый вектор соответствует фазовый вектор 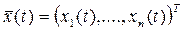 (траектория). (траектория).
Если определена цель управления, то имеет смысл искать наилучшее (оптимальное) управление для достижения этой цели. В большинстве случаев цель управления можно задать в форме вариационной задачи – поиска экстремума некоторого функционала I
[u
(t
)] на классе допустимых управлений U
.
Тогда задача оптимального управления
: найти оптимальное управление u
*(t
) и соответствующую ему оптимальную траекторию 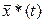 , для которых , для которых
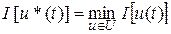 (другая форма записи: (другая форма записи: 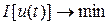 ), ),
или 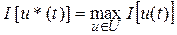 ( (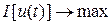 ). ).
Функционал I
[u
] называется критерием качества управления
. Например, в так называемой «задаче Лагранжа» роль критерия качества выполняет интегральный функционал вида
 (9) (9)
где 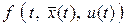 – заданная функция. – заданная функция.
Рассмотрим простейшую задачу управления: задана модель системы управления  , где , где 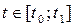 , , 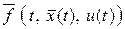 – непрерывная вектор-функция, – непрерывная вектор-функция, 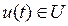 – функция управления, и критерий качества управления – функция управления, и критерий качества управления
 . .
Пусть каждому управлению  соответствует траектория соответствует траектория 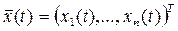 , переводящая систему из состояния , переводящая систему из состояния  в в  , где , где 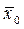 и и  фиксированы. фиксированы.
Требуется найти оптимальное управление u
*(t
) и соответствующую ему оптимальную траекторию 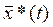 , для которых , для которых 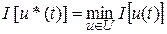 . Это задача Лагранжа с фиксированным временем и закрепленными концами траекторий: . Это задача Лагранжа с фиксированным временем и закрепленными концами траекторий: 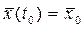 , , 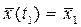 . .
Допустим, существует оптимальное управление  и соответствующая ему оптимальная траектория и соответствующая ему оптимальная траектория  , удовлетворяющие условиям задачи. , удовлетворяющие условиям задачи.
Введем вспомогательную вектор-функцию 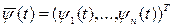 , где , где  –
неизвестные функции, кусочно-непрерывные на –
неизвестные функции, кусочно-непрерывные на 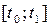 , и построим функцию Гамильтона-Понтрягина (гамильтониан): , и построим функцию Гамильтона-Понтрягина (гамильтониан):
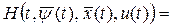 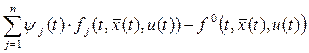 . (10) . (10)
Очевидно, что 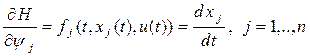 . .
При фиксированных 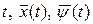 гамильтониан является функцией управления. Можно доказать, что если u
*(t
) – оптимальное управление, то при u
= u
*(t
) гамильтониан достигает максимума по управлению и выполняются условия гамильтониан является функцией управления. Можно доказать, что если u
*(t
) – оптимальное управление, то при u
= u
*(t
) гамильтониан достигает максимума по управлению и выполняются условия

Принцип максимума Понтрягина
.
Если  – оптимальное управление, переводящее систему из состояния – оптимальное управление, переводящее систему из состояния 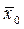 в в 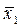 и и  – соответствующая ему оптимальная траектория, которая в первый раз достигает точки – соответствующая ему оптимальная траектория, которая в первый раз достигает точки 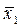 в момент t
1
, то в момент t
1
, то
1) существует вектор  , соответствующий u
*(t
) и , соответствующий u
*(t
) и 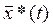 , причем , причем  и и 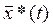 являются решениями системы дифференциальных уравнений являются решениями системы дифференциальных уравнений
 (11) (11)
удовлетворяющими условиям
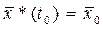 , ,  ; (12) ; (12)
2) в каждой точке непрерывности функции u
*(t
) достигается максимум гамильтониана по управлению:
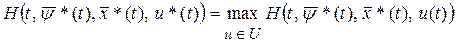 . (13) . (13)
Система (11) называется канонической системой задачи оптимального управления
. Для получения ее частного решения (определения констант интегрирования) используют граничные условия (12).
Принцип максимума представляет собой необходимое условие оптимальности. Если получается несколько управлений, удовлетворяющих условиям (11)-(13), то проверяют выполнение достаточных условий, или выбирают одно из них, исходя из смысла задачи.
Идея принципа максимума: чтобы найти u
*(t
) – оптимальное управление, минимизирующее функционал I
[u
(t
)], нужно найти управление, максимизирующее гамильтониан: 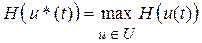 . .
Решение примерного варианта контрольной работы
Задача 1.
Дана формула алгебры логики: 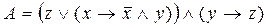 . .
Требуется:
1) при помощи равносильных преобразований упростить формулу;
2) построить релейно-контактные схемы для исходной и упрощенной формул.
Решение
.
1). Упростим заданную формулу, используя принятый порядок выполнения операций  . Сначала выразим импликации через дизъюнкции согласно формуле 12 основных равносильностей: . Сначала выразим импликации через дизъюнкции согласно формуле 12 основных равносильностей:
x
® y
º 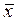 Ú y Ú y
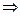 x
®
x
®  Ù y
º Ù y
º  Ú ( Ú ( Ù y
), y
® z
º Ù y
), y
® z
º 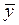 Ú z
, Ú z
,
затем используем формулы 16, 11 и 21:
x
Ù y
º y
Ù x
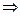
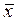 Ù y
º y
Ù Ù y
º y
Ù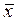 , , 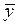 Ú z
º z
Ú Ú z
º z
Ú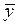 , ,
x
Ú (y
Ù x
) º x
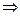
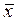 Ú (y
Ù Ú (y
Ù ) º ) º 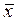 , ,
x
Ú (y
Ù z
) º (x
Ú y
) Ù (x
Ú z
) 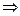 (z
Ú
(z
Ú ) Ù (z
Ú ) Ù (z
Ú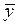 ) º z
Ú ( ) º z
Ú (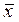 Ù Ù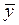 ), ),
откуда получаем:  º º
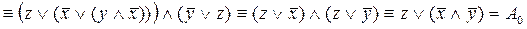 . .
2). Построим РКС для исходной формулы А
, используя таблицу простейших РКС и соответствующих им формул логики:
– конъюнкции  Ù y
соответствует последовательное соединение элементов Ù y
соответствует последовательное соединение элементов 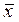 и y
; и y
;
– импликации x
® 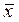 Ù y
соответствует параллельное соединение элементов Ù y
соответствует параллельное соединение элементов 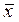 и ( и (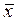 Ù y
); Ù y
);
дизъюнкции z
Ú (x
® 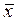 Ù y
) соответствует параллельное соединение элементов z
и (x
® Ù y
) соответствует параллельное соединение элементов z
и (x
®  Ù y
); Ù y
);
– импликации y
® z
соответствует параллельное соединение элементов  и z
; и z
;
– конъюнкции  соответствует последовательное соединение элементов (z
Ú (x
® соответствует последовательное соединение элементов (z
Ú (x
® 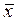 Ù y
)) и (y
® z
). Ù y
)) и (y
® z
).
Построим РКС для упрощенной формулы 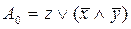 : конъюнкции : конъюнкции 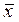 Ù Ù соответствует последовательное соединение элементов соответствует последовательное соединение элементов 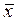 и и  , а дизъюнкции z
Ú ( , а дизъюнкции z
Ú ( Ù Ù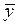 ) соответствует параллельное соединение элементов z
и ( ) соответствует параллельное соединение элементов z
и (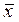 Ù Ù ). ).
Полученные в результате РКС изобразим на рис. 5.
Ответы:
1) результат упрощения формулы A
: 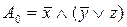 ; ;
2) РКС, соответствующие исходной формуле А
и упрощенной формуле А
0
приведены на рис. 5.

Задача 2.
Дана булева функция f
(x
, y
) = (x
Ú y
) ® (x
Ù Ú Ú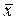 ® ® ). Составить таблицу значений функции и указать значение f
(0, 1). ). Составить таблицу значений функции и указать значение f
(0, 1).
Решение.
Известно, что порядок выполнения операций определен следующим образом:  . Используя таблицы истинности для отрицания, конъюнкции, дизъюнкции, импликации составим вспомогательную таблицу значений каждой из операций функции f
(x
, y
). . Используя таблицы истинности для отрицания, конъюнкции, дизъюнкции, импликации составим вспомогательную таблицу значений каждой из операций функции f
(x
, y
).
| x
|
y
|
x
Ú y
|
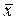
|

|
x
Ù
|
x
Ù Ú Ú
|
x
Ù Ú Ú ® ®
|
(x
Ú y
)®
(x
Ù Ú Ú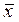 ® ® ) )
|
| 1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
| 1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
| 0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
Составим таблицу значений функции f
(x
, y
):
| x
|
y
|
f
(x
, y
) = (x
Ú y
)®(x
Ù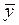 Ú Ú ® ®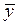 ) )
|
| 1
|
1
|
1
|
| 1
|
0
|
1
|
| 0
|
1
|
0
|
| 0
|
0
|
1
|
По таблице значений функции найдем значение f
(0, 1), соответствующее значениям аргументов x
= 0, y
= 1 (третья строка): f
(0, 1) = 0.
Ответы:
таблица значений функции приведена выше; f
(0, 1) = 0.
Задача 3.
Составить список дуг ориентированного графа, изображенного на рисунке 6. Сформировать матрицу инцидентности и матрицу смежности этого орграфа.
 Решение. Решение.
1. Для составления списка дуг орграфа G
составим вспомогательную таблицу, каждая строка которой соответствует одной дуге. В строке записываем обозначение дуги и номера вершин, инцидентных этой дуге, причем сначала указываем начальную вершину, затем – конечную, т.к. граф ориентированный.
| Дуга
|
Вершины
|
| x
1
|
v
2
, v
1
|
| x
2
|
v
2
, v
3
|
| x
3
|
v
1
, v
4
|
| x
4
|
v
4
, v
1
|
| x
5
|
v
2
, v
4
|
Получаем список дуг орграфа:
X
= {(v
2
, v
1
), (v
2
, v
3
), (v
1
, v
4
), (v
4
, v
1
), (v
2
, v
4
)}.
2. Для построения матрицы инцидентности орграфа G
составим таблицу, используя формулы (1). Заполняем таблицу по столбцам, соответствующим дугам орграфа: в j
-
м столбце ставим i
-й строке «–1», если вершина vi
является началом дуги х
j
, ставим «1», если вершина vi
является концом дуги х
j
и ставим «0», если вершина vi
и дуга х
j
не инцидентны.
При заполнении таблицы можно использовать список дуг орграфа.
| |
x
1
|
x
2
|
x
3
|
x
4
|
x
5
|
Получили матрицу инцидентности:
В
(G
2) = 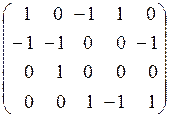 . .
|
| v
1
|
1
|
0
|
–1
|
1
|
0
|
| v
2
|
–1
|
–1
|
0
|
0
|
–1
|
| v
3
|
0
|
1
|
0
|
0
|
0
|
| v
4
|
0
|
0
|
1
|
–1
|
1
|
3. Для построения матрицы смежности орграфа G
составим таблицу, используя формулы (2). Так как граф G
ориентированный, то элемент матрицы aij
равен количеству ребер с началом в i
-й вершине, а концом в j
-й вершине.
| |
v
1
|
v
2
|
v
3
|
v
4
|
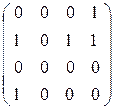
Получили матрицу смежности
A
(G
) = 
|
| v
1
|
0
|
0
|
0
|
1
|
| v
2
|
1
|
0
|
1
|
1
|
| v
3
|
0
|
0
|
0
|
0
|
| v
4
|
1
|
0
|
0
|
0
|
Ответы:
список дуг орграфа X
= {(v
2
, v
1
), (v
2
, v
3
), (v
1
, v
4
), (v
4
, v
1
), (v
2
, v
4
)};
матрица инцидентности и матрица смежности:
В
(G
) = 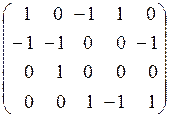 ; A
(G
) = ; A
(G
) = 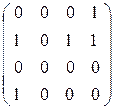 . .
Задача 4.
Дан функционал  . Найти экстремали функционала, удовлетворяющие граничным условиям y
(0) = –1, y
(π
) = 0. . Найти экстремали функционала, удовлетворяющие граничным условиям y
(0) = –1, y
(π
) = 0.
Решение.
Запишем уравнение Эйлера 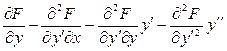 = 0 для данного функционала. = 0 для данного функционала.
Для подынтегральной функции  получаем частные производные: получаем частные производные:
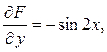 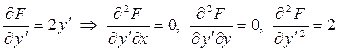 . .
Тогда уравнение Эйлера имеет вид: 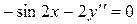 или или  – простейшее дифференциальное уравнение второго порядка. Его общее решение получаем двукратным интегрированием: – простейшее дифференциальное уравнение второго порядка. Его общее решение получаем двукратным интегрированием:
   . .
Определим произвольные постоянные С
1
, С
2
из граничных условий
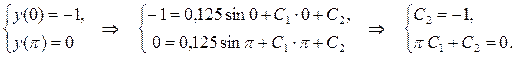
Отсюда получаем С
1
= 1/π
, С
2
= –1, следовательно, экстремалью функционала является функция 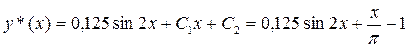 . .
Ответ.
 . .
Задача 5.
Дана модель объекта управления, описываемая системой дифференциальных уравнений 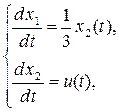 и граничными условиями x
1
(0) = 0, x
2
(0) = 3, x
1
(3) = 2, x
2
(3) = –
1, где t
–
время (t и граничными условиями x
1
(0) = 0, x
2
(0) = 3, x
1
(3) = 2, x
2
(3) = –
1, где t
–
время (t
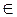 [0; 3]), [0; 3]), 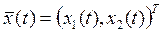 –
фазовый вектор (траектория объекта), u
(t
) –
функция управления объектом. –
фазовый вектор (траектория объекта), u
(t
) –
функция управления объектом.
Требуется найти оптимальное управление объектом u
*(t
) и соответствующую ему оптимальную траекторию  , если задан критерий качества управления: , если задан критерий качества управления: 
Решение.
1. Введем вспомогательный вектор  , где , где  –
неизвестные функции, и построим гамильтониан данной задачи: –
неизвестные функции, и построим гамильтониан данной задачи:
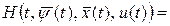 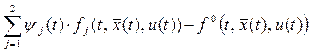 = =
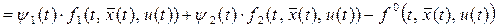 , ,
где функции  –
это правые части дифференциальных уравнений –
это правые части дифференциальных уравнений 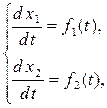 а а  –
подынтегральная функция критерия качества управления –
подынтегральная функция критерия качества управления 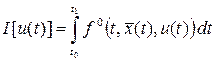 . .
По условию задачи 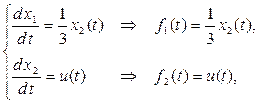

Отсюда получаем  = =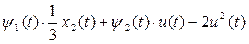 . .
2. Находим максимум гамильнониана по управлению:  , , 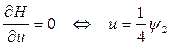 – критическая точка. Вторая производная – критическая точка. Вторая производная  , следовательно, при , следовательно, при 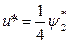 достигается максимум гамильнониана по управлению. достигается максимум гамильнониана по управлению.
3. Составим каноническую систему дифференциальных уравнений, подставив в формулу (8)  и частные производные гамильнониана и частные производные гамильнониана 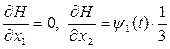 , и решим эту систему. Каноническая система имеет вид: , и решим эту систему. Каноническая система имеет вид:
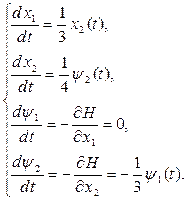
Общее решение системы находим последовательным интегрированием:

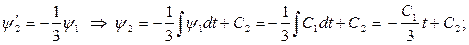 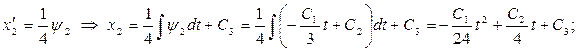  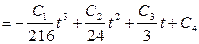 . .
Найдем частное решение системы, удовлетворяющее граничным условиям x
1
(0) = 0, x
2
(0) = 3, x
1
(3) = 2, x
2
(3) = –
1.
Из первых двух условий получаем: 
Подставив эти значения в другие два условия 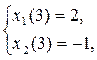 получаем:
получаем:
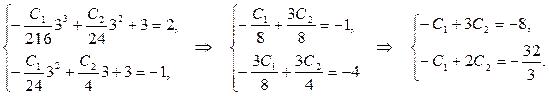
Вычитая из 1-го уравнения 2-е, получаем 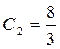 , затем
, затем 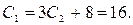
Подставив найденные значения констант, получим оптимальную траекторию и оптимальное управление:
 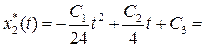
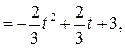 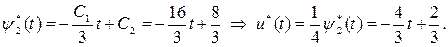
Ответы
: оптимальная траектория  , где , где  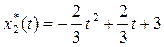 ; оптимальное управление ; оптимальное управление 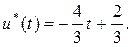
Рекомендуемая литература
1. Лихтарников Л. М. Математическая логика / Л.М. Лихтарников, Т.Г. Сукачева.– Санкт-Петербург: Лань, 1998.– 288 с.
2. Нефедов В.Н. Курс дискретной математики: учебное пособие. / В.Н. Нефедов, В.А.Осипова – М. Изд-во МАИ, 1992. – 264 с.
3. Баврин, И.И. Основы высшей математики: учебник / И. И. Баврин.– М.: Высш. шк., 2004.– 520 с.
4. Карташев А. П. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. / А. П. Карташев, Б. Л. Рождественский.– М.: Наука, 1986.– 288 с.
5. Краснов М. Л. Вариационное исчисление. / М. Л. Краснов, Г. И. Макаренко, А. И. Киселев.– М.: Наука, 1973.–192 с.
6. Ланина Н. Р. Дискретная математика: учебное пособие. В 2 ч. Ч.1 / Н.Р. Ланина. – Мурманск: Изд-во МГТУ, 1998. – 123 с.
7. Данко, П.Е. Высшая математика в упражнениях и задачах: учебное пособие для втузов. В 2 ч. Ч.2 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Оникс: Мир и образование, 2005.– 416 с.
8. Сборник задач по математике для втузов: специальные курсы. (Ч. 3). Под ред. А. В. Ефимова. / Э. А. Вуколов, А. В. Ефимов, В. Н. Земсков и др.– М.: Наука, 1984.– 608 с.
9. Пантелеев, А.В. Теория управления в примерах и задачах: Учебное пособие / А.В. Пантелеев, А.С. Бортаковский.– М.: Высш. шк., 2003.– 583 с.
|