Учебное пособие: Рекомендации по работе с потенциометром Мостовые методы измерения сопротивлений

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Физический факультет

Кафедра общей физики

«ИЗМЕРИТЕЛЬНЫЙ ПРАКТИКУМ»

А.В. Багинский, О.А. Брагин, А.А. Дорошкин

Работа 4.1-4.2

КОМПЕНСАЦИОННЫЕ МЕТОДЫ ИЗМЕРЕНИЙ

Учебно-методическое пособие

Новосибирск

2008

Представлено описание модернизированной лабораторной работы измерительного практикума кафедры общей физики НГУ. Работа выполняется студентами 1–2-го курсов физического факультета, факультета информационных технологий, геолого-геофизического, медицинского факультетов и факультета естественных наук.

При выполнении работы студенты знакомятся с компенсационными методами измерений ЭДС и сопротивления. Работа может быть использована при обучении студентов других естественнонаучных и технических факультетов.

Рецензент

Д.ф.-м.н. А. Д. Косинов

© Новосибирский государственный университет, 2008

Содержание

Введение…………………………………………………………………………4

4.1 Потенциометр……………………………………………………………….4

Принцип действия потенциометра…………………………………………….4

Одноконтурный потенциометр………………………………………………...6

Многоконтурные потенциометры.…………………………………………….7

Термопара….……………………………………………………………………8

Задания…………………………………………………………………………12

Приложение. Органы управления потенциометра и некоторые

рекомендации по работе с потенциометром………………………………...14

4.2 Мостовые методы измерения сопротивлений…………………………...17

Одинарный мост ………………………………………………………………17

Двойной мост………………………………………………………………..…19

Органы управления и клеммы для подключения

внешних элементов моста……………………………………………….……21

Задания…………………………………………………………………………21

Лабораторная работа 4 (4.1, 4.2)

КОМПЕНСАЦИОННЫЕ МЕТОДЫ ИЗМЕРЕНИЙ

Цель работы: изучение компенсационных методов измерения ЭДС, напряжений и сопротивлений.

Оборудование

4.1. Потен­циометр постоянного тока; нормальный элемент Вестона; батарея питания потенциометра; нуль-индикатор, милливольтметр; термопара; нуль-термостат; печь с тиглем; источник питания печи; регистратор ЭДС термопары.

4.2. Мост постоянного тока, нуль-индикатор, источник питания моста (батарея, аккумулятор или др.), плата с сопротивлениями, малое проволочное сопротивление, образцовое сопротивление или магазин сопротивлений, катушка из тонкого медного провода, рамка с натянутой медной проволокой и подвижными потенциальными контактами, амперметр, переключатель полярности, реостат, штангенциркуль, микрометр.

Введение

Существует класс электроизмерительных приборов, принцип действия которых основан на сравнения измеряемой (неизвестной) величины с известной, образцовой. В качестве элемента сравнения в таких приборах используются, как правило, рабочие эталоны единиц соответствующих величин: эталон напряжения, эталон сопротивления, эталон индуктивности и другие. Этим обеспечивается высокая точность и надежность измерений. Представителями данного класса приборов являются мосты и потенциометры.

4.1 потенциометр

Принцип действия потенциометра

Потенциометры предназначены для измерения электродвижущих сил (ЭДС) и напряжений методом компенсации измеряемого напряжения эталонным. Суть компенсационного метода измерения напряжения ясна из рис. 1.1. Источник измеряемого напряжения U_x включается встречно регулируемому образцовому источнику U_обр . Меняя напряжение образцового источника, можно добиться нулевых показаний нуль-индикатора А (чувствительного вольтметра или амперметра) и тем самым произвести измерение U_x = U_обр .

Выше отмечалось, что для обеспечения высокой точности измерений в качестве элемента сравнения U_обр необходимо применять эталон напряжения. К сожалению, регулируемых эталонов напряжения не существует. Поэтому измерение проводится в два этапа, как показано на рис. 1.2. Здесь регулируемое опорное напряжение снимается с движка переменного сопротивления R ₀ , к которому поочередно подключаются источник эталонного напряжения E _N (рис. 1.2а) и источник измеряемого напряжения E _x (рис. 1.2б). Если U больше E _N и E _x , то, перемещая движок R ₀ , мы всегда “найдем” точку, в которой напряжение, снимаемое с делителя, равно напряжению подключенного к нему источника (E _N или E _x ) и скомпенсирует его (нуль-индикатор А покажет ноль). Пусть компенсация E _N и E _x произошла при сопротивлениях делителя R _N (рис. 1.2а) и R _x (рис. 1.2б), т.е.:

, .

Отсюда:

.

Таким образом, зная R _N и R _X , мы, тем самым, определили отношение измеряемого напряжения к эталонному. Именно эта методика (немного модифицированная) реализована в потенциометрах.

Одноконтурный потенциометр

Схема измерений, показанная на рис. 1.2, вполне работоспособна, однако процедура измерений не удобна и, кроме того, возникают определенные технические трудности, связанные с очень большим внутренним сопротивлением рабочего эталона напряжения – нормального элемента Вестона. В реальном потенциометре строго фиксируют ток, протекающий через R ₀ (рабочий ток потенциометра). Если ток, протекающий через R ₀ всегда один и тот же, то делитель напряжения можно заранее отградуировать (т.е. разметить и оцифровать положения движка R ₀ ) непосредственно в Вольтах (а не в Омах), что делает процедуру измерений гораздо более удобной – сразу после компенсации напряжения E _x его значение можно прочитать по оцифровке делителя. Рабочий ток настраивается с использованием эталона напряжения (нормального элемента) перед началом измерений.

Упрощенная схема потенциометра, показанная на рис. 1.3, отличается от схемы, приведенной на рис. 1.2, дополнительным сопротивлением R _б , предназначенным для регулирования тока в цепи R ₀ , отдельным входом для подключения рабочего эталона напряжения (нормального элемента Вестона) и переключателем П , при помощи которого можно подключать к делителю R ₀ либо измеряемое, либо эталонное напряжение. Для настройки рабочего тока при подготовке потенциометра к работе нормальный элемент, как видно из схемы, подключается в фиксированную точку делителя. Эта специальная контрольная точка, выбранная таким образом, чтобы при протекании через R ₀ рабочего тока напряжение в этой точке было в точности равным ЭДС нормального элемента Вестона. Поэтому, если при помощи переключателя П подключить нормальный элемент к делителю, то при токе равном рабочему нуль-индикатор должен показать ноль. Если же это не так, то ток следует отрегулировать при помощи R _б , добившись нулевых показаний индикатора. После того как рабочий ток установлен, потенциометр готов к работе. Более подробно о настройке потенциометра прочтите в приложении.

Многоконтурные потенциометры

Из изложенного выше ясно, что настроенный потенциометр представляет собой не что иное, как регулируемый источник напряжения с высокой дискретностью его изменения. Так 6-декдый потенциометр перекрывает диапазон более 1 В с дискретностью 1 мкВ (см. приложение). Создание прецизионного источника с таким большим динамическим диапазоном является сложной технической задачей. Проще использовать два или три включенных последовательно источника, каждый из которых обладает меньшей относительной дискретностью изменения выходного напряжения. Так, если вернуться к схеме, приведенной на рис 1.1, то вместо одного источника U_обр с выходным напряжением, например, 0…1 В и дискретностью его установки 1 мкВ можно включить последовательно два источника: 0…1 В с дискретностью 1 мВ и 0…1 мВ с дискретностью 1 мкВ. Многоконтурный потенциометр построен именно по этому принципу и представляет собой два (или больше) одноконтурных потенциометров, смонтированных в одном корпусе и соединенных так, чтобы снимаемые с них напряжения суммировались на едином входе многоконтурного потенциометра.

Часть имеющихся в лаборатории потенциометров являются двухконтурными. При подготовке такого потенциометра к работе, необходимо установить два рабочих тока. Ток в “старшем” контуре настраивается с использованием нормального элемента, точно так же как у одноконтурного потенциометра. Образцовое напряжение для настройки рабочего тока во втором контуре поступает с делителя первого контура. Поэтому настройка многоконтурного потенциометра, должна производиться в строгом порядке – нельзя настраивать ток в “младшем” контуре, не настроив предварительно ток в “старшем” контуре. Что же касается собственно процесса измерений, то он ничем не отличается от описанного ранее.

Термопара

Термопара (термоэлектрический преобразователь) представляет собой очень простой, надежный и, в то же время, достаточно точный датчик температуры. Принцип действия термопары можно пояснить воспользовавшись моделью свободных электронов. Согласно этой модели, электроны проводимости рассматриваются как электронный газ, заполняющий кристаллическую решетку металла. Работа выхода и концентрация свободных электронов являются индивидуальными характеристиками вещества и у разных металлов различны. В результате, если два разнородных проводника соединить в одной точке, то часть электронов продиффундирует из одного проводника в другой, исходно электронейтральные проводники зарядятся, и на их свободных концах появится разность потенциалов – контактная ЭДС. Величина контактной ЭДС зависит от температуры – Е =Е (Т ). Поэтому простейшая конструкция состоящая из двух, соединенных в одной точке проводников может служить термометром, если для этой пары металлов зависимость Е =Е (Т ) известна. В данном контексте контактная ЭДС называется термо-ЭДС, проводники, из которых изготовлена термопара, называются термоэлектродами, а точка их соединения – спаем термопары.

Таким образом, чтобы измерить температуру какого-то объекта достаточно измерить термо-ЭДС термопары, спай которой находится в тепловом контакте с этим объектом, и затем рассчитать температуру, используя таблицу либо аналитическую зависимость Е (Т ). Как измерить ЭДС термопары? Очевидно, что если подключить термоэлектроды непосредственно к регистрирующему прибору (потенциометру или микровольтметру с большим входным сопротивлением), мы получим еще два "термопарных спая" в точках контактов термоэлектродов с клеммами прибора. В результате регистрирующий прибор покажет суммарную ЭДС

E = E _AB (t _x ) + E _{A Кл} (t ₀ ) + E _{B Кл} (t ₀ ) ,

где E _AB – термо-ЭДС рабочего спая; E _AКл , E _BКл – термо-ЭДС возникающие в местах контактов термоэлектродов с клеммами прибора; t _x – температура рабочего спая термопары; t ₀ – температура клемм прибора.

Так как при равенстве температур всех спаев суммарная ЭДС термопары должна равняться нулю это выражение можно преобразовать к виду:

E =E _AB (t _x ) – E _AB (t ₀ ) .

Отсюда видно, что термопарой измеряется разность t _x – t ₀ . Поэтому значение t ₀ нужно знать и при проведении измерений поддерживать постоянным, причем тем же самым, что и при градуировке термопары, когда определялась зависимость Е (Т ). Каких-либо физических ограничений на выбор величины t ₀ не существует, но общепринято термостатировать свободные концы термоэлектродов при t ₀ = 0° С . В таблицах номинальных статических характеристик термопар всегда приводят значения Е (t ) соответствующее температуре t ₀ = 0° С .

Таким образом, если термоэлектроды подключить непосредственно к клеммам прибора, температуру клемм придется поддерживать равной 0° С , что технически сложно. Поэтому применяют специальные способы подключения термопар.

Основной способ подключения термопары показан на рис. 1.4. Здесь термоэлектроды “надставлены” медными проводами, которые и присоединены к клеммам прибора. Так как клеммы потенциометров и чувствительных вольтметров изготавливают из меди или из сплавов, имеющих близкую к нулю контактную ЭДС в паре с медью, “паразитных” контактных ЭДС здесь не возникает, какую бы температуру не имели клеммы. Соединения медных проводов с термоэлектродами (так называемые “холодные спаи” термопары) помещают в сосуд с плавящимся льдом – термостатируют при температуре 0° С .

Другой способ подключения термопары показан на рис. 1.5. Здесь изображена так называемая дифференциальная термопара, представляющая собой, как видно из рис. 1.5, две “обычные” термопары, включенные встречно. Контактные ЭДС на клеммах прибора здесь взаимно компенсируются, т.к. они одинаковы по величине и противоположны по знаку. ЭДС дифференциальной термопары пропорциональна разности температур ее спаев. Поэтому дифференциальную термопару используют обычно не для абсолютного измерения температуры, а для измерения разности температур (различных объектов или в разных точках одного объекта). Однако ее можно использовать и для абсолютных измерений. В этом случае один из спаев (все равно какой) дифференциальной термопары используется, как рабочий, второй (“холодный спай”) – термостатируется при 0°С так же, как и у “обычной” термопары.

Чувствительностью термопары называется величина К = dE /dt (E – ЭДС термопары, t – температура). При подборе материалов термоэлектродов стремятся к тому, чтобы чувствительность была максимальной и не зависела от температуры. Наилучшей линейностью характеристики среди термопар с термоэлектродами из неблагородных металлов обладает хромель-алюмелевая (ХА) термопара (К = 40 мкВ/К при 0°С, К = 43 мкВ/К при 500°С), наивысшей чувствительностью – хромель-копелевая (ХК) термопара (К = 63 мкВ/К при 0°С, К = 88 мкВ/К при 500°С). Как видно из приведенных численных значений, чувствительность термопары зависит от температуры. Однако если измерения производятся в сравнительно небольшом интервале температур, можно в первом приближении считать К = const . В этом случае температура может быть рассчитана по формуле (при термостатировании “холодных” спаев при t ₀ = 0°С):

t _x = К ^-1 ×Е , °С.

Значение К можно рассчитать по экспериментально измеренной ЭДС термопары Е ^* при какой-либо известной температуре t ^* .

Задания.

Измерение температуры термопарой .

Измерьте ЭДС термопары при температуре плавления олова (231,9 ºС). Определите, воспользовавшись таблицами номинальных статических характеристик термопреобразователей, тип термопары (у вас может быть либо ХА-термопара, либо ХК-термопара).

Схема измерения температуры плавления олова показана на рис. 1.6. Измерительная термопара 3, один спай которой помещен в тигель с оловом, а другой – в нуль-термостат, подключена к аналого-цифровому преобразователю (АЦП) 4, при помощи которого осуществляется периодическое (с заданным периодом) измерение ЭДС термопары. Результаты измерений отображаются в графическом виде на экране монитора персонального компьютера 5 и запоминаются в файле экспериментальных данных. Так как фазовые переходы первого рода протекают при постоянной температуре, на зависимости ЭДС от времени (термограмме) будет наблюдаться характерная “полка” при температуре плавления олова.

Определив тип термопары, подключите ее к потенциометру и измерьте температуру кипящей воды и температуру собственного тела в нескольких точках (лабораторная работа комплектуется двумя совершенно одинаковыми термопарами, одна из которых используется в экспериментах с оловом, а вторая – для измерения температуры кипения воды и температуры тела ).

В линейном приближении, как указано в разделе “Термопара”, вычислите чувствительность термопары по результатам измерения ее ЭДС при температурах кипения воды (К ₀ ) и плавления олова (К ₁ ) Воспользовавшись значением К ₀ , рассчитайте (по измеренному значению ЭДС в точке плавления олова) температуру плавления олова и, наоборот, воспользовавшись значением К ₁ , рассчитайте температуру кипения воды. Проанализируйте результаты.

Работа с автоматизированной системой измерения ЭДС термопары .

Включите регистратор и персональный компьютер.

Найдите на рабочем столе иконку с подписью "tx_ measure ", и двойным нажатием левой клавиши мыши раскройте программу измерения зависимости температуры от времени.

Выставьте "Port com 1 ".

Установите периодичность отсчета, равной 1 сек: "period 1 сек ".

Кнопкой "RUN " проведите запуск программы.

Введите имя для сохранения экспериментальных данных в файле.

Включите нагреватель, и запишите зависимость температуры от времени как при нагревании, так и при остывании образца.

Замечание. В зависимости от наполнения нагревателя исследуемым веществом, рекомендуемая мощность нагрева различна. При наполнении ~0,5 объема оптимальная мощность соответствует 3 делениям регулятора нагревателя.

По окончании эксперимента нажмите кнопку "STOP& Write " и сохраните файл под своим именем с расширением .dat.

Контрольные вопросы

Как увеличить диапазон измерений потенциометром в два раза?

Приложение.

Органы управления потенциометра и некоторые рекомендации по работе с потенциометром.

Делитель напряжения . Делитель напряжения R ₀ , являющийся самым важным элементом потенциометра, показан на рис. 1.3 как простое переменное сопротивление. Очевидно, однако, что для точной компенсации измеряемого напряжения, а затем точного отсчета результата, делитель должен быть составным (т.е. состоять из нескольких последовательно включенных переменных сопротивлений разной величины, по принципу "грубо" → "средне" →"точно"→ ...) и дискретным (для точного отсчета). Схема делителя приведена на рис. 1.7. Здесь каждое из переменных сопро

Балластное сопротивление R _б (рис. 1.3) для настройки рабочего тока состоит из 3-х или 4-х (в зависимости от типа потенциометра) переменных сопротивлений разного номинала (“грубо” ® “средне” ® “точно”).

Коррекция точки подключения нормального элемента. Погрешность измерения ЭДС или напряжения потенциометром целиком и полностью определяется точностью подбора сопротивлений делителя напряжения (см. выше) и точностью установки рабочего тока. Класс потенциометра – это предельная погрешность, которая может быть достигнута при измерениях этим прибором. Очевидно, что погрешность установки рабочего тока не должна превосходить величины класса прибора (подгонка сопротивлений делителя не в компетенции экспериментатора). Так, для потенциометра класса 0,001 ток через делитель должен быть установлен с погрешностью не хуже 10^-3 %. Ясно, что для обеспечения такой точности никакой амперметр не годится и калибровка рабочего тока осуществляется методом сличения (как описано выше) с использованием эталонов напряжения – устройств, значение ЭДС которых известно с высокой точностью. В качестве рабочих эталонов напряжения используются гальванические элементы специальной конструкции – нормальные элементы Вестона. Каждому элементу Вестона после его аттестации в метрологическом институте методом сличения с первичным (в конечном счете) эталоном напряжения присваивается индивидуальное значение ЭДС, после чего он и становится эталоном определенного класса.

ЭДС нормального элемента Вестона хотя и слабо, но зависит от температуры (в диапазоне рабочих температур от 1,018 В до 1,019 В). В соответствии с этим в потенциометрах предусмотрена возможность изменения точки подключения нормального элемента к делителю напряжения. На панели потенциометра имеется рукоятка, рядом с которой выгравировано число 1,018 – это начальные цифры ЭДС нормального элемента Вестона. Для выполнения температурной коррекции рукоятку необходимо повернуть так, чтобы дополнить число 1.018 до значения ЭДС нормального элемента при текущей температуре. ЭДС нормального элемента при текущей температуре рассчитывают, руководствуясь его паспортными данными. При работе с потенциометрами класса ~ 0,01 ЭДС нормального элемента, которым комплектуется данная работа, можно рассчитывать по формуле:

e = 1,01864 – [40,6×(t – 20) + 0,95×(t – 20)² – 0,01×(t – 20)³ ]×10^-6

e – в Вольтах, t – в °С.

В потенциометрах класса 0,05 и ниже температурная коррекция не требуется.

Кнопки “Измерение” и переключатель чувствительности. Кнопки “Измерение грубо” и “Измерение точно” предназначены для замыкания измерительной цепи и изменения чувствительности нуль-индикатора. Когда они отжаты, переключатель П подключен к клеммам нуль-индикатора не непосредственно, как показано на рис. 1.3, а через очень большое, порядка нескольких Мом, сопротивление. Соответственно, источник измеряемого напряжения E _x подключен к делителю R ₀ через это сопротивление, а чувствительность нуль-индикатора сильно загрублена. При нажимании кнопки “Измерение грубо” указанное сопротивление шунтируется сопротивлением ~ 500 кОм, при нажимании кнопки “Измерение точно” - закорачивается и таким образом ступенчато меняется чувствительности нуль-индикатора. Начиная процедуру измерения, когда вы еще не знаете ни величины измеряемого напряжения, ни его полярности, нажимайте кнопку “измерение грубо ” лишь на мгновение. Определив, в каком направлении и как быстро перемещается указатель нуль-индикатора, выполните предварительную компенсацию напряжений, а при необходимости измените полярность подключения E _x . Убедившись, что нуль-индикатор не перегружается, кнопку “Измерение грубо” можно зафиксировать в нажатом положении поворотом на 90° и произвести более точную компенсацию напряжения. Затем следует повторить эту же процедуру на чувствительном пределе.

У некоторых потенциометров (например, Р37) кнопка “измерение” с переключателем чувствительности не совмещена и предназначена только для замыкания измерительной цепи. У этих потенциометров есть отдельный многоступенчатый переключатель чувствительности. Устроен он так же как и описано выше, но имеет не одно, а несколько различных добавочных сопротивлений. Позиции переключателя оцифрованы в величинах этих добавочных сопротивлений.

Кнопка "успокоение" закорачивает вход нуль-индикатора и используется в случае его "зашкаливания". Нажимать кнопку "успокоение" следует при отпущенной кнопке “измерение”. После устранения причины перегрузки индикатора кнопку "успокоение" отпускают.

Внешние подключения. Практически все потенциометры имеют два идентичных входа. Соответственно, переключатель рода работ П имеет три рабочих положения: НЭ – к делителю напряжения подключен нормальный элемент, Х ₁ - к делителю напряжения подключен первый вход (клеммы “Х ₁ ”), Х ₂ - к делителю напряжения подключен второй вход (клеммы “Х ₂ ”). Назначение остальных клемм ясно из рис.1. 3. Замечание. При подготовке потенциометра к работе нормальный элемент следует присоединять к клеммам прибора после того, как подключен источник питания U (не наоборот!), строго соблюдая полярность подключения. Ошибка может привести к выходу из строя нормального элемента. При демонтаже схемы первым отсоединяется нормальный элемент.

4.2. Мостовые методы измерения сопротивлений

Мостами называются приборы, предназначенные для изме­рения сопротивлений методом сравнения. Для измерения сопротивлений более 50 Ом применяют одинарный мост – мост Уитстона. При измерении малых сопротивлений применяют двойной мост – мост Томпсона.

Одинарный мост

Схема одинарного моста приведена на рис. 2.1. По сути, он представляет собой два делителя напряжения, включенных параллельно. Сопротивления R _1, R ₂ и R являются элементами моста и их значения известны. Сопротивление R _x - это неизвестное (измеряемое) сопротивление. Одно из сопротивлений моста (по схеме - это сопротивление R ) можно изменять в широких пределах, меняя, тем самым, коэффициент деления правого по схеме делителя напряжения, и, следовательно, потенциал в точке В. В процессе измерений мы меняем R в ту или иную сторону, добиваясь нулевых показаний индикатора Г , включенного в измерительную диагональ моста – уравновешиваем мост. В этот момент потенциалы в точках А и В равны

,

и, следовательно:

.

Поскольку значения всех сопротивлений в правой части этого выражения нам известны, мы можем рассчитать R _x .

Значения сопротивления R должны воспроизводиться очень точно и стабильно. Поэтому оно выполнено в виде магазина (набора) образцовых сопротивлений. Эти сопротивления соединены последовательно, группами по 10 шт. Величины сопротивлений в каждой группе одинаковы и отличаются от величин сопротивлений в соседних группах в 10 раз (например, группа 100-Омных сопротивлений, группа 10-Омных сопротивлений ... группа 0.01-Омных сопротивлений). Сопротивления внутри каждой группы коммутируются отдельным декадным переключателем. “Линейка” переключателей ´100 Ом, ´10 Ом, ´1 Ом, ´0,1 Ом, ´0,01 Ом смонтирована на лицевой панели моста. При помощи этой "линейки" можно выставить любое значение R до 1 кОм с дискретностью 0,01 Ом.

В процессе измерения сопротивления R ₁ и R ₂ остаются постоянными, но их значения можно изменить (кратно десяти: 1 Ом, 10 Ом, 100 Ом ...) при помощи штепсельного переключателя на лицевой панели моста. Меняя отношение R ₁ /R ₂ , мы меняем диапазон измерений. Так, при R ₁ /R ₂ = 1 диапазон измерений составит (для рассмотренного выше примера) 0,01 Ом ... 1111,10 Ом. Установив R ₁ /R ₂ = 100, мы будем иметь диапазон 1 Ом ... 111110 Ом, а при R ₁ /R ₂ = 0,1 – 0,001 Ом ...111,110 Ом. Подбирая диапазон измерений, следует стремиться к тому, чтобы максимально "задействовать" линейку декадных переключателей магазина R . Этим минимизируется погрешность измерения. Так, предположим, что вам нужно измерить сопротивление менее 100 Ом, например, 15 Ом. Если R ₁ /R ₂ = 1, то погрешность ваших измерений будет больше, чем можно бы было достичь, т.к. “старший” декадный переключатель линейки R не будет задействован, и вы будете иметь в результате не 5, а только 4 значащие цифры. В данном случае, для того чтобы выполнить измерения максимально точно, необходимо ввести отношение R ₁ /R ₂ = 0,1.

Если внимательно проанализировать схему на рис. 2.1а, то можно увидеть, что при уравновешивании моста измеряется не R _x , а R _x + r ₁ + r ₂ , где r ₁ и r ₂ – сопротивления подводящих проводов, которыми R _x присоединяется к клеммам моста. Когда вкладом сопротивлений подводящих проводов пренебречь нельзя, можно использовать трехпроводную схему подключения R _x , показанную на рис. 2.1б. Условие равновесия моста при таком включении имеет вид (обратите внимание, что мост симметричный):

R _x + r ₁ = R + r ₂

и при r ₁ = r ₂ сопротивления подводящих проводов взаимно компенсируются. Такая схема позволяет расширить диапазон измерений R _x в область малых значений (до единиц Ом), а также измерять R _x удаленные от измерительной аппаратуры, т.е. не когда R _x мало, а когда r ₁ + r ₂ велико. Условие r ₁ = r ₂ сравнительно нетрудно выполнить с точностью ~10^-1 Ом, вырезав из одной бухты провода куски одинаковой длины. Исходя из этого ограничения (с учетом, конечно, допустимой погрешности измерений и технических характеристик моста) можно оценить нижний предел значений величины R _x при использовании данной схемы измерений.

Двойной мост

При измерении малых сопротивлений трехпроводная схема подключения R _x не эффективна, т.к. вряд ли удастся обеспечить одинаковость сопротивлений подводящих проводов с приемлемой точностью, если R _x меньше этих сопротивлений.

На рис. 2.2 показана схема измерения сопротивлений, в которой задача исключения сопротивления подводящих проводов решается практически полностью. Обратите внимание, что здесь к каждому выводу сопротивления присоединено по два проводника. Это так называемая четырехпроводная схема включения сопротивлений в измерительную цепь. Два “токовых” проводника включаются в цепь источника питания, два “потенциальных” – присоединены к основаниям выводов сопротивления и идут к вольтметру. Очевидно, что токовые провода вообще не оказывают никакого влияния на результат измерений. Влияние потенциальных проводов при высоком входном сопротивлении вольтметра пренебрежимо мало. Сопротивление R _x рассчитывается здесь исходя из очевидного соотношения

по экспериментально измеренным значениям напряжений U _x и U _N . R _N – это образцовое сопротивление, значение которого известно с очень высокой точностью.

К сожаления эту схему невозможно применить в области очень больших и очень малых сопротивлений. Если R _x очень велико, то на результаты неизбежно скажется шунтирующее действие входного сопротивления вольтметра. При очень малых R _x ток в цепи R _x – R _N должен быть очень большим, чтобы обеспечить необходимую точность измерения U _x и U _N .

Задача измерения больших сопротивлений успешно решается с помощью одинарного моста Уитстона. Для измерения малых сопротивлений используется двойной мост Томпсона, схема которого показана на рис. 2.3. Собственно мост, как прибор, выделен на схеме пунктиром. В нижней части рисунка показана схема внешних цепей. Видно, что эта часть схемы тождественна схеме на рис. 2.2. Можно показать, что при балансе двойного моста, т.е. когда потенциалы в точках А и Б одинаковы, имеет место следующее соотношение:

,

где U _x – падение напряжения на сопротивлении R _x , U _N – падение напряжения на сопротивлении R _N .

Таким образом, при помощи моста Томпсона осуществляется непосредственное измерение отношения напряжений на последовательно включенных неизвестном и эталонном сопротивлениях. Равенство потенциалов в точках А и Б означает, к тому же, что через R _x и R _N течет один и тот же ток. Принимая это во внимание, получаем из предыдущего выражения:

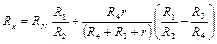
Параметры схемы двойного моста выбираются так, чтобы второе слагаемое этого выражения обращалось в нуль. Для этого переключатели магазинов R ₁ и R ₃ располагают на одной оси (R ₁ = R ₃ при любом положении переключателя), а штепсельными магазинами выставляют одинаковые значения R ₂ = R ₄ . При этих условиях формула для расчета R _x приобретает вид:

.

Рассматривая двойной мост, мы проводили аналогию между схемами, приведенными на рис. 2.2 и рис. 2.3. Однако если вы внимательно проанализируете эти схемы, то увидите, что полной аналогии здесь нет. Действительно, по потенциальным проводам, которыми R _x и R _N подключаются к клеммам двойного моста, течет ток и, следовательно, сопротивления этих проводников необходимо было бы учитывать. Однако в схеме двойного моста подводящие провода включаются не последовательно с R _x , как в схеме одинарного, а последовательно с R ₁ и R ₃ , которые можно выбрать произвольно большими, что и делается. То же самое относится к подключению R _N . В результате оказывается возможным пренебречь как сопротивлением потенциальных проводов, так и контактными сопротивлениями переключателей.

Органы управления и клеммы для подключения внешних

элементов моста

Мосты, как правило, бывают универсальными, одинарно–двойными. Это означает, что прибор можно включить и по схеме одинарного моста, и по схеме двойного. В связи с этим не все клеммы моста задействованы в том или другом случаях. Общими являются только клеммы “Г” для подключения нуль-индикатора. При работе в режиме одинарного моста источник питания подключается к соответствующим клеммам прибора, сопротивление R _x – к клеммам “X₀ ” (одинарный). Остальные клеммы остаются свободными. При работе в режиме двойного моста вначале собирается внешняя цепь (см. рис. 2.3), а затем потенциальные выводы с R _x и R _N подключаются соответственно к клеммам “X_Д ” (двойной) и “X_N ”. Клеммы “X₀ ” и “Б” остаются свободными. Некоторые одинарно–двойные мосты комплектуются встроенными одним или двумя образцовыми сопротивлениями. Отсек с этими сопротивлениями располагается рядом с клеммами “X_N ”. Для соединения потенциальных выводов встроенных R _N с клеммами “X_N ” имеются специальные перемычки. Перемычки снимаются, если используется внешнее образцовое сопротивление. При работе в режиме одинарного моста наличие или отсутствие этих перемычек не играет роли.

Магазин сопротивлений плеча сравнения и штепсельные магазины общие для одинарного и двойного моста.

Кнопка “измерение” предназначена для подключения нуль-индикатора к измерительной диагонали моста. Она фиксируется в нажатом положении поворотом на 90°.

Замечание. Обозначения сопротивлений в формулах соответствуют обозначениям рисунков и могут не совпадать с обозначениями на приборе. У разных типов мостов могут быть и некоторые другие различия в обозначениях. Поэтому, приступая к работе, ознакомьтесь с описанием прибора.

Задания

Одинарный мост Уитстона.

1. Одинарным мостом и тестером измерьте значения сопротивлений, имеющихся на рабочем столе в виде сборки на плате. Сопоставьте полученные значения со значениями, написанными на сопротивлениях (номинальными значениями).

2. Измерение температуры термометром сопротивления. Термометр сопротивления представляет собой резистор (как правило, это проволочный резистор специальной конструкции) с большим и стабильным температурным коэффициентом сопротивления (ТКС). В данной лабораторной работе в качестве термометра сопротивления используется малогабаритная катушка из тонкого медного провода. Измерьте сопротивление этой катушки при нулевой (в стакане с водно-ледяной смесью) и комнатной температурах. (Какое из этих измерений следует выполнить первым?) Полагая следующую зависимостью сопротивления медного провода от температуры

R (Т ) = R (Т ₀ ) × (1 + 4,3×10^-3 (Т – Т ₀ )),

рассчитайте комнатную температуру. Сопоставите полученный результат с показанием ртутного термометра.

Замечание. Любой контактный датчик температуры (термометр сопротивления, термопара, ртутный термометр и т.д.) измеряет не температуру объекта, в который он помещен, а температуру своего чувствительного элемента. Эти температуры всегда различаются. Задача экспериментатора – сделать это различие пренебрежимо малым. В данном случае систематическая погрешность возникает из-за нагрева термометра измерительным током. Поэтому прежде чем проводить основные измерения необходимо определить рабочий ток моста. Для этого выполните серию измерений сопротивления вашего термометра (на воздухе) при различных напряжениях питания моста и определите напряжение, при уменьшении которого показания моста не будут систематически меняться. В этих экспериментах необходимо использовать внешний регулируемый источник питания моста и, возможно, внешний нуль-индикатор. Дальнейшие (основные) измерения следует проводить при этом (или меньшем) напряжении питания.

Двойной мост Томпсона.

1. Измерьте с максимальной точностью значения сопротивлений образцовых резисторов и двух проволочных образцов, имеющихся на рабочем месте.

2. Измерьте сопротивление медного провода, используя устройство с подвижными потенциальными контактами, имеющееся на рабочем месте. Измерения выполните как минимум для пяти различных длин образца, изменяя положение подвижных потенциальных контактов. Постройте график зависимости сопротивления проводника от его длины. Измерьте диаметр проволоки микрометром как минимум в десяти разных точках. Рассчитайте удельное сопротивление меди и сравните свой результат со справочным значением.