| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«Нижегородский государственный университет им. Н.И.Лобачевского»
Чалиев А.А., Овчаров А.О.
СТАТИСТИКА
Часть 1
Учебно-методическое пособие
Рекомендовано методической комиссией финансового факультета
для студентов высших учебных заведений экономических специальностей
Нижний Новгород
2007
УДК 311(075.8)
ББК У051
Ч–12
Ч–12 Чалиев А.А., Овчаров А.О. СТАТИСТИКА. Учебно-методическое пособие. Часть 1. – Нижний Новгород: Издательство Нижегородского госуниверситета, 2007.– 87 с.
Рецензент: к.э.н., доцент Козлов А.И.
Настоящее издание содержит учебную программу и основные разделы теоретической и прикладной статистики. В учебно-методическом пособии даны примеры решения типовых задач, а также предлагаются задачи для самостоятельного решения.
Пособие предназначено для студентов всех специальностей финансового факультета ННГУ.
УДК 311(075.8)
ББК У051
© Нижегородский государственный
университет им. Н.И.Лобачевского, 2007
Содержание
Введение.. 4
1. Цели и задачи дисциплины... 4
2. Программа курса.. 6
3. Тематика контрольных (курсовых) работ.. 13
4. Методические указания и контрольные задания.. 15
Часть 1. Теоретическая статистика. 15
Тема 1. Абсолютные и относительные статистические величины.. 15
Тема 2. Средние величины и показатели вариации.. 22
Тема 3. Выборочное наблюдение. 29
Тема 4. Ряды динамики.. 33
Тема 5. Индексы.. 41
Тема 6. Статистическое изучение взаимосвязей.. 47
Часть 2. Социально-экономическая статистика. 56
Тема 1. Социально-демографическая статистика.. 56
Тема 2. Статистика уровня жизни населения. 61
Тема 3. Статистика национального богатства.. 66
Тема 4. Статистика труда.. 72
5. Экзаменационные вопросы... 83
6. Литература.. 84
Приложения.. 85
Приложение 1. Значения F-критерия Фишера. 85
Приложение 2. Значения t-критерия Стьюдента. 86
Введение
Учебная дисциплина «Статистика» является обязательным компонентом в подготовке дипломированных специалистов по экономическим специальностям. Основное назначение данной дисциплины состоит в повышении экономико-математической подготовки студентов в области современных методов сбора, обработки и анализа статистической информации, достижении высокого и устойчивого уровня профессионализма. Современный специалист должен обладать глубокими знаниями, уметь проводить количественный анализ сложных экономических проблем, применять математические расчеты в решении экономических задач. Поэтому изучение данной дисциплины поможет сформировать у студентов целостный взгляд на место и роль статистической науки в современной экономике.
1. Цели и задачи дисциплины
1.1.
Цель курса:
Цель преподавания курса «Статистика» – подготовка специалистов, владеющих современными методами сбора, обработки и анализа статистической информации, принятыми в отечественной и международной практике учета и статистики.
Структурно изучаемая дисциплина состоит из двух разделов: общей теории статистики и экономической статистики. В первом разделе рассматриваются общие понятия и методы сбора, обработки и обобщения массовых данных. Во втором – система показателей и их экономическая интерпретация для конкретных социально-экономических процессов.
1.2.
Задачи курса:
– овладение комплексом статистических методов наблюдения, сводки и группировки массовых данных;
– освоение системы статистических величин, характеризующих количественную сторону социально-экономических явлений и процессов;
– применение методов статистического анализа при исследовании различных сфер экономики.
1.3.
Место курса в профессиональной подготовке выпускника:
Эффективное изучение дисциплины «Статистика» предполагает знание основ экономической теории, математики и теории бухгалтерского учета.
1.4.
Требования к уровню освоения содержания курса:
В результате изучения дисциплины студенты должны:
а) знать:
─ основные категории и классификации в статистике;
─ методы расчета обобщающих показателей, выявления тенденций и закономерностей социально-экономических процессов;
─ принципы построения системы национальных счетов;
б) уметь:
─ анализировать результаты статистического наблюдения в виде таблиц и графиков;
─ рассчитывать статистические величины и делать аргументированные выводы;
─ применять теоретические положения статистики на практическом уровне;
в) иметь представление:
─ об органах государственной статистики в РФ;
─ о международных сопоставлениях макроэкономических показателей;
─ об организации практической статистической работы.
2. Программа курса
2.1. Содержание лекционных занятий.
Тема 1.
Предмет и метод статистики.
Предмет статистики. Статистика как наука. Ее связь с другими науками. Категории и задачи статистики.
Три группы методов статистики. Статистическое наблюдение как первый этап статистического исследования. Понятие, назначение и задачи статистического наблюдения. Виды статистического наблюдения. Способы статистического наблюдения. Программно-методологические основы наблюдения: цель, объект, единица и время наблюдения. Программа наблюдения и требования к ней. Статистический формуляр: понятие, назначение, виды и особенности применения. Статистическая инструкция, ее назначение и содержание.
Статистические сводки и группировки как второй этап статистического исследования. Понятие о сводке, ее назначение и задачи. Виды сводок.
Простая (монотетическая) и сложная (политетическая) группировки. Виды группировок: типологическая, структурная, аналитическая. Комбинационная группировка. Целевые задачи каждого вида группировки.
Принципы группировки: выбор основания группировки и группировочного признака; распределение единиц совокупности по группам; определение числа групп и интервалов группировки. Интервалы: равномерные и неравномерные, закрытые и открытые. Серединное значение интервала, центрирование интервалов. Формула Стерджесса для определения числа групп и интервала равномерной группировки.
Вторичная группировка, ее назначение и виды. Алгоритм укрупнения и разукрупнения первичных группировок. Многомерные группировки в статистике. Методы многомерных классификаций.
Тема 2
. Статистические величины и показатели вариации.
Абсолютная величина: сущность, виды и единицы измерения. Классификация относительных величин, способы их расчета.
Средняя величина как обобщающий показатель. Виды и принципы применения средних величин. Классификация средних величин: степенные и структурные; простые и взвешенные; пространственные и временные. Виды степенных средних – простые и взвешенные; арифметическая, гармоническая, геометрическая. Правило мажорантности этих средних.
Свойства степенных средних величин. Математические свойства средней арифметической. Расчет средней в интервальных рядах и методом условного нуля. Групповые средние. Расчет средней для совокупности на основе групповых средних.
Структурные средние величины: мода и медиана. Способы расчета для интервальных статистических совокупностей.
Причины и необходимость изучения вариации. Абсолютные и относительные показатели вариации: размах вариации; среднее линейное и квадратическое отклонение; коэффициенты осцилляции, относительного линейного отклонения, вариации.
Понятие о дисперсии. Математические свойства дисперсии. Общая, внутригрупповая и межгрупповая дисперсии. Расчет общей дисперсии четырьмя методами: методом прямого счета (по определяющей формуле); методом условного нуля; методом средних величин (разность между средним квадратом и квадратом средней); по правилу сложения внутригрупповой и межгрупповой дисперсий.
Тема 3.
Ряды динамики.
Сущность ряда динамики, его элементы и правила построения. Показатели анализа рядов динамики: абсолютный прирост, темпы роста и прироста, абсолютное значение одного процента прироста. Средние показатели ряда динамики. Графическое изображение рядов динамики.
Сопоставимость в рядах динамики. Причины несопоставимости. Преобразование рядов в сопоставимый вид. Смыкание рядов динамики при территориальных изменениях.
Понятие об общей тенденции развития ряда, ее значение и методы выявления. Метод укрупнения временных периодов. Метод усреднения краткосрочных отрезков за ряд лет (временных периодов), метод скользящей средней. Метод аналитического выравнивания по способу наименьших квадратов. Метод экстраполяции. Индекс сезонности.
Тема 4.
Выборочное наблюдение.
Понятие о выборочном наблюдении. Необходимость, принципы и задачи выборочного наблюдения.
Генеральная и выборочная совокупность, доля и средняя. Индивидуальный и групповой отбор. Методы отбора.
Определение средней и предельной ошибок выборочного наблюдения. Необходимая численность выборки. Способы распространения выборочных данных на генеральную совокупность.
Тема 5.
Индексы.
Экономическая сущность индексов и сферы их применения. Классификация индексов. Агрегатный индекс как основная форма индексов. Индексный метод. Типовые экономические задачи с применением статистических индексов.
Двухфакторный индексный анализ. Мультипликативная (алгебраическая) связь индексов и аддитивная (арифметическая) связь приростов, полученных за счет переменных индексных факторов.
Средние индексы. Индексы переменного, постоянного составов и структурных сдвигов: методика расчетов и экономический смысл. Трехфакторный индексный анализ сложных явлений.
Территориальные индексы: принципы построения и сфера применения.
Тема 6 .
Статистическое изучение взаимосвязей.
Основные понятия корреляционно-регрессионного анализа. Парная корреляция. Расчет линейного коэффициента корреляции. Эмпирическое корреляционное отношение. Множественная корреляция. Коэффициент множественной корреляции и коэффициент детерминации. Непараметрические методы оценки связи.
Однофакторный регрессионный анализ. Нахождение теоретической формы связи. Выравнивание по прямой. Коэффициент эластичности. Нелинейные зависимости.
Многофакторный корреляционно-регрессионный анализ. Парные и частные коэффициенты корреляции. Применение корреляционно-регрессионного анализа в прогнозировании социально-экономических процессов.
Тема 7.
Социально-демографическая статистика.
Демография как отрасль статистической науки. Категории и группировки населения. Показатели численности и размещения населения. Естественное и механическое движение населения: понятие и расчет основных коэффициентов. Демографический прогноз: сущность и виды. Прогнозирование будущей численности населения по методу передвижки возрастов. Основные показатели социальной характеристики населения.
Тема 8.
Статистика уровня жизни населения.
Понятие и система показателей уровня жизни населения. Номинальные, располагаемые и реальные доходы. Индексация доходов.
Группировка потребительских расходов по целевому назначению. Показатели объема, состава и динамики потребления материальных благ и услуг населением. Расчет коэффициента эластичности потребления. Баланс доходов и расходов населения.
Дифференциация населения по уровню доходов. Коэффициент фондов и децильный коэффициент. Модальный и медианный доход. Коэффициент Джини. Кривая Лоренца. Величина прожиточного минимума, его структура, натуральное и денежное выражение. Агрегированные показатели бедности: глубины и остроты. Индексы развития человеческого потенциала и нищеты населения.
Тема 9.
Статистика национального богатства.
Определение и структура национального богатства. Национальное имущество и природные ресурсы. Финансовые и нефинансовые активы.
Статистика природных ресурсов. Земельный и лесной фонды. Показатели их состояния и использования. Водные ресурсы, показатели их состояния, использования и эффективности очистки. Полезные ископаемые, их классификация и показатели запасов, добычи, эффективности использования. Система экологического и экономического учета.
Основные фонды: сущность, способы оценки и методы амортизации. Производственные и непроизводственные основные фонды. Статистическая группировка основных производственных фондов. Натурально-вещественный состав основных фондов в отдельных отраслях народного хозяйства – производственной и непроизводственной сферы. Активная и пассивная части основных фондов.
Показатели состояния основных фондов: коэффициенты ввода, выбытия, обновления, износа, годности. Показатели эффективности использования фондов: фондовооруженность труда, фондоотдача, фондоемкость. Увязка изменения фондоотдачи со структурными сдвигами в активной части фондов. Индексный анализ эффективности использования основных фондов. Двух- и трехфакторные модели изменения объема продукции.
Понятие, состав и классификация оборотных фондов. Производственные и непроизводственные оборотные фонды, формы их статистического учета. Количественные показатели оборотных фондов. Процессы ускорения и замедления оборачиваемости, их оценка.
Тема 10.
Система национальных счетов.
Система национальных счетов (СНС): сущность, принципы построения и основные показатели. Счет как элемент СНС. Методы балансировки счета. Две стороны счетов. Группы счетов СНС, их характеристика. Использование СНС в макроэкономическом анализе и прогнозировании.
Валовой внутренний продукт (ВВП) как ключевой макроэкономический показатель СНС. Методы расчета ВВП. Анализ динамики ВВП. Индекс–дефлятор ВВП. Методы переоценки ВВП в сопоставимые цены. Международные сопоставления ВВП.
Национальный доход и другие показатели доходов в СНС. Концепция дохода Дж. Хикса.
Межотраслевой баланс производства и использования товаров и услуг (МОБ) как элемент СНС. Основное уравнение МОБ. Виды МОБ и методы оценки его показателей.
Тема 11.
Статистика труда.
Рынок труда и его элементы. Экономически активное население. Группировка населения по статусу занятости. Показатели движения трудовых ресурсов.
Рабочее время и его использование. Единицы измерения рабочего времени. Календарный, табельный и максимально возможный фонды рабочего времени, способы их расчета. Баланс рабочего времени. Статистика трудовых конфликтов.
Понятие и элементы фонда оплаты труда. Методика расчета средней заработной платы. Коэффициент дифференциации заработной платы. Индексный метод анализа динамики оплаты труда.
Производительность труда: сущность и показатели ее уровня. Производительность общественного труда. Анализ выработки и трудоемкости. Натуральный, трудовой и стоимостной методы анализа динамики производительности труда. Двухфакторная модель изменения стоимости продукции.
Тема 12.
Статистика финансов.
Финансы как объект статистического учета. Статистика государственных и негосударственных финансов. Бюджетная статистика: понятие, задачи, классификации доходов и расходов. Анализ исполнения бюджетов всех уровней. Статистика налогов. Применение абсолютных и относительных показателей в налоговой статистике.
Прибыль: понятие, экономическое значение, виды, статистический учет. Статистический анализ балансовой прибыли, прибыли от реализации продукции (работ, услуг), прибыли от реализации иных ценностей, внереализационной прибыли, налогооблагаемой прибыли, чистой прибыли.
Рентабельность как важнейший показатель экономической эффективности. Виды рентабельности, их статистический учет и анализ. Факторный анализ прибыли и рентабельности в их причинно-следственной зависимости.
Коэффициентный анализ ликвидности, устойчивости и платежеспособности предприятия.
Система показателей статистики денежного обращения: денежный оборот, денежная масса, денежная база, скорость обращения, продолжительность оборота. Структура денежной массы. Факторный анализ динамики денежной массы. Влияние инфляции на состояние денежного оборота.
Понятие фондового рынка и задачи статистики. Индивидуальные характеристики ценных бумаг, их рейтинг. Расчет биржевых индексов. Индексы рынка государственных ценных бумаг. Статистика валютного курса.
Основные абсолютные показатели статистики страхования. Статистический учет страховых рисков. Показатели эффективности страхования.
Задачи статистики кредита. Основные статистические показатели кредита: средний размер задолженности, средний срок ссуды, средняя процентная ставка. Анализ динамики кредитных вложений. Система показателей банковской деятельности. Рейтинг банков. Виды и способы начисления банковских процентов. Расчет наращенной суммы и современной стоимости. Финансовые ренты: сущность, параметры и виды.
Тема 13.
Статистика коммерческой деятельности.
Задачи статистики коммерческой деятельности. Статистическое изучение торговли товарами и услугами; статистика товарных запасов и товарооборачиваемость. Статистика инфраструктуры коммерческой деятельности, статистика финансов и инвестиций в коммерции, статистика труда и обслуживания потребителей в коммерческой деятельности. Статистические методы оценки и прогнозирования коммерческой деятельности.
Задачи и система показателей статистики цен. Средняя арифметическая и средняя гармоническая цена. Состав и структура цен. Виды цен в РФ. Экономические элементы отпускной и розничной цены. Тарифы.
Динамика цен. Индексы потребительских цен, методы их расчета. Количественные оценки инфляции. Влияние инфляции на динамику цен. Индексы цен во внешней торговле.
Тема 14.
Статистика отраслей народного хозяйства.
Общие принципы исчисления показателей отраслей и секторов экономики. Статистика продукции промышленности. Натуральные и стоимостные показатели объема продукции. Расчет показателей качества и сортности продукции.
Система показателей продукции сельского хозяйства. Урожайность и валовой сбор: экономическая сущность и индексный метод анализа. Расчет показателей численности и продуктивности животноводства.
Классификация строительной деятельности. Производственный метод исчисления продукции строительства.
2.2. Распределение часов по темам и видам работ
| № п/п
|
Тема
|
Количество часов
|
| Очное отделение
|
Очно-заочное отделение
|
Заочное отделение
|
| Лекции
|
Семинары
|
Лекции
|
Семинары
|
Лекции
|
Семинары
|
| 1
|
Предмет и метод статистики
|
4
|
4
|
1
|
1
|
1
|
| 2
|
Статистические величины и показатели вариации
|
6
|
6
|
2
|
2
|
1
|
1
|
| 3
|
Ряды динамики
|
4
|
4
|
2
|
2
|
1
|
1
|
| 4
|
Выборочное наблюдение
|
4
|
4
|
1
|
1
|
1
|
| 5
|
Индексы
|
6
|
8
|
2
|
2
|
1
|
1
|
| 6
|
Статистическое изучение взаимосвязей
|
4
|
4
|
1
|
1
|
1
|
| 7
|
Статистика населения
|
4
|
6
|
2
|
2
|
1
|
1
|
| 8
|
Статистика национального богатства
|
4
|
6
|
2
|
2
|
1
|
| 9
|
Система национальных счетов
|
6
|
8
|
2
|
2
|
2
|
1
|
| 10
|
Статистика уровня жизни населения
|
6
|
8
|
2
|
2
|
1
|
1
|
| 11
|
Статистика труда
|
4
|
6
|
2
|
2
|
1
|
| 12
|
Статистика финансов
|
8
|
10
|
4
|
4
|
2
|
1
|
| 13
|
Статистика коммерческой деятельности
|
4
|
6
|
1
|
1
|
1
|
1
|
| 14
|
Статистика отраслей народного хозяйства
|
4
|
4
|
1
|
1
|
1
|
| Итого
|
68
|
84
|
25
|
25
|
16
|
8
|
Примечание: предложенное распределение бюджета времени относится к специальности «Финансы и кредит», для других специальностей изложение материала ведется по сокращенному бюджету времени.
3. Тематика контрольных (курсовых) работ
Задания к контрольной (курсовой) работе составлены в 10 вариантах. Курсовая работа должна содержать 2 части – теоретическую и практическую. Первая часть включает теоретическое изложение конкретной темы курса, вторая – решение комплексных задач по важнейшим разделам статистики.
При выполнении контрольной работы необходимо выполнить только практическую часть, задания к которой приведены в следующем разделе.
Выбор варианта зависит от последней цифры зачетной книжки студента:
| Последняя цифра зачетки
|
Номер варианта
|
| 0
|
10
|
| 1
|
1
|
| 2
|
2
|
| 3
|
3
|
| и т.д.
|
и т.д.
|
При выполнении курсовой работы необходимо руководствоваться следующими требованиями:
1. На титульном листе работы должны быть указаны фамилия, имя, отчество студента, выполнившего работу, номер группы и номер варианта. Задачи нужно решать в том порядке, в каком они даны в задании.
2. Перед решением задачи должно быть полностью приведено ее условие. Само решение следует сопровождать необходимыми расчетами и пояснениями с указанием применяемых формул, анализом и выводами.
3. Все расчеты относительных показателей нужно производить с точностью до 0,001, а процентов – до 0,01, используя при этом правила округления.
4. Работа должна быть оформлена аккуратно, написана разборчиво без помарок, зачеркиваний и сокращений слов. Допускается выполнение работы на компьютере в каком-либо текстовом редакторе.
В конце работы следует привести список использованной литературы, составленной в соответствии с общепринятыми правилами.
Задания к теоретической части курсовой работы
| Номер варианта
|
Тема
|
| 1
|
Задачи и основные показатели статистики цен
|
| 2
|
Социально-демографическая статистика
|
| 3
|
Статистика денежного обращения и кредита
|
| 4
|
Статистический анализ рынка труда
|
| 5
|
Система показателей уровня жизни населения
|
| 6
|
Статистика государственных финансов
|
| 7
|
Расчет и оценка макроэкономических показателей
|
| 8
|
Статистика национального богатства
|
| 9
|
Особенности статистического анализа окружающей среды и природных ресурсов
|
| 10
|
Статистика внешней торговли
|
4. Методические указания и контрольные задания
Часть 1. Теоретическая статистика
Тема 1. Абсолютные и относительные статистические величины
Методические указания по теме
Задача 1
.
Расход топлива на производственные нужды предприятия характеризуется в отчетном периоде следующими данными:
| Вид топлива
|
Теплотворная способность, МДж/кГ
|
Расход, т
|
| по плану
|
фактически
|
| Дизельное топливо
|
41,9
|
1000
|
1050
|
| Мазут
|
40,1
|
750
|
730
|
| Уголь
|
26,4
|
500
|
555
|
Определить общее количество потребленного условного топлива (1 т.у.т. = 29,3 МДж/кГ) по плану и фактически, а также процент выполнения плана по общему расходу топлива.
Решение. Учитывая стандартную теплотворную способность 29,3 МДж/кГ, определяем количество потребленного условного топлива каждого вида по плану (X
’1
i
) и фактически (X
1
i
):
– дизельное топливо: X
’1дт
= 41,9/29,3*1000 = 1430,034 т.у.т.
дизельное топливо: X
1дт
= 41,9/29,3*1050 = 1501,536 т.у.т.;
– мазут: X
’1м
= 40,1/29,3*750 = 1026,451 т.у.т.
мазут: X
1м
= 40,1/29,3*730 = 999,078 т.у.т.;
– уголь: X
’1у
= 26,4/29,3*500 = 450,512 т.у.т.
уголь: X
1у
= 26,4/29,3*555 = 500,068 т.у.т.
Суммируя количество потребленного условного топлива каждого вида, получим общее количество потребленного условного топлива:
– по плану X
’1
= ∑X
’1
i
= 2906,997 т.у.т.;
– фактически X
1
= ∑X
1
i
= 3000,682 т.у.т.
Для определения процента выполнения плана необходимо рассчитать индекс выполнения плана
, то есть отношение значений по факту и плану отчетного периода:
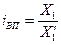 , (
1) , (
1)
Применяя формулу (1), имеем: 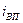 = 3000,682/2906,997 = 1,032, то есть план по общему расходу топлива перевыполнен на 3,2%. = 3000,682/2906,997 = 1,032, то есть план по общему расходу топлива перевыполнен на 3,2%.
Задача 2
.
Рассчитать индекс и темп изменения, если в марте произведено продукции 130 тонн, а в феврале 100 тонн.
Решение. Индекс изменения (динамики)
характеризует изменение какого-либо явления во времени. Он представляет собой отношение значений одной и той же абсолютной величины в разные периоды времени. Данный индекс определяется по формуле (2):
 , (
2) , (
2)
где подиндексы означают: 1 — отчетный или анализируемый период, 0 — прошлый или базисный период.
Критериальным значением индекса динамики (темпа роста) служит единица, то есть если  >1, то имеет место рост явления во времени; если >1, то имеет место рост явления во времени; если  =1 – стабильность; если =1 – стабильность; если  <1 – наблюдается спад явления. Применяя формулу (2), имеем: <1 – наблюдается спад явления. Применяя формулу (2), имеем:  = 130/100 = 1,3 (или 130%) > 1 – рост объема произведенной продукции. = 130/100 = 1,3 (или 130%) > 1 – рост объема произведенной продукции.
Темп изменения (прироста)
определяется по формуле (3):
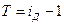 . (
3) . (
3)
Применяя формулу (3), имеем: Т
= 1,3 – 1 = 0,3 (или 30%), то есть объем произведенной продукции вырос в марте по сравнению с февралем на 30%.
Задача 3
.
Рассчитать индексы планового задания, выполнения плана и динамики, если выпуск продукции в отчетном году составил 100 млн. рублей, на следующий год планировалось 140 млн. рублей, а фактически получено 112 млн. рублей.
Решение. Индекс планового задания
– это отношение значений одной и той же абсолютной величины по плану анализируемого периода и по факту базисного. Он определяется по формуле (4):
 , (
4) , (
4)
где X
’1
— план анализируемого периода; X
0
— факт базисного периода.
Применяя формулу (4) имеем:  = 140/100 = 1,4 (или 140%), то есть на следующий год планировалось выпустить продукции в размере 140% от объема предыдущего года. = 140/100 = 1,4 (или 140%), то есть на следующий год планировалось выпустить продукции в размере 140% от объема предыдущего года.
Индекс выполнения плана определим, применяя формулу (1): 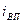 = 112/140 = 0,8 (или 80%), то есть план по увеличению выпуска продукции выполнили лишь на 80% или недовыполнили на 20%. = 112/140 = 0,8 (или 80%), то есть план по увеличению выпуска продукции выполнили лишь на 80% или недовыполнили на 20%.
Индекс динамики можно определить по формуле (2) или перемножая индексы планового задания и выполнения плана, то есть 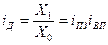 = 1,12. = 1,12.
Задача 4
.
Суммарные денежные доходы россиян в 2005 г. составили 13522,5 млрд. руб., из которых 8766,7 млрд. руб. составила оплата труда, 1748,4 млрд. руб. – социальные выплаты, 1541,7 млрд. руб. – доход от предпринимательской деятельности, 1201,5 млрд. руб. – доходы от собственности, остальное – прочие доходы. Рассчитать относительные величины структуры и координации, приняв за основу оплату труда. Построить секторную (круговую) диаграмму структуры доходов.
Решение. Индекс структуры (доля
) – это отношение какой-либо части величины (совокупности) ко всему ее значению. Он определяется по формуле (5):
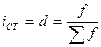 (
5) (
5)
Применяя формулу (5) и округляя значения до 3-х знаков после запятой, имеем:
– доля оплаты труда d
ОТ
= 8766,7/13522,5 = 0,648 или 64,8%;
– доля социальных выплат d
СВ
=1748,4/13522,5 = 0,129 или 12,9%;
– доля доходов от предпринимательской деятельности d
ПД
=1541,7/13522,5 = 0,114 или 11,4%;
– доля доходов от собственности d
ДС
=1201,5/13522,5 = 0,089 или 8,9%.
Долю прочих доходов найдем, используя формулу (6), согласно которой сумма всех долей равна единице:
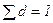 . (
6) . (
6)
Таким образом, доля прочих доходов d
проч
= 1 – 0,648 – 0,129 – 0,114 – 0,089 = 0,020 или 2,0%.
Для иллюстрации структуры (составных частей) доходов построим секторную диаграмму (рис.1):

Рис.1. Структура денежных доходов населения РФ в 2005 году.
Таким образом, очевидно, что наибольшую долю в суммарных денежных доходах составляет оплата труда (64,8%), на 2-м месте – социальные выплаты (12,9%), затем следуют предпринимательский доход (11,4%), доходы от собственности (8,9%), а прочие доходы составляют лишь 2%.
Индекс координации
– это отношение какой-либо части величины к другой ее части, принятой за основу (базу сравнения). Он определяется по формуле (7):
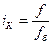 . (
7) . (
7)
Применяя формулу (7) и принимая за основу оплату труда, имеем:
– индекс координации социальных выплат 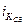 = 1748,4/8766,7 ≈ 0,129/0,648 = 0,199; = 1748,4/8766,7 ≈ 0,129/0,648 = 0,199;
– индекс координации предпринимательского дохода 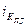 =1541,7/8766,7 ≈ 0,114/0,648 = 0,176; =1541,7/8766,7 ≈ 0,114/0,648 = 0,176;
– индекс координации доходов от собственности 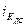 = 1201,5/8766,7 ≈ 0,089/0,648 = 0,137; = 1201,5/8766,7 ≈ 0,089/0,648 = 0,137;
– индекс координации прочих доходов 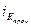 ≈ 0,02/0,648 = 0,031. ≈ 0,02/0,648 = 0,031.
Таким образом, социальные выплаты составляют 19,9% от оплаты труда, предпринимательский доход – 17,6%, доходы от собственности – 13,7%, а прочие доходы – 3,1%.
Задача 5
.
Запасы воды в озере Байкал составляют 23000 км3
, а в Ладожском озере 911 км3
. Рассчитать относительные величины сравнения запасов воды этих озер.
Решение. Индекс сравнения
– это отношение значений одной и той же величины в одном периоде или моменте времени, но для разных объектов или территорий. Он определяется по формуле (8):
 , (
8) , (
8)
где А
, Б
— признаки сравниваемых объектов или территорий.
Применяя формулу (8) и принимая за объекты А
и Б
, соответственно, озера Байкал и Ладожское, найдем индекс сравнения: 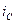 = 23000/911 = 25,25, то есть запасов воды в озере Байкал в 25,25 раза больше, чем в Ладожском озере. = 23000/911 = 25,25, то есть запасов воды в озере Байкал в 25,25 раза больше, чем в Ладожском озере.
Меняя базу сравнения, найдем индекс сравнения Ладожского озера с Байкалом по той же формуле: 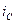 = 911/23000 = 0,0396 или 3,96%, то есть запасы воды в Ладожском озере составляют 3,96% запасов воды в озере Байкал. = 911/23000 = 0,0396 или 3,96%, то есть запасы воды в Ладожском озере составляют 3,96% запасов воды в озере Байкал.
Задача 6
.
Рассчитать относительную величину интенсивности валового внутреннего продукта (ВВП) в сумме 1416,1 млрд. $ на душу населения в России в 2004 году при численности населения в 144,2 млн. человек.
Решение. Показатель интенсивности
– это отношение значений двух разнородных абсолютных величин для одного периода времени и одной территории или объекта. Он определяется по формуле (9):
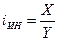 . (
9) . (
9)
Применяя формулу (9) имеем: i
ИН
= 1416,1/0,1442 = 9820,39 $/чел в год.
Контрольные задания по теме
Вариант 1.
Определить общее производство моющих средств в условных тоннах (условная жирность 40%) по плану и фактически, а также процент выполнения плана по следующим данным:
| Вид продукта
|
Жирность, %
|
Физическая масса, т
|
| по плану
|
фактически
|
| Мыло хозяйственное
|
60
|
500
|
600
|
| Мыло туалетное
|
80
|
1000
|
1500
|
| Стиральный порошок
|
10
|
50000
|
40000
|
Вариант 2.
По данным о численности жителей двух крупнейших городов России (тыс. чел) определить индексы сравнения и динамики.
| Город Год
|
2004
|
2005
|
| Москва
|
10391
|
10407
|
| Санкт-Петербург
|
4624
|
4600
|
Вариант 3.
1. По плану на 2005 год намечалось увеличение товарооборота на 3%. В 2005 году плановое задание перевыполнили на 600 млн. руб. или на 2,5%. Определить фактический прирост товарооборота (в млн. руб.) в 2005 году по сравнению с 2004 годом.
2. По данным о товарообороте из предыдущей задачи, состоящего из реализации собственной продукции и продажи покупных товаров, определить относительные величины координации и структуры собственной и покупной продукции в 2004 и 2005 годах, если известно, что доля собственной продукции в 2004 году составила 65%, а в 2005 году она увеличилась на 10%.
Вариант 4.
Жилищный фонд и численность населения России следующие (на начало года):
| Год
|
2002
|
2003
|
2004
|
2005
|
| Весь жилищный фонд, млн. м2
|
2853
|
2885
|
2917
|
2949
|
| Численность населения, млн. чел.
|
145,6
|
145,0
|
144,2
|
143,5
|
Охарактеризовать изменение обеспеченности населения жилой площадью с помощью относительных величин динамики и координации.
Вариант 5.
1. В России в 2004 численность женщин составила 77144,3 тыс. чел, а мужчин – 67023,9 тыс. чел. Рассчитать относительные величины структуры и координации.
2. По плану объем продукции в отчетном году должен возрасти по сравнению с прошлым годом на 2,5%. План выпуска продукции перевыполнен на 3,0%. Определить фактический выпуск продукции в отчетном году, если известно, что объем продукции в прошлом году составил 25,3 млн. руб.
Вариант 6.
Определить общий объем фактически выпущенной продукции по следующим данным по трем филиалам предприятия, выпускающих однородную продукцию:
| Номер филиала
|
Планируемый объем выпуска продукции, млн. руб.
|
Выполнение намеченного плана, %
|
| 1
|
500
|
104
|
| 2
|
750
|
92
|
| 3
|
250
|
116
|
Вариант 7.
По промышленному предприятию за отчетный год имеются следующие данные о выпуске продукции:
| Наименование
продукции
|
План на I квартал,
тыс. т
|
Фактический выпуск, тыс. т
|
Отпускная цена
за 1 т, у.е.
|
| январь
|
февраль
|
март
|
| Сталь арматурная
|
335
|
110
|
115
|
108
|
1700
|
| Прокат листовой
|
255
|
75
|
90
|
100
|
2080
|
Определить процент выполнения квартального плана: 1) по выпуску каждого вида продукции; 2) в целом по выпуску всей продукции.
Вариант 8.
Определить процент выполнения плана по продажам условных школьных тетрадей (1 у.ш.т. – 12 листов) по каждому виду тетрадей и в целом по магазину по следующим данным:
| Вид тетради
|
Цена, руб./шт.
|
Объем продаж, тыс. шт.
|
| по плану
|
фактически
|
| Тетрадь общая 90 листов
|
20
|
50
|
40
|
| Тетрадь общая 48 листов
|
13
|
200
|
350
|
| Тетрадь общая 16 листов
|
9
|
700
|
500
|
Вариант 9.
В России на начало 2005 года численность населения составила 144,2 млн. чел., в течение года: родилось 1,46 млн. чел., умерло – 2,3 млн. чел., мигрировало из других государств 2,09 млн. чел., мигрировало за границу – 1,98 млн. чел. Охарактеризовать изменение численности населения в 2005 году с помощью относительных величин.
Вариант 10.
Определить общий объем фактически выпущенной условной консервной продукции (1 у.к.б. = 0,33 л) по следующим данным:
| Вид продукции
|
Планируемый объем выпуска продукции, тыс. шт.
|
Выполнение плана, %
|
| Томатная паста 1 л
|
500
|
85
|
| Томатная паста 0,5 л
|
750
|
104
|
| Томатная паста 0,2 л
|
250
|
130
|
Тема 2. Средние величины и показатели вариации
Методические указания по теме
Задача 1
.
Имеются следующие данные о возрастном составе студентов группы заочного отделения ВУЗа (лет): 19; 19; 19; 20; 20; 20; 20; 20; 20; 20; 20; 20; 21; 21; 21; 22; 23; 23; 24; 25; 25; 25; 26; 27; 29.
Для анализа распределения студентов по возрасту требуется: 1) построить интервальный ряд распределения и его график; 2) рассчитать модальный, медианный и средний возраст, установить его типичность с помощью коэффициентов вариации; 3) проверить распределение на нормальность с помощью коэффициентов асимметрии и эксцесса.
Решение. Для построения интервального ряда из дискретного используется формула Стерджесса, с помощью которой определяется оптимальное количество интервалов (n
):
n = 1 +3,322 lg N,
(10)
где N
– число величин в дискретном ряде.
В нашей задаче n
= 1 + 3,322lg
25 = 1 + 3,322*1,398 = 5,64. Так как число интервалов не может быть дробным, то округлим его до ближайшего целого числа, т.е. до 6.
После определения оптимального количества интервалов определяем размах интервала по формуле:
h = H / n,
(11)
где H
– размах вариации, определяемый по формуле (12).
H
= Хмах
–Х
min
,
(
12)
где X
м
a
x
и Xmin
— максимальное и минимальное значения в совокупности.
В нашей задаче h
=
(29 – 19)/6 = 1,67.
Интервальная группировка данных приведена в первом столбце таблицы 1, которая содержит также алгоритм и промежуточные расчеты.
Таблица
1. Вспомогательные расчеты для решения задачи
| Xi
, лет
|
fi
|
ХИ
|
XИ
fi
|
ХИ
-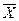
|

|
(ХИ
-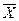 )2 )2
|
(ХИ
-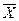 )2
fi )2
fi
|
(ХИ
-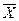 )3
fi )3
fi
|
(ХИ
-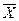 )4
fi )4
fi
|
| до 20,67
|
12
|
19,833
|
237,996
|
-2,134
|
25,602
|
4,552
|
54,623
|
-116,539
|
248,638
|
| 20,67-22,33
|
4
|
21,5
|
86,000
|
-0,467
|
1,866
|
0,218
|
0,871
|
-0,406
|
0,189
|
| 22,33-24
|
3
|
23,167
|
69,501
|
1,200
|
3,601
|
1,441
|
4,323
|
5,190
|
6,231
|
| 24-25,67
|
3
|
24,833
|
74,499
|
2,866
|
8,599
|
8,217
|
24,650
|
70,659
|
202,543
|
| 25,67-27,33
|
2
|
26,5
|
53,000
|
4,533
|
9,067
|
20,552
|
41,105
|
186,348
|
844,806
|
| более 27,33
|
1
|
28,167
|
28,167
|
6,200
|
6,200
|
38,446
|
38,446
|
238,383
|
1478,091
|
| Итого
|
25
|
—
|
549,163
|
—
|
54,937
|
—
|
164,018
|
383,636
|
2780,498
|
На основе этой группировки строится график распределения возраста студентов (рис.2).
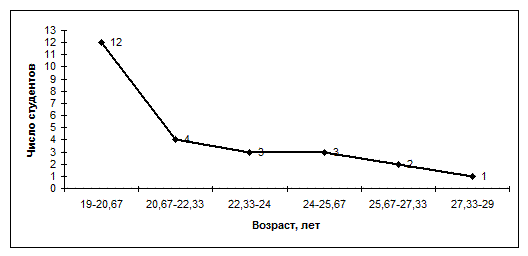
Рис.2. График распределения возраста студентов.
Мода
– это наиболее часто повторяющееся значение признака. Для интервального ряда с равными интервалами величина моды определяется по формуле (13):
 , (
13) , (
13)
где ХMo
– нижнее значение модального интервала; f
Mo
– число наблюдений или объем взвешивающего признака (вес признака) в модальном интервале; f
Mo-1
– то же для интервала, предшествующего модальному; f
Mo+1
– то же для интервала, следующего за модальным; h
– величина интервала изменения признака в группах.
В нашей задаче чаще всего повторяется (12 раз) первый интервал возраста (до 20,67), значит, это и есть модальный интервал. Используя формулу (13), определяем точное значение модального возраста:
Мо
= 19 + 1,667*(12-0)/(2*12-4-0) = 20 (лет).
Медиана –
это такое значение признака, которое приходится на середину ранжированного ряда. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака больше медианы, другая – меньше медианы. Для интервального ряда с равными интервалами величина медианы определяется так:
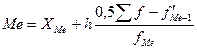 , (
14) , (
14)
где XMe
– нижняя граница медианного интервала; h
– его величина (размах); 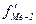 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; f
Me
– число наблюдений или объем взвешивающего признака в медианном интервале.
– сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; f
Me
– число наблюдений или объем взвешивающего признака в медианном интервале.
В нашей задаче второй интервал возраста (от 20,67 до 22,33) является медианным, так как на него приходится середина ряда распределения возраста. Используя формулу (14), определяем точное значение медианного возраста:
Ме
= 20,67 + 1,667*(12,5-12)/4 = 20,878 (года).
Средняя величина
– это обобщающий показатель совокупности, характеризующий уровень изучаемого явления или процесса. Средние величины могут быть простыми
и взвешенными.
Простая средняя рассчитывается при наличии двух и более статистических величин, расположенных в произвольном (несгруппированном)
порядке, по общей формуле (15). Взвешенная средняя величина рассчитывается по сгруппированным
статистическим величинам с использованием общей формулы (16).
 =
=
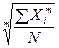 ;
(
15) ;
(
15) 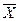 =
=
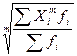 . (
16)
. (
16)
При этом обозначено: Xi
– значения отдельных статистических величин или середин группировочных интервалов; m
- показатель степени, от значения которого зависят виды
средних величин. Используя формулы (15) и (16) при разных показателях степени m
, получаем частные формулы каждого вида (см. таблицу 2).
Таблица
2. Виды степенных средних и их применение
| m
|
Название
средней
|
Формула расчета средней
|
Когда применяется
|
| простая
|
взвешенная
|
| 1
|
Арифметическая
|
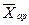 = = (
17)
(
17)
|
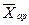 = =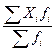 (
18)
(
18)
|
Чаще всего, кроме тех случаев, когда должны применяться другие виды средних
|
| –1
|
Гармоническая
|
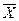 ГМ
= ГМ
= 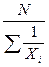 (
19)
(
19)
|
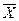 ГМ
= ГМ
= 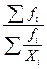 (
20)
(
20)
|
Для осреднения величин с дробной размерностью при наличии дополнительных данных по числителю дробной размерности
|
| 0
|
Геометрическая
|
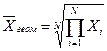 (
21) (
21)
|
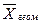 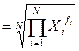 (
22)
(
22)
|
Для осреднения цепных индексов динамики
|
| 2
|
Квадратическая
|
 = = (
23)
(
23)
|
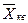 = =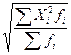 (
24)
(
24)
|
Для осреднения вариации признака (расчет средних отклонений)
|
| 3
|
Кубическая
|
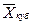 = = (
25)
(
25)
|
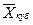 = =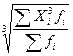 (
26)
(
26)
|
Для расчета индексов нищеты населения
|
| 1
|
Хронологическая
|
 (
27) (
27)
|
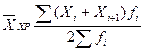 (28) (28)
|
Для осреднения моментных статистических величин
|
Выбор вида формулы средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять. Показатель степени m
в общей формуле средней величины оказывает существенное влияние на значение средней величины: по мере увеличения степени возрастает и средняя величина (правило мажорантности средних величин), то есть  < <  < <  < <  < <  .
Так, если .
Так, если 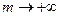 , то , то  , а если
, а если 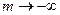 , то , то 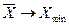 .
.
В нашей задаче, применяя формулу (18) и подставляя вместо 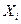 середины интервалов возраста ХИ
, определяем средний возраст студентов: середины интервалов возраста ХИ
, определяем средний возраст студентов: 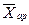 =
549,163/25 = 21,967 (года). Теперь осталось определить типичность или нетипичность найденной средней величины. Это осуществляется с помощью расчета показателей вариации. Чем ближе они к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности. При этом критериальным значением коэффициента вариации служит 1/3. =
549,163/25 = 21,967 (года). Теперь осталось определить типичность или нетипичность найденной средней величины. Это осуществляется с помощью расчета показателей вариации. Чем ближе они к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности. При этом критериальным значением коэффициента вариации служит 1/3.
Коэффициенты вариации рассчитываются как отношение среднего отклонения к средней величине. Поскольку среднее отклонение может определяться линейным и квадратическим способами, то соответствующими могут быть и коэффициенты вариации.
Среднее линейное отклонение
определяется по формулам (29) и (30):
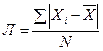 – простое; (
29) – простое; (
29) 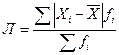 – взвешенное. (
30) – взвешенное. (
30)
Среднее квадратическое отклонение
определяется как корень квадратный из дисперсии, то есть по формуле (31):
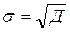 . (
31) . (
31)
Дисперсия
определяется по формулам (32) или (33):
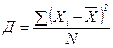 – простая; (
32) – простая; (
32)  – взвешенная. (
33)
– взвешенная. (
33)
В нашей задаче, применяя формулу (30), определим ее числитель и внесем в расчетную таблицу. В итоге получим среднее линейное отклонение: Л
= 54,937/25 = 2,198 (года). Разделив это значение на средний возраст, получим линейный коэффициент вариации
: 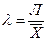 = 2,198/21,967 = 0,100. По значению этого коэффициента для рассмотренной группы студентов делаем вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,100 < 0,333). = 2,198/21,967 = 0,100. По значению этого коэффициента для рассмотренной группы студентов делаем вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,100 < 0,333).
Применяя формулу (33), получим в итоге дисперсию: Д
= 164,018/25 = 6,561. Извлечем из этого числа корень и получим в результате среднее квадратическое отклонение: 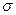 = = 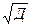 = 2,561 (года). Разделив это значение на средний возраст, получим квадратический коэффициент вариации
: = 2,561 (года). Разделив это значение на средний возраст, получим квадратический коэффициент вариации
: 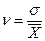 = 2,561/21,967 = 0,117. По значению этого коэффициента для рассмотренной группы студентов можно сделать вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,117 < 0,333).
= 2,561/21,967 = 0,117. По значению этого коэффициента для рассмотренной группы студентов можно сделать вывод о типичности среднего возраста, т.к. расчетное значение коэффициента вариации не превышает критериального (0,117 < 0,333).
В качестве показателей асимметрии
используются: коэффициент асимметрии – нормированный момент третьего порядка (34) и коэффициент асимметрии Пирсона (35):
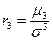 , (
34) , (
34) 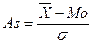 . (
35) . (
35)
Если значение коэффициента асимметрии положительно, то в ряду преобладают варианты, которые больше средней (правосторонняя скошенность), если отрицательно – левосторонняя скошенность. Если коэффициент асимметрии равен 0, то вариационный ряд симметричен.
В нашей задаче  = =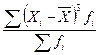 =383,636/25 = 15,345; =383,636/25 = 15,345; 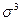 =2,5613
= 16,797; =2,5613
= 16,797; 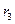 =15,345/16,797 = 0,914 > 0, значит, распределение студентов по росту с правосторонней асимметрией. Это подтверждает и значение коэффициента асимметрии Пирсона: As
= (21,967-20)/2,561 = 0,768. =15,345/16,797 = 0,914 > 0, значит, распределение студентов по росту с правосторонней асимметрией. Это подтверждает и значение коэффициента асимметрии Пирсона: As
= (21,967-20)/2,561 = 0,768.
Для характеристики крутизны распределения
используется центральный момент 4-го порядка:
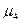 = =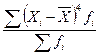 . (36) . (36)
Для образования безразмерной характеристики определяется нормированный момент 4-го порядка  , который и характеризует крутизну (заостренность) графика распределения. При измерении асимметрии эталоном служит нормальное (симметричное) распределение, для которого , который и характеризует крутизну (заостренность) графика распределения. При измерении асимметрии эталоном служит нормальное (симметричное) распределение, для которого 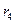 =3. Поэтому для оценки крутизны данного распределения в сравнении с нормальным вычисляется эксцесс распределения (37): =3. Поэтому для оценки крутизны данного распределения в сравнении с нормальным вычисляется эксцесс распределения (37):
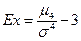 . (
37) . (
37)
Для приближенного определения эксцесса может быть использована формула Линдберга (38):
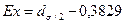 , (
38) , (
38)
где 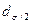 – доля количества вариант, лежащих в интервале, равном половине – доля количества вариант, лежащих в интервале, равном половине 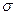 (в ту и другую сторону от средней величины). (в ту и другую сторону от средней величины).
В нашей задаче числитель центрального момента 4-го порядка рассчитан в последнем столбце расчетной таблицы. В итоге по формуле (37) имеем: Ex
= (2780,498/25)/2,5614
–3 = 111,220/43,017–3 = -0,415. Так как Ex<0, то распределение низковершинное. Это подтверждает и приблизительный расчет по формуле (38): в интервале 21,967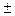 0,5*2,561, то есть от 20,687 до 23,248 находится примерно 21,4% студентов. Таким образом, Ex
= 0,214 – 0,3829 = –0,169. 0,5*2,561, то есть от 20,687 до 23,248 находится примерно 21,4% студентов. Таким образом, Ex
= 0,214 – 0,3829 = –0,169.
Контрольные задания по теме
По имеющимся в следующей таблице данным по группе из 20 студентов заочного отделения необходимо:
1) построить интервальный ряд распределения признака и его график;
2) рассчитать модальное, медианное и среднее значение, установить его типичность с помощью коэффициентов вариации;
3) проверить распределение на нормальность с помощью коэффициентов асимметрии и эксцесса.
| №
п/п
|
Вариант
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Рост,
см
|
Вес,
кг
|
Доход,
у.е./мес.
|
IQ (тест Айзенка)
|
Тет-радь,
листов
|
Воз-раст,
лет
|
Соот-ношение
«рост/вес»
|
Стаж
работы, мес.
|
Кол-во
друзей, чел.
|
Время решения контрольной, час.
|
| 1
|
159
|
45
|
430
|
95
|
24
|
20
|
3,533
|
26
|
5
|
8,5
|
| 2
|
160
|
61
|
640
|
115
|
32
|
25
|
2,623
|
63
|
7
|
6,2
|
| 3
|
161
|
56
|
610
|
111
|
24
|
28
|
2,875
|
94
|
10
|
6,8
|
| 4
|
162
|
48
|
330
|
97
|
24
|
19
|
3,375
|
16
|
4
|
12,0
|
| 5
|
162
|
54
|
420
|
105
|
60
|
23
|
3,000
|
49
|
2
|
7,5
|
| 6
|
164
|
58
|
290
|
98
|
16
|
20
|
2,828
|
14
|
6
|
10,0
|
| 7
|
166
|
51
|
480
|
109
|
90
|
26
|
3,255
|
78
|
9
|
7,2
|
| 8
|
169
|
62
|
610
|
120
|
24
|
19
|
2,726
|
10
|
5
|
4,2
|
| 9
|
170
|
70
|
840
|
122
|
48
|
30
|
2,429
|
130
|
10
|
3,5
|
| 10
|
170
|
72
|
330
|
92
|
24
|
20
|
2,361
|
20
|
3
|
9,5
|
| 11
|
171
|
73
|
560
|
110
|
16
|
28
|
2,342
|
86
|
8
|
7,8
|
| 12
|
171
|
64
|
450
|
102
|
48
|
21
|
2,672
|
29
|
4
|
8,0
|
| 13
|
172
|
73
|
350
|
108
|
32
|
26
|
2,356
|
75
|
7
|
6,0
|
| 14
|
174
|
68
|
310
|
100
|
48
|
21
|
2,559
|
22
|
4
|
4,8
|
| 15
|
176
|
81
|
380
|
104
|
64
|
20
|
2,173
|
32
|
1
|
8,6
|
| 16
|
176
|
84
|
340
|
104
|
48
|
19
|
2,095
|
21
|
5
|
10,0
|
| 17
|
178
|
76
|
660
|
128
|
90
|
27
|
2,342
|
96
|
8
|
4,5
|
| 18
|
181
|
90
|
450
|
106
|
48
|
26
|
2,011
|
70
|
9
|
12,5
|
| 19
|
183
|
68
|
540
|
105
|
32
|
23
|
2,691
|
59
|
6
|
10,5
|
| 20
|
192
|
95
|
750
|
117
|
60
|
27
|
2,021
|
98
|
4
|
6,5
|
Тема 3. Выборочное наблюдение
Методические указания по теме
Задача 1
.
На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за месяц:
| Доход, у.е.
|
до 300
|
300-500
|
500-700
|
700-1000
|
более 1000
|
| Число рабочих
|
8
|
28
|
44
|
17
|
3
|
С вероятностью 0,950 определить:
1) среднемесячный размер дохода работников данного предприятия;
2) долю рабочих предприятия, имеющих месячный доход более 700 у.е.;
3) необходимую численность выборки при определении среднемесячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е.;
4) необходимую численность выборки при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.
Решение. Выборочный метод (выборка) используется, когда применение сплошного наблюдения физически невозможно из-за огромного массива данных или экономической нецелесообразности. Учитывая, что на основе выборочного обследования нельзя точно оценить изучаемый параметр (например, среднее значение – 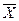 или долю какого-то признака – р
) генеральной совокупности, необходимо найти пределы, в которых он находится. Для этого необходимо определить изучаемый параметр по данным выборки (выборочную среднюю –
или долю какого-то признака – р
) генеральной совокупности, необходимо найти пределы, в которых он находится. Для этого необходимо определить изучаемый параметр по данным выборки (выборочную среднюю – 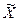 и/или выборочную долю – w
) и его дисперсию (Дв
). Для этого построим вспомогательную таблицу 3. и/или выборочную долю – w
) и его дисперсию (Дв
). Для этого построим вспомогательную таблицу 3.
Таблица
3. Вспомогательные расчеты для решения задачи
| Xi
|
fi
|
Х
И
|
X
И
fi
|
(Х
И
-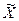 )
2 )
2
|
(Х
И
- )
2
fi )
2
fi
|
| до 300
|
8
|
200
|
1600
|
137641
|
1101128
|
| 300 - 500
|
28
|
400
|
11200
|
29241
|
818748
|
| 500 - 700
|
44
|
600
|
26400
|
841
|
37004
|
| 700 - 1000
|
17
|
850
|
14450
|
77841
|
1323297
|
| более 1000
|
3
|
1150
|
3450
|
335241
|
1005723
|
| Итого
|
100
|
57100
|
4285900
|
По формуле (18) получим средний доход в выборке: 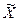 = 57100/100 = 571 (у.е.). Применив формулу (33) и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода: Дв
= 4285900/100 = 42859. = 57100/100 = 571 (у.е.). Применив формулу (33) и рассчитав ее числитель в последнем столбце таблицы, получим дисперсию среднего выборочного дохода: Дв
= 4285900/100 = 42859.
Затем необходимо определить предельную ошибку выборки
по формуле (39)[1]
:
 =
t =
t ,
(
39)
,
(
39)
где t
– коэффициент доверия
, зависящий от вероятности, с которой определяется предельная ошибка выборки;  –
средняя ошибка выборки
, определяемая для повторной выборки по формуле (40), а для бесповторной – по формуле (41):
–
средняя ошибка выборки
, определяемая для повторной выборки по формуле (40), а для бесповторной – по формуле (41):
 = = 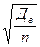 ,
(
40) ,
(
40)  = =  ,
(
41) ,
(
41)
где n
– численность выборки; N
– численность генеральной совокупности.
В нашей задаче выборка бесповторная, значит, применяя формулу (41), получим среднюю ошибку выборки при определении среднего возраста в генеральной совокупности:  = =  = 19,640 (у.е.). = 19,640 (у.е.).
Для определения средней ошибки выборки при определении доли рабочих с доходами более 700 у.е. в генеральной совокупности необходимо определить дисперсию этой доли. Дисперсия доли альтернативного признака w
(признак, который может принимать только два взаимоисключающих значения – например, больше или меньше определенного значения) определяется по формуле (42):
 . (
42) . (
42)
В нашей задаче долю альтернативного признака (рабочие с доходами более 700 у.е.) найдем как отношение числа таких рабочих к общему числу рабочих в выборке: w
= 20/100 = 0,2 или 20%. Теперь определим дисперсию этой доли по формуле (42): 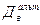 =0,2*(1-0,2) = 0,16. Теперь можно рассчитать среднюю ошибку выборки по формуле (41): =0,2*(1-0,2) = 0,16. Теперь можно рассчитать среднюю ошибку выборки по формуле (41):  = = 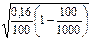 = 0,038 или 3,8%. = 0,038 или 3,8%.
Значения вероятности 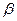 и коэффициента доверия t
имеются в математических таблицах нормального закона распределения вероятностей (если в выборке более 30 единиц), из которых в статистике широко применяются сочетания, приведенные в таблице 4: и коэффициента доверия t
имеются в математических таблицах нормального закона распределения вероятностей (если в выборке более 30 единиц), из которых в статистике широко применяются сочетания, приведенные в таблице 4:
Таблица
4. Значения интеграла вероятностей Лапласа
| 
|
0,683
|
0,866
|
0,950
|
0,954
|
0,988
|
0,997
|
| t
|
1
|
1,5
|
1,96
|
2
|
2,5
|
3
|
В нашей задаче  = 0,950, значит t
= 1,96 (то есть предельная ошибка выборки в 1,96 раза больше средней). Предельная ошибка выборки по формуле (39) будет равна: = 0,950, значит t
= 1,96 (то есть предельная ошибка выборки в 1,96 раза больше средней). Предельная ошибка выборки по формуле (39) будет равна: 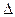 =
1,96*19,64 = 38,494 (у.е.) при определении среднего дохода; =
1,96*19,64 = 38,494 (у.е.) при определении среднего дохода; 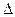 =
1,96*0,038 = 0,075 или 7,5% при определении доли рабочих с доходами более 700 у.е. =
1,96*0,038 = 0,075 или 7,5% при определении доли рабочих с доходами более 700 у.е.
После расчета предельной ошибки находят доверительный интервал
обобщающей характеристики генеральной совокупности по формуле (43) – для средней величины и по формуле (44) – для доли альтернативного признака:
(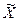 - - ) ) 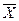  ( (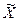 + + ) (
43) (w
- ) (
43) (w
- ) )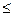 p p 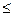 (w
+ (w
+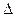 ) (
44) ) (
44)
В нашей задаче по формуле (43): 571-38,494   571+38,494 или 532,506 у.е. 571+38,494 или 532,506 у.е.    609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е. 609,494 у.е., то есть средний доход всех рабочих предприятия с вероятностью 95% будет лежать в пределах от 532,5 до 609,5 у.е.
Аналогично определяем доверительный интервал для доли по формуле (44): 0,2-0,075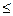 p p
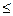 0,2+0,075 или 0,125 0,2+0,075 или 0,125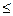 p p
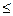 0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%. 0,275, то есть доля рабочих с доходами более 700 у.е. на всем предприятии с вероятностью 95% будет лежать в пределах от 12,5% до 27,5%.
При разработке программы выборочного наблюдения очень часто задается конкретное значение предельной ошибки ( ) и уровень вероятности ( ) и уровень вероятности (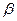 ). Неизвестной остается минимальная численность выборки (n
), обеспечивающая заданную точность. Ее можно получить, если подставить формулу (40) или (41) в формулу (39) и выразить из них n
. В результате получатся формулы для вычисления необходимой численности повторной (45) и бесповторной (46) выборок. ). Неизвестной остается минимальная численность выборки (n
), обеспечивающая заданную точность. Ее можно получить, если подставить формулу (40) или (41) в формулу (39) и выразить из них n
. В результате получатся формулы для вычисления необходимой численности повторной (45) и бесповторной (46) выборок.
n
повт
=
 ; (
45) n
б/повт
=
; (
45) n
б/повт
=
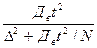 . (
46) . (
46)
В нашей задаче выборка бесповторная, значит, воспользуемся формулой (46), в которую подставим уже рассчитанные дисперсии среднего выборочного дохода рабочих (Дв
= 42859) и доли рабочих с доходами более 700 у.е. (Дв
= 0,16):
n
б/повт
=
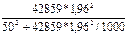 = 62 (чел.), n
б/повт
= = 62 (чел.), n
б/повт
=
 = 197 (чел.). = 197 (чел.).
Таким образом, необходимо включить в выборку не менее 62 рабочих при определении среднего месячного дохода работников предприятия, чтобы не ошибиться более чем на 50 у.е., и не менее 197 рабочих при определении доли рабочих с размером месячного дохода более 700 у.е., чтобы при этом не ошибиться более чем на 5%.
Контрольные задания по теме
Для изучения вкладов населения в коммерческом банке города была проведена 5%-я случайная выборка лицевых счетов, в результате которой получено следующее распределение клиентов по размеру вкладов:
| Размер вклада, у.е.
|
Число вкладчиков, чел.
|
Вариант
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| до 5000
|
10
|
80
|
100
|
50
|
60
|
30
|
90
|
20
|
70
|
40
|
| 5 000 – 15 000
|
40
|
60
|
150
|
30
|
40
|
110
|
75
|
65
|
90
|
80
|
| 15 000 – 30 000
|
25
|
35
|
70
|
90
|
120
|
90
|
130
|
140
|
60
|
95
|
| 30 000 – 50 000
|
30
|
45
|
40
|
5
|
80
|
30
|
60
|
75
|
20
|
115
|
| свыше 50 000
|
15
|
10
|
30
|
25
|
50
|
15
|
25
|
5
|
10
|
5
|
С вероятностью 0,954 определить:
1) средний размер вклада во всем банке;
2) долю вкладчиков во всем банке с размером вклада свыше 15000 у.е.;
3) необходимую численность выборки при определении среднего размера вклада, чтобы не ошибиться более чем на 500 у.е.;
4) необходимую численность выборки при определении доли вкладчиков во всем банке с размером вклада свыше 30 000 у.е., чтобы не ошибиться более чем на 10%.
Тема 4. Ряды динамики
Методические указания по теме
Задача 1
.
Смертность от болезней системы кровообращения в России за период 1995-2004 гг. характеризуется следующим рядом динамики.
| Год
|
1995
|
1996
|
1997
|
1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
2004
|
| Умершие,
тыс. чел.
|
1163,5
|
1113,7
|
1100,3
|
1094,1
|
1187,8
|
1231,4
|
1253,1
|
1308,1
|
1330,5
|
1287,7
|
Вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Проверить ряд на наличие в нем линейного тренда, на основе которого рассчитать интервальный прогноз на 2005 год с вероятностью 95%.
Решение. Любое изменение уровней ряда динамики определяется базисным
(сравнение с первым уровнем) и цепным
(сравнение с предыдущим уровнем) способами. Оно может быть абсолютным
(разность уровней ряда) и относительным
(соотношение уровней).
Базисное абсолютное изменение
представляет собой разность конкретного и первого уровней ряда (47), а цепное абсолютное изменение
представляет собой разность конкретного и предыдущего уровней ряда (48).
 (
47)
(
47) 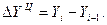 (
48)
(
48)
По знаку абсолютного изменения делается вывод о характере развития явления: при 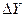 > 0 — рост, при > 0 — рост, при 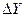 < 0 — спад, при < 0 — спад, при 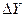 = 0 — стабильность. = 0 — стабильность.
В нашей задаче эти изменения определены в 3-м и 4-м столбцах таблицы 5. Для проверки правильности расчетов применяется правило, согласно которому сумма цепных абсолютных изменений равняется последнему базисному. В нашей задаче это правило выполняется:  =
124,2 и =
124,2 и 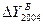 =
124,2. =
124,2.
Базисное относительное изменение
представляет собой соотношение конкретного и первого уровней ряда (49), а цепное относительное изменение
представляет собой соотношение конкретного и предыдущего уровней ряда (50).
 (
49)
(
49) 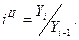 (
50)
(
50)
Относительные изменения уровней — это по существу индексы динамики, критериальным значением которых служит 1. Если они больше ее, имеет место рост явления, меньше ее — спад, а при равенстве единице наблюдается стабильность явления.
В нашей задаче эти изменения определены в 5-м и 6-м столбцах таблицы 5.
Вычитая единицу из относительных изменений, получают темп изменения
уровней, критериальным значением которого служит 0. При положительном темпе изменения имеет место рост явления, при отрицательном — спад, а при нулевом темпе изменения наблюдается стабильность явления. В нашей задаче темпы изменения определены в 7-м и 9-м столбцах таблицы 5, а в 8-м и 10-м сделан вывод о характере развития изучаемого явления. Для проверки правильности расчетов применяется правило, согласно которому произведение цепных относительных изменений равняется последнему базисному. В нашей задаче это правило выполняется: 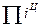 =1,107 и
=1,107 и 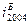 =1,107.
=1,107.
Таблица
5. Вспомогательные расчеты для решения задачи
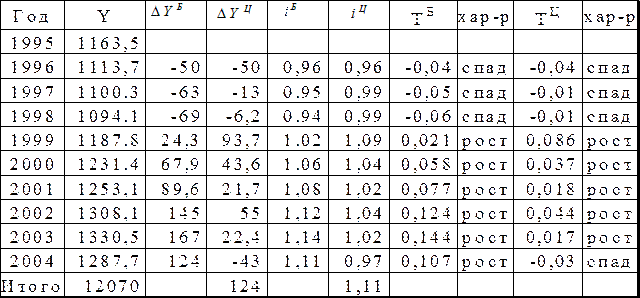
Обобщенной характеристикой ряда динамики является средний уровень ряда
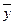 . Способ расчета . Способ расчета 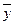 зависит от того, моментный ряд или интервальный (см. рис.3): зависит от того, моментный ряд или интервальный (см. рис.3):

Рис.3. Методы расчета среднего уровня ряда динамики.
В нашей задаче ряд динамики интервальный, значит, применяем формулу средней арифметической простой (17):  = 12070,2 / 10 = 1207,02 (тыс. чел.). То есть за период 1995-2004 в России в среднем за год от болезней системы кровообращения умирало 1207,02 тыс. чел. = 12070,2 / 10 = 1207,02 (тыс. чел.). То есть за период 1995-2004 в России в среднем за год от болезней системы кровообращения умирало 1207,02 тыс. чел.
Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.
Базисное среднее абсолютное изменение
– это частное от деления последнего базисного абсолютного изменения на количество изменений уровней (51). Цепное среднее абсолютное изменение
уровней ряда – это частное от деления суммы всех цепных абсолютных изменений на количество изменений (52).
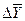 Б
=
Б
=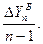 (
51)
(
51)  Ц
= Ц
=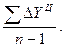 (
52)
(
52)
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность. Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными. В нашей задаче 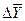 = 124,2/9 = 13,8, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 13,8 тыс. чел. = 124,2/9 = 13,8, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 13,8 тыс. чел.
Наряду со средним абсолютным изменением рассчитывается и среднее относительное. Базисное среднее относительное изменение
определяется по формуле (53), а цепное среднее относительное изменение
– по формуле (54):
 Б
= Б
=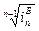 = = 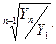 (
53)
(
53) 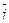 Ц
= Ц
=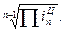 (
54)
(
54)
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. В нашей задаче  =
= 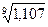 = 1,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет в 1,0114 раза. = 1,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет в 1,0114 раза.
Вычитанием 1 из среднего относительного изменения образуется соответствующий средний
темп изменения
, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашей задаче 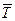 = 1,0114 – 1 = 0,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 1,14%.
= 1,0114 – 1 = 0,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 1,14%.
Проверка ряда динамики на наличие в нем тренда
(тенденции развития ряда) возможна несколькими способами (метод средних, Фостера и Стюарта, Валлиса и Мура и пр.), но наиболее простым является графическая модель, где на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально. Тренд может представлять собой прямую линию, параболу, гиперболу и т.п. В итоге приходим к трендовой модели вида:
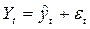 , (
55) , (
55)
где 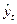 – математическая функция развития; – математическая функция развития; 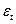 – случайное или циклическое отклонение от функции; t
– время в виде номера периода (уровня ряда). Цель такого метода – выбор теоретической зависимости – случайное или циклическое отклонение от функции; t
– время в виде номера периода (уровня ряда). Цель такого метода – выбор теоретической зависимости 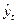 в качестве одной из функций: в качестве одной из функций:
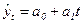 – прямая линия; – прямая линия;  – гипербола; – гипербола; 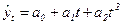 – парабола; – парабола; 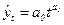 – степенная; – степенная;  – ряд Фурье. – ряд Фурье.
Для выявления тренда
(тенденции развития ряда) в нашей задаче построим график Y
(
t
)
(рис.4):
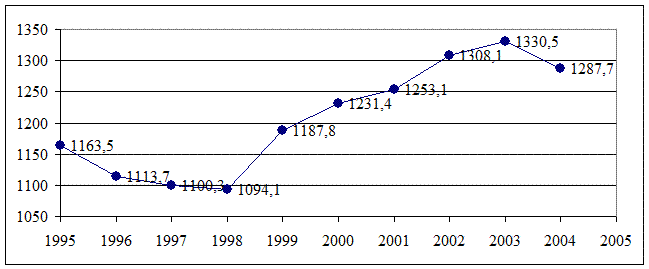
Рис.4. График динамики смертности от болезней системы кровообращения в РФ.
Из данного графика видно, что есть все основания принять уравнение тренда в виде линейной функции.
Определение параметров  в этих функциях может вестись несколькими способами, но самые незначительные отклонения аналитических (теоретических) уровней ( в этих функциях может вестись несколькими способами, но самые незначительные отклонения аналитических (теоретических) уровней (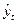 – читается как «игрек, выравненный по t
») от фактических ( – читается как «игрек, выравненный по t
») от фактических ( ) дает метод наименьших квадратов – МНК
. При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней ) дает метод наименьших квадратов – МНК
. При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней 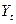 от теоретических уровней от теоретических уровней  : :
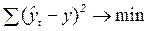 . (
56) . (
56)
В нашей задаче при выравнивании по прямой вида 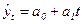 параметры параметры 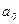 и и  отыскиваются по МНК следующим образом. В формуле (55) вместо отыскиваются по МНК следующим образом. В формуле (55) вместо 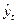 записываем его конкретное выражение записываем его конкретное выражение  . Тогда . Тогда 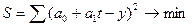 . Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении . Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении  и и 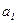 функция двух переменных S
может достигнуть минимума. Как известно, для этого надо найти частные производные S
по функция двух переменных S
может достигнуть минимума. Как известно, для этого надо найти частные производные S
по 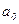 и и  , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными. , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с вышеизложенным найдем частные производные:

Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с y
в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений:
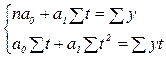 (
57) (
57)
где n
– количество уровней ряда; t
– порядковый номер в условном обозначении периода или момента времени; y
– уровни эмпирического ряда.
Эта система и, соответственно, расчет параметров  и и 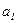 упрощаются, если отсчет времени ведется от середины ряда. Например, при нечетном
числе уровней серединная точка (год, месяц) принимается за нуль. Тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном
числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала: упрощаются, если отсчет времени ведется от середины ряда. Например, при нечетном
числе уровней серединная точка (год, месяц) принимается за нуль. Тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном
числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала: 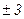 , , 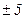 , ,  и т.д. и т.д.
При таком порядке отсчета времени (от середины ряда) 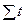 = 0, поэтому, система нормальных уравнений упрощается до следующих двух уравнений, каждое из которых решается самостоятельно: = 0, поэтому, система нормальных уравнений упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
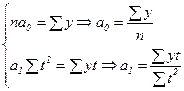 (
58) (
58)
Как видим, при такой нумерации периодов параметр  представляет собой средний уровень ряда. Определим по формуле (58) параметры уравнения прямой, для чего исходные данные и все расчеты необходимых сумм представим в таблице 6. представляет собой средний уровень ряда. Определим по формуле (58) параметры уравнения прямой, для чего исходные данные и все расчеты необходимых сумм представим в таблице 6.
Из таблицы получаем, что  = 12070,2/10 = 1207,02 и = 12070,2/10 = 1207,02 и  = 4195/330 = 12,7121. Отсюда искомое уравнение тренда = 4195/330 = 12,7121. Отсюда искомое уравнение тренда  =1207,02+12,7121
t
. В 6-м столбце таблицы 6 приведены трендовые уровни, рассчитанные по этому уравнению. Для иллюстрации построим график эмпирических (маркеры-кружочки) и трендовых уровней (рис.5).
=1207,02+12,7121
t
. В 6-м столбце таблицы 6 приведены трендовые уровни, рассчитанные по этому уравнению. Для иллюстрации построим график эмпирических (маркеры-кружочки) и трендовых уровней (рис.5).
Рис.5. График эмпирических и трендовых уровней смертности от болезней системы кровообращения в РФ.
По полученной модели для каждого периода (каждой даты) определяются теоретические уровни тренда (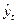 ) и оценивается надежность (адекватность) выбранной модели тренда
. Оценку надежности проводят с помощью критерия Фишера, сравнивая его расчетное значение F
р
с теоретическими значениями F
Т
(приложение 1). При этом расчетный критерий Фишера определяется по формуле: ) и оценивается надежность (адекватность) выбранной модели тренда
. Оценку надежности проводят с помощью критерия Фишера, сравнивая его расчетное значение F
р
с теоретическими значениями F
Т
(приложение 1). При этом расчетный критерий Фишера определяется по формуле:
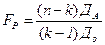 , (
59) , (
59)
где k
– число параметров (членов) выбранного уравнения тренда; ДА
– аналитическая дисперсия, определяемая по формуле (61); До
– остаточная дисперсия (62), определяемая как разность фактической дисперсии ДФ
(60) и аналитической дисперсии:
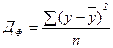 ; (
60) ; (
60)
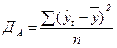 ; (
61) ; (
61)
 . (
62) . (
62)
Сравнение расчетного и теоретического значений критерия Фишера ведется обычно при уровне значимости  с учетом степеней свободы с учетом степеней свободы  и и 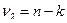 . Уровень значимости . Уровень значимости  связан с вероятностью связан с вероятностью  следующей формулой следующей формулой 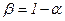 . При условии F
р
>
F
Т
считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд. . При условии F
р
>
F
Т
считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
Таблица
6. Вспомогательные расчеты для решения задачи
| Год
|
y
|
t
|
t
2
|
yt
|

|
(y –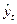 )2 )2
|
(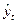 – –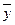 )2 )2
|
(y – 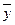 )2 )2
|
| 1995
|
1163,5
|
-9
|
81
|
-10471,5
|
1092,611
|
5025,263
|
13089,44
|
1893,9904
|
| 1996
|
1113,7
|
-7
|
49
|
-7795,9
|
1118,035
|
18,79354
|
7918,3033
|
8708,6224
|
| 1997
|
1100,3
|
-5
|
25
|
-5501,5
|
1143,459
|
1862,733
|
4039,9506
|
11389,1584
|
| 1998
|
1094,1
|
-3
|
9
|
-3282,3
|
1168,884
|
5592,592
|
1454,3822
|
12750,9264
|
| 1999
|
1187,8
|
-1
|
1
|
-1187,8
|
1194,308
|
42,35249
|
161,59803
|
369,4084
|
| 2000
|
1231,4
|
1
|
1
|
1231,4
|
1219,732
|
136,1394
|
161,59803
|
594,3844
|
| 2001
|
1253,1
|
3
|
9
|
3759,3
|
1245,156
|
63,10136
|
1454,3822
|
2123,3664
|
| 2002
|
1308,1
|
5
|
25
|
6540,5
|
1270,581
|
1407,705
|
4039,9506
|
10217,1664
|
| 2003
|
1330,5
|
7
|
49
|
9313,5
|
1296,005
|
1189,915
|
7918,3033
|
15247,3104
|
| 2004
|
1287,7
|
9
|
81
|
11589,3
|
1321,429
|
1137,652
|
13089,44
|
6509,2624
|
| Итого
|
12070,2
|
0
|
330
|
4195
|
12070,2
|
16476,25
|
53327,348
|
69803,596
|
Проверим тренд в нашей задаче на адекватность по формуле (59), для чего в 7-м столбце таблицы 6 рассчитан числитель остаточной дисперсии, а в 8-м столбце – числитель аналитической дисперсии. В формуле (59) можно использовать их числители, так как оба они делятся на число уровней n
(n
сократятся): F
Р
= 53327,348*8/(16476,25*1) = 25,893 > F
Т
, значит, модель адекватна и ее можно использовать для прогнозирования (F
Т
= 5,32 находим по приложению 1 в 1-ом столбце [ = k
– 1
= 1] и 8-й строке [ = k
– 1
= 1] и 8-й строке [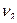 = n
–
k
= 8]). = n
–
k
= 8]).
При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза
. Границы интервалов определяются по формуле (63):
 , (
63) , (
63)
где 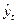 – точечный прогноз, рассчитанный по модели тренда; – точечный прогноз, рассчитанный по модели тренда;  – коэффициент доверия по распределению Стьюдента
при уровне значимости – коэффициент доверия по распределению Стьюдента
при уровне значимости  и числе степеней свободы и числе степеней свободы 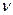 =
n
–1
(приложение 2); =
n
–1
(приложение 2); 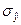 – ошибка аппроксимации
, определяемая по формуле (64): – ошибка аппроксимации
, определяемая по формуле (64):
 , (
64) , (
64)
где 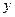 и и 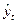 – соответственно фактические и теоретические (трендовые) значения уровней ряда динамики; n
– число уровней ряда; k
– число параметров (членов) в уравнении тренда. – соответственно фактические и теоретические (трендовые) значения уровней ряда динамики; n
– число уровней ряда; k
– число параметров (членов) в уравнении тренда.
Определим доверительный интервал в нашей задаче на 2005 год с уровнем значимости  = (1–0,95) = 0,05. Для этого найдем ошибку аппроксимации по формуле (64): = (1–0,95) = 0,05. Для этого найдем ошибку аппроксимации по формуле (64): 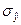 = =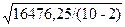 = 45,38. Коэффициент доверия по распределению Стьюдента = 45,38. Коэффициент доверия по распределению Стьюдента  = 2,2622 при = 2,2622 при  =
10 – 1=9. =
10 – 1=9.
Прогноз на 2005 с вероятностью 95% осуществим по формуле (63):
Y
2005
=
(1207,02+12,7121*11) 2,2622*45,38 или 1244,19<Y
2005
<1449,51 (тыс.чел.). 2,2622*45,38 или 1244,19<Y
2005
<1449,51 (тыс.чел.).
Контрольные задания по теме
По статистическим данным по России за 2000 – 2005 гг. вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Проверить ряд на наличие в нем линейного тренда, на основе которого рассчитать интервальный прогноз на 2006 год с вероятностью 95%.
| Год
|
Вариант
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Валовой сбор сахарной свеклы, млн.т.
|
Валовой сбор картофеля, млн.т.
|
Число заключенных браков, тыс.
|
Число построенных жилых домов, млн.м2
|
Поголовье крупного рогатого скота, млн.голов (на конец года)
|
Производство мяса, млн.т.
|
Производство яиц, млрд.шт.
|
Численность населения, тыс.чел. (на начало года)
|
Среднегодовая численность занятых в экономике, тыс.чел.
|
Доля расходов на оплату ЖКХ в бюджете домохозяйств, %
|
| 2000
|
14,1
|
34
|
897,3
|
30,3
|
16,5
|
4,4
|
34,1
|
146890
|
64327
|
4,6
|
| 2001
|
14,6
|
35
|
1001,6
|
31,7
|
15,8
|
4,5
|
35,2
|
146304
|
64710
|
5,2
|
| 2002
|
15,7
|
32,9
|
1019,8
|
33,8
|
15,0
|
4,7
|
36,3
|
145649
|
65359
|
6,2
|
| 2003
|
19,4
|
36,7
|
1091,8
|
36,4
|
13,5
|
4,9
|
36,5
|
144964
|
65666
|
7,2
|
| 2004
|
21,8
|
35,9
|
979,7
|
41,0
|
12,1
|
5,0
|
35,8
|
144168
|
66407
|
7,7
|
| 2005
|
21,4
|
37,3
|
1066,4
|
43,6
|
11,1
|
4,9
|
36,8
|
143474
|
66939
|
8,3
|
Тема 5. Индексы
Методические указания по теме
Задача 1
.
Имеются следующие данные о продажах торговой точкой двух видов товара:
| Товар
|
Цена за кг, руб.
|
Объем продаж, тыс. кг
|
| Январь
|
Февраль
|
Январь
|
Февраль
|
| Апельсины
|
20
|
18
|
100
|
160
|
| Бананы
|
22
|
25
|
150
|
120
|
Определить: 1) индивидуальные индексы цен, физического объема и выручки; 2) общие индексы цен, физического объема и выручки; 3) абсолютное изменение выручки за счет изменений цен, структурного сдвига и объемов продаж (для каждого фактора в отдельности) по всей продукции и по каждому товару в отдельности. По итогам расчетов сделать аргументированные выводы.
Решение. В основе решения задачи лежит формула (65):
Q
=
pq
,
(
65)
где p
– цена товара, q
– физический объем (количество), Q
– выручка (товарооборот).
Применив формулу (65) к нашей задаче, рассчитаем выручку по каждому товару в январе (Q
0
j
) и феврале (Q
1
j
) в таблице 7.
Таблица
7. Расчет выручки и ее изменения по каждому товару
| Товар
j
|
Январь
Q
0
j
|
Февраль
Q
1
j
|
Изменение выручки
∆
Qj
=
Q
1
j
–
Q
0
j
|
| Апельсины
|
20*100 = 2000
|
18*160 = 2880
|
880
|
| Бананы
|
22*150 = 3300
|
25*120 = 3000
|
-300
|
| Итого
|
5300
|
5880
|
580
|
Из таблицы видно, что абсолютное изменение общей выручки составило:
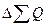 = ∑
Q
1
–∑
Q
0
= 5880-5300 = 580 тыс. руб., то есть она выросла на 580 тыс. руб. = ∑
Q
1
–∑
Q
0
= 5880-5300 = 580 тыс. руб., то есть она выросла на 580 тыс. руб.
Общий индекс изменения выручки равняется:
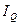 = ∑
Q
1
/∑
Q
0
= 5880/5300 = 1,1094, то есть выручка от продажи фруктов увеличилась в 1,1094 раза или на 10,94% в феврале по сравнению с январем. = ∑
Q
1
/∑
Q
0
= 5880/5300 = 1,1094, то есть выручка от продажи фруктов увеличилась в 1,1094 раза или на 10,94% в феврале по сравнению с январем.
Определим индивидуальные индексы цен (ip
), физического объема (iq
), выручки (iQ
) и доли товара (id
) по формуле (2), используя в качестве Xi
цены (p
), физический объем (q
), выручки (Q
) и доли товара (d
=
q
/∑
q
) каждого вида фруктов соответственно. Результаты расчетов представим в таблице 8.
Таблица
8. Расчет индивидуальных индексов
| Индивидуальный индекс
|
апельсины
|
бананы
|
| количества iq
|
160/100 = 1,6
|
120/150 = 0,8
|
| отпускных цен ip
|
18/20 = 0,9
|
25/22 = 1,136
|
| выручки iQ
|
2880/2000=1,44
|
3000/3300=0,909
|
| доли товара id
|
(160/280)/(100/250) = 1,429
|
(120/280)/(150/250) = 0,714
|
Правильность выполненных расчетов проверяется следующим образом:
1) общее изменение выручки должно равняться сумме ее частных (по каждому товару в отдельности) изменений: 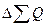 = 880+(-300) = 580 (тыс. руб.); = 880+(-300) = 580 (тыс. руб.);
2) произведение факторных индивидуальных индексов по периодам должно равняться соответствующему индивидуальному индексу выручки: iQ
А
=1,6*0,9 =1,44; iQ
Б
= 0,8*1,136 = 0,909.
Из таблицы видно, что в феврале по сравнению с январем:
– количество проданных апельсинов увеличилось в 1,6 раза или на 60%, а бананов – уменьшилось в 0,8 раза или на 20%;
– цена апельсинов понизилась в 0,9 раза или на 10%, а бананов – повысилась в 1,136 раза или на 13,6%;
– выручка по апельсинам выросла в 1,44 раза или на 44%, а по бананам – снизилась в 0,909 раза или на 9,1%;
– доля проданных апельсинов увеличилась в 1,429 раза или на 42,9%, а бананов – уменьшилась в 0,714 раза или на 28,6%.
Агрегатный общий индекс физического объема Ласпейреса определяется по формуле (66):
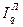 = =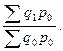 (
66)
(
66)
В нашей задаче 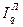 = =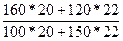 = 5840/5300 = 1,10189, то есть количество проданных фруктов в базисных (январских) ценах выросло в 1,10189 раза или на 10,189% в феврале по сравнению с январем. = 5840/5300 = 1,10189, то есть количество проданных фруктов в базисных (январских) ценах выросло в 1,10189 раза или на 10,189% в феврале по сравнению с январем.
Агрегатный общий индекс цен Пааше рассчитывается по формуле (67):
 = =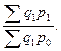 (
67)
(
67)
В нашей задаче  = =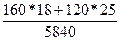 = 5880/5840 = 1,00685, то есть цена проданных фруктов при объемах продаж отчетного (февральского) периода выросла в 1,00685 раза или на 0,685% в феврале по сравнению с январем. = 5880/5840 = 1,00685, то есть цена проданных фруктов при объемах продаж отчетного (февральского) периода выросла в 1,00685 раза или на 0,685% в феврале по сравнению с январем.
Контроль осуществляется по формуле: IQ
=
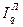  = 1,10189*1,00685 = 1,1094. = 1,10189*1,00685 = 1,1094.
Агрегатный общий индекс цен Ласпейреса вычисляется по формуле (68):
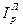 = =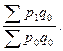 (
68)
(
68)
В нашей задаче 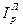 = =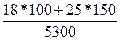 = 5550/5300 = 1,04717, то есть цена проданных фруктов при объемах продаж базисного (январского) периода выросла в 1,04717 раза или на 4,717% в феврале по сравнению с январем. = 5550/5300 = 1,04717, то есть цена проданных фруктов при объемах продаж базисного (январского) периода выросла в 1,04717 раза или на 4,717% в феврале по сравнению с январем.
Агрегатный общий количественный индекс Пааше рассчитывается по формуле (69):
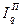 = = (
69)
(
69)
В нашей задаче 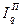 = 5880/5550 =1,05946, то есть количество проданных фруктов в отчетных (февральских) ценах выросло в 1,05946 раза или на 5,946% в феврале по сравнению с январем. = 5880/5550 =1,05946, то есть количество проданных фруктов в отчетных (февральских) ценах выросло в 1,05946 раза или на 5,946% в феврале по сравнению с январем.
Контроль осуществляется по формуле: IQ
=
  =
1,04717*1,05946 =1,1094. =
1,04717*1,05946 =1,1094.
Средняя геометрическая величина определяется из индексов Ласпейреса и Пааше (по методике Фишера) по формуле (70) для количества товаров и по формуле (71) – для цен:
 = = (
70)
(
70)  = = (
71)
(
71)
В нашей задаче 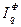 = = =1,0805, то есть в среднем количество проданных фруктов выросло в 1,0805 раза или на 8,05%; =1,0805, то есть в среднем количество проданных фруктов выросло в 1,0805 раза или на 8,05%; 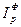 = =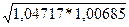 =1,0268, то есть в среднем цена проданных фруктов выросла в 1,0268 раза или на 2,68%. =1,0268, то есть в среднем цена проданных фруктов выросла в 1,0268 раза или на 2,68%.
Далее выполняется факторный анализ общей выручки. В его основе лежит следующая трехфакторная мультипликативная модель выручки:
IQ
= 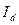 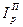 , (
72) , (
72)
где  = = , ,
 – индекс структурных сдвигов, показывающий как изменилась выручка под влиянием фактора изменения долей проданных фруктов в отчетном периоде по сравнению с базисным периодом. Он определяется по формуле (73): – индекс структурных сдвигов, показывающий как изменилась выручка под влиянием фактора изменения долей проданных фруктов в отчетном периоде по сравнению с базисным периодом. Он определяется по формуле (73):
 = = = =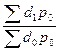 . (
73) . (
73)
В нашей задаче  = =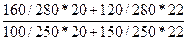 = 0,9838, то есть структурный сдвиг должен был уменьшить отчетную выручку в базисных ценах в 0,9838 раза или на 1,62%. = 0,9838, то есть структурный сдвиг должен был уменьшить отчетную выручку в базисных ценах в 0,9838 раза или на 1,62%.
Тогда изменение выручки за счет изменения общего количества фруктов определяется по формуле (74):
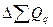 = =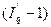  . (
74) . (
74)
В нашей задаче  = (1,12-1)*5300 = 636 (тыс. руб.), то есть изменение количества проданных фруктов увеличило выручку на 636 тыс. руб. = (1,12-1)*5300 = 636 (тыс. руб.), то есть изменение количества проданных фруктов увеличило выручку на 636 тыс. руб.
Изменение общей выручки за счет структурных сдвигов находится по формуле (75):
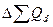 = =   .
(
75) .
(
75)
В нашей задаче 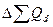 = 1,12*(0,9838-1)*5300 = –96 (тыс. руб.), то есть структурный сдвиг в количестве проданных фруктов уменьшил выручку на 96 тыс. руб. = 1,12*(0,9838-1)*5300 = –96 (тыс. руб.), то есть структурный сдвиг в количестве проданных фруктов уменьшил выручку на 96 тыс. руб.
Изменение общей выручки за счет изменения отпускных цен рассчитывается по формуле (76):
 = =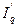 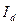 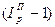  .
(
76) .
(
76)
В нашей задаче  =1,12*0,9838*(1,00685-1)*5300 = 40 (тыс. руб.), то есть изменение цен на фрукты увеличило выручку на 40 тыс. руб. =1,12*0,9838*(1,00685-1)*5300 = 40 (тыс. руб.), то есть изменение цен на фрукты увеличило выручку на 40 тыс. руб.
Контроль правильности расчетов производится по формуле (77), согласно которой общее изменение выручки равно сумме ее изменений за счет каждого фактора в отдельности.
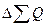 = =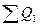 - - = =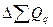 + +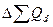 + + . (
77)
. (
77)
В нашей задаче 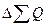 = 636 + (–96) + 40 = 580 тыс. руб. = 636 + (–96) + 40 = 580 тыс. руб.
Результаты факторного анализа общей выручки заносятся в последнюю строку факторной таблицы 9.
Таблица
9. Результаты факторного анализа выручки
| Товар
j
|
Изменение выручки,
тыс. руб.
|
В том числе за счет
|
| количества продукта
|
структурных сдвигов
|
отпускных цен
|
| А
|
880
|
240
|
960
|
–320
|
| Б
|
-300
|
396
|
–1056
|
360
|
| Итого
|
580
|
636
|
–96
|
40
|
Наконец, ведется факторный анализ изменения частной (по каждому j
-му товару в отдельности) выручки на основе следующей трехфакторной мультипликативной модели:
 = = 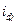 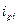  . (78)
. (78)
Тогда изменение частной выручки за счет каждого из 3-х факторов (количество, структурный сдвиг и цена) по j
-му виду товара определяется соответственно по формулам (79) – (81).
 = =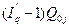 ; (
79) ; (
79)
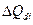 = = ; (
80) ; (
80)
 = = . (
81) . (
81)
Так, по апельсинам изменение выручки за счет первого фактора (изменения общего количества проданных фруктов) по формуле (79) равно:
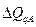 =(1,12-1)*2000 = 240 (тыс. руб.). =(1,12-1)*2000 = 240 (тыс. руб.).
Аналогично по бананам: 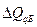 = (1,12-1)*3300 = 396 (тыс. руб.) = (1,12-1)*3300 = 396 (тыс. руб.)
Контроль правильности расчетов:
 = =  , то есть 240 + 396 = 636 (тыс. руб.). , то есть 240 + 396 = 636 (тыс. руб.).
Так, по апельсинам изменение выручки за счет второго фактора (структурных сдвигов в количестве проданных фруктов) по формуле (80) равно:
 =1,12*(1,429-1)*2000 = 960 (тыс. руб.). =1,12*(1,429-1)*2000 = 960 (тыс. руб.).
Аналогично по бананам:  =1,12*(0,714-1)*3300 = –1056 (тыс. руб.). =1,12*(0,714-1)*3300 = –1056 (тыс. руб.).
Контроль правильности расчетов:
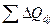 = =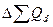 , то есть 960 + (–1056) = –96 (тыс. руб.). , то есть 960 + (–1056) = –96 (тыс. руб.).
И, наконец, по апельсинам изменение выручки за счет 3-го фактора (изменения отпускной цены) по формуле (81) равно:
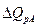 =1,12*1,429*(0,9-1)*2000 = –320 (тыс. руб.). =1,12*1,429*(0,9-1)*2000 = –320 (тыс. руб.).
Аналогично по бананам: 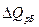 =1,12*0,714*(1,136-1)*3300 = 360 (тыс. руб.). =1,12*0,714*(1,136-1)*3300 = 360 (тыс. руб.).
Контроль правильности расчетов:
 = =  , то есть (–320) + 360= 40 (тыс. руб.) , то есть (–320) + 360= 40 (тыс. руб.)
Результаты факторного анализа частной выручки также заносятся в таблицу 9, в которой все числа оказались взаимно согласованными.
Контрольные задания по теме
Имеются следующие данные о продажах минимаркетом 3-х видов товаров (A, B и C):
| Товар
|
Цена за единицу продукта, руб.
|
Объем продаж, тыс. штук
|
| 1 квартал
|
2 квартал
|
1 квартал
|
2 квартал
|
| 1 вариант
|
| А
|
102
|
105
|
205
|
195
|
| В
|
56
|
51
|
380
|
423
|
| С
|
26
|
30
|
510
|
490
|
| 2 вариант
|
| А
|
112
|
109
|
202
|
260
|
| В
|
51
|
48
|
365
|
420
|
| С
|
22
|
26
|
477
|
316
|
| 3 вариант
|
| А
|
99
|
103
|
198
|
182
|
| В
|
55
|
59
|
370
|
361
|
| С
|
20
|
18
|
502
|
456
|
| 4 вариант
|
| А
|
99
|
109
|
188
|
182
|
| В
|
55
|
56
|
380
|
385
|
| С
|
20
|
21
|
508
|
444
|
| 5 вариант
|
| А
|
120
|
110
|
170
|
220
|
| В
|
60
|
58
|
350
|
390
|
| С
|
19
|
20
|
550
|
490
|
| Товар
|
Цена за единицу продукта, руб.
|
Объем продаж, тыс. штук
|
| 1 квартал
|
2 квартал
|
1 квартал
|
2 квартал
|
| 6 вариант
|
| А
|
130
|
125
|
138
|
198
|
| В
|
50
|
56
|
339
|
264
|
| С
|
20
|
21
|
613
|
511
|
| 7 вариант
|
| А
|
107
|
110
|
220
|
189
|
| В
|
46
|
44
|
490
|
550
|
| С
|
18
|
20
|
720
|
680
|
| 8 вариант
|
| А
|
95
|
98
|
264
|
197
|
| В
|
48
|
50
|
360
|
294
|
| С
|
26
|
25
|
448
|
640
|
| 9 вариант
|
| А
|
89
|
92
|
360
|
294
|
| В
|
58
|
56
|
410
|
482
|
| С
|
24
|
25
|
558
|
593
|
| 10 вариант
|
| А
|
120
|
125
|
150
|
108
|
| В
|
44
|
46
|
513
|
461
|
| С
|
16
|
19
|
891
|
550
|
Определить:
1. Индивидуальные индексы цен, физического объема и товарооборота;
2. Общие индексы цен, физического объема и товарооборота;
3. Абсолютные приросты товарооборота за счет изменений цен, структурного сдвига и объемов продаж (для каждого фактора в отдельности) по всей продукции и по каждому товару в отдельности.
По итогам расчетов сделать аргументированные выводы.
Тема 6. Статистическое изучение взаимосвязей
Методические указания по теме
Задача 1
.
По условным данным таблицы 10 о стоимости основных фондов х
и валовом выпуске продукции у
(в порядке возрастания стоимости основных фондов) выявить наличие и характер корреляционной связи между признаками x
и y
.
Таблица
10. Стоимость основных фондов и валовой выпуск по 10 однотипным предприятиям
| Предприятия
i
|
Основные производственные
фонды, млн. руб.
xi
|
Валовой выпуск
продукции, млн. руб.
yi
|
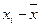
|

|
| 1
2
3
4
5
6
7
8
9
10
|
12
16
25
38
43
55
60
80
91
100
|
28
40
38
65
80
101
95
125
183
245
|
–
–
–
–
–
+
+
+
+
+
|
–
–
–
–
–
+
–
+
+
+
|
| Итого
|
520
|
1000
|
Решение. Для выявления наличия и характера корреляционной связи между двумя признаками в статистике используется ряд
методов
.
 1. Графический метод
,
когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n
взаимосвязанных пар значений x
и y
и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x
и y
. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии
(см. рисунок справа). Анализируя эту линию, визуально можно определить характер зависимости между признаками x
и y
. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции. 1. Графический метод
,
когда корреляционную зависимость для наглядности можно изобразить графически. Для этого, имея n
взаимосвязанных пар значений x
и y
и пользуясь прямоугольной системой координат, каждую такую пару изображают в виде точки на плоскости с координатами x
и y
. Соединяя последовательно нанесенные точки, получают ломаную линию, именуемую эмпирической линией регрессии
(см. рисунок справа). Анализируя эту линию, визуально можно определить характер зависимости между признаками x
и y
. В нашей задаче эта линия похожа на восходящую прямую, что позволяет выдвинуть гипотезу о наличии прямой зависимости между величиной основных фондов и валовым выпуском продукции.
2. Рассмотрение параллельных данных
(значений x
и y
в каждой из n
единиц). Единицы наблюдения располагают по возрастанию значений факторного признака х
и затем сравнивают с ним (визуально) поведение результативного признака у
. В нашей задаче в большинстве случаев по мере увеличения значений x
увеличиваются и значения y
(за несколькими исключениями – 2 и 3, 6 и 7 предприятия), поэтому, можно говорить о прямой связи между х
и у
(этот вывод подтверждает и эмпирическая линия регрессии). Теперь необходимо ее измерить, для чего рассчитывают несколько коэффициентов.
3. Коэффициент корреляции знаков (Фехнера
)
– простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений каждого признака (x
и y
) от своей средней величины. При этом во внимание принимаются не величины отклонений (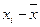 ) и ( ) и ( ), а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С
) и несовпадений (Н
). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц: ), а их знаки («+» или «–»). Определив знаки отклонений от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений (С
) и несовпадений (Н
). Тогда коэффициент Фехнера рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:
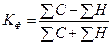 . (82) . (82)
Очевидно, что если знаки всех отклонений по каждому признаку совпадут, то КФ
=
1, что характеризует наличие прямой связи. Если все знаки не совпадут, то КФ
=–
1 (обратная связь). Если же å
С=
å
Н
, то КФ
=
0. Итак, как и любой показатель тесноты связи, коэффициент Фехнера может принимать значения от 0 до  1. Однако, если КФ
=
1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х
и у
. 1. Однако, если КФ
=
1, то это ни в коей мере нельзя воспринимать как свидетельство функциональной зависимости между х
и у
.
В нашей задаче  ; ; 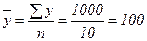 . .
В двух последних столбцах таблицы 10 приведены знаки отклонений каждого х
и у
от своей средней величины. Число совпадений знаков – 9, а несовпадений – 1. Отсюда КФ
= =0,8
. Обычно такое значение показателя тесноты связи характеризует сильную зависимость, однако, следует иметь в виду, что поскольку КФ
зависит только от знаков и не учитывает величину самих отклонений х
и у
от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление. =0,8
. Обычно такое значение показателя тесноты связи характеризует сильную зависимость, однако, следует иметь в виду, что поскольку КФ
зависит только от знаков и не учитывает величину самих отклонений х
и у
от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление.
4.
Линейный коэффициент корреляции
применяется в случае линейной зависимости между двумя количественными признаками x
и y
. В отличие от КФ
в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t
:
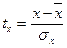 и и 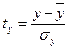 . .
Линейный коэффициент корреляции r
представляет собой среднюю величину из произведений нормированных отклонений для x
и у
:
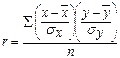 , (
83) или , (
83) или  . (
84) . (
84)
Числитель формулы (84), деленный на n
, т.е. 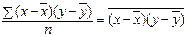 , представляет собой среднее произведение отклонений значений двух признаков от их средних значений, именуемое ковариацией
. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х
и у
на произведение их средних квадратических отклонений. Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции, например: , представляет собой среднее произведение отклонений значений двух признаков от их средних значений, именуемое ковариацией
. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х
и у
на произведение их средних квадратических отклонений. Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции, например:
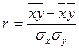 . (
85) . (
85)
Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения. Например, если 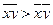 , то r
по формуле (85) будет положительным, что характеризует прямую зависимость между х
и у
, в противном случае (r
<
0) – обратную связь. Если , то r
по формуле (85) будет положительным, что характеризует прямую зависимость между х
и у
, в противном случае (r
<
0) – обратную связь. Если 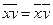 , то r
=
0, что означает отсутствие линейной зависимости между х
и у
, а при r
=
1 – функциональная зависимость между х
и у
. Следовательно, всякое промежуточное значение r
от 0 до 1 характеризует степень приближения корреляционной связи между х
и у
к функциональной. Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х
и у
к линейной. Поэтому близость значения r
к 0 в одних случаях может означать отсутствие связи между х
и у
, а в других свидетельствовать о том, что зависимость не линейная. , то r
=
0, что означает отсутствие линейной зависимости между х
и у
, а при r
=
1 – функциональная зависимость между х
и у
. Следовательно, всякое промежуточное значение r
от 0 до 1 характеризует степень приближения корреляционной связи между х
и у
к функциональной. Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х
и у
к линейной. Поэтому близость значения r
к 0 в одних случаях может означать отсутствие связи между х
и у
, а в других свидетельствовать о том, что зависимость не линейная.
В нашей задаче для расчета r
построим вспомогательную таблицу 11.
Таблица
11. Вспомогательные расчеты линейного коэффициента корреляции
| i
|
xi
|
yi
|
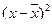
|
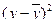
|
tx
|
ty
|
tx
ty
|

|

|
| 1
|
12
|
28
|
1600
|
5184
|
-1,36526
|
-1,10032
|
1,502223
|
288
|
33,6
|
| 2
|
16
|
40
|
1296
|
3600
|
-1,22873
|
-0,91693
|
1,126667
|
216
|
64
|
| 3
|
25
|
38
|
729
|
3844
|
-0,92155
|
-0,9475
|
0,873167
|
167,4
|
95
|
| 4
|
38
|
65
|
196
|
1225
|
-0,47784
|
-0,53488
|
0,255587
|
49
|
247
|
| 5
|
43
|
80
|
81
|
400
|
-0,30718
|
-0,30564
|
0,093889
|
18
|
344
|
| 6
|
55
|
101
|
9
|
1
|
0,102394
|
0,015282
|
0,001565
|
0,3
|
555,5
|
| 7
|
60
|
95
|
64
|
25
|
0,273052
|
-0,07641
|
-0,02086
|
-4
|
570
|
| 8
|
80
|
125
|
784
|
625
|
0,955681
|
0,382056
|
0,365124
|
70
|
1000
|
| 9
|
91
|
183
|
1521
|
6889
|
1,331128
|
1,268425
|
1,688436
|
323,7
|
1665,3
|
| 10
|
100
|
245
|
2304
|
21025
|
1,638311
|
2,215924
|
3,630373
|
696
|
2450
|
| Итого
|
520
|
1000
|
8584
|
42818
|
9,516166
|
1824,4
|
7024,4
|
В нашей задаче: 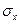 = = 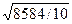 =29,299; =29,299;  = = =65,436. Тогда по формуле (83) r
= 9,516166/10 = 0,9516. Аналогичный результат получаем по формуле (84): r
= 1824,4/(29,299*65,436) = 0,9516 или по формуле (85): r
= (7024,4 – 52*100) / (29,299*65,436) = 0,9516, то есть связь между величиной основных фондов и валовым выпуском продукции очень близка к функциональной. =65,436. Тогда по формуле (83) r
= 9,516166/10 = 0,9516. Аналогичный результат получаем по формуле (84): r
= 1824,4/(29,299*65,436) = 0,9516 или по формуле (85): r
= (7024,4 – 52*100) / (29,299*65,436) = 0,9516, то есть связь между величиной основных фондов и валовым выпуском продукции очень близка к функциональной.
Проверка коэффициента корреляции на значимость (существенность).
Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x
и y
, на основе которых он рассчитан. Другими словами, как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями. Для того, чтобы оценить существенность (значимость) самого r
и, соответственно, реальность измеряемой связи между х
и у
, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции σ
r
. Оценка существенности (значимости) r
основана на сопоставлении значения r
с его средней квадратической ошибкой:  . .
Существуют некоторые особенности расчета σ
r
в зависимости от числа наблюдений (объема выборки) – n
.
1. Если число наблюдений достаточно велико (n
>30), то σ
r
рассчитывается по формуле (86):
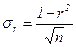 . (
86) . (
86)
Обычно, если  >3, то r
считается значимым (существенным), а связь – реальной. Задавшись определенной вероятностью, можно определить доверительные пределы (границы)
r
=
( >3, то r
считается значимым (существенным), а связь – реальной. Задавшись определенной вероятностью, можно определить доверительные пределы (границы)
r
=
( ), где t
– коэффициент доверия, рассчитываемый по интегралу Лапласа (см. таблицу 4). ), где t
– коэффициент доверия, рассчитываемый по интегралу Лапласа (см. таблицу 4).
2. Если число наблюдений небольшое (n
<30), то σ
r
рассчитывается по формуле (87):
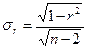 ,
(
87) ,
(
87)
а значимость r
проверяется на основе t
-
критерия Стьюдента, для чего определяется расчетное значение критерия по формуле (88) и сопоставляется c t
ТАБЛ
.
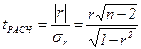 . (
88) . (
88)
Табличное значение t
ТАБЛ
находится по таблице распределения t
-критерия Стьюдента (см. приложение 2) при уровне значимости α=1-β
и числе степеней свободы ν=
n
–2
. Если t
РАСЧ
>
t
ТАБЛ
,
то r
считается значимым, а связь между х
и у
– реальной. В противном случае (t
РАСЧ
<
t
ТАБЛ
) считается, что связь между х
и у
отсутствует, и значение r
, отличное от нуля, получено случайно.
В нашей задаче число наблюдений небольшое, значит, оценивать существенность (значимость) линейного коэффициента корреляции будем по формулам (87) и (88): 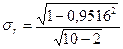 = 0,3073/2,8284 = 0,1086; = 0,3073/2,8284 = 0,1086; 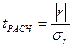 = 0,9516/0,1086 = 8,7591. При вероятности 95% t
табл
=
2,306, а при вероятности 99% t
табл
=
3,355, значит, t
РАСЧ
>
t
ТАБЛ
, что дает возможность считать линейный коэффициент корреляции r
= 0,9516 значимым. = 0,9516/0,1086 = 8,7591. При вероятности 95% t
табл
=
2,306, а при вероятности 99% t
табл
=
3,355, значит, t
РАСЧ
>
t
ТАБЛ
, что дает возможность считать линейный коэффициент корреляции r
= 0,9516 значимым.
5.
Подбор уравнения регрессии
представляет собой математическое описание изменения взаимно коррелируемых величин по эмпирическим (фактическим) данным. Уравнение регрессии должно определить, каким будет среднее значение результативного признака у
при том или ином значении факторного признака х,
если остальные факторы, влияющие на у
и не связанные с х,
не учитывать, т.е. абстрагироваться от них. Другими словами, уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь величины результативного признака у
со значениями факторного признака х.
Уравнение регрессии можно также назвать теоретической линией регрессии.
Рассчитанные по уравнению регрессии значения результативного признака называются теоретическими
. Они обычно обозначаются  (читается: «игрек, выравненный по х»)
и рассматриваются как функция от х
, т.е. (читается: «игрек, выравненный по х»)
и рассматриваются как функция от х
, т.е. 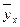 =
f
(
x
).
(Иногда для простоты записи вместо =
f
(
x
).
(Иногда для простоты записи вместо 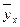 пишут пишут 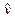 .
) .
)
Найти в каждом конкретном случае тип функции, с помощью которой можно наиболее адекватно отразить ту или иную зависимость между признаками х
и у, —
одна из основных задач регрессионного анализа. Выбор теоретической линии регрессии часто обусловлен формой эмпирической линии регрессии; теоретическая линия как бы сглаживает изломы эмпирической линии регрессии. Кроме того, необходимо учитывать природу изучаемых показателей и специфику их взаимосвязей.
Для аналитической связи между х
и у
могут использоваться следующие простые виды уравнений:
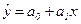 – прямая линия; – прямая линия;  – парабола; – парабола;
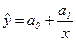 – гипербола; – гипербола;  – показательная функция; – показательная функция;
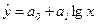 – логарифмическая функция и др. – логарифмическая функция и др.
Обычно зависимость, выражаемую уравнением прямой, называют линейной
(или прямолинейной),
а все остальные — криволинейными зависимостями
.
Выбрав тип функции, по эмпирическим данным определяют параметры уравнения. При этом отыскиваемые параметры должны быть такими, при которых рассчитанные по уравнению теоретические значения результативного признака  были бы максимально близки к эмпирическим данным. были бы максимально близки к эмпирическим данным.
Существует несколько методов нахождения параметров уравнения регрессии. Наиболее часто используется метод наименьших квадратов
(МНК). Его суть заключается в следующем требовании: искомые теоретические значения результативного признака  должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е. должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е.
 . .
Поставив данное условие, легко определить, при каких значениях 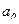 , , 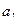 и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в методических указаниях к теме 4 «Ряды динамики», поэтому, воспользуемся формулой (57) для нахождения параметров теоретической линии регрессии в нашей задаче, заменив параметр t
на x
. и т.д. для каждой аналитической кривой эта сумма квадратов отклонений будет минимальной. Данный метод уже использовался нами в методических указаниях к теме 4 «Ряды динамики», поэтому, воспользуемся формулой (57) для нахождения параметров теоретической линии регрессии в нашей задаче, заменив параметр t
на x
.
 (
89) (
89)
Исходные данные и все расчеты необходимых сумм представим в таблице 12.
Таблица
12. Вспомогательные расчеты для решения задачи
| i
|
x
|
y
|
x*x
|
y*x
|
y'
|

|
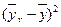
|
| 1
|
12
|
28
|
144
|
336
|
15
|
5184
|
7225
|
| 2
|
16
|
40
|
256
|
640
|
23,5
|
3600
|
5852,25
|
| 3
|
25
|
38
|
625
|
950
|
42,625
|
3844
|
3291,891
|
| 4
|
38
|
65
|
1444
|
2470
|
70,25
|
1225
|
885,0625
|
| 5
|
43
|
80
|
1849
|
3440
|
80,875
|
400
|
365,7656
|
| 6
|
55
|
101
|
3025
|
5555
|
106,375
|
1
|
40,64063
|
| 7
|
60
|
95
|
3600
|
5700
|
117
|
25
|
289
|
| 8
|
80
|
125
|
6400
|
10000
|
159,5
|
625
|
3540,25
|
| 9
|
91
|
183
|
8281
|
16653
|
182,875
|
6889
|
6868,266
|
| 10
|
100
|
245
|
10000
|
24500
|
202
|
21025
|
10404
|
| Итого
|
520
|
1000
|
35624
|
70244
|
1000
|
42818
|
38762,125
|
 ; ; 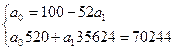 ; ; 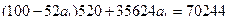 ; ;
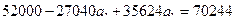 ; ; 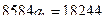 ; ; 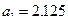 ; ;  =100–52*2,125 = – 10,5. =100–52*2,125 = – 10,5.
Отсюда искомая линия регрессии: =–10,5+2,125
x
. Для иллюстрации построим график эмпирической (маркеры-кружочки) и теоретической (маркеры-квадратики) линий регрессии.
=–10,5+2,125
x
. Для иллюстрации построим график эмпирической (маркеры-кружочки) и теоретической (маркеры-квадратики) линий регрессии.
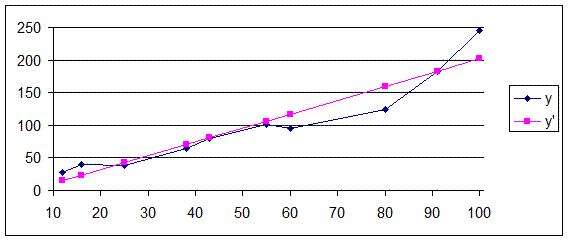
Рис.6. График эмпирической и теоретической линий регрессии.
6. Теоретическое корреляционное отношение
представляет собой универсальный показатель тесноты связи. Измерить тесноту связи между коррелируемыми величинами – это значит определить, насколько вариация результативного признака обусловлена вариацией факторного признака. Ранее были рассмотрены показатели, с помощью которых можно выявить наличие корреляционной связи между двумя признаками x
и y
и измерить тесноту этой связи: коэффициент Фехнера и линейный коэффициент корреляции.
Наряду с ними существует универсальный показатель – корреляционное отношение
(или коэффициент корреляции по Пирсону
), применимое ко всем случаям корреляционной зависимости независимо от формы этой связи. Следует различать эмпирическое и теоретическое корреляционные отношения. Эмпирическое корреляционное отношение
рассчитывается на основе правила сложения дисперсий как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии, т.е.
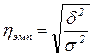 . (90) . (90)
Теоретическое корреляционное отношение  определяется на основе выравненных (теоретических) значений результативного признака определяется на основе выравненных (теоретических) значений результативного признака  , рассчитанных по уравнению регрессии. , рассчитанных по уравнению регрессии. 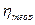 представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических значений результативного признака со средним квадратическим отклонением в ряду эмпирических значений. Если обозначить дисперсию эмпирического ряда игреков через представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических значений результативного признака со средним квадратическим отклонением в ряду эмпирических значений. Если обозначить дисперсию эмпирического ряда игреков через 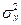 , а теоретического ряда – , а теоретического ряда – 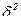 , то каждая из них выразится формулами: , то каждая из них выразится формулами:
 , (91) , (91)
 . (92) . (92)
Сравнивая вторую дисперсию с первой, получим теоретический коэффициент детерминации:
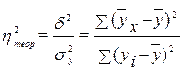 , (
93) , (
93)
который показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора x
на вариацию y
. Извлекая корень квадратный из коэффициента детерминации, получаем теоретическое корреляционное отношение:
 . (
94) . (
94)
Оно может находиться в пределах от 0 до 1. Чем ближе его значение к 1, тем теснее связь между вариацией y
и x
. При  <0,3 говорят о малой зависимости между коррелируемыми величинами, при 0,3< <0,3 говорят о малой зависимости между коррелируемыми величинами, при 0,3< <0,6 – о средней, при 0,6< <0,6 – о средней, при 0,6< <0,8 – о зависимости выше средней, при <0,8 – о зависимости выше средней, при  >0,8 – о большой, сильной зависимости. Корреляционное отношение применимо как для парной, так и для множественной корреляции независимо от формы связи. При линейной зависимости >0,8 – о большой, сильной зависимости. Корреляционное отношение применимо как для парной, так и для множественной корреляции независимо от формы связи. При линейной зависимости 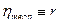 . .
В нашей задаче расчет необходимых сумм для использования в формуле (93) приведен в последних двух столбцах таблицы 12. Тогда теоретический коэффициент детерминации по формуле (93) равен: 2
теор
= 38762,125 / 42818 = 0,9053, то есть дисперсия, выражающая влияние вариации фактора x
на вариацию y
, составляет 90,53%. 2
теор
= 38762,125 / 42818 = 0,9053, то есть дисперсия, выражающая влияние вариации фактора x
на вариацию y
, составляет 90,53%.
Теоретическое корреляционное отношение по формуле (94) равно:  теор
= теор
=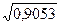 = 0,9515, что совпадает со значением линейного коэффициента корреляции и, следовательно, можно говорить о большой, сильной зависимости между коррелируемыми величинами. = 0,9515, что совпадает со значением линейного коэффициента корреляции и, следовательно, можно говорить о большой, сильной зависимости между коррелируемыми величинами.
Контрольные задания по теме
На основе исходных данных контрольных заданий по теме 2 определить наличие и характер корреляционной связи между признаками x
и y
6-ю методами.
| При-знак
|
Вариант
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| x
|
Рост
|
Доход
|
Возраст
|
IQ
|
Доход
|
Возраст
|
рост/вес
|
Стаж
|
Доход
|
IQ
|
| y
|
Вес
|
Вес
|
Доход
|
Доход
|
Тетрадь
|
рост/вес
|
Кол-во друзей
|
Доход
|
Кол-во друзей
|
Время решения
|
Часть 2. Социально-экономическая статистика
Тема 1. Социально-демографическая статистика
Методические указания по теме
Задача 1
.
Численность населения города составляла 3000 тыс. чел. на начало года. На конец года она возросла до 3050 тыс. чел. Число родившихся за год составило 35 тыс.чел., число умерших – 15 тыс.чел. Определить:
1) коэффициенты естественного, механического и общего движения населения, установить его тип;
2) перспективную численность населения через 4 года при условии, что коэффициент общего движения населения будет: а) сохраняться на прежнем уровне; б) снижаться ежегодно на 1%0
.
Решение. Численность населения (S
) в конкретном пункте существенно меняется с течением времени, поэтому, рассчитывается ее среднегодовое значение
по разным формулам средних величин в зависимости от полноты исходных данных. В нашей задаче среднегодовая численность определяется по формуле средней арифметической простой (17) как полусумма S
в начале и конце года: 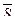 = (
S
н
+
S
к
)/2
= (3000 + 3050)/2 = 3025 (тыс. чел.). = (
S
н
+
S
к
)/2
= (3000 + 3050)/2 = 3025 (тыс. чел.).
Изменение численности населения за счет рождений и смертей называется естественным движением
населения, которое характеризуется рядом коэффициентов: рождаемости
(95), смертности
(96) и естественного движения
(97):
Кр
=
N
/ 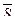 *1000%0
,
(
95) *1000%0
,
(
95)
Ксм
=
M
/  *1000%0
,
(
96) *1000%0
,
(
96)
КЕД
= (
N
–
M
)/
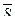 *1000%0
= Кр
– Ксм
,
(
97) *1000%0
= Кр
– Ксм
,
(
97)
где N
– число родившихся за год, M
– число умерших за год.
В нашей задаче по формуле (95) получаем: Кр
=
35 / 3025 * 1000%0
= 11,57%0
, то есть на каждую 1000 населения приходится 11 младенцев.
По формуле (96) получаем: Ксм
=
15 / 3025*1000%0
= 4,96%0
, то есть на каждую 1000 населения приходится 5 умерших.
И, наконец, по формуле (97) получаем: КЕД
=
Кр
– Ксм
,=
11,57%0
– 4,96%0
= 6,61%0
, то есть рождаемость превышает смертность на 6,61 промилле (это естественный прирост населения).
Движением населения может происходить и за счет миграции
, показывающей, куда и откуда, в каком количестве происходит перемещение населения в стране и в международном масштабе. Основными показателями миграции населения являются: сальдо миграции
(98) и коэффициент механического движения населения
(99):
∆
V
=
V
+
–
V
–
,
(
98)
КМД
= ∆
V
/
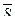 *1000%0
,
(
99) *1000%0
,
(
99)
где V
+
и V
–
–
численность, соответственно, прибывшего и выбывшего на постоянное жительство населения.
В нашей задаче число прибывших и выбывших неизвестно, но можно найти сальдо миграции, так как данные о миграционном сальдо вместе с данными об естественном движении населения служат основой для расчета коэффициента общего движения
населения (100):
КОД
= КЕД
+ КМД
= (
S
к
–
S
н
)/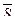 *1000%0
.
(
100) *1000%0
.
(
100)
В нашей задаче по формуле (100) получаем: КОД
=
(3050 – 3000) / 3025 * 1000%0
= 16,53%0
, тогда КМД
= КОД
– КЕД
=
16,53%0
– 6,61%0
= 9,92%0
, то есть численность прибывших в город больше выбывших на 9,92 промилле (это механический приток или прирост населения).
В социально-демографической статистике различают 8 типов общего движения населения:
1. Естественный прирост превышает механический отток;
2. Естественный прирост превышает механический приток;
3. Механический приток больше естественного прироста;
4. Механический приток больше естественной убыли;
5. Естественная убыль превышает механический приток;
6. Естественная убыль превышает механический отток;
7. Механический отток больше естественной убыли;
8. Механический отток больше естественного прироста.
 Их можно изобразить графически (см. рис. 7), если по оси абсцисс отложить КМД
, а по оси ординат – КЕД
. Их можно изобразить графически (см. рис. 7), если по оси абсцисс отложить КМД
, а по оси ординат – КЕД
.
Типы 1 – 4 (выше жирной диагонали) свидетельствуют о росте населения территории, а типы 5 – 8 (серый цвет) о сокращении ее населения.
В нашей задаче механический приток больше естественного прироста (│КМД
│>│КЕД
│), значит это 3-й тип общего движения.
Рис. 7. Типы движения населения.
Перспективную численность населения через t
лет можно определить по формуле (101):
S
н+
t
= 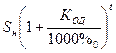 . (
101) . (
101)
В нашей задаче, считая, что КОД
сохранится на прежнем уровне, определим S
через 4 года по формуле (101):
S
4
= 3050*(1+16,53/1000)4
= 3256,27 (тыс. чел.).
Считая, что КОД
будет ежегодно снижаться на 1%0
:
S
1
= 3000*(1+16,53/1000) = 3050 (тыс. чел.);
S
2
= 3050*(1+15,53/1000) = 3097,363 (тыс. чел.);
S
3
= 3097,363*(1+14,53/1000) = 3142,364 (тыс. чел.);
S
4
= 3142,364*(1+13,53/1000) = 3184,877 (тыс. чел.).
Задача 2
.
Определить среднюю продолжительность предстоящей жизни по следующим данным о числе умирающих из 100 000 человек при переходе от возраста x
к x
+1 лет (dx
):
| Возраст х
, лет
|
0-1
|
1-4
|
5-9
|
10-14
|
15-19
|
20-24
|
25-29
|
30-34
|
35-39
|
40-44
|
| dx
|
1802
|
316
|
184
|
183
|
550
|
749
|
681
|
766
|
1061
|
1583
|
| Возраст х
, лет
|
45-49
|
50-54
|
55-59
|
60-64
|
65-69
|
70-74
|
75-79
|
80-84
|
85 и более
|
| dx
|
2454
|
3631
|
5341
|
7171
|
9480
|
11562
|
14192
|
14751
|
23543
|
Решение. Исходные данные – это элементы укрупненной в интервалы таблицы смертности. Эти данные показывают, как постепенно с увеличением возраста население выбывает под влиянием смертности. На их основе рассчитываются частные коэффициенты смертности по отдельным возрастным группам. Для определения средней продолжительности предстоящей жизни необходимо рассчитать следующие показатели для каждого возраста х
:
1) lx
– число доживающих до возраста х
, которое показывает, сколько из 100 000 лиц условного поколения доживают до каждого следующего года (102):
lx
+1
=
lx
–
dx
; (
102)
2) dx
– число умирающих возрасте x
;
3) px
– вероятность дожить до возраста x
+
1, которая показывает, какая доля из достигших данного возраста х
проживает еще полный год и достигнет очередного возраста х+
1 (103):
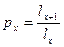 ; (
103) ; (
103)
4) qx
– вероятность умереть в возрасте х
(104) (при этом должно выполняться условие: px
+
qx
=
1):
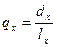 ; (
104) ; (
104)
5) Lx
– среднее число живущих в возрастном интервале от х
до x
+1 года (105):
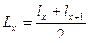 ; (
105) ; (
105)
6) Т
x
– число человеко-лет, которые проживет население, достигшее х
лет до максимального возраста w
(106):
 ; (
106) ; (
106)
7) Ex
– средняя продолжительность предстоящей жизни, которая показывает, сколько лет в среднем предстоит прожить лицам, достигшим возраста х
(107):
 ; (
107) ; (
107)
Показатель (107) является важнейшим обобщающим демографическим показателем, зависящим от социальной ситуации в стране.
В нашей задаче расчет перечисленных показателей приведен в таблице 13. Поскольку возраст задан интервально, то во втором столбце этой таблицы рассчитаны середины интервалов X
сер
как полусумма нижней и верхней границы интервала, а формула (106) примет следующий вид:
T
х
= (87,5 – X
сер
)*L
х
.
Таблица
13. Таблица смертности с укрупненными возрастными интервалами в 10 лет
| Возраст X
, лет
|
X
сер
|
lx
|
dx
|
px
|
qx
|
Lx
|
Т
x
|
Ex
|
| 0-1
|
0,5
|
100000
|
1802
|
0,982
|
0,018
|
99099,0
|
8621613,0
|
86,216
|
| 1-4
|
3
|
98198
|
316
|
0,997
|
0,003
|
98040,0
|
8284380,0
|
84,364
|
| 5-9
|
7,5
|
97882
|
184
|
0,998
|
0,002
|
97790,0
|
7823200,0
|
79,925
|
| 10-14
|
12,5
|
97698
|
183
|
0,998
|
0,002
|
97606,5
|
7320487,5
|
74,930
|
| 15-19
|
17,5
|
97515
|
550
|
0,994
|
0,006
|
97240,0
|
6806800,0
|
69,803
|
| 20-24
|
22,5
|
96965
|
749
|
0,992
|
0,008
|
96590,5
|
6278382,5
|
64,749
|
| 25-29
|
27,5
|
96216
|
681
|
0,993
|
0,007
|
95875,5
|
5752530,0
|
59,788
|
| 30-34
|
32,5
|
95535
|
766
|
0,992
|
0,008
|
95152,0
|
5233360,0
|
54,780
|
| 35-39
|
37,5
|
94769
|
1061
|
0,989
|
0,011
|
94238,5
|
4711925,0
|
49,720
|
| 40-44
|
42,5
|
93708
|
1583
|
0,983
|
0,017
|
92916,5
|
4181242,5
|
44,620
|
| 45-49
|
47,5
|
92125
|
2454
|
0,973
|
0,027
|
90898,0
|
3635920,0
|
39,467
|
| 50-54
|
52,5
|
89671
|
3631
|
0,960
|
0,040
|
87855,5
|
3074942,5
|
34,291
|
| 55-59
|
57,5
|
86040
|
5341
|
0,938
|
0,062
|
83369,5
|
2501085,0
|
29,069
|
| 60-64
|
62,5
|
80699
|
7171
|
0,911
|
0,089
|
77113,5
|
1927837,5
|
23,889
|
| 65-69
|
67,5
|
73528
|
9480
|
0,871
|
0,129
|
68788,0
|
1375760,0
|
18,711
|
| 70-74
|
72,5
|
64048
|
11562
|
0,819
|
0,181
|
58267,0
|
874005,0
|
13,646
|
| 75-79
|
77,5
|
52486
|
14192
|
0,730
|
0,270
|
45390,0
|
453900,0
|
8,648
|
| 80-84
|
82,5
|
38294
|
14751
|
0,615
|
0,385
|
30918,5
|
154592,5
|
4,037
|
| 85 и более
|
87,5
|
23543
|
23543
|
0,000
|
1,000
|
11771,5
|
0,0
|
0,000
|
| Итого
|
1568920
|
100000
|
1518920
|
79011963
|
50,361
|
Таким образом, в итоговой строке таблицы 13 в последнем столбце по формуле (107) определена средняя продолжительность предстоящей жизни в 50,361 года.
Контрольные задания по теме
Задание 1.
Имеются следующие условные данные о численности населения города, тыс. чел.:
| Вариант
|
1
|
2
|
3
|
4
|
5
|
| Численность в начале года
|
320
|
750
|
105
|
400
|
1500
|
| Численность в конце года
|
315
|
700
|
109
|
440
|
1475
|
| Число родившихся за год
|
8,5
|
15
|
5,5
|
15
|
25
|
| Число умерших за год
|
12,0
|
11
|
6,0
|
10
|
37
|
Определить:
1) коэффициенты естественного, механического и общего движения населения, установить его тип;
2) перспективную численность населения через 5 лет при условии, что коэффициент общего движения населения будет:
а) сохраняться на прежнем уровне;
б) ежегодно расти на 1%0
.
Задание 2.
Определить среднюю продолжительность предстоящей жизни по следующим данным о числе умирающих из 100 000 человек при переходе от возраста x
к x
+1 лет:
| Возраст X, лет
|
Вариант
|
| 6
|
7
|
8
|
9
|
10
|
| 0-10
|
2300
|
2170
|
2139
|
1856
|
4020
|
| 10-20
|
735
|
865
|
831
|
395
|
1980
|
| 20-30
|
1420
|
1420
|
1323
|
1176
|
5601
|
| 30-40
|
1837
|
1967
|
1934
|
1693
|
6810
|
| 40-50
|
4017
|
3887
|
3919
|
3973
|
9820
|
| 50-60
|
8992
|
9122
|
9090
|
9136
|
11968
|
| 60-70
|
16650
|
16520
|
16549
|
16894
|
21856
|
| 70-80
|
25755
|
25885
|
25856
|
26099
|
33295
|
| 80-90
|
38294
|
38164
|
38359
|
38778
|
4650
|
Тема 2. Статистика уровня жизни населения
Методические указания по теме
Задача 1.
По приведенным в следующей таблице данным (первые три столбца) о распределении населения РФ по ежемесячному среднедушевому доходу (СДД) в 2004 году рассчитать показатели дифференциации доходов (численность населения России в 2004 году составила 144,2 млн. чел.).
| №
групп i
|
Месячный
СДД, руб./чел.
|
Доля населения
di
|
Численность населения, млн. чел.
|
Доход, млн. руб.
|
Доля доходов
qi
|
Кумулятивные доли
|
| населения
d’i
|
дохода
q’
i
|
| 1
|
до 1000
|
0,019
|
2,7398
|
2054,85
|
0,00284829
|
0,019
|
0,00284829
|
| 2
|
1000-1500
|
0,043
|
6,2006
|
7750,75
|
0,01074355
|
0,062
|
0,01359184
|
| 3
|
1500-2000
|
0,062
|
8,9404
|
15645,7
|
0,02168699
|
0,124
|
0,03527883
|
| 4
|
2000-3000
|
0,146
|
21,0532
|
52633
|
0,07295623
|
0,27
|
0,10823506
|
| 5
|
3000-4000
|
0,139
|
20,0438
|
70153,3
|
0,09724166
|
0,409
|
0,20547671
|
| 6
|
4000-5000
|
0,118
|
17,0156
|
76570,2
|
0,10613632
|
0,527
|
0,31161303
|
| 7
|
5000-7000
|
0,17
|
24,514
|
147084
|
0,20387767
|
0,697
|
0,51549071
|
| 8
|
свыше 7000
|
0,303
|
43,6926
|
349540,8
|
0,48450929
|
1
|
1
|
| Итого
|
1
|
144,2
|
721432,6
|
1
|
Решение. Сначала определяем абсолютные величины дифференциации. Так, больше всего людей (их доля – 0,303) имели доход свыше 7000 руб./чел. В этом интервале и находится модальный доход, точное значение которого согласно формуле (13)[2]
определяется следующим образом:
Mo
= 7000 + 2000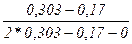 = 7610 руб./чел. = 7610 руб./чел.
Доход в интервале 4000-5000 руб./чел. является граничным для половины людей, поэтому согласно формуле (14) значение медианного дохода равно:
Ме
= 4000 + 1000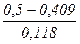 = 4771,19 руб./чел. = 4771,19 руб./чел.
Затем рассчитываем простейшие относительные величины дифференциации – децильный
(108) и фондовый
(109) коэффициенты. Децильный (дециль составляет 10%) коэффициент – это отношение минимального СДД 10% самого богатого населения (minСДД10%бог
) к максимальному СДД 10% самого бедного населения (maxСДД10%бед
). Коэффициент фондов – это отношение среднего СДД 10% самого богатого населения к среднему же СДД 10% самого бедного населения.
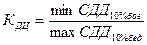 , (
108) , (
108)  . (
109) . (
109)
По исходным данным необходимо отобрать 10% самых бедных людей, т.е. первые три группы (их кумулятивная доля равна 0,124, что ближе всего к необходимым 0,1). Так как первый интервал СДД является открытым, следовательно, представляем его в закрытом виде, используя размах соседнего интервала в размере 500 руб./чел. (т.е. границы 1-й группы составят от 500 до 1000 руб./чел.). Тогда первые три группы самых бедных (12,4%) предстанут в границах 500-2000 с серединой 1250 руб./чел. Если 12,4% бедных имеют размах доходов 1500 руб./чел., то 10% будут иметь размах доходов: 10%*1500/12,4%=1209,68 (руб./чел.). Значит maxСДД10%бед
= 500 + 1209,68 = 1709,68 (руб./чел.), а  = 500 + 1209,68 / 2 = 1104,84 (руб./чел.). = 500 + 1209,68 / 2 = 1104,84 (руб./чел.).
Теперь отберем 10 % самых богатых людей – это 8-я группа с доходами от 7000 до 9000 руб./чел. (так как интервал открытый, то применили размах соседнего интервала в размере 2000 руб./чел.), т.е. 30,3% самого богатого населения имеет размах доходов 2000 руб./чел.[3]
. Нам нужно отобрать не 30,3%, а 10%, поэтому, решая пропорцию, находим размах доходов 10% самого богатого населения. Он равен 660,07 руб./чел. Отсюда minСДД10%бог
= 9000 - 660,07 = 8339,93 руб./чел., а его среднее значение  = 9000 - 660,07/2 = 8669,97 (руб./чел.). = 9000 - 660,07/2 = 8669,97 (руб./чел.).
Таким образом, по формуле (108) децильный коэффициент КДЦ
= 8339,93/1709,68=4,88, а по формуле (109) коэффициент фондов КФ
= 8669,97/1104,84=7,85.
Для расчета более сложных относительных величин дифференциации определим доход и его долю в каждой группе людей, используя середины интервалов СДД и количество людей в группах. Так, доход первой группы составит: 750 руб./чел. * 2,7398 млн. чел. = 2054,85 млн.руб., а его доля равняется 2054,85/721432,6=0,00284829. Аналогично, например, для четвертой группы: 2500*21,0532 = 52633 млн. руб. и 52633/721432,6=0,07295623. Естественно, доли доходов надо определять после суммирования доходов по группам (получается 721432,6 млн. руб.).
Полученные доли людей и доходов вписываются в таблицу, после чего определяются соответствующие кумулятивные доли (нарастающим итогом). Например, кумулятивная доля людей 3-й группы составит 0,019+0,043+0,062=0,1240, а кумулятивная доля их доходов – соответственно 0,00284829+0,01074355+0,02168699=0,03527883. Сумма долей как в обычном, так и в кумулятивном виде должна равняться 1.
Кумулятивные доли также вписываются в таблицу, после чего можно определять коэффициенты локализации
(определяется по формуле Лоренца (110)) и концентрации
(определяется по формуле Джини (111)) доходов:
 ; (
110) ; (
110)  . (
111) . (
111)
Значения коэффициентов Лоренца и Джини изменяются от 0 до 1. Нулевое их значение свидетельствует об абсолютной равномерности распределения доходов по группам населения. Чем ближе эти коэффициенты к единице, тем в большей мере доходы сосредоточены в отдельной группе населения. Естественно, при этом часть населения оказывается живущей в бедности.
Так, по формуле (110) коэффициент локализации Лоренца равняется:
Кл
= 0,5 * (│0,19–0,002848│ + │0,043–0,010744│ + │0,062–0,021687│ + │0,146–0,072956│ + + │0,139–0,09242│ + │0,118–0,10614│ + │0,17–0,20388│ + │0,303–0,4845│) = 0,215.
Для наглядности неравномерность распределения доходов изобразим графически в виде кривой Лоренца (рис.8).
По формуле (111) коэффициент концентрации Джини равняется:
КД
= 0,019*0,013592 + 0,062*0,03528 + 0,124*0,108235 + 0,27*0,2055 + 0,409*0,3116 + 0,527*0,5155 + 0,697*1 – 0,00285*0,062 – 0,0136*0,124 – 0,0353*0,27 – 0,108234*0,409 – 0,2055*0,527 – 0,3116*0,697 – 0,51549*1 = 1,168 – 0,897 = 0,271.
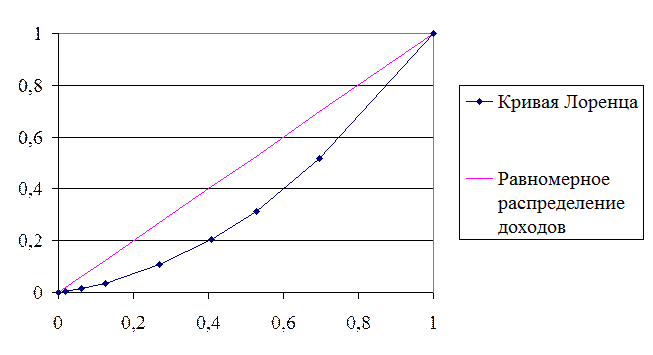 Рис.8. Кривая распределения доходов. Рис.8. Кривая распределения доходов.
Таким образом, коэффициенты Лоренца и Джини показали, что 0,215–0,271 доходов населения или 21,5–27,1% сосредоточено в руках 10% самых богатых людей, что говорит о неравномерности распределения доходов в России.
Задача 2.
Рассчитать индекс развития человеческого потенциала на 2006 год по следующим данным:
| Ожидаемая продолжительность жизни, лет
|
63
|
| Доля грамотных / учащихся
|
0,82 / 0,65
|
| Паритет покупательной способности валют
|
1,1
|
| Среднегодовой индекс инфляции
|
1,03
|
| Среднедушевой ВВП в мес., $/чел
|
1200
|
Решение. В качестве обобщающего критерия уровня жизни используется разработанный Программой развития ООН в 1993 г. индекс развития человеческого потенциала (ИРЧП), который базируется на расчете трех индексов и представляет собой простую среднюю арифметическую величину:
 . (
112) . (
112)
где I
ОБР
– международный индекс уровня образования, определяемый по формуле (113); I
ОЖ
– индекс ожидаемой при рождении продолжительности жизни, определяемый по формуле (114); I
ВВП
– индекс валового внутреннего продукта (ВВП), определяемый по формуле (116).
 , (
113) , (
113)
где 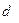 – доля грамотных, – доля грамотных,  – доля учащихся. – доля учащихся.
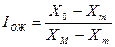 , (
114) , (
114)
где Xm
, XM
—минимально и максимально возможная продолжительность жизни, Х
0
– ожидаемая при рождении продолжительность жизни, определяемая по формуле (115).
По мировым стандартам Xm
= 25 лет, а XM
= 85 лет, значит, для международных сопоставлений надо принимать:
X
0
= 85(1- К'мс
), (
115)
где К'мс
– коэффициент младенческой смертности, выраженный в долях единицы.
 , (
116) , (
116)
где  – фактический в стране среднедушевой валовой внутренний продукт; ВВП
m
и ВВП
M
– минимальный и максимальный размеры среднедушевого ВВП по мировым стандартам; ППСВ
– паритет покупательной способности валют. – фактический в стране среднедушевой валовой внутренний продукт; ВВП
m
и ВВП
M
– минимальный и максимальный размеры среднедушевого ВВП по мировым стандартам; ППСВ
– паритет покупательной способности валют.
В качестве минимального размера ВВП принято $100 на человека в месяц, а максимальным размером для разумно высокого благосостояния в 1992 г. считалось $5120 на человека в месяц. Максимальный размер на последующие годы корректируется с учетом среднегодового индекса инфляции по формуле (117):
ВВП
M
= 5120* ,
(
117) ,
(
117)
где t
– количество лет с 1992 до расчетного года, а индекс инфляции i
ф
можно принять по предыдущему перед расчетным годом.
В нашей задаче индекс образования по формуле (113):
I
ОБР
= 2/3*0,82 + 1/3*0,65 = 0,763.
Находим индекс ожидаемой при рождении продолжительности жизни по формуле (114):  = (63 – 25)/(85 – 25) = 0,633. = (63 – 25)/(85 – 25) = 0,633.
Определяем максимальный ВВП по формуле (117):
ВВП
M
= 5120*1,0314
=
7744,459.
Индекс валового внутреннего продукта находим по формуле (116):
I
ВВП
= (1200*1,1–100)/(7744,459–100) = 0,160.
ИРЧП по определяем по формуле (112):
ИРЧП
= (0,763 + 0,633 + 0,160) / 3 = 0,519.
Контрольные задания по теме
Задание 1.
Определить показатели дифференциации доходов населения России по следующим данным.
| №
п/п
|
СДД,
руб./чел.
|
Доли населения, %
|
| Вариант
|
| 1
|
2
|
3
|
4
|
| 1
|
до 1000
|
20,4
|
12,5
|
6,8
|
3,3
|
| 2
|
1000-1500
|
19,9
|
15,0
|
10,6
|
6,6
|
| 3
|
1500-2000
|
16,4
|
14,4
|
11,8
|
8,5
|
| 4
|
2000-3000
|
20,7
|
21,7
|
21,0
|
17,7
|
| 5
|
3000-4000
|
10,4
|
13,4
|
15,2
|
15,1
|
| 6
|
4000-5000
|
5,3
|
8,2
|
10,4
|
11,7
|
| 7
|
5000-7000
|
4,4
|
8,2
|
11,9
|
15,4
|
| 8
|
более 7000
|
2,5
|
6,6
|
12,3
|
21,7
|
| Число жителей, млн.чел. (год)
|
146,9
(2000)
|
146,3
(2001)
|
145,6
(2002)
|
145,0
(2003)
|
| СДД,
руб./чел.
|
Доли населения, %
|
| Вариант
|
| 6
|
7
|
8
|
9
|
| до 1500
|
17,3
|
9,9
|
6,2
|
3,2
|
| 1500-2500
|
23
|
17,5
|
13,2
|
8,9
|
| 2500-3500
|
18,1
|
16,7
|
14,4
|
11,5
|
| 3500-4500
|
12,6
|
13,4
|
12,8
|
11,5
|
| 4500-6000
|
11,8
|
14,3
|
15
|
15
|
| 6000-8000
|
8,2
|
11,4
|
13,4
|
14,9
|
| 8000-12000
|
6,1
|
10,2
|
13,7
|
17,3
|
| более 12000
|
2,9
|
6,6
|
11,3
|
17,7
|
| Число жителей, млн.чел. (год)
|
145,6
(2002)
|
145,0
(2003)
|
144,2
(2004)
|
143,5
(2005)
|
Задание 2.
Рассчитать индекс развития человеческого потенциала на 2006 год:
| Исходные данные
|
Вариант 5
|
Вариант 10
|
| Ожидаемая продолжительность жизни, лет
|
61
|
72
|
| Доля грамотных/учащихся
|
0,78 / 0,45
|
0,98 / 0,56
|
| Паритет покупательной способности валют
|
1,5
|
0,84
|
| Среднегодовой индекс инфляции
|
1,05
|
1,02
|
| Среднедушевой ВВП в мес., $/чел
|
1500
|
2500
|
Тема 3. Статистика национального богатства
Методические указания по теме
Задача 1.
Имеются следующие данные о динамике балансовой стоимости основных фондов (Ф)
предприятия:
| Дата
|
1.01
|
1.02
|
1.03
|
1.04
|
1.05
|
1.06
|
1.07
|
1.08
|
1.09
|
1.10
|
1.11
|
1.12
|
31.12
|
| Ф
, млн. руб.
|
130
|
128
|
120
|
125
|
135
|
124
|
118
|
115
|
119
|
122
|
128
|
125
|
122
|
Износ фондов в начале года – 26 млн. руб., норматив отчислений на реновацию (амортизация) - 5%, ликвидационная стоимость - 15% от стоимости выбывших фондов, годовой объем выпущенной продукции - 300 млн. руб., среднесписочная численность персонала - 1000 чел.
1. Определить среднегодовую балансовую стоимость основных фондов.
2. Составить балансы основных фондов по первоначальной полной и остаточной стоимостям.
3. Рассчитать показатели состояния, движения и использования фондов.
Решение. Среднегодовая балансовая стоимость определяется по формуле средней хронологической простой (если временные интервалы равны) или взвешенной (если временные интервалы неравны). В нашей задаче интервалы равные (по 1 месяцу), значит, используем формулу (27):
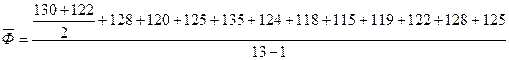 =123,75 (млн.руб.) =123,75 (млн.руб.)
Балансы показывают динамику фондов за год. Они строятся по полной первоначальной
стоимости и по остаточной
стоимости. Уравнение баланса по полной первоначальной стоимости имеет вид (118):
Фк
= Фн
+ П – В,
(
118)
где Фк
и Фн
– стоимость фондов на конец и начало года, соответственно; П
и В
– стоимость поступивших и выбывших, соответственно, фондов за год.
В нашей задаче по формуле (118) определяем стоимость Ф
на конец года:
Фк
= 130 + (5+10+4+3+6) – (2+8+11+6+3+3+3) =130 + 28 – 36 = 122 (млн. руб.).
В таблице 14 построим баланс основных фондов по полной первоначальной стоимости.
Таблица
14. Баланс основных фондов по полной первоначальной стоимости
| Виды
основ-ных фондов
|
Наличие
на начало года
|
Поступило в отчетном году
|
Выбыло в отчетном году
|
Наличие
на конец года
|
| Всего
|
В том числе
|
Всего
|
В том числе
|
| ввод в действие новых фондов
|
прочие поступ-ления
|
ликвидировано основных фондов
|
прочее выбытие
|
| Ф
|
130
|
28
|
28
|
0
|
36
|
36
|
0
|
122
|
Схема баланса по полной первоначальной стоимости во многом совпадает с балансом основных фондов по остаточной стоимости (табл. 15). Отличие заключается в том, что в таком балансе помимо учета поступления и выбытия объектов по остаточной (за вычетом износа) стоимости учитывается уменьшение их стоимости за год вследствие износа (А
), равное сумме начисленной амортизации за год. В основе баланса основных фондов по остаточной стоимости лежит уравнение (119):
Ф
' к
= Ф
' н
+ П
' – В
' – А,
(
119)
где ' – знак остаточной стоимости.
Остаточная стоимость выбывших фондов за год (В’
) включает стоимость: проданных (по рыночной стоимости), переданных безвозмездно (по остаточной стоимости) другим предприятиям и ликвидированных (по ликвидационной стоимости) из-за ветхости и износа основных фондов.
В нашей задаче, считая, что продажи и безвозмездной передачи не было, имеем: В'
= 0,15*36 = 5,4 (млн. руб.). Тогда, считая все поступившие фонды новыми, по формуле (119) имеем: Ф'к
= (130-26) + 28 – 5,4 – 0,05*130 = 104 + 28 – 5,4 – 6,5 =120,1 (млн. руб.).
Проверка: Фк
'
= Фк
- Ик
, где Ик
= Ин
+ А
+ В' – В
, поэтому, в нашей задаче Фк
'
= 122 - (26+6,5+5,4-36) = 120,1 (млн. руб.). В таблице 15 построим баланс основных фондов по остаточной стоимости.
Таблица
15. Баланс основных фондов по остаточной стоимости
| Виды основ-ных фондов
|
Наличие
на начало года
|
Поступило в отчетном году
|
Выбытие и износ за год
|
Наличие
на конец года
|
| Всего
|
В том числе
|
Всего
|
В том числе
|
| ввод в действие новых фондов
|
прочие поступления
|
износ основных
фондов
за год
|
ликвиди-ровано
основных
фондов
|
прочее выбытие
|
| Ф
|
104
|
28
|
28
|
0
|
11,9
|
6,5
|
5,4
|
0
|
120,1
|
Используя сведения о наличии фондов по полной и остаточной стоимости, находят их следующие обобщающие показатели:
1) состояния (коэффициенты износа и годности);
2) интенсивности движения (коэффициенты поступления, выбытия, движения и обновления);
3) использования (фондоотдача, фондоемкость и фондовооруженность).
Коэффициент износа
определяется на определенную дату (на начало или конец года) как отношение суммы износа основных фондов (И
) к их полной стоимости (Ф
), то есть по формуле (120):
Кизн
=И/Ф
. (
120)
В нашей задаче полная стоимость Ф
на начало года составляет 130 млн. руб., а износ - 26 млн. руб., следовательно, Кизн(н
)
= 26/130 = 0,20, то есть в начале года 20% фондов были изношенными.
Сумму износа на конец года (Ик
) можно получить как разность между полной (Фк
) и остаточной стоимостью на эту дату (Ф
'к
) фондов, то есть по формуле (121):
Ик
= Фк
– Ф
'к
. (
121)
В нашей задаче по формулам (120) и (121) получаем: Кизн(к)
= (122–120,1) / 122 = 0,016, то есть коэффициент износа уменьшился с 20% в начале года до 1,6% в конце.
Разность между единицей и коэффициентом износа дает величину коэффициента
годности
, отражающего долю неизношенной части основных фондов. Его можно также рассчитать по формуле (122):
Кгодн
= Ф'/Ф
. (
122)
В нашей задаче Кгодн(н)
= 1 – 0,2 = 0,8; Кгодн(к)
= 1 – 0,016 = 0,984 или по формуле (122): Кгодн(н)
= (130-26) / 130 = 0,8; Кгодн(к)
= 120,1 / 122 = 0,984, то есть степень неизношенности фондов увеличилась с 80% в начале года до 98,4% в конце.
К показателям движения основных фондов относят коэффициенты
поступления
(123) и выбытия
(124):
Кп
= П /Фк
;
(
123) Кв
= В /Фн
. (
124)
В нашей задаче Кп
= 28 / 122 = 0,230, то есть за год поступило 23% от стоимости всех фондов.
Кв
= 36 / 130 = 0,277, то есть за год выбыло 27,7% от стоимости фондов.
Дополнительно можно определить коэффициенты
движения
(125) и обновления
(126):
Кд
=(П - В)/  ;
(
125) Ко
= П / В.
(
126) ;
(
125) Ко
= П / В.
(
126)
В нашей задаче Кд
= (28–36)/123,75 = – 0,065, то есть поступило фондов на 6,5% меньше, чем выбыло.
Ко
= 28 / 36 = 0,778, то есть поступило за год 77,8% от стоимости выбывших фондов.
К показателям использования основных фондов относят фондоотдачу
(127), фондоемкость
(128) и фондовооруженность
(129):
Н =
Q
/ ;
(
127) h
= ;
(
127) h
=  /
Q
=
1 / Н;
(
128) V
= /
Q
=
1 / Н;
(
128) V
=  / / ,
(
129) ,
(
129)
где Q
– объем выпущенной за год продукции;  – среднесписочная численность персонала.
– среднесписочная численность персонала.
В нашей задаче по формуле (127): H
= 300 / 123,75 = 2,42, то есть на 1 руб. фондов произведено 2,42 руб. продукции; по формуле (128): h
=
123,75 / 300 = 0,42, то есть на 1 руб. произведенной продукции приходится 42 коп. стоимости фондов; по формуле (129): V
= 123,75 млн. руб. / 1000 чел. = 123,75 тыс. руб./чел., то есть на 1 работника приходится 123,75 тыс. руб. стоимости фондов.
Задача 2.
Имеются следующие данные об использовании материальных запасов
(З
) предприятия:
| Показатель
|
Базисный год (0
)
|
Отчетный год (1
)
|
| Стоимость З
в начале года, млн. руб.
|
30
|
45
|
| Стоимость З
в конце года, млн. руб.
|
12
|
23
|
| Среднесуточный расход З
, млн. руб./сут.
|
0,25
|
0,3
|
| Годовой объем выпущенной продукции, млн. руб.
|
80
|
99
|
Определить абсолютные и относительные изменения показателей использования З
предприятия.
Решение. Средний запас  предприятия определяется по формуле средней арифметической простой (17) как полусумма стоимости запасов на начало и конец года: предприятия определяется по формуле средней арифметической простой (17) как полусумма стоимости запасов на начало и конец года:
 0
= (30 + 12) / 2 = 21 (млн. руб.); 0
= (30 + 12) / 2 = 21 (млн. руб.);  1
= (42 + 23) / 2 = 32,5 (млн. руб.) 1
= (42 + 23) / 2 = 32,5 (млн. руб.)
Для характеристики использования запасов используют следующие относительные показатели: коэффициент
(скорость) оборачиваемости
(130), коэффициент
закрепления
(131) и время обращения
(средняя продолжительность оборота в днях) (132):
С = Р /  ,
(
130) K
закр
= ,
(
130) K
закр
=  / Р = 1 / С,
(
131) В = 360*
K
закр
,
(
132) / Р = 1 / С,
(
131) В = 360*
K
закр
,
(
132)
где Р
– стоимость реализованной выпущенной продукции за год.
В нашей задаче по формуле (130) определяем: С0
= 80 / 21 = 3,810 (оборотов в год); С1
= 100 / 32,5 = 3,077 (оборотов в год), то есть оборачиваемость запасов уменьшилась с 3,81 оборотов в базисном году до 3,077 оборотов в отчетном.
Абсолютное изменение оборачиваемости ∆С = С1
– С0
= 3,077 – 3,810 = – 0,733, то есть оборачиваемость уменьшилась на 0,733 раза в год.
Относительное изменение оборачиваемости i
С
= С1
/С0
= 3,077/3,81 = 0,808, то есть оборачиваемость запасов уменьшилась в 0,808 раза или на 19,2%.
По формуле (131) получаем: K
закр0
= 0,2625; K
закр1
= 0,325, то есть для реализации каждых 100 руб. продукции потребовалось материальных запасов: в базисном периоде – 26,3 руб., а в отчетном периоде – 32,5 руб.
Абсолютное изменение коэффициента закрепления ∆
K
закр
= K
закр1
–
K
закр0
=
0,325 – 0,2625 = 0,0625, то есть коэффициент закрепления вырос на 0,0625 в отчетном году по сравнению с базисным.
Относительное изменение коэффициента закрепления iK
закр
= K
закр1
/
K
закр0
=
0,325 / 0,2625 =1,238, то есть коэффициент закрепления вырос в 1,238 раза или на 23,8% в отчетном году по сравнению с базисным годом.
По формуле (132) получаем: В =
360*0,2625 = 94,5 (дня); В =
360*0,325 = 117 (дней), то есть средняя продолжительность оборота возросла с 94,5 дня в базисном году до 117 дней в отчетном.
Абсолютное изменение времени обращения ∆В= В1
– В0
=
117 – 94,5 = 22,5 (дня), то есть время обращения запасов выросло на 22,5 дня в отчетном году по сравнению с базисным.
Относительное изменение времени обращения i
В
= В1
/В0
=
117 / 94,5 = 1,238, то есть время обращения выросло в 1,238 раза или на 23,8% в отчетном году по сравнению с базисным.
Обеспеченность предприятия запасами в днях определяется путем деления размера запаса в начале периода (года) на среднесуточный расход (а
), то есть по формуле (133):
Одн
= З / а
. (
133)
В нашей задаче по формуле (133) получаем: Одн0
= 30 / 0,25 = 120 (дней); Одн1
= 45 / 0,3 = 150 (дней), то есть обеспеченность запасами выросла со 120 дней в базисном году до 150 дней в отчетном.
Абсолютное изменение обеспеченности запасами ∆Одн
= Одн1
– Одн0
=
150 – 120 = 30 (дней), то есть обеспеченность запасами возросла на 30 дней в отчетном году по сравнению с базисным.
Относительное изменение обеспеченности запасами i
Одн
= Одн1
/ Одн0
=
150 / 120 = 1,25, то есть обеспеченность запасами возросла в 1,25 раза или на 25% в отчетном году по сравнению с базисным.
Контрольные задания
Задание 1.
Имеются следующие данные о динамике балансовой стоимости основных фондов
(Ф
):
| Вариант
|
Дата
|
1.01
|
1.02
|
1.03
|
1.04
|
1.05
|
1.06
|
1.07
|
1.08
|
1.09
|
1.10
|
1.11
|
1.12
|
31.12
|
| 1
|
Стои-мость
Ф,
млн. руб.
|
90
|
85
|
75
|
71
|
81
|
80
|
90
|
77
|
65
|
70
|
75
|
85
|
95
|
| 2
|
260
|
280
|
300
|
250
|
240
|
220
|
235
|
245
|
255
|
| 3
|
33
|
31
|
35
|
39
|
29
|
32
|
34
|
36
|
40
|
45
|
42
|
41
|
39
|
| 4
|
150
|
150
|
148
|
146
|
144
|
154
|
151
|
149
|
155
|
150
|
145
|
140
|
130
|
| 5
|
400
|
450
|
425
|
420
|
435
|
445
|
475
|
450
|
425
|
Годность основных фондов в начале года составляла 75%, норматив отчислений на реновацию - 10%, ликвидационная стоимость - 5% от стоимости выбывших фондов, годовая выручка - 200 млн. руб., среднесписочная численность производственного персонала - 1500 чел.
1. Определить среднегодовую балансовую стоимость основных фондов.
2. Составить балансы фондов по первоначальной полной и остаточной стоимостям.
3. Рассчитать показатели состояния, движения и использования основных фондов.
Задание 2.
Имеются следующие условные данные по предприятию за базисный (БП) и отчетный (ОП) периоды:
| Вариант
|
6
|
7
|
8
|
9
|
10
|
| Период
|
БП
|
ОП
|
БП
|
ОП
|
БП
|
ОП
|
БП
|
ОП
|
БП
|
ОП
|
| Стоимость запасов в начале года, млн. руб.
|
15
|
20
|
50
|
40
|
110
|
105
|
1,5
|
0,9
|
70
|
80
|
| Стоимость запасов в конце года, млн. руб.
|
10
|
18
|
20
|
15
|
105
|
95
|
0,8
|
0,4
|
60
|
50
|
| Среднесуточный расход запасов, млн. руб./сут.
|
0,14
|
0,15
|
0,5
|
0,75
|
1,5
|
1,6
|
0,05
|
0,03
|
2,5
|
3,5
|
| Годовой объем выпущенной продукции, млн. руб.
|
45
|
52
|
110
|
85
|
300
|
250
|
2,5
|
1,5
|
175
|
195
|
Определить абсолютные и относительные изменения показателей использования запасов предприятия, сделать выводы.
Тема 4. Статистика труда
Методические указания по теме
Задача 1.
Имеются следующие данные по России на конец 2005 года, млн. человек: численность населения – 142,8, всего занято в экономике – 68,603, численность безработных – 5,2083.
Определить: 1) численность экономически активного населения (ЭАН); 2) коэффициент экономической активности населения; 3) коэффициенты занятости и безработицы.
Решение. ЭАН (рабочая сила)
– это часть населения, которая предлагает свой труд для производства товаров и услуг. Численность ЭАН определяется как сумма занятых и безработных по формуле (134):
P
ЭАН
=
P
зан
+
P
безр
. (
134)
В нашей задаче по формуле (134) получаем: P
ЭАН
=
68,603 + 5,2083 = 73,8113 (млн. чел.).
Коэффициент экономической активности
населения определяется как отношение численности ЭАН к общей численности населения, то есть по формуле (135):
КЭАН
=
P
ЭАН
/
P
. (
135)
В нашей задаче по формуле (135) получаем: КЭАН
=
73,8113 / 142,8 = 0,517, то есть численность ЭАН в общей численности населения составляет 51,7%.
Коэффициент занятости
населения определяется как отношение численности занятого населения к численности ЭАН, то есть по формуле (136):
Кзан
=
P
зан
/
P
ЭАН
. (
136)
В нашей задаче по формуле (136) получаем: Кзан
=
68,603 / 73,8113 = 0,929, то есть численность занятого населения составляет 92,9% от численности ЭАН.
Коэффициент безработицы
определяется как отношение численности безработного населения к численности ЭАН, то есть по формуле (137):
Кбезр
=
P
безр
/
P
ЭАН
. (
137)
В нашей задаче по формуле (137) получаем: Кбезр
=
5,2083 / 73,8113 = 0,071, то есть численность безработного населения составляет 7,1% от численности ЭАН.
Задача 2.
Имеются следующие условные данные по области, тыс. человек:
| На начало года:
|
| – численность трудоспособного населения в трудоспособном возрасте (ТТВнг
)
|
500
|
| – численность работающих лиц за пределами трудоспособного возраста (ТвнеТВнг
)
|
15
|
| В течение года:
|
| – вступило в трудоспособный возраст трудоспособного населения
|
30
|
| – вовлечено для работы в отраслях экономики лиц пенсионного возраста
|
3
|
| – прибыло из других областей трудоспособного населения в трудоспособном возрасте
|
20
|
| – выбыло из состава трудовых ресурсов (в связи с переходом в пенсионный возраст,
инвалидность, вследствие смерти и т.д.) трудоспособного населения
|
10
|
| – выбыло из состава трудовых ресурсов подростков
|
4
|
| – выбыло трудоспособного населения в трудоспособном возрасте в другие области
|
5
|
Определить:
1) численность трудовых ресурсов на начало года (ТНГ
);
2) на конец года:
а) численность трудоспособного населения в трудоспособном возрасте (ТТВкг
)
;
б) численность работающих лиц, находящихся за пределами трудоспособного возраста (ТвнеТВкг
)
;
в) численность трудовых ресурсов (Ткг
);
3) среднегодовую численность трудовых ресурсов;
4) коэффициенты естественного, механического и общего движения трудовых ресурсов;
5) перспективную численность трудовых ресурсов на предстоящие 3 года, при условии, что коэффициент общего движения трудовых ресурсов будет ежегодно расти на 1%0
.
Решение. Численность трудовых ресурсов (Т
) определяется как численность трудоспособного населения в трудоспособном возрасте ТТВ
и работающих лиц за пределами трудоспособного возраста ТвнеТВ
(лица пенсионного возраста и подростки), то есть по формуле (138):
Т = ТТВ
+ ТвнеТВ
. (
138)
В нашей задаче по формуле (138) получаем: Тнг
= ТТВнг
+ ТвнеТВнг
= 500 + 15 = 515 (тыс. чел.).
В течение года происходит постоянное изменение численности населения трудоспособного возраста по причинам:
1) естественного движения – выбытия за пределы трудоспособного возраста (в пенсионный возраст), а также пополнения при переходе в трудоспособный возраст;
2) механического движения – миграция населения трудоспособного возраста (приезд из других регионов и отъезд в другие регионы).
Таким образом, численность трудоспособного населения в трудоспособном возрасте в конце года можно определить путем корректировки этой численности в начале года на величину приростов естественного (∆ест
) и механического движения (∆мех
):
ТТВкг
= ТТВнг
+ ∆ест
+ ∆мех
. (
139)
В нашей задаче по формуле (139) получаем: ТТВкг
= 500 + (30 – 10) + (20 – 5) = 535 (тыс. чел.).
Для определения численности работающих лиц, находящихся за пределами трудоспособного возраста на конец года, необходимо прибавить к этой численности в начале года численность вовлеченных для работы лиц нетрудоспособного возраста (ТвнеТВвовлеч
) и вычесть численность выбывших из состава трудовых ресурсов лиц нетрудоспособного возраста (ТвнеТВвыб
):
ТвнеТВкг
= ТвнеТВнг
+ ТвнеТВвовлеч
– ТвнеТВвыб
. (
140)
В нашей задаче по формуле (140) получаем: ТвнеТВкг
= 15 + 3 – 4 = 14 (тыс. чел.).
Численность трудовых ресурсов на конец года определим по формуле (138): Ткг
= ТТВкг
+ ТвнеТВкг
=
535 + 14 = 549 (тыс. чел.).
Среднегодовая численность трудовых ресурсов определяем по формуле средней арифметической простой (17) как полусумма численности трудовых ресурсов на начало и конец года:
 = (515 + 549) / 2 = 532 (тыс. чел.). = (515 + 549) / 2 = 532 (тыс. чел.).
Коэффициенты естественного, механического и общего движения трудовых ресурсов рассчитываются путем деления соответствующих приростов на среднегодовую численность трудовых ресурсов по следующим формулам:
Кест
=  , (
141) , (
141)
Кмех
= 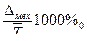 , (
142) , (
142)
Кобщ
= 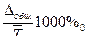 = =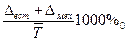 = Кест
+ Кмех
.
(
143) = Кест
+ Кмех
.
(
143)
В нашей задаче по формуле (141) получаем: Кест
= (30 + 3 – 10 – 4) / 532 * 1000%0
= 35,7%0
, а по формуле (142): Кмех
= (20 – 5) / 532 * 1000%0
= 28,2%0
, и, наконец, по формуле (143): Кобщ
= (30 + 3 – 10 – 4 + 20 – 5) / 532 * 1000%0
= 35,7%0
+ 28,2%0
= 63,9%0
.
Перспективную численность трудовых ресурсов на следующий год можно найти по формуле (144):
 .
(
144) .
(
144)
В нашей задаче по формуле (144) численность трудовых ресурсов через год составит:  1
= 535 * (1 + 64,9 / 1000) = 566 (тыс. чел.), а еще через год по той же формуле: 1
= 535 * (1 + 64,9 / 1000) = 566 (тыс. чел.), а еще через год по той же формуле: 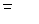 2
= 566 * (1 + 65,9 / 1000) = 603,299 (тыс. чел.), и, наконец, через три года: 2
= 566 * (1 + 65,9 / 1000) = 603,299 (тыс. чел.), и, наконец, через три года: 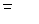 3
= 603,299 * (1 + 66,9 / 1000) = 643,66 (тыс. чел.). 3
= 603,299 * (1 + 66,9 / 1000) = 643,66 (тыс. чел.).
Задача 3.
Заполните годовой баланс рабочего времени предприятия (табл. 16) недостающими данными.
Таблица
16. Баланс рабочего времени за год
| Фонды времени
|
Условные обозначения
|
Чел.-дней
|
Использование рабочего времени
|
Условные обозначения
|
Чел.-дней
|
| Календарный фонд рабочего времени
|
КФРВ
|
Отработанное время
|
ОВ
|
| Неявки вследствие праздничных и выходных дней
|
ПВД
|
145500
|
Целодневные простои
|
ЦП
|
100
|
| Табельный фонд рабочего времени
|
ТФРВ
|
Неявки по уважительным причинам, всего
|
УП
|
20000
|
| Неявки в связи с очередными отпусками
|
ОО
|
31500
|
Неявки по неуважительным причинам, всего
|
НП
|
5000
|
| Максимально возможный фонд рабочего времени
|
МВФРВ
|
| Баланс
|
Баланс
|
Среднесписочная численность работников данного предприятия  =
1500 чел., установленная продолжительность рабочего дня в этой отрасли – 8 ч, отработано за год 2625040 чел.-часов. =
1500 чел., установленная продолжительность рабочего дня в этой отрасли – 8 ч, отработано за год 2625040 чел.-часов.
Определить:
1. Календарный, табельный и максимально возможный фонды рабочего времени;
2. Коэффициенты использования этих фондов времени;
3. Коэффициенты использования рабочего периода и рабочего дня;
4. Интегральный коэффициент использования рабочего времени.
Решение. КФРВ – это сумма человеко-дней, которые отработали бы в течение года все работники предприятия при ежедневной работе. Календарный фонд определяется по формулам (145) и (146):
КФРВ =  d
год
,
(
145)
d
год
,
(
145)
где d
год
– число календарных дней в году.
КФРВ =ОВ + ЦП + (ПВД+ОО) + УП + НП.
(
146)
В нашей задаче по формуле (145) получаем: КФРВ
=1500 * 365 = 547500 (чел.-дней), то есть если бы каждый из 1500 работников предприятия работал все календарные дни года, то фонд рабочего времени всех работников за год составил 547500 чел.-дней.
Из формулы (146) можно найти отработанное время: ОВ
= 547500 – 100 – (145500+31500) – 20000 – 5000 = 345400 (чел.-дней).
ТФРВ – это сумма человеко-дней, которые отработали бы в течение года все работники предприятия, если бы их неявки на работу были связаны только с праздничными и выходными днями. Табельный фонд определяется по формулам (147) или (148):
ТФРВ = КФРВ – ПВД,
(
147)
ТФРВ = ОВ + ЦП + ОО + УП + НП.
(
148)
В нашей задаче по формуле (147) получаем: ТФРВ =
547500 – 145500 = 402000 (чел.-дней) или по формуле (148): ТФРВ
= 345400 + 100 + 31500 + 20000 + 5000 = 402000 (чел.-дней), то есть если бы каждый работник предприятия не являлся на работу только по причине праздничных и выходных дней, то фонд рабочего времени всех работников за год составил 402000 чел.-дней.
МВФРВ – это сумма человеко-дней, которые отработали бы в течение года все работники предприятия, если бы их неявки на работу были связаны только с реализацией права на отдых (праздничные, выходные дни и очередные отпуска). Максимально возможный фонд определяется по формулам (149) – (151):
МВФРВ = КФРВ – (ПВД + ОО),
(
149)
МВФРВ = ТФРВ – ОО,
(
150)
МВФРВ = ОВ + ЦП + УП + НП.
(
151)
В нашей задаче по формуле (149) получаем: МВФРВ
= 547500 – (145500 + 31500) = 370500 (чел.-дней). Аналогичный результат получаем по формуле (150): МВФРВ
= 402000 – 31500 = 370500 (чел.-дней) или по формуле (151): МВФРВ
= 345400 + 100 + 20000 + 5000 = 370500 (чел.-дней), то есть если бы каждый работник предприятия не являлся на работу только по причине реализации права на отдых, то фонд рабочего времени всех работников за год составил бы 370500 чел.-дней.
Коэффициент использования того или иного фонда времени – это доля отработанного времени в соответствующем фонде. Данные коэффициенты определяются по формулам (152) – (154):
КиспКФРВ
= ОВ / КФРВ,
(
152)
КиспТФРВ
= ОВ / ТФРВ,
(
153)
КиспМВФРВ
= ОВ / МВФРВ.
(
154)
В нашей задаче по формуле (152) получаем: КиспКФРВ
=
345400 / 547500 = 0,631, то есть из-за неявок по всем причинам и целодневных простоев фактически отработанный фонд рабочего времени составляет 63,1% от календарного, то есть фонд недоиспользован на 36,9% или на 202100 (345400 – 547500) чел.-дней.
По формуле (153) получаем: КиспТФРВ
=
345400 / 402000 = 0,859, то есть из-за неявок по всем причинам, кроме выходных и праздничных дней и целодневных простоев фонд недоиспользован на 14,1%.
По формуле (154) получаем: КиспМВФРВ
=
345400 / 370500 = 0,932, то есть из-за неявок по всем причинам, кроме выходных и праздничных дней и очередных отпусков, а также целодневных простоев фонд недоиспользован на 6,8%.
Коэффициент использования рабочего периода (года) определяется по формуле (155):
Кисп.года
= 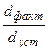 , (
155)
, (
155)
где d
факт
– фактическая продолжительность года, d
уст
– установленная продолжительность года.
Фактическая и установленная продолжительности года определяются по формулам (156) и (157):
d
факт
=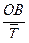 , (
156) d
уст
= , (
156) d
уст
= . (
157) . (
157)
В нашей задаче по формуле (156) получаем: d
факт
= 345400 / 1500 = 230,2 (дня), то есть из-за неявок по всем причинам и целодневных простоев каждый работник отработал в среднем не 365 календарных дней года, а только 230,2 дня.
По формуле (157) получаем: d
уст
= 370500 / 1500 = 247 (дней), то есть с учетом неявок вследствие выходных и праздничных дней и очередных отпусков каждый работник должен отработать в среднем 247 дней в году.
И, наконец, по формуле (155) получаем: Кисп.года
=
230,267 / 247 = 0,9323, то есть из-за неявок по всем причинам, кроме выходных и праздничных дней, а также очередных отпусков, фактическая рабочая продолжительность года недоиспользована на 6,77%, или на 16,8 (230,2 – 247) дня.
Коэффициент использования рабочего дня определяется по формуле (158):
Кисп.дня
=
 ,
(
158) ,
(
158)
где t
факт
– фактическая продолжительность дня, определяемая как соотношение количества отработанных человеко-часов и человеко-дней; t
уст
– установленная продолжительность дня, определяемая нормативами в зависимости от сферы деятельности.
В нашей задаче по формуле (158) получаем: Кисп.дня
= (2625040/345400) / 8 = 7,6 / 8 = 0,95, то есть продолжительность рабочего дня недоиспользована на 5% или на 0,4 (7,6 – 8) часа.
Интегральный коэффициент использования рабочего времени учитывает использование как рабочего года, так и рабочего дня. Он определяется по формулам (159) – (161):
Кинт
= 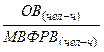 = = 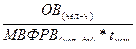 , (
159) , (
159)
Кинт
=  , (
160) , (
160)
Кинт
= Кисп.года
* Кисп.дня
, (
161)
где ОВчел.-ч.
– отработанное время за год в человеко-часах; МВФРВчел.-ч.
– максимально возможный фонд рабочего времени в человеко-часах; МВФРВчел.-дн.
– максимально возможный фонд рабочего времени в человеко-днях; МВФРВч/чел.
– установленное для работника время на год в часах, МВФРВч/чел.
= d
уст
t
уст
; ОВч/.чел.
– отработанное время за год одним работником.
В нашей задаче по формуле (159) получаем: Кинт
= 2625040 / (370500*8) = 0,886. Аналогичный результат получаем по формуле (160): Кинт
= (2625040 / 1500) / (247*8) = 0,886 или по формуле (161): Кинт
= 0,9323 * 0,95 = 0,886, то есть рабочее время за год недоиспользовано на 11,4%.
Задача 4.
Имеются следующие данные по предприятию:
| Показатель
|
Базисный период
|
Отчетный период
|
| Среднесписочная численность работающих ( ), чел. ), чел.
|
3200
|
3926
|
| Произведенная продукция (выручка – Q
), тыс. руб.
|
42400
|
53000
|
| Фонд заработной платы (F
), тыс. руб.
|
35200
|
39072
|
Определить влияние экстенсивного и интенсивного факторов на изменение: 1) выручки; 2) фонда заработной платы.
Решение. Изменение выручки определим по формуле (2):
iQ
= 53000/ 42400 = 1,25.
Это означает, что в отчетном периоде по сравнению с базисным выручка возросла в 1,25 раза (на 25%) или на 10600 (53000 – 42400) тыс. руб. Данное изменение выручки было получено в результате влияния двух факторов: изменения численности работающих (экстенсивный фактор) и изменения производительности труда (интенсивный фактор). Производительность труда определяется по формуле (162):
w
= 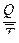 .
(
162) .
(
162)
В нашей задаче по формуле (162) получаем: w
0
= 42400 / 3200 = 13,25 (тыс.руб./чел.), то есть в базисном периоде на одного работающего приходилось 13,25 тыс. руб. продукции; а в отчетном периоде w
1
= 53000 / 3926 = 13,50 (тыс.руб./чел.). Тогда по формуле (2) изменение производительности труда составит: iw
= 13,5 / 13,25 = 1,0189, то есть производительность труда в отчетном периоде по сравнению с базисным возросла примерно в 1,0189 раза (на 1,89%) или на 0,25 (13,5 – 13,25) тыс.руб./чел.
Изменение среднесписочной численности работающих по формуле (2) составило: iT
=
3926 / 3200 = 1,2269, то есть среднесписочная численность работающих возросла примерно в 1,2269 раза (на 22,69%) или на 726 (2926 – 3200) чел.
Для проверки правильности расчетов влияния экстенсивного и интенсивного факторов на изменение выручки воспользуемся следующей двухфакторной мультипликативной моделью (163):
iQ
= iT
iw
.
(
163)
В нашей задаче по формуле (163) получаем: 1,25 = 1,2269*1,0189, то есть выручка возросла за счет увеличения среднесписочной численности работающих (экстенсивный фактор) в 1,2269 раза и за счет увеличения производительности труда каждого работающего (интенсивный фактор) в 1,0189 раза. Для определения влияния этих факторов в абсолютных величинах (в рублях) воспользуемся формулами (164) и (165):
∆QT
= (iT
– 1)Q0
,
(
164)
∆Qw
= iT
(iw
– 1)Q0
. (
165)
В нашей задаче по формуле (164) получаем: ∆
QT
=
(1,2269–1)*42400 = 9620 (тыс. руб.), то есть вследствие увеличения численности работающих на 22,69% выручка увеличилась на 9620 тыс. руб., что составляет примерно 90,8% от общего изменения (9620 /10600*100%).
По формуле (165) получаем: ∆
Qw
=
1,2269*(1,0189–1)*42400 = 980 (тыс. руб.), то есть вследствие увеличения производительности труда работающих на 1,89% выручка увеличилась на 980 тыс. руб., что составляет примерно 9,2% от общего изменения (980/10600*100%).
Для проверки правильности расчетов воспользуемся формулой (166):
∆
QT
+∆
Qw
=
Q
1
–
Q
0
.
(
166)
В нашей задаче по формуле (166) получаем: 9620 + 980 = 53000 – 42400 = 10600.
Изменение фонда заработной платы F
определим по формуле (2):
iF
= 39072 / 35200 = 1,11.
Это означает, что в отчетном периоде по сравнению с базисным фонд возрос в 1,11 раза или на 11%. В абсолютном выражении данный прирост составил 3872 (39072 – 35200) тыс. руб. Он был получен в результате влияния двух факторов: изменения численности работающих (экстенсивный фактор) и изменения уровня заработной платы (интенсивный фактор). Уровень заработной платы определяется по формуле (167):
f
= 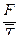 .
(
167) .
(
167)
В нашей задаче по формуле (167) получаем: f
0
= 35200 / 3200 = 11 (тыс. руб./чел.), то есть в базисном периоде средний уровень заработной платы составлял 11 тыс. руб./чел.; а в отчетном периоде – f
1
= 39072 / 3926 = 9,952 (тыс.руб./чел.). Тогда по формуле (2) изменение уровня заработной платы составит: if
= 9,952 / 11 = 0,9047. Это означает, что средний уровень заработной платы в отчетном периоде по сравнению с базисным уменьшился в 0,9047 раза (на 9,53%) или на 1,048 (9,952 – 11) тыс. руб./чел.
Для проверки правильности расчетов влияния экстенсивного и интенсивного факторов на изменение фонда заработной платы воспользуемся следующей двухфакторной мультипликативной моделью (168):
iF
= iT
if
.
(
168)
В нашей задаче по формуле (168) получаем: 1,11 = 1,2269*0,9047, то есть фонд возрос за счет увеличения среднесписочной численности работающих (экстенсивный фактор) в 1,2269 раза и за счет уменьшения уровня заработной платы каждого работающего (интенсивный фактор) в 0,9047 раза. Для определения влияния этих факторов в абсолютных величинах (в рублях) воспользуемся формулами (169) и (170):
∆FT
= (iT
– 1)F0
,
(
169)
∆Ff
= iT
(if
– 1)F0
.
(
170)
В нашей задаче по формуле (169) получаем: ∆
FT
=
(1,2269–1)*35200 = 7986,88 (тыс. руб.), а по формуле (170): ∆
Ff
=
1,2269*(0,9047 – 1)*35200 = – 4115,71 (тыс. руб.), то есть вследствие увеличения численности работающих на 22,69% фонд заработной платы должен был увеличиться на 7986,88 тыс. руб., однако, за счет уменьшения уровня заработной платы на 9,53% он уменьшился на 4115,71 тыс. руб.
Для проверки правильности расчетов воспользуемся формулой (171):
∆FT
+∆Ff
= F1
– F0
.
(
171)
В нашей задаче по формуле (171) получаем: 7986,88 + (–4115,71) = 39072 – 35200 = 3872.
Контрольные задания
Задание 1.
Имеются следующие условные данные по стране, млн. человек:
| Вариант
|
1
|
2
|
3
|
4
|
5
|
| Численность населения
|
53
|
186
|
42
|
24
|
94
|
| Всего занято в экономике
|
31
|
105
|
28
|
15,5
|
41
|
| Численность безработных
|
4
|
21
|
2,5
|
1,8
|
18
|
Определить: 1) численность экономически активного населения; 2) коэффициент экономической активности населения; 3) коэффициенты занятости и безработицы.
Задание 2.
Имеются следующие условные данные за год по предприятию:
| Вариант
|
1
|
2
|
3
|
4
|
5
|
| Неявки вследствие праздничных и выходных дней, тыс. чел.-дн.
|
100
|
475
|
33,6
|
247,5
|
9,5
|
| Неявки в связи с очередными отпусками, тыс. чел.-дн.
|
20,5
|
95
|
7
|
42,5
|
2,05
|
| Целодневные простои, чел.-дн.
|
80
|
700
|
30
|
190
|
5
|
| Неявки по уважительным причинам, всего, тыс. чел.-дн.
|
25
|
90
|
10
|
44
|
3
|
| Неявки по неуважительным причинам, всего, тыс. чел.-дн.
|
4
|
15
|
1,5
|
5,5
|
0,25
|
| Среднесписочная численность работников, чел
|
1000
|
5000
|
350
|
2500
|
100
|
| Всего отработано за год, тыс. чел-часов
|
1838,64
|
8941,875
|
660,946
|
4649,453
|
171,157
|
| Установленная продолжительность рабочего дня, часов
|
8
|
7,5
|
7,9
|
7,7
|
7
|
Составьте годовой баланс рабочего времени предприятия и определите:
1. Календарный, табельный и максимально возможный фонды рабочего времени;
2. Коэффициенты использования этих фондов времени;
3. Коэффициенты использования рабочего периода и рабочего дня;
4. Интегральный коэффициент использования рабочего времени.
Задание 3.
Имеются следующие условные данные по области, тыс. человек:
| Вариант
|
6
|
7
|
8
|
9
|
10
|
| На начало года:
|
| – численность трудоспособного населения в трудоспособном возрасте
|
53
|
186
|
42
|
24
|
94
|
| – численность работающих лиц за пределами трудоспособного возраста
|
4
|
21
|
2,5
|
1,8
|
18
|
| В течение года:
|
| – вступило в трудоспособный возраст трудоспособного населения
|
3
|
6
|
2
|
1
|
5
|
| – вовлечено для работы в отраслях экономики лиц пенсионного возраста
|
1,5
|
2,5
|
3
|
0,6
|
1,3
|
| – прибыло из других областей трудоспособного населения в трудоспособном возрасте
|
1
|
2
|
6
|
3
|
5
|
| – выбыло из состава трудовых ресурсов (в связи с переходом в пенсионный возраст, инвалидность, вследствие смерти и т.д.) трудоспособного населения
|
2
|
1
|
5
|
3
|
6
|
| – выбыло из состава трудовых ресурсов подростков
|
2
|
3
|
4
|
1,5
|
6
|
| – выбыло трудоспособного населения в трудоспособном возрасте в другие области
|
2,5
|
3,5
|
7
|
4
|
1,5
|
Определить:
1) численность трудовых ресурсов на начало года;
2) на конец года:
а) численность трудоспособного населения в трудоспособном возрасте;
б) численность работающих лиц, находящихся за пределами трудоспособного возраста;
в) численность трудовых ресурсов;
3) среднегодовую численность трудовых ресурсов;
4) коэффициенты естественного, механического и общего движения трудовых ресурсов;
5) перспективную численность трудовых ресурсов на предстоящие 3 года, при условии, что коэффициент общего движения трудовых ресурсов будет ежегодно снижаться на 1%0
.
Задание 4.
Имеются следующие условные данные по предприятию за базисный (БП) и отчетный (ОП) периоды:
| Вариант
|
6
|
7
|
8
|
9
|
10
|
| Период
|
БП
|
ОП
|
БП
|
ОП
|
БП
|
ОП
|
БП
|
ОП
|
БП
|
ОП
|
| Среднесписочная численность работающих, чел.
|
1000
|
1500
|
500
|
450
|
2500
|
2900
|
5000
|
4000
|
200
|
250
|
| Товарная продукция, млн. руб.
|
50
|
60
|
20
|
15
|
100
|
110
|
300
|
200
|
10
|
11
|
| Фонд заработной платы, тыс. руб.
|
40
|
45
|
15
|
14
|
90
|
94
|
250
|
190
|
8
|
10
|
Определить влияние экстенсивного и интенсивного факторов на изменение: 1) выручки; 2) фонда заработной платы.
5. Экзаменационные вопросы
- Предмет и метод статистики. Структура статистики.
- Статистическое наблюдение, его виды.
- Сводка и группировка статистических данных.
- Абсолютные и относительные величины.
- Общая характеристика средних величин.
- Средняя арифметическая и ее свойства, способы расчета.
- Средняя гармоническая, правила выбора формы средней.
- Структурные средние.
- Показатели вариации, свойства дисперсии.
- Ряды динамики: классификация и правила построения.
- Показатели анализа рядов динамики.
- Проверка ряда динамики на наличие тренда.
- Общая характеристика статистических индексов. Их классификация.
- Индивидуальные и общие индексы.
- Средние индексы.
- Индексный метод анализа факторов динамики.
- Индексы постоянного и переменного составов, индекс структурных сдвигов.
- Основные понятия корреляционного анализа.
- Методы регрессионного анализа.
- Сущность социально-демографической статистики. Характеристика численности населения.
- Естественное и механическое движение населения.
- Демографический прогноз.
- Статистика экономической активности населения, занятости и безработицы.
- Статистика рабочего времени.
- Статистика оплаты труда.
- Производительность труда: сущность и показатели ее уровня.
- Методы анализа динамики производительности труда.
- Сущность и основные элементы СНС.
- Расчет макроэкономических показателей баланса народного хозяйства.
- Расчет показателей системы национальных счетов.
- Понятие уровня жизни населения. Показатели доходов и расходов (потребления) населения.
- Показатели дифференциации доходов населения.
- Понятие и структура национального богатства.
- Основные фонды: классификация, виды оценок и износ.
- Показатели основных фондов.
- Статистика оборотных фондов.
- Показатели уровня и структуры цен.
- Виды цен в РФ.
- Расчет индекса потребительских цен.
- Статистика государственных финансов.
- Основные показатели страховой статистики.
- Статистические показатели денежной массы.
- Механизм начисления банковских процентов.
- Финансовые ренты: сущность, виды и методы анализа.
45. Система показателей финансовой деятельности предприятий.
6. Литература
Рекомендуемая литература (основная)
1. Воронин В.Ф., Жильцова Ю.В. Статистика: учебное пособие для ВУЗов. – М.: Экономистъ, 2004. – 301 с.
2. Статистика: Учеб. пособие/Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. В.Г.Ионина. – Изд.2-е, перераб. и доп. – М.: ИНФРА-М, 2006. – 384 с.
3. Экономическая статистика: Учебник / Под ред. Иванова Ю.Н. – М.: ИНФРА-М, 2004. – 480 с.
4. Ефимова М.Р., Рябцев В.Н. Общая теория статистики. – М.: Финансы и статистика, 1999. – 304 с.
Рекомендуемая литература (дополнительная)
1. Теория статистики: Учебник / Под ред. Р.А. Шмойловой. М.: Финансы и статистика, 2004.
2. Ковалевский Г.В. Индексный метод в экономике. М.: Финансы и статистика, 1989.
3. Симчера В.М. Методы сравнительного анализа статистических данных: Учебное пособие. М.: Изд-во ВЗФИ, 1987.
4. Практикум по статистике: Учеб пособие для вузов / Под ред. В.М. Симчеры. – М.: ЗАО «Финанстатинформ», 1999.
5. Башкатов Б.И. Практикум о международной экономической статистике. – М.: Издательство «Дело и сервис», 2003.
6. Гусаров В.М. Экономическая статистика: Учеб. Пособие. – М.: Экономическое образование, 2004.
7. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2000.
8. Теория статистики: Учебник. / Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2002.
Приложения
Приложение 1. Значения
F-критерия Фишера
при уровне значимости 0,05
| 1
|
2
|
3
|
4
|
5
|
6
|
8
|
12
|
24
|

|
| 1
|
161,5
|
200
|
215,7
|
224,6
|
230,2
|
234
|
238,9
|
243,9
|
249
|
254,3
|
| 2
|
18,5
|
19
|
19,16
|
19,25
|
19,3
|
19,33
|
19,37
|
19,41
|
19,45
|
19,5
|
| 3
|
10,13
|
9,55
|
9,28
|
9,12
|
9,01
|
8,94
|
8,84
|
8,74
|
8,64
|
8,53
|
| 4
|
7,71
|
6,94
|
6,59
|
6,39
|
6,26
|
6,16
|
6,04
|
5,91
|
5,77
|
5,63
|
| 5
|
6,61
|
5,79
|
5,41
|
5,19
|
5,05
|
4,95
|
4,82
|
4,68
|
4,53
|
4,36
|
| 6
|
5,99
|
5,14
|
4,76
|
4,53
|
4,39
|
4,28
|
4,15
|
4
|
3,84
|
3,67
|
| 7
|
5,59
|
4,74
|
4,35
|
4,12
|
3,97
|
3,87
|
3,73
|
3,57
|
3,41
|
3,23
|
| 8
|
5,32
|
4,46
|
4,07
|
3,84
|
3,69
|
3,58
|
3,44
|
3,28
|
3,12
|
2,93
|
| 9
|
5,12
|
4,26
|
3,86
|
3,63
|
3,48
|
3,37
|
3,23
|
3,07
|
2,9
|
2,71
|
| 10
|
4,96
|
4,1
|
3,71
|
3,48
|
3,33
|
3,22
|
3,07
|
2,91
|
2,74
|
2,54
|
| 11
|
4,84
|
3,98
|
3,59
|
3,36
|
3,2
|
3,09
|
2,95
|
2,79
|
2,61
|
2,4
|
| 12
|
4,75
|
3,88
|
3,49
|
3,26
|
3,11
|
3
|
2,85
|
2,69
|
2,5
|
2,3
|
| 13
|
4,67
|
3,8
|
3,41
|
3,18
|
3,02
|
2,92
|
2,77
|
2,6
|
2,42
|
2,21
|
| 14
|
4,6
|
3,74
|
3,34
|
3,11
|
2,96
|
2,85
|
2,7
|
2,53
|
2,35
|
2,13
|
| 15
|
4,54
|
3,68
|
3,29
|
3,06
|
2,9
|
2,79
|
2,64
|
2,48
|
2,29
|
2,07
|
| 16
|
4,49
|
3,63
|
3,24
|
3,01
|
2,85
|
2,74
|
2,59
|
2,42
|
2,24
|
2,01
|
| 17
|
4,45
|
3,59
|
3,2
|
2,96
|
2,81
|
2,7
|
2,55
|
2,38
|
2,19
|
1,96
|
| 18
|
4,41
|
3,55
|
3,16
|
2,93
|
2,77
|
2,66
|
2,51
|
2,34
|
2,15
|
1,92
|
| 19
|
4,38
|
3,52
|
3,13
|
2,9
|
2,74
|
2,63
|
2,48
|
2,31
|
2,11
|
1,88
|
| 20
|
4,35
|
3,49
|
3,1
|
2,87
|
2,71
|
2,6
|
2,45
|
2,28
|
2,08
|
1,84
|
| 21
|
4,32
|
3,47
|
3,07
|
2,84
|
2,68
|
2,57
|
2,42
|
2,25
|
2,05
|
1,81
|
| 22
|
4,3
|
3,44
|
3,05
|
2,82
|
2,66
|
2,55
|
2,4
|
2,23
|
2,03
|
1,78
|
| 23
|
4,28
|
3,42
|
3,03
|
2,8
|
2,64
|
2,53
|
2,38
|
2,2
|
2
|
1,76
|
| 24
|
4,26
|
3,4
|
3,01
|
2,78
|
2,62
|
2,51
|
2,36
|
2,18
|
1,98
|
1,73
|
| 25
|
4,24
|
3,38
|
2,99
|
2,76
|
2,6
|
2,49
|
2,34
|
2,16
|
1,96
|
1,71
|
| 26
|
4,22
|
3,37
|
2,98
|
2,74
|
2,59
|
2,47
|
2,32
|
2,15
|
1,95
|
1,69
|
| 27
|
4,21
|
3,35
|
2,96
|
2,73
|
2,57
|
2,46
|
2,3
|
2,13
|
1,93
|
1,67
|
| 28
|
4,2
|
3,34
|
2,95
|
2,71
|
2,56
|
2,44
|
2,29
|
2,12
|
1,91
|
1,65
|
| 29
|
4,18
|
3,33
|
2,93
|
2,7
|
2,54
|
2,43
|
2,28
|
2,1
|
1,9
|
1,64
|
| 30
|
4,17
|
3,32
|
2,92
|
2,69
|
2,53
|
2,42
|
2,27
|
2,09
|
1,89
|
1,62
|
| 35
|
4,12
|
3,26
|
2,87
|
2,64
|
2,48
|
2,37
|
2,22
|
2,04
|
1,83
|
1,57
|
| 40
|
4,08
|
3,23
|
2,84
|
2,61
|
2,45
|
2,34
|
2,18
|
2
|
1,79
|
1,52
|
| 45
|
4,06
|
3,21
|
2,81
|
2,58
|
2,42
|
2,31
|
2,15
|
1,97
|
1,76
|
1,48
|
| 50
|
4,03
|
3,18
|
2,79
|
2,56
|
2,4
|
2,29
|
2,13
|
1,95
|
1,72
|
1,44
|
| 60
|
4
|
3,15
|
2,76
|
2,52
|
2,37
|
2,25
|
2,1
|
1,92
|
1,7
|
1,39
|
| 70
|
3,98
|
3,13
|
2,74
|
2,5
|
2,35
|
2,23
|
2,07
|
1,89
|
1,67
|
1,35
|
| 80
|
3,96
|
3,11
|
2,72
|
2,49
|
2,33
|
2,21
|
2,06
|
1,88
|
1,65
|
1,31
|
| 90
|
3,95
|
3,1
|
2,71
|
2,47
|
2,32
|
2,2
|
2,04
|
1,86
|
1,64
|
1,28
|
| 100
|
3,94
|
3,09
|
2,7
|
2,46
|
2,3
|
2,19
|
2,03
|
1,85
|
1,63
|
1,26
|
| 125
|
3,92
|
3,07
|
2,68
|
2,44
|
2,29
|
2,17
|
2,01
|
1,83
|
1,6
|
1,21
|
| 150
|
3,9
|
3,06
|
2,66
|
2,43
|
2,27
|
2,16
|
2
|
1,82
|
1,59
|
1,18
|
| 200
|
3,89
|
3,04
|
2,65
|
2,42
|
2,26
|
2,14
|
1,98
|
1,8
|
1,57
|
1,14
|
| 300
|
3,87
|
3,03
|
2,64
|
2,41
|
2,25
|
2,13
|
1,97
|
1,79.
|
1,55
|
1,1
|
| 400
|
3,86
|
3,02
|
2,63
|
2,4
|
2,24
|
2,12
|
1,96
|
1,78
|
1,54
|
1,07
|
| 500
|
3,86
|
3,01
|
2,62
|
2,39
|
2,23
|
2,11
|
1,96
|
1,77
|
1,54
|
1,06
|
| 1000
|
3,85
|
3
|
2,61
|
2,38
|
2,22
|
2,1
|
1,95
|
1,76
|
1,53
|
1,03
|
| 
|
3,84
|
2,99
|
2,6
|
2,37
|
2,21
|
2,09
|
1,94
|
1,75
|
1,52
|
Приложение 2. Значения
t-критерия Стьюдента
при уровне значимости
a
:
0,10, 0,05, 0,01
| Число степеней свободы
|
a
|
Число степеней свободы
|
a
|
| 0,1
|
0,05
|
0,01
|
0,1
|
0,05
|
0,01
|
| 1
|
6,314
|
12,706
|
63,66
|
18
|
1,734
|
2,101
|
2,878
|
| 2
|
2,92
|
4,3027
|
9,925
|
19
|
1,729
|
2,093
|
2,861
|
| 3
|
2,353
|
3,1825
|
5,841
|
20
|
1,725
|
2,086
|
2,845
|
| 4
|
2,132
|
2,7764
|
4,604
|
21
|
1,721
|
2,08
|
2,831
|
| 5
|
2,015
|
2,5706
|
4,032
|
22
|
1,717
|
2,074
|
2,819
|
| 6
|
1,943
|
2,4469
|
3,707
|
23
|
1,714
|
2,069
|
2,807
|
| 7
|
1,895
|
2,3646
|
3,5
|
24
|
1,711
|
2,064
|
2,797
|
| 8
|
1,86
|
2,306
|
3,355
|
25
|
1,708
|
2,06
|
2,787
|
| 9
|
1,833
|
2,2622
|
3,25
|
26
|
1,706
|
2,056
|
2,779
|
| 10
|
1,813
|
2,2281
|
3,169
|
27
|
1,703
|
2,052
|
2,771
|
| 11
|
1,796
|
2,201
|
3,106
|
28
|
1,701
|
2,048
|
2,763
|
| 12
|
1,782
|
2,1788
|
3,055
|
29
|
1,699
|
2,045
|
2,756
|
| 13
|
1,771
|
2,1604
|
3,012
|
30
|
1,697
|
2,042
|
2,75
|
| 14
|
1,761
|
2,1448
|
2,977
|
40
|
1,684
|
2,021
|
2,705
|
| 15
|
1,753
|
2,1315
|
2,947
|
60
|
1,671
|
2
|
2,66
|
| 16
|
1,746
|
2,1199,
|
2,921
|
120
|
1,658
|
1,98
|
2,617
|
| 17
|
1,74
|
2,1098
|
2,898
|

|
1,645
|
1,96
|
2,576
|
Александр Александрович Чалиев
Антон Олегович Овчаров
СТАТИСТИКА
Часть 1
Учебно-методическое пособие
Государственное образовательное учреждение высшего
профессионального образования
«Нижегородский государственный университет им. Н.И.Лобачевского».
603950, Нижний Новгород, пр. Гагарина, 23.
Подписано в печать . Формат 60х84 1/16.
Бумага офсетная. Печать офсетная. Гарнитура Таймс.
Усл. печ. л. 5,0. Уч.-изд. л. 5,4.
Заказ № Тираж 1000 экз.
Отпечатано в типографии Нижегородского госуниверситета
им. Н.И.Лобачевского
603600, г. Нижний Новгород, ул. Большая Покровская, 37
Лицензия ПД № 18-0099 от 14.05.01
[1]
Если в выборке более 30 единиц генеральной совокупности
[2]
Формулы (13) и (14) должны применяться к распределениям с одинаковым размахом интервалов (СДД), в нашей задаче это условие не соблюдается, а значит, и результаты получены приблизительные
[3]
Очевидно, что данное допущение о максимуме СДД в 9000 руб./чел. является чисто теоретическим, на самом же деле, есть люди, получающие гораздо больше, поэтому полученные показатели являются лишь приблизительными
|