| Министерство образования Российской Федерации
Ярославский государственный университет имени П.Г. Демидова
Математический факультет
Курсовая работа
на тему:
Факторизация полиномов над конечными полями (Алгоритм Берлекампа)
Выполнил: Степанов А.Ю.
Группа КБ-21
Ярославль, 2004
Краткий план.
1. Введение в алгебру полиномов.
2. Наибольшие общие делители полиномов над полем.
3. Неприводимые сомножители полиномов.
4. Разложение полиномов на свободные от квадратов множители.
5. Основные факты о конечных полях.
6. Разложение полиномов на множители в конечных полях.
7. Вычисление числа неприводимых полиномов над конечным полем.
8. Подход к алгоритму Берлекампа.
9. Алгоритм Берлекампа.
10. Пример.
1. Введение в алгебру полиномов.
Пусть K – область целостности, x – независимая переменная – её можно рассматривать как просто формальный символ, а не как независимый аргумент области К. Тогда выражение вида
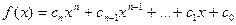 , где , где 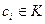 для для 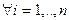
называется полиномом от переменной х над K.
Полиномы называются равными, если у них равны коэффициенты при соответствующих степенях х
Определим так сумму и произведение полиномов:
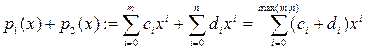
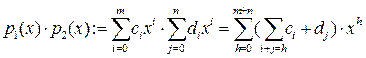
Очевидно, что сумма и произведение полиномов от х над К также представляют собой полином над K. Mножество полиномов от х над областью целостности К само является областью целостности, которая обозначается как K[x]. Покажем это. Возьмём полиномы 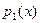 и и 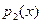 . Тогда их произведение . Тогда их произведение 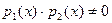 . Знаком 0 здесь обозначен нулевой многочлен - . Знаком 0 здесь обозначен нулевой многочлен - 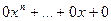 . Предположим . Предположим 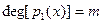 и и 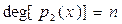 , так что , так что 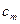 и и 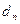 не обращаются в 0. Следствием из этого является не обращаются в 0. Следствием из этого является 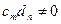 так как так как 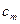 и и 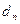 являются элементами области целостности К. Но являются элементами области целостности К. Но 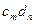 - коэффициент при старшем члене полинома-произведения, т.е. - коэффициент при старшем члене полинома-произведения, т.е. 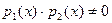 , что означает отсутствие в K[x] делителей нуля. , что означает отсутствие в K[x] делителей нуля.
Рассмотрим полином  - не равный тождественно 0 полином над К. Тогда полином - не равный тождественно 0 полином над К. Тогда полином 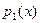 делит полином делит полином 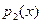 если если 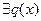 - некоторый полином над К, что - некоторый полином над К, что 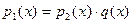 . В этом случае используется запись . В этом случае используется запись 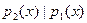 . Полином . Полином 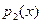 называется делителем полинома называется делителем полинома 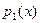 . .
Докажем важный факт, известный как свойство евклидовости:
Пусть К – область целостности, а 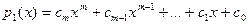 и и 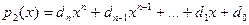 - два полинома над К[x] и пусть - два полинома над К[x] и пусть 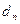 обратим в К. Тогда существуют единственные полиномы обратим в К. Тогда существуют единственные полиномы 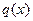 и и  (частное и остаток соответственно), что (частное и остаток соответственно), что
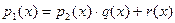 , ,  . .
Доказательство производится индукцией по степени делимого 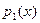 .Если .Если 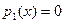 или или 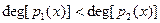 то положим то положим  и и 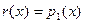 . В противном случае пусть . В противном случае пусть 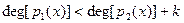 , , 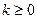 и образуем полином и образуем полином 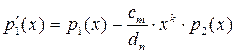 . При этом . При этом  так как убрана старшая степень х. В случае так как убрана старшая степень х. В случае  или или 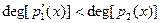 - всё доказано. В противном случае по индукции - всё доказано. В противном случае по индукции  для некоторых для некоторых 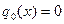 и и  , таких что , таких что 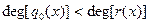 . Поэтому . Поэтому  , что и доказывает существование полиномов , что и доказывает существование полиномов 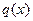 и и  . Ясно, что . Ясно, что 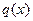 и и  - полиномы в кольце К[x], при этом либо - полиномы в кольце К[x], при этом либо 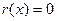 либо либо  . Для доказательства единственности предположим наличие другой пары . Для доказательства единственности предположим наличие другой пары 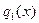 и и 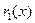 , такой что , такой что  , , 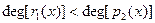 . Тогда . Тогда  и и 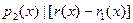 . A это может иметь место только в случае . A это может иметь место только в случае  . Следовательно . Следовательно  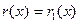 и и 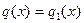
Следует заметить, что если К – поле, то для наличия свойства евклидовости достаточно чтобы полином-делитель 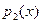 не был нулевым полиномом. не был нулевым полиномом.
Легко можно составить алгоритм полиномиалного деления над полем, который более известен как алгоритм PDF (P
olynomial D
ifvision over the F
ield).
Вход:  и и 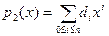 - два полинома, - два полинома, 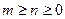 , причём , причём 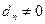
(кстати, алгоритм будет работать и над областью целостности, если в ней 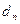 обратим) обратим)
Выход: 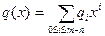 и и  , обладающие свойством евкидовости. , обладающие свойством евкидовости.
Cам алгоритм будет состоять из двух частей:
1. FOR k=m-n DOWNTO 0 // основной вычислительный цикл
BEGIN
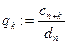
FOR j=n+k-1 DOWNTO k
BEGIN
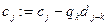
END
END
2. FOR i=0 TO m-n // выдача результатов
BEGIN
RETURN 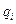

RETURN 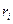
END
Очевидно что доминирует первый цикл, который выполняется m-n+1 раз. В каждом цикле происходит одно деление и пересчитывается ряд коэффициентов. Таким образом трудоёмкость алгоритма PDF есть O[n(m-n+1)]. Это как раз то время, которое нужно для вычисления произведения 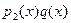 над полем. над полем.
Наибольшие общие делители полиномов над полем
. Дадим следующее
Определение. Пусть К – область целостности и 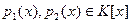 , причём , причём 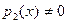 . .
Полином  называется Наибольшим Общим Делителем (НОД) полиномов называется Наибольшим Общим Делителем (НОД) полиномов 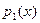 и и 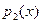 если выполнены следующие условия: если выполнены следующие условия:
1. 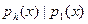 и и 
2. Если 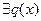 ,такой что ,такой что  и и 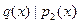 ,то ,то 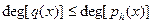 и и 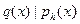 . .
Отсюда виден так называемый алгоритм Евклида для нахождения НОД двух полиномов, также использующий теорему делимости, который работает следующим образом:
 , при этом , при этом 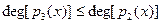
. . .
. . .
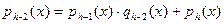 , при этом , при этом 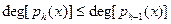
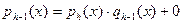
Так как  , то очевидно что эта последовательность закончится самое большее за , то очевидно что эта последовательность закончится самое большее за  шагов. При этом справедлива следующая шагов. При этом справедлива следующая
Теорема. Последний отличный от нуля остаток  это и есть НОД( это и есть НОД(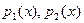 ). ).
Cледует учесть что НОД может быть определён не однозначно если в области целостности имеются обратимые элементы.
Теперь пусть имеется некоторое поле F, 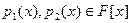 , , 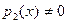 . Применяя PDF можно вычислить НОД( . Применяя PDF можно вычислить НОД( ). ).
Пусть  и и 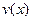 - некоторые произвольные полиномы из - некоторые произвольные полиномы из  . Тогда справедлива . Тогда справедлива
Теорема. Если 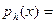 НОД( НОД( ), то в ), то в  найдутся полиномы найдутся полиномы  и и 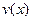 , такие что , такие что 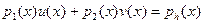
Доказательство: Из всех полиномов вида 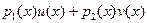 выберем любой из полиномов наименьшей степени и обозначим его выберем любой из полиномов наименьшей степени и обозначим его  . Если . Если  не делит не делит 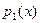 , то , то  , ,  , ,  . Но тогда полином . Но тогда полином 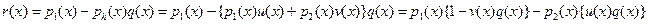 имеет вид имеет вид 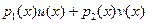 , в противоречие с выбором , в противоречие с выбором  . .
Из теоремы следует, что для взаимной простоты полиномов 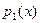 и и 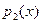 необходимо и достаточно чтобы необходимо и достаточно чтобы 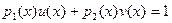 для некоторых для некоторых 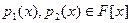 . .
Неприводимые сомножители полиномов. Для начала нужно сформулировать ряд известных теорем:
1. Основная теорема алгебры. Каждый полином 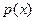 из из 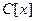 - поля комплексных чисел - поля комплексных чисел 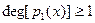 имеет корень в имеет корень в 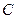 . .
2. Отличный от константы полином 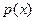 из R[x] неприводим если и только если он имеет степень 1 либо это квадратный трёхчлен с отрицательным дискриминантом. из R[x] неприводим если и только если он имеет степень 1 либо это квадратный трёхчлен с отрицательным дискриминантом.
Имеет место обратное утверждение.
Теперь для полиномов над полем K – поле.
3.Если неприводимый полином 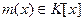 делит произведение делит произведение 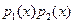 то то 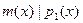 или или 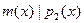 . .
4. Пусть 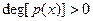 . Тогда полином . Тогда полином 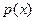 может быть однозначно представлен в произведение неприводимых нормированных полиномов над K[x]. Разложение является единственным с точностью до порядка сомножителей. может быть однозначно представлен в произведение неприводимых нормированных полиномов над K[x]. Разложение является единственным с точностью до порядка сомножителей.
Назовём полином  примитивным, ecли его коэффициенты – целые числа, НОД которых равен 1. Тогда любой полином из примитивным, ecли его коэффициенты – целые числа, НОД которых равен 1. Тогда любой полином из 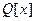 ассоциирован с некоторым примитивным полиномом (два полинома называются ассоциированными, если один из них является скалярным кратным другого). Верна теорема ассоциирован с некоторым примитивным полиномом (два полинома называются ассоциированными, если один из них является скалярным кратным другого). Верна теорема
5. Произведение двух примитивных полиномов из 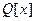 снова примитивный полином. снова примитивный полином.
Доказательство: Пусть p – простое число. По определению примитивности для простого числа p имеем:
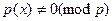 , ,  , откуда , откуда 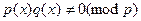
Иначе говоря никакое простое число не делит все коэффициенты многочлена 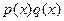 что и доказывает его примитивность. что и доказывает его примитивность.
6. (Gauss) Если  , причём , причём 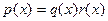 , то , то  , где , где 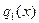 и и 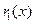 - полиномы, ассоциированные с - полиномы, ассоциированные с 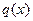 и и  соответственно. соответственно.
Полином в 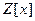 неприводим если он не разлагается в произведение двух полиномов с целыми коэффициентами. В силу вышеприведённой теоремы видно, что полином неприводим в неприводим если он не разлагается в произведение двух полиномов с целыми коэффициентами. В силу вышеприведённой теоремы видно, что полином неприводим в  , если и только если он неприводим как полином из , если и только если он неприводим как полином из 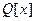 . При этом справедлива теорема . При этом справедлива теорема
7. Если 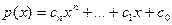 - полином в - полином в 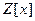 и и  - его корень, такой что НОД(r,
s
)=1, то - его корень, такой что НОД(r,
s
)=1, то 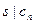 и и 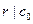 . .
8. (критерий Эйзенштейна) Пусть  - полином в - полином в  . Если существует такое простое число p, что p не делит . Если существует такое простое число p, что p не делит 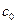 и делит остальные коэффициенты и делит остальные коэффициенты 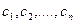 , но , но 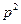 не делит не делит  , тогда полином , тогда полином 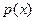 неприводим. неприводим.
Доказательство большинства из этих теорем опускается, иначе это уведёт от главной цели.
Разложение полиномов на свободные от квадратов множители
. Полином 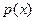 называется свободным от квадратов, если не найдётся полинома называется свободным от квадратов, если не найдётся полинома  положительной степени, такого что положительной степени, такого что 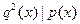 . Cправедлива . Cправедлива
Теорема. Пусть K - область с однозначным разложением на множители, характеристики нуль. И пусть 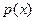 - примитивный полином в K[x], отличный от константы. Возьмём его однозначное разложение на множители - примитивный полином в K[x], отличный от константы. Возьмём его однозначное разложение на множители 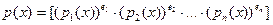 . Его производную обозначим . Его производную обозначим 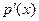 . Тогда НОД( . Тогда НОД(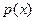 , ,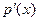 )= )=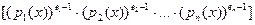
Доказательство: Обозначим  и r(
x)
= НОД( и r(
x)
= НОД(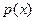 , ,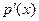 ). Тогда ). Тогда 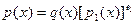 и и  , откуда следует что , откуда следует что 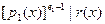 . Методом от противного можно показать что . Методом от противного можно показать что 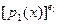 не делит r(
x).
Предположим что не делит r(
x).
Предположим что  . Тогда . Тогда  , откуда можно заключить что , откуда можно заключить что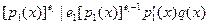 . Отсюда после сокращений . Отсюда после сокращений 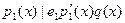 . Cтало быть . Cтало быть 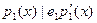 потому что НОД( потому что НОД(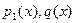 )=1. Из этого можно заключить что )=1. Из этого можно заключить что  . Очевидное противоречие. . Очевидное противоречие.
Из теоремы легко выводятся два следствия.
Следствие1. Простые корни полинома не являются корнями его производной.
Cледствие2. Пусть K – поле, 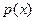 - неприводимый полином в K[x], который делит - неприводимый полином в K[x], который делит  . Тогда . Тогда 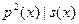 если и только если если и только если 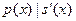 . .
Пусть 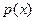 - примитивный полином, определённый на области с однозначным разложением на множители K, - примитивный полином, определённый на области с однозначным разложением на множители K, 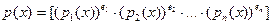 . Пусть . Пусть  . Для . Для 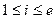 положим положим  , ,  . Тогда . Тогда 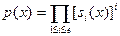 называется разложением полинома называется разложением полинома 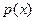 на свободные от квадратов множители. на свободные от квадратов множители.
Замечание. Некоторые из полиномов 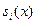 могут быть единицей, могут быть единицей, 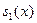 - произведение всех линейных множителей, cоответствующим простым корням, - произведение всех линейных множителей, cоответствующим простым корням, 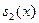 - произведение всех линейных множителей, cоответствующим двойным корням и т.д. - произведение всех линейных множителей, cоответствующим двойным корням и т.д.
Так как r(
x)
= НОД(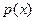 , , )= )=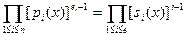 (здесь без (здесь без 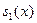 ). ).
Наибольший свободный от квадратов делитель полинома 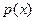 равен равен 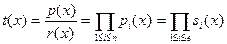 . .
Cледовательно,
НОД( , , )= )= . .
Поэтому 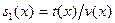 . Повторяя процесс с . Повторяя процесс с  вместо вместо 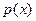 мы можем вычислить мы можем вычислить 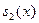 как первый свободный от квадратов сомножитель как первый свободный от квадратов сомножитель  , и в конце можно получить все свободные от квадратов сомножители , и в конце можно получить все свободные от квадратов сомножители 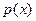 . Таким образом получен алгоритм, известный под названием PSQFF(P
olynomial Sq
uare F
ree F
actorization). . Таким образом получен алгоритм, известный под названием PSQFF(P
olynomial Sq
uare F
ree F
actorization).
Вход: 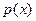 - примитивный полином, определённый на области с однозначным разложением на множители K, - примитивный полином, определённый на области с однозначным разложением на множители K, 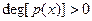 , char(K)=0. , char(K)=0.
Выход: полиномы 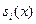 и вышеопределённое число e, определяющие разложение и вышеопределённое число e, определяющие разложение 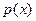 на свободные от квадратов множители. на свободные от квадратов множители.
На условном языке программирования алгоритм выглядит примерно так:
BEGIN // первоначальная инициализация
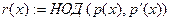
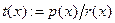
j:=1
label:
IF 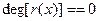 THEN // выход? THEN // выход?
BEGIN
e:=j
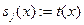
EXIT
END
v(x)
:=  // вычисляем // вычисляем 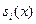
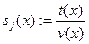
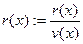 // обновляем // обновляем

INCR(j)
GOTO label
END
Основные факты о конечных полях
. Из определения поля видно, что каждое поле – область целостности, обратное утверждение в общем случае неверно. Но имеет место следующее утверждение:
Каждая конечная область целостности – поле.
Если взять два неравных элемента a,
b
из конечной области целостности K , то для всех ненулевых элементов  по правилу сокращения по правилу сокращения 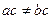 . Поэтому сК=К
и найдется такой . Поэтому сК=К
и найдется такой 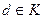 , что , что  , что и означает наличие у каждого ненулевого элемента конечной области целостности мультипликативного обратного элемента, что и подтверждает что K- поле. , что и означает наличие у каждого ненулевого элемента конечной области целостности мультипликативного обратного элемента, что и подтверждает что K- поле.
Так как ненулевые элементы любого конечного поля из q элементов образуют абелеву группу порядка q-1 относительно умножения, то справедлива
Теорема1. Если F
- поле, |F|=q, 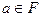 , , 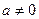 , то , то 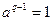 . .
Cледствие. При условиях теоремы любой 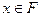 удовлетворяет уравнению удовлетворяет уравнению 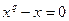
Теорема2. Пусть F
- поле, |
F|=
q
, 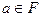 , , 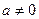 . Если n – порядок элемента a, то n|(q-1). . Если n – порядок элемента a, то n|(q-1).
Теорема3. Пусть F
– поле, |
F|=
q
, тогда 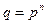 , p – простое, , p – простое, 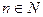 . .
Cледствие. Если F
– конечное поле, то оно имеет характеристику p – простое натуральное число, таким образом содержит подполе, изоморфное 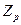 . .
Теорема о примитивном корне (4). Элемент группы называется примитивным корнем, если его степени 0,1,2,… пробегают все элементы группы. Cуть теоремы в том, что в поле F из q элементов найдётся элемент а
, что каждый ненулевой элемент поля представляет степень а
, т.е. a
– примитивный корень, и порядок элемента а
равен q-1.
Теорема 5. Пусть F
– поле и 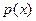 - нормализованный полином из F[х]. Тогда существует таккое содержащее F
поле K
, что в К
[x] полином - нормализованный полином из F[х]. Тогда существует таккое содержащее F
поле K
, что в К
[x] полином 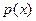 разлагается в произведение линейных сомножителей. Это поле К называют полем расщепления для разлагается в произведение линейных сомножителей. Это поле К называют полем расщепления для 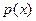 . К примеру, . К примеру,
C
– поле расщепления для любого полинома из Q
[x].
Пусть  - корень некоторого ненулевого полинома из F
[x
]. Тогда элемент х
называют алгебраичным над F. Иначе – трансцендентным. - корень некоторого ненулевого полинома из F
[x
]. Тогда элемент х
называют алгебраичным над F. Иначе – трансцендентным.
Теорема 6. Пусть 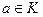 алгебраичен над F
. Тогда существует единственный неприводимый нормированный полином алгебраичен над F
. Тогда существует единственный неприводимый нормированный полином 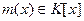 , что , что 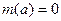 , и каждый полином , и каждый полином 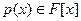 с корнем а
делится на m(
x).
Этот полином называют минимальным полиномом элемента а
над F
. с корнем а
делится на m(
x).
Этот полином называют минимальным полиномом элемента а
над F
.
Разложение полиномов на множители в конечных полях.
Любой полином степени n в 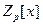 может быть разложен на множители за конечное число шагов, так как существует может быть разложен на множители за конечное число шагов, так как существует 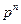 возможных полиномов степени <n, но такой алгоритм "проб и ошибок” чрезмерно трудоёмкий(этот алгоритм осуществляется через PDF). Так что неплохо бы иметь более быстрые алгоритмы. возможных полиномов степени <n, но такой алгоритм "проб и ошибок” чрезмерно трудоёмкий(этот алгоритм осуществляется через PDF). Так что неплохо бы иметь более быстрые алгоритмы.
Если взять полином 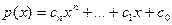 , то его производная , то его производная 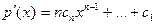 равна нулю тогда и только тогда равна нулю тогда и только тогда  для каждого i. Это будет выполнено в случаях p|
i
или для каждого i. Это будет выполнено в случаях p|
i
или 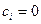 для каждого i. Поэтому для каждого i. Поэтому 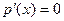 если если 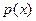 - полином от - полином от 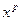 . Теперь несколько обобщим данную ранее теорему о НОД( . Теперь несколько обобщим данную ранее теорему о НОД(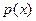 , , ): ):
Теорема. Пусть K - область с однозначным разложением на множители, произвольной характеристики . И пусть 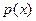 - примитивный полином в K[x], отличный от константы. Возьмём его однозначное разложение на множители - примитивный полином в K[x], отличный от константы. Возьмём его однозначное разложение на множители 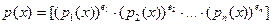 .Пусть .Пусть 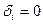 , если , если  , в противном случае , в противном случае 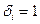 . Тогда НОД( . Тогда НОД(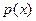 , , )= )=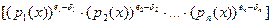 . .
Доказательство данной полностью аналогично доказательству уже доказанной теоремы.
На этой теореме также основана некоторая модификация алгоритма PSQFF, но перед этим нужно доказать ещё две вспомогательные теороемы.
Теорема 1. Пусть 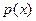 - полином в - полином в 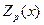 . Тогда . Тогда  . .
Доказательство:Пусть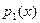 , ,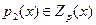 .Тогда .Тогда 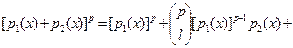
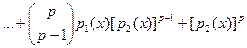 = =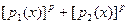 (все биномиальные коэффициенты делятся на р
). Так как (все биномиальные коэффициенты делятся на р
). Так как 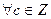 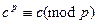 (малая теорема Ферма) то (малая теорема Ферма) то  = = . .
Теорема 2. Пусть 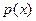 - полином в - полином в 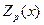 . Тогда . Тогда 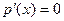 в том и только в том случае, когда p(x) eсть р-ая степень некоторого полинома в том и только в том случае, когда p(x) eсть р-ая степень некоторого полинома 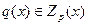 . .
Доказательство:
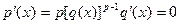 . Обратно, если . Обратно, если 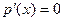 , то , то 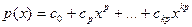 . Тогда . Тогда  . .
Таким образом получен следующий алгоритм PSQFFF разложения на свободные от квадратов множители над конечным полем (P
olynomial Sq
uare-free F
actorization over a F
inite F
ield) :
Вход: 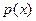 - нормированный полином из - нормированный полином из  , не являющийся константой, p>0 – простое число. , не являющийся константой, p>0 – простое число.
Выход: 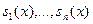 и е
, такие что и е
, такие что 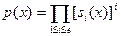 - разложение полинома - разложение полинома 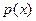 на свободные от квадратов множители. на свободные от квадратов множители.
Реализация:
BEGIN
k:=0; m:=1; e:=0 // инициализировали
label3:
j:=1; 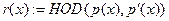 ; ; 
IF 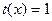 THEN GOTO label1 THEN GOTO label1
label2:
e1:=j*m; IF e1>e THEN FOR i:=e to e1-2 do  ; ;
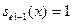 ; e:=e1; ; e:=e1;
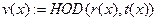 ; ; 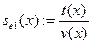 // вычислили // вычислили 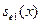
IF 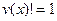 THEN THEN
BEGIN
 ; ; 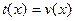 ; incr(j); GOTO label2 ; incr(j); GOTO label2
END
IF 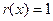 THEN EXIT THEN EXIT
label1: 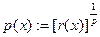 ; inkr(k); m:=m*p; GOTO label3; ; inkr(k); m:=m*p; GOTO label3;
END
Вычисление числа неприводимых полиномов над конечным полем
. Согласно ранее доказанным фактам в  найдётся неприводимый полином степени n для любого n. Также найдётся неприводимый полином степени n для любого n. Также 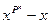 - произведение всех неприводимых полиномов в - произведение всех неприводимых полиномов в  , степени которых делят n. Отсюда степень произведения всех неприводимых полиномов, степени которых делят n равна , степени которых делят n. Отсюда степень произведения всех неприводимых полиномов, степени которых делят n равна 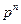 . Число всех нормированных полиномов степени n в . Число всех нормированных полиномов степени n в  будет обозначаться будет обозначаться 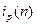 . .
Введём для  функцию Мёбиуса функцию Мёбиуса  следующим образом: следующим образом:
 если если 
если 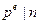 для некоторого простого p и некоторого для некоторого простого p и некоторого 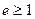
если n раскладывается в произведение r различных простых чисел
Если n делится на квадрат простого числа, то 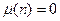 ; для простого числа p ; для простого числа p
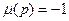 . Также m и n – взаимно простые числа, то . Также m и n – взаимно простые числа, то 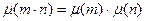 , то есть , то есть  - мультипликативная функция. А для мультипликативных функций верна теорема - мультипликативная функция. А для мультипликативных функций верна теорема
Если f
– мультипликативная функция, а функция F
определена соотношением 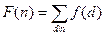 , то F
– также мультипликативная функция. , то F
– также мультипликативная функция.
Доказательство: Пусть числа m и n – взаимно простые. Тогда каждый делитель в числа 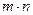 может быть представлен в виде произведения взаимно простых может быть представлен в виде произведения взаимно простых 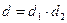 , таких что , таких что 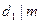 и и  . Поэтому . Поэтому
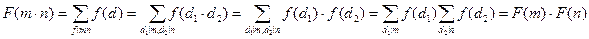
Теперь ещё небольшой факт:
Если  , то , то 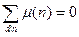 . .
Доказательство: Функция 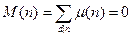 является мультипликативной, если e=0 является мультипликативной, если e=0
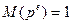 и в то же время и в то же время 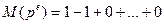 , если , если  . Если n делится на простое число, то . Если n делится на простое число, то  , из этого всего и следует это утверждение. , из этого всего и следует это утверждение.
Формула обращения Мёбиуса. Для любой функции f, определённой на множестве натуральных чисел (не обязательно мультипликативной), если
 для каждого для каждого 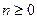 , то , то 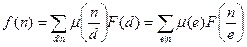 . .
Доказательство: Положим 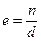 . Тогда суммы очевидно равны. По определению F . Тогда суммы очевидно равны. По определению F
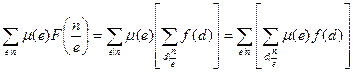 . .
Теперь изменим порядок суммирования и воспользуемся тем, что если  , то , то 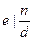 далее следует далее следует  . .
В последней сумме коэффициент при  равен 0, кроме случаев равен 0, кроме случаев 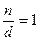 или или  . Эта сумма сводится к единственному члену . Эта сумма сводится к единственному члену  . .
Теорема. Число всех нормированных неприводимых полиномов степени n над 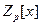 задаётся формулой задаётся формулой 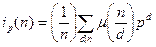 . .
Доказательство: Возьмём  , , 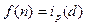 , подставим в предидущую формулу. , подставим в предидущую формулу.
Теперь можно перейти к тестам неприводимости полиномов в  . .
Тест1. Полином 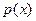 степени n>1
неприводим в степени n>1
неприводим в  тогда и только тогда когда тогда и только тогда когда
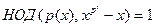 для для 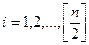 . .
Причём если полином приводим то тест сработает достаточно быстро. Для неприводимых полиномов этот тест становится медлительным из-за вычислений НОД в 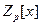 . Для исправления этого создан . Для исправления этого создан
Тест2. Полином 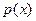 степени n>1
неприводим в степени n>1
неприводим в  тогда и только тогда когда тогда и только тогда когда 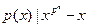 и и 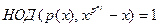 для всех для всех 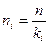 , , 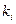 - простые делители n
. - простые делители n
.
Алгоритм Берлекампа разложения на множители над конечными полями. Идея Берлекампа основана на китайской теореме об остатках для полиномов:
Пусть 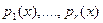 - полиномы из - полиномы из  , причём , причём  взаимно прост с взаимно прост с 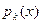 при при 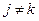 . Пусть . Пусть 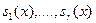 - произвольные полиномы из - произвольные полиномы из  . Тогда существует единственный полином . Тогда существует единственный полином 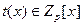 , такой что , такой что  и и 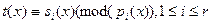 . Это же можно сформулировать на языке отображений: . Это же можно сформулировать на языке отображений:
Отображение, ставящее в соответствие полиному 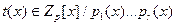 вектор вектор 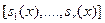 , где , где 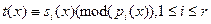 , является биекцией между , является биекцией между 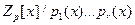 и и 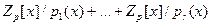 . .
Доказательство: Проводится расширенным алгоритмом Евклида. То есть определяются полиномы 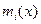 , такие что , такие что 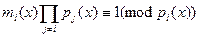 . Полагаем . Полагаем 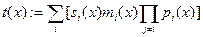 . Тогда . Тогда  , , 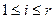 . Если бы нашёля такой . Если бы нашёля такой  , который бы был решением этих сравнений, то полином , который бы был решением этих сравнений, то полином 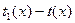 должен делиться на все должен делиться на все 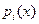 . Поэтому . Поэтому 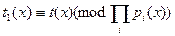 . .
Теорема. В поле GF(p) – поле Галуа (конечное поле, содержащее p (простое число) элементов) имеет место разложение:
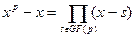 . .
Доказательство: В поле Галуа  (а также по малой теореме Ферма) . Значит s является корнем полинома (а также по малой теореме Ферма) . Значит s является корнем полинома 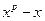 , то есть (x-
s
) является делителем , то есть (x-
s
) является делителем 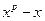 . А так как это выполнено для всех . А так как это выполнено для всех 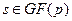 то то 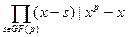 . Также следует заметить, что . Также следует заметить, что 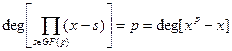 и это два нормированных полинома, из этого всего и следует их равенство. и это два нормированных полинома, из этого всего и следует их равенство.
Следствие. Для 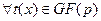 имеет место равенство: имеет место равенство:
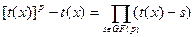 . .
Теорема. Пусть 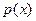 и и 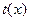 - два нормированных полинома над GF(p), такие что - два нормированных полинома над GF(p), такие что
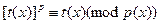 , , 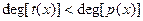 . .
Тогда 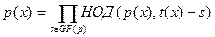
Доказательство: Из предположения следует, что  . Поэтому . Поэтому
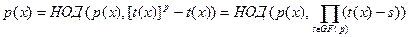
Помимо этого 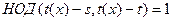 для для 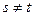 , и полиномы , и полиномы  и и 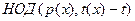 также взаимно просты. Поэтому также взаимно просты. Поэтому 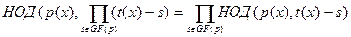 . .
Таким образом, пусть 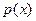 - свободный от квадратов полином степени n, который нужно разложить на множители над GF(p), и предположим, удалось найти полиномы - свободный от квадратов полином степени n, который нужно разложить на множители над GF(p), и предположим, удалось найти полиномы 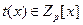 , , 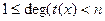 , такие что , такие что 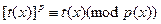 . По одной из ранее доказанных теорем, полином . По одной из ранее доказанных теорем, полином 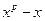 имеет в имеет в 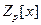 ровно p корней. А именно 0,1…p-1. Значит он раскладывается следующим образом ровно p корней. А именно 0,1…p-1. Значит он раскладывается следующим образом 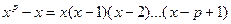 . Заменив х на . Заменив х на 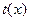 , в кольце , в кольце 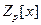 получим получим 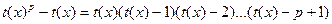 . Так как . Так как  , то , то 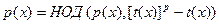 . Кроме того поскольку полиномы . Кроме того поскольку полиномы 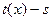 и и 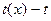 - взаимно простые при - взаимно простые при 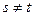 , то , то 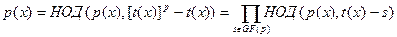 - нетривиальное разложение полинома над GF(p). - нетривиальное разложение полинома над GF(p).
Теперь задача состоит в определении полиномов 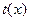 . Это можно осуществить с помощью решения систем линейных уравнений, получаемой следующим образом. Пусть . Это можно осуществить с помощью решения систем линейных уравнений, получаемой следующим образом. Пусть
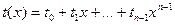 , где коэффициенты требуется найти. Нужно сначала проверить делит ли , где коэффициенты требуется найти. Нужно сначала проверить делит ли 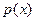 полином полином  . Ранее доказано, что . Ранее доказано, что 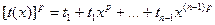 . .
Разделив 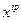 на на 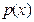 получаем получаем 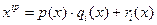 , где , где 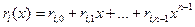 . Теперь, заменив . Теперь, заменив 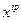 на соответствующие выражения, получим на соответствующие выражения, получим
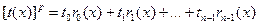 +[кратное +[кратное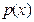 ]. ].
Таким образом 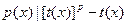 тогда и только тогда когда тогда и только тогда когда 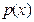 делит полином делит полином 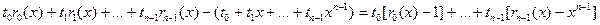 , степень которого , степень которого 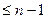 . Поэтому полином степени n будет делить этот полином если только он равен нулю. Приравняв его нулю и собрав коэффициенты при степенях х,
получаем систему из n линейных уравнений . Поэтому полином степени n будет делить этот полином если только он равен нулю. Приравняв его нулю и собрав коэффициенты при степенях х,
получаем систему из n линейных уравнений  . Это и есть коэффициенты того полинома . Это и есть коэффициенты того полинома 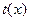 . .
Пусть 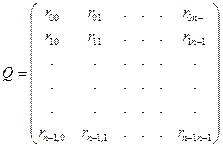 - матрица, строки которой образуют - матрица, строки которой образуют
коэффициенты полиномов остатков. По этому всему имеет место
Теорема. Полином  является решением сравнения является решением сравнения 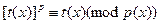 тогда и только тогда, когда тогда и только тогда, когда 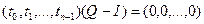 . .
Пусть N – множество векторов  , таких что , таких что 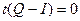 называется нуль-пространством
матрицы называется нуль-пространством
матрицы 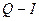 . У этого пространства имеется базис и размерность. . У этого пространства имеется базис и размерность.
Теорема. Число различных неприводимых сомножителей 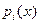 полинома полинома 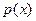 в в 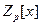 равно размерности нуль-пространства матрицы равно размерности нуль-пространства матрицы 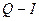 . .
Доказательство: Полином 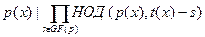 тогда и только тогда когда каждый тогда и только тогда когда каждый 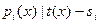 , , 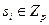 . По ранее доказанным фактам для набора . По ранее доказанным фактам для набора  существует единственный существует единственный 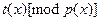 , такой что , такой что  . Существует . Существует 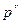 решений сравнения решений сравнения 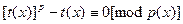 . . 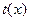 является решением сравнения если является решением сравнения если  . Для вопроса о неприводимости получен . Для вопроса о неприводимости получен
Тест3. Полином 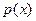 степени n>1
неприводим в степени n>1
неприводим в  тогда и только тогда когда нуль-пространство матрицы тогда и только тогда когда нуль-пространство матрицы 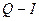 одномерно и одномерно и 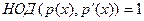 . .
Доказательство: Нуль-пространство матрицы 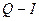 одномерно тогда и только тогда когда одномерно тогда и только тогда когда 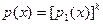 - степень неприводимого полинома. Тогда берём r(x)=1. - степень неприводимого полинома. Тогда берём r(x)=1.
Теорема. Пусть 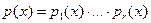 в в  и и 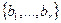 - базис нуль-пространства. Тогда для каждого - базис нуль-пространства. Тогда для каждого 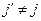 , ,  , существует k , существует k  и и 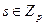 , такие что , такие что 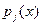 делит, а делит, а  не делит не делит  . .
Доказательство: В нуль-пространстве существует вектор, 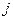 -ая компонента которой отлична от -ая компонента которой отлична от 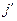 -ой. Значит найдётся такое k, -ой. Значит найдётся такое k,  , , 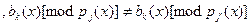 . Положим . Положим 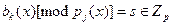 . .
Алгоритм
BA
(
Berlecamp
’
s
Algorithm
)
Вход: Нормированный, свободный от квадратов полином 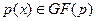 , ,  . .
Выход: Неприводимые над 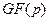 сомножители полинома сомножители полинома 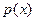 . .
Описание реализации:
- Построить матрицу Q.
2. Триангуляция этой матрицы. Привести матрицу Q к треугольному виду, вычислив её ранг n-r и найдя нуль-пространство (т.е. его базис 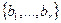 ). Здесь r – число неприводимых сомножителей полинома. Так как решением уравнения сравнения являются ). Здесь r – число неприводимых сомножителей полинома. Так как решением уравнения сравнения являются 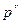 полиномов, соответствующие векторам полиномов, соответствующие векторам 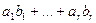 при любом выборе чисел при любом выборе чисел 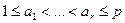 . И если r=1 то полином неприводим и алгороитм завершает работу. . И если r=1 то полином неприводим и алгороитм завершает работу.
3. Вычисление сомножителей. Пусть 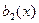 - полином, соответствующий вектору - полином, соответствующий вектору 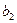 . Вычислим . Вычислим  для всех для всех 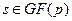 . Если с помощью . Если с помощью 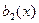 получено менее r сомножителей, вычислим получено менее r сомножителей, вычислим 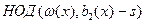 для всех для всех  и всех сомножителей и всех сомножителей 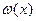 , найденных к данному времени, k=3,4,…,r, пока не найдётся r сомножителей. Это гарантируется предидущими теоремами. , найденных к данному времени, k=3,4,…,r, пока не найдётся r сомножителей. Это гарантируется предидущими теоремами.
На шаге 2 этого алгоритма матрица матрица Q приводится к треугольному виду, затрачивается время 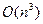 . Так как требуется не более p вычислений НОД для каждого базисного вектора и не более r из этих вычислений будут нетривиальны, то . Так как требуется не более p вычислений НОД для каждого базисного вектора и не более r из этих вычислений будут нетривиальны, то 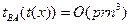 . Так что алгоритм не очень эффективен при больших p. Разберём . Так что алгоритм не очень эффективен при больших p. Разберём
Пример. Разложим над GF(13) полином  , свободный от квадратов. , свободный от квадратов.
Решение. Вместо данного полинома рассмотрим нормированный эквивалентный полином 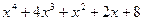 . .
Для начала вычислим обратные элементы ненулевым элементам GF(13) (1,…,12). Это соответственно будут (1,7,9,10,8,11,2,5,3,4,6,12).
Первая строка матрицы Q [4x4] всегда представляет собой (1,0,0,0), соответствуя полиному 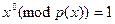 . Вторая строка представляет . Вторая строка представляет 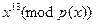 , третья , третья  , четвёртая , четвёртая  . .
Пусть 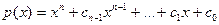 . Предположим, что . Предположим, что 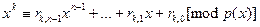 . Тогда . Тогда 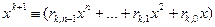 или или
 . Что означает . Что означает
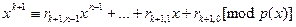 . Здесь . Здесь  , , 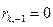 . .
Эти формулы объясняют вычисление 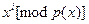 . Вычисления можно проводить используя массив . Вычисления можно проводить используя массив 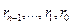 . В цикле . В цикле  , ,  ,…, ,…, 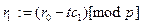 , , 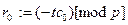 . Результаты отображаем в таблице: . Результаты отображаем в таблице:
| 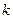
|
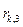
|
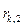
|
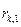
|
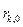
|
| 0
|
0
|
0
|
0
|
1
|
| 1
|
0
|
0
|
1
|
0
|
| 2
|
0
|
1
|
0
|
0
|
| 3
|
1
|
0
|
0
|
0
|
| 4
|
9
|
12
|
11
|
5
|
| 5
|
2
|
2
|
0
|
6
|
| 6
|
7
|
11
|
2
|
10
|
| 7
|
9
|
8
|
9
|
9
|
| 8
|
11
|
0
|
4
|
6
|
| 9
|
8
|
6
|
9
|
3
|
| 10
|
0
|
2
|
0
|
1
|
| 11
|
2
|
0
|
1
|
0
|
| 12
|
5
|
12
|
9
|
10
|
| 13
|
5
|
4
|
0
|
12
|
Нетрудно видеть вторую строку матрицы Q: (12,0,4,5). Аналогично строим для k=26,39 и получаем матрицу
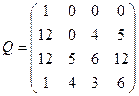 , , 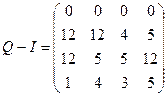 . .
Теперь нужно находить нуль-пространство матрицы Q-
I
. На основании эквивалентных преобразований матрицы составляется следующий алгоритм NS (Null-Space algorithm):
Вход: Матрица размера n  , , 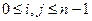 , с элементами из поля. , с элементами из поля.
Выход: Линейно независимые вектора  , такие что , такие что 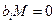 , n-
r
– ранг матрицы М
. , n-
r
– ранг матрицы М
.
Реализация:
- r:=0;
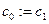 ,…, ,…, 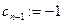
2. Для h от 0 до n-1 : если найдётся столбец с номером h и 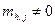 , , 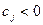 , j=0,…,n-1, то , j=0,…,n-1, то
j-тый столбец матрицы M умножаем на 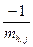 , чтобы , чтобы 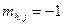 , затем для всех , затем для всех 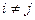 прибавляем умноженный на прибавляем умноженный на  столбец j
к столбцу i
. И столбец j
к столбцу i
. И 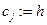 . Если не найдётся столбца j
, чтобы . Если не найдётся столбца j
, чтобы 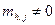 , то положить , то положить 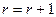 , выдать вектор , выдать вектор 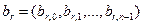 , где для , где для 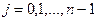

если 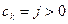 , если таких k не одно, то взять любое. , если таких k не одно, то взять любое.
если 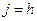
в противном случае.
При 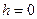 получится вектор получится вектор 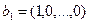 . Он соответствует полиному-константе 1. При . Он соответствует полиному-константе 1. При  можно взять j равным 0,1,2,3, поскольку можно взять j равным 0,1,2,3, поскольку 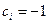 для i=1,2,3 – выбор на данном этапе полностью произволен, хотя он и влияет на получаемые при выходе векторы. Берём j=0 и после ранее описанных преобразований матрица Q имеет вид: для i=1,2,3 – выбор на данном этапе полностью произволен, хотя он и влияет на получаемые при выходе векторы. Берём j=0 и после ранее описанных преобразований матрица Q имеет вид:
 . .
Второй элемент в первом столбце 12 – означает 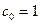 . Для h=2 матрица будет . Для h=2 матрица будет
 . .
Третий элемент второго столбца означает, что 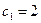 . Два последние столбца, состоящие только из нулей, обуславливают на выходе вектор . Два последние столбца, состоящие только из нулей, обуславливают на выходе вектор 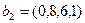 при h=3. Соответствующий полином будет при h=3. Соответствующий полином будет 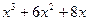 . .
Из вида матрицы Q-I при h=3 видно, что векторы 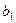 и и 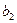 удовлетворяют условию удовлетворяют условию  . Так как эти вычисления дали только два линейно независимых вектора, то . Так как эти вычисления дали только два линейно независимых вектора, то 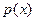 должен иметь только два неприводимых сомножителя над GF(13). должен иметь только два неприводимых сомножителя над GF(13).
Теперь нужно переходить к третьему шагу алгоритма Берлекампа, в котором непосредственно найдутся эти сомножители. Этот шаг состоит в нахождении 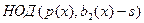 для всех для всех  . Здесь . Здесь 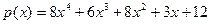 и и  . После вычислений получаем при . После вычислений получаем при 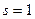 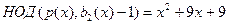 и при и при 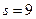 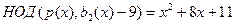 . Непосредственная проверка показывает, что полиномы найдены правильно. . Непосредственная проверка показывает, что полиномы найдены правильно.
Но если p
достаточно велико, то алгоритм имеет огромную трудоёмкость, связанную с вычислением НОДов для всех 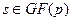 . Лучший способ вычислений был предложен Кантором и Пассенхаузом, и с ними мне предстоит разобраться в следующей курсовой работе. . Лучший способ вычислений был предложен Кантором и Пассенхаузом, и с ними мне предстоит разобраться в следующей курсовой работе.
|