|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОУ ВПО УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ – УПИ
Радиотехнический институт – РТФ
Курсовая работа
<<Проектирование пассивных электрических фильтров>>
Подпись Дата Ф.И.О.
Преподаватель _____________________________________________Шилов Ю.В.
Студент группы
Р - 24044 ______________________________________________Зверев А.М.
2006 г.
Содержание
Содержание............................................................................................................................................................................................... 2
Реферат.......................................................................................................................................................................................................... 3
Характеристики аналоговых фильтров......................................................................................................................................... 3
Классификация фильтров по виду частотных характеристик........................................................................................... 4
Этапы проектирования фильтра........................................................................................................................................................ 5
Нормирование параметров фильтра и преобразование частоты...................................................................................... 6
Правила преобразования элементов и расчетные соотношения для основных видов преобразований....... 7
Расчет и реализация пассивных LС-фильтров............................................................................................................................ 8
Алгоритм расчета комплексной частотной характеристики лестничной цепи........................................................ 9
Перечень условных обозначений, единиц и терминов................................................................................ 12
Задание........................................................................................................................................................................................................ 13
Основная часть................................................................................................................................................................................... 14
1. Нормировка параметров................................................................................................................................................................ 14
2. Выбор порядка фильтра................................................................................................................................................................... 14
3. Параметры нормированного прототипа ФНЧ...................................................................................................................... 14
4. Преобразование ФНЧ®
ФВЧ........................................................................................................................................................... 14
5. Денормировка параметров............................................................................................................................................................ 15
6. АЧХ и ФЧХ фильтра............................................................................................................................................................................ 15
7. Влияние на АЧХ и ФЧХ разброса параметров индуктивностей и емкостей.......................................................... 16
8. Нули и полюсы системной функции........................................................................................................................................ 16
Заключение............................................................................................................................................................................................ 17
Библиографический список................................................................................................................................................... 18
Приложение............................................................................................................................................................................................ 19
Реферат
Фильтрующие цепи играют важную роль в системах связи и в электрических контрольно-измерительных устройствах. В современной радиотехнике под фильтрацией сигналов на фоне помех понимают любое выделение параметров случайных процессов, отражающих полезную информацию (сообщение). Вместе с тем сохраняется и традиционное, более узкое, представление о фильтрации, связанное с частотной селекцией сигналов.
Под электрическим фильтром в традиционном смысле понимается цепь, обладающая избирательностью реакции на внешнее воздействие. Характеристики фильтра могут задаваться во временной или частотной области, в последнем случае требования к фильтру обычно диктуют определенную избирательность в заданном диапазоне частот.
Электрические фильтры можно классифицировать по различным признакам. По способу построения и используемой элементной базе различаются следующие типы фильтров: фильтры на сосредоточенных элементах (LC-фильтры), кварцевые и керамические, электромеханические фильтры, фильтры на отрезках длинных линий (СВЧ-фильтры), активные RС-фильтры на сосредоточенных и распределенных элементах, коммутируемые и цифровые фильтры, фильтры на поверхностных акустических волнах.
Характеристики аналоговых фильтров.
Ниже рассматриваются фильтры с одним входом и одним выходом, состоящие из линейных элементов, параметры которых не зависят от времени (рис. 1).
Выходной сигнал такого фильтра линейно связан с входным. Эта связь во временной области описывается интегралом свертки: где h
(
t
)
-.импульсная характеристика фильтра.
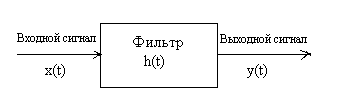
Рис.1. Линейный фильтр
Связь между входным и выходным сигналами в частотной области можно получить, применив к выше приведенной формуле преобразование Лапласа:
Y
(
p
)=
H
(
p
)
X(p)
Здесь Н(р)
- преобразование Лапласа для h
(
t
)
(передаточная функция фильтра). При p
=jω
она является комплексной частотной характеристикой (КЧХ) H(
jω
)
. Таким образом, где Н(jω)
- амплитудно-частотная характеристика (АЧХ) фильтра;
φ(ω) -
фазо-частотная характеристика (ФЧХ) фильтра.
В зависимости от вида входной и выходной переменных передаточная функция и КЧХ могут иметь размерность сопротивления, проводимости либо быть безразмерными. В частности, КЧХ по напряжению определяется как где U
вых
(jω)
и U
вх
(
jω
)
-
комплексные амплитуды входного и выходного напряжений.
Наряду с этой характеристикой широко используется частотный коэффициент передачи мощности: В отличие от КЧХ, частотный коэффициент передачи мощности является действительной функцией частоты и поэтому в ряде случаев удобен для задания исходных данных при проектировании фильтров. Однако эта функция не содержит в общем случае сведений о ФЧХ фильтра.
Передаточная функция физически реализуемого фильтра представляет собой отношение полиномов: где Н,а,
b
- действительные постоянные коэффициенты; т,п = 1,2,..., т≤п.
Степень полином знаменателя определяет порядок фильтра.
Наряду с частотными характеристиками передачи (в переменных выход-вход) широко применяются частотные характеристики затухания (в переменных вход-выход), использующие не само отношение переменных, а логарифм При этом А(
ω)
называется логарифмической амплитудно-частотной характеристикой (ЛАЧХ) фильтра и измеряется в децибелах.
Для расчета фильтров, я пользуюсь специальным справочником по расчету фильтров, автора Зааля Р. Он специально предназначен в помощь инженеру при решении большинства задач по расчету фильтров, он позволяет избежать трудоемких вычислений, которые требуют синтезы цепей, и составления сложных машинных программ или применение вычислительных машин.
Классификация фильтров по виду частотных характеристик.
Диапазон частот, в котором затухание фильтра минимально (для идеального фильтра равно нулю), называется полосой пропускания. Обычно это диапазон частот, занимаемый преимущественно полезным сигналом.
Диапазон частот, в котором затухание фильтра максимально (для идеального фильтра равно бесконечности), называется полосой подавления (задерживания). Обычно это диапазон частот, занимаемый преимущественно помехой.
Диапазон частот, лежащий между полосой пропускания и полосой подавления, называют переходной полосой;
В зависимости от взаимного расположения полос подавления и пропускания различают следующие типы фильтров:
1 Фильтр нижних частот (ФНЧ) - фильтр с полосой пропускания от 0 до частоты ωс и с полосой подавления от ωс до бесконечности (ωс<ωs).
2. Фильтр верхних частот (ФВЧ) - фильтр с полосой пропускания от частоты ωс до бесконечности и с полосой подавления от 0 до ωс (ωс >ωs).
3. Полосовой фильтр (ПФ) - обе границы полосы пропускания представляют собой ненулевые частоты ωсн, ωсв, а с каждой из сторон от полосы пропускания имеется по одной полосе подавления (от 0 до ωsh и от ωsh до ∞).
4. Режекторный (заграждающий) фильтр (РФ) - фильтр с двумя полосами пропускания (от 0 до ωсн и от ωсв до ∞) и одной полосой подавления.
5. Гребенчатый фильтр (ГФ) - фильтр с несколькими полосами подавления и несколькими полосам пропускания.
6. Все пропускающий фильтр постоянного затухания (ФПЗ) - фильтр с единичной (постоянной) передачей для всех частот (т. е. с полосой пропусками от 0 до ∞); используется для обеспечения требуемой фазовой коррекции и фазового сдвига.
Требования к амплитудно-частотной характеристике фильтра в первую очередь включают параметры полосы подавления, полосы пропускания и переходной полосы.
В идеальном случае затухание фильтра должно быть равным нулю в полосе пропускания и стремиться к бесконечности в полосе подавления. В теории цепей на основе так называемого критерия Пели-Виннера доказывается, что фильтры с прямоугольной АЧХ физически нереализуемы. Поэтому первая задача построения фильтра - аппроксимация идеальной прямоугольной характеристики функцией цепи, удовлетворяющей условиям физической реализуемости. Эта задача имеет многочисленные решения, доведенные до ряда стандартных функциональных построений, которые основаны на различных способах аппроксимации.
Наиболее употребительными являются следующие типы фильтров, отличающиеся видом аппроксимирующей функции:
1. Фильтр Баттерворта, имеющий максимально плоскую АЧХ в полосе пропускания и монотонно возрастающее затухание в полосе задерживания.
2. Фильтр Чебышева с равно волновой АЧХ в полосе пропускания и монотонно возрастающим затуханием в полосе подавления.
3. Инверсный фильтр Чебыщева с монотонно возрастающим в полосе пропускания затуханием и равно волновой АЧХ в полосе подавления.
4. Эллиптический фильтр (фильтр Золотарева-Кауэра) с равно волновой АЧХ, как в полосе пропускания, так и в полосе подавления.
5. Фильтр Бесселя (фильтр с максимально плоской характеристикой группового времени
запаздывания) с аппроксимацией ФЧХ рядом Тейлора.
Фильтры с характеристиками указанных типов могут быть реализованы как пассивными LC-цепями, так и активными RC-схемами, а также цифровыми методами.
Этапы проектирования фильтра.
Проектирование фильтра начинается с задания технических характеристик фильтра, которые обычно формируются в виде требований к АЧХ в полосе пропускания и полосе подавления, ширине переходной полосы, требований к ФЧХ или характеристике группового времени запаздывания, а также к другим параметрам, например, к сопротивлению нагрузки, внутреннему сопротивлению источника, уровню сигнала и т. п.
На втором этапе решается задача нахождения подходящей передаточной функции, удовлетворяющей заданным требованиям. Эта задача сводится к выбору аппроксимирующей функции, то есть к выбору фильтра соответствующего типа.
Третий этап - схемная реализация выбранной на втором этапе передаточной функции. Решение этой задачи для основных типов фильтров (Баттерворта, Чебышева, эллиптических), реализуемых как в виде пассивных LC-схем, так и в виде активных четырехполюсников на базе операционных усилителей (ОУ), охваченных обратной связью, доведено до обширных таблиц и графиков. Тем самым в инженерных приложениях второй и третий этапы сводятся к выбору типа фильтра (вида аппроксимирующей функции) и определению по таблицам или графикам соответствующих коэффициентов передаточной функции, устанавливающих в конечном итоге параметры элементов фильтра.
Четвертый этап - анализ фильтра, то есть исследование его характеристик на соответствие требуемым допускам, чувствительности к изменению параметров схемы, возможностям настройки и т. п.
Сначала такой анализ выполняется при номинальных значениях параметров, чтобы проверить правильность расчетов, произведенных на втором и третьем этапах. Затем учитываются погрешности элементов. Необходимость этого объясняется следующими причинами. При изготовлении спроектированного фильтра невозможно абсолютно точно подобрать его элементы. Разброс параметров реальных резисторов; конденсаторов и катушек индуктивности обычно находится в пределах нескольких процентов. В связи с этим анализ должен дать ответ на вопрос о допустимом разбросе параметров элементов фильтра, при котором еще выполняется техническое задание на проектирование.
Кроме того, в процессе эксплуатации неизбежно изменение параметров элементов фильтра за счет старении, изменения климатических условий и т.п. Анализ позволяет учесть и этот фактор и принять соответствующие меры для стабилизации характеристик фильтра.
При достаточно большом числе элементов фильтра такой анализ выполнить вручную весьма сложно, а порой и просто невозможно (например, при попытках учесть случайный характер изменения параметров элементов). Поэтому эти расчеты и моделирование выполняют на ПЭВМ с использованием различных пакетов прикладных программ анализа электронных схем.
На следующей стадии проектирования осуществляется сравнение технических требований с характеристиками, рассчитанными на этапе анализа. Если требования не выполняются, необходимо изменить параметры фильтра, выбрать другой тип или снизить требования к характеристикам и повторить расчеты. После получения удовлетворительных характеристик переходят к этапу экспериментальной реализации фильтра.
Нормирование параметров фильтра и преобразование частоты.
Для использования на этапе расчета фильтра графиков и таблиц, помещенных в справочниках, то есть для обращения к «каталогу фильтров», необходимо проектируемый фильтр привести к каноническому виду. Это приведение основано на двух процедурах: нормировании параметров фильтра и частотного диапазона и преобразовании частоты.
Нормирование заключается в переходе от размерных физических величин к безразмерным и близким к 1 за счет выбора подходящих нормирующих величин.
Преобразование частоты представляет собой процедуру, с помощью которой требования к ФВЧ, ПФ, ЗФ преобразуются в требования к ФНЧ, называемому фильтром-прототипом. Эта же процедура после расчета фильтра-прототипа дает простой способ перехода от ФНЧ к более сложным типам фильтров.
При выборе нормирующих величин следует учитывать, что полное сопротивление, частота, индуктивность и емкость связаны между собой. Поэтому только две переменные могут быть нормированы независимо. Чаще всего это полное сопротивление и частота. Если взять нормирующую частоту f
в
в Гц и нормирующее сопротивление R
в
в Ом, то получим прочие нормирующие величины:
нормирующее время в секундах
T
в
= 1/2п
f
в
= 1/
ω
в
= 1/6.283185
f
в
нормирующую индуктивность в генри
L
в
=
R
в
/2п
f
в
нормирующую емкость в фарадах
С
в
= 1/2п
f
в
R
в
Тогда нормированные(безразмерные) значения определятся следующими выражениями:
значения частоты
Ω =
f
/
f
в
=
ω
/
ω
в
времени
t = T/T
в
групповой задержки
τ
g
=
T
g
/
T
в
сопротивления
r
=
R
/
R
в
индуктивности
ι
=
L
/
L
в
и емкости
с = С
/C
в
В качестве основных нормирующих величин R
в
и f
в
обычно выбираются сопротивления нагрузки R
2
(или внутреннее сопротивление источника R
1
) и частота в некоторой удобной точке (чаще всего частота среза f
с
).
Сущность преобразования частоты заключается в замене частотной переменной ω
нч
во всех частотных характеристиках фильтра-прототипа на функцию ω
нч
=
W(ω)
.
Такое преобразование приводит к замене индуктивного и емкостного сопротивлений прототипа на новые реактивные сопротивления, характер и величина которых могут быть определены из выражений.
ω
нч
L
нч
=
W(ω)L
нч
1
/ω
нч
C
нч
= 1/ W(ω)
Правила преобразования элементов и расчетные соотношения для основных видов преобразований. Обратный переход от нормированных к денормированным (размерным) значениям физических параметров схемы фильтра осуществляется путем соответствующего выбора конкретных значении fв и Rв.
Правила преобразования элементов и расчетные соотношения для основных видов преобразований.
Преобразование ФНЧ-ФНЧ (масштабирование по частоте)
осуществляется путем следующей замены переменной:
Ω =
W(ω) = ω/ω
c
Таким образом, если фильтр прототип имел частоту cpеза, равную 1, то новый фильтр будет иметь частоту среза ω
с
.
Характер реактивных сопротивлений в преобразованной схеме сохраняется, изменяется только величина элементов:
Преобразования ФНЧ-ФВЧ
осуществляется путем следующей смены переменной: При этом индуктивное сопротивление прототипа ωнчLнч преобразуется в емкостное
где
и наоборот, емкостное, в индуктивное
где
Преобразование частоты приводит к тому, что точки на АЧХ фильтра-прототипа, соответствующие частоте среза ωср и границе полосы подавления (частоте гарантированного затухания) ωsнч, отображаются в точки, соответствующие частоте среза и частоте гарантированного затухания ФВЧ.
В частности, если преобразованию подвергается нормированный фильтр прототип с частотой среза Ωснч=1, то параметр преоброзования А
равен частоте среза проектируемого ФВЧ.
При задании требований к характеристике затухания ФВЧ необходимая избирательность фильтра-прототипа, определяющая его порядок, вычисляется из соотношения
Расчет и реализация пассивных
LС-фильтров.
 Под пассивным фильтром подразумевается реактивный четырехполюсник (четырехполюсник без потерь), нагруженный со стороны выходных зажимов на сопротивление нагрузки R
2
, а со стороны входных - на внутреннее сопротивление генератора R
1
,
как это показано на рис.2. Под пассивным фильтром подразумевается реактивный четырехполюсник (четырехполюсник без потерь), нагруженный со стороны выходных зажимов на сопротивление нагрузки R
2
, а со стороны входных - на внутреннее сопротивление генератора R
1
,
как это показано на рис.2. Рис.2. Реактивный четырехполюсник с нагрузкой на входе и выходе
При расчете таких фильтров для их описания вводят два коэфицента – коэфициент передачи мощности и коэффициент отражения – определяемые по следующей методике.
Максимальная мощность, которая может поступить от источника в нагрузку, рассчитывается по формуле
Мощность, поступающая в нагрузку через реактивный четырехполюсник, определяется выражением
С учетом этого коэффициент передачи мощности определяется отношением
оэффицент отражения определяется как дополнение оэффицента передачи мощности до 1:
Отсюда следует, что изменение коэффициента отражения в полосе пропускания приводит к изменению затухания на величину, дБ,
Иначе В справочниках по расчету фильтров используют как максимально допустимый коэффицент отражения, так и максимальную неравномерность АЧХ затухания.
Часто вместо коэффицента передачи мощности используется характеристическая функция θ(
iω
)
, определяемая из соотношения
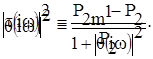 |
Откуда следует, что Существует несколько методов реализации заданной передаточной функции пассивной цепью. Наибольшее распространение получили три основные схемные структуры: лестничные схемы, мостовые схемы и схемы Дарлингтона. Тематика курсовой работы предполагает разработку пассивного LС -фильтра лестничной структуры. Лестничные схемы обладают важным преимуществом, вытекающим из следующего свойства: нуль передачи лестничной цепи достигается на тех частотах, на которых полное сопротивление последовательной ветви или полная проводимость параллельной ветви равны бесконечности. Из этого следует, что каждой ветвью обусловлен нуль передачи (полюс затухания). Это делает настройку лестничного фильтра относительно простой. Также благодаря этому нули передачи (полюса затухания) менее чувствительны к изменению параметров элементов по сравнению со схемами, в которых частота полюса (нуля) определяется условием баланса моста.
Расчет пассивного LC-фильтра лестничной структуры осуществляется в следующей последовательности.
1. Нормирование частоты и определение нормирующих параметров у элементов фильтра.
2. Переход к фильтру-прототипу и определение параметра избирательности фильтра-прототипа.
3. Выбор типа и порядка фильтра-прототипа.
4. Определение по таблицам и графикам нормированных параметров фильтра-прототипа.
5. Преобразование частоты - переход от фильтра-прототипа к ФВЧ или ПФ.
5. Денормирование параметров элементов фильтра.
Нормирование частоты можно производить и после перехода к фильтру-прототипу.
Алгоритм расчета комплексной частотной характеристики лестничной цепи.
Под лестничной цепью понимают пассивный линейный четырехполюсник, образованный путем каскадного соединения обратных Г-образных звеньев (рис.6). Пассивные фильтры чаще всего строятся на основе именно таких структур.
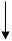  
При расчете КЧХ продольные ветви такой цепи удобно обозначать как сопротивления с нечетными индексами. Внутренне сопротивление источника включается в состав сопротивления Z1, а проводимость нагрузки – в состав проводимости Y2n.
Составляя уравнения Кирхгофа последовательно для первого контура и первого узла, затем для второго контура и второго узла и т.д., получаем систему из 2n уравнений и с 2n неизвестными (токи и напряжения). I
1Z
1 + U
2 = E (1 контур),
-I
1 + Y
2U
2 + I
3 = 0 (1 узел),
-U
2 + I
3Z
3 + U
4 = 0 (2
контур
),
-I
3 + Y
4U
4 + I
5 = 0 (2
узел
),
………………………………….
-U
2n + I
2nZ
2n + U
2n = 0 (n-й
контур
),
-I
2n-1 + Y
2nU
2n =
0 (n-
й узел
).
Или в матричной форме где [IU] = [I1,U2,I3,U4,…,I2n-1,U2n] – вектор-столбец электрических переменных схемы (токов и напряжений);
[E] – вектор-столбец источников; [ZY] – матрица параметров схемы, имеющая следующий вид;
Уравнение всегда разрешимо: Можно избежать трудностей вычисления обратной матрицы [ZY], если воспользоваться некоторыми свойствами трехдагональных матриц, к которым относится матрица параметров [ZY]
Решение системы линейных уравнений методом Крамера дает: где ∆ - определитель матрицы параметров;
∆2n – определитель матрицы, полученной из [ZY] путем замены последнего столбца на вектор-столбец [E].
Раскладывая определитель ∆2n по элементам последнего столбца и учитывая, что остающийся при этом определитель треугольный, получаем: Передаточная функция по напряжению по определению
Откуда с учетом выше приведенных формул получаем, что КЧХ по напряжению и ее модуль определяются выражениями:
а затухание – соответственно
Таким образом, задача построения АЧХ сводиться к расчету определителя матрицы, выполняемому по рекуррентной схеме:
Далее, пользуясь методом математической индукции, приходим к следующему рекуррентному соотношению: Подчеркнем, что в общем случае элементы матрицы [ZY] носят комплексный характер, поэтому необходимо отдельно вычислять действительные и мнимые части определителя.

Перечень условных обозначений, единиц и терминов.
fc
-частота среза фильтра, кГц;
fs
-частота гарантированного затухания, кГц; граница полосы подавления;
Аs
-гарантированное затухание в полосе подавления, дБ;
Ad
-неравномерность частотной характеристики в полосе пропускания, дБ;
r-коэффициент отражения, %;
R-сопротивление нагрузки, Ом.
Задание
1. Спроектировать фильтр в виде реактивного четырехполюсника лестничной структуры с нагрузкой на входе и выходе, удовлетворяющий ниже перечисленным требованиям.
2. Привести полную схему фильтра и рассчитать АЧХ и ФЧХ фильтра в диапазоне (0¸3)fс
.
3. Исследовать влияние на АЧХ и ФЧХ разброса параметров индуктивностей и емкостей в пределах ±dL% и ±dC% относительно номинального значения.
Тип фильтра-ФВЧ Кауэра (эллиптический).
Значения параметров:
fс
=375 кГц
fs
=325 кГц
Аs
=25 дБ
r=7%
dL=0,5%
dС=0,5%
Основная часть
1. Нормировка параметров
2. Выбор порядка фильтра
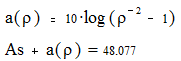
по графику выбираем порядок фильтра: n=7.
3. Параметры нормированного прототипа ФНЧ
Аs
=36,6 дБ Ws
=1,154700538 Аd
=0,0109 дБ
| n
|
C`2
n
-1
|
l`2
n
|
c`2
n
|
W¥
2
n
|
Wo
n
|
-an
|
±bn
|
| 1
|
0,655615
|
1,174721
|
0,197222
|
2,077564703
|
0
|
0,858149
|
0
|
| 2
|
1,137083
|
0,698751
|
1,047479
|
1,168869467
|
0,5557952234
|
0,534179
|
0,7795035
|
| 3
|
0,985395
|
0,680458
|
0,838932
|
1,323536714
|
0,8724355936
|
0,193429
|
1,0084229
|
| 4
|
0,286352
|
0,9878780920
|
0,044815
|
1,0538538
|
Cof=11.491824010
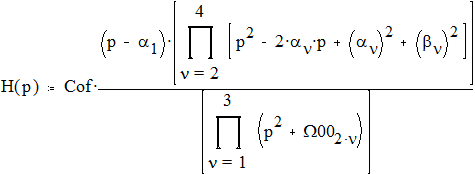
4. Преобразование ФНЧ
®ФВЧ
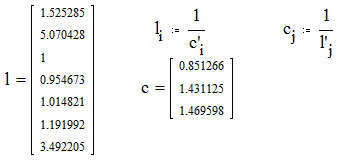
5. Денормировка параметров
6. АЧХ и ФЧХ фильтра
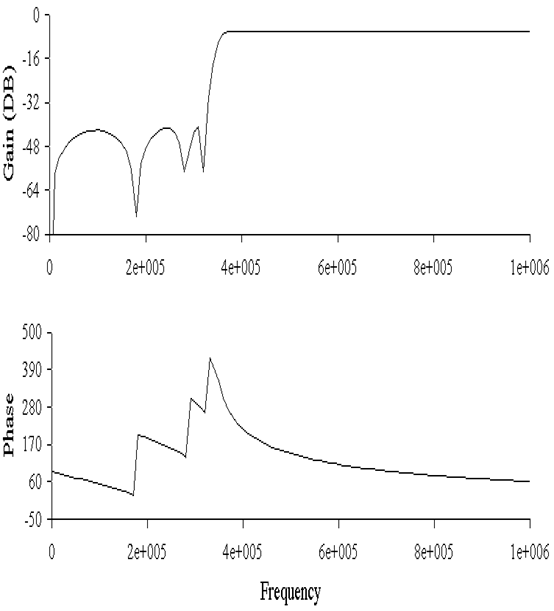
Расчет АЧХ и ФЧХ фильтра проводился при помощи программы Electronics Workbench v.5.0c, в ветвях цепи, содержащих индуктивности задавались сопротивления потерь равные 10-7
Ом.
7. Влияние на АЧХ и ФЧХ разброса параметров индуктивностей и емкостей
Точные параметры индуктивности увеличены на 0,5 %
Емкости увеличены на 0,5 % индуктивности и емкости увеличены на 0,5%
L увеличены, C уменьшены на 0,5 % емкости увеличены, инд. уменьшены на 0,5 %
В результате проведенного анализа можно сделать вывод что в пределах разброса параметров индуктивностей и емкостей ± 0.5 % схема сохраняет необходимые избирательные свойства. При изменении параметров меняются только максимальные значения затухания без сдвига их по частоте.
8. Нули и полюсы системной функции
Заключение
Библиографический список
1. Г. И. Атабеков Теоретические основы электротехники М.: Энергия, 1966
2. Зааль Р. Справочник по расчету фильтров: Пер. с нем. М.: Радто и связь, 1985
3. Коберниченко В. Г., Мальцев А.П. Шилов Ю.В. Проектирование пассивных и активных фильтров: Методические указания. Екатеринбург:ГОУ ВПО УГТУ-УПИ, 2001
Приложение.
Пассивный фильтр лестничной структуры. |