| РОССИЙСКАЯ АКАДЕМИЯ НАУК
Ордена Ленина
Институт прикладной математики
им. М.В. Келдыша
М.П. Галанин, С.А. Лазарева
Локальная гладкость и асимптотика решения
метода конечных суперэлементов
в угловых точках разбиения
Москва – 2008
Аннотация(*)
В работе представлены результаты теоретических исследований характеристик метода конечных суперэлементов Федоренко (МКСЭ). Определены регулярность приближенного решения МКСЭ, его асимптотика в окрестности угловых точек разбиения области на подобласти-суперэлементы.
M. Galanin, S. Lazareva
Local regularity and asymptotic behavior of the
finite superelement method solution
near the corner points of decomposition
Abstract
In this paper characteristics of Fedorenko finite superelement method (FSEM) is theoretically investigated. Regularity of the approximate solution is given. Asymptotics near the corner points of decomposition on subdomains-superelements is examined.
Содержание
Введение .……………………………………………………………………....3
1. Принципы МКСЭ.. 4
2. Обозначения и определения. 8
3. Локальная гладкость приближенного решения МКСЭ.. 14
4. Оценки решения по шкале H
M
(Ω) 23
Заключение. 28
Список литературы.. 28
Введение
Основанием для разработки и развития метода конечных суперэлементов Федоренко (МКСЭ) является проблема численного решения сложных вычислительных задач, содержащих резкие особенности, или “сингулярности”, решения. В этих случаях размеры расчетной области составляют значительную величину в сравнении с областью проявления особенностей.
Данная работа является продолжением исследований [3 – 12] по выявлению качественных характеристик МКСЭ. В ней определены регулярность приближенного решения МКСЭ, установлена его асимптотика в окрестностях угловых точек разбиения области на подобласти-суперэлементы (СЭ). Работа выполнена на примере задачи Дирихле для уравнения Лапласа. Для достижения поставленной цели использованы теория весовых пространств Соболева и Кондратьева, теория эллиптических задач в областях с угловыми точками, свойства регулярности решений вариационных задач в негладких областях. Работа направлена на поиск оптимальных аппроксимаций метода и способов его применения.
МКСЭ позволяет решать задачи, содержащие мелкие “сингулярности” в расчётной области в пространстве слабых решений, обладая при этом погрешностями, оцениваемыми через ограничения этого решения на гладкие части суперэлементных границ. Это не требует использования сеток, сгущающихся в окрестностях “сингулярностей”, и связано с выбором особых аппроксимирующих пространств. Однако поведение приближений МКСЭ в пространствах сильных и гладких решений также представляет интерес.
При решении задачи рассматриваемая проблема возникает естественным образом. Как правило, искомое решение при достаточно гладкой границе области и подходящих граничных условиях обладает производными (например, суммируемыми с квадратом) до порядка 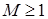 . Вторым распространенным вариантом является гладкое, обладающее производными высокого порядка, решение в окрестностях границ разбиения области на подобласти-суперэлементы. . Вторым распространенным вариантом является гладкое, обладающее производными высокого порядка, решение в окрестностях границ разбиения области на подобласти-суперэлементы.
Производные представляют важные (а часто и определяющие) физические характеристики поставленной задачи. Например, такими характеристиками могут быть скорости и ускорения в механике, гидродинамике; напряжения, деформации и скорость их роста в теории упругости; напряженности и силы в теории поля; мощность тепловых источников и потоки газа в теории переноса теплоты и др. Полученные в работе результаты позволяют определить поведение погрешностей приближения производных решения первого и более высокого порядков.
Связующим звеном такого исследования является определение гладкости приближений МКСЭ, их асимптотического поведения в окрестностях углов декомпозиции. Помимо того, определение возможной гладкости приближенного решения в пределах СЭ и во всей области и нахождение его асимптотики представляют самостоятельный интерес.
Метод конечных суперэлементов (МКСЭ) предложен в работах Федоренко и его коллег [1–2] и входит в класс численных методов, основанных на декомпозиции области в сочетании с выбором особой аппроксимации решения. Функции, с помощью разложения по которым разыскивается приближенное решение МКСЭ, являются решениями исходной системы уравнений в части области со специальными условиями на ее границе и, следовательно, заведомо содержат в себе ряд характеристик решения рассматриваемой задачи. Для авторов метода и данной работы главный интерес представляют задачи, характеризующиеся наличием ряда резких особенностей, проявляющихся на малых по сравнению с основной областью пространственных подобластях. Такие особенности могут представлять собой “сингулярности” решения, порожденные резкими неоднородностями геометрии области либо физической или математической модели. В работах [1–12] эффективность МКСЭ подтверждена примерами решения задач разнообразного физического происхождения.
Все дальнейшие рассмотрения мы проведем на примере задачи Дирихле для уравнения Лапласа в двумерной области 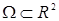 . Область . Область 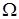 представляет собой квадрат с исключенными из него кругами, радиус которых мал по сравнению с размерами Ω (рис. 1). Полагаем, что в окрестностях таких мелких отверстий сосредоточены все резкие “сингулярности” решения. представляет собой квадрат с исключенными из него кругами, радиус которых мал по сравнению с размерами Ω (рис. 1). Полагаем, что в окрестностях таких мелких отверстий сосредоточены все резкие “сингулярности” решения.
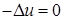 в в 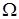 , ,
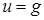 на на  , ,
где 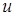 – искомая функция, – искомая функция,  – граница расчетной области, – граница расчетной области, 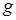 – некоторая известная функция на – некоторая известная функция на  . .
Как и в обычном методе конечных элементов (МКЭ) для численного решения задачи разобьем расчетную область на некоторое число подобластей, называемых суперэлементами
. Каждое предполагаемое место сосредоточения особенности (отверстие, неоднородность и т.п.) при этом должно быть заключено строго внутри одного СЭ. На рис. 2 показан пример равномерного разбиения области 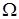 на квадратные СЭ на квадратные СЭ 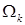 с границей с границей 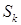 , , 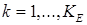 , где , где  – общее число подобластей-суперэлементов. Функции, разложением по которым разыскивается приближенное решение, для краткости будем называть базисными. Они являются финитными, их носители связаны с СЭ. При этом задание аппроксимаций в МКСЭ связано не со всей двумерной подобластью – общее число подобластей-суперэлементов. Функции, разложением по которым разыскивается приближенное решение, для краткости будем называть базисными. Они являются финитными, их носители связаны с СЭ. При этом задание аппроксимаций в МКСЭ связано не со всей двумерной подобластью 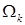 , а только с её одномерной границей. , а только с её одномерной границей.
Рассмотрим аппроксимации МКСЭ в одном СЭ 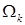 , где , где  - некоторое фиксированное число. На его одномерной границе - некоторое фиксированное число. На его одномерной границе 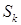 зададим набор функций зададим набор функций 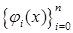 , , 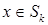 , которые назовем граничными базисными функциями
. В узлах СЭ , которые назовем граничными базисными функциями
. В узлах СЭ  и на границе его отверстия и на границе его отверстия  они равны они равны
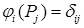 , ,  , , 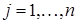 , ,
где  – символ Кронекера. Узлы СЭ – символ Кронекера. Узлы СЭ 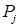 расположены только на его ребрах и в углах (рис. 3). Символ расположены только на его ребрах и в углах (рис. 3). Символ  , имеющий нулевой индекс, обозначает не один узел, а всю границу отверстия. В том случае, если СЭ , имеющий нулевой индекс, обозначает не один узел, а всю границу отверстия. В том случае, если СЭ 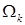 не содержит отверстия, полагаем, что не содержит отверстия, полагаем, что  на всей на всей 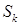 . .
Ранее в [6; 9] предложены и исследованы различные варианты продолжения этих функций с узлов 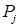 на ребра СЭ. Варианты заключаются в представлении базисных граничных функций на каждом из ребер границы некоторым “стандартным” интерполянтом [19]: полиномиальным, кусочно-линейным, сплайном и т.д. Одна из таких функций на ребра СЭ. Варианты заключаются в представлении базисных граничных функций на каждом из ребер границы некоторым “стандартным” интерполянтом [19]: полиномиальным, кусочно-линейным, сплайном и т.д. Одна из таких функций  при кусочно-линейной зависимости представлена на рис. 4, а при полиномиальной зависимости второго порядка на ребрах границы СЭ – на рис. 5. при кусочно-линейной зависимости представлена на рис. 4, а при полиномиальной зависимости второго порядка на ребрах границы СЭ – на рис. 5.
Граничные базисные функции заданы для всех узлов и СЭ в области 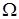 . Предполагается, что функции . Предполагается, что функции  , , 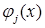 , определенные на одном и том же ребре соседних СЭ , определенные на одном и том же ребре соседних СЭ 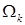 и и 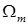 , на нем совпадают, т.е. , на нем совпадают, т.е.
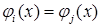 , , 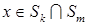 , ,
для всех 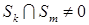 и всех соседних СЭ и всех соседних СЭ 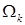 , , 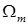 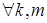 . Кроме того, на внешней границе . Кроме того, на внешней границе  необходимо удовлетворить главное граничное условие : необходимо удовлетворить главное граничное условие :
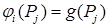 , , 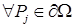 , , 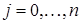 . .
Каждая построенная граничная базисная функция  однозначно определяет функцию однозначно определяет функцию 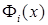 в СЭ в СЭ 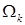 . Она является решением задачи Дирихле следующего вида: . Она является решением задачи Дирихле следующего вида:
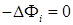 в в 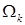 , ,
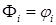 на на 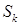 . .
Функции 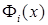 , , 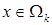 , задают базисные функции МКСЭ
в СЭ , задают базисные функции МКСЭ
в СЭ  . Базисные функции единообразно задаются в каждом из СЭ . Базисные функции единообразно задаются в каждом из СЭ 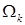 , , 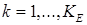 , области расчета , области расчета 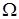 . Пример базисной функции . Пример базисной функции 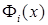 показан на рис. 6. Он соответствует граничной базисной функции показан на рис. 6. Он соответствует граничной базисной функции  , заданной полиномом второго порядка (рис. 5). Представляет интерес дальнейшее рассмотрение вариантов МКСЭ при полиномиальной или сплайновой интерполяции. , заданной полиномом второго порядка (рис. 5). Представляет интерес дальнейшее рассмотрение вариантов МКСЭ при полиномиальной или сплайновой интерполяции.
Заметим, что сингулярности решения задачи в окрестностях отверстий учтены посредством базисной функции с нулевым индексом  в каждом из СЭ. Остальные функции в каждом из СЭ. Остальные функции 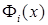 , , 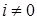 , при наличии отверстия в СЭ , при наличии отверстия в СЭ 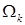 обращаются в ноль на его границе согласно . Если в СЭ отверстия нет, то обращаются в ноль на его границе согласно . Если в СЭ отверстия нет, то 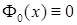 . .
При помощи построенного базиса решение исходной задачи внутри каждого отдельного СЭ разыскивается в следующем виде:
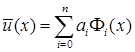 , , 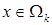 . .
Таким образом определяется приближенное решение МКСЭ
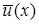 во всей расчетной области во всей расчетной области 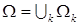 . При этом неизвестные значения . При этом неизвестные значения 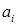 находятся с помощью обычного метода Бубнова-Галеркина при выборе функций находятся с помощью обычного метода Бубнова-Галеркина при выборе функций  в качестве базисных и пробных [3–12]. в качестве базисных и пробных [3–12].
В классическом случае эллиптических уравнений второго порядка при должных оговорках относительно гладкости границы, коэффициентов и граничных функций слабые решения принадлежат пространству Соболева  . Следы этих решений на границе . Следы этих решений на границе 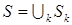 суперэлементного разбиения области принадлежат пространству Соболева суперэлементного разбиения области принадлежат пространству Соболева  с полуцелым показателем гладкости [16; 18]. Выбор функции, аппроксимирующей след решения на границе разбиения в норме пространства с полуцелым показателем гладкости [16; 18]. Выбор функции, аппроксимирующей след решения на границе разбиения в норме пространства  , и применение МКСЭ приведут к приближенному решению, аппроксимирующему в , и применение МКСЭ приведут к приближенному решению, аппроксимирующему в 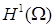 точное решение. точное решение.
В предыдущих работах исследовано влияние выбора метода аппроксимации на границе разбиения на результирующую точность расчетов метода. Получены теоретические (априорные) оценки погрешностей метода в зависимости от способа приближения [10–12]. Неясным остался вопрос о сходимости или расходимости ошибок производных сильного решения разного порядка. Такое исследование изначально затруднено особым “нестандартным” видом получаемого приближенного решения МКСЭ и его ограничениями по гладкости.
Данная работа посвящена теоретическому анализу МКСЭ Федоренко. В ней рассмотрена регулярность приближенного решения, получена его асимптотика в углах суперэлементного разбиения. Она представляет как отдельный интерес, так и служит для получения оценок погрешности производных различного порядка. Результаты получены на примере задачи – .
Будем предполагать наличие такой гладкости функции 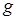 в (2) и границы области в (2) и границы области  , которые достаточны для того, чтобы искомое решение принадлежало , которые достаточны для того, чтобы искомое решение принадлежало 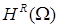 [16; 23]. Сохраним далее введенные обозначения: [16; 23]. Сохраним далее введенные обозначения: 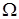 – расчетная область (рис. 2), – расчетная область (рис. 2), 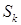 – граница СЭ – граница СЭ 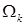 , , 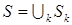 – совокупность всех суперэлементных границ, – совокупность всех суперэлементных границ, 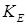 – общее число СЭ в области, – общее число СЭ в области,  – искомое и – искомое и  – приближенное решение МКСЭ. – приближенное решение МКСЭ.
Как правило, СЭ 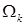 является многоугольником, так что необходимо учитывать тот факт, что является многоугольником, так что необходимо учитывать тот факт, что 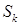 принадлежит классу принадлежит классу  непрерывности. Будем рассматривать лишь случай, когда непрерывности. Будем рассматривать лишь случай, когда 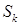 – граница многоугольника либо граница, состоящая из конечного числа гладких кривых. В таком случае – граница многоугольника либо граница, состоящая из конечного числа гладких кривых. В таком случае  , ,  , где L
– число сторон , где L
– число сторон  (или гладких частей границы) СЭ (или гладких частей границы) СЭ 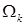 . Полагаем, что все вершины углов границы СЭ направлены во внешность области, то есть раствор углов не превышает π
. Рассмотрим варианты МКСЭ, использующие полиномиальной либо сплайн-интерполяцию на границах СЭ. В случае сплайн-интерполяции . Полагаем, что все вершины углов границы СЭ направлены во внешность области, то есть раствор углов не превышает π
. Рассмотрим варианты МКСЭ, использующие полиномиальной либо сплайн-интерполяцию на границах СЭ. В случае сплайн-интерполяции  обозначают те отрезки разбиения суперэлементных границ, на каждом из которых интерполянт представляет собой полином (L
– их число). обозначают те отрезки разбиения суперэлементных границ, на каждом из которых интерполянт представляет собой полином (L
– их число).
Определим объекты нашего рассмотрения.
Пространство всех полиномов
порядка не выше  на отрезке на отрезке  обозначим через обозначим через  . Введем . Введем  – пространство заданных на границе S
полиномов порядка не выше – пространство заданных на границе S
полиномов порядка не выше  на каждой из частей на каждой из частей  границы.
Обозначим символом границы.
Обозначим символом  пространство всех сплайнов
порядка не выше пространство всех сплайнов
порядка не выше  , построенных на разбиении , построенных на разбиении  на на  отрезок длины отрезок длины  . При этом . При этом  . Полиномиальная интерполяция служит частным случаем интерполяции сплайнами, в которой . Полиномиальная интерполяция служит частным случаем интерполяции сплайнами, в которой  – число отрезков – число отрезков  на S
, поэтому при её рассмотрении вариант полиномиальной граничной интерполяции МКСЭ отдельным образом не выделяется. на S
, поэтому при её рассмотрении вариант полиномиальной граничной интерполяции МКСЭ отдельным образом не выделяется.
Аппроксимирующее пространство
 МКСЭ
– линейная оболочка, образованная всеми базисными функциями МКСЭ с граничной интерполяцией посредством сплайнов МКСЭ
– линейная оболочка, образованная всеми базисными функциями МКСЭ с граничной интерполяцией посредством сплайнов  , т.е. , т.е.
 . .
Здесь след функции на
S
определен равенством  . Оператор взятия следа . Оператор взятия следа  , заданный на , заданный на  соотношением соотношением
 , ,  , ,
непрерывно действует из пространства  в в  для всех для всех  . При этом существует непрерывный оператор, обратный к . При этом существует непрерывный оператор, обратный к  и действующий из и действующий из  в в  . Такой общий случай действия оператора . Такой общий случай действия оператора  справедлив как для гладкой, так и для многоугольной или просто липшицевой границы справедлив как для гладкой, так и для многоугольной или просто липшицевой границы  [16; 31]. Отметим, что определение [16; 31]. Отметим, что определение  содержит условие содержит условие
 почти всюду на почти всюду на  , ,
для всех  и всех соседних СЭ и всех соседних СЭ  , ,   . Это соотношение, очевидно, не всегда выполнено для пространства слабых решений задачи . Это соотношение, очевидно, не всегда выполнено для пространства слабых решений задачи  (см., например, [36]). Аппроксимирующее пространство МКСЭ содержит его как “главное условие”, накладываемое на все базисные функции. Соотношение не включено в для сохранения более компактной записи. Иногда, если это не вызовет недоразумений, мы будем использовать также символ (см., например, [36]). Аппроксимирующее пространство МКСЭ содержит его как “главное условие”, накладываемое на все базисные функции. Соотношение не включено в для сохранения более компактной записи. Иногда, если это не вызовет недоразумений, мы будем использовать также символ  без обозначения множества, на котором определена область значений оператора взятия следа. без обозначения множества, на котором определена область значений оператора взятия следа.
Аналогичным образом определено и а
ппроксимирующее пространство
 МКСЭ
, представляющее собой линейную оболочку, образованную базисными функциями МКСЭ с граничной интерполяцией посредством полиномов МКСЭ
, представляющее собой линейную оболочку, образованную базисными функциями МКСЭ с граничной интерполяцией посредством полиномов  порядка не выше ν. порядка не выше ν.
В определение аппроксимирующего пространства не входят условия совместности функций в узлах  СЭ вида: СЭ вида:
 , ,  , ,
на соседних отрезках  границы S границы S
 , ,  . Условие , как правило, в МКСЭ выполнено, поскольку введено в определение граничных базисных функций . Условие , как правило, в МКСЭ выполнено, поскольку введено в определение граничных базисных функций  (см. ). Оно связано с расчетом базисных функций МКСЭ, являющихся решениями задач – , и заданием интерполянта (см. ). Оно связано с расчетом базисных функций МКСЭ, являющихся решениями задач – , и заданием интерполянта  для них, непрерывного на всей границе для них, непрерывного на всей границе  . Линейная оболочка таких базисных функций МКСЭ согласно определению и составляет аппроксимирующее пространство. Тем не менее, условие можно ввести без ограничения общности метода, если непрерывность искомой функции в окрестностях узлов СЭ заведомо известна, а все особенности задач заключены строго внутри СЭ. В частности, всегда для сильного решения . Линейная оболочка таких базисных функций МКСЭ согласно определению и составляет аппроксимирующее пространство. Тем не менее, условие можно ввести без ограничения общности метода, если непрерывность искомой функции в окрестностях узлов СЭ заведомо известна, а все особенности задач заключены строго внутри СЭ. В частности, всегда для сильного решения  , ,  . .
Отметим, что в определении использован оператор Лапласа, определяющий гармоническую функцию в СЭ. Под гармоничностью
некоторого слабого решения  в произвольной области Ω мы понимаем его удовлетворение уравнению Лапласа в следующей обобщенной постановке: в произвольной области Ω мы понимаем его удовлетворение уравнению Лапласа в следующей обобщенной постановке:
  . .
Далее как для слабого, так и для сильного решения продолжаем формально пользоваться кратким обозначением  . .
Характерным свойством аппроксимации слабых решений МКСЭ является возможность рассмотрения задачи – не просто в энергетическом пространстве  , а в некотором его подпространстве, обозначаемом здесь , а в некотором его подпространстве, обозначаемом здесь  . Это пространство . Это пространство  снабжено дополнительным свойством гармоничности входящих в него функций в каждом из СЭ снабжено дополнительным свойством гармоничности входящих в него функций в каждом из СЭ  по отдельности: по отдельности:
 . .
Аппроксимирующее пространство МКСЭ является подпространством данного пространства. Определение  включает в себя условие : включает в себя условие :
 почти всюду на почти всюду на  , ,
для всех  и всех соседних СЭ и всех соседних СЭ  , ,   . Перепишем его эквивалентно также в виде: . Перепишем его эквивалентно также в виде:

Здесь и далее везде мы будем использовать оператор следа  , поэтому сделаем несколько замечаний о смысле данного определения. , поэтому сделаем несколько замечаний о смысле данного определения.
Глобальное
задание следа на границе  мы связываем с его стандартным определением. На пространстве мы связываем с его стандартным определением. На пространстве  оператор следа оператор следа  задан формулой . Если бы граница задан формулой . Если бы граница  обладала бесконечной гладкостью, то было бы выполнено соотношение обладала бесконечной гладкостью, то было бы выполнено соотношение  при любом значении при любом значении  . Для произвольной замкнутой липшицевой области . Для произвольной замкнутой липшицевой области  оператор следа оператор следа  действует из пространства действует из пространства  в в  , однозначно определен, ограничен и имеет ограниченный обратный только при выполнении условия , однозначно определен, ограничен и имеет ограниченный обратный только при выполнении условия  . При этом, если . При этом, если  , то область значений шире, чем , то область значений шире, чем  , см. [31; 30; 34; 15; 27]. В случае , см. [31; 30; 34; 15; 27]. В случае  для шкалы пространств Соболева в липшицевой области известно немного (то же и для более общего случая пространств Бесова), но, если для шкалы пространств Соболева в липшицевой области известно немного (то же и для более общего случая пространств Бесова), но, если  , то , то  действует из действует из  в в  [28; 14]. Кроме того, гармонические функции обладают дополнительной гладкостью, и имеет смысл рассмотрение случая пространств Бесова [29; 31]. [28; 14]. Кроме того, гармонические функции обладают дополнительной гладкостью, и имеет смысл рассмотрение случая пространств Бесова [29; 31].
Учитывая тот факт, что  – многоугольная область с границей, гладкой вне стратифицированных особенностей, далее возможно “улучшить” этот результат, вводя определение следа локально. Оператор следа – многоугольная область с границей, гладкой вне стратифицированных особенностей, далее возможно “улучшить” этот результат, вводя определение следа локально. Оператор следа  определен только на каждой из L
гладких частей (ребер) определен только на каждой из L
гладких частей (ребер)  границы границы  , ,  . Локальное
определение следа . Локальное
определение следа  [26; 20] мы связываем именно с таким заданием, а именно: [26; 20] мы связываем именно с таким заданием, а именно:  . Тогда локальный оператор . Тогда локальный оператор  при при  непрерывен и действует из непрерывен и действует из  в в  . Для следа на всей S
: . Для следа на всей S
:  . Обозначение . Обозначение  в зависимости от случая мы далее не меняем. Локальный след, очевидно, совпадает с глобальным, если последний корректно определен. При действии оператора в зависимости от случая мы далее не меняем. Локальный след, очевидно, совпадает с глобальным, если последний корректно определен. При действии оператора  на функцию из пространства Соболева с произвольным показателем гладкости на функцию из пространства Соболева с произвольным показателем гладкости  считаем оператор следа локальным. Это необходимо учитывать, например, при использовании граничных интегральных уравнений и работе с ними. Локальные следы более высокого порядка также обладают общими свойствами на многоугольной границе, см., напр., [26]. В дальнейшем мы используем запись вида считаем оператор следа локальным. Это необходимо учитывать, например, при использовании граничных интегральных уравнений и работе с ними. Локальные следы более высокого порядка также обладают общими свойствами на многоугольной границе, см., напр., [26]. В дальнейшем мы используем запись вида  , которая является условным обозначением, и , которая является условным обозначением, и  . .
Нам понадобятся следующие пространства, обозначаемые через  : :
 , ,
для любых  , ,  . При . При  имеем определение пространства имеем определение пространства  . В определение . В определение  включено и условие . Рост показателя R
характеризует увеличение гладкости функций включено и условие . Рост показателя R
характеризует увеличение гладкости функций  из этого пространства на всех гладких частях суперэлементных границ. Поскольку для следа любой функции из этого пространства на всех гладких частях суперэлементных границ. Поскольку для следа любой функции  из пространства из пространства  справедливо включение справедливо включение  , то выполнено включение: , то выполнено включение:
 . .
Обратное вложение при  на границе класса на границе класса  не имеет места. Кроме того, любая функция не имеет места. Кроме того, любая функция  однозначно определена своим следом однозначно определена своим следом 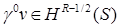 на S
(см. напр., [32]). на S
(см. напр., [32]).
Если при аппроксимации решения в пространстве 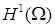 для ошибки решения, очевидно, справедлива эквивалентность для ошибки решения, очевидно, справедлива эквивалентность 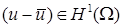  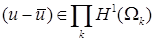  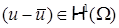 , то в пространствах более высокой гладкости , то в пространствах более высокой гладкости 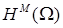 , , 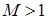 , и многоугольной границей разбиения , и многоугольной границей разбиения 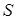 подобное несправедливо. Более того, показатель гладкости произвольной функции подобное несправедливо. Более того, показатель гладкости произвольной функции 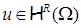 на на  , имеющей гладкие следы на частях негладкой границы , имеющей гладкие следы на частях негладкой границы  , ограничен сверху [13]. Это относится к регулярности решения задачи Дирихле в отдельном СЭ , ограничен сверху [13]. Это относится к регулярности решения задачи Дирихле в отдельном СЭ  [32; 33; 24]. Ограничение по гладкости может оказаться достаточно жестким и связано с локальным поведением решения в суперэлементных углах. Показатель гладкости зависит как от гладкости правой части граничного условия на отдельных сторонах границы [32; 33; 24]. Ограничение по гладкости может оказаться достаточно жестким и связано с локальным поведением решения в суперэлементных углах. Показатель гладкости зависит как от гладкости правой части граничного условия на отдельных сторонах границы  , их совместности в вершинах углов, так и от величины раствора углов, кривизны их сторон и вида исходного уравнения. , их совместности в вершинах углов, так и от величины раствора углов, кривизны их сторон и вида исходного уравнения.
3.1. Свойства гладкости приближенного решения МКСЭ
Пусть Λ – один из углов СЭ с границей 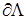 раствора α
, раствора α
,  ; P
– его вершина; ; P
– его вершина; 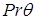 – полярная система координат, связанная с Λ. В данном пункте мы рассмотрим преимущественно отдельный угол Λ, полученные таким образом результаты обобщаются на всю расчетную область. – полярная система координат, связанная с Λ. В данном пункте мы рассмотрим преимущественно отдельный угол Λ, полученные таким образом результаты обобщаются на всю расчетную область.
Помимо самого приближенного решения 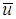 исследуем также его интерполянт исследуем также его интерполянт 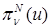 . Отметим, что все полученные здесь результаты для . Отметим, что все полученные здесь результаты для  справедливы и для приближенного решения справедливы и для приближенного решения 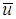 , а коэффициенты в его разложении, указанные через интерполянт , а коэффициенты в его разложении, указанные через интерполянт 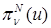 , должны быть заменены аналогичными, заданными через приближенное решение , должны быть заменены аналогичными, заданными через приближенное решение 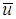 . .
Интерполянт 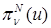 МКСЭ в области СЭ МКСЭ в области СЭ  является решением задачи: является решением задачи:
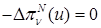 в в  , ,
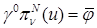 на на  , ,
где  , , 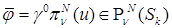 – граничный сплайн-интерполянт решения. Дальнейшие выкладки мы проводим в предположении, что следы совместны для всех углов Λ в СЭ – граничный сплайн-интерполянт решения. Дальнейшие выкладки мы проводим в предположении, что следы совместны для всех углов Λ в СЭ  так, что так, что
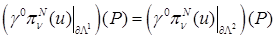 , ,
и аналогично для приближенного решения:
 , ,
где 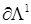 и и 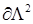 – отдельные стороны угла Λ, составляющие его границу – отдельные стороны угла Λ, составляющие его границу 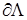 и пересекающиеся в точке P
. и пересекающиеся в точке P
.
Утверждение 1
. Пусть граничные базисные функции МКСЭ в некоторой окрестности угла
Λ СЭ  , на его границах , на его границах  и и 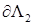 , – полиномы порядка не выше ν. Интерполянт приближенного решения , – полиномы порядка не выше ν. Интерполянт приближенного решения 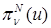 МКСЭ в этой окрестности представим в виде: МКСЭ в этой окрестности представим в виде:
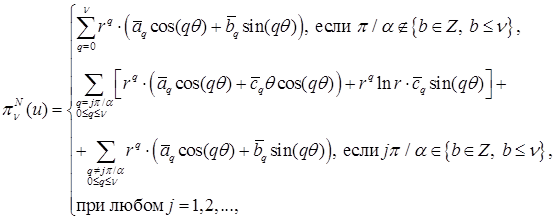
где
 , ,  , , 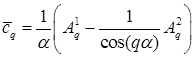 , ,
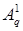 , , 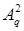 – коэффициенты решения (граничного полинома – коэффициенты решения (граничного полинома 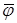 ) на границах ) на границах  , , 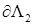 перед перед 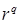 , ,  . Аналогичное утверждение справедливо и для приближенного решения . Аналогичное утверждение справедливо и для приближенного решения 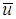 . .
Доказательство.
Будем искать решение задачи – в угле Λ СЭ как сумму решений 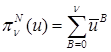 задач следующего вида: задач следующего вида:
 в в 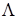 , ,
 на на 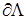 , ,
где  – константы, – константы,  . При этом . При этом 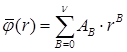 на на 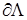 . Согласно [17, с. 47] асимптотика этой задачи в угле Λ такова: . Согласно [17, с. 47] асимптотика этой задачи в угле Λ такова:
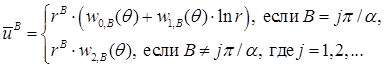
Здесь коэффициенты разложения по переменной r
(функции 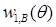 , , 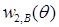 и и  ) бесконечно дифференцируемы по θ
(*)
. ) бесконечно дифференцируемы по θ
(*)
.
Получим представление интерполянта приближенного решения:
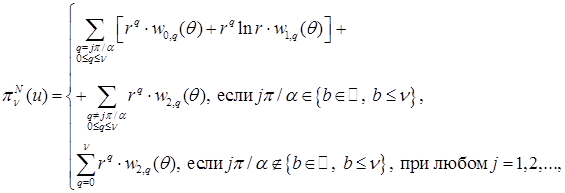
где 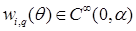 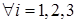 . .
Уточним результат, рассмотрев константные коэффициенты разложений. Они представляют интерес для дальнейшего рассмотрения. Выбранные полиномиальные граничные значения бесконечно дифференцируемы в окрестности угла. Решение задачи согласно результату [17, с. 50] может быть найдено в виде:
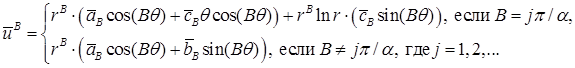
Находим коэффициенты 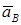 , , 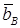 , , 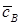 , подставляя в задачу . Тогда , подставляя в задачу . Тогда
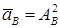 , ,  , , 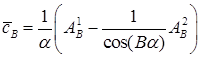 , ,
где 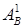 , ,  – коэффициенты граничных значений – коэффициенты граничных значений  для различных сторон угла для различных сторон угла 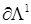 и и 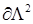 соответственно. Граница соответственно. Граница 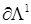 соответствует значениям угла соответствует значениям угла 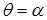 , и , и  – значению – значению  . .
Отметим, что в первой сумме выражения  . Суммирование по всем B
дает разложение приближенного решения . Суммирование по всем B
дает разложение приближенного решения 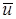 в области Λ (где символ B
заменен на q
): в области Λ (где символ B
заменен на q
):
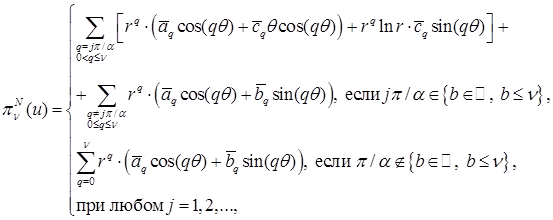
с коэффициентами , 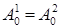 , ,  . Выпишем слагаемое при . Выпишем слагаемое при 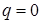 : :
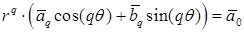
в обоих случаях принадлежности 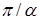 . # . #
Замечание.
Из проведенного рассмотрения следует также: 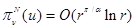 , ,  при при 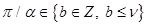 , ,  ; в противном случае решение ; в противном случае решение  и и  ограничено. ограничено.
Пример.
Для угла квадратного СЭ значение 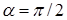 . Приближенное решение МКСЭ . Приближенное решение МКСЭ 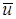 , а также его интерполянт в некоторой окрестности углов СЭ представимы в виде следующей конечной суммы: , а также его интерполянт в некоторой окрестности углов СЭ представимы в виде следующей конечной суммы:
при линейной интерполяции граничного решения
 ; ;
при любой полиномиальной интерполяции порядка выше единицы:
 . # . #
Выражение определяет гладкость интерполянта приближенного решения 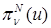 МКСЭ в соболевских пространствах. Если МКСЭ в соболевских пространствах. Если 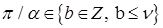 и и 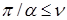 , то , то 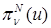 нерегулярна по отношению к граничному условию так, что нерегулярна по отношению к граничному условию так, что 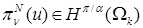 для произвольных для произвольных  , , 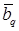 , , 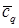 . В противном случае решение в угле Λ обладает бесконечной гладкостью, поэтому приближенное решение в СЭ . В противном случае решение в угле Λ обладает бесконечной гладкостью, поэтому приближенное решение в СЭ 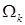 имеет максимальную гладкость по отношению к граничному условию на имеет максимальную гладкость по отношению к граничному условию на  . То же относится к приближенному решению . То же относится к приближенному решению 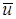 МКСЭ. МКСЭ.
Рассмотрим пространство  . Согласно в его определение включено условие . Мы вводим ещё одно важное предположение о совместности следов в узлах . Согласно в его определение включено условие . Мы вводим ещё одно важное предположение о совместности следов в узлах 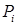 СЭ, а именно: СЭ, а именно: 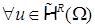 считаем выполненным условие считаем выполненным условие
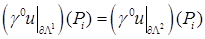 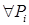 . .
Считаем также, что все углы СЭ направлены во внешность их области:  . Пространство . Пространство  , дополненное условием совместности следов
, и условием , дополненное условием совместности следов
, и условием
 на раствор углов
, обозначим на раствор углов
, обозначим 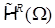 . .
Утверждение 2
. Приближенное решение МКСЭ из пространства  принадлежит соболевскому пространству принадлежит соболевскому пространству  в пределах каждого СЭ в пределах каждого СЭ 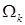 . То же верно для интерполянта . То же верно для интерполянта 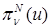 . .
Доказательство
. Предыдущие выкладки показывают, что  в области СЭ в области СЭ  , если , если  . Нерегулярный случай . Нерегулярный случай 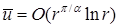 при минимальном значении при минимальном значении 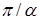 из множества из множества 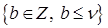 дает дает 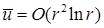 . Значит, выполнено . Значит, выполнено 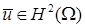 . Аналогично для . Аналогично для 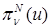 . Заметим, что для дальнейших выкладок это не принципиально, но упрощает некоторые записи. # . Заметим, что для дальнейших выкладок это не принципиально, но упрощает некоторые записи. #
3.2. Асимптотическое разложение функции класса
HR
(Λ)
Приведем некоторые известные сведения об асимптотическом разложении некоторой функции в многоугольном СЭ. Совместно с пунктом 0 эта информация может быть употреблена для получения ряда оценок. Кроме того, она дает представление и о других возможных вариантах задания граничных базисных функций, не указанных ранее и характеризуемых любой гладкостью по шкале Соболева. Как мы уже отмечали, показатель гладкости такой функции в СЭ всегда ограничен сверху. Это связано с гладкостью  его границы. Получим асимптотическое разложение в окрестностях угловых точек. его границы. Получим асимптотическое разложение в окрестностях угловых точек.
Произвольное решение уравнения Лапласа с граничными данными 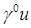 в угле Λ СЭ в угле Λ СЭ 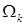 (в некоторой окрестности угловой точки P
) разложимо в сумму гладкой и сингулярной частей [24; 25; 35]: (в некоторой окрестности угловой точки P
) разложимо в сумму гладкой и сингулярной частей [24; 25; 35]:
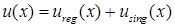 , , 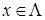 , ,
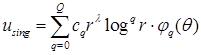 , ,
где 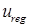 обладает максимальной гладкостью, порожденной гладкостью функции обладает максимальной гладкостью, порожденной гладкостью функции 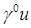 граничного условия, а наличие граничного условия, а наличие  обусловлено видом области Λ. Здесь обусловлено видом области Λ. Здесь 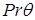 – локальная система координат в угле Λ; набор параметров λ
определен некоторыми характеристическими числами, связанными с уравнением, и может быть дополнен конечным числом положительных действительных параметров – локальная система координат в угле Λ; набор параметров λ
определен некоторыми характеристическими числами, связанными с уравнением, и может быть дополнен конечным числом положительных действительных параметров 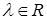 , , 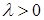 ; причем и в том, и в другом случае диапазон λ
ограничен сверху гладкостью граничных данных; Q
– конечное число; ; причем и в том, и в другом случае диапазон λ
ограничен сверху гладкостью граничных данных; Q
– конечное число; 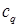 – константы. Рассматриваемое нами эллиптическое уравнение не содержит членов порядка меньше максимального. Кроме того, границы – константы. Рассматриваемое нами эллиптическое уравнение не содержит членов порядка меньше максимального. Кроме того, границы  СЭ в некоторой окрестности каждого из углов Λ считаем прямыми линиями. СЭ в некоторой окрестности каждого из углов Λ считаем прямыми линиями.
Классическим способом определения регулярности решения линейного эллиптического уравнения с постоянными коэффициентами является метод В.А. Кондратьева(*)
, использующий преобразование Меллина [21] исходного уравнения в угле Λ в задачу на отрезке  , , 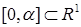 , , 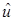 – изображение. Выписанное уравнение на собственные значения – изображение. Выписанное уравнение на собственные значения 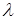 можно получить и определенной заменой переменных, преобразовывающей задачу в угле в задачу на некоторой простой области, например, полосе [17], полупространстве [33] в случае уравнения Лапласа. Несложно определить его решение как решение задачи Штурма-Лиувилля. Оно имеет вид: можно получить и определенной заменой переменных, преобразовывающей задачу в угле в задачу на некоторой простой области, например, полосе [17], полупространстве [33] в случае уравнения Лапласа. Несложно определить его решение как решение задачи Штурма-Лиувилля. Оно имеет вид: 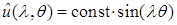 , , 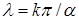 , , 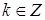 . Обратное преобразование Меллина даст разложение решения: . Обратное преобразование Меллина даст разложение решения: 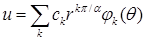 , где , где 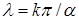 принадлежит конечному промежутку, принадлежит конечному промежутку, 
В случае уравнения Лапласа коэффициенты λ
разложения включают в себя конечный ряд из полученных характеристических чисел 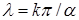 для для  [25; 32]. [25; 32].
Наличие неоднородных граничных условий на 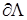 приводит к возникновению дополнительных слагаемых в таком разложении, гладкость которых измеряется в пространствах Соболева с весом приводит к возникновению дополнительных слагаемых в таком разложении, гладкость которых измеряется в пространствах Соболева с весом  [35]. Для определения их полной асимптотики и регулярности в рамках шкалы “обыкновенных” пространств Соболева требуется дополнительное исследование. Например, полиномиальная правая часть в угле раствора [35]. Для определения их полной асимптотики и регулярности в рамках шкалы “обыкновенных” пространств Соболева требуется дополнительное исследование. Например, полиномиальная правая часть в угле раствора 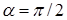 (см. пункт 0) приводит к разложению с порядком (см. пункт 0) приводит к разложению с порядком 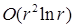 . Величина . Величина  регулярна при рассмотрении пространства с показателем гладкости регулярна при рассмотрении пространства с показателем гладкости 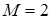 , она регулярна также и для некоторых пространств Соболева с весом. При работе в шкале соболевских пространств , она регулярна также и для некоторых пространств Соболева с весом. При работе в шкале соболевских пространств 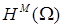 , ,  , её уже необходимо учитывать как нерегулярную часть. Отметим, что шкала весовых пространств “с однородной нормой”, возникающих при использовании метода Кондратьева, не имеет пересечений со шкалой пространств Соболева , её уже необходимо учитывать как нерегулярную часть. Отметим, что шкала весовых пространств “с однородной нормой”, возникающих при использовании метода Кондратьева, не имеет пересечений со шкалой пространств Соболева 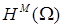 [32]. Мы ее не используем. [32]. Мы ее не используем.
Нас интересует множество функций, удовлетворяющих уравнению Лапласа в областях 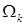 , условиям и со следами класса , условиям и со следами класса 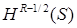 , , 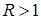 . Ранее оно было обозначено через . Ранее оно было обозначено через 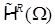 . Вообще говоря, пространство . Вообще говоря, пространство 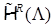 в угле Λ содержит в себе набор весовых пространств “с неоднородной нормой” в угле Λ содержит в себе набор весовых пространств “с неоднородной нормой”  , см. [32], характеризующийся индексами , см. [32], характеризующийся индексами 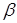 , ,  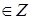 определенного диапазона. Уточнение асимптотики выражения – со следами из определенного диапазона. Уточнение асимптотики выражения – со следами из 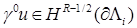 , , 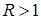 , может быть выписано согласно [32, p.p. 284, 300]. А именно, в угле Λ справедливо представление: , может быть выписано согласно [32, p.p. 284, 300]. А именно, в угле Λ справедливо представление:
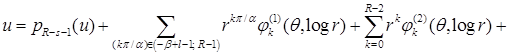
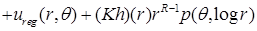 , ,
где 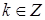 , , 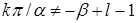 ; ; 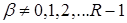 ; ;  ; ;  для некоторого для некоторого  . Слагаемое . Слагаемое 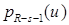 является полиномом от функции u
порядка не выше является полиномом от функции u
порядка не выше 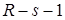 . Функции . Функции 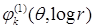 , , 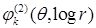 , , 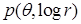 – полиномы от переменной – полиномы от переменной 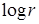 с коэффициентами (зависящими от с коэффициентами (зависящими от 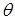 ) класса ) класса 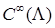 . Функция . Функция 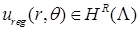 обладает максимальной гладкостью по отношению к заданному граничному условию обладает максимальной гладкостью по отношению к заданному граничному условию 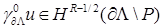 . Функция . Функция 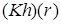 действует в пространство действует в пространство 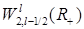 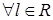 , , 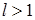 . Из общих теорем вложения для данных весовых пространств (напр., [26]) следует, что . Из общих теорем вложения для данных весовых пространств (напр., [26]) следует, что  для для  . При этом для функции u
при . При этом для функции u
при  справедливо условие справедливо условие 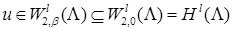 . .
Такое разложение достаточно громоздко, но содержит все необходимые нам факты, связанные с асимптотикой 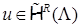 в угле СЭ. Подчеркнем, что вид разложения является общим, его коэффициенты могут зависеть от раствора угла [33], величины R
, граничных условий [37] и т.п. в угле СЭ. Подчеркнем, что вид разложения является общим, его коэффициенты могут зависеть от раствора угла [33], величины R
, граничных условий [37] и т.п.
Заметим, что для  , асимптотика содержит слагаемое , асимптотика содержит слагаемое 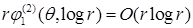 , его гладкость не выше , его гладкость не выше 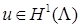 . Для . Для 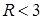 в общем случае для решения справедливо соотношение в общем случае для решения справедливо соотношение 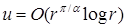 . При этом . При этом 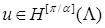 , где , где 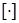 – обозначение целой части числа. Если – обозначение целой части числа. Если 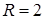 , то первая сумма содержит слагаемые только в случае угла , то первая сумма содержит слагаемые только в случае угла  . .
Отсюда для пространства 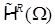 следует вложение следует вложение
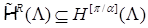 . .
Напомним, что из общего определения выполнено вложение вида
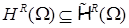 , , 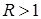 . .
Отметим, что достаточно хорошо известны результаты и оценки, связанные с сильным решением задачи Дирихле 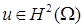 в многоугольной области в многоугольной области 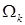 (см. [22; 23]). При этом достаточно легко заметить, что все соотношения в данных работах полностью согласуются с выписанным разложением . Мы не используем данные результаты, поскольку нас интересует весь диапазон возможной гладкости. Используем асимптотику либо её более общий вид . Последующие рассуждения относятся к уточнению таких оценок, что не представляется возможным, оставаясь лишь в рамках шкалы (см. [22; 23]). При этом достаточно легко заметить, что все соотношения в данных работах полностью согласуются с выписанным разложением . Мы не используем данные результаты, поскольку нас интересует весь диапазон возможной гладкости. Используем асимптотику либо её более общий вид . Последующие рассуждения относятся к уточнению таких оценок, что не представляется возможным, оставаясь лишь в рамках шкалы 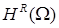 . .
Введем ещё одно определение. Оператор следа
m-го порядка
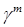 в пространстве в пространстве  задан соотношением задан соотношением
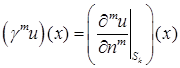 , , 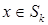 , ,
где n
– внешняя единичная нормаль к границе  , , 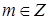 . Оператор . Оператор 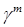 действует из действует из 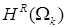 в в  для для 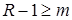 , и допускает “обычное” расширение в слабом смысле, например, , и допускает “обычное” расширение в слабом смысле, например, 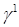 : : 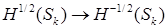 для для  . .
Пусть задача – обладает гладким решением 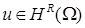 , , 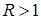 . Рассмотрим вопрос об аппроксимации первых производных . Рассмотрим вопрос об аппроксимации первых производных  , как и ранее, в норме пространства , как и ранее, в норме пространства 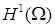 . Из того факта, что . Из того факта, что
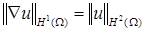 , ,
следует, что нам нужны оценки погрешностей решения u
в норме пространства 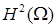 . Обобщая на произвольный порядок производных . Обобщая на произвольный порядок производных  , ,  , ,  , можно исследовать поведение погрешностей решения u
в нормах пространств , можно исследовать поведение погрешностей решения u
в нормах пространств  и, следовательно, определяя свойства МКСЭ о приближении производных порядка и, следовательно, определяя свойства МКСЭ о приближении производных порядка 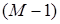 в норме пространства Соболева в норме пространства Соболева 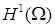 . .
Рассмотрим пример M
= 2. Из гармоничности градиентов искомого и приближенного решений имеем
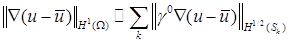 , ,
где, вообще говоря, 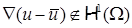 , так как условие совместности для градиентов не выполнено. Пункт 0 показывает, что , так как условие совместности для градиентов не выполнено. Пункт 0 показывает, что  в области СЭ в области СЭ 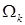 , если , если 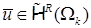 , поэтому запись ошибки решения в норме , поэтому запись ошибки решения в норме 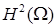 корректна. корректна.
Запишем с использованием стандартных преобразований:
 , ,
где  – производная по направлению касательного вектора – производная по направлению касательного вектора  на отрезке на отрезке  ; ; 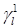 – след первого порядка – след первого порядка 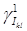 на на 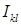 , см. . , см. .
Если бы выражение для ошибки 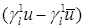 допускало принадлежность классу допускало принадлежность классу  , , 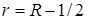 , ,  , на отдельном отрезке , на отдельном отрезке 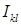 , то стала бы возможной запись неравенства , то стала бы возможной запись неравенства 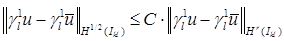 как следствие непрерывного вложения соответствующих пространств. Тогда слагаемые под знаком нормы в правой части выражения оценивались бы согласно “стандартным” выкладкам [10–12]. Заметим, что здесь нас интересуют не только априорные оценки погрешностей производных, но и сама сходимость производных приближенного решения МКСЭ к точному решению. как следствие непрерывного вложения соответствующих пространств. Тогда слагаемые под знаком нормы в правой части выражения оценивались бы согласно “стандартным” выкладкам [10–12]. Заметим, что здесь нас интересуют не только априорные оценки погрешностей производных, но и сама сходимость производных приближенного решения МКСЭ к точному решению.
Ясно, что 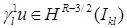 . Для следа первого порядка (нормальной производной) приближенного решения . Для следа первого порядка (нормальной производной) приближенного решения 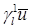 на отрезке на отрезке 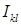 нет точного аналитического выражения, оно известно лишь для следа нет точного аналитического выражения, оно известно лишь для следа 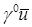 . Можно определить регулярность . Можно определить регулярность  лишь в окрестности узлов лишь в окрестности узлов 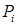 , благодаря пункту 0. , благодаря пункту 0.
Рассмотрим далее угол Λ, поэтому через 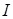 будем обозначать произвольную его сторону будем обозначать произвольную его сторону  ; как и ранее, P
– вершина угла Λ. ; как и ранее, P
– вершина угла Λ.
Несложно показать, что на границе угла 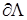 справедливо равенство: справедливо равенство:
 . .
Тогда из разложения для интересующего диапазона 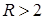 получим следующий результат: получим следующий результат:
 ; ;
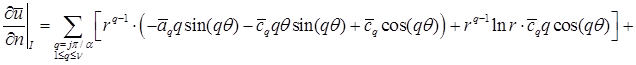
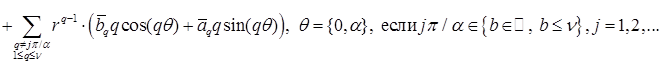 Отметим, что первым слагаемым, характерным для каждого из разложений и имеющим минимальный показатель Отметим, что первым слагаемым, характерным для каждого из разложений и имеющим минимальный показатель 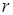 (либо (либо  ) является величина ) является величина 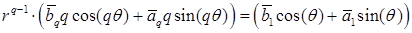 при при 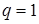 , зависящая от переменной , зависящая от переменной 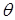 . Здесь также . Здесь также 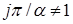 , поскольку , поскольку  . .
Перепишем полученные выражения, подставляя 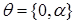 во вторую сумму(*)
: во вторую сумму(*)
:
 Отсюда ясно, что в окрестности вершины P
произвольного угла СЭ Λ раствора α
справедливы соотношения: Отсюда ясно, что в окрестности вершины P
произвольного угла СЭ Λ раствора α
справедливы соотношения:  и и  для для  или производная или производная  регулярна, если регулярна, если  . .
Более того, свойства гладкости 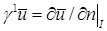 можно определить, воспользовавшись следующими результатами. можно определить, воспользовавшись следующими результатами.
Утверждение 3
[26].
Элемент 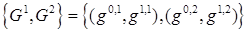 из пространства из пространства 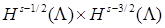 является образом некоторой функции является образом некоторой функции 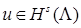 в угле в угле 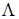 раствора α с вершиной P в результате действия согласно оператора раствора α с вершиной P в результате действия согласно оператора  , тогда и только тогда, когда выполнены соотношения , тогда и только тогда, когда выполнены соотношения
 , ,
 , ,
 , ,
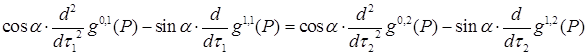
и для 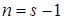 , ,
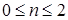 , выполнено некоторое
интегральное
условие
, где
, выполнено некоторое
интегральное
условие
, где  – существующие конечные производные по отношению к касательным векторам – существующие конечные производные по отношению к касательным векторам  для границы для границы  , , 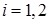 . .
В том случае, когда 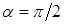 , условия
– принимают вид: , условия
– принимают вид:
 , ,
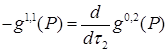 , ,
 , ,

и для 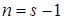 , ,
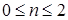 ,
,
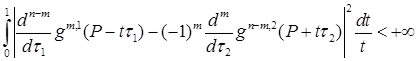 , при , при 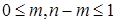 . .
Отметим, что число условий совместности ограничено, несмотря на увеличение показателя s
. Это связано с тем, что мы исследуем лишь величины 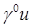 и и  ; это число таким образом связано непосредственно с порядком рассматриваемой нормы M
. ; это число таким образом связано непосредственно с порядком рассматриваемой нормы M
.
Вариант 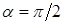 выписан для примера вследствие простоты записи. Не составляет труда перенести результаты на общий случай. Для квадратного СЭ выписан для примера вследствие простоты записи. Не составляет труда перенести результаты на общий случай. Для квадратного СЭ 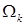 с узлами с узлами 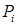 и сторонами и сторонами 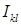 ,
,  , , 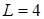 , справедливо утверждение. , справедливо утверждение.
Утверждение 4
[26].
Пусть 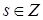 и и 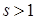 . Элемент . Элемент 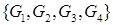 , , 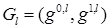 , , 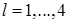 , из пространства , из пространства 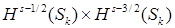 есть образ при отображении есть образ при отображении 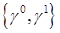 некоторой функции из пространства Соболева некоторой функции из пространства Соболева 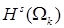 тогда и только тогда, когда для всех тогда и только тогда, когда для всех  и для всех и для всех  , , 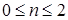 , , 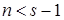 , выполнено , выполнено
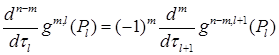 , где , где
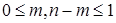 , ,
для 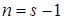 , , 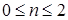 , выполнено , выполнено
 , ,
и принято обозначение 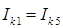 , ,  – касательные вектора для границы – касательные вектора для границы  . .
Замечание
Пространство 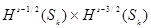 , дополненное набором таких условий, не является замкнутым в , дополненное набором таких условий, не является замкнутым в 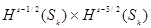 в стандартной норме. Оператор в стандартной норме. Оператор  непрерывно действует из непрерывно действует из 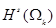 в такое модифицированное пространство и допускает непрерывный обратный при s > 2 в том случае, когда оно снабжено нормой с добавлением слагаемого, совпадающего с левой частью или , см. также [26].# в такое модифицированное пространство и допускает непрерывный обратный при s > 2 в том случае, когда оно снабжено нормой с добавлением слагаемого, совпадающего с левой частью или , см. также [26].#
Таким образом, для исследования свойств нормальной производной 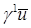 в соответствии с приведенными утверждениями нам нужны только значения в соответствии с приведенными утверждениями нам нужны только значения 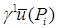 в вершинах в вершинах 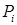 углов СЭ. углов СЭ.
Из условий – утверждения 3 в некоторой окрестности угла Λ СЭ раствора 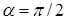 при при  , , 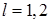 , не выполнены условия и для , не выполнены условия и для  , то есть , то есть 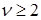 . Действительно, согласно разложению для . Действительно, согласно разложению для 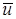 и разложению и разложению  для данного случая несложно проверить, что в вершине угла P
: для данного случая несложно проверить, что в вершине угла P
:
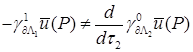 , ,
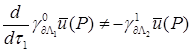 . .
Подобный же результат мы получим, исследуя целый СЭ 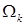 (см. утверждение 4) для произвольного раствора α
. Следовательно, нормальная производная (см. утверждение 4) для произвольного раствора α
. Следовательно, нормальная производная 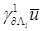 не является образом локального оператора следа не является образом локального оператора следа  , действующего из , действующего из 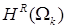 в в 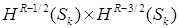 , а элемент , а элемент 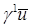 не обладает гладкостью не обладает гладкостью  . .
В дальнейшем необходимо дополнительное исследование полученных результатов, а “стандартная” схема не применима для получения верных априорных оценок МКСЭ и определения сходимости производных в энергетической норме пространства 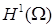 . Последующие работы посвящены более точному определению свойств . Последующие работы посвящены более точному определению свойств 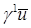 и погрешностей производных. и погрешностей производных.
В работе представлены результаты теоретических исследований МКСЭ Федоренко. Определены регулярность приближенного решения МКСЭ, его асимптотика в окрестностях угловых точек разбиения области на подобласти - суперэлементы. Исследование проведено на примере задачи Дирихле. Определение гладкости приближенного решения в пределах СЭ и во всей области и его асимптотического поведения в окрестностях “неестественного” разбиения исходной области на многоугольные СЭ представляет большой самостоятельный интерес. Помимо этого выполненная работа служит связующим звеном при переходе к определению теоретических оценок погрешностей производных приближенного решения.
[1] Федоренко Р.П. Введение в вычислительную физику
. – МФТИ, Москва, 1994. – 528с.
[2] Жуков В.Т, Новикова Н.Д., Страховская Л.Г., Федоренко Р.П., Феодоритова О.Б. Метод конечных суперэлементов в задачах конвекции-диффузии //
Препринт ИПМ им. М.В.Келдыша РАН, n. 8, 2001. – 36 с.
[3] Галанин М.П., Савенков Е.Б. К обоснованию метода конечных суперэлементов // Журн. вычисл. мат. и мат. физики
, т. 43, n. 5, 2003, c. 711 – 727.
[4] Галанин М.П., Савенков Е.Б. Метод конечных суперэлементов для задачи о скоростном скин-слое
// Препринт ИПМ им. М.В. Келдыша РАН, n. 3, 2004.
[5] Galanin M., Savenkov E., Temis J. Finite Superelements Method for Elasticity Problems // Mathematical Modelling and Analysis
, v. 10, n. 3, 2005, p. 237 – 246.
[6] Галанин М.П., Лазарева С.А., Савенков Е.Б. Численное исследование метода конечных суперэлементов на примере решения задачи о скважине для уравнения Лапласа
// Препринт ИПМ им. М.В. Келдыша РАН, n. 79, 2005.
[7] Галанин М.П., Савенков Е.Б. Совместное использование метода конечных элементов и метода конечных суперэлементов // Журн. вычисл. мат. и мат. физики
, т. 46, n. 2, 2006, c. 270 – 283.
[8] Galanin M., Lazareva S., Savenkov E. Numerical investigation of the Finite Superelement Method for the 3D elasticity problems // Mathematical Modelling and Analysis
, v. 12, n. 1, 2007, p. 39 – 50.
[9] Galanin M., Lazareva S., Savenkov E. Fedorenko Finite Superelement Method and its Applications // Computational Methods in Applied Mathematics
, v. 7, n. 1, 2007, p. 3 – 24.
[10] Галанин М.П., Лазарева С.А., Савенков Е.Б.
Качественный анализ и численное исследование метода конечных суперэлементов Федоренко // Тезисы всероссийской конференции по вычислительной математике “КВМ – 2007”, 18 – 20 июня, 2007, Академгородок, Новосибирск, Россия, с. 23.
[11] Лазарева С.А.
Априорные оценки погрешностей и гладкость приближенного решения МКСЭ Федоренко // Тезисы конференции “Студенческая научная весна – 2007”, МГТУ им. Н.Э. Баумана, Москва, Россия.
[12] Лазарева С.А.
Аппроксимационные свойства метода конечных суперэлементов Федоренко // Вычислительные технологии
, 2008, в печати
[13][1]
Агранович М.С. Обобщенные функции и соболевские пространства
// Лекции Независимого московского университета, 2005. – 60 с.
[14][2]
Агранович М.С. Спектральные задачи для сильно эллиптических систем второго порядка в областях с гладкой и негладкой границей // Успехи математических наук
, т. 57, вып. 5, 2002, с. 3 – 78.
[15][3]
Агранович М.С. Регулярность вариационных решений линейных граничных задач в липшицевых областях // Функциональный анализ и его приложения
, т. 40, вып. 4, 2006.
[16] Лионс Ж.-Л., Мадженес Э. Неоднородные граничные задачи и их приложения
. Мир, Москва, 1971. – 371 с.
[17] Назаров С.А, Пламеневский Б.А. Эллиптические задачи в областях с кусочно гладкой границей.
– Наука, Москва, 1991. – 336 с.
[18] Обэн Ж.-П. Приближенное решение эллиптических краевых задач.
Мир, Москва, 1977. – 383 с.
[19] Рябенький В.С. Введение в вычислительную математику.
Физматлит, Москва, 1994. – 336 с.
[20] Васильчик М.Ю. Граничные свойства функций из пространства Соболева, определенных в плоской области с угловыми точками // Сибирский математический журнал
, т. 36, n. 4, 1995, с. 787 – 804.
[21] Математическая энциклопедия.
В 5 т. Т.3: Меллина преобразование
/ гл. ред. Виноградов И.М. – Советская Энциклопедия, Москва, 1977.
[22][4]
Bacuta C., Bramble J.H., Xu J. Regularity estimates for elliptic boundary value problems with smooth data on polygonal domains // Journal of Numerical Mathematics
, v. 11, n. 2, 2003, p. 75 – 94.
[23] Borsuk M., Kondratiev V. Elliptic boundary value problems of second order in piecewise smooth domains
. – Elsevier, North-Holland, 2006. – 538 p.
[24][5]
Costabel M., Dauge M. Construction of corner singularities for Agmon-Douglis-Nirenberg elliptic systems//Mathematische Nachrichten,
v.162,n.1,1993,p.209– 237
[25][6]
Costabel M., Dauge M. Stable asymptotics for elliptic systems on plane domains with corners // Commu
nications in Partial Differential Equations,
v. 19, n. 9–10, 1994, p. 1677 – 1726.
[26][7]
Bernardi Ch., Dauge M., Maday Y. Polynomials in the Sobolev World
// Internal Report, Laboratoire Jacques-Louis Lions,Université Pierre et Marie Curie, 2003.–97p.
[27][8]
Dahlke St., DeVore R.A. Besov Regularity for Elliptic Boundary Value Problems // Communications in Partial Differential Equations
, n. 22, 1997, p. 1 – 16.
[28][9]
Ding Z. A proof of the trace theorem of Sobolev spaces on Lipschitz domains // Proceedings of American Mathematical Society
, v. 124, n. 2, 1996, p. 591 – 600.
[29] DeVore R.A. Nonlinear approximation // Acta Numerica
, n. 7, 1998, p.51 – 150.
[30] Fabes E., Mendez O., Mitrea M. Boundary Layers on Sobolev-Besov Spaces and Poisson’s Equation for the Laplacian in Lipschitz Domains // Journal of Functional Analysis
, n. 159, 1998, p. 323 – 368.
[31] Jerison J., Kenig C.E. The inhomogeneous Dirichlet problem in lipschitz domains // Journal of Functional Analysis
, n. 130, 1995, p. 161 – 219.
[32][10]
Kozlov V.A., Maz’ya V.G., Rossmann J. Elliptic boundary value problems in domains with point singularities
. – American Mathematical Society, 1997. – 414 p.
[33] Lehman R.Sh. Developments at an analytic corner of solutions of elliptic partial differential equations // Journal of Mathematics and Mechanics
, v. 8, n. 5, 1959, p. 727 – 760.
[34] Mitrea M., Taylor M. Potential Theory on Lipschitz Domains in Riemannian Manifolds: Sobolev-Besov Space Results and the Poisson Problem // Journal of Functional Analysis
, n. 176, 2000, p. 1 – 79.
[35][11]
Sändig A.-M. Regularity results for linear elliptic boundary value problems in polygons
// Lectures at the Charles university Prague, 2005. – 38 p.
[36][12]
Showalter R.E. Hilbert space methods for partial differential equations
. – Electronic Journal of Differential Equations: Monographs, n. 01, 1994 (Originally of 1977). – 214 p.
[37][13]
Sweers G. Hopf’s lemma and two dimensional domains with corners // Rendiconti dell'Istituto di Matematica dell'Università di Trieste
, vol. 28, 1997, p. 383 – 419.
(*)
Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект РФФИ № 06 - 01 - 00421).
(*)
Коэффициенты разложений имеют вид 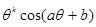 , , 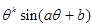 для любого линейного эллиптического уравнения [25]. для любого линейного эллиптического уравнения [25].
(*)
Кондратьев В.А. Краевые задачи для эллиптических уравнений в областях с коническими или угловыми точками
// Труды московского математического общества, т. 16, 1967, с. 209 – 292.
(*)
В случае  и разложения перед логарифмом стоит и разложения перед логарифмом стоит  вместо вместо  для для 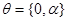 , и , и 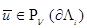 , как это и предполагалось граничным условием. Здесь ситуация обратная. , как это и предполагалось граничным условием. Здесь ситуация обратная.
[1]
Web access: http://www.agranovich.nm.ru/
[2]
Web access: http://www.agranovich.nm.ru/
[3]
Web access: http://www.agranovich.nm.ru/
[4]
Web access: http://www.math.psu.edu/ccma/reports.html
[5]
Web access: http://perso.univ-rennes1.fr/monique.dauge/core/
[6]
Web access: http://perso.univ-rennes1.fr/monique.dauge/core/
[7]
Web access: http://perso.univ-rennes1.fr/monique.dauge/core/
[8]
Web access: http://citeseer.ist.psu.edu/dahlke95besov.html
[9]
Web access: http:// www.ams.org/proc/1996-124-02/
[10]
Web access: http://www.ams.org/online_bks/surv52/
[11]
Web access: http://preprints.ians.uni-stuttgart.de
[12]
Web access: http://www.emis.ams.org/journals/EJDE/
[13]
Web access: http://aw.twi.tudelft.nl/~sweers/
|