Министерство образования Российской Федерации
Саратовский государственный технический университет
Технологический институт (филиал) СГТУ
Кафедра Материаловедение
ПРОЕКТИРОВАНИЕ МЕХАНИЗМОВ
ЗУБОДОЛБЕЖНОГО СТАНКА
Методические указания и задания
к курсовому проекту
по курсу «Теория механизмов и машин»
для студентов специальности ТМС
Саратов 2005
Содержание курсового проекта.
1. Введение.
2. Проектирование механизма привода долбяка.
2.1. Определение геометрических параметров шарнирного четырехзвенника. Построение плана положений механизма.
2.2. Построение плана скоростей для 13-ти положений.
2.3. Построение плана ускорений для №-ого положения.
2.4. Построение диаграмм перемещения, скорости и ускорения долбяка.
3. Синтез кулачкового механизма подвода и отвода стола.
3.1. Построение диаграммы скорости толкателя.
3.2. Построение диаграммы перемещения толкателя методом графического интегрирования.
3.3. Построение диаграммы ускорения толкателя методом графического дифференцирования.
3.4. Определение радиуса начальной окружности кулачка и положения центра кулачка.
3.5. Построение теоретического и практического профилей кулачка.
4. Синтез планетарного механизма.
4.1. Определение числа зубьев зубчатых колес и числа сателлитов.
4.2. Построение внешнего эвольвентного зацепления.
5. Расчет маховика.
5.1. Построение диаграммы приведенного момента сил сопротивления.
5.2. Построение диаграммы работы движущих сил и сил сопротивления, приведенного момента движущих сил.
5.3. Построение диаграммы кинетической энергии механизма.
5.4. Построение диаграммы приведенного момента инерции.
5.5. Построение диаграммы энергомасс.
5.6. Расчет массы и геометрических параметров маховика.
6. Заключение.
7. Список используемой литературы.
Исходные данные к курсовому проекту по ТММ
«Проектирование механизмов зубодолбежного станка» (специальность ТМС)
Угловой ход коромысла 
 ; АS2
=0,5АВ ; АS2
=0,5АВ
Максимальное перемещение толкателя 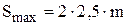
График скорости толкателя кулачка- синусоидальный.
Угол зубчатого зацепления 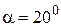
| №
|
Число оборотов двигателя nдв
, об/мин
|
Число оборотов кулачка nк
, об/мин
|
Максимальный ход долбяка Нmax
, м
|

|
Скорость резания Vр, м/мин
|
Положение кривошипа при построении плана ускорений , град
|
Усилие резания (полезного сопротивления) Р пс, кН
|
Передаточное число планетарного
редуктора iпл
|
Модуль зубчатых колес m, мм
|
Фазовые углы поворота
кулачка , град.
|
Максимальный угол давления , град

|
Коэффициент неравномерности вращения кривошипа
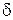
|
Момент инерции кривошипа J1
, кг м2
|
Момент инерции шатуна J S
2
, кг м2
|
Момент инерции коромысла J S
3
,кг м2
|
Масса шатуна m2
, кг
|
Масса коромысла m3
, кг
|
Масса долбяка m4
, кг
|
| 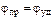
|

|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
12
|
9
|
10
|
11
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
| 1
|
1000
|
100
|
0,22
|
0,85
|
15
|
30
|
3,5
|
4
|
4
|
55
|
25
|
35
|
0,05
|
0,13
|
0,05
|
0,08
|
30
|
50
|
60
|
| 2
|
1100
|
110
|
0,21
|
0,80
|
20
|
60
|
3,0
|
5
|
3
|
60
|
10
|
36
|
0,08
|
0,10
|
0,04
|
0,10
|
40
|
60
|
70
|
| 3
|
1200
|
120
|
0,20
|
0,75
|
25
|
120
|
2,5
|
6
|
4
|
65
|
10
|
38
|
0,03
|
0,11
|
0,03
|
0,11
|
50
|
70
|
80
|
| 4
|
1300
|
130
|
0,19
|
0,70
|
30
|
150
|
2,0
|
4
|
3
|
70
|
0
|
40
|
0,04
|
0,12
|
0,06
|
0,12
|
60
|
80
|
90
|
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
12
|
9
|
10
|
11
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
| 5
|
1400
|
140
|
0,18
|
0,65
|
35
|
210
|
1,5
|
5
|
4
|
65
|
15
|
35
|
0,03
|
0,15
|
0,05
|
0,13
|
70
|
90
|
100
|
| 6
|
1500
|
150
|
0,17
|
0,60
|
40
|
240
|
1,8
|
6
|
3
|
60
|
20
|
36
|
0,06
|
0,12
|
0,04
|
0,10
|
80
|
100
|
110
|
| 7
|
1450
|
150
|
0,16
|
0,55
|
45
|
300
|
2,1
|
4
|
4
|
55
|
10
|
38
|
0,04
|
0,11
|
0,03
|
0,12
|
90
|
110
|
120
|
| 8
|
1400
|
140
|
0,15
|
0,50
|
50
|
330
|
2,4
|
5
|
3
|
60
|
0
|
40
|
0,07
|
0,12
|
0,04
|
0,08
|
100
|
120
|
130
|
| 9
|
1350
|
140
|
0,14
|
0,85
|
55
|
30
|
2,7
|
6
|
4
|
65
|
20
|
35
|
0,08
|
0,13
|
0,05
|
0,09
|
110
|
130
|
140
|
| 10
|
1300
|
130
|
0,13
|
0,80
|
60
|
60
|
3,0
|
4
|
3
|
55
|
15
|
36
|
0,05
|
0,10
|
0,06
|
0,10
|
120
|
140
|
150
|
| 11
|
1250
|
130
|
0,12
|
0,75
|
65
|
120
|
3,3
|
5
|
4
|
55
|
25
|
38
|
0,05
|
0,13
|
0,05
|
0,11
|
130
|
150
|
160
|
| 12
|
1200
|
120
|
0,11
|
0,70
|
70
|
150
|
3,6
|
6
|
3
|
60
|
10
|
40
|
0,08
|
0,10
|
0,06
|
0,12
|
140
|
160
|
170
|
| 13
|
1150
|
120
|
0,22
|
0,65
|
75
|
210
|
3,5
|
4
|
4
|
65
|
10
|
35
|
0,03
|
0,11
|
0,04
|
0,13
|
150
|
170
|
180
|
| 14
|
1100
|
110
|
0,21
|
0,60
|
80
|
240
|
3,0
|
5
|
3
|
70
|
10
|
36
|
0,04
|
0,12
|
0,02
|
0,08
|
160
|
180
|
190
|
| 15
|
1050
|
110
|
0,20
|
0,55
|
85
|
300
|
2,5
|
6
|
4
|
65
|
0
|
38
|
0,03
|
0,13
|
0,03
|
0,09
|
170
|
190
|
200
|
| 16
|
1000
|
100
|
0,19
|
0,50
|
90
|
330
|
2,0
|
4
|
3
|
60
|
20
|
40
|
0,06
|
0,14
|
0,05
|
0,10
|
180
|
200
|
210
|
| 17
|
1200
|
120
|
0,18
|
0,85
|
95
|
30
|
1,8
|
5
|
4
|
55
|
10
|
35
|
0,04
|
0,15
|
0,06
|
0,11
|
190
|
85
|
95
|
| 18
|
1400
|
140
|
0,17
|
0,80
|
100
|
60
|
2,2
|
6
|
3
|
60
|
0
|
36
|
0,07
|
0,11
|
0,03
|
0,12
|
200
|
95
|
105
|
| 19
|
1600
|
160
|
0,16
|
0,75
|
105
|
120
|
2,6
|
4
|
4
|
65
|
20
|
38
|
0,08
|
0,12
|
0,04
|
0,13
|
85
|
105
|
115
|
| 20
|
1500
|
150
|
0,15
|
0,70
|
110
|
150
|
3,0
|
5
|
3
|
55
|
15
|
40
|
0,05
|
0,13
|
0,05
|
0,08
|
95
|
135
|
145
|
| 21
|
1400
|
140
|
0,14
|
0,65
|
115
|
210
|
3,4
|
6
|
4
|
65
|
15
|
35
|
0,05
|
0,14
|
0,06
|
0,09
|
105
|
150
|
160
|
| 22
|
1300
|
130
|
0,13
|
0,60
|
120
|
240
|
3,8
|
4
|
3
|
60
|
20
|
36
|
0,08
|
0,10
|
0,04
|
0,10
|
135
|
165
|
175
|
| 23
|
1200
|
120
|
0,12
|
0,55
|
125
|
300
|
4,2
|
5
|
4
|
55
|
10
|
38
|
0,03
|
0,11
|
0,02
|
0,11
|
150
|
180
|
190
|
| 24
|
1100
|
110
|
0,11
|
0,45
|
130
|
330
|
4,6
|
6
|
3
|
60
|
0
|
40
|
0,04
|
0,12
|
0,03
|
0,12
|
165
|
200
|
210
|
| 25
|
1000
|
100
|
0,10
|
0,40
|
140
|
30
|
2,5
|
4
|
4
|
65
|
20
|
35
|
0,03
|
0,13
|
0,04
|
0,13
|
180
|
160
|
170
|
Исходные данные.
1. Число оборотов двигателя 
2. Число оборотов кулачка 
3. Максимальный ход долбяка 
4. 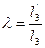
5. Скорость резания 
6. Положение кривошипа при построении плана ускорений [град
]
7. Усилие резания (полезного сопротивления) 
8. Модуль зубчатых колес 
9. Фазовые углы поворота кулачка 
10. Передаточное число планетарного редуктора 
11. Максимальный угол давления 
12. Коэффициент неравномерности вращения кривошипа 
13. Момент инерции кривошипа 
14. Момент инерции шатуна 
15. Момент инерции коромысла 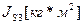
16. Масса шатуна 
17. Масса коромысла 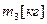
18. Масса долбяка 
1. Введение.
В первой части курсового проекта – введении - необходимо сформулировать цели и задачи курсового проектирования, как заключительного этапа в изучении дисциплины, его роль в формировании у студентов профессиональных качеств инженера, самостоятельности, творческой инициативы.
Дать краткое описание методов получения эвольвентных профилей зубьев, проанализировать плюсы и минусы каждого метода. Дать описание оборудования по обработке зубьев (зубодолбежные, зубострогальные станки и т.д.). Привести краткое описание проектируемого зубодолбежного станка (5В12 или его модификаций), принципа его работы, основных узлов станка, дать техническую характеристику.
Объем первой части проекта 5-7 страниц рукописного текста с вложенной ксерокопией схемы проектируемого станка.
2. Проектирование механизма привода долбяка.
(Лист 1)
2.1. Определение геометрических параметров шарнирного
четырехзвенника. Построение плана положений механизма.
Определение геометрических параметров шарнирного четырехзвенника и построение плана положений механизма заключается в следующем.
1. Откладываем в выбранном масштабе половину хода долбяка  вверх и вниз от горизонтали (точки С1
,С7
рис.1). вверх и вниз от горизонтали (точки С1
,С7
рис.1).
2. Задан угол хода коромысла  определяем длину определяем длину  по формуле: по формуле:
 [м] [м]
С помощью циркуля на горизонтали из точек С1
и С7
находим центр качания коромысла – точку О2
,
откладывая расстояние  в выбранном масштабе. в выбранном масштабе.
3. Исходя из заданного отношения 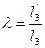 , находим длину , находим длину  и откладываем ее на продолжении коромысла (получаем точки В1
и В7
): и откладываем ее на продолжении коромысла (получаем точки В1
и В7
):
 [
м
]
[
м
]

Рис.1.
4. Измеряем длину  , равную расстоянию В1
В7
,определяем , равную расстоянию В1
В7
,определяем  . Рассчитываем длину . Рассчитываем длину 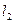 по формуле: по формуле: 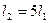 . Откладывая длину . Откладывая длину 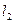 от точек В1
и В7
по вертикали, получаем точки А1
и А7
. от точек В1
и В7
по вертикали, получаем точки А1
и А7
.
5. Находим центр вращения кривошипа – т.О1
, достраиваем окружность радиусом  и тринадцать положений механизма через каждые 30˚(точки А1
– А13
). и тринадцать положений механизма через каждые 30˚(точки А1
– А13
).
6. Переносим длину 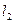 из каждой точки А1
-А13
на дугу АВ
, получая точки В1
-В13
. Точки В1
-В13
соединяем с центром качания коромысла О2
, продолжив полученные лучи, получаем тоски С1
-С13
. Точки долбяка Д1
-Д13
находим горизонтальным переносом соответствующих точек С1
-С13
. Указываем центры тяжести звеньев, учитывая, что из каждой точки А1
-А13
на дугу АВ
, получая точки В1
-В13
. Точки В1
-В13
соединяем с центром качания коромысла О2
, продолжив полученные лучи, получаем тоски С1
-С13
. Точки долбяка Д1
-Д13
находим горизонтальным переносом соответствующих точек С1
-С13
. Указываем центры тяжести звеньев, учитывая, что 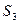 совпадает с О2
, а совпадает с О2
, а  есть половина длины есть половина длины 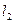 : : . .
7. Определяем частоту вращения кривошипа  и угловую скорость кривошипа и угловую скорость кривошипа  : : 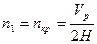 [ [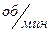 ] , ] , 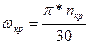 [ [ ] ]
8. Проверяем условие существования кривошипа - условие, при котором звено можно назвать кривошипом:
 , ,  , , 



2.2. Построение планов скоростей
для тринадцати положений.
План скоростей – это векторное изображение скоростей звеьев для заданного положения механизма.
Построение плана скоростей для тринадцати положений кривошипа производится следующим образом.
Рассчитываем скорость точки А
кривошипа:  [ [ . ] . ]
Скорость этой точки всегда направлена перпендикулярно кривошипу в сторону вращения этого звена. (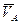 ^
О1
А
). ^
О1
А
).
Векторное уравнение для построения планов скоростей:
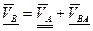
 ВА
, ВА
,  О2
В
. О2
В
.
Скорость точки С определяем по правилу рычага:
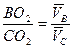 Þ Þ [м/с
] [м/с
]
Скорость направлена в сторону, противоположную 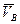 . .
Скорость  определяем из векторного уравнения: определяем из векторного уравнения:
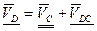 
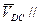 ВС, ВС,
 - по вертикали. - по вертикали.
Для определения скорости центра тяжести звена АВ
, который находится на его середине, находим середины отрезков а1
в1
, а2
в2
, а3
в3
и т.д. и соединяем их с полюсом Р
. Таким образом получаем длины векторов скорости  [мм
] и умножая на масштабный коэффициент скорости, определяем численные значения. [мм
] и умножая на масштабный коэффициент скорости, определяем численные значения.
Построение.
Проводим окружность с центром в произвольно выбранном полюсе Р
и радиусом приблизительно 100мм
(рис.2.).
Через каждые 30о
проводим радиусы и обозначаем векторы скорости вращения кривошипа для тринадцати положений этого звена ( ), отмечаем точки (а1
¸
а13
). ), отмечаем точки (а1
¸
а13
).
Рассчитаем масштабный коэффициент скорости – отношение численного значения физической величины, в свойственных единицах, к длине отрезка в миллиметрах, изображающего эту величину:
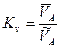 [ [  ] ]

Рис.2.
Проводим направления векторов 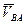 и и  для тринадцати положений, определяем точки их пересечения (в1
¸
в13
). для тринадцати положений, определяем точки их пересечения (в1
¸
в13
).
Учитывая, что  , то есть , то есть  , откладываем соответствующие длины векторов скорости , откладываем соответствующие длины векторов скорости  в противоположную сторону от в противоположную сторону от  , получаем точки (с1
¸
с13
). Проводим направления скорости , получаем точки (с1
¸
с13
). Проводим направления скорости 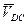 до пересечения с до пересечения с  (вертикаль). (вертикаль).
Заполняем таблицу 1.
Таблица 1
| |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|  , град , град
|
0
|
30
|
60
|
90
|
120
|
150
|
180
|
210
|
240
|
270
|
300
|
330
|
360
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|  
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 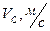
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 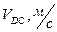
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Угловая скорость коромысла: [1/с
] [1/с
]
Угловая скорость шатуна [1/с
] [1/с
]
2.3. Построение плана ускорений для №-ого положения.
Ускорение точки А
кривошипа рассчитывается как  , но так как , но так как  , то , то  и направлено к центру вращения, то есть параллельно О1
А
от А
к О1
. и направлено к центру вращения, то есть параллельно О1
А
от А
к О1
.
Ускорение точки В
шатуна: 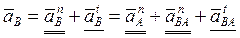

 [ [ ] ]
 [ [ ] ]
Ускорение точки С
коромысла определяем по правилу рычага.

Ускорение 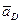 долбяка находим по векторному уравнению: долбяка находим по векторному уравнению:

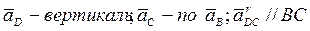
Ускорение Кориолиса рассчитывается как  , его направление можно определить, повернув линейную скорость , его направление можно определить, повернув линейную скорость 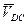 на 90° в сторону вращения коромысла в данном положении механизма на 90° в сторону вращения коромысла в данном положении механизма , так как , так как 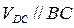 , то , то  . .
Построение.
Из произвольно выбранного полюса Q откладываем произвольной длины вектор 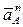 //АО1
от А
к О1
, отмечаем точку а
(рис.3.). Вводим //АО1
от А
к О1
, отмечаем точку а
(рис.3.). Вводим

Рис.3.
масштабный коэффициент ускорения [ [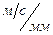 ]. Рассчитываем ]. Рассчитываем  [мм
] , [мм
] ,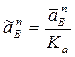 [мм
]. Откладываем от точки а
ускорение [мм
]. Откладываем от точки а
ускорение 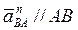 и отмечаем точку m
, через эту точку проводим направление ускорения и отмечаем точку m
, через эту точку проводим направление ускорения 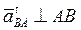 . Из полюса откладываем ускорение . Из полюса откладываем ускорение  , конец вектора обозначим точкой n
, через нее проводим направление вектора , конец вектора обозначим точкой n
, через нее проводим направление вектора  и на пересечении с проведенным направлением и на пересечении с проведенным направлением  получаем точку в
. Соединив полученную точку с полюсом, получаем вектор ускорения получаем точку в
. Соединив полученную точку с полюсом, получаем вектор ускорения  . Предварительно рассчитав длину вектора . Предварительно рассчитав длину вектора  по правилу рычага, откладываем ее в противоположную сторону от полюса Q и отмечаем точку с
. Через эту точку проводим направление ускорения Кориолиса по правилу рычага, откладываем ее в противоположную сторону от полюса Q и отмечаем точку с
. Через эту точку проводим направление ускорения Кориолиса  и откладываем предварительно рассчитанную его длину , конец вектора обозначаем точкой k
. Через эту точку проводим направление ускорения и откладываем предварительно рассчитанную его длину , конец вектора обозначаем точкой k
. Через эту точку проводим направление ускорения  до пересечения с вертикалью, так как по вертикали направлено ускорение долбяка до пересечения с вертикалью, так как по вертикали направлено ускорение долбяка  . Точку пересечения обозначаем –d
, измеряем длину вектора ускорения долбяка и рассчитываем умножая на масштабный коэффициент его значение . Точку пересечения обозначаем –d
, измеряем длину вектора ускорения долбяка и рассчитываем умножая на масштабный коэффициент его значение  [ [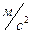 ]. Аналогично определяем величины и других ускорений, результаты расчетов заносим в таблицу 2. ]. Аналогично определяем величины и других ускорений, результаты расчетов заносим в таблицу 2.
Таблица 2
2.4. Построение диаграмм перемещения, скорости и ускорения.
Пользуясь таблицей 1 строим диаграмму скорости долбяка  с учетом ее направления. Построение диаграмм перемещения и ускорения производится методами графического интегрирования и графического дифференцирования. с учетом ее направления. Построение диаграмм перемещения и ускорения производится методами графического интегрирования и графического дифференцирования.
Построение диаграммы ускорения методом графического дифференцирования.
Произвольно выбираем полюс Q в системе координат (а-
t
). Две соседние точки графика скорости соединяем хордами, каждую из которых параллельно переносим в полюс Q до пересечения с вертикалью. Полученные на вертикали точки сносим на середины временных промежутков. Соединив полученные точки, достраиваем диаграмму ускорения.
Построение диаграммы перемещения методом графического интегрирования
. Произвольно выбираем полюс Р в системе координат (V
-
t
), из середины отрезков временных промежутков графика скорости восстанавливаем перпендикуляры до пересечения с графиком. Полученные точки сносим горизонтально до пересечения с вертикалью, соединяем их с полюсом Р, полученные таким образом лучи сносим в границы промежутков на графике перемещений, получаем диаграмму перемещений.
Определяем масштабные коэффициенты по следующим формулам:
Масштабный коэффициент времени:
 , ,
где 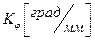 -масштабный коэффициент угла поворота; -масштабный коэффициент угла поворота;
  .- число оборотов кривошипа .- число оборотов кривошипа
Масштабный коэффициент перемещения:
 , ,
где  - максимальный ход долбяка; - максимальный ход долбяка;
 - максимальный ход долбяка, взятый с диаграммы перемещений. - максимальный ход долбяка, взятый с диаграммы перемещений.
Масштабный коэффициент скорости:
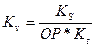  , ,
где  - полюсное расстояние, мм
. - полюсное расстояние, мм
.
Масштабный коэффициент ускорения:
 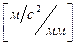
где  - полюсное расстояние, мм
. - полюсное расстояние, мм
.
Компоновка листа №1.

Лист №1.Проектирование привода долбяка.
«Схема положений четырехзвенника М 1: __»
«План скоростей Kv
= __»
«План ускорений Ka
=___»
«Кинематическая диаграмма перемещения долбяка Ks
=__
»
«Кинематическая диаграмма скорости долбяка Kv
=__;
K
j=__
»
«Кинематическая диаграмма ускорения долбяка Ka
=__
»
3. Синтез кулачкового механизма подвода и отвода стола.
3.1. Построение диаграммы скорости толкателя.
Вид кулачкового механизма- дисковый кулачок с поступательно движущимся толкателем с роликом с силовым замыканием (рис.4., на схеме станка обозначен как К2). График изменения скорости толкателя задан в виде синусоиды. Заданы фазовые углы кулачка: 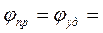 ; ;  ; тогда ; тогда 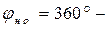   = . = .

Рис.4.
Построение синусоиды
. На оси абсцисс угла поворота звена откладываем фазовые углы поворота кулачка: угол приближения и угол удаления, угол верхнего останова, угол нижнего останова. Углы приближения и удаления делим на шесть равных частей. С центром в начале координат роводим полуокружность произвольным радиусом. Делим полученную полуокружность на шесть равных частей. Проводим горизонтали из точек на полуокружности до пересечения с соответствующими перпендикулярами восстановленными из отрезков в углах приближения и удаления. Полученные таким образом точки соединяем и получаем диаграмму скорости толкателя.
3.2. Построение диаграммы перемещения толкателя
методом графического интегрирования.
Построение диаграммы перемещения толкателя методом графического интегрирования заключается в следующем. На оси угла поворота звена в системе координат (S
-
t
)откладываем фазовые углы поворота кулачка (рис.5.). Углы приближения и удаления разбиваем на шесть равных частей. На оси угла поворота произвольно выбираем полюс Р1
. Из середин временных промежутков графика скорости восстанавливаем перпендикуляры до пересечения с графиком. Полученные таким образом точки горизонтально переносим до пересечения с вертикалью и соединяем лучами с полюсом Р1
. Лучи параллельно переносим в границы промежутков на графике перемещений. Кривая, являющаяся результатом проведенных построений, есть диаграмма перемещения толкателя.
Рассчитываем максимальное перемещение толкателя по формуле:
 [м], [м],
где  - модуль зубчатых колес, [мм]. - модуль зубчатых колес, [мм].
Рассчитываем масштабный коэффициент перемещения по формуле:
  , ,
где 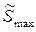 - максимальное перемещение толкателя, взятое с кинематической диаграммы перемещения толкателя, [мм]
. - максимальное перемещение толкателя, взятое с кинематической диаграммы перемещения толкателя, [мм]
.
Рассчитываем масштабный коэффициент времени по формуле:
  , ,
где  [об/мин]
- число оборотов кулачка, [об/мин]
- число оборотов кулачка,
 - масштабный коэффициент угла поворота. - масштабный коэффициент угла поворота.
Рассчитываем масштабный коэффициент скорости по формуле:
  , ,
где  - полюсное расстояние, [мм]
. - полюсное расстояние, [мм]
.

Рис.5.
3.3. Построение диаграммы ускорения толкателя
методом графического дифференцирования.
Построение диаграммы ускорения толкателя методом графического дифференцирования заключается в следующем. На оси угла поворота звена откладываем фазовые углы поворота кулачка. Углы приближения и удаления разбиваем на шесть равных частей. На оси угла поворота произвольно выбираем полюс Р2
. Две соседние точки графика изменения скорости толкателя соединяем хордами. Каждую хорду параллельно переносим в полюс Р2
до пересечения с вертикалью. Полученные на вертикали точки сносим на середины временных промежутков до пересечения с восстановленными из них перпендикулярами. Соединив полученные точки, получим кинематическую диаграмму ускорения толкателя.
Рассчитываем масштабный коэффициент ускорения, используя ранее найденные масштабные коэффициенты скорости и времени, по формуле:
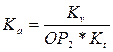 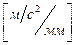 , ,
где  - полюсное расстояние, [мм]. - полюсное расстояние, [мм].
Найдем угловую скорость кулачка по формуле:
 
3.4. Определение радиуса начальной окружности кулачка
и положения центра кулачка.
По построенным диаграммам скорости и перемещения толкателя и с учетом масштабных коэффициентов заполняем таблицу 3.
Таблица 3
| №
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|  , град , град
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 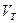 , м/с , м/с
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
|  м. м.
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
| 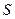 , м , м
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
Для определения радиуса начальной окружности кулачка и положения центра кулачка необходимо построить вспомогательный эллипс (рис.6.), который представляет собой зависимость величины  от перемещения толкателя от перемещения толкателя  . На двух взаимно перпендикулярных осях по вертикали откладываем ход толкателя . На двух взаимно перпендикулярных осях по вертикали откладываем ход толкателя 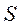 из таблицы 3 в предварительно выбранном масштабе, а по горизонтали от каждого положения влево и вправо- величину из таблицы 3 в предварительно выбранном масштабе, а по горизонтали от каждого положения влево и вправо- величину 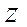 , равную отношению линейной скорости толкателя к угловой скорости кулачка. Соединив полученные точки, получаем вспомогательный эллипс. К крайним точкам эллипса проводим касательные под углами , равную отношению линейной скорости толкателя к угловой скорости кулачка. Соединив полученные точки, получаем вспомогательный эллипс. К крайним точкам эллипса проводим касательные под углами  (максимальный угол давления), они отсекают на вертикали точку О2
, ниже которой находится геометрическое место точек центра кулачка. Так как (максимальный угол давления), они отсекают на вертикали точку О2
, ниже которой находится геометрическое место точек центра кулачка. Так как  , то минимальный радиус кулачка увеличиваем на 8-10%, откладывая ниже точку О1
: , то минимальный радиус кулачка увеличиваем на 8-10%, откладывая ниже точку О1
:  , мм , мм

Рис.6.
Таким образом, расстояние  - есть радиус минимальной окружности кулачка. - есть радиус минимальной окружности кулачка.
Рассчитаем радиус ролика по формуле:
 , мм
, мм
3.5. Построение теоретического и практического
профилей кулачка.
Построение теоретического профиля кулачка начинается с проведения окружности радиусом 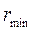 с центром в точке О1
. Разбиваем ее на фазовые углы. Углы приближения и удаления делим на шесть равных частей. На полученных лучах откладываем перемещение, взятое из таблицы 3. Профиль кулачка в углах верхнего и нижнего останова очерчиваем дугами окружностей. Соединив полученные точки кривой, получим теоретический профиль кулачка. с центром в точке О1
. Разбиваем ее на фазовые углы. Углы приближения и удаления делим на шесть равных частей. На полученных лучах откладываем перемещение, взятое из таблицы 3. Профиль кулачка в углах верхнего и нижнего останова очерчиваем дугами окружностей. Соединив полученные точки кривой, получим теоретический профиль кулачка.
Для построения практического профиля кулачка проводим окружности радиусом 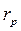 с центрами на полученном теоретическом профиле. Затем вычерчиваем эквидистантную кривую, как бы касающуюся окружностей ролика, получаем практический профиль кулачка ( на рис.6. не показан), который меньше теоретического на величину радиуса ролика с центрами на полученном теоретическом профиле. Затем вычерчиваем эквидистантную кривую, как бы касающуюся окружностей ролика, получаем практический профиль кулачка ( на рис.6. не показан), который меньше теоретического на величину радиуса ролика 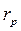 . .
Компоновка листа №2.

Лист №2.Синтез кулачкового механизма подвода и отвода стола.
«Кинематическая диаграмма перемещения толкателя Ks
=__
»
«Кинематическая диаграмма скорости толкателя Kv
=__;
K
j=__
»
«Кинематическая диаграмма ускорения толкателя Ka
=__
»
«Вспомогательный эллипс. Теоретический и практический профили кулачка М 1:____»
4. Синтез планетарного механизма.
4.1. Определение числа зубьев зубчатых колес
и числа сателлитов.
Синтез планетарного механизма начинаем с того, что задаемся числом зубьев центральной шестерни. Так как все зубчатые колеса механизма будем считать нулевыми, то минимальное число зубьев центральной шестерни принимаем 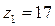 , для того чтобы избежать эффекта подрезания ножки зуба. Далее по предложенному ниже алгоритму подбираем числа зубьев остальных шестерен зубчатого механизма. В случае невыполнения какого-либо из условий, следует это отметить фразой «Условие не выполняется» и принять число зубьев центральной шестерни , для того чтобы избежать эффекта подрезания ножки зуба. Далее по предложенному ниже алгоритму подбираем числа зубьев остальных шестерен зубчатого механизма. В случае невыполнения какого-либо из условий, следует это отметить фразой «Условие не выполняется» и принять число зубьев центральной шестерни  и так далее до выполнения всех условий. и так далее до выполнения всех условий.
Задаемся числом зубьев центральной шестерни 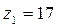 . .
1. Определяем число зубьев шестерни  по заданному передаточному отношению: по заданному передаточному отношению:

Рис.7.
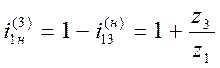
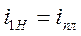

(рассчитанное значение  должно быть целым числом) должно быть целым числом)
2. Определяем число зубьев сателлита  из условия соосности
: из условия соосности
:
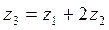

(рассчитанное значение  должно быть целым числом) должно быть целым числом)
3. Определяем предельно допускаемое число сателлитов из условия соседства:
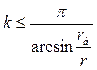
rа
- радиус окружности выступов сателлитов, мм
r-
радиус окружности центров сателлитов, мм
p
=180o


(число сателлитов принимаем равным ближайшему меньшему целому числу
)
4. Проверяем соответствие планетарного механизма условию сборки
:
 , ,
где g-
целое число
( если
g не получится целым числом, то принимаем число сателлитов
k меньшим на единицу и т.д.)
Рассчитываем диаметры начальных окружностей и вычерчиваем в масштабе схему планетарного редуктора:
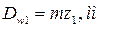

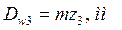
4.2. Построение внешнего эвольвентного зацепления.
Определяем параметры зубчатых колес:
- высота головки зубьев 
- высота ножки зубьев 

Рис.8.
- диаметры начальных окружностей:


- диаметры выступов зубьев:


- диаметры впадин зубьев:


Межцентровое расстояние:
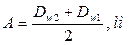
Шаг по начальной окружности:

Угол зацепления:  . .

Рис.9.
При вычерчивании элементов зубчатого зацепления масштаб построения выбираем таким образом, чтобы высота зубьев на чертеже была не менее 50 мм,
учитываем, что высота зуба 
Построение.
Откладываем межцентровое расстояние А=О1
О2
. Из центров проводим начальные окружности. Отмечаем полюс зацепления Р
. Через полюс под углом  проводим линию зацепления
. На линию зацепления из центров опускаем перпендикуляры, отмечаем точки M
и N
. MN
– теоретическая линия зацепления
. O1
M
и O2
N
– радиусы основных окружностей. Проводим основные окружности. Строим профиль центральной шестерни 1. Отрезок PN
разбиваем на шесть равных отрезков. На основной окружности отмечаем такие же отрезки по обе стороны от точки N
. В каждой полученной точке строим касательную к окружности. На них отмечаем отрезки, увеличивая их количество, если касательная выше линии зацепления и уменьшая, если ниже. Соединяя крайние точки, получаем эвольвенту
. Проводим окружности выступов и впадин. По начальной окружности от полюса Р
откладываем половину толщины зуба: проводим линию зацепления
. На линию зацепления из центров опускаем перпендикуляры, отмечаем точки M
и N
. MN
– теоретическая линия зацепления
. O1
M
и O2
N
– радиусы основных окружностей. Проводим основные окружности. Строим профиль центральной шестерни 1. Отрезок PN
разбиваем на шесть равных отрезков. На основной окружности отмечаем такие же отрезки по обе стороны от точки N
. В каждой полученной точке строим касательную к окружности. На них отмечаем отрезки, увеличивая их количество, если касательная выше линии зацепления и уменьшая, если ниже. Соединяя крайние точки, получаем эвольвенту
. Проводим окружности выступов и впадин. По начальной окружности от полюса Р
откладываем половину толщины зуба:  Соединяем с центром О2
и получаем ось симметрии зуба. Достраиваем вторую стенку зуба. Соседние зубья вычерчиваем на расстоянии шага Соединяем с центром О2
и получаем ось симметрии зуба. Достраиваем вторую стенку зуба. Соседние зубья вычерчиваем на расстоянии шага 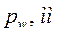 .Аналогично строим зубья второго колеса. .Аналогично строим зубья второго колеса.
Определяем практическую линию зацепления АВ
. Точка А
– точка пересечения образующей с окружностью выступов колеса 1. Точка В
– точка пересечения образующей с окружностью выступов колеса 2. Отмечаем рабочие участки зубьев радиусами О2
А
и О1
В
. делаем засечки на стенках зубьев, находящихся в зацеплении, заштриховываем шириной 2-4мм
.
Построение диаграммы работы зубьев.
От точек А
и В
восстанавливаем перпендикуляры к образующей, чертим прямоугольник произвольной ширины и от каждой стороны откладываем отрезки равные шагу по основной окружности:  . Заштриховываем зоны работы зубьев. . Заштриховываем зоны работы зубьев.
Коэффициент перекрытия (зацепления):

Анализ значения коэффициента перекрытия (демонстрируется на примере):
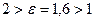
 - таким образом, 40% времени в зацеплении находится одна пара зубьев. - таким образом, 40% времени в зацеплении находится одна пара зубьев.
 - таким образом, 60% времени в зацеплении находятся две пары зубьев. - таким образом, 60% времени в зацеплении находятся две пары зубьев.
Компоновка листа №3.

Лист №3.Синтез планетарного механизма.
«Схема планетарного механизма М __
»
«Эвольвентное зацепление М ____»
5. Расчет маховика.
5.1. Построение диаграммы приведенного момента
сил сопротивления.
Силы полезного сопротивления действуют только во время рабочего хода машины, в курсовом проекте этот период соответствует процессу резания долбяком. Исходя из предложенной циклограммы механизма зубодолбежного станка (приложение №2), для  от 0° до 30° и от 150° до 360° момент сил сопротивления от 0° до 30° и от 150° до 360° момент сил сопротивления  . .
Момент сил сопротивления, приведенных к кривошипу:
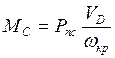 
Значение  определено в п.2.1. Значения скорости долбяка сведены в таблице 1. Результаты расчетов приведенного момента сил сопротивления заносим в таблицу 4. определено в п.2.1. Значения скорости долбяка сведены в таблице 1. Результаты расчетов приведенного момента сил сопротивления заносим в таблицу 4.
Таблица 4
| №
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
| 
|
0
|
30
|
60
|
90
|
120
|
150
|
180
|
210
|
240
|
270
|
300
|
330
|
360
|
| 
|
0
|
|
|
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
По полученным данным строим диаграмму приведенного момента сил сопротивления (рис.10). Рассчитываем масштабные коэффициенты:
 
 , ,
5.2. Построение диаграммы работы движущих сил
и сил сопротивления, приведенного момента движущих сил.
Диаграмма работы сил сопротивления 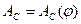 строим методом графического интегрирования диаграммы строим методом графического интегрирования диаграммы 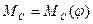 . .
При установившемся движении работа движущих сил равна работе сил сопротивления: 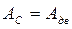 . Поэтому на диаграмме работы сил сопротивления соединяем крайние точки графика . Поэтому на диаграмме работы сил сопротивления соединяем крайние точки графика 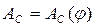 прямой линией, которая соответствует графику работы движущих сил прямой линией, которая соответствует графику работы движущих сил  . .
Рассчитываем масштабный коэффициент работы:  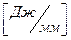
Методом графического дифференцирования строим график приведенного момента движущих сил  . .
5.3. Построение диаграммы изменения
кинетической энергии механизма.
Изменение кинетической энергии равно разности работ движущих сил и сил сопротивления: 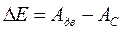 . Поэтому диаграмму . Поэтому диаграмму  строим графически из диаграмм строим графически из диаграмм  и и  с учетом знака разности. Масштабный коэффициент: с учетом знака разности. Масштабный коэффициент: 

Рис.10
5.4. Построение диаграммы
приведенного момента инерции.
При определении закона движения механизма массы всех подвижных звеньев заменяют массой звена приведения. Если звено приведения совершает вращательное движение, то пользуются понятием приведенного момента инерции.


где 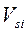 - линейная скорость центра тяжести i-того звена; - линейная скорость центра тяжести i-того звена;
 - масса i-того звена; - масса i-того звена;
 - угловая скорость i-того звена; - угловая скорость i-того звена;
 - центральный момент инерции i-того звена. - центральный момент инерции i-того звена.
В курсовом проекте звеном приведения является кривошип, совершающий вращательное движение, поэтому:
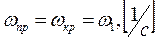
 
Рассчитываем приведенный момент инерции для 13 положений и результаты заносим в таблицу 5. Значения VD
,VS2
,
w
2
и w
3
берем из таблицы 1.
Таблица 5
| №
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
| 
|
0
|
30
|
60
|
90
|
120
|
150
|
180
|
210
|
240
|
270
|
300
|
330
|
360
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По полученным значениям строим график приведенного момента инерции. Определяем масштабный коэффициент:  
5.5. Построение диаграммы энергомасс методом Виттенбауэра.
Диаграмма энергомасс строится исключением параметра 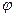 из диаграмм из диаграмм  и и  . .
К полученной диаграмме проводим касательные под углами 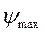 и и  . .


w
ср
=
w
кр
d
- коэффициент неравномерности
Касательные отсекаются на вертикали отрезок kl
, тогда момент инерции маховика:
 , ,
Если  и и  имеют значения близкие к 90о
, то касательные пересекут вертикаль далеко за пределами чертежа. Поэтому отрезок kl
определяют аналитически. имеют значения близкие к 90о
, то касательные пересекут вертикаль далеко за пределами чертежа. Поэтому отрезок kl
определяют аналитически.
Из треугольника Domk
следует:
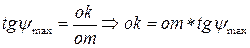
Из треугольника Donl
следует:

(длины om
и on [мм]
измеряем на диаграмме).
Тогда kl=
ol-
ok [мм]
5.6. Расчет массы и геометрических параметров маховика.
Принимаем средний диаметр маховика в пределах:  . .
Масса обода маховика:  [кг] [кг]

Рис.11.
Окружная скорость маховика:  
Если  , то материал маховика- чугун. , то материал маховика- чугун.  , если , если 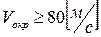 , то материал маховика- сталь. , то материал маховика- сталь.
Определяем геометрические параметры сечения маховика.
Площадь сечения маховика: 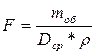 
Принимаем  , и так как , и так как  [м] [м]
Вычерчиваем в масштабе сечение маховика в виде колеса со спицами.
Компоновка листа №4.

Лист №4.Расчет маховика.
«Диаграмма приведенного момента движущих сил и сил сопротивления»
«Диаграмма работы движущих сил и сил сопротивления»
«Диаграмма изменения кинетической энергии»
«Диаграмма приведенного момента инерции»
«Диаграмма энергомасс (метод Виттенбауэра)»
6. Заключение.
В заключительной части курсового проекта следует кратко описать основные этапы проектирования, изложить основные его результаты , дать анализ полученных расчетов.
Общее руководство и контроль за ходом выполнения курсового проекта осуществляется преподавателем дисциплины. По ходу выполнения курсового проекта руководителем просматривается каждая часть пояснительной записки и подписывается каждый лист графической части. Готовый курсовой проект, оформленный соответствующим образом, передается руководителю на окончательную проверку. Проверенный проект с замечаниями руководителя возвращается студенту. По указаниям руководителя студент исправляет допущенные ошибки и дорабатывает курсовой проект.
Защита курсового проекта является обязательной и проводится за счет времени, отведенного на изучение дисциплины. Защита производится только при наличии разрешающих надписей на чертежах и пояснительной записке. Проект защищается студентом перед комиссией в составе не менее двух преподавателей.
Студент должен уметь кратко (за 3-5 минут) доложить основные положения проекта и ответить по существу на предложенные вопросы.
Курсовой проект оценивается по пятибалльной системе. Студентам, получившим неудовлетворительную оценку по курсовому проекту , предоставляется право выбора новой темы курсового проекта или, по решению преподавателя, доработки прежней темы, и определяется новый срок для ее выполнения. После защиты все материалы курсового проекта сдаются в архив кафедры.
ЛИТЕРАТУРА
1. Артоболевский И.И. Теория механизмов.- М.: Изд-во Наука, 1965.-776 с.: ил.
2. Кореняко А.С. Курсовое проектирование по теории механизмов и машин. Изд. 3-е, перераб. и доп / А.С. Кореняко, Л.И. Кременштейн, С.Д. Петровский и др.-М.:МАШГИЗ,1960.-262 с.:ил.
3. Левитская О.Н. Курс теории механизмов и машин: Учебник для вузов/ О.Н.Левитская, Н.И.Левитский.- М.: Высш.школа, 1978.-269 с.:ил.
4. Попов С.А. Курсовое проектирование по теории механизмов и механике машин: Учеб. Пособие для машиностроит. Спец.вузов/Под ред. К..Фролова.- М.: Высш.школа, 1986.-295 с.:ил.
5. Тепинкишев В.К.Металлорежущие станки.
6. Чернов Н.Н.Металлорежущие станки.- М.,1978.
7. Юдин В.А. Теория механизмов и машин.: Учеб. пособие для вузов. Изд.2-е, перераб. и доп./ В.А.Юдин, Л.В.Петрокас.-М.: Высш. школа, 1977.-527 с.:ил.
Приложение 1
Саратовский государственный технический университет
Энгельсский технологический институт(филиал) СГТУ
Кафедра Материаловедение
РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту
по дисциплине Теория механизмов и машин
Разработал: студент группы ___________
(группа)
_____________________________________
(ФИО)
Проверил: доцент каф. Материаловедение
_______________________________________
(ФИО)
Энгельс 200__ г.
Приложение 2

ПРОЕКТИРОВАНИЕ МЕХАНИЗМОВ
ЗУБОДОЛБЕЖНОГО СТАНКА
Методические указания и задания
к курсовому проекту
по курсу «Теория механизмов и машин»
для студентов специальности ТМС
Составил: МИЛОВАНОВА Людмила Руслановна
Рецензент
|