| 
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
высшего профессионального образования
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ
им. Н.И.ЛОБАЧЕВСКОГО
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

Факультет вычислительной математики и кибернетики
Кафедра информатики и автоматизации научных исследований
МЕТОДИЧЕСКИЕ УКАЗАНИЯ (СБОРНИК ЗАДАЧ) ПО КУРСУ «СИСТЕМЫ ПРИНЯТИЯ РЕШЕНИЙ»
Нижний Новгород, 2010
Методические указания (сборник задач) для самостоятельной работы студентов специальности «Прикладная информатика» факультета ВМК по курсу «Системы принятия решений» / Нижегородский государственный университет, 2010, с 20.
Данная методическая разработка содержит задания, связанные с применением необходимых и достаточных условий оптимальности в различных классах оптимизационных задач.
Методическая разработка подготовлена доцентом Коротченко А.Г., Сморяковой В.М., Кучиной О.М., Малаховской Д.А.
Рецензент: кандидат физ.-мат. наук, доцент В.А.Гришагин
В данной разработке приведены оптимизационные задачи, для которых требуется доказать существование решения, задачи на доказательство некоторых свойств выпуклых множеств и выпуклых функций, а также задачи на использование необходимых и достаточных условий оптимальности.
Напомним основные обозначения, используемые при решении задач данного раздела:
 - - 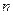 -мерные вектора; -мерные вектора;
 - - 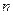 -мерное евклидово пространство со скалярным произведением -мерное евклидово пространство со скалярным произведением  ; ;
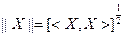 - норма вектора X; - норма вектора X;
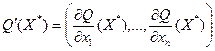 - градиент функции - градиент функции  в точке в точке 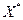 ; ;
 - матрица вторых частных производных (гессиан) функции - матрица вторых частных производных (гессиан) функции  в точке в точке 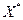 . .
Задача математического программирования

 (1) (1)
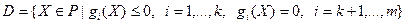 - допустимое множество задачи математического программирования, - допустимое множество задачи математического программирования,
 . .
 - функция Лагранжа задачи (1), где - функция Лагранжа задачи (1), где  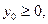  . .
 - градиент функции Лагранжа по координатам вектора - градиент функции Лагранжа по координатам вектора  , то есть вектор, составленный из частных производных функции Лагранжа по координатам вектора
, то есть вектор, составленный из частных производных функции Лагранжа по координатам вектора  :
:
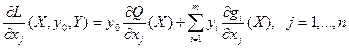 . .
 - матрица вторых частных производных функции Лагранжа по координатам вектора - матрица вторых частных производных функции Лагранжа по координатам вектора  .
.
Сформулируем известный из курса математического анализа результат о существовании решения задачи (1):
Теорема 1
(Теорема Вейерштрасса)
Пусть  - компакт (ограниченное и замкнутое множество) в - компакт (ограниченное и замкнутое множество) в  , ,  - непрерывная функция на - непрерывная функция на  . Тогда точка глобального минимума функции . Тогда точка глобального минимума функции  на на  (глобальное решение задачи (1)) существует. (глобальное решение задачи (1)) существует.
1. Пусть  - замкнутое множество на - замкнутое множество на  , ,  - непрерывная функция на - непрерывная функция на  , причём при некотором , причём при некотором  множество множество  ограничено. Доказать, что тогда точка глобального минимума функции ограничено. Доказать, что тогда точка глобального минимума функции  на на  существует. существует.
2. Известно, что функция  непрерывна на непрерывна на  и удовлетворяет следующему условию: и удовлетворяет следующему условию:  для любой последовательности для любой последовательности  такой, что такой, что 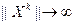 , , 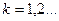 . Доказать, что тогда функция . Доказать, что тогда функция  достигает своего минимального значения на любом замкнутом множестве из достигает своего минимального значения на любом замкнутом множестве из  . .
3. Пусть непрерывная функция  имеет точку глобального минимума на имеет точку глобального минимума на  . Следует ли отсюда, что функция . Следует ли отсюда, что функция  имеет точку глобального минимума на любом замкнутом множестве из имеет точку глобального минимума на любом замкнутом множестве из  ? ?
4. Пусть  - точка строгого локального минимума функции - точка строгого локального минимума функции 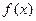 на на 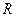 ( ( ). Можно ли утверждать, что ). Можно ли утверждать, что 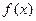 убывает в некоторой левой полуокрестности точки убывает в некоторой левой полуокрестности точки  и возрастает в некоторой правой полуокрестности и возрастает в некоторой правой полуокрестности  ? ?
5. Убедиться, что функция 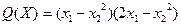 достигает локального минимума в точке достигает локального минимума в точке 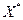 = (0,0) вдоль каждой прямой, проходящей через = (0,0) вдоль каждой прямой, проходящей через 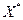 , но , но 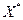 не является точкой локального минимума этой функции. не является точкой локального минимума этой функции.
Задача математического программирования (1) называется задачей безусловной оптимизации, если 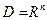 , то есть , то есть
 (2) (2)
Теорема 2
(Необходимое условие локальной оптимальности первого порядка)
Пусть функция  дифференцируема в точке дифференцируема в точке 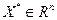 . Если . Если 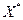 - локальное решение задачи (2), то - локальное решение задачи (2), то
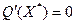 . (3) . (3)
Теорема 3
(Необходимое условие локальной оптимальности второго порядка)
Пусть функция  дважды дифференцируема в точке дважды дифференцируема в точке 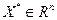 . Если . Если 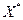 - локальное решение задачи (2), то матрица - локальное решение задачи (2), то матрица  - неотрицательно определена, то есть - неотрицательно определена, то есть
 при всех при всех  . (4) . (4)
Теорема 4
(Достаточное условие локальной оптимальности)
Пусть функция  дважды дифференцируема в точке дважды дифференцируема в точке 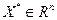 и и 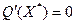 , а матрица , а матрица  положительно определена, то есть положительно определена, то есть
 при всех при всех  , , 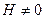 . (5) . (5)
Тогда 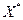 - строгое локальное решение задачи (2). - строгое локальное решение задачи (2).
Теорема 5
(Критерий Сильвестра)
Симметрическая матрица является неотрицательно (положительно) определенной, тогда и только тогда, когда все её главные (угловые) миноры неотрицательны (положительны).
Пример 1.
Рассмотрим задачу безусловной оптимизации:
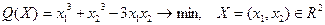 . .
Решение:
- Выпишем необходимое условие локальной оптимальности первого порядка:
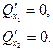 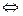 
Решениями этой системы являются точки  = (0,0), = (0,0), 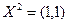
- Рассмотрим гессиан функции
 в точках в точках  и и  : :
 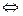 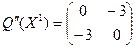 , ,  . .
Матрица  по критерию Сильвестра не является неотрицательно определённой, то есть необходимое условие локальной оптимальности второго порядка не выполняется. Отсюда следует, что точка по критерию Сильвестра не является неотрицательно определённой, то есть необходимое условие локальной оптимальности второго порядка не выполняется. Отсюда следует, что точка  = (0,0) не может быть решением задачи. = (0,0) не может быть решением задачи.
Матрица  положительно определена. Следовательно, выполняется достаточное условие локальной оптимальности. Точка положительно определена. Следовательно, выполняется достаточное условие локальной оптимальности. Точка 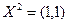 – строгое локальное решение задачи. – строгое локальное решение задачи.
В следующих задачах требуется привести примеры функций одной или двух переменных, в которых выполняются указанные ниже требования.
6. Глобальные максимум и минимум достигаются в бесконечном числе точек.
7. Функция ограничена, глобальный максимум достигается, а глобальный минимум не достигается.
8. Функция ограничена, но глобальные минимум и максимум не достигаются.
9. Функция ограничена, имеет локальные минимумы и максимумы, но глобальные максимум и минимум не достигается.
10. Имеется единственный локальный экстремум, не являющийся глобальным.
11. Имеется бесконечное число локальных минимумов, но нет ни одного локального максимума.
12. Найти все точки локального минимума и локального максимума функции  на на 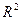 . .
Найти локальные решения в задачах 13-16.
13. 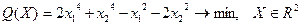 . .
14. 
15. 
16. 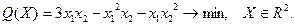
17. Найти наименьшее значение функции 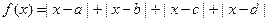 , где , где  ; ; 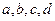 - заданные числа. - заданные числа.
18. Показать, что в методе наискорейшего спуска направления 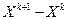 и и  - ортогональны. - ортогональны.
Напомним, что метод наискорейшего спуска предназначен для отыскания локального минимума функции  и задаётся расчётной формулой и задаётся расчётной формулой 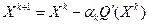 для заданной точки для заданной точки 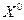 и и  , которые выбираются из условия минимизации функции вдоль направления антиградиента для каждого , которые выбираются из условия минимизации функции вдоль направления антиградиента для каждого  . .
Задача математического программирования (1) называется классической задачей на условный экстремум, если  , то есть , то есть
 (6) (6)
Функция Лагранжа классической задачи на условный экстремум определена при 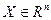 , ,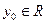 , , 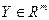 . .
Теорема 6
(Необходимое условие локальной оптимальности первого порядка)
Пусть функции 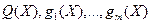 непрерывно дифференцируемы в некоторой окрестности точки непрерывно дифференцируемы в некоторой окрестности точки 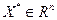 . Если . Если 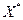 - локальное решение задачи (6), то существует число - локальное решение задачи (6), то существует число  и вектор и вектор  не равные нулю одновременно и такие, что не равные нулю одновременно и такие, что
 . (7) . (7)
Если градиенты  линейно независимы, то линейно независимы, то  . .
Условие линейной независимости градиентов ограничений в точке 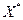 называется условием регулярности. Числа называется условием регулярности. Числа 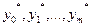 называются множителями Лагранжа. Функция Лагранжа, для которой называются множителями Лагранжа. Функция Лагранжа, для которой  , называется регулярной. , называется регулярной.
Теорема 7
(Необходимое условие локальной оптимальности второго порядка)
Пусть функции  дважды дифференцируемы в точке дважды дифференцируемы в точке 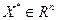 и непрерывно дифференцируемы в некоторой её окрестности, причём градиенты и непрерывно дифференцируемы в некоторой её окрестности, причём градиенты  линейно независимы. Если линейно независимы. Если 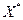 - локальное решение задачи (6), то - локальное решение задачи (6), то
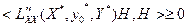 (8) (8)
при любых 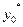 , , 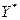 , удовлетворяющих (7), и всех , удовлетворяющих (7), и всех  таких, что таких, что
 (9) (9)
Теорема 8
(Достаточное условие локальной оптимальности)
Пусть функции 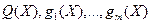 дважды дифференцируемы в точке дважды дифференцируемы в точке 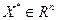 , удовлетворяющей ограничениям , удовлетворяющей ограничениям 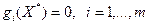 . Предположим, что при некоторых . Предположим, что при некоторых  , , 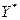 выполняется условие (7), и кроме того выполняется условие (7), и кроме того
 (10) (10)
при всех ненулевых  , удовлетворяющих условию (9). , удовлетворяющих условию (9).
Тогда  - строгое локальное решение задачи (6). - строгое локальное решение задачи (6).
Пример 2.
Рассмотрим классическую задачу на условный экстремум:
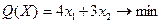
 , ,
 . .
Решение:
1. Составим функцию Лагранжа:
 = = . .
2. Выпишем необходимые условия оптимальности и ограничение задачи:
  
Ясно, что условие регулярности для данной задачи выполнено, но иногда бывает удобно рассмотреть отдельно два случая  и и  . .
Если  то и то и  , что противоречит необходимому условию оптимальности (не все множители Лагранжа равны нулю). Полагаем , что противоречит необходимому условию оптимальности (не все множители Лагранжа равны нулю). Полагаем  . Таким образом, имеем регулярную функцию Лагранжа: . Таким образом, имеем регулярную функцию Лагранжа:
 = = . .
Необходимые условия перепишутся в виде:

Данная система имеет два решения:
1) 
2) 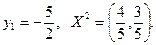
3. Далее рассмотрим матрицу вторых частных производных функции Лагранжа:
 . .
Для указанных решений матрица принимает соответственно вид:
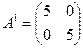 , ,  . .
Выпишем условие (9):
 , ,  . .
Исследуем полученные точки  и и  : :
3.1. Условие (9) для точки  выглядит следующим образом: выглядит следующим образом:  . Отсюда . Отсюда  . Нетрудно проверить, что матрица . Нетрудно проверить, что матрица 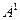 удовлетворяет условию (10). Достаточное условие оптимальности выполнено, следовательно, точка удовлетворяет условию (10). Достаточное условие оптимальности выполнено, следовательно, точка  - строгое локальное решение исходной задачи. - строгое локальное решение исходной задачи.
3.2. Из условия (9) для точки  получаем получаем  . Проверим условие (8) для таких . Проверим условие (8) для таких 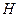 . Получаем . Получаем 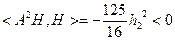 , при , при  . Необходимое условие оптимальности второго порядка не выполняется. Точка . Необходимое условие оптимальности второго порядка не выполняется. Точка  не является решением задачи. не является решением задачи.
19. Из данного треугольника вырезать два равных круга наибольшего радиуса.
20. Доказать, что из всех треугольников с общим углом при вершине и данной суммой длин боковых сторон равнобедренный треугольник имеет наименьшее основание.
21. Из всех треугольников с одинаковым основанием и одним и тем же углом при вершине найти треугольник с наибольшим периметром.
22. Даны две параллельные прямые и точка  между ними, лежащая на расстоянии между ними, лежащая на расстоянии  от одной прямой и на расстоянии от одной прямой и на расстоянии 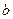 от другой прямой. Точка от другой прямой. Точка  служит вершиной прямых углов прямоугольных треугольников, две другие вершины которых лежат на каждой из параллельных прямых. Какой из треугольников имеет наименьшую площадь? служит вершиной прямых углов прямоугольных треугольников, две другие вершины которых лежат на каждой из параллельных прямых. Какой из треугольников имеет наименьшую площадь?
23. В треугольной пирамиде проводятся сечения, параллельные двум её непересекающимся рёбрам. Найти сечение с наибольшей площадью.
24. Окно имеет форму прямоугольника, который сверху заканчивается полукругом. Каково должно быть основание прямоугольника для того, чтобы при данном периметре 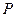 окно пропускало бы больше света? окно пропускало бы больше света?
25. Дан квадратный лист картона. Какой величины должны быть вырезаны квадраты в каждом из четырёх углов этого листа, чтобы из оставшейся крестообразный фигуры можно было сделать коробку наибольшей вместимости?
26. В эллипс  вписать прямоугольник наибольшей площади. вписать прямоугольник наибольшей площади.
27. Из всех эллипсов, у которых сумма осей постоянна и равна 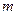 , найти наибольший по площади. , найти наибольший по площади.
В задачах 28-31 требуется определить локальные минимумы и максимумы функции 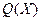 при выполнении ограничения при выполнении ограничения  . .
28. 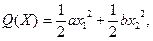  , , 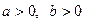 . .
29.  , , 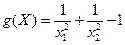 . .
30. 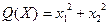 , , 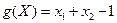 . .
В задачах 28-30  . .
31.  , ,  , , 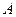 - симметрическая матрица размера - симметрическая матрица размера  , ,  . .
32. Доказать, что для любых двух векторов 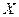 , ,  таких, что таких, что  , ,  справедливо неравенство справедливо неравенство  . .
Найти решения задач на условный экстремум:
33. 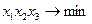 , , 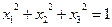 , ,  . .
34.  , ,  , ,  . .
35. 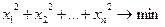 , , 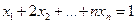 . .
- Число
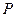 разложить на разложить на  множителей так, чтобы сумма их была наименьшей. множителей так, чтобы сумма их была наименьшей.
Выпуклые множества и выпуклые функции
Непустое множество  называется выпуклым, если называется выпуклым, если  при всех при всех  , , 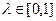 . .
Функция 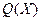 , определенная на выпуклом множестве , определенная на выпуклом множестве  , называется выпуклой, если , называется выпуклой, если
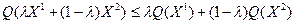 (11) (11)
при всех  , , 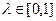 . Если при всех . Если при всех  , ,  , , 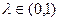 неравенство (11) выполняется как строгое, то неравенство (11) выполняется как строгое, то 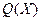 называется строго выпуклой. называется строго выпуклой.
Функция 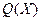 , определенная на выпуклом множестве , определенная на выпуклом множестве  , называется сильно выпуклой с константой , называется сильно выпуклой с константой  , если , если
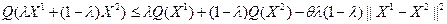
при всех  , ,  . .
Ниже приведены необходимые и достаточные условия выпуклости и сильной выпуклости дифференцируемых функций. Для краткости формулировок выпуклые функции рассматриваются как сильно выпуклые с параметром  . .
Теорема 9
(Первый дифференциальный критерий сильной выпуклости)
Пусть функция 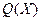 дифференцируема на выпуклом множестве дифференцируема на выпуклом множестве  . Тогда для того, чтобы . Тогда для того, чтобы 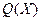 была сильно выпуклой с параметром была сильно выпуклой с параметром  на на  , необходимо и достаточно выполнения условия: , необходимо и достаточно выполнения условия:
 , при всех , при всех 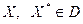 . .
Теорема 10
(Второй дифференциальный критерий сильной выпуклости)
Пусть функция 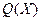 непрерывно дифференцируема на выпуклом множестве непрерывно дифференцируема на выпуклом множестве  . Тогда для того, чтобы . Тогда для того, чтобы 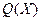 была сильно выпуклой с параметром была сильно выпуклой с параметром  на на  , необходимо и достаточно выполнения условия: , необходимо и достаточно выполнения условия:
 , при всех , при всех 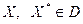 . .
Теорема 11
(Третий дифференциальный критерий сильной выпуклости)
Пусть 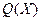 дважды непрерывно дифференцируема на выпуклом множестве дважды непрерывно дифференцируема на выпуклом множестве  , причем внутренность множества , причем внутренность множества  не пуста ( не пуста ( 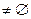 ). Тогда для того, чтобы ). Тогда для того, чтобы  была сильно выпуклой с параметром была сильно выпуклой с параметром  на на  , необходимо и достаточно выполнения условия: , необходимо и достаточно выполнения условия:
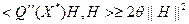 для всех для всех  . .
37. Показать, что множество  выпукло тогда и только тогда, когда выпукло тогда и только тогда, когда  при всех при всех  . Здесь . Здесь  - алгебраическая сумма множеств - алгебраическая сумма множеств 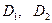 ( (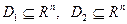 ). ).
38. Являются ли выпуклыми множествами следующие множества на плоскости:
а) круг 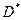 с центром в начале координат; с центром в начале координат;
в) часть круга 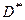 , получающаяся из него путём вырезания сектора, лежащего в правом квадранте. , получающаяся из него путём вырезания сектора, лежащего в правом квадранте.
39. Верно ли, что объединение и пересечение двух выпуклых множеств выпукло?
40. Пусть 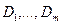 - выпуклые множества, - выпуклые множества, 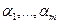 - произвольные числа. Доказать, что множество - произвольные числа. Доказать, что множество  выпукло. выпукло.
41. Перечислить все выпуклые множества, принадлежащие числовой прямой  . .
42. Показать, что следующие множества являются выпуклыми:
а) 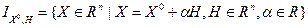 - прямая, проходящая через точку - прямая, проходящая через точку 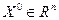 в направлении в направлении  ; ;
в)  - луч, выходящий из точки - луч, выходящий из точки 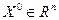 в направлении в направлении  ; ;
с)  - гиперплоскость с нормалью - гиперплоскость с нормалью  ( (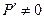 ) )  ; ;
d) 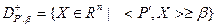 , ,
 - порождаемые гиперплоскостью с нормалью - порождаемые гиперплоскостью с нормалью  ( ( ) полупространства. Здесь ) полупространства. Здесь  . .
43. Показать, что множество , где , где 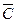 - некоторая матрица размера ( - некоторая матрица размера ( ) со строками ) со строками  , , 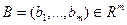 , является выпуклым. , является выпуклым.
44. Показать, что множество 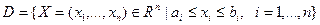 является выпуклым. Здесь является выпуклым. Здесь 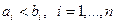 , - заданные числа. , - заданные числа.
Точка  выпуклого множества выпуклого множества  называется крайней, если её нельзя представить в виде называется крайней, если её нельзя представить в виде 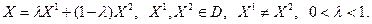
45. Определить все крайние точки множества  , заданного в задаче 44. , заданного в задаче 44.
46. Определить все крайние точки множества  , где , где  . .
47. Указать все крайние точки множества  , определённого в задаче 42. , определённого в задаче 42.
В задачах 48-53 множество  предполагается выпуклым. предполагается выпуклым.
48. Доказать, что функция 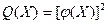 - выпукла, если - выпукла, если 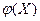 выпукла и выпукла и 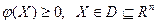 . .
49. Доказать, что функция 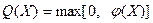 - выпукла, если - выпукла, если 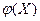 выпукла, выпукла, 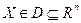 . .
50. Проверить, что функция  - выпукла на - выпукла на 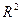 . .
51. Пусть 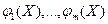 - выпуклые функции на множестве - выпуклые функции на множестве 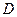 . Доказать, что функция . Доказать, что функция  - выпукла на - выпукла на  . .
52. Пусть 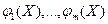 - выпуклые функции на множестве - выпуклые функции на множестве 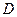 , , 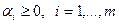 , и хотя бы при одном , и хотя бы при одном 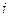 функция функция  строго (сильно) выпукла, строго (сильно) выпукла,  . Доказать, что . Доказать, что 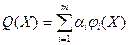 - строго (сильно) выпукла на - строго (сильно) выпукла на  . .
53. Доказать, что функция 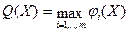 - выпукла на - выпукла на 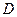 , если функции , если функции  , ,  , выпуклы на , выпуклы на  . .
54. Пусть  - выпуклая функция на выпуклом множестве - выпуклая функция на выпуклом множестве 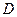 . Показать, что . Показать, что  при всех при всех  , для которых , для которых  . .
55. Доказать, что функция 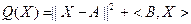 сильно выпукла на сильно выпукла на  , ,  . .
56. Доказать, что строго вогнутая функция может достигать своего минимального значения только в крайних точках выпуклого множества 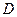 , на котором она определена. , на котором она определена.
57. Найти максимальное значение функции  при выполнении ограничений: при выполнении ограничений:


58. Пусть функция  - непрерывная, монотонно неубывающая функция на отрезке - непрерывная, монотонно неубывающая функция на отрезке  . Показать, что функция . Показать, что функция 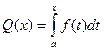 является выпуклой на отрезке является выпуклой на отрезке  . .
- Проверить, что функция
 выпукла на выпукла на  . .
Задача
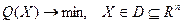 (12) (12)
называется выпуклой, если  - выпуклое множество, а - выпуклое множество, а  выпуклая функция на выпуклая функция на 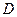 . .
60. Доказать, что в выпуклой задаче любое её локальное решение является также и глобальным.
61. Пусть функция  выпукла на выпукла на 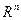 и дифференцируема в точке и дифференцируема в точке  . Доказать, что если . Доказать, что если  , то , то 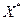 - точка минимума функции - точка минимума функции  на на  . .
62. Известно, что выпуклая задача (12) имеет решение. Доказать, что тогда множество её решений выпукло, если при этом  строго выпукла на строго выпукла на 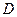 , то решение задачи (12) единственно. , то решение задачи (12) единственно.
Условия оптимальности
Пусть  - множество направлений убывания функции - множество направлений убывания функции  в точке в точке  , а , а  - множество возможных направлений относительно множества - множество возможных направлений относительно множества 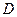 в точке в точке 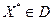 . Напомним, что вектор . Напомним, что вектор 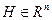 задаёт направление убывания функции задаёт направление убывания функции  в точке в точке  , если , если 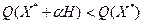 при всех достаточно малых при всех достаточно малых 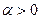 , и возможное направление относительно множества , и возможное направление относительно множества  в точке в точке  , если точка , если точка 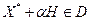 при всех достаточно малых при всех достаточно малых 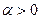 . .
63. Доказать, что если 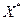 - локальное решение задачи (3) без каких-либо предположений на множество - локальное решение задачи (3) без каких-либо предположений на множество  и функцию и функцию  , то , то 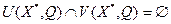 . .
64. Пусть в задаче (12) множество  выпукло, а функция выпукло, а функция  - дифференцируема в точке - дифференцируема в точке  . Доказать, что тогда, если . Доказать, что тогда, если  - локальное решение задачи (12), то - локальное решение задачи (12), то
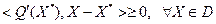 , (13) , (13)
если же  выпукла на выпукла на  и выполняется (13), то и выполняется (13), то 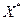 - глобальное решение задачи (12). - глобальное решение задачи (12).
65. Доказать, что если  ( (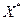 - внутренняя точка множества - внутренняя точка множества 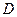 ), то (13) эквивалентно условию ), то (13) эквивалентно условию  . .
66. Пусть множество  имеет вид имеет вид  , где , где  , , 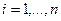 (если (если  или или  , то соответствующий знак неравенства в задании множества , то соответствующий знак неравенства в задании множества  следует понимать как строгий). Доказать, что тогда условие (13) эквивалентно условию: для любого следует понимать как строгий). Доказать, что тогда условие (13) эквивалентно условию: для любого 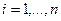

67. Пусть множество  имеет вид имеет вид  , , 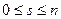 ( ( соответствует случаю соответствует случаю 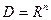 ). Доказать, что тогда (13) эквивалентно условиям: ). Доказать, что тогда (13) эквивалентно условиям:
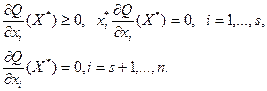
68. Решить задачу:

69. Решить задачу:

70. Пусть  - дифференцируемая сильно выпуклая функция на - дифференцируемая сильно выпуклая функция на  . Показать, что при любом . Показать, что при любом  решение уравнения решение уравнения  на на  существует и единственно. существует и единственно.
71. Пусть  - дифференцируемая выпуклая функция на - дифференцируемая выпуклая функция на  . Показать, что при любом . Показать, что при любом  решение уравнения решение уравнения  на на  существует и единственно. существует и единственно.
Напомним необходимое условие оптимальности (Принцип Лагранжа) в задаче математического программирования (1).
Теорема 12
(Принцип Лагранжа)
Пусть в задаче (1) множество  - выпукло, функции - выпукло, функции 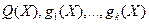 дифференцируемы в точке дифференцируемы в точке 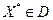 , функции , функции  непрерывно дифференцируемы в некоторой окрестности точки непрерывно дифференцируемы в некоторой окрестности точки 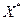 . Если . Если 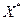 - локальное решение задачи (1), то существует число - локальное решение задачи (1), то существует число  и вектор и вектор 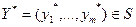 не равные нулю одновременно и такие, что не равные нулю одновременно и такие, что
 (14) (14)
 . (15) . (15)
Используемые здесь обозначения пояснены после формулировки задачи (1) на странице 3, а числа  , также как в классической задаче на условный экстремум, называются множителями Лагранжа. , также как в классической задаче на условный экстремум, называются множителями Лагранжа.
Теорема 13
(Достаточное условие оптимальности)
Пусть в задаче (1) множество  выпукло, функции выпукло, функции 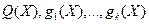 выпуклы на выпуклы на 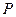 и дифференцируемы в точке и дифференцируемы в точке 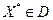 , функции , функции  линейны. Если при линейны. Если при  и некотором и некотором  выполняются условия (14), (15), то выполняются условия (14), (15), то 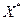 - глобальное решение задачи (1). - глобальное решение задачи (1).
Теорема 14
(Условия регулярности)
Пусть в задаче (1) множество  выпукло, функции выпукло, функции  дифференцируемы в точке дифференцируемы в точке 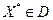 , функции , функции 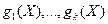 выпуклы на выпуклы на  , функции , функции 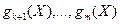 линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий: линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
1) ограничения-равенства отсутствуют (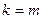 ) и существует точка ) и существует точка 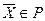 такая, что такая, что 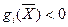 при всех при всех 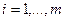 ; ;
2)  , функции , функции 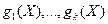 линейны. линейны.
Тогда, если 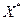 - локальное решение задачи (1), то существует - локальное решение задачи (1), то существует  такой, что при такой, что при  будут выполнены условия (14), (15). будут выполнены условия (14), (15).
Условие 1) теоремы называется условием регулярности Слейтера.
Теорема 15
(Теорема Куна-Таккера в дифференциальной форме)
Пусть в дополнение к условиям теоремы 14 функция  выпукла на выпукла на 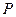 . Тогда точка . Тогда точка  является решением задачи (1) в том и только том случае, если существует вектор является решением задачи (1) в том и только том случае, если существует вектор  такой, что при такой, что при  выполняются условия (14), (15). выполняются условия (14), (15).
Пример 3.
Рассмотрим задачу:

Решение:
1. Очевидно, что данная задача - задача выпуклого программирования.
2. Условия регулярности Слейтера выполнено, следовательно, функция Лагранжа регулярная:
 . .
- Выпишем необходимые условия:
  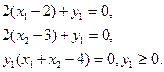
Пусть 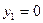 , тогда , тогда 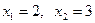 , но данная точка не удовлетворяет ограничению задачи. Отсюда следует, что , но данная точка не удовлетворяет ограничению задачи. Отсюда следует, что  . Система перепишется в виде: . Система перепишется в виде:
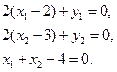
Разрешая систему, получим:
 . .
4. Для задачи выпуклого программирования необходимые условия оптимальности являются и достаточными (теорема 13), то есть 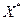 - глобальное решение задачи. - глобальное решение задачи.
72. Опираясь на решение задач 65-67, конкретизировать условие (14) в случае, когда 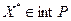 и когда и когда  имеет вид, указанный в задачах 66, 67. имеет вид, указанный в задачах 66, 67.
Проекцией точки 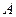 на множество D
называется точка на множество D
называется точка  , ближайшая к , ближайшая к 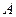 среди всех точек из D
. Иными словами, среди всех точек из D
. Иными словами, 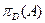 является решением задачи проектирования является решением задачи проектирования
 . .
Заметим, что понятие проекции точки на множество используется в численных методах условной оптимизации, основанных на идее проектирования очередной точки, вырабатываемой методом решения безусловной задачи, на допустимое множество задачи с ограничениями.
Доказать следующие утверждения для произвольной точки  . .
73. Если  - сфера, то - сфера, то  . .
74. Если  - координатный параллелепипед, то - координатный параллелепипед, то

75. Если  - неотрицательный октант, то - неотрицательный октант, то  . .
76. Если  - гиперплоскость ( - гиперплоскость (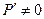 ), то ), то 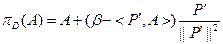 . .
77. Если 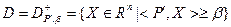 - полупространство ( - полупространство (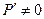 ), то ), то  . .
78. Если  - аффинное множество, причём строки матрицы - аффинное множество, причём строки матрицы 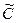 линейно независимы, то линейно независимы, то 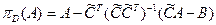 , где , где  - транспонированная матрица, - транспонированная матрица,  . .
79. Решить задачу:


80. Доказать, что решением задачи выпуклого программирования


является точка  . .
81. Показать, что других решений, кроме  , в задаче 80 нет. , в задаче 80 нет.
82. Доказать, что решением задачи выпуклого программирования
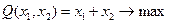

является точка  . .
83. Показать, что других решений, кроме  , в задаче 82 нет. , в задаче 82 нет.
В задачах 84-88 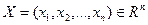 . .
84. Используя необходимые условия оптимальности (14), (15), разработать численный метод отыскания решения задачи
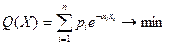
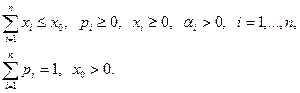
Решить задачи:
85. 

 - положительные числа, - положительные числа, 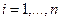 . .
86. 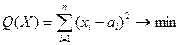
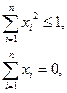
 - произвольные числа, - произвольные числа, 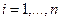 . .
87. 

88. 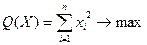
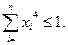
89. 

90. 

91. 
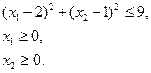
92. 

93. 

- Доказать, что если
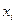 , , 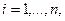 - положительные числа, причём - положительные числа, причём  , то , то  . .
Пусть
 , ,
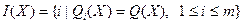
 (17) (17)
95. Показать, что если 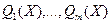 дифференцируемы в точке дифференцируемы в точке  и и 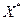 - локальное решение задачи (17), то существуют числа - локальное решение задачи (17), то существуют числа  , такие, что , такие, что
 . .
Предполагая, что в задаче (1) 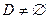 , обозначим через , обозначим через  точную нижнюю грань целевой функции задачи (1) на её допустимом множестве: точную нижнюю грань целевой функции задачи (1) на её допустимом множестве:  . Вектор . Вектор 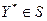 называется вектором Куна-Таккера задачи (1), если называется вектором Куна-Таккера задачи (1), если  при всех при всех  . .
Двойственной к задаче (1) называется задача
 (18) (18)
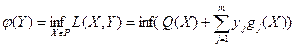 , ,  . .
При этом задача (1) называется прямой. Предполагая, что 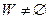 , обозначим через , обозначим через  . .
96. Показать, что в задаче (18) множество  выпукло, а функция выпукло, а функция 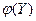 вогнута на вогнута на  . .
97. Показать, что для любых 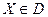 и и  справедливо неравенство справедливо неравенство  . Если . Если 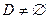 , ,  , то , то  . .
Теорема 16
(Теорема существования вектора Куна-Таккера)
Пусть в задаче (1) множество  выпукло, функции выпукло, функции 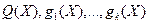 выпуклы на выпуклы на 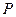 , функции , функции  линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий: линейны. Предположим, что дополнительно выполняется хотя бы одно из следующих условий:
1) ограничения равенства отсутствуют ( ) и существует точка ) и существует точка 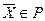 такая, что такая, что 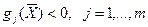 ; ;
2)  , функции , функции  линейны, множество линейны, множество 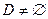 . .
Тогда вектор Куна-Таккера задачи (1) существует.
Теорема 17
(Теорема двойственности)
Пусть вектор Куна-Таккера задачи (1) существует. Если значение прямой задачи (1) конечно ( ) в частности, если она имеет решение, то множество решений двойственной задачи (18) непусто и совпадает с множеством векторов Куна-Таккера задачи (1). При этом справедливо соотношение двойственности ) в частности, если она имеет решение, то множество решений двойственной задачи (18) непусто и совпадает с множеством векторов Куна-Таккера задачи (1). При этом справедливо соотношение двойственности
 . (19) . (19)
98. Показать, что если вектор Куна – Таккера задачи (1) существует, а допустимое множество  двойственной задачи непусто, то она имеет решение. Если же двойственной задачи непусто, то она имеет решение. Если же 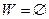 , то , то 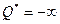 . .
99. Для задачи

построить двойственную и найти её решение. Убедится в справедливости соотношения (19).
Теорема 18
(Теорема Куна-Таккера в форме двойственности).
Пусть вектор Куна-Таккера задачи (1) существует. Тогда точка  является решением задачи (1) в том и только том случае, если существует вектор является решением задачи (1) в том и только том случае, если существует вектор 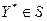 такой, что справедливо соотношение двойственности такой, что справедливо соотношение двойственности
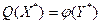 , (20) , (20)
равносильное условиям
 , ,
 . .
Множество векторов 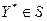 , удовлетворяющее (20), совпадает с множеством решений двойственной задачи (18) или же с множеством векторов Куна-Таккера прямой задачи (1). , удовлетворяющее (20), совпадает с множеством решений двойственной задачи (18) или же с множеством векторов Куна-Таккера прямой задачи (1).
100. Решить задачу:
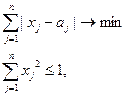
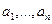 - заданные числа. - заданные числа.
Литература
1. Давыдов Н.А., Коровкин П.П., Никольский В.Н. Сборник задач по математическому анализу. –М.: Просвещение, 1964.
2. Лидский В.Б., Овсянников Л.В., Тулайков А.Н., Шабунин М.И. Задачи по элементарной математике. –М.: Наука, 1965.
3. Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. –М.: Наука, 1984.
4. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации.
–М.: Наука, 1986.
5. Морозов В.В., Сухарев А.Г., Федоров В.В. Исследование операций в задачах и упражнениях. –М.: Высшая школа, 1986.

|