| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Факультет Киберенетики
Кафедра интеллектуальных
технологий и систем
Курсовая работа
Тема: Методологический базис ТПР
Дисциплина: Теория принятий решений
Студент: Юнцевич А.Г.
Yср = 4
|{5}|= 10
|{4}|= 5
|{3}|= 10
|{3,4,5}|= 25
Группа: ИИ-1-03
Руководитель Панченко В.М.
Консультант Шорохов М.И.
МОСКВА 2005
Реферат
Отчет 44 с, 4 ч.,9 рис., 18 табл., 3 источника.
Методологический базис теории принятий решений.
Цель работы – построить циклограмму, которая демонстрирует работу парикмахерской, рассчитать транспортную задачу и задачу линейного программирования и найти ее оптимальное решение.
В процессе работы проводились вычисления и анализ транспортной и линейной задач, ее суть - имея исходные данные о перевозимом грузе, предусмотреть расходы и найти наиболее оптимальный по цене вариант решения.
Содержание
| Введение…………………………………………………………………………………………..
|
4
|
| 1. Моделирование процессов в системе G/G/3/3…………………………..…………………..
|
5
|
| 2. Анализ данных единичного эксперимента…………………………………………………..
|
18
|
| 3. Транспортная задача (ТЗ) линейного программирования…………………………………..
|
25
|
| 3.1. Составление опорного плана ТЗ по методу Северо-западного угла (СЗУ)…………….
|
25
|
| 3.2. Составление опорного плана ТЗ по методу минимума стоимостей перевозки………..
|
26
|
| 3.3. Сравнение планов по критерию стоимости………………………………………………
|
27
|
| 3.4. Проверка лучшего опорного плана на оптимальность…………………………………..
|
28
|
| 3.5. Улучшение плана по методу циклических перестановок……………………………….
|
29
|
| 4. Решение задачи линейного программирования……………………………………………..
|
32
|
| 4.1. Условие задачи линейного программирования ………………………………………….
|
32
|
| 4.1.1. Граф-схема решения задачи линейного программирования….……………………..
|
32
|
| 4.1.2. Алгебраическая модель решения задачи линейного программирования…………..
|
33
|
| 4.1.3. Геометрическая форма представления процесса решения………………………….
|
35
|
| 4.1.4. Свойства задач линейного программирования………………………………………
|
37
|
| 4.2. Симплекс-метод решения задачи линейного программирования………………………
|
38
|
| 4.2.1. Иллюстрация процесса поиска решения……………………………………………...
|
38
|
| 4.2.2. Алгебраическое решение………………………………………………………………
|
41
|
| 4.2.2.1. Поиск опорного решения………………………………………………………...
|
41
|
| Заключение………………………………………………………………………………………..
|
43
|
| Список использованной литературы…………………………………………………………...
|
44
|
Введение
В основе системного анализа лежит системный подход. При системном подходе объект /реальная система/ рассматривается как комплекс систем рационально-эмпирического типа, полнота которого проверяется практикой взаимодействия субъекта с объектом.
Системный анализ как совокупность методов и средств подготовки и обоснования решений применяется к системам, выделенным для описания объекта.
Системный анализ образует базис для изучения наук о системах: «Исследования операций», «Теории систем», «Теории принятия решений» и др.
В курсовой работе мы используем метод имитационного моделирования и метод линейного программирования.
В ходе имитационного эксперимента формируется комплекс эмпирических систем для системного анализа, проводимого в условиях неопределённости, нечёткости или риска.
Имитационное моделирование в широком смысле определяет методологию исследований, в основу которой положен способ имитации реальных процессов и явлений. Методология – это учение о структуре, логической организации, методах и средствах деятельности. Методология имитационного моделирования опирается на теорию вероятностей как науку о принципах построения, формах и способах познания явлений стохастической природы [1].
Линейное программирование – это метод математического моделирования, разработанный для оптимизации использования ограниченных ресурсов. На алгоритмах ЛП (учитывая их компьютерную эффективность) базируются оптимизационные алгоритмы для других, более сложных типов моделей и задач, включая целочисленное, нелинейное и стохастическое программирование[2].
1 Моделирование процессов в системе
G/
G/3/3.
Представим результаты моделирования одного рабочего дня системы. Описание процессов будем строить в форме циклограмм по каждому часу функционирования системы с указанием и анализом особенностей принимаемых решений.
Циклограмму имитационного процесса будем строить в форме, принятой при описании работы переключающих схем.
Циклограмма работы системы является удобной формой представления процессов имитации для относительно несложных систем при моделировании вручную, на АВМ и гибридных средствах при наличии многоканальных устройств вывода сигналов[1].
При моделировании на ЦВМ следует учитывать особенности средств отображения цифровой информации и устройств ввода-вывода.
На Рис.1-1.4. показана циклограмма работы парикмахерской с тремя рабочими каналами и тремя каналами ожидания за один рабочий день.
В таблице 1 показана выборка случайных чисел.
| N(dT)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
| r
|
81
|
53
|
77
|
58
|
84
|
28
|
31
|
10
|
10
|
47
|
62
|
93
|
86
|
30
|
7
|
12
|
43
|
| N(S)
|
1
|
2
|
3
|
4
|
5,6
|
7
|
| n1
|
1
|
1
|
1
|
1
|
1
|
4
|
4
|
4
|
4
|
4
|
| n2
|
2
|
2
|
2
|
2
|
5
|
5
|
5
|
| n3
|
3
|
3
|
3
|
6
|
6
|
6
|
6
|
| m1
|
| m2
|
| m3
|
Рис.1. Циклограмма
| 18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
32
|
| 2
|
58
|
71
|
85
|
74
|
54
|
90
|
40
|
69
|
1
|
63
|
12
|
41
|
12
|
70
|
| 8
|
9
|
10
|
11,12
|
13
|
14
|
15
|
16
|
17
|
| перерыв
|
перерыв
|
перерыв
|
перерыв
|
перерыв
|
Перерыв
|
11
|
11
|
11
|
11
|
11
|
15
|
15
|
15
|
| 8
|
8
|
8
|
10
|
10
|
10
|
10
|
10
|
10
|
перерыв
|
перерыв
|
перерыв
|
перерыв
|
| 9
|
9
|
9
|
9
|
13
|
13
|
13
|
13
|
14
|
14
|
14
|
14
|
| 10
|
11
|
14
|
14
|
14
|
| 15
|
15
|
Рис.1.1. Циклограмма
| 33
|
34
|
35
|
36
|
37
|
38
|
39
|
40
|
41
|
42
|
43
|
44
|
45
|
46
|
47
|
48
|
49
|
50
|
| 37
|
61
|
42
|
87
|
84
|
5
|
8
|
70
|
45
|
75
|
7
|
76
|
27
|
9
|
47
|
38
|
3
|
1
|
| 18
|
19
|
20
|
21,22
|
23,24
|
25
|
26
|
27,28
|
29,3
|
| 15
|
15
|
19
|
19
|
19
|
22
|
22
|
23
|
23
|
23
|
23
|
23
|
30
|
30
|
30
|
30
|
| перерыв
|
перерыв
|
20
|
20
|
20
|
20
|
20
|
20
|
24
|
24
|
27
|
27
|
27
|
27
|
27
|
| 14
|
18
|
18
|
18
|
21
|
21
|
21
|
21
|
26
|
26
|
26
|
29
|
29
|
29
|
29
|
29
|
29
|
29
|
| 18
|
19
|
21
|
23
|
23
|
23
|
27
|
30
|
| 22
|
22
|
| 24
|
24
|
24
|
24
|
Рис.1.2. Циклограмма
| 51
|
52
|
53
|
54
|
55
|
56
|
57
|
58
|
59
|
60
|
61
|
62
|
63
|
64
|
65
|
66
|
67
|
| 87
|
30
|
16
|
72
|
54
|
74
|
15
|
85
|
12
|
37
|
49
|
99
|
88
|
29
|
2
|
91
|
2
|
| 31
|
32
|
33
|
34
|
35,36,37
|
38
|
39,4
|
| 31
|
31
|
31
|
31
|
33
|
33
|
33
|
33
|
33
|
35
|
35
|
35
|
35
|
35
|
39
|
| 32
|
32
|
32
|
34
|
34
|
34
|
36
|
36
|
36
|
36
|
38
|
38
|
| перерыв
|
перерыв
|
перерыв
|
перерыв
|
перерыв
|
перерыв
|
37
|
37
|
37
|
37
|
37
|
40
|
| 38
|
38
|
38
|
39
|
| 40
|
Рис.1.3. Циклограмма
| 68
|
69
|
70
|
71
|
72
|
73
|
74
|
75
|
76
|
77
|
78
|
79
|
80
|
81
|
82
|
83
|
84
|
85
|
| 58
|
94
|
30
|
12
|
81
|
81
|
48
|
76
|
95
|
60
|
15
|
31
|
12
|
76
|
27
|
60
|
90
|
| 41,42
|
43
|
44
|
45
|
46,47
|
48
|
49
|
50
|
51,52
|
| 39
|
39
|
42
|
42
|
43
|
43
|
43
|
43
|
46
|
46
|
46
|
49
|
49
|
49
|
51
|
51
|
| 38
|
41
|
41
|
44
|
44
|
44
|
44
|
48
|
48
|
48
|
48
|
48
|
50
|
50
|
50
|
| 40
|
40
|
40
|
40
|
45
|
45
|
45
|
52
|
52
|
| 42
|
Рис.1.4. Циклограмма
| 86
|
87
|
88
|
| 51
|
51
|
| 50
|
50
|
| 52
|
52
|
52
|
Рис.1.5. Циклограмма
Таблица 1
Выборка
| Rl
|
Rm
|
Rr
|
Rt
|
| 1
|
81
|
90
|
7
|
75
|
| 2
|
53
|
60
|
76
|
45
|
| 3
|
77
|
27
|
27
|
70
|
| 4
|
58
|
76
|
9
|
8
|
| 5
|
84
|
12
|
47
|
5
|
| 6
|
28
|
31
|
38
|
84
|
| 7
|
31
|
15
|
3
|
87
|
| 8
|
10
|
60
|
1
|
42
|
| 9
|
10
|
95
|
87
|
61
|
| 10
|
47
|
76
|
30
|
37
|
| 11
|
62
|
48
|
16
|
70
|
| 12
|
93
|
81
|
72
|
12
|
| 13
|
86
|
81
|
54
|
41
|
| 14
|
30
|
12
|
74
|
12
|
| 15
|
7
|
30
|
15
|
63
|
| 16
|
12
|
94
|
85
|
1
|
| 17
|
43
|
58
|
12
|
69
|
| 18
|
2
|
2
|
37
|
40
|
| 19
|
58
|
91
|
49
|
90
|
| 20
|
71
|
2
|
99
|
54
|
| 21
|
85
|
29
|
88
|
74
|
| 22
|
74
|
88
|
29
|
85
|
| 23
|
54
|
99
|
2
|
71
|
| 24
|
90
|
49
|
91
|
58
|
| 25
|
40
|
37
|
2
|
2
|
| 26
|
69
|
12
|
58
|
43
|
| 27
|
1
|
85
|
94
|
12
|
| 28
|
63
|
15
|
30
|
7
|
| 29
|
12
|
74
|
12
|
30
|
| 30
|
41
|
54
|
81
|
86
|
| 31
|
12
|
72
|
81
|
93
|
| 32
|
70
|
16
|
48
|
62
|
| 33
|
37
|
30
|
76
|
47
|
| 34
|
61
|
87
|
95
|
10
|
| 35
|
42
|
1
|
60
|
10
|
| 36
|
87
|
3
|
15
|
31
|
| 37
|
84
|
38
|
31
|
28
|
| 38
|
5
|
47
|
12
|
84
|
| 39
|
8
|
9
|
76
|
58
|
| 40
|
70
|
27
|
27
|
77
|
| 41
|
45
|
76
|
60
|
53
|
| 42
|
75
|
7
|
90
|
81
|
| 43
|
7
|
75
|
| 44
|
76
|
45
|
| 45
|
27
|
70
|
| 46
|
9
|
8
|
| 47
|
47
|
5
|
| 48
|
38
|
84
|
| 49
|
3
|
87
|
| 50
|
1
|
42
|
| 51
|
87
|
61
|
| 52
|
30
|
37
|
| 53
|
16
|
70
|
| 54
|
72
|
12
|
| 55
|
54
|
41
|
| 56
|
74
|
12
|
| 57
|
15
|
63
|
| 58
|
85
|
1
|
| 59
|
12
|
69
|
| 60
|
37
|
40
|
| 61
|
49
|
90
|
| 62
|
99
|
54
|
| 63
|
88
|
74
|
| 64
|
29
|
85
|
| 65
|
2
|
71
|
| 66
|
91
|
58
|
| 67
|
2
|
2
|
| 68
|
58
|
43
|
| 69
|
94
|
12
|
| 70
|
30
|
7
|
| 71
|
12
|
30
|
| 72
|
81
|
86
|
| 73
|
81
|
93
|
| 74
|
48
|
62
|
| 75
|
76
|
47
|
| 76
|
95
|
10
|
| 77
|
60
|
10
|
| 78
|
15
|
31
|
| 79
|
31
|
28
|
| 80
|
12
|
84
|
| 81
|
76
|
58
|
| 82
|
27
|
77
|
| 83
|
60
|
53
|
| 84
|
90
|
81
|
Рис.2. Продолжение табл.1
Частота событий 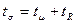 по результатам моделирования в единицах по результатам моделирования в единицах 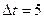 мин показана в табл.2. мин показана в табл.2.
Таблица 2
Частота событий
| Tr\Tm
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
E
|
| 0
|
7
|
0
|
1
|
9
|
9
|
8
|
1
|
1
|
36
|
| 1
|
0
|
0
|
1
|
3
|
2
|
3
|
1
|
0
|
10
|
| 2
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
2
|
| 3
|
0
|
0
|
0
|
1
|
0
|
2
|
0
|
0
|
3
|
| 4
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
| 5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 7
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| E
|
7
|
0
|
4
|
13
|
11
|
14
|
2
|
1
|
52
|
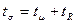 , ,
где 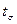 - время нахождения заявки в системе; - время нахождения заявки в системе;
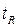 -время в очереди; -время в очереди; 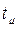 - время на обслуживание. - время на обслуживание.
При 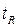 =0 имеем 36 заявок, т.е. те которые не ждали, а сразу поступали на рабочий канал или сразу уходили: 7 ушли сразу, 1 заявка обслуживалась 2 пятиминутных интервала, 9 - по 3 , 9 - по 4, 8 – по 5, 1 – по 6, и 1 заявка обслуживалась 7 пятиминутных интервалов. Самое длительное =0 имеем 36 заявок, т.е. те которые не ждали, а сразу поступали на рабочий канал или сразу уходили: 7 ушли сразу, 1 заявка обслуживалась 2 пятиминутных интервала, 9 - по 3 , 9 - по 4, 8 – по 5, 1 – по 6, и 1 заявка обслуживалась 7 пятиминутных интервалов. Самое длительное 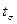 = 40 ( = 40 (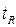 = 3, = 3, 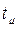 = 5), самое короткое - = 5), самое короткое - 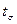 =10. =10.
При построении циклограммы одного рабочего дня системы мы придерживались правила последовательной выборки случайных чисел по мере необходимости по системе обусловленных адресов.
При этом для удобства имитации было принято лишь одно соглашение: выборка из таблицы случайных чисел производилась для каждого вида МСВ (Механизм случайной выборки) своего начального адреса.
Можно было бы обойтись и без этого соглашения, выбирая числа последовательно с любого начального адреса вне зависимости от типа МСВ. Назовём подобный путь организации статических испытаний последовательным.
Однако установить соответствие без проведения имитационного эксперимента в этом случае не представляется возможным из-за случайности протекающего процесса, в функции которого производится выборка случайных чисел из таблицы [1].
f({rv};E;P)=Sv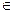 S, где rv- принятая последовательность случайных чисел до шага v; Е-структура системы; Р- правила функционирования, принятые при моделировании; Sv-состояние системы на шаге v, f-функция от случайной последовательности случайных чисел rv и констант Е, Р, определяемых моделью системы и правилами проведения имитационного моделирования [1]. S, где rv- принятая последовательность случайных чисел до шага v; Е-структура системы; Р- правила функционирования, принятые при моделировании; Sv-состояние системы на шаге v, f-функция от случайной последовательности случайных чисел rv и констант Е, Р, определяемых моделью системы и правилами проведения имитационного моделирования [1].
В моделируемый день. В систему поступило 52 заявки.
Первый канал обслужил 17 заявок и из 88 пятиминутных интервалов он был свободен 21 интервалов.
Второй канал обслужил 15 заявок и был свободен 30 интервалов .
Третий канал обслужил 13 заявок и был свободен 33 интервалов.
Всего обслужено 45 заявки. Покинуло систему 7 заявок.
Для анализа средних величин временных параметров
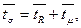
где  среднее время нахождения заявки в системе; среднее время нахождения заявки в системе;
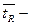 среднее время ожидания в очереди среднее время ожидания в очереди
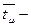 среднее время обслуживания, среднее время обслуживания,
а также связанных с ними параметров, в частности 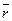 и и 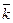 (средняя длина очереди и среднее число занятых каналов), представим результаты моделирования в виде табл.3. (средняя длина очереди и среднее число занятых каналов), представим результаты моделирования в виде табл.3.
Таблица 3
Число кортежей
| w
|
Tr
|
Tm
|
Ts
|
n
|
Заявки
|
| 1
|
0
|
0
|
0
|
7
|
7;12;16;17;25;28;47;
|
| 2
|
0
|
2
|
2
|
1
|
41;
|
| 3
|
0
|
3
|
3
|
9
|
3;5;8;26;32;34;45;46;49;
|
| 4
|
0
|
4
|
4
|
9
|
2;6;9;13;31;36;43;44;51;
|
| 5
|
0
|
5
|
5
|
8
|
1;4;33;35;37;48;50;52;
|
| 6
|
0
|
6
|
6
|
1
|
20;
|
| 7
|
0
|
7
|
7
|
1
|
29;
|
| 8
|
1
|
2
|
3
|
1
|
42;
|
| 9
|
1
|
3
|
4
|
3
|
18;19;39;
|
| 10
|
1
|
4
|
5
|
2
|
21;30;
|
| 11
|
1
|
5
|
6
|
3
|
11;27;40;
|
| 12
|
1
|
6
|
7
|
1
|
10;
|
| 13
|
2
|
2
|
4
|
1
|
22;
|
| 14
|
2
|
5
|
7
|
1
|
15;
|
| 15
|
3
|
3
|
6
|
1
|
38;
|
| 16
|
3
|
5
|
8
|
2
|
14;23;
|
| 17
|
4
|
2
|
6
|
1
|
24;
|
Общее время обслуживания и его составляющие определяются суммированием данных, приведённых в табл.2.
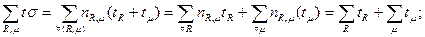
где 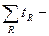 суммарное время, проведённое заявками в очереди; суммарное время, проведённое заявками в очереди;
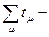 суммарное время обслуживания заявок. суммарное время обслуживания заявок.
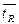 Общее число заявок пребывающих в очереди: n(R)= 19. Общее число заявок пребывающих в очереди: n(R)= 19.
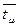 = (10*1+2*2+3*3+1*4)/16=1,69 пятимин. интервала или 8,45 мин. = (4*2+13*3+11*4+14*5+2*6+1*7)/45=4 пятиминутных интервала или 20 мин. = (10*1+2*2+3*3+1*4)/16=1,69 пятимин. интервала или 8,45 мин. = (4*2+13*3+11*4+14*5+2*6+1*7)/45=4 пятиминутных интервала или 20 мин.
В очереди потрачено время 45*5 мин = 225; на обслуживание затрачено 180*5=900 мин.; среднее время, проведенное заявкой в системе, составило 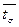 =(8,45+20,00)мин=28,45 мин. =(8,45+20,00)мин=28,45 мин.
Работу отдельных каналов обслуживания можно оценить, представив данные эксперимента в виде табл.4: производительнее всех работал 2-й канал (19,333 мин/s), обслуживший 15 заявок.
Таблица 4
Данные эксперимента
| N1 ед.
|
N1dT
|
N2 ед.
|
N2dT
|
N3 ед.
|
N3dT
|
E ед
|
E dT
|
Мин
|
| 1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 3
|
2
|
4
|
2
|
4
|
0
|
0
|
4
|
8
|
40
|
| 4
|
4
|
12
|
5
|
15
|
4
|
12
|
13
|
39
|
195
|
| 5
|
4
|
16
|
3
|
12
|
4
|
16
|
11
|
44
|
220
|
| 6
|
7
|
35
|
3
|
15
|
4
|
20
|
14
|
70
|
350
|
| 7
|
0
|
0
|
2
|
12
|
0
|
0
|
2
|
12
|
60
|
| E мин
|
17
|
67
|
15
|
58
|
13
|
55
|
45
|
180
|
900
|
| 0
|
335
|
0
|
290
|
0
|
275
|
0
|
20
|
0
|
| T m
|
19,706
|
19,333
|
21,154
|
Очевидно, при сдельной оплате труда по затратам времени, если общий фонд зарплаты принять равным единице, заработок q следует распределить:
1-ый канал – 335/Q; q1=0,37;
2-ой канал – 290/Q; q2=0,32;
2-ой канал – 275/Q; q2=0,31;
Q=900 мин.
Для выравнивания загрузки по числу обслуженных за день заявок можно ввести очередь между каналами на обслуживание очередной заявки. Это равносильно изменению правил функционирования системы и потребует проведения самостоятельных имитационных исследований системы.
Среднее число занятых каналов 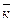 через коэффициент перегрузки одного канала: через коэффициент перегрузки одного канала:
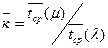 , ,
где 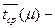 среднее время обслуживания заявки в моделируемый день. среднее время обслуживания заявки в моделируемый день.
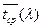 - среднее время поступления одной заявки. - среднее время поступления одной заявки.
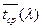 = 350/52=6,73 = 350/52=6,73
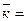 (20 мин/s)/(6,73 мин/s)=2,97 (20 мин/s)/(6,73 мин/s)=2,97
По данным эксперимента в системе наблюдается следующие состояния:
S0- система свободна; S1 –один канал занят; S2 –два канала занято;S3-три канала,S4-одно место в очереди занято;S5-два места в очереди занято;S6- три места в очереди занято.
В табл.5 указаны данные о количестве переходов типа Si - Sj.
Таблица 5
Количество переходов
| S0
|
S1
|
S2
|
S3
|
S4
|
S5
|
S6
|
E
|
P(S)
|
| S0
|
4
|
3
|
0
|
1
|
0
|
0
|
0
|
8
|
0,0909
|
| S1
|
1
|
3
|
7
|
1
|
0
|
0
|
0
|
12
|
0,1364
|
| S2
|
2
|
5
|
6
|
6
|
0
|
0
|
0
|
19
|
0,2159
|
| S3
|
0
|
2
|
6
|
12
|
8
|
1
|
0
|
29
|
0,3295
|
| S4
|
0
|
0
|
0
|
8
|
4
|
2
|
0
|
14
|
0,1591
|
| S5
|
0
|
0
|
0
|
1
|
2
|
1
|
1
|
5
|
0,0568
|
| S6
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0,0114
|
| E
|
7
|
13
|
19
|
29
|
14
|
5
|
1
|
88
|
Рабочий день можно представить в виде случайного процесса показанного на рис.3. Внизу на рисунке суммировано число интервалов 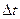 , когда система находиться в данном состоянии. , когда система находиться в данном состоянии.

Рис.3. Процесс смены состояний в ходе
имитационного моделирования системы.
В табл.6 приведены метапараметры и их значения.
Таблица 6
Метапараметры
| №
|
Параметр
|
Значение
|
| Ф1
|
52
|
| Ф(R1)
|
11 | 4
|
| Ф(R2)
|
4 | 3
|
| Ф(R3)
|
0 | 0
|
| Ф(R4)
|
0 | 0
|
| Ф(T)
|
1 | 0
|
| Ф1(E)
|
7
|
| Ф(n=1)
|
17
|
| Ф(n=2)
|
15
|
| Ф(n=3)
|
13
|
| Ф2(E)
|
45
|
| k(Tm/Tl)
|
2,142857
|
| r(Tr/Tl)
|
0,321429
|
| tl(Ф1)
|
8,076923
|
| t(Ф2+Фt)
|
9,333333
|
| tl(Ф2)
|
9,333333
|
| tm
|
20
|
| tr
|
6,412698
|
| t(t)
|
26,4127
|
| M[r]
|
0,306818
|
| M[k]
|
2,238636
|
2 Анализ данных единичного эксперимента.
Таблица 7
Порядок предметов в зачетной книжке
| №
|
Предмет
|
Дата
|
Оценка
|
№ согл.
|
| 1
|
2
|
3
|
4
|
5
|
| 1.1
|
Начертательная геометрия (э)
|
05.01.04
|
Отл.
|
1
|
| 1.2
|
Физика (э)
|
09.01.04
|
Удовл.
|
2
|
| 1.3
|
Алгебра и геометрия (э)
|
13.01.04
|
Хор.
|
3
|
| 1.4
|
Математический анализ (э)
|
17.01.04
|
Удовл.
|
4
|
| 1.5
|
Информатика (к/р)
|
19.12.03
|
Хор.
|
5
|
| 2.1
|
Английский язык (э)
|
10.06.04
|
Отл.
|
6
|
| 2.2
|
Алгебра и геометрия (э)
|
10.06.04
|
Хор.
|
7
|
| 2.3
|
Физика (э)
|
16.06.04
|
Хор.
|
8
|
| 2.4
|
Отечественная история (э)
|
22.06.04
|
Отл.
|
9
|
| 2.5
|
Программирование (э)
|
28.06.04
|
Отл.
|
10
|
| 2.6
|
Дискретная математика (к/р)
|
14.04.04
|
Отл.
|
11
|
| 3.1
|
Дифференциальные уравнения (э)
|
10.01.05
|
Удовл.
|
12
|
| 3.2
|
Математический анализ (э)
|
14.01.05
|
Хор.
|
13
|
| 3.3
|
Физика (э)
|
18.01.05
|
Удовл.
|
14
|
| 3.4
|
Математическая логика (э)
|
24.01.05
|
Отл.
|
15
|
| 3.5
|
Электротехника (э)
|
28.01.05
|
Удовл.
|
16
|
| 3.6
|
Математическая логика (к/р)
|
30.11.04
|
Отл.
|
17
|
| 3.7
|
ЯПВУ (к/р)
|
17.12.04
|
Отл.
|
18
|
| 4.1
|
Дискретный анализ (э)
|
30.05.05
|
Удовл.
|
19
|
| 4.2
|
ТФКП (э)
|
30.05.05
|
Удовл.
|
20
|
| 4.3
|
Вычислительная математика (э)
|
4.06.05
|
Удовл.
|
21
|
| 4.4
|
Философия (э)
|
18.05.05
|
Отл.
|
22
|
| 4.5
|
Теория вероятностей (э)
|
24.06.05
|
Удовл.
|
23
|
| 4.6
|
Логическое программирование(к/р)
|
18.05.05
|
Отл.
|
24
|
| 4.7
|
Теория информационных процессов(к/р)
|
20.05.05
|
Удовл.
|
25
|
| ИИ-1-03
|
| Альсаад Я.
|
| Андриченко Д.
|
| Гатаулина Н.
|
| Губин М.
|
| Жужман М.
|
| Ижбулатов Р.
|
| Киричук И.
|
| Комаров А.
|
| Кондаков А.
|
| Конов А.
|
| Коновалов И.
|
| Коновалов С.
|
| Космынин В.
|
| Кругликов Л.
|
| Носков А.
|
| Пелипенко О.
|
| Понкратова О.
|
| Приходько В.
|
| Тычинин Е.
|
| Филиппова К.
|
| Юнцевич А.
|
| № семестра
|
Кол-во оценок в семестре
|
| Семестр 1
|
5
|
| Семестр 2
|
6
|
| Семестр 3
|
7
|
| Семестр 4
|
7
|
Рис.4. Исходные данные
| Семестр
|
№ предм.
|
Название
|
Цикл
|
| Семестр 1
|
1
|
Начертательная геометрия
|
ОПД
|
| 2
|
Физика
|
ЕН
|
| 3
|
Алгебра и геометрия
|
ЕН
|
| 4
|
Математический анализ
|
ЕН
|
| 5
|
Информатика
|
ЕН
|
| Семестр 2
|
6
|
Английский язык
|
ГСЭ
|
| 7
|
Алгебра и геометрия
|
ЕН
|
| 8
|
Физика
|
ЕН
|
| 9
|
Отечественная история
|
ГСЭ
|
| 10
|
Программирование
|
ОПД
|
| 11
|
Дискретная математика
|
ЕН
|
| Семестр 3
|
12
|
Дифференциальные уравнения
|
ЕН
|
| 13
|
Математический анализ
|
ЕН
|
| 14
|
Физика
|
ЕН
|
| 15
|
Математическая логика
|
ЕН
|
| 16
|
Электротехника
|
ОПД
|
| 17
|
Математическая логика
|
ЕН
|
| 18
|
ЯПВУ
|
ОПД
|
| Семестр 4
|
19
|
Дискретный анализ
|
ЕН
|
| 20
|
ТФКП
|
ЕН
|
| 21
|
Вычислительная математика
|
ЕН
|
| 22
|
Философия
|
ГСЭ
|
| 23
|
Теория вероятностей
|
ЕН
|
| 24
|
Логическое программирование
|
СД
|
| 25
|
Теория информационных процессов
|
СД
|
Рис.5. Предметы
Таблица 8
Оценки
| Гр.
|
ИИ-1-03
|
Семестр 1
|
Семестр 2
|
Семестр 3
|
Семестр 4
|
| №
|
Фамилия
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
| 1
|
Альсаад Я.
|
4
|
3
|
3
|
3
|
4
|
5
|
3
|
3
|
3
|
5
|
4
|
3
|
3
|
4
|
5
|
4
|
5
|
5
|
4
|
5
|
5
|
4
|
4
|
4
|
| 2
|
Андриченко Д.
|
4
|
3
|
4
|
4
|
5
|
5
|
3
|
3
|
5
|
5
|
5
|
3
|
4
|
3
|
5
|
4
|
5
|
5
|
5
|
4
|
5
|
5
|
4
|
5
|
5
|
| 3
|
Гатаулина Н.
|
4
|
5
|
5
|
3
|
4
|
5
|
4
|
4
|
5
|
4
|
3
|
4
|
4
|
4
|
5
|
4
|
5
|
3
|
4
|
4
|
5
|
5
|
3
|
3
|
3
|
| 4
|
Губин М.
|
3
|
4
|
4
|
4
|
5
|
5
|
5
|
4
|
5
|
4
|
5
|
5
|
5
|
3
|
5
|
4
|
5
|
5
|
5
|
5
|
4
|
5
|
4
|
5
|
4
|
| 5
|
Жужман М.
|
5
|
4
|
4
|
4
|
4
|
5
|
3
|
3
|
4
|
5
|
5
|
3
|
4
|
3
|
3
|
3
|
4
|
4
|
3
|
3
|
4
|
4
|
3
|
4
|
3
|
| 6
|
Ижбулатов Р.
|
4
|
3
|
4
|
4
|
5
|
5
|
4
|
4
|
4
|
5
|
4
|
3
|
4
|
3
|
5
|
4
|
5
|
5
|
5
|
5
|
5
|
3
|
5
|
4
|
| 7
|
Киричук И.
|
4
|
3
|
3
|
4
|
4
|
5
|
3
|
3
|
5
|
4
|
4
|
3
|
3
|
3
|
3
|
4
|
5
|
4
|
3
|
3
|
3
|
5
|
3
|
5
|
3
|
| 8
|
Комаров А.
|
5
|
5
|
4
|
4
|
5
|
5
|
4
|
5
|
5
|
5
|
5
|
4
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
4
|
5
|
5
|
3
|
5
|
4
|
| 9
|
Кондаков А.
|
3
|
4
|
4
|
3
|
4
|
5
|
3
|
3
|
5
|
4
|
5
|
3
|
3
|
3
|
5
|
4
|
5
|
5
|
5
|
3
|
3
|
4
|
3
|
3
|
3
|
| 10
|
Конов А.
|
4
|
4
|
4
|
3
|
4
|
5
|
4
|
3
|
5
|
5
|
5
|
3
|
3
|
4
|
5
|
4
|
5
|
5
|
4
|
3
|
5
|
3
|
4
|
4
|
3
|
| 11
|
Коновалов И.
|
5
|
3
|
3
|
3
|
5
|
5
|
4
|
3
|
5
|
4
|
5
|
4
|
4
|
4
|
5
|
4
|
5
|
5
|
5
|
4
|
4
|
5
|
5
|
5
|
5
|
| 12
|
Коновалов С.
|
5
|
3
|
3
|
3
|
5
|
5
|
3
|
3
|
5
|
4
|
5
|
5
|
4
|
4
|
5
|
4
|
5
|
5
|
5
|
4
|
4
|
5
|
5
|
5
|
5
|
| 13
|
Космынин В.
|
4
|
4
|
3
|
4
|
3
|
5
|
3
|
3
|
5
|
3
|
3
|
4
|
4
|
4
|
5
|
4
|
5
|
5
|
3
|
4
|
4
|
4
|
3
|
3
|
3
|
| 14
|
Кругликов Л.
|
5
|
5
|
4
|
3
|
5
|
5
|
5
|
4
|
5
|
5
|
5
|
4
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
| 15
|
Носков А.
|
4
|
3
|
3
|
3
|
4
|
5
|
3
|
3
|
5
|
5
|
5
|
3
|
3
|
3
|
3
|
3
|
5
|
5
|
3
|
3
|
3
|
4
|
3
|
3
|
5
|
| 16
|
Пелипенко О.
|
3
|
3
|
3
|
3
|
3
|
5
|
3
|
3
|
5
|
4
|
3
|
3
|
3
|
3
|
3
|
3
|
4
|
4
|
3
|
3
|
5
|
3
|
3
|
3
|
| 17
|
Понкратова О.
|
4
|
3
|
3
|
3
|
5
|
4
|
3
|
4
|
4
|
5
|
4
|
4
|
3
|
3
|
4
|
4
|
5
|
5
|
3
|
3
|
4
|
5
|
3
|
3
|
4
|
| 18
|
Приходько В.
|
3
|
4
|
3
|
3
|
3
|
5
|
4
|
4
|
4
|
4
|
4
|
4
|
3
|
4
|
5
|
4
|
4
|
4
|
3
|
4
|
5
|
4
|
3
|
3
|
| 19
|
Тычинин Е.
|
4
|
4
|
4
|
3
|
5
|
5
|
3
|
4
|
5
|
4
|
5
|
5
|
4
|
3
|
5
|
4
|
5
|
5
|
5
|
3
|
4
|
5
|
4
|
5
|
3
|
| 20
|
Филиппова К.
|
4
|
4
|
3
|
4
|
4
|
5
|
5
|
4
|
4
|
5
|
4
|
4
|
4
|
4
|
5
|
4
|
4
|
4
|
3
|
3
|
4
|
5
|
3
|
3
|
3
|
| 21
|
Юнцевич А.
|
5
|
3
|
4
|
3
|
4
|
5
|
4
|
4
|
5
|
5
|
5
|
3
|
4
|
3
|
5
|
3
|
5
|
5
|
3
|
3
|
3
|
5
|
3
|
5
|
3
|
Таблица 9
Значения единичного эксперимента
| ОПД
|
ЕН
|
ЕН
|
ЕН
|
ЕН
|
ГСЭ
|
ЕН
|
ЕН
|
ГСЭ
|
ОПД
|
ЕН
|
ЕН
|
ЕН
|
ЕН
|
ЕН
|
ОПД
|
ЕН
|
ОПД
|
ЕН
|
ЕН
|
ЕН
|
ГСЭ
|
ЕН
|
СД
|
СД
|
| |{5}|
|
6
|
3
|
1
|
0
|
9
|
20
|
3
|
1
|
15
|
11
|
12
|
3
|
3
|
2
|
16
|
2
|
17
|
15
|
9
|
1
|
7
|
16
|
3
|
10
|
5
|
| |{4}|
|
11
|
8
|
10
|
8
|
9
|
1
|
7
|
9
|
5
|
9
|
6
|
8
|
10
|
8
|
1
|
15
|
4
|
5
|
3
|
6
|
9
|
4
|
6
|
3
|
5
|
| |{3}|
|
4
|
10
|
10
|
13
|
3
|
0
|
11
|
11
|
1
|
1
|
3
|
10
|
8
|
11
|
4
|
4
|
0
|
1
|
9
|
9
|
5
|
1
|
12
|
8
|
11
|
| |{3,4,5}|
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
21
|
16
|
21
|
21
|
21
|
21
|
21
|
| Yср.
|
4,09524
|
4
|
4
|
3
|
4
|
5
|
4
|
4
|
5
|
4
|
4
|
4
|
4
|
4
|
5
|
4
|
5
|
5
|
4
|
4
|
4
|
5
|
4
|
4
|
4
|
| P5
|
0,28571
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
| P4
|
0,52381
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| P3
|
0,19048
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
| P5*ldP5
|
0,51639
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
| P4*ldP4
|
0,48865
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
| P3*ldP3
|
0,45568
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
| H
|
0,92161
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
| D
|
0,9026
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
2
|
2
|
4
|
4
|
5
|
6
|
7
|
7
|
8
|
11
|
16
|
14
|
14
|
18
|
19
|
21
|
Таблица 10
Значения единичного эксперимента
| №
|
Фамилия
|
|{5}|
|
|{4}|
|
|{3}|
|
|{3,4,5}|
|
Yср.
|
P5
|
P4
|
P3
|
P5*ldP5
|
P4*ldP4
|
P3*ldP3
|
H
|
D
|
| 1
|
Альсаад Я.
|
7
|
9
|
8
|
24
|
4
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
| 2
|
Андриченко Д.
|
13
|
7
|
5
|
25
|
4
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
| 3
|
Гатаулина Н.
|
8
|
11
|
6
|
25
|
4
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
| 4
|
Губин М.
|
14
|
9
|
2
|
25
|
4
|
0
|
0
|
##
|
1
|
0
|
##
|
0
|
| 5
|
Жужман М.
|
4
|
11
|
10
|
25
|
4
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
| 6
|
Ижбулатов Р.
|
10
|
10
|
4
|
24
|
4
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
| 7
|
Киричук И.
|
5
|
7
|
13
|
25
|
4
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
| 8
|
Комаров А.
|
18
|
6
|
1
|
25
|
5
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
| 9
|
Кондаков А.
|
7
|
6
|
12
|
25
|
4
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
| 10
|
Конов А.
|
8
|
10
|
7
|
25
|
4
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
| 11
|
Коновалов И.
|
13
|
8
|
4
|
25
|
4
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
| 12
|
Коновалов С.
|
14
|
6
|
5
|
25
|
4
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
| 13
|
Космынин В.
|
5
|
10
|
10
|
25
|
4
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
| 14
|
Кругликов Л.
|
20
|
3
|
1
|
24
|
5
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 15
|
Носков А.
|
7
|
3
|
15
|
25
|
4
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
| 16
|
Пелипенко О.
|
3
|
3
|
18
|
24
|
3
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
| 17
|
Понкратова О.
|
5
|
10
|
10
|
25
|
4
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
| 18
|
Приходько В.
|
3
|
13
|
8
|
24
|
4
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
| 19
|
Тычинин Е.
|
11
|
9
|
5
|
25
|
4
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
| 20
|
Филиппова К.
|
5
|
14
|
6
|
25
|
4
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
| 21
|
Юнцевич А.
|
10
|
5
|
10
|
25
|
4
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
Таблица 11
Рейтинг группы ИИ-1-03
| Гр.
|
ИИ-1-03
|
Семестр 1
|
Семестр 2
|
Семестр 3
|
Семестр 4
|
| №
|
Фамилия
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
| 1
|
Альсаад Я.
|
2
|
4
|
5
|
5
|
7
|
7
|
7
|
9
|
9
|
10
|
11
|
10
|
10
|
9
|
10
|
10
|
9
|
9
|
11
|
12
|
10
|
9
|
11
|
11
|
11
|
| 2
|
Андриченко Д.
|
2
|
4
|
4
|
3
|
4
|
4
|
4
|
6
|
5
|
5
|
5
|
6
|
6
|
6
|
6
|
6
|
6
|
6
|
6
|
6
|
5
|
5
|
5
|
5
|
5
|
| 3
|
Гатаулина Н.
|
2
|
2
|
1
|
2
|
3
|
3
|
2
|
3
|
3
|
3
|
5
|
5
|
5
|
4
|
4
|
4
|
4
|
6
|
7
|
7
|
6
|
6
|
7
|
7
|
8
|
| 4
|
Губин М.
|
3
|
4
|
4
|
3
|
4
|
4
|
2
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
3
|
| 5
|
Жужман М.
|
1
|
2
|
2
|
2
|
3
|
3
|
3
|
5
|
5
|
5
|
5
|
6
|
6
|
6
|
7
|
7
|
7
|
8
|
11
|
13
|
11
|
12
|
15
|
13
|
14
|
| 6
|
Ижбулатов Р.
|
2
|
4
|
4
|
3
|
4
|
4
|
3
|
4
|
4
|
4
|
5
|
6
|
6
|
6
|
6
|
6
|
6
|
6
|
6
|
5
|
4
|
4
|
6
|
6
|
6
|
| 7
|
Киричук И.
|
2
|
4
|
5
|
4
|
6
|
6
|
6
|
8
|
7
|
8
|
9
|
8
|
9
|
8
|
11
|
11
|
10
|
11
|
14
|
16
|
14
|
13
|
16
|
14
|
15
|
| 8
|
Комаров А.
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
2
|
2
|
| 9
|
Кондаков А.
|
3
|
4
|
4
|
4
|
6
|
6
|
6
|
8
|
7
|
8
|
8
|
7
|
8
|
7
|
8
|
8
|
7
|
7
|
9
|
10
|
10
|
10
|
12
|
12
|
12
|
| 10
|
Конов А.
|
2
|
3
|
3
|
3
|
5
|
5
|
4
|
6
|
5
|
5
|
5
|
6
|
7
|
6
|
6
|
6
|
6
|
6
|
7
|
8
|
7
|
7
|
8
|
8
|
9
|
| 11
|
Коновалов И.
|
1
|
3
|
4
|
4
|
5
|
5
|
4
|
6
|
5
|
6
|
6
|
6
|
6
|
5
|
5
|
5
|
5
|
5
|
5
|
4
|
5
|
5
|
4
|
4
|
4
|
| 12
|
Коновалов С.
|
1
|
3
|
4
|
4
|
5
|
5
|
5
|
7
|
6
|
7
|
7
|
6
|
6
|
5
|
5
|
5
|
5
|
5
|
5
|
4
|
5
|
5
|
4
|
4
|
4
|
| 13
|
Космынин В.
|
2
|
3
|
4
|
3
|
6
|
6
|
6
|
8
|
7
|
9
|
11
|
9
|
9
|
7
|
8
|
8
|
7
|
7
|
10
|
11
|
10
|
10
|
12
|
12
|
12
|
| 14
|
Кругликов Л.
|
1
|
1
|
1
|
2
|
2
|
2
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
2
|
1
|
1
|
1
|
| 15
|
Носков А.
|
2
|
4
|
5
|
5
|
7
|
7
|
7
|
9
|
8
|
8
|
8
|
7
|
8
|
7
|
10
|
11
|
10
|
10
|
13
|
15
|
13
|
13
|
16
|
15
|
15
|
| 16
|
Пелипенко О.
|
3
|
5
|
6
|
6
|
9
|
9
|
8
|
10
|
9
|
11
|
12
|
11
|
11
|
10
|
12
|
12
|
11
|
12
|
15
|
17
|
15
|
14
|
17
|
16
|
16
|
| 17
|
Понкратова О.
|
2
|
4
|
5
|
5
|
6
|
7
|
7
|
8
|
8
|
8
|
9
|
7
|
8
|
7
|
9
|
9
|
8
|
8
|
11
|
13
|
11
|
11
|
14
|
13
|
12
|
| 18
|
Приходько В.
|
3
|
4
|
5
|
5
|
8
|
8
|
7
|
8
|
8
|
9
|
10
|
8
|
9
|
7
|
8
|
8
|
8
|
9
|
12
|
14
|
12
|
11
|
13
|
12
|
13
|
| 19
|
Тычинин Е.
|
2
|
3
|
3
|
3
|
4
|
4
|
4
|
5
|
4
|
5
|
5
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
4
|
5
|
5
|
5
|
5
|
7
|
| 20
|
Филиппова К.
|
2
|
3
|
4
|
3
|
5
|
5
|
3
|
4
|
4
|
4
|
5
|
5
|
5
|
4
|
4
|
4
|
5
|
6
|
8
|
9
|
8
|
7
|
9
|
10
|
11
|
| 21
|
Юнцевич А.
|
1
|
3
|
3
|
3
|
5
|
5
|
4
|
5
|
4
|
4
|
4
|
5
|
5
|
5
|
5
|
6
|
6
|
6
|
8
|
9
|
9
|
8
|
10
|
9
|
10
|
3 Транспортная задача (ТЗ) линейного программирования.
3.1 Составление опорного плана ТЗ по методу
северо-западного угла (СЗУ).
Название этого метода связано с особой разметкой транспортной таблицы: стороны таблицы называют по сторонам света (верхняя – северная, нижняя - южная), а углы соответственно помечают как промежуточные направления (левый верхний – северо-западный угол или СЗУ и т.д.)(табл.12) [2].
Составление опорного плана начинают с СЗУ таблицы – заполняют клетку А1В1 меньшим из чисел a1 и b1, т.е. х11=min{a1,b1}. От соотношения a1 и b1 зависит последовательность заполнения таблицы.
Если a1>b1, то х11=b1 – это значит, что заявка потребителя B1 удовлетворена полностью. В этом случае говорят, что столбец B1 «закрыт» и переходят к заполнению клетки A1B2(т.е. передвигаются по строке вправо, к следующему потребителю). При этом х12=min{a1-b1,b2}.
Если a1<b1, то запасы поставщика исчерпаны А1 исчерпаны (строка А1 «закрыта»), а заявка потребителя В1 удовлетворена, но не полностью. Поэтому, чтобы закончить обслуживание заявки В1, переходим к клетке А2В1(т.е. к следующему поставщику) и записываем в нее значение х21=min{a2,b1-a1} [2].
Если a1=b1,то закрываем строку А1 и строку В1, а затем переходим к клетке А2В2.
Таблица 12
Результат решения ТЗ по методу СЗУ
| Пункт назначения
|
Запасы
|
| В1
|
В2
|
В3
|
В4
|
В5
|
В6
|
аi
|
| Пункт отправления
|
A1
|
8
20
|
1
11
|
5
|
3
|
7
|
7
|
31
|
| A2
|
5
|
8
6
|
8
20
|
4
9
|
2
|
8
|
35
|
| A3
|
3
|
1
|
1
|
1
1
|
1
7
|
1
|
8
|
| A4
|
4
|
7
|
6
|
2
|
9
12
|
3
19
|
31
|
| Заявки
|
bi
|
20
|
17
|
20
|
10
|
19
|
19
|
105
|
Процесс продолжается до тех пор, пока не будут исчерпаны запасы ai, и заявки bj не будут полностью удовлетворены. Это всегда возможно, т.к. по условию задача сбалансирована, т.е. предложение товаров равно спросу на них. Основным свойством транспортной задачи является то, что она всегда имеет решение.
3.2 Составление опорного плана ТЗ по методу минимума стоимостей перевозки.
Метод минимума стоимостей перевозок аналогичен методу СЗУ, только надо заполнять в первую очередь те клетки, для которых стоимости перевозок стоимости наименьшие. Если таких клеток несколько, целесообразнее сначала заполнить клетки, соответствующие наибольшим объёмам заявок. Результат решения транспортной задачи методом минимума стоимостей представлен в табл.13.
Таблица 13
Результат решения ТЗ по методу минимума стоимостей
| Пункт назначения
|
Запасы
|
| В1
|
В2
|
В3
|
В4
|
В5
|
В6
|
аi
|
| Пункт отправления
|
A1
|
8
|
1
17
|
5
14
|
3
|
7
|
7
|
31
|
| A2
|
5
10
|
8
|
8
6
|
4
|
2
19
|
8
|
35
|
| A3
|
3
|
1
|
1
|
1
8
|
1
|
1
|
8
|
| A4
|
4
10
|
7
|
6
|
2
2
|
9
|
3
19
|
31
|
| Заявки
|
bi
|
20
|
17
|
20
|
10
|
19
|
19
|
105
|
3.3 Сравнение планов по критерию стоимости.
Необходимо подсчитать суммарные затраты на транспортировку (значение целевой функции):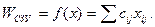
Для задач рассмотренных выше в табл. 12 и табл.13, получим:
- для плана, построенного по методу СЗУ:
WСЗУ=20*8+1*11+6*8+20*8+4*9+1*1+1*7+9*12+3*19=588;
- для плана, построенного по методу минимума стоимостей:
WМС=17*1+14*5+10*5+6*8+19*2+8*1+10*4+2*2+19*3=332;
Лучшим считается план с меньшей суммарной стоимостью перевозок.
WМС < WСЗУ.
3.4 Проверка лучшего опорного плана на оптимальность.
Для проверки плана на оптимальность можно применить метод потенциалов.
Для этого надо ввести так называемые псевдостоимости  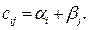 Входящие в псевдостоимости величины Входящие в псевдостоимости величины 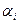 и и 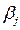 называют потенциалами. Псевдостоимости обладают следующими свойствами: называют потенциалами. Псевдостоимости обладают следующими свойствами:
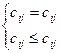 (1) (1)
Для транспортной задачи 4х6 введём величины 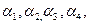 соответствующие первым четырём ограничениям, и соответствующие первым четырём ограничениям, и  остальным ограничениям. остальным ограничениям.
Согласно табл.13 запишем условия в виде:
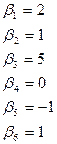 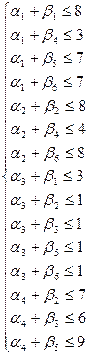 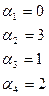 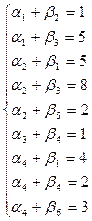
Так как у нас восемь уравнений и десять неизвестных, то мы имеем восемь независимых переменных и две свободных – за свободные мы взяли 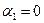 и и 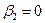 и нашли величины. и нашли величины.
Таблица 14
Проверка плана ТЗ на оптимальность и первый цикл пересчета
| 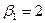
|
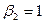
|
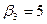
|
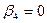
|
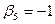
|
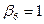
|
| 
|
2 8 8
|
1=1
|
5=5
|
0 3 3
|
-1 7 7
|
1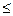 7 7
|
| 17
|
14
|
| 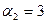
|
5=5
|
4 8 8
|
8=8
|
3 4 4
|
2=2
|
4 8 8
|
| 10
|
6
|
19
|
| 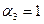
|
3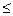 3 3
|
2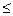 1 1
|
6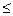 1 1
|
1=1
|
2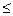 1 1
|
2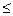 1 1
|
| 8
|
| 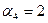
|
4=4
|
3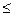 7 7
|
7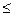 6 6
|
2=2
|
1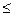 9 9
|
3=3
|
| 10
|
2
|
19
|
Полученное решение не оптимально его необходимо улучшить.
3.5 Улучшение плана по методу циклических перестановок
Для получения нового плана надо перераспределить перевозимы груз между поставщиками и покупателями таким образом, чтобы снизить суммарную стоимость перевозок, не нарушив при этом условий задачи. Решать эту задачу мы будем с помощью метода циклических перестановок.
Сначала намечаем маршрут циклической перестановки – определяем так называемый цикл пересчета.
Циклом пересчёта называют ломаную линию, начинающуюся в свободной клетке, остальные вершины которой помещены в базисные клетки, а звенья лежат вдоль строк и столбцов таблицы. В каждой вершине встречаются только два звена, причём одно из них расположено по строке, другое по столбцу. Свободной клетке в цикле присваивается знак «+», другим вершинам – чередующиеся по ходу знаки «-», «+» и т.д.
Так как число «положительных» и «отрицательных» вершин цикла одинаково, то баланс не нарушиться если в «отрицательных» вершинах вычесть какое- либо число, а в «положительных» вершинах прибавить это же число.
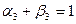 -
пишем в базис -
пишем в базис
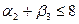 - записываем в свободную клетку - записываем в свободную клетку
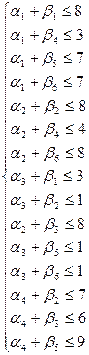 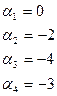 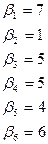 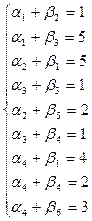
Таблица 15
Проверка плана ТЗ на оптимальность и второй цикл пересчета
| 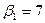
|
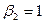
|
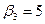
|
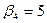
|
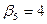
|
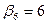
|
| 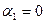
|
7 8 8
|
1=1
|
5=5
|
5 3 3
|
4 7 7
|
6 7 7
|
| 17
|
14
|
| 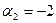
|
5=5
|
-1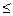 8 8
|
3 8 8
|
3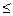 4 4
|
2=2
|
4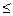 8 8
|
| 16
|
|
19
|
| 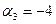
|
3 3 3
|
-3 1 1
|
1=1
|
1=1
|
0 1 1
|
2 1 1
|
| 6
|
2
|
| 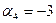
|
4=4
|
-2 7 7
|
2 6 6
|
2=2
|
1 9 9
|
3=3
|
| 4
|
8
|
19
|
Полученное решение не оптимально его необходимо улучшить.
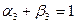 -
пишем в базис -
пишем в базис
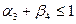 - записываем в свободную клетку - записываем в свободную клетку
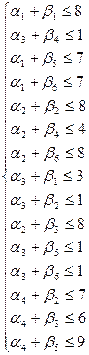 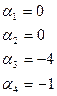 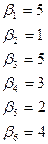 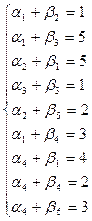
Таблица 16
Оптимальное решение транспортной задачи
| 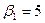
|
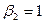
|
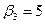
|
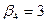
|
|
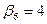
|
| 
|
5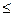 8 8
|
1=1
|
5=5
|
3=3
|
2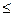 7 7
|
4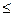 7 7
|
| 17
|
12
|
2
|
| 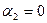
|
5=5
|
1 8 8
|
5 8 8
|
3 4 4
|
2=2
|
4 8 8
|
| 16
|
|
19
|
| 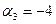
|
1 3 3
|
-3 1 1
|
1=1
|
-1 1 1
|
-2 1 1
|
0 1 1
|
| 8
|
| 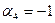
|
4=4
|
0 7 7
|
4 6 6
|
2=2
|
1 9 9
|
3=3
|
| 4
|
8
|
19
|
Оптимальному решению соответствует следующее значение суммарной стоимости перевозок (оптимальное значение):
Wmin
=17*1+12*5+2*3+16*5+19*2+8*1+4*4+8*2+19*3=298
4 Решение задачи линейного программирования.
4.1 Условие задачи линейного программирования.
Условия задачи
Имеются две бетономешалки {А, В} и три стройки {1,2,3} (потребители бетона). В сутки стройкам требуется 700 т бетона, соответственно: 200т, 280т, 220т. Производительность источников А И В равна 320 т и 380 т. Удельная стоимость доставки за тонну определена матрицей 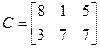 , ,
в условных единицах.
Требуется
.
Определить неизбежные суточные затраты на операцию доставки грузов.
4.1.1 Граф-схема решения задачи линейного программирования.
Первая модель решения:
на полном двудольном графе отношений.
Задача имеет очевидное решение, вытекающее из метода минимума транспортных расходов. Решение представлено на рис.6.
По дуге графа (А,2) при СА1 = 1 транспортировать 280 тонн и платить 1*280=280 усл.ед. стоимости.
Остаток бетона 320-280=40 отправляется на строку 5 при затратах на транспортировку 5*40=200 усл.ед. На стройку 1 по 8 усл.ед. за тонну его отправлять не выгодно.
Аналогично имеем дугу (В,1) с минимальными затратами 3*200=600 усл.ед. Остаток по дуге (В,3) с неизбежными затратами 7*180=1260 усл.ед.
Общая стоимость суточных затрат составит 2340 усл.ед. из единственности приведённого решения вытекает и его оптимальность.
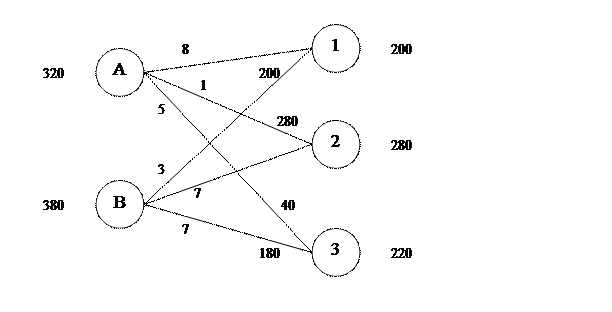
W=CX=1*280+3*200+5*40+7*180=280+600+200+1260=2340 усл.ед.
Рис.6. Решение задачи на графе К2,3 :
осуществляется последовательность в соответствии с разметкой
графа: (А,2)-280; (A,3)-40; (B,1)-200;(В,3)-180
4.1.2 Алгебраическая модель решения задачи линейного программирования.
Вторая модель
.
Алгебраический уровень описания задачи. В общем случае задачи размерности 2х3, где |{A,B}| и 3=|{1,2,3}|- обозначение мощности множества, т.е. числа элементов в множествах, имеет вид:
Дано:
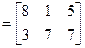 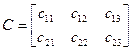
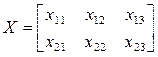
Найти:
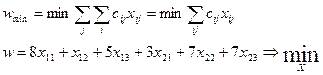
Однако не все переменные множества Х является независимыми.
Табл.16 позволяет облегчить поиск зависимых переменных с помощью уравнений. Для случая  х1=х11 и х2=х12 имеем: х1=х11 и х2=х12 имеем:
x13=х3=320-(х1+х2)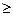 0 0
x21=x4=200-x1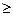 0 0
x22=x5=280-x2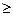 0 0
x23=x6=220-x3=x1+x2-100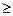 0 0
x1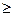 0 и x2 0 и x2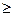 0. 0.
Подстановка системы уравнений-ограничений (знак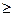 0 ) в W даёт: 0 ) в W даёт:
Wmin=3460+7x1-4x2=> min.
Таблица 17
Для поиска зависимых переменных
| 1
|
2
|
3
|
4
|
| А
|
х11
|
х12
|
Х13
|
320
|
| В
|
х21
|
х22
|
X23
|
380
|
| bj
|
200
|
230
|
220
|
700
|
В итоге была получена следующая задача линейного программирования в неравенствах (Табл 17).
Таблица 18
Задача линейного программирования в неравенствах
| х1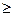 0 и х2 0 и х2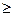 0 0
|
| 320-(х1+х2)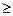 0 0
|
х3=f3(x1;x2)
|
| 200-х1 0 0
|
х4=f4(x1)
|
| 280-х2 0 0
|
х5=f5(x2)
|
| х1+х2-100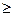 0 0
|
х6=f6(x1;x2)
|
| Wmin=3880+4х1-2х2
|
W=fw(x1;x2)
|
4.1.3 Геометрическая форма представления процесса решения.
Третья модель
.
Геометрическое решение задачи.
В случае двух независимых переменных поиск точки решения, соответствующей Wmin, нагляднее произвести методами алгебраической геометрии в топологии Евклида.
С этой целью воспользуемся декартовой системой координат (х1;х2).
На рис.7 приведена область допустимых решений, определённая неравенствами уравнений-ограничений.
Выделена точка х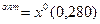 , соответствующая Wmin . Определено значение Wmin (х , соответствующая Wmin . Определено значение Wmin (х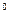 )=2340 усл.ед. Решение, полученное на модели 3, совпадает с решением, полученным на модели 1. )=2340 усл.ед. Решение, полученное на модели 3, совпадает с решением, полученным на модели 1.

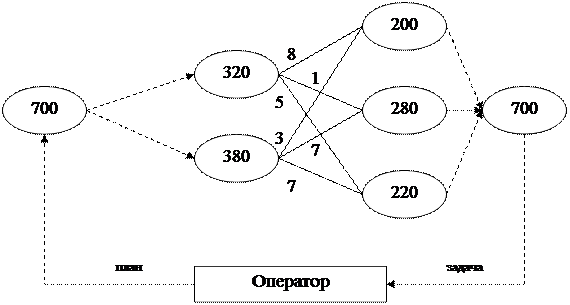
Рис.7. Задача «Бетон»: топология на графе и в проекции
для метрического пространства
4.1.4 Свойства задач линейного программирования.
Задача математического программирования, сводимая к системе линейных уравнений или неравенств, включая критерий эффективности, становится задачей линейного программирования.
Уравнения – ограничения определяют область допустимых решений(ОДР).
Критерий эффективности определяет выбор вершины ОДР. ОДР представляет собой выпуклую оболочку. Если критерий эффективности параллелен грани оболочки, которой принадлежит оптимальное решение, то любая точка этой грани может быть принята в качестве решения в силу эквивалентности по величине значения оценки эффективности [2].
Из линейности граней и выпуклости ОДР, линейности w вытекает следующие свойства ЗЛП [2]:
· Решение задачи лежит, по крайне мере, в одной из вершин выпуклой оболочки, если ОДР ограничена в направлении перемещения опорной поверхности.
· Решение отсутствует, если ОДР не ограничена в направлении перемещения опорной поверхности.
· В невырожденном случае в вершине ОДР все свободные переменные равны нулю, число свободных переменных определяется мерностью пространства представления ОДР.
· В вырожденном случае число равных нулю переменных в вершине ОДР больше числа свободных переменных.
· Множество переменных естественно разбивается на два подмножества: свободные и базовые. Поисковые методы решения в случае многомерных пространств ориентированы на невырожденный случай ЗЛП и процесс поэтапной замены свободных переменных на базовые.
4.2 Симплекс-метод решения задачи линейного программирования.
Симплекс-метод представляет собой организацию процедуры поиска решения путем перемещения от опорной вершины, принадлежащей ОДР, к соседствующей с ней вершиной в сторону оптимальной вершины путём одношаговых замен одной из свободных переменных на одну из базовых вплоть до выполнения критерия эффективности [2].
4.2.1 Иллюстрация процесса поиска решения.
На рис.8 используем для иллюстрации симплекс-метода решения конкретной задачи линейного программирования.
Дано:
ЗЛП в виде алгебраической модели системы уравнений ОДР:
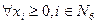 - общее условие допустимости решений, где при х1=х2=0 имеем: х1=х2=0; х3=320;х4=200;х5=280;х6=-100; - общее условие допустимости решений, где при х1=х2=0 имеем: х1=х2=0; х3=320;х4=200;х5=280;х6=-100;
W=3460.
Согласно условиям, т.к. х<0 (равно -100), то решение в точке (0,0) – начало координат на рис.8 - не является допустимым. Точка (0,0) не принадлежит области допустимых решений:
{(x1;x2)=(0,0)}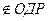 . .

Рис.8. Схема ЗЛП
Далее рассуждения ведутся согласно принятой разметке ОДР в симплексах ОДР.
Итак, чтобы получить допустимое решение необходимо из точки «0» прейти в одну из точек симплекса {Ai;Bi; или Ci}, где 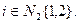
Задача невырожденная, т.к. во всех точках симплекса только две свободные переменные равны нулю, а именно (см. Рис.8):
А1:х2=х6=0;
А2:х1=х6=0
В1:х2=х4=0
В2:х1=х5=0
С1:х3=х4=0
С2:х3=х5=0
Переходим из точки «0», где х1=х2=0 в любую из точек {A1;A2;B1;B2} соответствует правилу замены одной свободной переменной на одну базовую[2].
На Рис.9 показаны возможные пути перехода при решении задачи ЛП, соответствующие замене одной свободной переменной на одну базовую. 
Рис.9. Смежность точек по свойству «замена только одной
свободной переменной»
Очевидно, имеются 4 допустимых маршрута перехода из точки «0» в оптимальную точку (симплекс-вершину)  : :
2……6 6…..5
  1) 0 А2 1) 0 А2 
2…..5
 2) 0 2) 0 
1…..6 6…..4 2…..3 4…..5 3…..1
     3) 0 А1 B1 C1 C2 3) 0 А1 B1 C1 C2 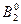
1…..4 2…..3 4…..5 3…..1
    4) 0 B1 C1 C2 B2 4) 0 B1 C1 C2 B2
Из них самый короткий путь - через точки (0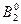 ), самый долгий – через точки (0, А1, В1, C1, C2, ), самый долгий – через точки (0, А1, В1, C1, C2, 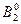 ). ).
4.2.2 Алгебраическое решение.
4.2.2.1 Поиск опорного решения.
Т.к. решение в точке «0» недопустимо из-за отрицательности значений х6 =-100, напрашивается замена переменной х2 на базовую переменную х6 или х1 на х6.
Уравнение х6=х1+х2-100 перерешим относительно х2:
х2=х6-х1+100.
Теперь свободными переменными стали х1 и х6.
При х1=х6=0 базовая переменная х2=100, и условие х2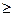 0 выполняется. 0 выполняется.
В остальные уравнения подставим полученное значение х2:
х3=320-х1-100-х6+х1=220-х6;
х4=200-х1;
х5=280-х6+ х1-100=180- х6+ х1;
w=3460-400-4х6+4х1+7х1=3060+11х1-4х6.
Опорное решение получено и равно:
х6=х1=0;х1=100;х3=220;х4=200;х5=180;w=3060.
Вывод.
Наличие отрицательных коэффициентов при свободных переменных в случае минимизации функции w указывает на не оптимальность данного решения.
Для анализа выпишем систему полученных уравнений:
х2=х6-х1+100;
х3=220-х6;
х4=200- х1;
х5=180-х6+ х1;
w=3060+11х1-4х6.
Увеличение х6 ограничено переменными х3 и х5, которые (при х1=0) стремятся с ростом х6 к уменьшению:
- при х6=220 имеем х3=0;
- при х6=180 имеем х5=0.
Следовательно, х5 ограничивает рост х6 раньше, чем х3. Делаем замену х6 на х5:
х6=180-х5+х1;
х4=200-х1;
х2=180-х5+х1 -х1+100=280-х5;
х3=40-х1+х5;
w=3060+11х1 -4(180-х5+х1)= 2340+4х5+7х1=wmin.
Итак, решение достигнуто в точке х5=х1=0;х1=200;х2=280;
х5=40;х6=180;w=2340.
Оно совпадает с результатами, полученными ранее в процессе применения других моделей.
Заключение
Основной целью изучения методов и средств теории принятий решений является выявление их системно-комплексного единства. В области линейного программирования наиболее явно данное свойство проявляется в изоморфизме отдельных моделей в процессе применения методологии «спора моделей». Каждая из указанных моделей возникает в результате рассмотрения объекта исследования на соответствующем уровне абстрактного описания рационально- эмпирического комплекса систем [2].
Задачи линейного программирования, рассмотренные в курсовой работе, представляют собой частные случаи более широких классов задач, имеющих важное научно-практическое значение и решаемых в инженерной деятельности.
Имитационное моделирование относиться к прикладным методам системного анализа системного анализа, применение которого на практике однозначно связано с решением задач творческого характера. В процессе решения подобного рода задач от исследователя требуется умение применять на практике формализованные модели и методы современной математики[1].
Методология решения проблемных творческих задач в настоящее время приобретает все большое значение, так как связана с активными процессами информатизации общественной жизни людей.
Список использованной литературы
1..Панченко В.М. Системный анализ. Метод имитационного моделирования: Учебное пособие – М.:МИРЭА, 1998.-132 с.
2..Панченко В.М., Панов А.В. Теория принятий решения. Линейное программирование: Учебное пособие.- М.: МИРЭА,2005.- 44 с
3..Панченко В.М. Теория систем: задачи и примеры: Учебное пособие. Часть1- М.: МИРЭА,1999.- 80 с.
|