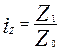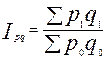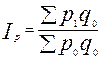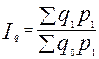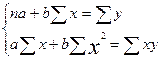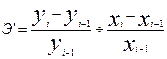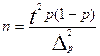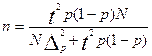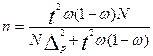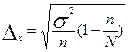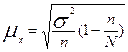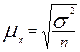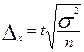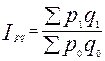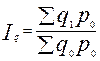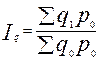Учебное пособие: Методические указания по написанию контрольной работы и проведению переаттестации для студентов заочного отделения всех экономических специальностей
|
Название: Методические указания по написанию контрольной работы и проведению переаттестации для студентов заочного отделения всех экономических специальностей Раздел: Остальные рефераты Тип: учебное пособие 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Уральский государственный экономический университет Центр дистанционного образования ОБЩАЯ ТЕОРИЯ СТАТИСТИКИМетодические указания по написанию контрольной работы и проведению переаттестации для студентов заочного отделения всех экономических специальностей Екатеринбург 2007 Составители: к.э.н., доцент Фёдорова Л.Н., к.э.н. Фёдорова А.Е, ст. преподаватель Рекечинская Т.Б. ВведениеКурс «Общая теория статистики» является базовой дисциплиной в подготовке экономистов, формирующей у них умение и навыки экономико-статистического исследования и имеющей большую практическую направленность. Статистика разрабатывает систему показателей, которая характеризует с различных сторон деятельность секторов, отраслей и предприятий экономики. Она вскрывает закономерности развития явлений, выявляет соотношение между ними, позволяет анализировать тенденции развития и на их основе прогнозировать будущие уровни и соотношения между финансовыми показателями. Целью курса «Статистика» является ознакомление студентов со статистической методологией сбора и анализа экономической информации, системой статистических показателей, отражающих состояние и развитие явлений и процессов в условиях рыночных отношений. Задачи дисциплины заключаются в следующем: 1. изучение существующей в РФ системы показателей статистики на всех уровнях экономики; 2. обучение студентов практическому применению методов статистического исследования; 3. ознакомление студентов с реальными параметрами, характеризующими экономическую деятельность субъектов на территории РФ; 4. развитие навыков работы со статистическими данными и использованием разнообразных источников статистической информации. Изучение данного курса закладывает основу для дальнейшего изучения других экономических дисциплин, использующих статистические методы и методологию исчисления статистических показателей. В процессе изучения дисциплины студенты выполняют контрольную работу и сдают переаттестацию. Переаттестация проводится преподавателем на одном из первых занятий по дисциплине в форме теста. Примерные вопросы тестов приведены в разделе «Переаттестация». Контрольная работа носит комплексный характер и охватывает основные методы статистического анализа. При выполнении работы необходимо руководствоваться следующими требованиями: - контрольная работа должна быть выполнена в отдельной тетради или распечатана на бумажном носителе в формате А4 на компьютере и представлена в срок; - контрольная работа должна выполняться в той последовательности, которая установлена в содержании задания; - решение следует обязательно сопровождать необходимыми формулами; - по окончании решения каждой задачи следует четко формулировать полные выводы; - таблицы следует оформлять в соответствии с правилами, установленными ГОСТом; - список литературы, использованной при написании контрольной работы, необходимо привести в ее конце. Задания контрольной работы разбиты на темы в соответствии с учебным планом. В каждой теме представлены необходимые формулы для вычислений. Работу следует выполнять по вариантам. В каждой теме номер варианта соответствует номеру задачи. Выбор варианта осуществляется в зависимости от начальной буквы фамилии:
По окончании изучения курса студенты должны: - знать сущность показателей статистики; - знать методологию исчисления важнейших показателей статистики финансов; - уметь систематизировать и обобщать информацию, анализировать структуру и тенденции развития процессов и явлений экономической деятельности на всех уровнях экономики РФ, прогнозировать эти процессы и явления; - приобрести навыки самостоятельной работы с исходными данными; - уметь использовать статистическую информацию при дальнейшем освоении специальных экономических дисциплин. Методические указания написаны в соответствии с требованиями образовательных стандартов высшего профессионального образования по экономическим специальностям. Контрольные заданияТема 1. Предмет и метод статистики. Сводка и группировка. Предмет изучения. Статистическая совокупность. Метод и основные элементы методологии. Основные категории статистики. Задачи статистики. Содержание сводки. Статистические ряды распределения. Группировка – основа научной обработки данных статистики. Статистика — общественная наука, изучающая количественную сторону качественно определенных массовых социально-экономических явлений и закономерностей их развития в конкретных условиях места и времени. Особенностью статистики, в отличие, например, от математики, является то, что она исследует количественную сторону общественных явлений в един стве с их качественной стороной. Поэтому она опирается на понятия тех наук, количественную сторону которых она исследует. Основные задачи статистики состоят в следующем: 1) изучение уровня, структуры и динамики массовых социально-экономических явлений; 2) изучение взаимосвязи массовых социально-экономических явлений и процессов; 3) количественная и качественная характеристика новых явлений, процессов и закономерностей; 4) совершенствование системы сбора, обработки информации, системы организации статистического наблюдения. Предметом статистики является количественная сторона качественно определенных массовых социально-экономических явлений и процессов, отображаемая посредством статистических показателей. Другими словами, статистика изучает размеры, объемы, уровни, количественные соотношения явлений общественной жизни. Статистическая информация, отобранная в ходе массового наблюдения, является первичной, при этом данные представляются по каждой единице. Полученная статистическая информация не является обобщенной. С ее помощью нельзя сделать выводы в целом об объекте и отдельных его частях без предварительной обработки имеющихся данных. Для целей статистического анализа полученную информацию необходимо обобщить (сжать) и представить в виде сводных (обобщенных) показателей, чаще всего в табличной форме. Выполняется данная операция с помощью сводки и группировки. Сводка — это ряд последовательных операций по обобщению и обработке первичной информации, выполняемых с целью выявления типичных черт и закономерностей, присущих изучаемому явлению. Сводка является особой стадией статистического исследования, в ходе которой систематизируются первичные материалы статистического наблюдения. Проведение сводки включает 3 этапа: • предварительный контроль материалов, т.е. проверку исходных данных; • группировку данных по заданным признакам, определение производных показателей; • оформление результатов сводки в виде статистических таблиц, удобных для восприятия информации. Задачи сводки - систематизация первичных данных и получение сводных характеристик объекта. Результатом сводки являются подробные данные, отражающие в целом всю совокупность. Группировка данных производится в соответствии с программой сводки для того, чтобы впоследствии представить полученную информацию в виде, доступном для восприятия. Группировка — объединение единиц совокупности в некоторые группы, имеющие свои характерные особенности, общие черты и сходные размеры изучаемого признака. Результаты группировки оформляются в виде группированных таблиц , делающих информацию обозримой. Группировки различают: • по задачам систематизации данных; • по числу группировочных признаков; • по используемой информации. Метод группировок применяется для решения задач, возникающих в ходе научного статистического исследования: • выделения социально-экономических типов явлений; • изучения структуры явления и структурных сдвигов, происходящих в нем; • выявления связей и зависимостей между отдельными признаками явления. Для решения этих задач применяют (соответственно) три вида группировок: типологические, структурные и аналитические (факторные). По числу группировочных признаков различают простые (по одному признаку) и сложные (по нескольким признакам — комбинированные и многомерные). Комбинированные группировки строятся путем разбивки каждой группы на подгруппы в соответствии с дополнительными признаками. Многомерные — строятся с помощью специальных алгоритмов, когда осуществляется поиск скопления в К-мерном пространстве, где каждый объект — точка, т.е. построить многомерную группировку — найти скопление точек. По используемой информации различают первичные и вторичные группировки. Первичные группировки производятся на основе исходных данных, полученных в результате статистических наблюдений. Вторичные — результат объединения или расщепления первичной группировки. Статистическая группировка данных осуществляется в следующем порядке: 1 этап Выбор признака, который закладывается в основание группировки. Разбивка единиц совокупности на отдельные группы проводится по группировоч ному признаку, его часто называют основанием группировки. В качестве основания группировки используются существенные признаки как количественные, гак и качественные. 2 этап Определение количества групп (зависит от задач исследования и вида признака). При построении групп по качественному признаку количество групп обычно соответствует числу градаций, типов, видов, состояний признака. Например, в случае проведения группировки населения по полу можно образовать только две группы: мужчины и женщины. Количество групп и величина интервала связаны между собой: чем больше образовано групп, тем меньше интервал, и наоборот. Количество групп зависит от числа единиц исследуемого объекта и степени колеблемости группировочного признака. При небольшом объеме совокупности нельзя образовывать большое число групп, так как группы будут малочисленными. При определении количества групп необходимо стремиться к тому, чтобы были учтены особенности изучаемого явления. Поэтому количество групп должно быть оптимальным , в каждую группу должно входить достаточно большое число единиц совокупности, что отвечает требованию закона больших чисел. При небольшом объеме совокупности не следует образовывать большое число групп, так как они будут малочисленны, а показатели, рассчитанные для таких групп, не будут представительными. Степень колеблемости учитывается так: чем больше разность между наибольшим и наименьшим значением признака, тем больше следует образовывать групп. Существует эмпирическое правило: чем больше групп, тем точнее будет воспроизведен характер исследуемого объекта. Кроме того, в одну группу не должно попасть более половины всех единиц совокупности, а средние iруппы должны содержать больше единиц, чем крайние. Определить количество групп можно эмпирическим (опытным) путем или используя формулу Стерджесса: n =1+3,322ln N ; где п - число групп; N - число единиц совокупности. 3 этап Определение величины интервала группировки. Интервал - это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, называемую шагом, а также верхнюю и нижнюю границы. Верхняя граница - наибольшее значение признака в рассматриваемом интервале, нижняя граница наименьшее значение признака. Величина равного интервала определяется по формуле
где h - величина равного интервала; R - размах вариации, R ~ Хтях ~ Xmin ; Хтах , Хтт - соответственно максимальное и минимальное значения признака в совокупности; п - количество групп. Полученную величину интервала (шаг интервала) принято округлять. Правило округления: дробные числа округляются до десятых (0,1); если размер шага имеет целых две значащие цифры и дробную часть, в этом случае округляют до целых. Целые трехзначные цифры округляются до ближайшего числа, кратного 10. Например, 678 следует округлить до 680. Формулы для вычислений
Задача 1. Имеется информация о количестве книг, полученных студентами по абонементу за прошедший учебный год.
Построить вариационный, ранжированный, дискретный ряд распределения, обозначив элементы ряда. Задача 2. Имеются данные о стоимости основных фондов у 50 предприятий, тыс. руб.:
Построить ряд распределения, выделив 5 групп предприятий (с равными интервалами). Задача 3. По ряду предприятий легкой промышленности получены следующие данные:
Произведите группировку предприятий по числу рабочих, образуя 6 групп с равными интервалами. Подсчитайте по каждой группе: 1. число предприятий 2. число рабочих 3. объем произведенной продукции за год 4. среднюю фактическую выработку одного рабочего 5. объем основных средств 6. средний размер основных средств одного предприятия 7. среднюю величину произведенной продукции одним предприятием Результаты расчета оформите в таблицы. Сделайте выводы. Задача 4. По ряду предприятий легкой промышленности получены данные, представленные в таблице. Произведите группировку предприятий по размеру основных средств, образуя 6 групп с равными интервалами. По каждой группе подсчитайте: 1. число предприятий 2. объем основных средств 3. средний размер основных средств одного предприятия 4. объем произведенной продукции 5. выпуск продукции на 1000 рублей основных средств
Результаты расчета оформите в таблицы. Сделайте выводы. Тема 2. Абсолютные и относительные величины Абсолютные обобщающие величины, их виды. Единицы измерения абсолютных величин. Относительные величины, их виды. Взаимосвязь абсолютных и относительных величин. Необходимость их комплексного использования. Абсолютными в статистике называются суммарные обобщающие показатели, характеризующие размеры (уровни, объемы) общественных явлений в конкретных условиях места и времени. Индивидуальными называют абсолютные статистические величины, характеризующие размеры признака у отдельных единиц совокупности (например, размер заработной платы отдельного работника, вклада гражданина в определенном банке и т.д.). В отличие от индивидуальных суммарные абсолютные статистические величины характеризуют итоговое значение признака по определенной совокупности объектов, охваченных статистическим наблюдением. Они являются суммой количества единиц изучаемой совокупности (численность совокупности) или суммой значений варьирующего признака всех единиц совокупности (объем варьирующего признака). Абсолютные статистические величины представляют собой именованные числа , т.е. имеют какую-либо единицу измерения. Натуральные единицы измерения в свою очередь могут быть простыми (тонны, штуки, метры, литры) и сложными, являющимися комбинацией нескольких разноименных величин (грузооборот железнодорожного транспорта выражается в тонно-километрах, производство электроэнергии — в киловатт-часах, затраты труда — в человеко-часах, человеко-днях). Стоимостные единицы измерения используются, например, для выражения объема разнородной продукции в стоимостной (денежной) форме — рублях. В трудовых единицах измерения (человеко-днях, человеко-часах) учитываются общие затраты труда на предприятии, трудоемкость отдельных операций технологического цикла. Относительная величина в статистике — это обобщающий показатель, который представляет собой частное от деления одного абсолютного показателя на другой и дает числовую меру соотношения между ними. Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием . Относительная величина динамики ( I ) рассчитывается как отношение уровня признака в определенный период или момент времени к уровню этого же признака в предшествующий период или момент времени, т.е. она характеризует изменение уровня какого-либо явления во времени. Относительные величины динамики называются темпами роста . Формулы для вычислений
Относительная величина выполнения плана задания (вып.пл.) представляет собой отношение фактически достигнутого в данном периоде уровня к запланированному. Относительными величинами структуры называются показатели, характеризующие долю отдельных частей изучаемой совокупности во всем ее объеме. Они рассчитываются делением числа единиц (или объема явления) в отдельных частях совокупности на общее число единиц совокупности (или объем явления). Относительными величинами интенсивности называют показатели, характеризующие степень распространения или уровень развития того или иного явления в определенной среде. Относительными величинами координации называют показатели, характеризующие соотношение отдельных частей целого между собой. Относительными величинами сравнения называют показатели, представляющие собой частное от деления одноименных абсолютных статистических величин, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.д.) и относящихся к одному и тому же периоду (или моменту) времени. Задача 1. В таблице приведены данные о продажах автомобилей в одном из автосалонов города за 1 квартал прошедшего года. Определите структуру продаж.
Задача 2. По региону имеются следующие данные о вводе в эксплуатацию жилой площади:
Определить: 1. динамику ввода жилья в эксплуатацию; 2. структуру введенного жилья. Задача 3. Закупочная цена пшеницы в августе текущего года в России составила 70 долларов за тонну. При этом планировалось, что цена закупки в сентябре сократится до 60 долларов. Фактически она составила 72 доллара за тонну. В то же время в США цена пшеницы достигла соответственно: 90 долларов в августе и 84 доллара в сентябре. Определить все возможные относительные величины. Задача 4. Натуральный баланс сахара в регионе характеризуется следующими данными, млн. тонн: Запасы на начало года 2,2 Произведено 23,4 Потреблено 16,6 в том числе: - производственное потребление 6,4 - потребление населением 10,2 Вывоз за пределы региона 7,0 Определить: 1) запасы сахара на конец года; 2) соотношение потребленного и вывезенного сахара; 3) структуру потребления. Тема 3. Средние величины Сущность и значение средних показателей. Виды средних и способы их вычисления. Средняя величина простая и взвешенная. Свойства средней величины. Исчисление средней из интервального ряда распределения по методу моментов. Структурные средние. Средний показатель - показатель в форме средней величины, представляющий собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средняя величина - наиболее распространенная форма статистических показателей, так как выражает типичные черты и дает общую характеристику но одному из варьирующих признаков. Так, например, одной из задач органов государственной статистики является характеристика уровня жизни населения, в том числе в проработке по социальным группам. При этом сравнение дохода каждой семьи без подразделения на подгруппы невозможно, так как количество членов семьи, их возрастной состав, социальный статус разные. Если выполнять сравнение по социальным группам, тогда также не достигнуть объективности, так как численности по группам разные. Поэтому для характеристики уровня жизни используют только средние показатели, такие как средняя годовая заработная плата по категориям и в целом по предприятию, среднедушевой доход с выделением социального положения и другие. Средние показатели, получаемые при таком подходе, являются типичными. В общем виде формула для расчета среднего показателя выглядит следующим образом:
В зависимости от того, в каком виде представлены исходные данные для расчета средней, различают среднюю арифметическую, среднюю гармоническую и среднюю геометрическую величину. Средняя арифметическая величина (х) - наиболее распространенный вид средней. Значения признака могут быть представлены в сгруппированном и не-сгруппированном виде, вследствие чего и расчет средней арифметической может выполняться с использованием различных формул. Если значение признака представлено в исходной совокупности без группировки, расчет ведется по формуле простой (невзвешенной) средней
Формулы для вычислений
Задача 1. Имеется информация о численности студентов ВУЗов города и удельном весе (%) обучающихся студентов на коммерческой основе:
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов. Задача 2. Сумма невыплаченной своевременно задолженности по кредитам на 1 июля составляла 92,4 млн. денежных единиц. По отдельным отраслям экономики она распределялась следующим образом:
Определить средний процент невыплаченной своевременно задолженности. Обоснуйте выбор формы средней. Задача 3. За прошлый квартал банком выплачено процентов по депозитам 98 тысяч денежных единиц, в том числе: по краткосрочным – 63, среднесрочным – 35. депозитная процентная ставка соответственно составляла 7,5 и 9%. Определите среднюю депозитную процентную ставку. Обоснуйте выбор формы средней. Задача 4. Имеются данные по 2-м заводам, вырабатывающим одноименную продукцию. Определить для каждого года отдельно средние затраты времени на единицу продукции по двум заводам вместе.
Тема 4. Показатели вариации Понятие вариации и ее значение. Абсолютные показатели вариации. Относительные показатели вариации. Виды дисперсии. Правило сложения дисперсий. Вариация альтернативного признака. Коэффициент детерминации и эмпирическое корреляционное отношение. Колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности называется вариацией. Измерение вариации дает возможность оценить степень воздействия на данный признак других варьирующих признаков. По степени вариации можно судить о многих сторонах развития явления: об однородности совокупности, об устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи признаков одного явления и признаков разных явлений. На основе показателей вариации в статистике разрабатываются другие показатели: тесноты связи между явлениями и их признаками, показатели точности выборочного наблюдения. Показатели вариации делятся на 2 группы: абсолютные и относительные. К абсолютным показателям вариации относятся: размах вариации (R); среднее линейное отклонение (d); дисперсия; среднее квадратическое отклонение. Относительные показатели вариации определяются как отношение абсолютных показателей вариации к средней арифметической или медиане.
Формулы для вычислений
Задача 1 При изучении влияния рекламы на размер среднемесячного вклада в банках района обследовано 2 банка. Получены следующие результаты:
Определить: 1) для каждого банка: а) средний размер вклада за месяц; б) дисперсию вклада; 2) средний размер вклада за месяц для двух банков вместе. 3) Дисперсию вклада для 2-х банков, зависящую от рекламы; 4) Дисперсию вклада для 2-х банков, зависящую от всех факторов, кроме рекламы; 5) Общую дисперсию используя правило сложения; 6) Коэффициент детерминации; 7) Корреляционное отношение. Задача 2. Имеются данные о распределении населения России по размеру денежного дохода в условном году
Определить:1)среднедушевой доход за изучаемый период в целом, используя упрощенный способ; 2) среднедушевой доход в форме моды и медианы для дискретного и интервального рядов; 3) дисперсию способом моментов; 4) среднее квадратическое отклонение; 5) коэффициент вариации Задача 3. Имеется группировка предприятий по величине товарной продукции:
Определить: 1) дисперсию величины товарной продукции; 2) среднее квадратическое отклонение; 3) коэффициент вариации Задача 4. Имеются следующие данные о расходах граждан в январе условного года:
Определить: 1) среднедушевой расход городских и сельских жителей; 2) дисперсии душевого расхода: среднюю из групповых, межгрупповую, общую; 3) зависимость расходов от места жительства, исчислив коэффициент детерминации и эмпирическое корреляционное отношение. Тема 5. Выборочное наблюдение Понятие о выборочном наблюдении и его задачи. Виды выборок. Ошибки выборки. Доверительная вероятность. Определение необходимого объема выборки. Оценка результатов выборочного наблюдения и распространение их на генеральную совокупность. Выборочное наблюдение проводится в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. Например, проверка качества отдельных видов продукции может быть связана с ее уничтожением, а некоторые совокупности настолько велики, что физически не возможно собрать данные в отношении каждого из их членов. Также выборочное наблюдение используют для проверки результатов сплошного наблюдения. Выборочной совокупностью
называют ту часть единиц, которые отобраны для наблюдения а генеральной
- всю совокупность единиц, из которых производится отбор Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, т.е., насколько выборка репрезентативна. Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц. Методы отбора единиц в выборочную совокупность подразделяют на повторный и бесповторный При повторном отборе каждая попавшая в выборку единица возвращается в генеральную совокупность и имеет шанс вторично попасть в выборку. При этом вероятность попадания в выборочную совокупность для всех единиц генеральной совокупности остается одинаковой. Бесповторный отбор означает, что каждая отобранная единица не возвращается в генеральную совокупность и не может подвергнуться вторичной регистрации, а поэтому для остальных единиц вероятность попадания в выборку увеличивается. Бесповторный отбор дает более точные результаты по сравнению с повторным, т.к. при одном и том же объеме выборки наблюдение охватывает больше единиц генеральной совокупности. При формировании выборочной совокупности используют следующие виды (способы) отбора: простой случайный отбор; механический отбор; серийная, расслоенная (типическая или стратифицированная), многоступенчатая, многофазовая и моментная выборки. Случайный отбор производится с помощью жеребьевки либо по таблице случайных чисел. В первом, случае всем элементам генеральной совокупности присваивается порядковый номер и на каждый элемент заводится жребий в виде пронумерованных шаров или карточек-фишек, которые перемешиваются и помещаются в ящик. Затем производится отбор «наудачу». Во втором случае из специальных таблиц производится выбор случайных чисел, которые образуют порядковые номера для отбора. Например, имеется ряд чисел: 60280, 88925. 99610. Применение комбинации этих чисел зависит от размера совокупности: если в ней 1000 единиц, то порядковый номер каждой единицы должен состоять из трех цифр от 000 до 999. В этом случае приведенный ряд чисел даст пять первых номеров единиц выборочной совокупности: 602,808, 892, 599, 610. Остальные номера получают аналогично до тех пор, пока не будет получен заданный объем выборочной совокупности. При механическом
способе отбирается каждый ральной совокупности. Например, если имеется совокупность из 100 тыс. единиц и требуется выборка в 1000 единиц, то в нее попадет каждый сотый элемент. Если единицы совокупности не ранжированы относительно изучаемого признака, то 1 -й элемент выбирается наугад, произвольно, а если ранжированы - то из середины 1-й сотни. При серийном способе в порядке случайной или механической выборки отбирают не единицы, а определенные районы, серии (гнезда), внутри которых проводится сплошное наблюдение. Расслоенным (стратифицированным) способом производится отбор единиц из неоднородной совокупности. Для этого генеральную совокупность с помощью типологической группировки разбивают на однородные группы, а затем из каждой группы случайным или механическим способом отбирают единицы в выборочную совокупность. При этом единицы разных групп включаются в выборку пропорционально их численности в генеральной совокупности.
Формулы для вычислений
Задача 1. Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:
Определить: 1) по предприятиям, включенным в выборку: а) средний размер произведенной продукции на одно предприятие; б) дисперсию объема производства; в) долю предприятий с объемом производства продукции более 400 тыс. руб.; 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать: а) средний объем производства продукции на одно предприятие; б) долю предприятий с объемом производства продукции более 400 тыс. руб.; 3) общий объем выпуска продукции по области. Задача 2. По результатам контрольной проверки налоговыми службами 400 бизнес-структур, у 140 из них в налоговых декларациях не полностью указаны доходы, подлежащие налогообложению. Определите в генеральной совокупности (по всему району) долю бизнес-структур, скрывших часть доходов от уплаты налогов, с вероятностью 0,954. Задача 3. Для изучения экономической активности населения района из 200 000 человек методом случайного бесповторного отбора опрошено 4 000 человек. Из них 1 600 человек вложили свои ваучеры в инвестиционные фонды или акции предприятий. С вероятностью 0,954 определить пределы населения всего района, в которых находиться доля экономически активного населения района. Задача 4. Для определения средней величины заработной платы работников малых предприятий необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество работников нужно отобрать, чтобы ошибка выборки с вероятностью 0,954 не превышала 2 тыс. руб. при среднем квадратическом отклонении 10 тыс. руб. Тема 6. Ряды динамики Понятие и классификация рядов динамики. Аналитические показатели изменения уровней ряда динамики. Средние показатели ряда динамики. Сопоставимость уровней и смыкание рядов динамики. Компоненты ряда динамики. Методы анализа основной тенденции (тренда) в рядах динамики. Модели сезонных колебаний. Рядом динамики в статистике называется ряд чисел, характеризующих изменение величины социально-экономических явлений во времени. Каждый ряд динамики состоит из двух элементов: 1) ряд уровней изучаемого явления (у); 2) ряд периодов времени, к которому относятся уровни ряда (t). Классификация рядов динамики 1. В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. 2. В зависимости от того, как выражают уровни ряда состояние явления на определенные моменты времени, различают моментные и интервальные ряды динамики. 3. В зависимости от расстояний между уровнями ряды динамики подразделяются на ряды с равностоящими и неравностоящими уровнями ряда во времени. Формулы для вычислений
Задача1. Данные о площадях под картофелем до и после изменения границ района, тысяч гектаров:
Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района. Задача 2. Имеется информация об экспорте продукции из региона за ряд лет.
Определить: 1) цепные и базисные: а) абсолютные приросты; б) темпы роста; в) темпы прироста; 2)абсолютное содержание одного процента прироста; 3) средние показатели: а) средний уровень ряда; б) среднегодовой абсолютный прирост; в) среднегодовой темп роста; г) среднегодовой темп прироста. Задача 3. По следующей информации определить средний размер имущества предприятия за квартал:
Задача 4. Имеется информация о списочном составе работников малого предприятия за октябрь месяц. На 1 сентября – 40 человек, 5 сентября уволилось 8 человек, 12 сентября принято 5 человек, 20 сентября уволилось 2 человека, 25 сентября принято 10 человек. Определить среднесписочный состав работников за сентябрь месяц. Тема 7. Экономические индексы Понятие экономических индексов и их классификация. Индивидуальные и общие индексы. Агрегатные и средневзвешенные индексы. Веса индексов. Индексный метод анализа выявления роли отдельных факторов. Свойства индексов Ласпейреса и Пааше. Анализ изменения среднего уровня индексируемой величины в относительных и абсолютных показателях. Индекс - относительный показатель, выражающий соотношение величин какого-либо явления во времени и пространстве или сравнение фактических данных с любым эталоном (планом, нормативом и т.д.). В переводе с латинского индекс (index) означает показатель. В международной практике индексы принято обозначать символами: индивидуальные (частные) индексы; Показатель, изменение которого определяется в индексе, называется ин дексируемым. В статистическом анализе приходится сталкиваться с простыми и сложными (несопоставимыми) явлениями, при этом для их характеристики используются разные индексы. Показатели, характеризующие изменение более или менее однородных явлений или объектов, входящих в состав сложною явления, называются инди видуальными индексами ( i ). При изучении изменения уровня цен. затрат, объема в текущем периоде, по сравнению с базисным по одному конкретному продукту, рассчитываются индивидуальные индексы цен, объема, себестоимости Показатели, характеризующие изменение уровней сложного явления или объекта, составные части которого несоизмеримы, называются сводными (общими) индексами ( J ). Например, изменение физического объема продукции, включающей разноименные товары (в случае многономенклатурного производства). Получить общую картину изменения объема, измеряемого в разных натуральных единицах, путем прямого суммирования показателя в текущем и базовом периодах невозможно. Поэтому на практике с целью сопоставления сложных явлений прибегают к показателю, называемому весами. Показатели, с помощью которых непосредственно несопоставимые явления приводятся в сопоставимый вид, называются весами. Формулы для вычислений
Задача1.По нижеприведенным данным ответить на вопросы, поставленные в таблице, т.е. определить недостающие показатели.
Задача 2. Имеется информация о выпуске продукции на предприятии, ее себестоимости за 2 квартала.
Определить: 1) индивидуальные индексы количества и себестоимости; 2) общие индексы затрат на производство, натурального выпуска и себестоимости; 3) абсолютное изменение затрат на выпуск продукции в целом и по факторам: а) за счет изменения себестоимости; б) за счет изменения натурального выпуска. Сделать выводы. Задача 3. Имеется информация о затратах на производство и индексах количества:
Определить: 1)индивидуальные индексы физического объема производства; 2) общий индекс физического объема производства; 3) общий индекс себестоимости, если известно, что общие затраты на производство выросли на 25%. Сделать выводы. Задача 4. Денежные затраты на строительно-монтажные работы увеличились в текущем периоде на 38%, а себестоимость работ – на 46,8%. Определить индекс объема строительно-монтажных работ. Тема 8. Основы корреляционного анализаВиды и формы связей. Функциональные и корреляционные связи. Методы измерения степени тесноты корреляционной связи между признаками и оценка их существенности. Линейный коэффициент корреляции и линейный коэффициент детерминации. Уравнение регрессии. Нахождение параметров уравнения регрессии и проверка их значимости. Показатели эластичности.
Формулы для вычислений
Задача 1. По пяти рабочим цеха имеются данные о квалификации и месячной выработке. Для изучения связи между квалификацией рабочих и их выработкой определить линейное уравнение связи и коэффициент корреляции. Дать интерпретацию коэффициентам регрессии и корреляции.
Задача 2. По группе предприятий отрасли имеются следующие данные:
1) постройте уравнение прямой и определите коэффициент регрессии; 2) определите тесноту связи; 3) сделайте экономические выводы. Задача 3. На предприятии цены на изделия снижены с 80 руб. за единицу до 60 руб. После снижения цен продажа возросла с 400 до 500 единиц в день. Определить абсолютную и относительную эластичность. Сделать оценку эластичности с целью возможности (или невозможности) дальнейшего снижения цен. Задача 4. По 8 однородным магазинам имеются следующие данные:
Найдите уравнение корреляционной связи товарооборота и уровня издержек обращения. Вычислите коэффициенты эластичности, показатели тесноты корреляционной связи. Сделайте выводы. ПереаттестацияТема 1. Предмет и метод статистики. Сводка и группировка. 1.Что является предметом статистики? А. Планирование и прогнозирование Б. Организация работы В. Количественная сторона массовых явлений в конкретных условиях места и времени Г. Координирование Д. контроль 2.Сущность метода статистики: А. Сбор данных, их обобщение, представление, анализ и интерпретация Б. Изучение динамики В. Составление балансов Г. Оценка затрат Д. Корреспондентский опрос 3.Основные стадии статистического исследования: А. Сбор данных Б. Группировка данных В. Составление таблиц Г. Организация работы Д. Планирование и прогнозирование 4. Что такое статистическая сводка? А. Выделение качественно однородных групп Б. Выявление взаимосвязей между признаками В. Определение интервалов Г. Приведение собранной информации к виду, удобному для проведения анализа Д. Подсчет структуры явления 5. Что такое группировка? А. Разработка системы показателей Б. Определение интервалов В. Образование однородных групп по существенным признакам Г. Ранжирование ряда распределения Д. Подсчет структуры распределения 6. Что такое атрибутивные признаки? А. Явление, информацию о котором собирают Б. Качественный (описательный) признак В. Первичный элемент объекта, подлежащий регистрации Г. Признак, выраженный числом Д. Интервал, имеющий нижнюю границу 7. Что называется рядом распределения? А. Совокупность явлений, информацию о которых собирают Б. Первичные элементы объекта, подлежащих регистрации В. Перечень вопросов, ответы на которые получают в процессе наблюдения Г. Величина интервала Д. Упорядоченное распределение единиц совокупности на группы по какому-либо признаку Тема 2. Абсолютные и относительные величины 1.Что такое абсолютные показатели в статистике? А. Первичный элемент объекта наблюдения Б. Варьирующие признаки, положенные в основу группировки В. Это частоты, рассчитанные на единицу ширины интервала Г. Показатели, характеризующие размеры (уровни, объемы) общественных явлений в конкретных условиях места и времени Д. Величины, представляющие собой частное от деления одного показателя на другой 2.Что такое относительная величина координации? А. Отношение фактически достигнутого в данном периоде уровня к запланированному Б. Показатель, характеризующий долю отдельных частей изучаемой совокупности В. Показатели, характеризующие долю отдельных частей изучаемой совокупности Г. Отношение фактических уровней, относящихся к разным периодам Д. Отношение одноименных показателей, относящихся к разным объектам 3.Что такое относительная величина сравнения? А. Отношение фактически достигнутого в данном периоде уровня к запланированному Б. Показатель, характеризующий долю отдельных частей изучаемой совокупности В. Показатели, характеризующие долю отдельных частей изучаемой совокупности Г. Отношение фактических уровней, относящихся к разным периодам Д. Отношение одноименных показателей, относящихся к разным объектам 4.Что такое относительная величина динамики? А. Отношение фактически достигнутого в данном периоде уровня к запланированному Б. Показатель, характеризующий долю отдельных частей изучаемой совокупности В. Показатели, характеризующие долю отдельных частей изучаемой совокупности Г. Отношение фактических уровней, относящихся к разным периодам Д. Отношение одноименных показателей, относящихся к разным объектам Тема 3. Средние величины 1. Что представляет собой средняя величина в статистике? А. Количественная характеристика соотношений явлений в пространстве Б. Обобщающая характеристика изменения явления во времени В. Обобщающая количественная характеристика какого-либо признака в совокупности 2. Что произойдет со средней арифметической, если все варианты ряда увеличить в 2 раза? А. Останется прежней Б. Увеличится в 2 раза В. Уменьшится в 2 раза Г. Увеличится на 2 3. Что произойдет со средней арифметической, если все варианты уменьшить на 100? А. Останется прежней Б. Увеличится на 100 В. Увеличится в 100 раз Г. Уменьшится на 100 4. Что произойдет со средней арифметической, если все частоты уменьшить в 4 раза? А. Останется без изменения Б. Увеличится в 4 раза В. Уменьшится в 4 раза Г. Уменьшится на 4 5. В каком случае используется мода? А. Для измерения колеблемости признака Б. Для характеристики наиболее часто встречающейся величины признака В. Для исчисления средних темпов роста Г. Для отыскания средней величины ранжированного ряда 6. В каком случае исчисляется медиана? А. Для измерения колеблемости признака совокупности Б. Для характеристики наиболее часто встречающейся величины признака В. Для отыскания центрального члена ранжированного ряда Г. При исчислении средних темпов роста 7. Какую из форм средних величин следует использовать при определении продукции, пользующейся наибольшим спросом? А. Средняя арифметическая Б. Медиана В. Средняя гармоническая Г. Мода 8. Какую цену записывает учетчик при регистрации цен на продукты? А. Среднюю арифметическую Б. Среднюю гармоническую В. Медианную Г. Модальную Тема 4. Показатели вариации 1. Для чего применяются показатели вариации? А. Оценка степени однородности Б. Характеристика темпов роста явления В. Определение среднего значения признака 2. В каких единицах измеряется среднее квадратическое отклонение? А. В процентах Б. В тех же единицах, что и варьирующий признак В. В тех же единицах, в каких выражены частоты 3. Что характеризует межгрупповая дисперсия? А. Вариацию признака под влиянием всех условий, вызвавших эту вариацию Б. Вариацию признака под влиянием фактора, положенного в основу группировки В. Вариацию признака, происходящую под влиянием неучтенных факторов Г. Вариацию признака, не зависящую от условия, положенного в основу группировки 4. Что характеризует внутригрупповая дисперсия? А. Вариацию признака под влиянием всех условий, вызвавших эту вариацию Б. Вариацию признака под влиянием фактора, положенного в основу группировки В. Вариацию признака, происходящую под влиянием неучтенных факторов Г. Вариацию признака, не зависящую от условия, положенного в основу группировки 5. Что характеризует общая дисперсия? А. Вариацию признака под влиянием всех условий, вызвавших эту вариацию Б. Вариацию признака под влиянием фактора, положенного в основу группировки В. Вариацию признака, происходящую под влиянием неучтенных факторов Г. Вариацию признака, не зависящую от условия, положенного в основу группировки 6. Что произойдет с дисперсией, если все варианты уменьшить в 3 раза? А. Останется неизменной Б. Уменьшится в 3 раза В. Увеличится в 9 раз Г. Уменьшится в 9 раз 7. По двум совокупностям имеется информация о коэффициенте вариации изучаемого признака: А. Первая Б. Вторая В. Одинаковы 8. В каком случае факторный признак влияет более сильно на вариацию результативного признака: при А. При Б. При В. Нет разницы Тема 5. Выборочное наблюдение 1.Как определяется необходимая численность выборки при случайном бесповторном отборе? А. Б. В. Г. Д. 2.Как определяется предельная ошибка выборочной средней при серийном бесповторном отборе? А. Б. В. Г. Д. 3.Как определяется предельная ошибка выборки при случайном бесповторном отборе для средней? А. Б. В. Г. Д. 4.Как оценивается доля признака? А. от 0 до 1 Б. В. Г. Д. 5.Как выглядит доверительный интервал для оценки средних значений? А. от 0 до 1 Б. В. Г. Д. Тема 6. Ряды динамики 1.Что характеризуют динамические ряды статистики? А. Изменение явлений в пространстве Б. Изменение явлений во времени В. Дают числовую меру соотношения двух статистических величин 2. По какой формуле определяется средний уровень моментного ряда динамики? А. Б. В. 3. По какой формуле определяется цепной темп роста? А. Б. В. 4. Что характеризует темп прироста? А. Отношение одного уровня к другому Б. Величину явления на ту или иную дату В. Относительная оценка абсолютного прироста 5. По какой формуле исчисляется средний темп динамики? А. Средняя арифметическая Б. Средняя гармоническая В. Средняя геометрическая 6. В каких единицах измеряется абсолютный прирост? А. В коэффициентах Б. В процентах В. В единицах измерения исходной информации 7. Чему равен средний абсолютный прирост? А. Б. В. 8. Назовите важнейшее условие правильного построения динамического ряда. А. Уровни ряда должны быть выражены в абсолютных величинах Б. Уровни ряда должны быть выражены в относительных величинах В. Сопоставимость уровней динамического ряда между собой Тема 7. Экономические индексы 1.Что такое статистические индексы? А. Абсолютные величины Б. Относительные величины структуры В. Относительные величины, характеризующие изменение явления во времени, пространстве или с эталоном 2. Что характеризуют индивидуальные индексы? А. Изменение одного элемента сложного явления вне связи его с другим элементом Б. Изменение сложного явления во времени В. Изменение сложного явления в пространстве 3. Как исчисляется агрегатный индекс стоимости продукции? А. Б. В. 4. Как определяется агрегатный индекс физического объема продукции? А. Б. В. 5. Какой вариант агрегатных индексов качественных показателей используют при расчете индекса потребительских цен (ИПЦ)? А. Б. В. 6. Что называется индексом переменного состава? А. Индекс абсолютных величин Б. Индекс относительных величин В. Индекс средних величин 7. Что называется индексом постоянного состава? А. Индекс, рассчитанный при разной структуре совокупности Б. Индекс, рассчитанный для средних величин В. Индекс, рассчитанный при фиксированной структуре 8. Что показывает разность между числителем и знаменателем общего индекса затрат на производство? А. Изменение затрат от изменения себестоимости Б. Изменение затрат от изменения натурального выпуска В. Общее изменение затрат 9. Что характеризует разность между числителем и знаменателем общего индекса цен? А. Общее применение товарооборота Б. Изменение товарооборота за счет изменения натуральных продаж В. Изменение товарооборота за счет изменения цен 10. В чем сущность индексов-дефляторов? А. Характеризуют изменение натурального выпуска продукции в стране Б. Характеризуют изменение затрат на выпуск продукции В. Характеризуют общее изменение цен или покупательной способности денег Тема 8. Основы корреляционного анализа1. В каком случае связь между переменными будет функциональной? А. Одному значению факторного признака может соответствовать несколько значений результативного признака Б. Одному значению факторного признака может соответствовать одно строго определенное значение результативного признака В. Одному значению результативного признака может соответствовать несколько значений факторного признака 2. В каком случае связь между переменными признаками будет корреляционной? А. Одному значению факторного признака может соответствовать одно строго определенное значение результативного признака Б. Изменение результативного признака не зависит от изменения факторных признаков В. Одному значению результативного признака может соответствовать несколько значений факторного признака и наоборот 3. Что служит основанием установления формы связи между переменными при небольшой (до 30) объеме совокупности? А. Нормальный закон распределения Б. Эмпирическая линия регрессии В. Теоретическая линия регрессии Г. Корреляционное поле 4. В каких пределах изменяется корреляционное отношение? А. Может принимать любое значение Б. Может быть в пределах от 0 до 1 В. Может быть в пределах от –1 до +1 5. Если коэффициент корреляции равен 0.76, то какая часть колеблемости результативного признака вызвана изменением факторного признака? А. 76% Б. 42% В. 58% Г. 24% 6. Из следующих коэффициентов корреляции один указывает наивысшую степень зависимости и равен (+0.7; -0.8; +0.25). Назовите этот коэффициент и поясните ваш выбор 7. Напишите единственное значение коэффициента корреляции, указывающее на абсолютное отсутствие зависимости между величинами двух переменных 8. При неизменном уровне дохода возрастает уровень личной задолженности и уменьшается объем планируемых закупок на последующий период. Какой знак имеет коэффициент корреляции, представляющий эту зависимость? 9. Расходы семьи на образование возрастают по мере увеличения уровня дохода. Напишите знак коэффициента корреляции, выражающего степень зависимости между этими двумя переменными; 10. В каком случае для оценки связи между признаками можно использовать коэффициент корреляции? А. При любой форме связи Б. Только при корреляционной связи В. Только при криволинейной связи Вопросы к зачету и экзамену 1. Понятие о статистике, ее характерные особенности 2. Основные задачи и принципы организации государственной статистики в РФ 3. Предмет статистической науки. Этапы статистического исследования. Особенности статистической методологии. Метод статистики 4. Понятие о статистическом наблюдении. Этапы его проведения 5. Задачи группировок и их значение в статистическом исследовании 6. Ряды распределения, их виды, принципы построения и использования 7. Относительные величины в статистике. Виды относительных величин, способы их расчета и формы выражения. 8. Сущность и значение средних показателей 9. Средняя арифметическая простая и взвешенная 10. Свойства средней арифметической и упрощенный способ ее расчета 11. Средняя гармоническая. Выбор формы средней 12. Мода и медиана в статистике. Способы их вычисления 13. Задачи статистического изучения вариации. Основные показатели вариации 14. Виды дисперсии. Правило сложения дисперсий 15. Понятие о выборочном наблюдении. Генеральная и выборочная совокупности и их основные характеристики 16. Оценка результатов выборочного наблюдения и распространение их на генеральную совокупность 17. Определение необходимого объема выборки 18. Понятие и классификация рядов динамики 19. Сопоставимость уровней и смыкание рядов динамики 20. Средние показатели в рядах динамики и методы их расчета 21. Изучение сезонных колебаний 22. Понятие экономических индексов. Классификация индексов 23. Индивидуальные и общие индексы 24. Агрегатные индексы как основная форма общих индексов 25. Среднеарифметический и среднегармонический индексы 26. Индексный метод анализа изменения сложных явлений в целом и по факторам 27. Индексы переменного состава, постоянного состава и структурных сдвигов 28. Взаимосвязь индексов 29. Парная регрессия на основе метода наименьших квадратов 30. Виды и формы связей 31. Показатели тесноты связи. Корреляционное отношение. Коэффициент корреляции 32. Показатели эластичности 33. Основные показатели естественного движения населения и формулы их расчета 34. коэффициенты рождаемости и смертности: общие и специальные ЛИТЕРАТУРАВопросы статистики – ежемесячный журнал Федеральной Службы Государственной Статистики РФ Громыко Г.Л. Общая теория статистики: практикум. М.: ИНФРА-М, 1999 Гусаров В.М. Статистика: Учебное пособие для ВУЗов. М.: ЮНИТИ-ДАНА, 2002. Елисеева И.И., Юзбашев М.М. Общая теория статистики. М.: ФиС, 2004 Ефимова М.Р., Рябцев В.М. Общая теория статистики. М.: ФиС, 2003 Калашникова М.И., Салин В.Н. Современная организация статистики финансов: учебное пособие. – М.: Прометей, 1998. Попова А.А., Салин В.Н. Статистика денежного обращения: учебное пособие. – М.: Финансовая академия, 1999. Родионова Н.С., Салин В.Н. Статистика финансов предприятий: учебное пособие. – М.: Финансовая академия,1998. Рябушкин Б.Т. Основы статистики финансов: учебное пособие. – М.: Финстатинформ, 1997. Салин В.Н., Шпаковская Е.П. Социально-экономическая статистика. – М.: Юристъ, 2000. Симчера В.М. Введение в финансовые и актуарные вычисления. – М.: Финансы и статистика, 2003. Симчера В.М. Учебное пособие для ВУЗов. М.: 2002 Ситникова О.Ю., Салин В.Н. Техника финансово-экономических расчетов: учебное пособие. – М.: Финансы и статистика, 2002. Социально-экономическая статистика. Практикум/под ред. В.Н. Салина, Е.П. Шпаковской. М.: ФиС, 2003 Статистика финансов: Учебник. / под ред. В.Н. Салина – М.: Финансы и статистика, 2003. Статистическое обозрение – М.: Федеральная служба государственной статистики Четыркин Е.М. Финансовая математика. – М.: Дело ЛТД, 2000. Шмойлова Р.А. Теория статистики. М.: ФиС, 2005 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






 ; d=
; d=
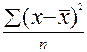 ;
; 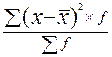

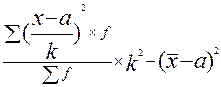
 ;
; 
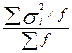
 ;
; 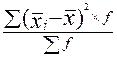

 ;
; 

 ;
; 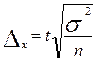
 ;
; 

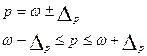
 ;
;  ;
; 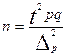
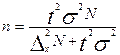 ;
; 
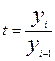 ;
; 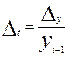 ;
; 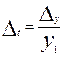 ;
; 
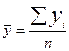 ;
; 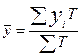 ;
; 
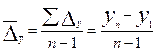
 ;
; 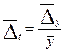 ;
;  ;
; 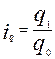 ;
;