МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра МО САПР
Использование факторного анализа для построения рейтинга банков.
Курсовая работа
студентов второй группы
третьего курса
факультета прикладной
математики и информатики
Бескоровайного А.А. и
Лейнова В. А.
Научный руководитель:
Ковалев М.М.
Минск, 1997.
Содержание
| Введение |
3 |
| Методология факторного анализа |
4 |
| Описание программы |
8 |
| Приложение |
9 |
| Формат файлов |
9 |
| Таблица исходных данных |
9 |
| Факторная матрица |
10 |
| Матрица факторного отображения |
11 |
| Графическое представление |
12 |
В факторном анализе предполагается, что наблюдаемые переменные являются линейной комбинацией некоторых латентных (гипотетических или ненаблюдаемых) факторов. Некоторые из этих факторов допускаются общими для двух и более переменных, а другие-- характерными для каждого параметра в отдельности.
Применительно к построению банковских рейтингов реальную картину состояния дает методика, основанная на применении двухфакторного анализа, которая позволяет представить банки точками на плоскости, координатными осями которой являются [построенные] факторы, что особенно удобно для составления динамических рейтингов, когда при анализе состояния системы во времени точки, указывающие на состояние банков, превращаются в диаграммы.
Методология факторного анализа.
Необходимо попытаться наиболее полно проанализировать разнообразные показатели, характеризующие в нашем случае состояние банков. Для этого необходимо свести их к меньшему числу некоторых факторов. Представим каждый рейтинговый показатель zj
как линейную комбинацию гипотетических факторов:
Zj
=aj1
F1
+aj2
F2
+...+ajm
Fm
(j=1,2...n),
где
Fi
– значение i-го фактора для данной (j-ой) компоненты;
aji
–
вес фактора i в компоненте j;
m – количество факторов;
n – количество показателей.
Можно выделить следующие этапы построения факторной матрицы:
1. Создаем исходную матрицу {{xij
}} размерности (n *
m), где m – количество характеристик, а n – количество исследуемых банков.
2. Строим корреляционную матрицу R={{rij
}},
имеющую размерность m *
m:
2.1 Строим ковариационную матрицу: C=XT
*
X/n :
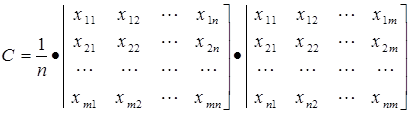
2.2 Строим корреляционную матрицу:
R={{rij
}}, 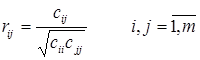
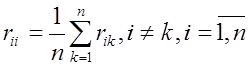
2.3 На основе построенной корреляционной матрицы строим редуцированную корреляционную матрицу:
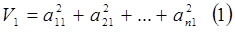
3. В методе главных факторов на 1-ом этапе вычислений ищут коэффициенты при первом факторе так, чтобы сумма вкладов в суммарную общность была максимальной
Максимум V1
должен быть обеспечен при условии
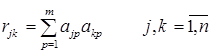
Чтобы максимизировать функцию n переменных воспользуемся методом множителей Лагранжа, с помощью которого приходим к выводу, что искомая функция является ничем иным как максимальным собственным значением уравнения
det(R-lE)=0 (2),
где R- редуцированная корреляционная матрица, полученная в пункте 2.
Далее, подставив найденное значение l1
и получив одно из возможных решений (q11
,q21, ... ,
 qn1)
уравнения (2), являющихся в свою очередь собственным вектором, соответствующим данному собственному значению и, для удовлетворения выражению (1), разделив на корень из суммы их квадратов и умножив на квадратный корень из собственного значения, получим
qn1)
уравнения (2), являющихся в свою очередь собственным вектором, соответствующим данному собственному значению и, для удовлетворения выражению (1), разделив на корень из суммы их квадратов и умножив на квадратный корень из собственного значения, получим
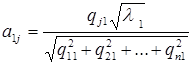
что представляет собой искомый коэффициент при факторе F1
в факторном отображении пункта 1.
l1
вычисляется по формуле:
l1
=max{p1j
}, где вектор p=R*
q1
Вектор q1
находится при помощи следующего итерационного процесса:
Вычисляем R, R2
, R4
,... до тех пор, пока не будет выполняться условие |b(
i)
-b(i/2)
|<e, где b(
i)
вектор, j-ый элемент которого равен частному от деления суммы j-ой строки матрицы Ri
на максимальную из сумм элементов строк матрицы Ri
, а в качестве e берется заранее выбранная точность вычислений. По окончании процесса в качестве вектора q берется вектор a(i)
.
4.Для определения коэффициентов при втором факторе F2
необходимо максимизировать функцию что делается аналогично вычислениям для 1-го фактора, только вместо матрицы R используется матрица

Полученную факторную матрицу F размерности m*
2 вращаем путем умножения на матрицу поворота
 , ,
где a-угол поворота, изменяющийся от 0 до p/2 с шагом p/720.
Окончательный поворот будет произведен на угол, при котором выполнится критерий Варимакс:Где r — число факторов.
Умножив справа исходную матрицу Х на построенную Fпов
, получим окончательную матрицу, показывающую расположение банков в новых координатах (факторах F1
, F2
).
Для компьютерной реализации описанного выше метода нами, с помощью среды Delphi 2.0, была создана программа rating, функционирующая под управлением операционной системы Windows-95.
1. После запуска программа предлагает пользователю загрузить исходные данные о состоянии банков за некоторые периоды времени. Исходные файлы хранятся в специальном формате (см. приложение 1).
2. Данные загружаются в таблицы (по годам), где и могут быть просмотрены (см. приложение 2)
В прилагаемом ниже примере исходными данными является файл по состоянию на 1995 код со следующими показателями, характеризующими банки :
a1=Активы
a2=Капитал
a3=Капитал/активы в %
a4=.Вложения в другие банки
a5=Вложения в экономику
a6=Вложения всего
3. По нажатию соответствующей кнопки на панели управления программой, будут построены и отображены матрицы факторного отображения (см приложение 4) ,за каждый из периодов времени. Данные матрицы образуются из факторных матриц, описывающих вклад каждого из показателей в общий фактор (см. приложение 3)
4. По желанию пользователя может быть построен график, показывающий положение банков на факторной плоскости и динамику их развития во времени (см. приложение 5).
1. Формат файлов
Файлы, используемые в нашей программе представляют собой текстовые файлы, в которых в качестве разделителей используются пробелы.
В первом столбце файла хранятся названия обрабатываемых банков, а в первой строке – названия показателей, характеризующих их деятельность.
2. Таблица исходных данных

3. Факторная матрица
| Показатель
|
F1 |
F2 |
| a1=Активы |
0.940 |
0.264 |
| a2=Капитал |
0.949 |
0.198 |
| a3=Капитал/активы в % |
0.829 |
0.436 |
| a4=Вложения в другие банки |
0.602 |
0.539 |
| a5=Вложенияв экономику |
0.834 |
0.425 |
| a6=Вложения всего |
0.922 |
0.335 |

4.Матрица факторного отображения
5. Графическое представление

Прямоугольной областью обозначается положение банка на факторной плоскости по состоянию на 1995 год, а круглой областью такого же цвета обозначается положение того же банка по состоянию на 1996 год.
|