ФИНАНСОВАЯ АКАДЕМИЯ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Кафедра математики
на тему:
Студент группы МЭК 1-1 - А.С. Кормаков
Научный руководитель - Солодовников А.С.
МОСКВА – 2001
Содержание
1. Двойственность в линейном программировании.................................... 3
2. Несимметричные двойственные задачи. Теорема двойственности... 4
3. Симметричные двойственные задачи........................................................ 9
4. Виды математических моделей двойственных задач........................... 11
5. Двойственный симплексный метод........................................................... 12
6. Список используемой литературы............................................................ 14
Понятие двойственности.
С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной.
Первоначальная задача называется исходной.
Связь исходной и двойственной задач состоит в том, что коэффициенты Cj
функции цели исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные члены B
i
системы ограничений исходной задачи служаткоэффициентами функции цели двойственной задачи, а матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи. Решение двойственной задачи может быть получено из решения исходной и наоборот.
В качестве примера рассмотрим задачу использования ресурсов. Предприятие имеет т
видов ресурсов в количестве bi
(i = 1, 2, ..., m
) единиц, из которых производится n
видов продукций. Для производства 1 ед. i
-й продукции расходуется aij
ед. t-гo ресурса, а ее стоимость составляет Cj
ед. Составить план выпуска продукции, обеспечивающий ее максимальный выпуск в стоимостном выражении. Обозначим через xj
(j
=1,2, ..., n)
количество ед. j
-й продукций, Тогда исходную задачу сформулируем так.
Найти вектор Х
=(x1
, x2
, …, xn
), который удовлетворяет ограничениям
 a11
x1
+ a12
x2
+ … + a1n
xn
£ b1, a11
x1
+ a12
x2
+ … + a1n
xn
£ b1,
a21
x1
+ a22
x2
+ … + a2n
xn
£ b2,
xj
³ 0 (j
=1,2, ..., n)
…………………………………
am1
x1
+ am2
x2
+ … + amn
xn
£ bm,
и доставляет максимальное значение линейной функции
Z = C1
x1
+ C2
x2
+ … + Cn
xn
,
Оценим ресурсы, необходимые для изготовления продукции. За единицу стоимости ресурсов примем единицу стоимости выпускаемой продукции. Обозначим через у
i
(j
=1,2, ..., m)
стоимость единицы i-
горесурса. Тогда стоимость всех затраченных ресурсов, идущих на изготовление единицы j
-й продукции, равна  . Стоимость затраченных ресурсов не может быть меньше стоимости окончательного продукта, поэтому должно выполняться неравенство . Стоимость затраченных ресурсов не может быть меньше стоимости окончательного продукта, поэтому должно выполняться неравенство  ³Cj
, j
=1,2, ..., n
. Стоимость всех имеющихся ресурсов выразится величиной ³Cj
, j
=1,2, ..., n
. Стоимость всех имеющихся ресурсов выразится величиной  . Итак, двойственную задачу
можно сформулировать следующим образом. . Итак, двойственную задачу
можно сформулировать следующим образом.
Найти вектор Y
=(y1
, y2
, …, yn
), который удовлетворяет ограничениям
 a11
y1
+ a12
y2
+ … + am1
ym
£ C1, a11
y1
+ a12
y2
+ … + am1
ym
£ C1,
a12
y1
+ a22
y2
+ … + am2
ym
£ C2,
yj
³ 0 (i
=1,2, ..., m)
…………………………………
a1n
y1
+ a2n
y2
+ … + amn
ym
£ Cm,
и доставляет минимальное значение линейной функции
f
= b1
y1
+ b2
y2
+ … + bm
ym
.
Рассмотренные исходная и двойственная задачи могут быть экономически интерпретированы следующим образом.
Исходная задача.
Сколько и. какой продукции xj
(j
=1,2, ..., n)
необходимо произвести, чтобы при заданных стоимостях Cj
(j
=1,2, ..., n)
единицы продукции и размерах имеющихся ресурсов bi
(i
=1,2, ..., n)
максимизировать выпуск продукции в стоимостном выражении.
Двойственная задача. Какова должна быть цена единицы каждого из ресурсов, чтобы при заданных количествах ресурсов b
i
и величинах стоимости единицы продукции C
i
минимизироватьобщую стоимость затрат?
Переменные у
i
называются оценками
или учетными, неявными
ценами.
Многие задачи линейного программирования первоначально ставятся в виде исходных или двойственных задач, поэтому имеет смысл говорить о паре двойственных задач линейного программирования.
В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной — в виде неравенств, причем в последней переменные могутбыть и отрицательными.Для простоты доказательств постановку задачи условимсязаписывать в матричной форме.
Исходная задача.
Найти матрицу-столбец X
= (x1
, x2
, …, xn
),
которая удовлетворяет ограничениям
(1.1) AX
= A0
, Х
³0
и минимизирует линейную функцию Z
= СХ
.
Двойственная задача.
Найти матрицу-строку Y
= (y1
, y2
, …, ym
),
которая удовлетворяет ограничениям
(1.2) YA
£
С
и максимизирует линейную функцию f
= YA0
В обеих задачах C
= (c1
, c2
, …, cn
) - матрица-строка, A0
= (b1
, b2
, …, bm
) — матрица-столбец, А
= (aij
) — матрица коэффициентов системы ограничений. Связь между оптимальными планами пары двойственных задач устанавливает следующая теорема.
Теорема (теорема двойственности).
Если из пары двойственных задач одна обладает оптимальным планом, то и другая имеет решение, причем для экстремальных значений линейных функций выполняется соотношение
min Z
= max f.
Если линейная функция одной из задач не ограничена, то другая не имеет решения.
Д о к а з а т е л ь с т в о. Предположим, что исходная задача обладает оптимальным планом, который получен симплексным методом. Не нарушая общности, можно считать, что окончательный базис состоит из т
первых векторов A
1
, A
2
, ..., A
m
. Тогда последняя симплексная таблица имеет вид табл. 1.1.
Т а б л и ц а 1.1
| i |
Базис |
С
базиса |
A0
|
C1
|
C2
|
… |
Cm
|
Cm+1
|
… |
cn
|
| A1
|
A2
|
… |
Am
|
Am+1
|
… |
An
|
1
2
.
.
.
m
|
A1
A2
.
.
.
Am
|
C1
C2
.
.
.
Cm
|
x1
x2
.
.
.
xm
|
1
0
.
.
.
0
|
0
1
.
.
.
0
|
...
...
.
.
.
.
|
0
0
.
.
.
1
|
x1, m+1
x2, m+1
.
.
.
xm, m+1
|
…
…
.
.
.
…
|
x1n
x2n
.
.
.
xmn
|
| m+1 |
Zi
- Cj
|
Z0
|
Z1
– C1
|
Z2
– C2
|
... |
Zm
– Cm
|
Zm+1
– Cm+1
|
… |
Zn
– Cn
|
Пусть D
— матрица, составленная из компонент векторов окончательного базиса A
1
, A
2
, ..., A
m
; тогда табл. 1.1 состоит из коэффициентов разложения векторов A
1
, A
2
, ..., A
n
исходной системы по векторам базиса, т. е. каждому вектору A
j
в этой таблице соответствует такой вектор X
j
что
(1.3) Aj
= DXj
(j= 1,2, ,.., n).
Для оптимального плана получаем
(1.4) A
0
=DX*
,
где X*
= (
x
*
1
, x
*
2
, …, x
*
m
)
.
Обозначим через 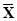 матрицу, составленную из коэффициентов разложения векторов А
j
(j = 1, 2, ..., n), записанных в табл. 1.1. Тогда, учитывая соотношения (1.3) и (1.4), получаем:
матрицу, составленную из коэффициентов разложения векторов А
j
(j = 1, 2, ..., n), записанных в табл. 1.1. Тогда, учитывая соотношения (1.3) и (1.4), получаем:
(1.5) A
=D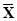 , D-1
A =
, D-1
A =
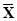 ,
,
(1.6) A
0
=DX*;
D
-1
A
0
=
X*
,
(1.7) min Z
= C*X*
,
(1.8)  =
C* =
C*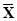 —C
£
0,
—C
£
0,
где С
* = (C*
1
, C*
2
, …, C*
m
),С
= (C1
, C2
, …, Cm
, Cm+1
, …, Cn
),
a  = (C*X
1
– C1
; С*Х
2
- С2
, ..., C*X
n
– Cn
) = (Z1
–С1
; Z2
- C2
; ..., Zn
— Cn
) — вектор, компоненты которого неположительны, так как они совпадают с Zj
— Cj
£ 0, соответствующими оптимальному плану. = (C*X
1
– C1
; С*Х
2
- С2
, ..., C*X
n
– Cn
) = (Z1
–С1
; Z2
- C2
; ..., Zn
— Cn
) — вектор, компоненты которого неположительны, так как они совпадают с Zj
— Cj
£ 0, соответствующими оптимальному плану.
Оптимальный план исходной задачи имеет вид X*
=D-1
А
0
, поэтому оптимальный план двойственной задачи ищем в виде
(1.9) Y*
=
C*D
-1
.
Покажем, что Y*
действительно план двойственной задачи. Для этого ограничения (1.2) запишем в виде неравенства YA
— С
£
0
, в левую часть которого подставим Y*
. Тогда на основании (1.9), (1.5) и (1.8) получим
Y
* А
–
С
=
С* D
-1
А
–
С
=
С* 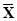 -
С
£
0,
-
С
£
0,
откуда находим Y*A
£
С.
Так как Y*
удовлетворяет ограничениям (1.2), то это и есть план двойственной задачи. При этом плане значение линейной функции двойственной задачи f
(Y
*) = Y*A
0
. Учитывая соотношения (1.9), (1.6) и (1.7), имеем
(1.10) f
(Y
*) = Y*A
0
= C*D-1
A0
=C*X*=minZ(X
).
Таким образом, значение линейной функции двойственной задачи от Y*
численно равно минимальному значению линейной функции исходной задачи.
Докажем теперь, что Y*
является оптимальным планом. Умножим (1.1) на любой план Y
двойственной задачи, а (1.2) — на любой план X
исходной задачи: YAX=YA
0
=
f
(
Y)
, YAX
£СХ
=
Z (X)
, отсюда следует, что для любых планов Х
и Y
выполняется неравенство
(1.11) f
(
Y)
£
Z
(X).
Этим же соотношением связаны и экстремальные значения max f
(
Y)
£min Z (Х)
.Из последнего неравенства заключаем, что максимальное значение линейной функции достигается только в случае, еслиmax f
(Y) = min Z (X), но это значение [см. (1.10)]f
(
Y)
достигает при плане Y*
, следовательно, план Y*
— оптимальный план двойственнойзадачи.
Аналогично можно доказать, что если двойственная задача имеет решение, то исходная также обладает решением и имеет место соотношение max f
(Y) = min Z (X).
Для доказательства второй части теоремы допустим, что линейная функция исходной задачи не ограничена снизу. Тогда из (1.11) следует, что f
(Y
) £ -¥ . Это выражение лишено смысла, следовательно, двойственная задача не имеет решений.
Аналогично предположим, что линейная функция двойственной задачи не ограничена сверху. Тогда из (1.11) получаем, что Z (X)
³ +¥. Это выражение также лишено смысла, поэтому исходная задача не имеет решений.
Доказанная теорема позволяет при решении одной из двойственных задач находить оптимальный план другой.
Исходная задача.
Найти минимальное значение линейной функции Z = x2
– x4
– 3x5
при ограничениях
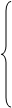 x1
+ 2x2
- x4
+ x5
= 1, x1
+ 2x2
- x4
+ x5
= 1,
- 4x2
+ x3
+ 2x4
– x5
= 2, xij
³ 0 (j
= 1, 2, …, 6)
3x2
+ x5
+ x6
= 5,
Здесь матрица-строка С = (0;. 1; 0; —1; — 3, 0), матрица-столбец
  1 1 2 0 -1 1 0 1 1 2 0 -1 1 0
A0
= 2 A
= 0 -4 1 2 -1 0
3 0 3 0 0 1 1
 1 0 0 1 0 0
2 -4 3
A
’’ = 0 1 0
-1 2 0
1 -1 0
0 0 1
Двойственная задача.
Найти максимальное значение линейной функции f
= y1
+ 2y2
+5y3
при ограничениях
 y1
£ 0, y1
£ 0,
2y1
– 4y2
+ 3y3
£ 1,
y2
£ 0,
-y1
+ 2y2
£ -1,
y1
– y2
+ y3
£ -3,
y3
£ 0.
Решение исходной задачи находим симплексным методом (табл. 1.2).
| i |
Базис |
С
базиса |
A0
|
0 |
1 |
0 |
-1 |
-3 |
0 |
| A1
|
A2
|
A3
|
A4
|
A5
|
A6
|
1
2
3
|
A1
A3
A6
|
0
0
0
|
1
2
5
|
1
0
0
|
2
-4
3
|
0
1
0
|
-1
2
0
|
1
-1
1
|
0
0
1
|
| m + 1 |
Zi
- Cj
|
0 |
0 |
-1 |
0 |
1 |
3 |
0 |
1
2
3
|
A5
A3
A6
|
-3
0
0
|
1
3
4
|
1
1
-1
|
2
-2
1
|
0
1
0
|
-1
1
1
|
1
0
0
|
0
0
1
|
| m + 1 |
Zi
- Cj
|
-3 |
-3 |
-7 |
0 |
4 |
0 |
0 |
1
2
3
|
A5
A4
A6
|
-3
-1
0
|
4
3
1
|
2
1
-2
|
0
-2
3
|
1
1
-1
|
0
1
0
|
1
0
0
|
0
0
1
|
| m + 1 |
Zi
- Cj
|
-15 |
-7 |
1 |
-4 |
0 |
0 |
0 |
1
2
3
|
A5
A4
A2
|
-3
-1
1
|
4
11/3
1/3
|
3
-1/3
-2/3
|
0
0
1
|
1
1/3
-1/3
|
0
1
0
|
1
0
0
|
0
2/3
1/3
|
| m + 1 |
Zi
- Cj
|
-46/3 |
-19/3 |
0 |
-11/3 |
0 |
0 |
-1/3 |
Оптимальный план исходной задачи X*
=(0; 1/3; 0; 11/3; 4; 0), при котором Zmin
= - 46/3, получен в четвертой итерации табл. 1.2. Используя эту итерацию, найдем оптимальный план двойственнойзадачи. Согласно теореме двойственности оптимальный план двойственной задачи находится из соотношения Y*
= C*D
-1
,
где матрица D
-1
- матрица, обратная матрице, составленной из компонент векторов, входящих в последний базис, при котором получен оптимальный план исходной задачи. В последний базис входят векторы A5
, A4
, A2
; значит,
 1 -1 2 1 -1 2
D
=
(
A5
, A4
, A2
)
= -1 2 -4
1 0 3
Обратная матрица D
-1
образована из коэффициентов, стоящих в столбцах A1
, A3
, A6
четвертой итерации:
 2 1 0 2 1 0
D-1
=
-1/3 1/3 2/3
-2/3 -1/3 1/3
 Из этой же итерации следует С*
= (— 3; —1; 1). Таким образом Из этой же итерации следует С*
= (— 3; —1; 1). Таким образом
2 1 0
Y =
С*
D-1
= (-3; -1; 1) · -1/3 1/3 2/3
-2/3 -1/3 1/3
Y*=(-19/3; -11/3; -1/3),
т. е. y
i
= С*Х
i
, где Х
i
— коэффициенты разложения последней итерации, стоящие в столбцах векторов первоначального единичного базиса.
Итак, i-ю двойственную переменную можно получить из значения оценки (m + 1)-й строки, стоящей против соответствующего вектора, входившего в первоначальный единичный базиc, если к ней прибавить соответствующее значение коэффициента линейной функции:
у
1
= —
19/3 + 0 = — 19/3; y2
= -11/3 + 0 = -11/3; у
3
= -1/3+0 = -1/3. При этом плане max f = -46/3.
Разновидностью двойственных задач линейного , программирования являются двойственные симметричные задачи, в которых система ограничений как исходной, так и двойственной задач задается неравенствами, причем на двойственные переменные налагается условие неотрицательности.
Исходная задача.
Найти матрицу-столбец Х
= (x1
, x2
, …, xn
), которая удовлетворяет системе ограничений
(1.12). АХ
>А0
, Х
>0
и минимизирует линейнуюфункцию Z
= СХ.
Двойственная задача.
Найти матрицу-строку Y
= (y1
, y2
, …, yn
), которая удовлетворяет системе ограничений YA
£C
, Y
³0 и максимизирует линейную функцию f
= YA
0
.
Систему неравенств с помощью дополнительных переменных можно преобразовать в систему уравнений, поэтому всякую пару симметричных двойственных задач можно преобразовать в пару несимметричных, для которых теорема двойственности уже доказана.
Используя симметричность, можно выбрать задачу, более удобную для решения. Объем задачи, решаемой с помощью ЭВМ, ограничен числом включаемых строк, поэтому задача, довольно громоздкая в исходной постановке, может быть упрощена в двойственной формулировке. При вычислениях без помощи машин использование двойственности упрощает вычисления.
Исходная задача.
Найти минимальное значение линейной функции Z =
x1
+ 2x2
+ 3x3
при ограничениях
 2x1
+ 2x2
- x3
³ 2, 2x1
+ 2x2
- x3
³ 2,
x1
- x2
- 4x3
£ -3, xi
³ 0 (i=1,2,3)
x1
+ x2
- 2x3
³ 6,
2x1
+ x2
- 2x3
³ 3,
Очевидно, для того чтобы записать двойственную задачу, сначала необходимо систему ограничений исходной задачи привести к виду (1.12). Для этого второе неравенство следует умножить на -1.
Двойственная задача.
Найти максимум линейной функции f
= 2y1
+ 3y2
+ 6y3
+ 3y4
при ограничениях
 2y1
- y2
+ y3
+ 2y4
£ 1, 2y1
- y2
+ y3
+ 2y4
£ 1,
2y1
+ y2
+ y3
+ y4
³ 2,
-y1
+ 4y2
- 2y3
- 2y4
³ 3,
Для решения исходной задачи необходимо ввести четыре дополнительные переменные и после преобразования системы - одну искусственную. Таким образом, исходная симплексная таблица будет состоять из шести строк и девяти столбцов, элементы которых подлежат преобразованию.
Для решения двойственной задачи необходимо ввести три дополнительные переменные. Система ограничений не требует предварительных преобразований, ее первая симплексная таблица содержит четыре строки и восемь столбцов.
Двойственную задачу решаем симплексным методом (табл. 1.3).
Оптимальный план двойственной задачи Y*
= (0; 1/2; 3/2; 0), f
max
=21/2.
Оптимальный план исходной задачи находим, используя оценки (
m + 1)-й строки последней итерации, стоящие в столбцах A5
, A6
, A7
: x1
= 3/2 + 0 = 3/2; x2
= 9/2 + 0 = 9/2; x3
= 0+ 0 = 0. При оптимальном плане исходной задачи X*
= (3/2; 9/2; 0) линейная функция достигает наименьшего значения: Zmin
=21/2.
Т а б л и ц а 1.3
| i |
Базис |
С
базиса |
A0
|
2 |
3 |
6 |
3 |
0 |
0 |
0 |
| A1
|
A2
|
A3
|
A4
|
A5
|
A6
|
A7
|
1
2
3
|
A5
A3
A7
|
0
0
0
|
1
2
3
|
2
2
-1
|
-1
1
4
|
1
1
-2
|
2
-1
-2
|
1
0
0
|
0
1
0
|
0
0
1
|
| m + 1 |
Zi
- Cj
|
0 |
-2 |
-3 |
-6 |
-3 |
0 |
0 |
0 |
1
2
3
|
A3
A6
A7
|
6
0
0
|
1
1
5
|
2
0
3
|
-1
2
6
|
1
0
0
|
2
-1
2
|
1
-1
2
|
0
1
0
|
0
0
1
|
| m + 1 |
Zi - Cj |
6 |
10 |
-9 |
0 |
9 |
6 |
0 |
0 |
1
2
3
|
A3
A2
A7
|
6
3
0
|
3/2
½
2
|
2
0
3
|
0
1
0
|
1
0
0
|
3/2
-1/2
4
|
½
-1/2
5
|
½
½
3
|
0
0
1
|
| m + 1 |
Zi
- Cj
|
21/2 |
10 |
0 |
0 |
9/2 |
3/2 |
9/2 |
0 |
На основании рассмотренных несимметричных и симметричных двойственных задач можно заключить, что математические модели пары двойственных задач могут иметь один из следующих видов.
Несимметричные задачи
(1) Исходная задача Двойственная задача
Zmin
= CX;
f
max
= YA0
;
AX
= A0
;
YA
£
С
.
X
³ 0.
(2) Исходная задача Двойственная задача
Zmax
= CX;
f
min
= YA0
;
AX
= A0
;
YA
³
С
.
X
³ 0.
Симметричные задачи
(3) Исходная задача Двойственная задача
Zmin
= CX;
f
max
= YA0
;
AX
³A0
;
YA
£
С
.
X
³ 0. Y
³
0.
(4) Исходная задача Двойственная задача
Zmax
= CX;
f
min
= YA0
;
AX
£A0
;
YA
³
С
.
X
³ 0. Y
³
0.
Таким образом, прежде чем записать двойственную задачу для данной исходной, систему ограничений исходной задачи необходимо привести к соответствующему виду. Запишем, например, математическую модель двойственной задачи для следующей исходной.
Найти минимальное значение линейной функции Z = 2x1
+ x2
+ 5x3
при ограничениях
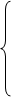 x1
– x2
– x3
£ 4, x1
– x2
– x3
£ 4,
x1
– 5x2
+ x3
³ 5, xj
³ 0 (j = 1, 2, 3).
2x1
– x2
+ 3x3
³6,
Рассматриваемая задача относится к симметричным двойственным задачам на отыскание минимального значения линейной функции. Для того чтобы было можно записать двойственную задачу, ее модель должна иметь вид (3). Переход осуществляется умножением первого неравенства на -1.
Исходная задача:
Zmin
= 2x1
+ x2
+ 5x3
при ограничениях
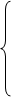 -x1
+ x2
+ x3
³ -4, -x1
+ x2
+ x3
³ -4,
x1
– 5x2
+ x3
³ 5, xj
³ 0 (j = 1, 2, 3).
2x1
– x2
+ 3x3
³6,
Двойственная задача:
f
min
= -4x1
+ 5x2
+ 6x3
при ограничениях
 -y1
+ y2
+ 2y3
£ 2, -y1
+ y2
+ 2y3
£ 2,
y1
– 5y2
- y3
£ 1, yi
³ 0 (i = 1, 2, 3).
2y1
+ y2
+ 3y3
£ 5,
Приведем без доказательства следующую теорему. Теорема 1.1.
Если при подстановке компонент оптимального плана в систему ограничений исходной задачи i-e ограничение обращается в неравенство, то i-я компонента оптимального плана двойственной задачи равна нулю.
Если i-я компонента оптимального плана двойственной задачи положительна, то
i-e ограничение исходной задачи удовлетворяется ее оптимальным решением как строгое равенство.
В п. 2 и п. 3 настоящего параграфа было показано, что для получения решения исходной задачи можно перейти к двойственной и используя оценки ее оптимального плана, определить оптимальное решение исходной задачи.
Переход к двойственной задаче не обязателен, так как если рассмотреть первую симплексную таблицу с единичным дополнительным базисом, то легко заметить, что в столбцах записана исходная задача, а в строках - двойственная. Причем оценками плана исходной задачи являются С
j
а оценками плана двойственной задачи – bi
. Решим "двойственную задачу по симплексной таблице, в которой записана исходная задача; найдем оптимальный план двойственной задачи, а вместе с ним и оптимальный план исходной задачи. Этот метод носит название двойственного симплексного метода,
Пусть необходимо решить исходную задачу линейного программирования, поставленную в общем виде: минимизировать функцию Z =СХ
при АХ
= A0
, Х
³ 0. Тогда в двойственной задаче необходимо максимизировать функцию f
= YA
0
при YA
£
С.
Допустим, что выбран такой базис D
= (A
1
, А
2
, ..., А
i
, ..., А
m
), при котором хотя бы одна из компонент вектора Х
= D
-1
A0
= (x1
, x2
, ..., xi
, ..., xm
) отрицательная (например, xi
< 0), но для всех векторов Aj
выполняется соотношение Zj
– Cj
£ 0 (i = 1,2, ..., n). Тогда на основании теоремы двойственности Y
= С
баз
D-1
- план двойственной задачи. Этот план не оптимальный, так как, с одной стороны, при выбранном базисе X
содержит отрицательную компоненту и не является планом исходной задачи, а с другой стороны, оценки оптимального плана двойственной задачи должны быть неотрицательными.
Таким образом, вектор Аi
, соответствующий компоненте xi
< 0, следует исключить из базиса исходной задачи, а вектор, соответствующий отрицательной оценке,— включить в базис двойственной задачи.
Для выбора вектора, включаемого в базис исходной задачи, просматриваем i
-ю
строку: если в ней не содержатся x
ij
< 0, то линейная функция двойственной задачи не ограничена на многограннике решений, а исходная задача не имеет решений. Если же некоторые x
ij
< 0, то для столбцов, содержащих эти отрицательные значения, вычисляем q0j
= min (xi
/xij
) ³ 0 и определяем вектор, соответствующий maxq0j
(Zj
— Cj
) при решении исходной задачи на минимум и minq0j
(Zj
— Cj
)при решении исходной задачи на максимум. Этот вектор и включаем в базис исходной задачи. Вектор, который необходимо исключить из базиса исходной задачи, определяется направляющей строкой.
Если q0j
= min (xi
/xij
) = 0, т. е. xi
= 0, то x
ij
берется за разрешающий элемент только в том случае, если x
ij
> 0. Такой выбор разрешающего элемента на данном этапе не приводит к увеличению количества отрицательных компонент вектора X
. Процесс продолжаем до получения Х
³ 0; при этом находим оптимальный план двойственной задачи, следовательно, и оптимальный план исходной задачи.
В процессе вычислений по алгоритму двойственного симплексного метода условие Zj
– Cj
£ 0 можно не учитывать до исключения всех х
i
<
0, затем оптимальный план находится обычным симплексным методом. Это удобно использовать, если все х
i
<
0;
тогда для перехода к плану исходной, задачи за одну итерацию необходимо q0j
определить не по минимуму, а по максимуму отношений, т. е. q0j
= max (xi
/xij
) > 0.
Двойственным симплексным методом можно решать задачи линейного программирования, системы ограничений которых при положительном базисе содержат свободные члены любого знака. Этот метод позволяет уменьшить количество преобразований системы ограничений, а также размеры симплексной таблицы.
6. Список используемой литературы
1. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. «Финансы и статистика», 1998 г.
2. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. «Наука», 1980 г.
|