АННОТАЦИЯ
Пояснительная записка курсовой работы «Решение задачи о загрузке (задача о рюкзаке), использую рекуррентные соотношения» содержит общие сведения о задачах динамического программирования, о методах их решения.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ……………………………………………………………………
1 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ………………………….
1.1 Задача динамического программирования………………………..
1.2 Примеры задач динамического программирования……………...
1.3 Общая структура динамического программирования…………...
2 ЗАДАЧА О ЗАГРУЗКЕ……………………………………………………
2.1 Общие сведения…………………………………………………………
2.2 Рекуррентные соотношения для процедур прямой и обратной прогонки………………………………………………………………………
2.3 Решение задачи о загрузке…………………………………………….
2.4 Анализ чувствительности решения…………………………………..
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………….
ПРИЛОЖЕНИЕ А……………………………………………………………
ПРИЛОЖЕНИЕ Б……………………………………………………………
ПРИЛОЖЕНИЕ В…………………………………………………………….
|
6
8
8
12
16
18
18
19
22
25
27
28
36
40
|
ВВЕДЕНИЕ
Работа над данным курсовым проектом позволяет закрепить знания по предмету «Математические методы исследования операций».
В наше время наука уделяет все большое внимание вопросам организации и управления, это приводит к необходимости анализа сложных целенаправленных процессов под углом зрения их структуры и организации. Потребности практики вызвали к жизни специальные методы, которые удобно объединять под названием «исследование операций». Под этим термином понимается применение математических, количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.
Целью исследования операций является выявление наилучшего способа действия при решение той или иной задачи. Главная роль при этом отводится математическому моделированию. Для построения математической модели необходимо иметь строгое представление о цели функционирования исследуемой системы и располагать информацией об ограничениях, которые определяют область допустимых значений. Цель и ограничения должны быть представлены в виде функций.
В моделях исследования операций переменные, от которых зависят ограничения и целевая функция, могут быть дискретными (чаще всего целочисленными) и континуальными (непрерывными). В свою очередь, ограничения и целевая функция делятся на линейные и нелинейные. Существуют различные методы решения данных моделей, наиболее известными и эффективными из них являются методы линейного программирования, когда целевая функция и все ограничения линейные. Для решения математических моделей других типов предназначены методы динамического программирования, целочисленного программирования, нелинейного программирования, многокритериальной оптимизации и методы сетевых моделей.
Практически все методы исследования операций порождают вычислительные алгоритмы, которые являются итерационными по своей природе. Это подразумевает, что задача решается последовательно (итерационно), когда на каждом шаге (итерации) получаем решение, постепенно сходящиеся к оптимальному решению.
Итерационная природа алгоритмов обычно приводит к объемным однотипным вычислениям. В этом и заключается причина того, что эти алгоритмы разрабатываются, в основном, для реализации с помощью вычислительной техники.
1 ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
1.1 Задача динамического программирования
Большинство методов исследования операций связано в первую очередь с задачами вполне определенного содержания. Классический аппарат математики оказался малопригодным для решения многих задач оптимизации, включающих большое число переменных и/или ограничений в виде неравенств. Несомненна привлекательность идеи разбиения задачи большой размерности на подзадачи меньшей размерности, включающие всего по нескольких переменных, и последующего решения общей задачи по частям. Именно на этой идее основан метод динамического программирования.
Динамическое программирование (ДП) представляет собой математический метод, заслуга создания и развития которого принадлежит прежде всего Беллману. Метод можно использовать для решения весьма широкого круга задач, включая задачи распределения ресурсов, замены и управления запасами, задачи о загрузке. Характерным для динамического программирования является подход к решению задачи по этапам, с каждым из которых ассоциирована одна управляемая переменная. Набор рекуррентных вычислительных процедур,связывающих различные этапы, обеспечивает получение допустимого оптимального решения задачи вцеломпри достижении последнего этапа.
Происхождение названия динамическое программирование,
вероятно, связано с использованием методов ДП в задачах принятия решений через фиксированные промежутки времени (например, в задачах управления запасами). Однако методы ДП успешно применяются также для решения задач, в которых фактор времени не учитывается. По этой причине более удачным представляется термин многоэтапное программирование,отражающий пошаговый характер процесса решения задачи.
Фундаментальным принципом, положенным в основу теории ДП, является принцип оптимальности.По существу, он определяет порядок поэтапного решения допускающей декомпозицию задачи (это более приемлемый путь, чем непосредственное решение задачи в исходной постановке) с помощью рекуррентных вычислительных процедур.
Динамическое программирование позволяет осуществлять оптимальное планирование управляемых процессов. Под «управляемыми» понимаются процессы, на ход которых мы можем в той или другой степени влиять.
Пусть предполагается к осуществлению некоторое мероприятие или серия мероприятий («операция»), преследующая определенную цель. Спрашивается: как нужно организовать (спланировать) операцию для того, чтобы она была наиболее эффективной? Для того, чтобы поставленная задача приобрела количественный, математический характер, необходимо ввести в рассмотрение некоторый численный критерий W, которым мы будем характеризовать качество, успешность, эффективность операции. Критерий эффективности в каждом конкретном случаи выбирается исходя из целевой направленности операции и задачи исследования (какой элемент управления оптимизируется и для чего).
Сформулируем общий принцип, лежащий в основе решения всех задач динамического программирования («принцип оптимальности»):
«Каково бы ни было состояние системы S перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным».
Динамическое программирование – это поэтапное планирование многошагового процесса, при котором на каждом этапе оптимизируется только один шаг. Управление на каждом шаге должно выбираться с учетом всех его последствий в будущем.
При постановке задач динамического программирования следует руководствоваться следующими принципами:
1. Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.
2. Расчленить операцию на этапы (шаги).
3. Выяснить набор шаговых управлений xi
для каждого шага и налагаемые на них ограничения.
4. Определить какой выигрыш приносит на i-ом шаге управление xi
, если перед этим система была в состоянии S, т.е. записать «функцию выигрыша»:
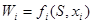 . .
5. Определить, как изменяется состояние S системы S под влиянием управление xi
на i-ом шаге: оно переходит в новое состояние
 . (1.1) . (1.1)
6. Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш Wi
(S) (начиная с i-го шага и до конца) через уже известную функцию Wi
+1
(S):
 . (1.2) . (1.2)
Этому выигрышу соответствует условное оптимальное управление на i-м шаге xi
(S) (причем в уже известную функцию Wi
+1
(S) надо вместо S подставить измененное состояние  ) )
7. Произвести условную оптимизацию последнего (m-го) шага, задаваясь гаммой состоянийS, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого из них условный оптимальный выигрыш по формуле 
8. Произвести условную оптимизацию (m-1)-го, (m-2)-го и т.д. шагов по формуле (1.2), полагая в ней i=(m-1),(m-2),…, и для каждого из шагов указать условное оптимальное управление xi
(S), при котором максимум достигается.
Заметим, что если состояние системы в начальный момент известно (а это обычно бывает так), то на первом шаге варьировать состояние системы не нужно - прямо находим оптимальный выигрыш для данного начального состояния S0
. Это и есть оптимальный выигрыш за всю операцию

9. Произвести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге. Взять найденное оптимальное управление на первом шаге  ; изменить состояние системы по формуле (1.1); для вновь найденного состояния найти оптимальное управление на втором шаге х2
*
и т.д. до конца. ; изменить состояние системы по формуле (1.1); для вновь найденного состояния найти оптимальное управление на втором шаге х2
*
и т.д. до конца.
Данные этапы рассматривались для аддитивных задач, в которых выигрыш за всю операцию равен сумме выигрышей на отдельных шагах. Метод динамического программирования применим также и к задачам с так называемым «мультипликативным» критерием, имеющим вид произведения:

(если только выигрыши wi
положительны). Эти задачи решаются точно так же, как задачи с аддитивным критерием, с той единственной разницей, что в основном уравнении (1.2) вместо знака «плюс» ставится знак «умножения»: 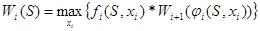
1.2 Примеры задач динамического программирования
Задача планирования рабочей силы
:
При выполнении некоторых проектов число рабочих, необходимых для выполнения какого-либо проекта, регулируется путем их найма и увольнения. Поскольку как наем, так и увольнение рабочих связано с дополнительными затратами, необходимо определить, каким образом должна регулироваться численность рабочих в период реализации проекта.
Предположим, что проект будет выполнятся в течение n недель и минимальная потребность в рабочей силе на протяжении i-й недели составит bi
рабочих. При идеальных условиях хотелось бы на протяжении i-й недели иметь в точности bi
рабочих. Однако в зависимости от стоимостных показателей может быть более выгодным отклонение численности рабочей силы как в одну, так и в другую сторону от минимальных потребностей.
Если xi
– количество работающих на протяжении i-й недели, то возможны затраты двух видов: 1) С1
(xi
- bi
)-затраты, связанные с необходимостью содержать избыток xi
- bi
рабочей силы и 2) С2
(xi
- xi
-1
)-затраты, связанные с необходимостью дополнительного найма (xi
- xi
-1
) рабочих.
Элементы модели динамического программирования определяются следующим образом:
1. Этап і представляется порядковым номером недели і, і=1,2,…n.
2. Вариантами решения на і-ом этапе являются значения xi
– количество работающих на протяжении і-й недели.
3. Состоянием на і-м этапе является xi
-1
– количество работающих на протяжении (і-1) –й недели (этапа).
Рекуррентное уравнение динамического программирования представляется в виде

где 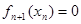
Вычисления начинаются с этапа n при xn
=bn
и заканчиваются на этапе 1.
Задача замены оборудования
:
Чем дольше механизм эксплуатируется, тем выше затраты на его обслуживание и ниже его производительность. Когда срок эксплуатации механизма достигает определенного уровня, может оказаться более выгодной его замена. Задача замены оборудования, таким образом, сводится к определению оптимального срока эксплуатации механизма.
Предположим, что мы занимаемся заменой механизмов на протяжении n лет. В начале каждого года принимается решение либо об эксплуатации механизма еще один год, либо о замене его новым.
Обозначим через r(t) и c(t) прибыль от эксплуатации t-летнего механизма на протяжении года и затраты на его обслуживание за этот же период. Далее пусть s(t) – стоимость продажи механизма, который эксплуатировался t лет. Стоимость приобретения нового механизма остается неизменной на протяжении всех лет и равна l.
Элементы модели динамического программирования таковы:
1. Этап і представляется порядковым номером года і, і=1,2,...n.
2. Вариантами решения на і-м этапе (т.е. для і-ого года) являются альтернативы: продолжить эксплуатацию или заменить механизм в начале і-ого года.
3. Состоянием на і-м этапе является срок эксплуатации t (возраст) механизма к началу і-ого года.
Пусть fi
(t)-максимальная прибыль, получаемая за годы от і до n при условии, что в начале і-ого года имеется механизм t-летнего возраста.
Рекуррентное уравнение имеет следующий вид:

(1)-если эксплуатировать механизм,
(2)-если заменить механизм.
Задача инвестирования
:
Предположим, что в начале каждого из следующих n лет необходимо сделать инвестиции P1
, P2
,…, Pn
соответственно. Вы имеете возможность вложить капитал в два банка: первый банк выплачивает годовой сложный процент r1
, а второй - r2
. Для поощрения депозитов оба банка выплачивают новым инвесторам премии в виде процента от вложенной суммы.
Премиальные меняются от года к году, и для і-ого года равны qi
1
и qi
2
в первом и втором банках соответственно. Они выплачиваются к концу года, на протяжении которого сделан вклад, и могут быть инвестированы в один из двух банков на следующий год. Это значит, что лишь указанные проценты и новые деньги могут быть инвестированы в один из двух банков. Размещенный в банке вклад должен находится там до конца рассматриваемого периода. Необходимо разработать стратегию инвестиции на следующие n лет.
Элементы модели динамического программирования следующие:
1. Этап і представляется порядковым номером года і, і=1,2,...n
2. Вариантами решения на і-м этапе (для і-ого года) являются суммы li
и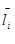 инвестиций в первый и второй банк соответственно. инвестиций в первый и второй банк соответственно.
3. Состоянием xi
на і-м этапе является сумма денег на начало і-ого года, которые могут быть инветсированы.
Заметим, что по определению 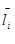 =xi
-li
. Следовательно, =xi
-li
. Следовательно,

где і=2,3,…n, x1
=P1
. Сумма денег xi
, которые могут быть инвестированы, включает лишь новые деньги и премиальные проценты за инвестиции, сделанные на протяжении (і-1)-го года.
Пусть fi
(xi
)- оптимальная сумма инвестиций для интервала от і-го до n-го года при условии, что в начале і-го года имеется денежная сумма xi
. Далее обозначим через si
накопленную сумму к концу n-го года при условии, что li
и (xi
-li
)-объемы инвестиций на протяжении і-го года в первый и второй банк соответственно. Обозначая  , і=1,2, мы можем сформулировать задачу в следующем виде. , і=1,2, мы можем сформулировать задачу в следующем виде.
Максимизировать z=s1
+s2
+…+sn
, где

Так как премиальные за n-й год являются частью накопленной денежной суммы от инвестиций, в выражения для sn
добавлены qn
1
и qn
2
.
Итак, в данном случае рекуррентное уравнение для обратной прогонки в алгоритме динамического программирования имеет вид

где xi
+1
выражается через xi
в соответствии с приведенной выше формулой, а fn
+1
(xn
+1
)=0.
1.3 Общая структура динамического программирования
Отыскание оптимальной стратегии принятия набора последовательных решений, в большинстве случаях, производится следующим образом: сначала осуществляется выбор последнего во времени решения, затем при движении в направлении, обратном течению времени, выбираются все остальные решения вплоть до исходного.
Для реализации такого метода необходимо выяснить все ситуации, в которых может происходить выбор последнего решения. Обычно условия, в которых принимается решение, называют «состоянием» системы. Состояние системы – это описание системы, позволяющее, учитывая будущие решения, предсказать ее поведение. Нет необходимости выяснять, как возникло то ил иное состояние или каковы были предшествующие решения. Это позволяет последовательно выбирать всего по одному решению в каждый момент времени. Независимо от того, отыскивают оптимальные решения с помощью табличного метода и последующего поиска или аналитическим путем, обычно быстрее и выгоднее производить выбор по одному решению в один момент времени, переходя затем к следующему моменту и т.д. К сожалению, таким методом можно исследовать не все процессы принятия решений. Необходимым условием применения метода динамического программирования является аддитивность цен всех решений, а также независимость будущих результатов от предыстории того или иного состояния.
Если число решений очень велико, то можно построить относительные оценки состояний так, чтобы оценки, отвечающие каждой паре последовательных решений, отличались друг от друга на постоянную величину, представляющую собой средний «доход» на решение. Также можно выполнять дисконтирование доходов от будущих решений. Необходимость в этом иногда появляется в том случае, когда решение принимаются редко, скажем раз в году. Тогда уже не нужно рассматривать последовательно 1,2,3…решения, чтобы достичь решения с большим номером. Вместо этого можно непосредственно оперировать функциональным уравнением, что, как правило, дает существенную выгоду с точки зрения сокращения объема вычислений.
2 ЗАДАЧА О ЗАГРУЗКЕ
2.1 Общие сведения
Задача о загрузке – это задача о рациональной загрузке судна (самолета, автомашины и т.п.), которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в определении загрузки судна такими грузами, которые приносят наибольшую суммарную прибыль.
Рекуррентное уравнение процедуры обратной прогонки выводится для общей задачи загрузки судна грузоподъемностью W предметов (грузов) n наименований. Пусть mi
-количество предметов і-го наименования, подлежащих загрузке, ri
-прибыль, которую приносит один загруженный предмет і-го наименования, wi
-вес одного предмета і-го наименования. Общая задача имеет вид следующей целочисленной задачи линейного программирования.
Максимизировать z=r1
m1
+r2
m2
+…+rn
mn
.
при условии, что
w1
m1
+w2
m2
+…+wn
mn
 W, W,
m1
,m2
,…,mn
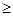 0 и целые. 0 и целые.
Три элемента модели динамического программирования определяются следующим образом:
1. Этап і ставится в соответствии предмету і-го наименования, і=1,2,…n.
2. Варианты решения на этапе і описываются количеством mi
предметов і-го наименования, подлежащих загрузке. Соответствующая прибыль равна ri
mi
. Значение mi
заключено в пределах от 0 до [W/wi
], где [W/wi
] – целая часть числа W/wi
.
3. Состояние xi
на этапе і выражает суммарный вес предметов, решения о погрузке которых приняты на этапах і,і+1,...n. Это определение отражает тот факт, что ограничения по весу является единственным, которое связывает n этапов вместе.
Пусть fi
(xi
)-максимальная суммарная прибыль от этапов і,і+1,...,n при заданном состоянии xi
. Проще всего рекуррентное уравнение определяется с помощью следующей двухшаговой процедуры.
Шаг 1. Выразим fi
(xi
) как функцию fi
+1
(xi
+1
) в виде

где fn
+1
(xn
+1
)=0.
Шаг 2. Выразим xi
+1
как функцию xi
для гарантии того, что левая часть последнего уравнения является функцией лишь xi
. По определению xi
-xi
+1
представляет собой вес, загруженный на этапе і, т.е. xi
-xi
+1
=wi
mi
или xi
+1
=xi
-wi
mi
. Следовательно, рекуррентное уравнение приобретает следующий вид:

2.2 Рекуррентные соотношения для процедур прямой и обратной прогонки
Фермеру принадлежит стадо овец, насчитывающее k
голов. Один раз в год фермер принимает решение о том, сколько овец продать и сколько оставить. Прибыль от продажи одной овцы в і-м году составляетpi
. Количество оставленных в i-м году овец удваивается в (1+1)-м году. По истечении п
лет фермер намеревается продать все стадо.
Этот чрезвычайно простой пример приводится для того, чтобы наглядно продемонстрировать преимущества алгоритма обратной прогонки по сравнению с алгоритмом прямой прогонки. Вычислительные схемы процедур прямой и обратной прогонки обладают различной эффективностью в случаях, когда этапы модели нумеруются в некотором специальном порядке. Такая ситуация имеет место в приводимом примере, где этап jставится в соответствие году j, т. е. этапы должны рассматриваться в хронологическом порядке.
Сначала построим рекуррентные соотношения для процедур прямой и обратной прогонки, а затем проведем сравнение двух вычислительных схем. Важное различие между двумя формулировками непосредственно следует из определения состояния.
Обозначим количества оставленных и проданных в j
-м
году овец через xj
и yj
,соответственно. Положим Zj
,=
xj
+
yj
.
Из условий задачи следует, что
z1
=2x0
=2k,
zj
=2xj
-1
,j=l,2, ...,n.
Состояние на этапе j можно описать с помощью переменной zj
, которая выражает количество имеющихся к концу этапа j овец для распределения на этапах j+1, j+2, ..., n, или с помощью переменной xj
, которая выражает количество имеющихся к началу этапа j+1 овец, обусловленное принятыми на этапах 1,2,...,j решениями. Первое определение ориентировано на построение рекуррентного соотношения
для процедуры обратной прогонки, тогда как второе определение приводит к использованию алгоритма прямой прогонки.
Алгоритм обратной прогонки
Обозначим через fi
(zi
) максимальную прибыль, получаемую на этапах j,j+1,…,n, при заданном zj
. Рекуррентное соотношение имеет следующий вид:
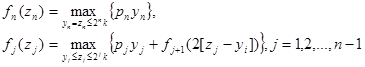
Заметим, что yj
и zj
- неотрицательные целые числа. Кроме того, уj
(количество овец, проданных в конце периода j) должно быть меньше или равно zj
. Верхней границей для значений zj
, является величина 2j
k (где k- исходный размер стада), которая соответствует отсутствию продажи.
Алгоритм прямой прогонки
Обозначим через gj
(xj
) максимальную прибыль, получаемую на этапах 1,2,...,j при заданном xj
, (где xj
— размер стада к началу этапа J+1). Рекуррентное соотношение записывается в следующем виде:

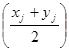 - целое. - целое.
Сравнение двух формулировок показывает, что представление xj
-1
через xj
создает более существенные препятствия для вычислений, чем представление zj
+1
через zj
.
В замене xj
-1
=(xj
+yj
)/2 подразумевается целочисленность правой части, тогда как на равенство zj
+1
=2(zj
-yj
) такое требование не накладывается. Таким образом в случае процедуры прямой прогонки значения yj
и xj
, связанные неравенством
Yj
<=2j
k -Xj
,
должны дополнительно удовлетворять условию целочисленности их полусуммы, связанному с видом зависимости хj
-1
от xj
,. Рассмотренный пример иллюстрирует трудности вычислительного характера, которые обычно возникают при использовании алгоритма прямой прогонки.
2.3 Решение задачи о загрузке
Контрольная работа содержит вопросы по N различным темам. Каждый вопрос типа i имеет вес Vi(i=1,2,…N), а также время, отводимое на ответ Wi. Максимально время, которое может затратить студент на контрольную работу W. Требуется определить максимальное количество баллов (вес), которое может набрать студент за отведенное время W=30. Данные приведены в таблице:
| I |
Wi |
Vi |
1 5 5
2 6 6
3 4 4
4 3 3
5
6 6 6
7 5 5
8 7 7
|
2
3
1
4
7
5
3
2
|
2
3
2
4
6
5
4
2
|
Решить задачу, приведя ее к рекуррентным соотношениям.
Сначала рассмотрим задачу в общей постановке. Если обозначить количество вопросов типа і через ki
, то задача принимает следующий вид:
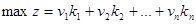
при ограничениях

ki
-неотрицательные числа.
Если отбросить требования целочисленности ki
, то решение задачи нетрудно найти с помощью симплекс-метода (см. Приложение В). В самом деле, так как остается лишь одно ограничение, базисной будет только одна переменная, и задача сводится к выбору типа і, для которого величина vi
W/wi
принимает максимальное значение. Исходная задача не является задачей линейного программирования, и для ее решения необходимо использовать метод динамического программирования. Следует отметить, что рассматриваемая задача может быть также решена с помощью методов целочисленного программирования.
Каждый из трех основных элементов модели ДП определяется следующим образом.
1. Этап j ставится в соответствии типу j, j=1,2,…,N.
2. Состояние yj
на этапе j выражает суммарный вес вопросов, количество ответов на которые приняты на этапах j,j+1,…,N; при этом y1
=W и yj
=0,1,…,W при j=2,3,…,N.
3. Варианты решения kj
на этапе j описываются количеством вопросов типа j. Значение kj
заключено в пределах от нуля до [W/wj
], где [W/wj
]-целая часть числа (W/wj
).
Пусть fi
(yi
)-максимальный суммарный вес вопросов, ответы на которые приняты на этапах j,j+1,…,N при заданном состоянии yj
.
Рекуррентное соотношение (для процедуры обратной прогонки) имеет следующий вид:


Заметим, что максимальное допустимое значение kj
ограничено величиной [yj
/wj
]. Это позволяет автоматически исключать все не являющиеся допустимыми варианты при заданном значении переменной состояния yj
.
Решение исходной задачи (см. приложении А):
Этап 8.

Этап 7.

Этап 6.

Этап 5.

Этап 4.
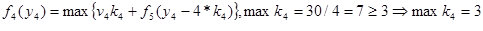
Этап 3.

Этап 2.

Этап 1.
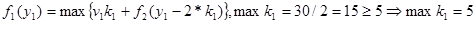
Оптимальное решение определяется теперь следующим образом. Из условия W=30 следует, что первый этап решения задачи при y1
=30 дает оптимальное решение k1
=0, которое означает, что на 0 (нуль) вопросов 1-го типа будут даны ответы. Далее находим:
| y1
=30 |
k1
=0 |
| y2
=y1
-2*k1
=30 |
k2
=0 |
| y3
=y2
-4*k2
=30 |
k3
=4 |
| y4
=y3
-k3
=26 |
k4
=1 |
| y5
=y4
-4*k4
=22 |
k5
=0 |
| y6
=y5
-7*k5
=22 |
k6
=0 |
| y7
=y6
-5*k6
=22 |
k7
=5 |
| y8
=y7
-3*k7
=7 |
k8
=7 |
Соответственно оптимальным решением задачи является (0,0,4,1,0,0,5,7), соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 46.
2.4 Анализ чувствительности решения
В таблице для первого этапа нам, по существу, необходимо получить оптимальное решение лишь для y1
=30, так как это последний этап, подлежащий рассмотрению (см. Приложение А). Однако в таблицу включены вычисления для y1
=0,1,…,30, которые позволяют провести анализ чувствительности решения.
Например, что произойдет, если время отводимое на контрольную работу будет 20, вместо 30 (см. Приложение А)?
| Y1
=20 |
k1
=0 |
| Y2
=y1
-2*k1
=20 |
k2
=0 |
| Y3
=y2
-4*k2
=20 |
k3
=4 |
| Y4
=y3
-k3
=16 |
k4
=0 |
| Y5
=y4
-4*k4
=16 |
k5
=0 |
| Y6
=y5
-7*k5
=16 |
k6
=0 |
| Y7
=y6
-5*k6
=16 |
k7
=3 |
| Y8
=y7
-3*k7
=7 |
k8
=7 |
соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 34.
Что произойдет, если время отводимое на контрольную работу будет 5, вместо 30 (см. Приложение А)?
| y1
=5 |
k1
=0 |
| y2
=y1
-2*k1
=5 |
k2
=0 |
| y3
=y2
-4*k2
=5 |
k3
=0 |
| y4
=y3
-k3
=5 |
k4
=0 |
| y5
=y4
-4*k4
=5 |
k5
=0 |
| y6
=y5
-7*k5
=5 |
k6
=0 |
| y7
=y6
-5*k6
=5 |
k7
=0 |
| Y8
=y7
-3*k7
=5 |
k8
=5 |
соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 10.
Что произойдет, если типов вопросов будет 4, вместо 8 (см. Приложение Б)?
Этап 4.

Этап 3.
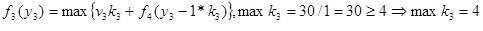
Этап 2.

Этап 1.
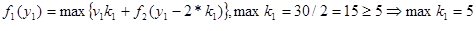
| y1
=30 |
k1
=5 |
| y2
=y1
-2*k1
=20 |
k2
=3 |
| y3
=y2
-4*k2
=8 |
k3
=4 |
| y4
=y3
-k3
=4 |
k4
=3 |
соответственно максимально количество баллов, которое студент может набрать за отведенное время равно 39.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Таха Х. Введение в исследование операций.–М.: Мир,1985.
2. Кузнецов Ю. Н. Математическое программирование. –М.: Наука,1976.
3. Вентцель Е. С. Исследование операций. –М.: Наука,1976.
4. Вентцель Е. С. Элементы динамического программирования. –М.: Наука,1987.
5. Акоф Р., Сасиени М. Основы исследования операций. –М.: Мир,1971.
6. Вентцель Е. С. Исследование операций: задачи, принципы, методология. –М.: Наука,1988.
7. Карманов В. Т. Математическое программирование. –М.:Наука,1986.
8. Зайченко Ю. П. Исследование операций. –К.: Высшая школа,1985.
9. Аоки М. Введение в методы оптимизации. –М.: Наука,1977.
10. Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. –М.: Наука,1965.
11. Муну М. Математическое программирование. Теория алгоритмов. –М.: Наука,1990.
ПРИЛОЖЕНИЕ А
Решение задачи методом динамического программирования
ПРИЛОЖЕНИЕ Б
Анализ чувствительности решения
ПРИЛОЖЕНИЕ В
Решение задачи симплекс-методом
|