Жизнь М. В. Остроградского.
Математическая жизнь в академии наук в середине десятых годов почти замерла и возродилась в конце двадцатых с приходом в Академию Остроградского и Буняковского, особенно первого из них.
Михаил Васильевич Остроградский родился 26 сентября 1801г. на Украине, в деревне Пашенной Кобелякского уезда Полтавской губернии в семье помещика. В 1816 г. он поступил в Харьковский университет. Остроградский успешно сдал кандидатские экзамены, и перед ним, казалось, открывалась прямая дорога к университетской профессуре. Однако острая идейная борьба, которая в те годы велась в Харьковском университете, помешала спокойному течению научной карьеры Остроградского.
Осиповский подверг критике идеалистическую немецкую философию, сторонники которой имелись и среди работавших в Харьковском университете иностранцев. В устных выступлениях Осиповский разоблачал и высмеивал мистиков, стоявших во главе министерства просвещения и учебных округов. Свое враждебное отношение к Осиповскому реакционная часть харьковской профессуры перенесла и на его лучшего ученика, также не любившего ни метафизики, ни мистики и бывшего, надо полагать, уже тогда “полным материалистом и атеистом”.
Когда ректор университета Осиповский предложил присвоить Остроградскому заслуженную им степень кандидата, в Совете университета произошли резкие столкновения. Один из реакционных профессоров, А. И. Дудрович, письменно донес попечителю округа З. Я. Корнееву, что по вине Осиповского студенты-математики не занимаются богословием, а Остроградского обвинил в том, что он, несмотря на предписание начальства, не слушал богопознания и христианского учения. Дело дошло до министра “духовных дел и народного просвещения” А. Н. Голицына, по указанию которого Осиповский был уволен из университета, Остроградскаму отказали в присуждении степени кандидата, издевательски предложив заново сдать экзамены, якобы сданные им раньше в неправильном порядке.
Остроградский мужественно перенес эти испытания и решил, несмотря ни на что, посвятить свою жизнь науке. Еще в Харьковском университете его особенно увлекали вопросы прикладной математики и в 1922 г. он отправился в Париж, где работали Лаплас и Фурье, Лежандр и Пуассон, Бине и Коши и другие первоклассные ученые, пролагавшие новые пути в математике, математической физике и механике. Курсы, читавшиеся в Политехнической школе, Сорбонне, Коллеж де Франс были образцовыми и привлекали молодежь из многих стран.
Быстрые успехи Остроградского завоевали ему дружбу и уважение многих французских математиков, как старших поколений, так и сверстников. Время парижской жизни явилось для Остроградского не только “годами странствий и учения”, но и интенсивного творчества. В 1824-1827 гг. он представил Академии наук в Париже несколько замечательных мемуаров на французском языке. В “Замечаниях об определенных интегралах” (1824) он дал вывод незадолго перед тем опубликованной Коши формулы для вычета функции относительно полюса п-
го порядка, вывод, по сути дела совпадающий с принятым ныне. В “Доказательстве одной теоремы интегрального исчисления” (1826) он разработал весьма важную составную часть общего метода разделения переменных для интегрирования уравнений математической физики. В том же году Остроградский подготовил “Мемуар о распространении волн в цилиндрическом бассейне”, где развил исследования Коши и Пуассона, изучивших движение малых волн в бассейне бесконечной глубины и не ограниченном стенками, а год спустя “Мемуар о распространении тепла внутри твердых тел”, содержавший новое сжатое изложение метода разделения и решения новой задачи о распространении тепла в некоторой треугольной призме. Из них только работа по гидродинамике увидела свет в издании Парижской Академии, другие же остались в ее архиве. Но и не опубликованные тогда его открытия по математической физике оказали существенное влияние на развитие математики. Основные результаты вошли в последующие печатные труды самого Остроградского; кроме того, в рукописи или в устном изложении самого Остроградского с ними ознакомились тогда же или вскоре Коши, Пуассон и другие.
Перечисленные работы показывают, что Остроградский в первые же годы парижской жизни не только полностью овладел новейшим аппаратом анализа и механики, но существенно развил его и мастерски применил к решению как весьма общих актуальных проблем, так и частных трудных задач. Коши с высокой похвалой отзывался о работах своего молодого ученика и сотрудника. Например, в основоположном мемуаре по теории интегралов в комплексной области 1825 г., Коши, рассказывая о своих предыдущих результатах писал:”Наконец, один молодой русский, одаренный большой проницательностью и весьма искусный в анализе бесконечно малых, г. Остроградский, также прибегнув к употреблению этих интегралов и их преобразованию в обыкновенные, дал новое доказательство формул, мною выше упомянутых, и обобщил другие формулы, которые я представил в 19-й тетради “Журнала Политехнической школы”. Г. Остроградский любезно сообщил нам главные результаты своей работы”. Столь же уважительны отзывы Коши об Остроградском в статьях по теории вычетов. Много позднее, в работе, в которой установлен ряд общих свойств интегралов линейных уравнений с частными производными, Коши вспоминал о парижских открытиях Остроградского:”Я хотел бы иметь возможность сравнить полученные мною здесь результаты с результатами, полученными г. Остроградским в мемуаре, в котором он установил несколько общих предложений относительно интегрирования линейных уравнений в частных производных.Но я только смутно помню этот мемуар и, так как не знаю, был ли он где-либо опубликован, я лишен возможности произвести это сравнение”.
Весной 1828 г. Остроградский приехал в Петербург и здесь на протяжении нескольких месяцев представил Академии наук три работы. Первая содержала оригинальный, основанный на новой концепции интеграла (Коши), вывод уравнения Пуассона, которому удовлетворяет объемный потенциал поля тяготения в точке, лежащей внутри притягиваемой массы или на ее границе. Следующая посвящена вопросу о перестановке порядка интегрирования в двойном интеграле в случае бесконечного разрыва подынтегральной функции и примыкает к аналогичным исследованиям Коши. Третьей был уже упомянутый мемуар “Доказательство одной теоремы интегрального исчисления”, который автор вскоре взял обратно для переработки и затем опубликовал для переработки и затем опубликовал под названием “Заметки по теории теплоты”. Коллинс представил о трудах Остроградского блестящий отзыв и 29 декабря 1828 г. молодой ученый был избран адъюнктом по прикладной математике. Два года спустя он был выбран экстраординарным академиком и в 1831 г. – ординарным.
Деятельность Остроградского в Академии была весьма разносторонней. Он сделал более 85 научных сообщений, частью неопубликованных; читал публичные лекции; писал подробные отзывы на поступавшие в Академию работы, участвовал в комиссиях по введению григорианского календаря и десятичных мер (что было сделано лишь после великой Октябрьской социалистической революции), по водоснабжению Петербурга и т. д., занимался по поручению правительства изысканиями по внешней баллистике, и т. д. Вместе с тем Остроградский много времени уделял преподаванию. С 1828 г. он начал читать лекции в Морском корпусе (впоследствии Морской академии), где преемниками его последовательно были В.Я. Буняковский, А.Н. Коркин, А.Н. Крылов. С годами педагогическая деятельность Остроградского становилась все более интенсивной. Он вел занятия по математике и механике в Институте инженеров путей сообщения, Главном инженерном и Главном артиллерийском училищах, Главном педагогическом институте. С 1847 г. и до своей смерти он работал на посту главного наблюдателя по преподаванию математических наук во всех военных заведениях страны. Ему принадлежат несколько руководств по элементарной и высшей математике.
Педагогические взгляды Остроградского были весьма прогрессивными. Он считал, что в гимназиях и кадетских корпусах нужны лаборатории и мастерские, где учащиеся приобретали бы трудовые навыки, производили опыты и наблюдения. Он выступал за наглядность обучения математике, особенно в раннем возрасте, и критиковал сухое и формальное изложение этого предмета в современной ему школе. Он был сторонником введения в специальных старших классах средних военных учебных заведений идеи функции и начал анализа; курс математики, с его точки зрения, должен быть связан с другими предметами, как физика, в которых применяются математические методы. Как видно, в ряде пунктов Остроградский предвосхитил идеи так называемого движения за реформу преподавания, возникшего в начале XX века. Кое-чего Остроградский достиг в этом направлении в кадетских корпусах. Однако более широкая реализация педагогических установок Остроградского стала возможной лишь много позднее. Свое общее педагогическое credo Остроградский изложил в написанной совместно с парижским математиком и инженером И.-О. Блюмом (1812-1877) брошюре “Размышления о преподавании”, вышедшей на французском языке. Чтение этого блестящего по изложению и глубокого по содержанию сочинения интересно и в наши дни. Школьное преподавание арифметики, алгебры и геометрии, - писали авторы, - ничем “не напоминает о насущной необходимости изучения этих предметов для насущной жизни” и на деле дает “только тот результат, что их усваивает очень небольшое число учеников”. Этому в брошюре ярко противопоставлены принципы обучения, воспитывающего наблюдательность и любознательность, техническую сноровку и научное мышление. Для повышения интереса и привлечения внимания учеников Блюм и Остроградский рекомендовали использовать историю наук и биографии выдающихся людей, “принесших пользу наукам и искусству”:”Это в одно и то же время отличная разрядка и средство с помощью живого рассказа запечатлеть то или иное основное положение, либо удачное приложение теоретических принципов”.
Школьная математика должна учитывать особенности детского восприятия, но следует избегать общепринятой недооценки возможностей детей уже с семилетнего возраста. В брошюре разобран вопрос об обучении ребят до 12 лет, причем только в гимназиях или специальных учебных заведениях; более массовые школы, где учат началам чтения, письма и счета оставлены были в стороне.
Остроградский оказал значительное влияние на развитие математики и механики. Он, в частности, подготовлял условия для создания математической школы, организованной Чебышевым, и сам основал русскую школу механики. К его исследованиям примыкают многие последующие работы по математической физике, по теории интегрирования иррациональных функций, по теории кратных интегралов и даже по теории вероятностей, которыми он сам занимался немного. Прямыми учениками Остроградского были создатель теории автоматического регулирования И. А. Вышнеградский (1831-1895), автор классических исследований по теории трения и влияния на него смазки и по теории механизмов Н. П. Петров (1822-1889) и другие. Все перечисленные математики вышли из Главного педагогического института, где Остроградский преподавал с 1832 по 1859 г..
Научные заслуги Остроградского были высоко оценены и за рубежом. Он был избран членом-корреспондентом французской Академии наук в 1856 г., а еще ранее членом Американской академии наук и академий в Турине и в Риме. Скончался он 1 января 1862 г.
Кратные интегралы.
Остановимся несколько подробнее на работах Остроградского по кратным интегралам.
Формула Остроградского для преобразования тройного интеграла в двойной, которую мы пишем обычно в виде
 (1) (1)
или
 , ,
где div A
– дивергенция поля вектора А, А
n
–
скалярное произведение вектора А
на единичный вектор внешней нормали n граничной поверхности, в математической литературе нередко связывалась ранее с именами Гаусса и Грина. На самом деле в работе Гаусса о притяжении сфероидов можно усмотреть только весьма частные случаи формулы (1), например при P=x, Q=R=0 и т. п. Что касается Дж. Грина, то в его труде по теории электричества и магнетизма формулы (1) вовсе нет; в нем выведено другое соотношение между тройным и двойным интегралами, именно, формула Грина для оператора Лапласа, которую можно записать в виде
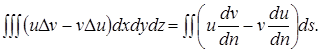 (2) (2)
Конечно, можно вывести формулу (1) и из (2), полагая
  
и точно так же можно получить формулу (2) из формулы (1), но Грин этого и не думал делать.
Все же вопрос об авторе интегральной формулы (1) оставался не вполне ясным. Дело в том, что, как было недавно замечено, в мемуаре Пуассона по теории упругости, выводится формула

где слева стоит интеграл по объему, а справа интеграл по граничной поверхности, причем  суть направляющие косинусы внешней нормали. суть направляющие косинусы внешней нормали.
Парижские рукописи Остроградского свидетельствуют, с полной несомненностью, что ему принадлежит и открытие, и первое сообщение интегральной теоремы (1). Впервые она была высказана и доказана, точно так, как это делают теперь в “Доказательстве одной теоремы интегрального исчисления”, представленном Парижской Академии наук 13 февраля 1826 г., после чего еще раз была сформулирована в той части “Мемуара о распространении тепла внутри твердых тел ”, которую Остроградский представил 6 августа 1827 г. “Мемуар” был дан на отзыв Фурье и Пуассону, причем последний его, безусловно читал, как свидетельствует запись на первых страницах обеих частей рукописи. Разумеется, Пуассону и не приходила мысль приписывать себе теорему, с которой он познакомился в сочинении Остроградского за два года до представления своей работы на теории упругости.
Что касается взаимоотношения работ по кратным интегралам Остроградского и Грина, напомним, что в “Заметке по теории теплоты” выведена формула, обнимающая собственную формулу Грина, как весьма частный случай. Непривычная теперь символика Коши, употребленная Остроградским в “Заметке”, до недавнего времени скрывала от исследователей это важное открытие. Разумеется, за Грином остается честь открытия и первой публикации в 1828 г. носящей его имя формулы для операторов Лапласа.
Открытие формулы преобразования тройного интеграла в двойной помогло Остроградскому решить проблему варьирования п-
кратного интеграла, именно, вывести понадобившуюся там общую формулу преобразования интеграла от выражения типа дивергенции по п-
мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид

 (3) (3)
Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала.
В “Мемуаре об исчислении вариаций кратных интегралов” рассмотрены еще два важных вопроса теории таких интегралов. Во-первых, Остроградский выводит формулу замены переменных в многомерном интеграле; во-вторых, впервые дает полное и точное описание приема вычисления п-
кратного интеграла с помощью п
последовательных интеграций по каждой из переменных в соответствующих пределах. Наконец, из формул, содержащихся в этом мемуаре, легко выводится общее правило дифференцирования по параметру многомерного интеграла, когда от этого параметра зависит не только подынтегральная функция, но и граница области интегрирования. Названное правило вытекает из наличных в мемуаре формул настолько естественным образом, что позднейшие математики даже отождествляли его с одною из формул этого мемуара.
Замене переменных в кратных интегралах Остроградский посвятил специальную работу. Для двойного интеграла соответствующее правило вывел с помощью формальных преобразований Эйлер, для тройного – Лагранж. Однако, хотя результат Лагранжа верен, рассуждения его были не точными: он как бы исходил из того, что элементы объемов в старых и новых переменных – координатах – между собою равны. Аналогичную ошибку допустил вначале в только что упомянутом выводе правила замены переменных Остроградский. В статье “О преобразовании переменных в кратных интегралах” Остроградский раскрыл ошибку Лагранжа, а также впервые изложил тот наглядный геометрический метод преобразования переменных в двойном интеграле, который, в несколько более строгом оформлении, излагается и в наших руководствах. Именно, при замене переменных в интеграле  по формулам по формулам  , , 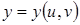 , область интегрирования разбивается координатными линиями двух систем u=const, v=const
на бесконечно малые криволинейные четырехугольники. Тогда интеграл можно получить, складывая сначала те его элементы, которые отвечают бесконечно узкой криволинейной полосе, а затем, продолжая суммировать элементы полосами, пока они все не будут исчерпаны. Несложный подсчет дает для площади, которая с точностью до малых высшего порядка может рассматриваться как параллелограмм, выражение , область интегрирования разбивается координатными линиями двух систем u=const, v=const
на бесконечно малые криволинейные четырехугольники. Тогда интеграл можно получить, складывая сначала те его элементы, которые отвечают бесконечно узкой криволинейной полосе, а затем, продолжая суммировать элементы полосами, пока они все не будут исчерпаны. Несложный подсчет дает для площади, которая с точностью до малых высшего порядка может рассматриваться как параллелограмм, выражение  , где , где  , выбирается так, чтобы площадь была положительной. В итоге получается известная формула , выбирается так, чтобы площадь была положительной. В итоге получается известная формула
 . .
Так дифференциальное выражение  , которое Эйлер формально подставлял вместо dydx,
а следуя рассуждениям Лагранжа для трехмерного случая, нужно было бы считать равным dydx,
приобрело у Остроградского простой и ясный геометрический смысл. , которое Эйлер формально подставлял вместо dydx,
а следуя рассуждениям Лагранжа для трехмерного случая, нужно было бы считать равным dydx,
приобрело у Остроградского простой и ясный геометрический смысл.
Дифференциальные уравнения.
В теории обыкновенных дифференциальных уравнений заслуживают внимания два результата Остроградского. В «Заметке о методе последовательных приближений», предложен метод решения нелинейных уравнений с помощью разложения в ряд по малому параметру, позволяющей избегать так называемых вековых членов, содержащих аргумент вне тригонометрических функций. Такие члены нередко появляются при употреблении обыкновенных приемов интегрирования с помощью степенных рядов; неограниченно возрастая вместе с аргументом, они порождают ошибочные приближения, а содержащее их решение оказывается неподходящим.С этим явлением встречались еще астрономы XVIII в. и задачей уничтожения вековых членов занимались Лаплас, Лагранж и другие. Свой метод, основанный на одновременном разложении по параметру как самого решения, так и периода входящих в него периодических функций, Остроградский кратко пояснил на примере:
 , , 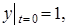  , ,
который записал в несколько иной форме:
 , ,
совпадающей с данным уравнением при  . Решение с точностью до величин первого порядка относительно . Решение с точностью до величин первого порядка относительно 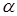 , найденное обычным способом, содержит вековой член: , найденное обычным способом, содержит вековой член:
 ; ;
решение по способу Остроградского от него свободно:
 , ,  . .
Найденное приближение Остроградский сопоставил с точным решением уравнения в эллиптических функциях Якоби. Остроградский ограничился получением первого приближения; в конце статьи он высказал намерение приложить этот метод к движению планет вокруг Солнца. Намерение это, видимо, не осуществилось, но как раз в работах по определению орбит небесных тел идея Остроградского получила дальнейшее развитие. Одним из первых таких трудов явилось исследование по теории возмущений шведского ученого А. Линдстедта, работавшего в 1879 – 1886 гг. в Дерптском университете. За этим последовали глубокие исследования А. Пуанкаре и А. М. Ляпунова и, уже в советский период, Н. М. Крылова, который применил к нему и другим, более общим классам линейных неоднородных уравнений второго порядка, содержащих малый параметр, несколько модифицированный им метод Ляпунова. В настоящее время метод малого параметра широко применяется к исследованию нелинейных задач механики, физики и техники.
Небольшая “Заметка о линейных дифференциальных уравнениях” Остроградского (1839) содержит классическую теорему, которая излагается теперь в любом курсе дифференциальных уравнений. Дано уравнение
 . .
и п
его решений  , которые предполагаются линейно независимыми. Согласно теореме Остроградского определитель , которые предполагаются линейно независимыми. Согласно теореме Остроградского определитель

выражается через коэффициент при (п-1)-
й производной:
 , ,
где а –
постоянная. Мы называем определитель  по имени впервые рассмотревшего его (в другой связи и более общей форме) польского математика Г. Вронского (1812). Та же теорема была одновременно получена из несколько иных соображений Ж. Лиувиллем (1838). по имени впервые рассмотревшего его (в другой связи и более общей форме) польского математика Г. Вронского (1812). Та же теорема была одновременно получена из несколько иных соображений Ж. Лиувиллем (1838).
Некоторые работы Остроградского были связаны с конкретными задачами современной ему военной техники. Так, например, в 1839-1842 гг. он по поручению артиллерийского ведомства занимался изучением стрельбы эксцентрическими сферическими снарядами, у которых центр фигуры отличен от центра инерции. Этому вопросу Остроградский посвятил три небольшие статьи, из которых одна содержала таблицы интегралов, нужных для решения задачи о движении снаряда в воздухе при квадратичном законе сопротивления. К работам по баллистике в свою очередь примыкали исследования Остроградского по приближенным вычислениям, в том числе и упоминавшаяся работа 1839 г., содержащая вывод остаточного члена формулы суммирования Эйлера-Маклорена.
План
:
1. Жизненный путь М. В. Остроградского.
2. Кратные интегралы.
3. Дифференциальные уравнения.
4. Заключение.
МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИМ. А. А. КУЛЕШОВА
Реферат
на тему
:
М. В. Остроградский
Выполнила
студентка
физико-математического
факультета
V
курса, группы
“B”
Семерикова Юлия
МОГИЛЕВ
2002.
|