Магнитогорский Государственный технический университет
Приближенное вычисление определенных интегралов.
Формула парабол (формула симпсона)
Подготовил: Студент группы ФГК-98 Григоренко М.В.
Магнитогорск –1999
е для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих случаях вычисление определенных интегралов по формуле Ньютона-Лейбница затруднительно, и применяются различные способы вычисления определенных интегралов. Один из них приведен ниже.
Формула парабол (формула Симпсона)
Разделим отрезок [a,b] на четное число равных частей n = 2m. Площадь криволинейной трапеции, соответствующей первым двум отрезкам [x0
,x1
] и [x1
,x2
] и ограниченной заданной кривой y = f(x), заменим площадью криволинейной трапеции, которая ограничена параболой второй степени, проходящей через три точки M(x0
,y0
), M1
(x1
,y1
), M2
(x2
,y2
) и имеющей ось, параллельную оси Оу (см. рисунок). Такую трапецию будем называть параболической трапецией.
Уравнение параболы с осью, параллельной оси Оу, имеет вид
y = Ax2
+ Bx + C.
Коэффициенты А, В и С однозначно определяются из условия, что парабола проходит через три заданные точки. Аналогичные параболы строим и для других пар отрезков. Сумма площадей параболических трапеций и даст приближенное значение интеграла.
Вычислим сначала площадь одной параболической трапеции.
Если криволинейная трапеция ограничена параболой
y
= Ax2
+ Bx + C,
осью Ох и двумя ординатами, расстояние между которыми равно 2h, то ее площадь равна
S = h/3 (y0
+ 4y1
+ y2
),
(☺)
где у0
и у2
– крайние ординаты, а у1
– ордината кривой в середине отрезка
Пользуясь формулой (☺), мы можем написать следующие приближенные равенства (h=Δx):| . . . . . . . . . . . . . . . . . . . . . . |
Складывая левые и правые части, получим слева искомый интеграл, справа его приближенное значение: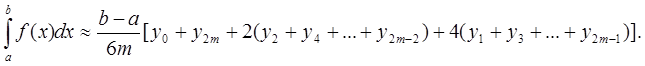
Это и есть формула Симпсона. Здесь число точек деления n = 2m произвольно, но чем больше это число, тем точнее сумма в правой части равенства дает значение интеграла.
Примеры
Было дано задания вычислить приблизительно следующие определенные интегралы:
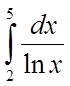  
И
Для вычисления данных интегралов мною были написаны специальные программы на языке Visual Basic for Application. (тексты программ приведены в приложении).
Программы осуществляют запрос количества отрезков, на которые следует разбить заданный отрезок. Структура программ универсальна и применима для вычисления любых определенных интегралов. Для этого необходимо изменить границы определенного интеграла в строках (*) и (**), а также подынтегральную функцию в строке (***).
Были получены следующие ответы:
При n = 20.
 Приложение Приложение
'Приближенное вычисление интегралов по формуле парабол
'(формула Симпсона)
Option Explicit
Sub integral_1()
Dim i As Integer, n As Integer
Dim t As Boolean
Dim b As Double, a As Double
Dim chet As Double, nechet As Double
Dim delta As Double, result As Double
a = 0 '(*)
b = 1 '(**)
t = True
Do
n = InputBox("Введите четное число n", "Запрос")
If n Mod 2 = 0 Then t = False
Loop While t
delta = (b - a) / n
chet = 0
nechet = 0
For i = 1 To n - 1
If (i Mod 2) = 0 Then
chet = chet + (f(a + (delta * i)))
Else
nechet = nechet + (f(a + (delta * i)))
End If
Next i
result = (delta / 3) * (f(a) + f(b) + (2 * chet) + (4 * nechet))
MsgBox result, vbInformation, "Результат"
End Sub
Function f(x) As Double
f = Sqr(1 + (x ^ 4)) '(***)
End Function
'Приближенное вычисление интегралов по формуле парабол
'(формула Симпсона)
Option Explicit
Sub integral_1()
Dim i As Integer, n As Integer
Dim t As Boolean
Dim b As Double, a As Double
Dim chet As Double, nechet As Double
Dim delta As Double, result As Double
a = 2 '(*)
b = 5 '(**)
t = True
Do
n = InputBox("Введите четное число n", "Запрос")
If n Mod 2 = 0 Then t = False
Loop While t
delta = (b - a) / n
chet = 0
nechet = 0
For i = 1 To n - 1
If (i Mod 2) = 0 Then
chet = chet + (f(a + (delta * i)))
Else
nechet = nechet + (f(a + (delta * i)))
End If
Next i
result = (delta / 3) * (f(a) + f(b) + (2 * chet) + (4 * nechet))
MsgBox result, vbInformation, "Результат"
End Sub
Function f(x) As Double
f = 1 / (Log(x)) '(***)
End Function

|