Лабораторная работа № 4.
Приближенный метод решения интегралов.
Метод прямоугольников (правых, средних, левых).
Гребенникова Марина
12-А класс
Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида 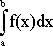 где f(x) -данная функция, непрерывная на отрезке [a; b]. Если функция f(x) задана формулой и мы умеем найти неопределенный интеграл F(x), то определенный интеграл вычисляется по формуле Ньютона-Лейбница: где f(x) -данная функция, непрерывная на отрезке [a; b]. Если функция f(x) задана формулой и мы умеем найти неопределенный интеграл F(x), то определенный интеграл вычисляется по формуле Ньютона-Лейбница: 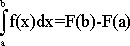
Если же неопределенный интеграл данной функции мы найти не умеем, или по какой-либо причине не хотим воспользоваться формулой Ньютона-Лейбница или если функция f(x) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла можно использовать метод прямоугольников (правых, левых, средних). При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла. Если f(x)>=0 на отрезке [a; b], то 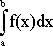 численно равен площади фигуры, ограниченной графиком функции y=f(x), отрезком оси абсцисс, прямой x=a и прямой x=b (рис. 1.1) Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции. численно равен площади фигуры, ограниченной графиком функции y=f(x), отрезком оси абсцисс, прямой x=a и прямой x=b (рис. 1.1) Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.

Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка  . .
Точки деления будут: x0
=a; x1
=a+h; x2
=a+2*h, ... , xn-1
=a+(n-1)*h; xn
=b.
Числа y0
, y1
, y2
, ... , yn
являются ординатами точек графика функции, соответствующих абсциссам x0
, x1
, x2
, ... , xn
(рис. 1.2).
Строим прямоугольники. Это можно делать несколькими способами:
 Левые прямоуголики (слева на право) Левые прямоуголики (слева на право)
Правые прямоугоники (построение справа на лево)

Средние прямоугольники (посредине)

Из рис. 1.2 следует, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.

h=(b-a)/n –ширина прямоугольников
Формула левых прямоугольников:
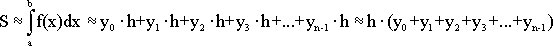 (1.3) (1.3)
Формула правых прямоугольников:
 (1.4) (1.4)
Формула средних прямоугольников.
Sсредих
= (Sправых
+ Sлевых
) /2
 (1.5) (1.5)
Программа вычисления
 по методу левых прямоугольников. по методу левых прямоугольников.
Programlevii;{Метод левых прямоугольников}
usescrt;
vari,n:integer; a,b,h,x,xb,s:real;
functionf(x:real):real;
beginf:=(1/x)*sin(3.14*x/2); end;
begin
clrscr;
write('Введите нижний предел интегрирования '); readln(a);
write('Введите верхний предел интегрирования '); readln(b);
write('Введите количество отрезков '); readln(n);
h:=(b-a)/n; s:=0; xb:=a;
fori:=0 ton-1 do
beginx:=xb+i*h; s:=s+f(x)*h; end;
writeln('Интеграл равен ',s:12:10); readln;
end.
a=1 b=2 n=10 S= 18,077
a=1 b=2 n=20 S= 18, 208
a=1 b=2 n=100 S= 18, 270
Программа вычисления
 по методу правых прямоугольников
. по методу правых прямоугольников
.
a=1 b=2 n=10 S=18,05455
a=1 b=2 n=20 S=18,55555
a=1 b=2 n=100 S= 18,2734
Программа вычисления
 по методу средних прямоугольников. по методу средних прямоугольников.
a=1 b=2 n=10 S=18,07667
a=1 b=2 n=20 S=18,368
a=1 b=2 n=100 S= 18,156
Заключение и выводы.
Таким образом очевидно, что при вычислении определенных интегралов методами прямоугольников не дает нам точного значения, а только приближенное.
Чем больше значение n, тем точнее значение интеграла..
|