| §1.Понятия статистики, статистическая закономерность и совокупность............................. 2
§2. Признаки единиц статистической совокупности, их классификация.............................. 2
§1. Понятие статистического наблюдения, его подготовка..................................................... 4
§2. Виды статистического наблюдения...................................................................................... 5
§3. Ошибки наблюдения.............................................................................................................. 6
§4. Сводка и группировка............................................................................................................ 6
§5. Виды статистических группировок...................................................................................... 6
§6. Статистические таблицы........................................................................................................ 7
§7. Статистические графики........................................................................................................ 8
§1. Фактическое и теоретическое распределение.................................................................... 21
§2. Кривая нормального распределения................................................................................... 21
§3. Проверка гипотезы о нормальном распределении............................................................ 21
§4. Критерии согласия: Пирсона, Романовского, Колмогорова............................................ 21
§5. Практическое значение моделирования рядов распределения........................................ 22
§1. Понятие выборочного наблюдения. Причины его применения..................................... 23
§3. Ошибки выборочного наблюдения..................................................................................... 24
§4. Задачи выборочного наблюдения....................................................................................... 25
§5. Распространение данных выборочного наблюдения на генеральную совокупность... 26
§6. Малая выборка....................................................................................................................... 26
§1. Понятие корреляционной связи и КРА.............................................................................. 27
§2. Условия применения и ограничения КРА......................................................................... 27
§3. Парная регрессия на основе метода наименьших квадратов........................................... 28
§4. Применение парного линейного уравнения регрессии................................................... 29
§6. Множественная
корреляция................................................................................................. 32
Тема 1.: Введение в статистику.
- понятия статистики, статистическая закономерность и совокупность.
- признаки единиц статистической совокупности, их классификация.
- предмет и метод статистики.
§1.Понятия статистики, статистическая закономерность и совокупность.
Слово статистика происходит от латинского “status
” в переводе – состояние, положение вещей.
Термин статистика возник во 2ой
половине 18 века. В связи с познанием государств, изучением их особенности. К этому же времени относится начало преподавания статистики в университете. В зависимости от отрасли статистического исследования различают: статистику населения, промышленности, с/х и т.д. - прикладная статистика.
Общая теория статистики – совокупность методов и приемов по сбору, обработке, представлению и анализу числовых данных. Термин статистика в наши дни употребляется в 3х
значениях:
- как синоним слова «данные»
- отрасль значений объединяющая принципы и методы работы с числовыми данными характеризующими массовые явления (продолжительность жизни мужчин ниже чем женщин)
- отрасль практической деятельности направленной на обработку и анализ числовых данных.
Статистика позволяет выявить и измерить закономерность развития социально-экономических процессов и явлений, а также взаимосвязи между ними в конкретных условиях места и времени.
Закономерность важнейшая категория статистики.
Под закономерностью понимается повторяемость, последовательность и порядок изменений в явлениях.
Статистическая закономерность – закономерность в которой необходимость неразрывно связанном в каждом отдельном явлении со случайностью и лишь во множестве явлений проявляет себя как закон. Понятию статистической закономерности противостоит понятие динамической закономерности проявляющейся в каждом явлении. (пример: Sкруга
=pr2
чем > r тем > Sкруга
). Объектом статистического исследования является статистическая совокупность – множество единиц обладающих массовостью, однородностью, определяемой целостностью и наличием вариации. Каждый отдельно взятый элемент называется – единицей статистической совокупности (ЕСС)
§2. Признаки единиц статистической совокупности, их классификация.
ЕСС обладают определенными свойствами которые называются признаками. Статистика изучает явления через их признаки, чем более однородна совокупность тем больше общих признаков имеют ее единицы и тем меньше варьируют значения этих признаков.
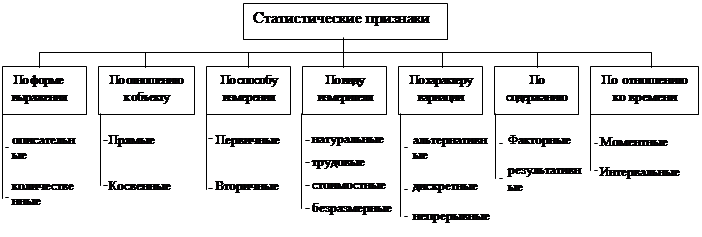
- Описательный признак – признак, который может быть выражен только словесно.
- Количественный признак – признак, который может быть выражен численно.
- Прямой признак – свойство непосредственно присуще характерному объекту.
- Косвенный признак – свойства не самого характеризуемого объекта, а объекта связанного с ним либо входящих в него.
- первичный признак – абсолютная величина, может быть измерен.
- вторичный признак – результат сопоставления первичных признаков, он измеряется непосредственно.
- натуральный признак – измеряется в штуках, кг, тоннах, литрах и т.д.
- трудовой признак – измеряется в человеко-днях, человеко-часах.
- стоимостной признак - измеряется в рублях, $, €, ₤.
- безразмерный признак – измерение в долях, %
- альтернативный признак – признак, который принимает только одно значение из нескольких возможных.
- дискретный признак – принимает только целое значение, без промежуточного.
- непрерывный признак – признак, принимающий любые значения в определенном диапазоне.
- факторный признак – признак, под действием которого изменяется другой признак.
- результативный признак – признак, который изменяется под признаком другого
- моментный признак – признак, измеренный на определенный момент времени.
- интервальный признак – признак за определенный интервал времени.
Один и тот же признак может быть классифицирован одновременно по разным классификациям.
§3. Предмет и метод статистики
.
Предметом статистического исследования являются статистические совокупности – множество одно-качественных варьирующих предметов.
Специфика предмета статистики обуславливает специфику метода, они включают в себя:
- сбор данных (статистическое наблюдение, публикация)
- обобщение данных (сводка, группировка)
- представление данных (таблицы и графики)
- анализ и интерпретация числовых данных (расчет средних, вариационных анализ, КРА, ряды динамики, индексы)
тема 2: Организация статистического наблюдения.
Сводка и группировка данных.
§1. Понятие статистического наблюдения, его подготовка.
§2. Виды статистического наблюдения.
§3 Ошибки наблюдения.
§4 Сводка и группировка
§5 Виды статистических группировок.
§6 Статистические таблицы.
§7 Статистические графики.
§1. Понятие статистического наблюдения, его подготовка.
Любое статистическое исследование начинается со сбора данных.
Источники информации:
1. различные публикации (газеты, журналы, и т.д.)
2. главный источник опубликованной статистической информации – издания органов государственной статистики («РФ в 2001 году» издательство ГОСКОМСТАТ).
3. проведение статистического наблюдения, т.е. научно организованного сбора данных.
Статистическое наблюдение – массовое, плановое , научно организованное наблюдение за явлением социальной и экономической жизни, которая заключается в регистрации признаков у каждой единицы изучаемой совокупности.
Процесс проведения наблюдения:
- Подготовка к наблюдению
- Проведение массового сбора данных
- Подготовка данных к обработке
- Разработка предложений по совершенствованию статистического наблюдения.
Подготовка наблюдения:
- Определение цели и объекта наблюдения
- Определение состава признаков подлежащих регистрации
- Разработка документов для сбора данных
- Выбор отчетной единицы и единицы относительно которой будет проводится наблюдение.
- Необходимо определить методы и средства получения данных.
Необходимо решить организационные проблемы:
- необходимо определить состав служб проводящих исследование
- проинструктировать персонал
- составить календарный план работы
- провести тиражирование документов для сбора данных
Объектом наблюдения являются социально-экономические явления и процессы.
Необходимо четко выделить признаки для регистрации.
Программа наблюдения – перечень признаков подлежащих регистрации признаков в процессе наблюдения.
Требования к программе наблюдения:
- Программа должна содержать существенные признаки, непосредственно характеризующие изучаемое явление, не следует включать в программу признаки, имеющие второстепенные явления или признаки, значения которых будут заведомо недостоверны или будут вообще отсутствовать.
- Вопросы программы наблюдения должны быть точными и не двусмысленными, а также легкими для понимания во избежании трудностей при получении ответов.
- Следует определить последовательность вопросов.
- В программу наблюдения следует включать вопросы непосредственного характера для проведения и уточнения собираемых данных.
- для обеспечения единообразия получаемых сведений программа оформляется в виде документа – называемый статистическим формуляром.
Статистический формуляр - это документ единого образца содержащий программу и результаты наблюдений.
Различают индивидуальный формуляр (ответы на вопросы по одной единице наблюдения) и списанный (сведения по нескольким единицам статистической совокупности).
Формуляр и инструкция по его заполнению являются инструментарием статистического наблюдения.
Выбор времени наблюдения заключается в решении 2х
вопросов: установлении критической даты либо интервала, определением периода наблюдения.
Критическая дата – конкретный день года, час дня по состоянию на который должны быть зарегистрированы признаки по каждой единице изучаемой совокупности.
Период наблюдения – время в течении которого происходит заполнение статистических формуляров т.е. время необходимое для сбора данных.
Следует учитывать, что отдаление периода наблюдения от критической даты или интервала может привести к снижению достоверности получаемых сведений.
§2. Виды статистического наблюдения.
В отечественной статистике используются три формы статистических наблюдений.
- статистическая отчетность предприятий, организаций, учреждений.
- специально организованное статистическое наблюдение (перепись и т.д.)
- регистр – форма непрерывного статистического наблюдения за долговременными процессами
Статистическое наблюдение классифицируется :
По времени наблюдения:
- текущее наблюдение – производится непрерывная регистрация признаков (загс, преступление, и т.д.).
- периодическое наблюдение – производится через определенные интервалы времени (уровень жизни в городе Челябинске, стоимость потребительской корзины, перепись населения).
- Единовременный – наблюдение, производимое один раз под конкретную цель.
По охвату единиц совокупности:
- Сплошное наблюдение – должна быть получена информация обо всех ЕСС
- Не сплошное наблюдение:
- Способ основного массива – обследованию подвергаются самые существенные единицы изучаемой совокупности (изучить предприятие машиностроения Челябинской области).
- Выборочное наблюдение – случайный отбор ЕСС подлежащих наблюдению.
- Монографическое наблюдение – когда наблюдению подвергается одна ЕСС, часто используются для составления программы массового наблюдения.
По способу сбора данных:
- Непосредственное наблюдение – сами регистраторы путем непосредственного замера, взвешивания устанавливают факт подлежащей регистрации (ребенок в возрасте до 1 года в поликлинике).
- Документальное наблюдение – используются различные документы (составление декларации)
Опрос – необходимые сведения получают со слов респондента.
- Экспедиционный опрос – осуществляется специально подготовленными работниками которые получают необходимую информацию на основе опроса соответствующих лиц и сами фиксируют ответы в формуляре. Экспедиционный опрос может быть прямым (лицом к лицу) и опосредованным (опрос по телефону)
- Корреспондентский опрос – сведения сообщает штат добровольных корреспондентов, данный способ требует малых финансовых затрат, но не дает точного значения проводимого наблюдения.
- Саморегистрация – формуляры заполняются самими респондентами, а регистраторы лишь раздают им бланки опросных листов и объясняют заполнение их.
§3. Ошибки наблюдения
Основное требование, применяемое к статистическому наблюдению - это точность.
Точность – степень соответствия какого-либо показателя признака определенным по материалам статистического наблюдения действительной величине.
Расхождение между расчетным и действительным значением называется ошибкой наблюдения в зависимости от причин возникновения различают: ошибки регистрации и ошибки репрезентативности. Ошибки регистрации делятся на случайные и систематические.
Случайные ошибки – результат действий случайных факторов (перепутаны строки, столбцы)
Систематические ошибки – всегда имеют тенденцию либо к завышению либо к занижению показателя. (возраст)
Ошибки репрезентативности – характер для не сплошного наблюдения и возникают в результате неточного воспроизведения выборной всей исходной совокупности.
После получения статистических формуляров необходимо:
1. провести проверку полноты собранных данных.
2. провести арифметический контроль, основанный на связи различных признаков между собой.
3. провести логический контроль основанный на знании логических связей между признаками.
§4. Сводка и группировка
На основе собранных данных нельзя произвести расчет и сделать выводы, для начала их нужно обобщить и свести в единую таблицу. Для этих целей служат сводка и группировка.
Сводка – комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность и выявление типичных черт и закономерностей присущих изучаемому явлению в целом.
Простая водка – подсчет общих итогов по совокупности.
Сложная сводка – комплекс операций по группировке единичных наблюдений, подсчет итогов по каждой группе и по всему объекту в целом и представлении результатов в виде статистических таблиц.
По форме обработки материала сводка бывает децентрализованная , централизованная – такая сводка проводится при единовременном статистическом наблюдении.
Группировка – расчленение множества единиц изучаемой совокупности на группы по определенным признакам.
§5. Виды статистических группировок
Группировки могут быть классифицированы по структуре и по содержанию.
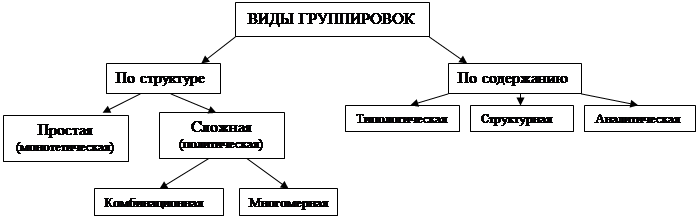
Типологическая – разделение совокупности на классы, социально-экономические типы (государственные предприятия, ОАО, ООО, ЗАО)
Структурная – разделение совокупности по какому-либо одному признаку.
Возраст
<трудоспособный
трудоспособный
трудоспособный>
 Аналитическая группировка характеризует взаимосвязь между признаками один из которых является факторным другой результативным. Аналитическая группировка характеризует взаимосвязь между признаками один из которых является факторным другой результативным.
| образование
|
0-5000
|
5000-10000
|
От 10000
|
| Среднее
|
2
|
1
|
-
|
| Незаконченное высшее
|
10
|
20
|
5
|
| Высшее
|
7
|
15
|
25
|
§6. Статистические таблицы
Результаты сводки и группировки должны быть представлены так, чтобы ими можно было пользоваться.
Существует 3 способа представления данных:
- данные могут быть включены в текст.
- представление в таблицах.
- графический способ
Статистическая таблица – система строк и столбцов, в которой в определенной последовательности излагается статистическая информация о социально-экономических явлениях.
Различают подлежащее и сказуемое таблицы.
Подлежащим называется объект характеризующийся числами, обычно подлежащее дается в левой части таблицы.
Сказуемое – система показателей с помощью которых характеризуется объект.
| Город
|
Численность
|
Плотность населения чел/км2
|
Площадь города км2
|
| Москва
|
| Челябинск
|
Статистическая таблица содержит 3 вида заголовков: общее, боковое
Общий заголовок должен отражать содержание всей таблицы, располагается над таблицей по центру.
Правило составления таблиц.
1. обязательны все три вида заголовков без сокращений слов, общие единицы измерения можно вынести в заголовок.
2. в таблице не должно быть лишних линий, вертикальная разметка может отсутствовать.
3.
Итоговая строка обязательна. Она может быть как в начале так и в конце документа. Если в начале документа то если в конце то ИТОГО: 4. цифровые данные в пределах одной графы записываются с одной степенью точности. Разряды записываются строго под разрядами, целая часть отделяется запятой.
5. в таблице не должно быть пустых клеток, если данные отсутствуют, то пишут «Сведений нет» или «…», если данные равны нулю, то «–». Если значение не равно нулю но первая значащая цифра появляется после заданной точности 0,01®0,0 – если принятая точность до десятых.
6. если в таблице много граф, то графы подлежащего обозначаются заглавными буквами, а графы сказуемого цифрами.
7. если таблица основана на заимствованных данных, то под таблицей указывается источник данных, в случае необходимости таблица может сопровождаться примечаниями.
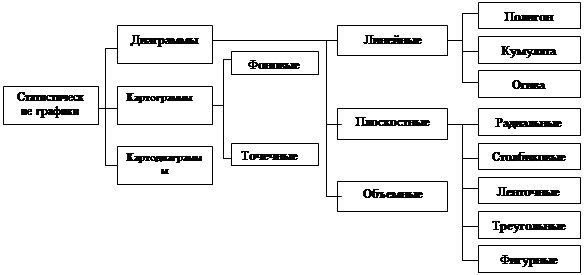
§7. Статистические графики
Статистические таблицы могут дополняться графиками.
Статистические графики – условные изображения числовых величин и их соотношений посредством линий, геометрических фигур, рисунков.
Плюсы графического изображения
1. наглядно, обозримо, выразительно.
2. сразу видны пределы изменения показателя, сравнительная скорость изменения и колеблемость
Минусы графического изображения
- Включают меньшее количество данных чем в таблице.
- на графике показываются округленные данные, общая ситуация, но не детали.
Тема 3: Статистические показатели.
§1. Сущность и значение статистического показателя, его атрибуты.
§2. Классификация статистических показателей.
§3. Виды относительных показателей. Принципы построения.
§4. Системы статистических показателей.
§1.
Статистический признак – свойство присущее ЕСС, он существует объективно от того изучает его как наука или нет
Статистический показатель – обобщающая характеристика какого-либо свойства совокупности.
Структура статистического показателя (его атрибуты):
| Качественная сторона : объект и его свойства
|
Количественная сторона: число и ед. измерения
|
Территориальные, отраслевые, либо др. границы
|
Интервал или момент времени
|
| Ввод в действие жилых домов
|
40800,5 млн./м2
|
РФ
|
1993 год
|
§2.
· Средние величины
· Показатели вариации
· Показатели связи признаков
· Показатели структуры и характера распределения
· Показатели динамики
· Показатели колебимости
· Показатели точности и надежности выборочных оценок
· Показатели точности и надежности прогнозов
По виду
: суммарное количество единиц либо суммарное свойство объекта. Это сумма первичных признаков, измеряется в шт., кг, м, $, и т.д.
Относительный показатель
– получаемый путем сопоставления абсолютных или относительных показателей в пространстве, во времени или в сравнении показателей разных свойств изучаемого объекта.
Относительный показатель 1го
порядка получается путем сопоставления 2х
абсолютных показателей. Относительный показатель 2го
порядка получается путем сопоставления относительных показателей 1го
порядка и т.д.
Относительный показатель 3го
порядка и выше встречаются очень редко.
Прямые показатели – такие показатели величина которых увеличивается с увеличением исследуемого явления .
Обратные показатели – показатели величина которых уменьшается с увеличением исследуемого явления.
 Пример: Пример:
§3. Относительные показатели
Показатели структуры
получаются путем отношения части к целому.
Относительные показатели динамики
- Показатели динамики (темпы роста, прироста)
- Индексы
Показатели взаимосвязи
характеризуют связи между признаками:
- Коэффициент корреляции
- Аналитические индексы
Показатели интенсивности
характеризуют отношение двух объектов по разным признакам.
- Трудоемкость – количество времени используемое для изготовления одной единицы изделия
- Выработка – количество продукции произведенное в единицу времени
ВЫРАБОТКА = 1/трудоемкость
Показатели отношения к нормативу
– соотношение фактических величин признака показателя к нормативным, плановым, оптимальным.
Показатели сравнения –
сравнение разных объектов по одному признаку.
Общие принципы построения статистических показателей:
1. статистические показатели объективно связаны.
2. сравниваемые показатели могут отличаться только одни атрибутом, нельзя сопоставлять показатель по двум и более атрибутам.
3. необходимо знать и учитывать границы показателя.
§4.
Для каждой характеристики объекта необходима система статистических показателей.
1. функция позновательская – основывается на анализе данных
2. пропагандистская
3. стимулирующая функция
тема 4: Средние величины
§1. понятие средней величины
§2. виды средних величин
§3. средняя арифметическая и ее свойства
§4. среднее гармоническое, геометрическое, квадратическое.
§5. многомерная средняя
§1.
Наиболее распространенной формой статистических показателей является средняя величина.
Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще каждой единице изучаемой совокупности, хотя значение признака отдельных единиц совокупности могут колебаться в ту или иную сторону.
Типичность средней непосредственно связана с однородностью изучаемой совокупности. В случае не однородной совокупности необходимо провести разбивку ее на качественно однородные группы и рассчитать среднюю по каждой по каждой из однородных групп.
Определить среднюю можно через исходное соотношение средней (ИСС) ее логическую формулу.
От того в каком виде представлены данные для расчета средней, зависит каким именно будет ИСС.
§2.
- Средняя арифметическая
- Средне гармоническая
- Средне квадратическая, кубическая
- Средне геометрическое
Правило мажерантности средних.
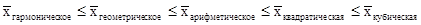
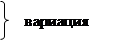 Структурные средние Структурные средние
Мода – Мо
Медиана – Ме
В рядах динамики рассчитывается средняя арифметическая, средняя хронологическая.
Средней арифметической
называется такое среднее значение признака при вычислении которого общий объем признака не изменяется.
Пример: вес.
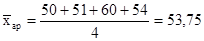
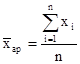 - ср. арифметическое простое - ср. арифметическое простое
xi
– индивидуальное значение признака
n – общее число изучаемой совокупности
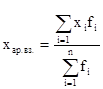 ср. арифметическое взвешенное ср. арифметическое взвешенное
Свойства ср. арифметической.
- Сумма отклонений индивидуальных значений признака от его средней величины равно нулю
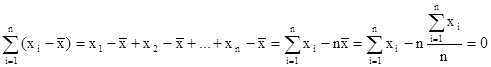
- если каждое индивидуальное значение признака умножить или разделить на одно и тоже постоянное число, то среднее увеличится или уменьшится во столько же раз.
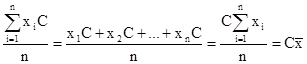
- если к каждому индивидуальному значению признака прибавить одно и тоже постоянное число, то средняя величина изменится соответственно на тоже самое число.
Доказательство
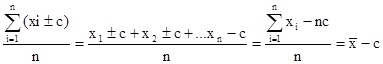
- если веса f средней взвешенной умножить или разделить на одно и тоже число, то средняя не изменится.
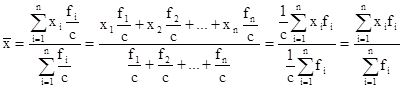
- сумма квадратов отклонений признака меньше чем от любого другого числа.
Другие виды средних
| Вид средней
|
Простая средняя
|
Взвешенная средняя
|
| гармоническая
|

|

|
| геометрическое
|
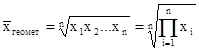
|
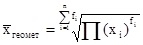
|
| Квадратическая
|
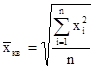
|

|
§5.
Очень трудно охарактеризовать группировку по одному признаку и мало остается информации в памяти.
Сохранить сложность описания групп и одновременно преодолеть недостатки комбинированной группировки позволяют многомерные группировки. Простейшим вариантом многомерной группировки является многомерная средняя.
Многомерная средняя – средняя величина для нескольких признаков Е.С.С.
Т.к. нельзя рассчитать ср. величину абсолютных значений разных признаков выраженных в разных единицах измерения, то многомерная средняя вычисляется из относительных величин.
Из отношений значений признака для Е.С. к средним значениям этих признаков.
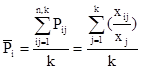
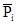 - многомерная средняя для i единицы - многомерная средняя для i единицы
xij
– значение признака j для i единицы
 - среднее значение признака j - среднее значение признака j
k – число признаков
j – номер признака и номер его совокупности
тема 5: Вариационный анализ
§1. Вариация признаков и ее причины
§2. Ряды распределения
§3. Структурные характеристики вариационного ряда.
§4. Показатели силы вариации.
§5. Показатели интенсивности вариации
§6. виды дисперсии. Правило сложения дисперсии.
§1.
Вариацией значения какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени.
Причина вариации: разные условия существования ЕСС именно вариация порождает необходимость в такой науке как статистика.
§2.
Проведение вариационного анализа начинается с построения вариационного ряда – упорядоченное распределение единиц совокупности по возрастающим или по убывающим признакам и подсчет соответствующих частот.
Ряды распределения
- ранжированные
- дискретные
- интервальные
Ранжированный вариационный ряд
– перечень отдельных ед. совокупности в порядке возрастания убывания ранжированного признака
| БАНК
|
Капитал тыс. руб.
|
| СБ РФ
|
96007237
|
| Внешторгбанк
|
47991724
|
Дискретный вариационный ряд –
таблица состоящая из 2х
строк – полимерных значений варьирующего признака и кол-во единиц с данным значением признака.
| Кол-во детей в семье
|
0
|
1
|
2
|
3
|
4
|
| Кол-во семей
|
20
|
40
|
45
|
10
|
5
|
Интервальный вариационный ряд строится в случаях:
1. признак принимает дискретные значения , но кол-во их слишком велико
2. признака принимает любые значения в определенном диапазоне
| Размер собственного капитала тыс. руб.
|
0 - 10000
|
10000-50000
|
Свыше 50000
|
| Количество банков
|
20
|
40
|
10
|
При построении интервального вариационного ряда необходимо выбрать оптимальное количество групп, самый распространенный способ по формуле Стерджесса
k=1+3.32lgn
k – количество интервалов
n – объем совокупности
При расчетах почти всегда получают дробные значения, округления производить до целого числа.
Длина интервала – l

Виды интервалов
1. нижняя граница последующего интервала повторяет верхнюю границу последующего интервала
2. С индивидуальными границами в интервал входят верхняя и нижняя границы
3. открытый интервал, интервал с одной границей
В случае открытого интервала l
принимается равной длине смежного с ним интервала, либо исходя из логических соображений.
| Стаж
|
До 5
|
5-7
|
7-9
|
| Кол-во рабочих
|
При расчетах по интервальному вариационному ряду за xi
принимается середина интервала.
Интервалы могут быть как равные так и нет. При изучении вариационного ряда существенную помощь оказывает графическое изображение. Дискретный вариационный ряд изображается с помощью полигона. Интервальный вариационный ряд изображается с помощью гистограммы.
Накопленная частота | xi
|
0
|
1
|
2
|
3
|
4
|
| fi
|
20
|
40
|
45
|
10
|
5
|
NME
=60 медиана = 1
Кумулята – распределение меньше чем
Огива – распределение больше чем §3.
Медиана – значение признака делящее всю совокупность на две равные части.
Для дискретного вариационного ряда расчет медианы: если n-четное, то №Ме
медианой единицы
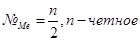
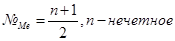
Интервальный вариационный ряд:
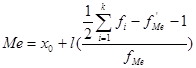
k – количество интервалов
х0
– нижняя граница медианного интервала
l
– длина медианного интервала
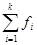 - сумма частот - сумма частот
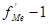 - накопленная частота интервала предшествующая медианному. - накопленная частота интервала предшествующая медианному.
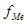 - частота медианного интервала - частота медианного интервала
Медианный интервал
– первый интервал накопленная частота которого превышает половину от общей суммы частот.
| 0-5
|
5-10
|
 10-15 10-15
|
15-20
|
| 15
|
20
|
40
|
25
|
Графически медиана находится по кумуляте.
2. Квартили – значение признака делящее совокупность на 4 равные части.
1ый
квартиль 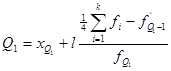
3ий
квартиль 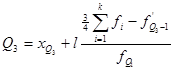
2ой
квартиль – медиана.
xQ
1
xQ
3
– нижняя граница интервала содержащего 1го
и 3го
квартили.
l – длина интервала
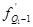 и и  - накопленные частоты интервалов предшествующих интервалов содержащих 1 и 3 квартили. - накопленные частоты интервалов предшествующих интервалов содержащих 1 и 3 квартили.
 - частоты квартильных интервалов. - частоты квартильных интервалов.
Для характеристики вариационного ряда используются:
Децили – делят совокупность на 10 равных частей, Перцитили – делят совокупность на 100 равных частей.
3. Мода – часто встречающаяся характеристика признака. Для дискретного вариационного ряда – наибольшая частота. Для интервального вариационного ряда мода рассчитывается по следующей формуле:

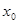 - нижняя граница модального интервала - нижняя граница модального интервала
l
– длина модального интервала
fMo
–
частота модального интервала
fMo
+1
– частота интервала следующего за модальным
Модальный интервал – интервал с наибольшей частотой.
Графически мода находится по гистограмме.
§4.
1. Размах вариации 
2. Среднее линейное отклонение
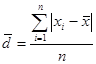
 - взвешенная - взвешенная
3. Дисперсия:
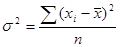
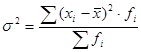 - взвешенная - взвешенная
4. Средне квадратическое отклонение
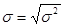
Свойство дисперсии.
1. 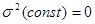
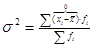
1. уменьшение всех значений признака на одну и ту же величину не меняет величину дисперсии.

2. Уменьшение всех значений признаков в к раз уменьшает величину дисперсии в к2
раз, а СКО в к
раз
3.  если исчислить средний квадрат отклонений от любой величины А отличающийся от средней арифметической, то он всегда будет больше среднего квадрата отклонений исчисленного из средней арифметической. Таким образом если исчислить средний квадрат отклонений от любой величины А отличающийся от средней арифметической, то он всегда будет больше среднего квадрата отклонений исчисленного из средней арифметической. Таким образом  от средней всегда меньше от средней всегда меньше  исчисленной от любой другой величины т.е. она имеет свойство минимальности. СКО=1,25 исчисленной от любой другой величины т.е. она имеет свойство минимальности. СКО=1,25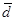 -при распределениях близких к нормальному. -при распределениях близких к нормальному.
В условиях нормального распределения существует следующая зависимость между  и количеством наблюдений в пределах и количеством наблюдений в пределах 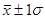 находится 68,3% наблюдений. находится 68,3% наблюдений.
В пределах 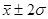 находится 95,4% наблюдений находится 95,4% наблюдений
В пределах 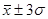 находится 99,7% наблюдений находится 99,7% наблюдений
§5.
Для сравнения вариации признаков в разных совокупностях или для сравнения вариации разных признаков в одной совокупности используются относительные показатели, базой служит средняя арифметическая.
1. Относительный размах вариации.

2. Относительное линейное отклонение

3. Коэффициент вариации
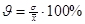
данные показатели дают не только сравнительную оценку но и образуют однородность совокупности. Совокупность считается однородной если коэффициент вариации не превышает 33%.
§6
На ряду с изучением вариации признака по всей совокупности в целом, часто бывает необходимо проследить количественные изменения признака, но группам, на которые делится совокупность и между ними. Эта достигается путем вычисления  разных видов. разных видов.
Виды дисперсии:
1. Общая дисперсия 
2. Межгрупповая дисперсия 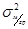
3. Внутригрупповая дисперсия (остаточная) 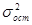
1.
измеряет вариацию признака во всей совокупности под влиянием все факторов обусловивших данную вариацию
Пример:
потребление йогурта: при выборке 100 человек
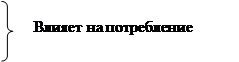 Возраст Возраст
Доход
Социальное положение

xi
–индивидуальное значение признака
 - среднее значение признака по всей совокупности - среднее значение признака по всей совокупности
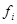 - частота этого признака. - частота этого признака.
2.
характеризует вариацию признака под влиянием признака фактора положенного в основу группировки.
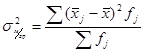
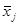 - средняя по группе - средняя по группе
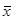 - общая средняя по группе - общая средняя по группе
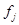 - частота по группе - частота по группе
3.
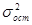 характеризует вариацию признака под влиянием факторов не включенных в группировку характеризует вариацию признака под влиянием факторов не включенных в группировку
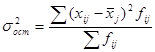
xij
–
i значение признака в j группе
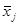 - среднее значение признака в j
группе - среднее значение признака в j
группе
fij
– частота
i-го признака в
j группе
Существует правило которое связывает 3 вида дисперсии, оно называется правило сложения дисперсии.

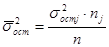
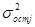 - остаточная дисперсия по j
группе - остаточная дисперсия по j
группе
 - сумма частот по j
группе - сумма частот по j
группе
n
– общая сумма частот
§7
основная задача анализа вариационных рядов – выявление закономерности распределения частот.
Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду в функционально связанным изменением значения признака.
Кривую распределения можно построить с помощью полигона и гистограммы. Целесообразно свести эмпирическое распределение к теоретическому, к одному из хорошо изученных виду.
Кривая нормального распределения.
Различают следующие разновидности кривых распределения:
- одновершинные
- много вершинные
Для однородных совокупностей характерны одновершинные кривые, много вершинная кривая говорит о неоднородности совокупности и необходимости перегруппировки.
Выяснение общего характера распределения предполагает оценку его однородности, и расчет асимметрии и эксцесса. Для симметричных распределений 
Для сравнительного изучения асимметрии различных распределений вычисляется коэффициент асимметрии As.
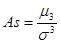 где где 
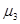 - центральный момент третьего порядка; - центральный момент третьего порядка; 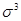 - СКО в кубе; - СКО в кубе;
Если 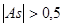 , то асимметрия значительная , то асимметрия значительная
Если As<0, то As – левосторонняя, если As>0, то As – правосторонняя.
Если  , то As незначительная. Для симметричных и умеренно асимметричных рассчитывается показатель эксцесса: , то As незначительная. Для симметричных и умеренно асимметричных рассчитывается показатель эксцесса: 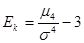 , если Ек
>0, то распределение островершинное, если Ek
<0, то распределение плосковершинное. , если Ек
>0, то распределение островершинное, если Ek
<0, то распределение плосковершинное.
§8.
Вариация альтернативного признака количественно проявляется следующим образом.
0 – единицы не обладающие данным признаком;
1 – единицы обладающие данным признаком;
Пусть:
р
– доля единиц обладающих данным признаком;
q
– доля единиц не обладающих данным признаком;
тогда p+
q=1.
Альтернативный признак принимает 2 значения 0 и 1 с весами p
и q.
 ; ; 
Прямые признаки
– это такие признаки, величина которых увеличивается с увеличением исследуемого явления.
Обратные признаки –
признаки, величина которых уменьшается с увеличением исследуемого явления.
Максимальная дисперсия доли равна 0,25.
Тема 6: Моделирование рядов распределения.
§1. Фактическое и теоретическое распределение
§2. Кривая нормального распределения.
§3. Проверка гипотезы о нормальном распределении.
§4. Критерии согласия: Пирсона, Романовского, Колмогорова.
§5. Практическое значение моделирования рядов распределения.
§1. Фактическое и теоретическое распределение
Одна из важнейших целей изучения рядов распределения состоит в том, чтобы выявить закономерность распределения и определить ее характер. Закономерности распределения наиболее отчетливо проявляются только при большом количестве наблюдений.
Фактическое распределение может быть изображено графически с помощью кривой распределения – графически изображается в виде непрерывной линии изменения частот в вариационном ряду функционально связанного с изменением варианта.
Под теоретической кривой распределения понимается кривая данного типа распределения в общем виде исключающего влияние случайных для закономерности факторов.
Теоретическое распределение может быть выражено аналитической формулой которая называется аналитической формулой. Наиболее распространенным является нормальное распространение.
§2. Кривая нормального распределения.
Закон нормального распределения:
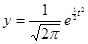 ; ;
у – ордината нормального распределения
t – нормированное отклонение.
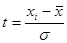 ; е=2,7218; xi
–
варианты вариационного ряда; ; е=2,7218; xi
–
варианты вариационного ряда;  - среднее; - среднее;
Свойства:
Функция нормального распределения – четная, т.е. f(t)=f(-t),  . Функция нормального распределения полностью определяется . Функция нормального распределения полностью определяется 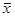 и СКО. и СКО.
§3. Проверка гипотезы о нормальном распределении.
Причиной частого обращения к закону распределения является то, что зависимость возникающая в результате действия множества случайных причин ни одна из которых не является преобладающей. Если в вариационном ряду рассчитали Мо=Ме, то это может указывать на близость к нормальному распределению. Наиболее точная проверка соответствия нормальному закону производится с помощью специальных критериев.
§4. Критерии согласия: Пирсона, Романовского, Колмогорова.
Критерий Пирсона.

 - теоретическая частота - теоретическая частота
 - эмпирическая частота - эмпирическая частота
Методика расчета теоретических частот.
- Определяется среднее арифметическое и
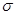 по интервальному вариационному ряду, считается t по каждому интервалу. по интервальному вариационному ряду, считается t по каждому интервалу.
- Находим значение плотности вероятности для нормированного закона распределения.
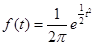 СТР.49 СТР.49
- Находим теоретическую частоту.
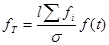
l – длина интервала
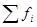 - сумма эмпирических частот - сумма эмпирических частот
 - плотность вероятности - плотность вероятности
округлить значение до целых
4. Расчет коэффициента Пирсона
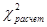
5. табличное значение 
d.f. – количество интервалов – 3
d.f. – количество степеней свободы.
6. если 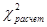 > >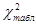 , то распределение не является нормальным, т.е. гипотеза о нормальном распределении отменяется. Если , то распределение не является нормальным, т.е. гипотеза о нормальном распределении отменяется. Если 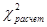 < <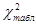 , то распределение является нормальным. , то распределение является нормальным.
Критерий Романовского.

 - критерий Пирсона расчетный; - критерий Пирсона расчетный;
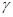 - число степеней. - число степеней.
Если С<3, то распределение близко к нормальному.
Критерий Колмогорова
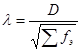 , D –
максимальное значение между накопленными эмпирическими и теоретическими частотами. Необходимое условие для использования Колмогорова: Число наблюдений более 100. По специальной таблице вероятностей , D –
максимальное значение между накопленными эмпирическими и теоретическими частотами. Необходимое условие для использования Колмогорова: Число наблюдений более 100. По специальной таблице вероятностей  с которой можно утверждать, что данное распределение является нормальным. с которой можно утверждать, что данное распределение является нормальным.
§5. Практическое значение моделирования рядов распределения.
1. возможность применить к эмпирическому распределению законов нормального распределения.
2. возможность использования правила 3х
сигм.
3. Возможность избежать дополнительных трудоемких и затратных расчетов, по исследованию совокупности зная, что распределение нормальное.
Тема 7: Выборочное наблюдение.
§1. Понятие выборочного наблюдения. Причины его применения.
§2. Виды выборочного наблюдения.
§3. Ошибки выборочного наблюдения.
§4. Задачи выборочного наблюдения
§5. Распространение данных выборочного наблюдения на генеральную совокупность.
§6. Малая выборка.
§1. Понятие выборочного наблюдения. Причины его применения.
Выборочное наблюдение
– такое не сплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные определенным образом.
Цель (задача) выборочного наблюдения: по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов статистического наблюдения.
Причины применения выборочного наблюдения:
- экономия материальных, трудовых затрат и времени;
- возможность более детально и подробно изучит отдельные единицы статистической совокупности и их группы.
- некоторые специфические задачи можно решить только с применением выборочного наблюдения.
- грамотное и хорошо организованное выборочное наблюдение дает высокую точность результатов.
Генеральная совокупность – совокупность единиц, из которых производится отбор.
Выборочная совокупность – совокупность отобранных для обследования единиц. В статистике принято различать параметры генеральной совокупности и выборочной совокупности.
| Совокупность
|
Средняя
|
Дисперсия
|
Объем
|
Доля
|
| Генеральная
|
m
|
s2
|
N
|
p
|
| Выборочная
|
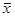
|
S2
|
n
|
p
|
Виды выборочного наблюдения
По методу отбора:
Повторное
Попавшая в выборку единица после регистрации наблюдаемых признаков возвращаются в генеральную совокупность для участия в дальнейшей процедуре отбора.
Объем генеральной совокупности остается неизменным, что обуславливает постоянное попадание в выборку какой-либо единицы.
Бесповторное
Попавшая в выборку единица не возвращается в совокупность, из которой происходит отбор.
По способу отбора:
Собственно-случайная
заключается в отношении единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем проводить такую выборку, нужно убедиться, что все единицы генеральной совокупности имеют равные шансы попасть в выборку, т.е. в полном перечне единиц статистической совокупности отсутствуют пропуски или игнорирования отдельных единиц. Следует, также, четко установить границы генеральной совокупности. Технически сложившейся отбор осуществляется методом жеребьевки или с помощью таблицы случайных чисел.
Механическая выборка
(каждый 5 по списку) применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в распределении единиц. При проведении механической выборки устанавливается пропорция отбора, которая устанавливается соотношением генеральной совокупности и выборочной совокупности.
Опасность ошибки при механической выборке может появляться вследствие: случайного совпадения выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности.
Районированная выборка
используется когда все единицы генеральной совокупности можно разбить на группы (районы, страны) по какому-либо признаку.
Комбинированная выборка.
Отбор единиц может быть произведен:
1. либо пропорционально объему группы
2. либо пропорционально внутригрупповой дифференциации признака
1. 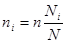 , где n – объем выборочной совокупности, N – объем генеральной совокупности, ni
–
объем выборки i
-группы, Ni
–
объем i
выборки. , где n – объем выборочной совокупности, N – объем генеральной совокупности, ni
–
объем выборки i
-группы, Ni
–
объем i
выборки.
2.  - этот способ является более точным, но в ходе проведения выборочного наблюдения очень трудно определить заранее о вариации. (до проявления наблюдения). - этот способ является более точным, но в ходе проведения выборочного наблюдения очень трудно определить заранее о вариации. (до проявления наблюдения).
Серийный отбор.
Используется когда ЕСС объединены в небольшие группы (серии), например упаковка с готовой продукцией, студенческие группы. Сущность серийной выборки – серии отбираются собственно случайным, либо механическим способом, а затем осуществляется сплошное обследование внутри отобранной серии.
Комбинированный отбор.
Это комбинация рассмотренных выше способов отбора чаще применяется комбинация типичных и серийных серии, т.е. отбор серий из нескольких типических групп.
Отбор моет быть еще многоступенчатым и одноступенчатым, многофразным и однофразным.
Многоступенчатый отбор:
из генеральной совокупности сначала извлекаются укрупненные группы, затем более мелкие, и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофразная выборка:
предполагает сохранение одной и той же единицы отбора на всех этапах его проведения. При этом отобранные на каждой последующей стадии единицы отбора подвергаются обследованию, программа которого расширяется (Пример: студенты всего института, затем студенты каких-то факультетов).
§3. Ошибки выборочного наблюдения.
Ошибки репрезентативности возникают только при выборочном наблюдении. Возникают в силу того, что выборочная совокупность не может в точности воспроизвести генеральную совокупность. Избежать их нельзя, но они легко поддаются прогнозированию и при необходимости их можно свести к минимуму.
Ошибка выборочного наблюдения – это разности между величиной параметра в генеральной совокупности и его величиной вычисленной по результатам выборочного наблюдения. Dх=-m+ , Dх – предельная ошибка в выборке, m - генеральная средняя; , Dх – предельная ошибка в выборке, m - генеральная средняя;  - выборочная средняя. - выборочная средняя.
Предельная ошибка выборки – величина случайная исследованию закономерностей случайны ошибок выборки посвящены работы Чебышева. В теореме Чебышева доказано, что Dх не превышает:  - средняя ошибка выборки.t-коэффициент доверия указывает на вероятность данной ошибки. Стр 42-43. - средняя ошибка выборки.t-коэффициент доверия указывает на вероятность данной ошибки. Стр 42-43.
В случае, когда нужно определить t по известной F(t) берем F(t) ближайшую большую и по ней определяем t.
Предельная ошибка доль
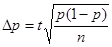 , р – доля. , р – доля.
Если отбор был осуществлен бесповторным способом, то в формулы предельных ошибок добавляется
 - поправка на бес повторность. - поправка на бес повторность.
Для каждого вида выборочного наблюдения представленная ошибка, рассчитываются по разному:
- собственно случайное и механическое наблюдение
 ; ; 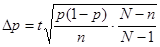
- Районированное наблюдение
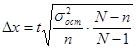
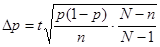
- Серийная выборка
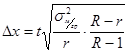
r – количество серий в выборке;
R – количество серий в генеральной совокупности;
 ; ;
 - меж групповая дисперсия доли. - меж групповая дисперсия доли.
§4. Задачи выборочного наблюдения
Применяется для следующих задач:
- n - ? для определения объема выборки по известной F(t), Dx.
- определение Dx выборки по известной F(t), n
- определение F(t) по известным Dx и n
1 задача n - ? Сначала n определяется по формуле повторного отбора  , , 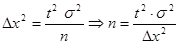 для бесповторного отбора: для бесповторного отбора: 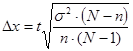
Способы для определения дисперсии:
- ее берут из предыдущих аналогичных исследований.
- СКО»
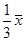
- СКО при нормальном распределении » 1/6 размаха вариации.
- если распределение заведомо асимметричное, то СКО » 1/5 размаха вариации
- Для доли применяется дисперсия максимально возможная р(1-р)=0,25
- при n³100, то s2
=S2
– выборочная дисперсия
30£ n
£100, то s2
=S2
(n/n-1), s2
– генеральная дисперсия
n<30, то S2
( малая, т.к. дисперсия выборочная) и все расчеты ведутся по S2
При расчете n не следует гнаться за большим значением t и за малыми предельными ошибками, т.к. это ведет к увеличению n следовательно, к увеличению затрат. По следующему закону аналогично.
§5. Распространение данных выборочного наблюдения на генеральную совокупность.
Конечной целью любого ВН является характеристика генеральной совокупности.
Величины, рассчитанные по результатам ВН распространяются на генеральную совокупность с учетом предела их предельной ошибки.
Предположим, что потребление йогурта в месяц одним человеком.
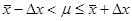
250-20£m£250+20; 230£m£270
А всего 1000 человек
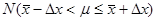
230000£m£270000
Для доли
p-Dp£p£p+Dp
48%-5%£p£48%+5%
43%£p£53%
§6. Малая выборка.
В практике статистического исследования в современных условиях все чаще приходится сталкиваться с небольшими по объему выборками.
Малая выборка –
выборка наблюдения численность единиц которого не превышает 30, n£30/
Разработка теории малой выборки была проделана английским статистом Госсет, писавшим под псевдонимом student в 1908 году.
Он доказал, что оценка расхождения между средствами малой выборки и генеральной выборки имеет особый закон распределения. При расчетах по малой выборке величина s2
не рассчитывается. tст
для возможных пределов ошибки пользуются критерием student. Стр.44-45. 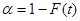 - вероятность обратного события. - вероятность обратного события.
Количество степеней свободы
d.f=n-1,
предельная ошибка малой выборки
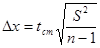
предельная ошибка доли

Тема 8: Корреляционно-регрессионный анализ и моделирование.
§1. Понятие корреляционной связи и КРА.
§2. Условия применения и ограничения КРА.
§3. Парная регрессия на основе метода наименьших квадратов.
§4. Применение парного линейного уравнения регрессии.
§5. Показатели тесноты связи и силы связи.
§6. Множественная корреляция.
§1. Понятие корреляционной связи и КРА.
Функциональная связь y=5x
Корреляционная связь 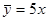
Различают 2 типа связей меду различными явлениями и их признаком функциональную и статистическую.
Функциональной называется такая связь когда с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е., значению одной переменной соответствует одно или несколько точно заданных значений другой переменной. Функциональная связь возможна лишь в том случае, когда переменная у зависит от переменной х и не от каких других факторов не зависит, но в реальной жизни такое невозможно.
Статистическая связь существует в том случае, когда с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения, но ее статистические характеристики изменяются по определенному закону.
Важнейший частный случай статистической связи – корреляционная связь. При корреляционной связи разным значениям одной переменной соответствуют различные средние значения другой переменной, т.е. с изменением значения признака х закономерным образом изменяется среднее значение признака у.
Слово корреляция ввел английский биолог и статист Френсис Галь (correlation)
Корреляционная связь может возникнуть разными путями:
- причинная зависимость вариации результативного признака от вариации факторного признака.
- Корреляционная связь может возникнуть между 2 следствиями одной причины (пожары, кол-во пожарников, размер пожара)
- Взаимосвязь признаков каждый из которых и причина и следствие одновременно (производительность труда и з/плата)
В статистике принято различать следующие виды зависимости:
- парная корреляция – связь между 2мя
признаками результативным и факторным, либо между двумя факторными.
- частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении другого факторного признака.
- множественная корреляция – зависимость результативного признака от двух и более факторных признаков включенных в исследование.
Задачей корреляционного анализа является количественная оценка тесноты связи между признаками. В конце 19 века Гальтон и Пирсон исследовали зависимость между ростом отцов и детей.
Регрессия исследует форму связи. Задача регрессионного анализа – определение аналитического выражения связи.
Корреляционно-регрессионный анализ как общее понятие включает в себя изменение тесноты связи и установления аналитического выражения связи.
§2. Условия применения и ограничения КРА.
1. наличие массовых данных, т.к. корреляционная связь является статистической
2. необходима качественная однородность совокупности.
3. подчинение распределения совокупности по результативному и факторному признаку, нормальному закону распределения, что связано с применением метода наименьших квадратов.
§3. Парная регрессия на основе метода наименьших квадратов.
Регрессионный анализ заключается в определении аналитического выражения связи. По форме различают линейную регрессию, которая выражается уравнением прямой 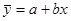 , и не линейную регрессию , и не линейную регрессию  или или  . .
По направлению связи различают на прямую т.е. с увеличением признака х увеличивается признак у.
Обратная т.е. с увеличением х уменьшается у.
1. способ графический – нанеся эмпирические данные на поле корреляции, но более точная оценка производится с помощью метода наименьших квадратов.
2. МНК
Х – признак фактический
У - признак результативный
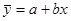

Разница между фактическим значением и значением рассчитанным по уравнению связи возведенное в квадрат должна стремиться к минимуму.
При МНК min сумма квадратов отклонений эмпирических значений у от теоретических полученных по выбранному уравнению регрессии.
Для линейной зависимости
 
для параболы

Для гиперболы

параметры a,b,c записываются в уравнение, затем подставляем полученное уравнение эмпирическое значение xi
и находим теоретическое значение yi
.
Затем сравниваем yi
теоретическое и yi
эмпирическое. Сумма квадратов разности между ними должна быть минимальна. Выбираем тот вид зависимости при котором выполняется данная зависимость.
В уравнении парной линейной регрессии:
b – коэффициент парной линейной регрессии,
он измеряет силу связи, т.е. характеризует среднее по совокупности отклонение у от его средней величины на принятую единицу измерения.
b
=20 при изменении х на 1 признак у отклониться от своего среднего значения на 20 в среднем по совокупности.
Положительный знак при коэффициенте регрессии говорит о прямой связи между признаками, знак «-» говорит об обратной связи между признаками.
§4. Применение парного линейного уравнения регрессии.
Основное применение – прогнозирование по уравнению регрессии. Ограничением при прогнозировании служат условия стабильности других факторов и условий процесса. Если резко измениться в нем среда протекающего процесса, то данное уравнение регрессии не будет иметь места.
Точечный прогноз получается подстановкой в уравнение регрессии ожидаемого значения фактора. Вероятность точной реализации такого прогноза крайне мала.
Если точечный прогноз сопровождается значением средней ошибки прогноза, то такой прогноз называется интервальным.
Средняя ошибка прогноза образуется из двух видов ошибок:
1. ошибок 1 рода – ошибка линии регрессии
2. ошибка 2 рода – ошибка связанная с ошибкой вариации.
Средняя ошибка прогноза.

 - ошибка положения линии регрессии в генеральной совокупности - ошибка положения линии регрессии в генеральной совокупности
n - объем выборки
xk
– ошибочное значение фактора
 - СКО результативного признака от линии регрессии в генеральной совокупности - СКО результативного признака от линии регрессии в генеральной совокупности
Корреляционный анализ предполагает оценку тесноты связи. Показатели:
- линейные коэффициент корреляции – характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости

при  =-1 связь функциональная обратная, =-1 связь функциональная обратная,  =1 связь функциональная прямая, при =1 связь функциональная прямая, при  =0 связь отсутствует. =0 связь отсутствует.
МИНУСЫ
Применяется только для линейных связей, используется для оценки связей между количественными признаками. Рассчитываются только по индивидуальным значениям.
Корреляционное отношение:
Эмпирическое:  оба вида дисперсии рассчитываются по результативному признаку. оба вида дисперсии рассчитываются по результативному признаку.
Теоретическое: 
 - дисперсия значений результативного признака рассчитанных по уравнению регрессии - дисперсия значений результативного признака рассчитанных по уравнению регрессии
 - дисперсия эмпирического значения результативного признака - дисперсия эмпирического значения результативного признака

ПЛЮСЫ
· высокая степень точности
· подходит для оценки тесноты связи между описательным и количественным признаком, но количественный должен быть результативным
· подходит для любых типов связей
Коэффициент корреляции Спирмена
Ранги
– порядковые номера единиц совокупности в ранжированном ряду. Ранжировать оба признака необходимо в одном и том же порядке от меньших к большим или наоборот. Если ранги единиц совокупности обозначить рх
и ру
, то коэффициент корреляции рангов примет следующий вид:

Преимущества коэффициента корреляционного ряда:
- Ранжировать можно и по описательным признакам, которые нельзя выразить численно, следовательно расчет коэффициента Спирмена возможен для следующих пар признаков: кол-во – кол-во; описательный – количественный; Описательный – описательный. (образование – описательный признак)
- показывает направление связи
Недостатки коэффициента Спирмена.
1. одинаковым разностям рангов могут соответствовать совершенно отличные разности значения признака (в случае количественных признаков). Пример: Выработка электроэнергии страны в год
США 2400 кВт/ч 1
РФ 800 кВт/ч 2
Канада 600 кВт/ч 3
Если среди значения Спирмена встречаются несколько одинаковых, то образуются связанные ранги т.е. одинаковые средние номера
800 1
600 2,5
600 2,5
400 4
В данном случае коэффициент Спирмена рассчитывается следующим образом:

j –
номера связок по порядку для признака х
Aj
–
число одинаковых рангов в j связи по х
k –
номера связок по порядку признака у
Bk
–
число одинаковых рангов в к-ой
связке по у
4.
Коэффициент корреляции ранга Кендалла
 - максимальная сумма ранга - максимальная сумма ранга
S – фактическая сумма рангов

Дает более строгую оценку чем коэффициент Спирмена. 
Для расчета  все единицы ранжируются по признаку х по признаку у
для каждого ранга подсчитывается число последующих рангов превышающих данный их сумму обозначим Р и число последующих рангов ниже данного обозначения Q. все единицы ранжируются по признаку х по признаку у
для каждого ранга подсчитывается число последующих рангов превышающих данный их сумму обозначим Р и число последующих рангов ниже данного обозначения Q.
S=P-Q
P+Q=1
/2
n(n-1)

5. Коэффициент корреляции ранга Фехнера.
| 
|
х
|
у
|

|

|

|
| 600
|
50
|
+
|
+ - C
|
| 700
|
40
|
+
|
0 – C
|
| 300
|
20
|
-
|
- - C
|
| 400
|
50
|
-
|
+ - H
|

Коэффициент Фехнера
– мера тесноты связи в виде отношения разности числа пар совпадающих и не совпадающих знаков к сумме этих чисел.
1. расчет средних по х и у
2. сравниваются индивидуальные значения xi
yi
со средними значениями с обязательным указанием знака «+» или «-». Если знаки совпадают по х и у, то мы относим их числу «С» если, нет, то к «Н».
3. подсчитываем количество совпадающих и несовпадающих пар.
 Коэффициент Фехнера очень грубый коэффициент оценки связи, не учитывающий величину отклонений от среднего значения, но он может служить ориентиром для оценки интенсивности связи. Коэффициент Фехнера очень грубый коэффициент оценки связи, не учитывающий величину отклонений от среднего значения, но он может служить ориентиром для оценки интенсивности связи.
| Часто а
|
Редко в
|
| Есть А
|
Аа 5
|
Ав 10
|
| Нет В
|
Ва 7
|
Вв 4
|
Задача измерения связи становится перед статисткой по отношению к описательным признакам, важным частным случаем такой задачи, измерения связи между 2 альтернативными признаками один из которых причина другой последствие.
Теснота связи между 2 альтернативными признаками может быть измерена с помощью 2х коэффициентов:
1. коэффициент ассоциации
2. коэффициент контингенции

Коэффициент контингенции имеет недостаток: при равных нулю одного из двух гетерогенных сочетаний Ав или Ва коэффициент обращается в единицу. Очень либерально оценивает тесноту связи – завышает ее.
Коэффициент Пирсона
При наличии не двух, а более возможных значений каждого из взаимосвязанных признаков рассчитываются следующие коэффициенты:
- Коэффициент Пирсона
- Коэффициент Чупрова для описательного признака
Коэффициент Пирсона рассчитывается по квадратным матрицам
| доход
|
Ниже нормы
|
Норма
|
2 нормы
|
3 нормы
|
| 1-3 ПМ
|
2
|
4
|
-
|
-
|
| 3-7 ПМ
|
5
|
3
|
5
|
-
|
| 7-12 ПМ
|
10
|
7
|
6
|
1
|
| Св. 12 ПМ
|

к1
и к2
– число группы по признакам 1 и 2 соответственно. Минус коэффициента Пирсона в том, он не достигает 1 даже при увеличении количества групп.
Коэффициент Чупрова (1874 –1926)
 коэффициент Чупрова более строже оценивает тесноту связи. коэффициент Чупрова более строже оценивает тесноту связи.
§6. Множественная корреляция.
Изучение связи между результативным и двумя или более факторными признаками называется множественной регрессией.
При исследовании зависимостей методами множественной регрессии ставят 2 задачи.
- определение аналитического выражения связи между результативным признаком у и фактическими признаками х1
, х2
, х3
, …хк
, т.е. найти функцию у=f(х1
, х2
, …хк
)
- Оценка тесноты связи между результативным и каждым из факторных признаков.
Корреляционно-регрессионная модель (КРМ) – такое уравнение регрессии, которое включает основные факторы, влияющие на вариацию результативного признака.
Построение модели множественной регрессии включает этапы:
- выбор формы связи
- отбор факторных признаков
- обеспечение достаточного объема совокупности для получения верных оценок.
I. все множество связей между переменными, встречающиеся на практике достаточно полно описывается функциями 5-ти видов:
- линейная:

- степенная:

- показательная:

- парабола:

- гипербола:

хотя все 5 функций присутствуют в практике КРА, наиболее часто используется линейная зависимость, как наиболее простая и легко поддающаяся интерпретации уравнение линейной зависимости:  , к – множество факторов включающихся в уравнение, bj
– коэффициент условно-чистой регрессии, который показывает среднее по совокупности отклонение результативного признака от его среднего значения при отклонении фактора xj
от своей средней величины на единицу при условии, что все остальные факторы, входящие в уравнение сохраняют средние значения. , к – множество факторов включающихся в уравнение, bj
– коэффициент условно-чистой регрессии, который показывает среднее по совокупности отклонение результативного признака от его среднего значения при отклонении фактора xj
от своей средней величины на единицу при условии, что все остальные факторы, входящие в уравнение сохраняют средние значения.
Параметры уравнения множественной регрессии и определение с помощью МНК.

  Пример:
0 – т.к. >0,7 следовательно на них обращаем особое внимание
ЭКО. Шкала тесноты связи:
Если связь 0 – 0,3 – слабая связь
0,3 – 0,5 – заметная
0,3 – 0,5 – тесная
0,7 – 0,9 – высокая
более 0,9 – весьма высокая
затем сравниваем два признака (доход и пол) <0,7, то включаем в уравнение множественной регрессии.
Отбор факторов для включения в уравнение множественной регрессии:
- между результативным и фактическим признаками должна быть причинно-следственная зависимость.
- результативный и фактический признаки должны быть тесно связаны между собой иначе возникает явление мультиколлинеарности (>06)
, т.е. включенные в уравнение факторные признаки влияют не только на результативный, но друг на друга, что влечет к неверной интерпретации числовых данных.
Методы отбора факторов для включения в уравнение множественной регрессии:
1.
экспертный метод
– основан на интуитивно логическом анализе который выполняется высококвалифицированными экспертами.
2.
использование матриц парных коэффициентов корреляции осуществляется параллельно с первым методом, матрица симметрична относительно единичной диагонали.
3.
пошаговый регрессионный анализ – последовательное включение факторных признаков в уравнение регрессии и проверки значимости проводится на основании значений двух показателей на каждом шаге. Показатель корреляции, регрессии.
Показатель корреляции: рассчитывают изменение теоретической корреляции отношения или изменение средней остаточной дисперсии. Показатель регрессии – изменение коэффициента условно чистой регрессии.
 Пример расчета: Пример расчета:
| Ниже среднего
|
Среднее
|
Выше среднего
|
Итого
|
| Ниже среднего
|
12
|
7
|
3
|
22
|
| Средний
|
15
|
10
|
9
|
34
|
| Выше среднего
|
3
|
15
|
10
|
29
|
| Итого
|
31
|
32
|
22
|
85
|

|