Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
1.
ПОНЯТИЕ О
СТАТИСТИЧЕСКОЙ
ТАБЛИЦЕ.
ЭЛЕМЕНТЫ
СТАТИСТИЧЕКОЙ
ТАБЛИЦЫ.
Результаты
сводки и группировки
материалов
статистического
наблюдения,
как правило,
излагаются
в виде таблиц.
Таблица
является наиболее
рациональной,
наглядной и
компактной
формой представления
статистического
материала.
Однако
не всякая таблица
является
статистической.
Таблица умножения,
опросный лист
социологического
обследования
и т.д. могут носить
табличную
форму, но еще
не являются
статистическими
таблицами.
Статистическую
таблицу от
других табличных
форм отличает
следующее:
Таким
образом, статистической
называется
таблица,
которая содержит
сводную числовую
характеристику
исследуемой
совокупности
по одному или
нескольким
существенным
признакам,
взаимосвязанным
логикой экономического
анализа.
Основные
элементы
статистической
таблицы, представленные
на рис.1, составляют
как бы ее основу.
Название
таблицы *
(общий
заголовок)
Содержание
строк
|
Наименование
граф (верхние
заголовки)
|
А
|
1 |
2 |
3 |
4 |
5 |
. . . |
Наименование
строк
(боковые
заголовки)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итоговая
строка
|
|
|
|
|
|
Итоговая
графа
|
*
Примечания
к таблице
Рис.
1. Остов
(основа) статистической
таблицы
Табличная
форма расположения
числовой информации
– это такая,
при которой
число располагается
на пересечении
четко сформулированного
заголовка по
вертикальному
столбцу, называемому
графой, и сформулированного
названия по
соответствующей
горизонтальной
полосе – строке.
Таким
образом, внешне
таблица представляет
собой пересечение
граф и строк,
которые формируют
ее состав. Каждое
пересечение
образует клетку
таблицы. Размер
таблицы определяется
произведением
числа строк
на число граф.
Статистическая
таблица содержит
три вида заголовков:
общий, верхние
и боковые. Общий
заголовок
отражает содержание
всей таблицы
(к какому месту
и времени она
относится),
располагается
над ее макетом
по центру и
является внешним
заголовком.
Верхние
заголовки
характеризуют
содержание
граф (заголовки
сказуемого),
а боковые (заголовки
подлежащего)
– срок. Они являются
внутренними
заголовками.
Остов
таблицы, заполненный
заголовками,
образует ее
макет. Если на
пересечении
граф и срок
записать цифры,
то получается
полная статистическая
таблица.
Цифровой
материал может
быть представлен
абсолютными
(численность
населения РФ),
относительными
(индексы цен
на продовольственные
товары) и средними
(среднемесячный
доход служащего
коммерческого
банка) величинами.
В
случае необходимости
таблицы могут
сопровождаться
примечанием,
используемым
с целью пояснения
заголовков,
методики расчета
некоторых
показателей,
источников
информации
и т.д.
По
логическому
содержанию
таблица представляет
собой «статистическое
предложение»,
основными
элементами
которого являются
подлежащее
и сказуемое.
Подлежащим
статистической
таблицы называется
объект, характеризующийся
цифрами. Это
могут быть одна
или несколько
совокупностей,
отдельные
единицы совокупностей
(фирмы, объединения)
в порядке их
перечня или
сгруппированные
по каким – либо
признакам
(отдельные
территориальные
единицы или
временные
периоды в
хронологических
таблицах и
т.д.). Обычно
подлежащее
таблицы дается
в левой части,
в наименовании
строк.
Сказуемое
статистической
таблицы образует
система показателей,
которыми
характеризуется
объект изучения,
т.е. подлежащее
таблицы. Сказуемое
формирует
верхние заголовки
и составляет
содержание
граф с логически
последовательным
расположением
показателей
слева направо.
Расположение
подлежащего
и сказуемого
может меняться
местами, что
зависит от
достижения
каждым исследователем
в отдельности
наиболее полного
и лучшего способа
прочтения и
анализа исходной
информации
об исследуемой
совокупности.
26
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
10.
ДИАГРАММЫ
СРАВНЕНИЯ
Наиболее
распространенными
диаграммами
сравнения
является столбиковые
диаграммы,
принцип построения
которых состоит
в изображении
статистических
показателей
в виде поставленных
по вертикали
прямоугольников
– столбиков.
Каждый столбик
изображает
величину отдельного
уровня исследуемого
статистического
ряда. Таким
образом, сравнение
статистических
показателей
возможно потому,
что все сравнимые
показатели
выражены в
одной единице
измерения.
При
построении
столбиковых
диаграмм необходимо
начертить
систему прямоугольных
координат, в
которой располагаются
столбики. На
горизонтальной
оси располагаются
столбики. На
горизонтальной
оси располагаются
основания
столбиков,
величина основания
столбиков,
величина основания
определяется
произвольно,
но устанавливается
одинаковой
для всех.
Шкала,
определяющая
масштаб столбиков
по высоте,
расположена
по вертикальной
оси. Величина
каждого столбика
по вертикали
соответствует
размеру изображаемого
на графике
статистического
показателя.
Таким образом,
у всех столбиков,
составляющих
диаграмму,
переменной
величиной
является только
одно измерение.
Покажем построение
столбиковой
диаграммы по
данным табл.
5, характеризующим
вклады граждан
в учреждения
Сбербанка в
1995 г. (рис. 7).
Таблица
5.
Вклады
граждан в учреждения
Сбербанка в
1995 г.
(цифры
условные)
Месяц
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Вклад,
млрд. руб.
|
550 |
560 |
560 |
640 |
640 |
1100 |
1100 |
1100 |
1630 |
1610 |
1610 |
2500 |
Р
ис.
7.
В
соответствии
с изложенными
выше правилами
на горизонтальной
оси размещаются
основания
двенадцати
столбиков на
одинаковом
расстоянии
друг от друга,
в данном случае
0,5 см. Ширина
столбиков
принята 0,5 см.
Масштаб на оси
ординат – 500 млрд
руб. – 1 см. Наглядность
данной диаграммы
достигается
сравнением
величины столбиков.
Размещение
столбиков в
поле графика
может быть
различным:
на
одинаковом
расстоянии
друг от друга
(рис. 7);
вплотную
друг от друга
(рис. 8);
в
частном наложении
друг на друга
(рис. 9).
Правила
построения
столбиков
диаграмм допускаются
одновременное
расположение
на одной горизонтальной
оси изображений
нескольких
показателей.
В этом случае
столбики
располагаются
группами, для
каждой из которых
может быть
принята разная
размерность
варьирующих
признаков (рис.
10).
Р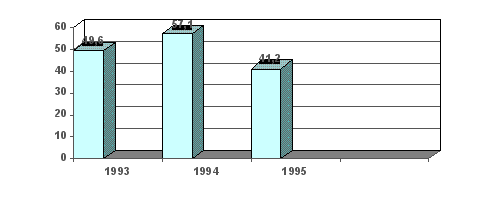
ис.
8. Динамика
выпуска книг
и брошюр в одном
из
регионов
России за 1993 –
1995 гг.
Р
ис.
9. Динамика
денежных доходов
населения в
регионе
за
1993 – 1995 гг.
Разновидности
столбиковых
диаграмм составляют
так называемые
ленточные
или
полосовые
диаграммы.
Их отличие
состоит в том,
что масштабная
шкала расположена
по горизонтали
сверху или
снизу и она
определяет
величину полос
по длине.
Р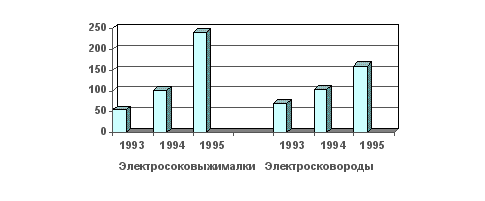
ис.
10. Динамика
производства
некоторых видов
товаров
хозяйственного
потребления
за 1993 – 1995 гг.
Область
применения
столбиковых
и полосовых
диаграмм одинакова,
так как идентичны
правила их
построения.
Одномерность
изображаемых
статистических
показателей
и их одномасштабность
для различных
столбиков
и полос требуют
выполнения
единственного
положения:
соблюдения
соразмерности
(столбиков –
по высоте, полос
– по длине) и
пропорциональности
изображаемых
величинам. Для
выполнения
этого требования
необходимо:
во-первых, чтобы
шкала, по которой
устанавливается
размер столбика
(полос), начиналась
с нуля; во-вторых,
эта шкала должна
быть непрерывной,
т.е. охватывать
все числа данного
статистического
ряда; разрыв
шкалы и соответственно
столбиков
(полос) не допускается.
Невыполнение
указанных
правил приводит
к искаженному
графическому
представлению
анализируемого
статистического
материала.
В
качестве примера
приведем полосовую
диаграмму
сравнения по
данным табл.
6 (рис.
11).
Таблица
6
Общий
объем промышленного
производства
в
некоторых
странах
СНГ в I
квартале 1995 г.
(в
% к I кварталу
1994 г.) (цифры условные)
Страны
СНГ
|
Общий
объем промышленного
производства
|
|
Казахстан
Беларусь
Россия
Кыргызстан
Таджикистан
Армения
|
88,7
83,5
80,7
77,6
71,8
41,6
|
Р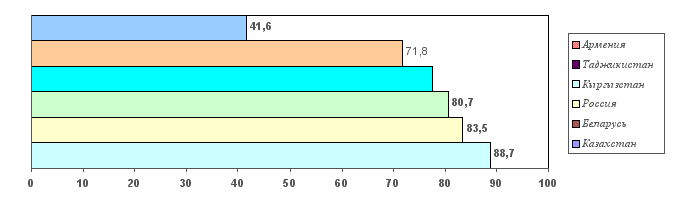
ис.
11. Общий
объем промышленного
производства
в странах СНГ
в
I
квартале 1995 г.
(в % к I
кварталу 1994 г.)
Столбиковые
и полосовые
диаграммы как
прием графического
изображения
статистических
данных, по существу,
взаимозаменяемы,
т.е. рассматриваемые
статистические
показатели
рано могут быть
представлены
как столбиками,
так и полосами.
И в этом, и в другом
случае для
изображения
величины явления
используется
одно измерение
каждого прямоугольника
– высота
столбика или
длина полосы.
Поэтому и сфера
применения
этих двух видов
диаграмм в
основном одинакова.
Разновидность
столбиковых
(ленточных)
диаграмм являются
направленные
диаграммы.
Они отличаются
от обычных
двусторонним
расположением
столбиков или
полос и имеют
начало отсчета
по масштабу
в середине.
Обычно такие
диаграммы
применяются
для изображения
величин противоположного
качественного
значения. Сравнение
между собой
столбиков
(полос), направленных
в разные стороны,
менее эффективно,
чем расположенных
рядом в одном
направлении.
Несмотря на
это, анализ
направленных
диаграмм позволяет
делать достаточно
содержательные
выводы, так как
особое расположение
придает графику
яркое изображение.
К группе двусторонних
относятся
диаграммы
числовых отклонений.
В них полосы
направлены
в обе стороны
от вертикальной
нулевой линии:
вправо – для
прироста; влево
– для уменьшения.
С помощью таких
диаграмм удобно
изображать
отклонения
от плана или
некоторого
уровня, принятого
за базу сравнения.
Важным достоинством
рассматриваемых
диаграмм является
возможность
видеть размах
колебаний
изучаемого
статистического
признака, что
само по себе
имеет большое
значение для
экономического
анализа (рис.
12).
П
роценты
Рис.
12. Распределение
населения
одного из регионов
России
по
полу и возрасту
в 1995 г.
Для
простого сравнение
независимых
друг от друга
показателей
могут также
использоваться
диаграммы,
принцип построения
которых состоит
в том, что сравниваемые
величины изображаются
в виде правильных
геометрических
фигур, которые
строятся так,
чтобы площади
их относились
между собой
как количества,
этими фигурами
изображаемые.
Иными словами,
эти
диаграммы
выражаются
величину
изображаемого
явления размером
явления размером
своей площади.
Для
получения
диаграмм
рассматриваемого
типа используют
разнообразные
геометрические
фигуры –
квадрат, круг,
реже – прямоугольник.
Известно, что
площадь квадрата
равна квадрату
его стороны,
а площадь круга
определяется
пропорционально
квадрату его
радиуса. Поэтому
для построения
диаграмм необходимо
сначала из
сравниваемых
величин извлечь
квадратный
корень. Затем
на базе полученных
результатов
определить
сторону квадрата
или радиус
круга соответственно
принятому
масштабу.
Например,
если изобразить
в виде квадрата
или круга поставки
российского
газа в ближайшее
зарубежье, то
сначала нужно
извлечь квадратные
корни из этих
цифр. (табл. 7)
Таблица
7
Поставки
российского
газа в страны
ближнего зарубежья,
январь
– август 1995 г.
| Страны
ближнего зарубежья |
Млн.
м3
|
|
Украина
Беларусь
Литва
|
44
460,1
10
250,0
2
458,0
|
Это
составит: для
Украины –
210,9; Беларуси –
101,2; Литвы – 49,6. Затем
установить
масштаб и по
этим данным
построить
квадраты. Для
нашего примера
прием 1 см равным
30 млн. м3.
Тогда сторона
первого квадрата
составит 7,03 см
(210,9 : 30); второго –
3,4 см; третьего
– 1,65 см (рис. 13).
 4 460,1
4 460,1
 Украина
Украина
  10 250,0
10 250,0
2 458,0
Беларусь
 
Литва
Рис.
13. Поставки
российского
газа в страны
ближнего
зарубежья,
январь – август
1995 г.
Для
правильного
построения
диаграмм квадраты
или круг необходимо
расположить
на одинаковом
друг от друга
расстоянии,
а в каждой фигуре
указать числовое
значение, которое
она изображает,
не приводя
масштаба измерения.
К
рассматриваемому
виду диаграмм
относится
графическое
изображение,
полученное
путем построения
один в другом
квадратов,
кругов или
прямоугольников
с различной
заштриховкой
или закраской.
Такие диаграммы
также позволяют
сравнивать
между собой
ряд исследуемых
величин. На
рис. 14 показан
такой вариант
круговой диаграммы.
Наиболее
выразительным
и легко воспринимаемым
является способ
построения
диаграмм сравнения
в виде фигур
– знаков. В этом
случае статистические
совокупности
изображаются
не геометрическими
фигурами, а
символами или
знаками, воспроизводящими
в какой – то
степени внешний
образ статистических
данных. Достоинство
такого способа
графического
изображения
заключается
в высокой степени
наглядности,
в получении
подобного
отображения,
отражающего
содержание
сравниваемых
совокупностей.
Важнейший
признак любой
диаграммы –
масштаб. Поэтому,
чтобы правильно
построить
фигурную диаграмму,
необходимо
определить
единицу
счета.
В качестве
последней
принимается
отдельная
фигура (символ),
которой условно
присваивается
конкретное
численное
значение. А
исследуемая
статистическая
величина
изображается
отдельным
количеством
одинаковых
по размеру
фигур, последовательно
располагающихся
на рисунке.
Однако в большинстве
случаев не
удается изобразить
статистический
показатель
целым количеством
фигур. Последнюю
из них приходится
делить на части,
так как по масштабу
один знак является
слишком крупной
единицей измерения.
Обычно эта
часть определяется
на глаз. Сложность
точного ее
определения
является недостатком
фигурных диаграмм.
Однако, если
большая точность
представления
статистических
данных не
преследуется,
то результаты
получаются
вполне удовлетворительными.
Рассмотрим
построение
фигурной диаграммы
по данным таб.
8 фермерских
хозяйств в
России за 1993 –
1995 гг.
Таблица
8
Численность
фермерских
хозяйств в
России за 1993 –
1995 гг.
(данные
условные)
| Год |
1993 |
1994 |
1995 |
Численность
фермерских
хозяйств
|
49
|
183
|
270
|
 
1993 -
49 тыс.
    
- 183 тыс.
- -
270 тыс.
  
-
40 тыс.
фермерских
хозяйств
Рис.
15. Динамика
численности
фермерских
хозяйств в
одном
из регионов
России за 1993 –
1995 гг.
Примем
условно за одни
знак 40 тыс. фермерских
хозяйств. Тогда
число хозяйств
в России
в 1993 г. в размере
49 тыс. будет
изображено
в количестве
1,22 хозяйства,
в 1994 г. – 4,6 хозяйства
и т.д. (Рис. 15).
Как
правило, фигурные
диаграммы
широко используются
для популяризации
статистических
данных и рекламы.
3
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
11.
СТРУКТУРНЫЕ
ДИАГРАММЫ
Основное
назначение
структурных
диаграмм заключается
в графическом
представлении
состава статистических
совокупностей,
характеризующихся
как соотношение
различных
частей каждой
из совокупностей.
Состав статистической
совокупности
графически
может быть
представлен
с помощью как
абсолютных,
так и относительных
показателей.
В первом случае
не только размеры
отдельных
частей, но и
размер графика
в целом определяются
статистическими
величинами
и измеряются
в соответствии
с изменениями
последних. Во
втором – размер
всего графика
не меняется
(так как сумма
всех частей
любой совокупности
составляет
100%), а меняются
только размеры
отдельных его
частей. Графическое
изображение
состава совокупности
по абсолютным
и относительным
показателям
способствует
проведению
более глубокого
анализа и позволяет
проводить
международные
сопоставления
и сравнения
социально –
экономических
явлений.
В
качестве графического
образа для
изображения
структуры
совокупностей
применяются
прямоугольники
– для построения
столбиковых
и полосовых
диаграмм и
круги – для
построения
секторных
диаграмм.
Покажем
построение
указанных выше
диаграмм на
конкретных
примерах.
Чтобы
по приведенным
данным табл.
9 построить
диаграмму,
отражающую
структуру
сравниваемых
совокупностей
по соотношению
в них отдельных
видов часов,
ряд абсолютных
показателей
заменяются
рядом относительных
величин. В этом
случае каждая
из полос диаграммы
будет иметь
одинаковую
длину, так как
при переходе
к относительным
величинам
погашаются
различия в
абсолютных
размерах
совокупностей.
В то же время
структурные
различия проявляются
значительно
четче. Графическое
изображение
структуры с
помощью столбиковых
(полосовых)
диаграмм позволяет
изучить особенности
многих изучаемых
экономических
явлений. Так,
приведенная
на рис. 16 диаграмма,
построенная
по данным таб.
9, характеризует
увеличение
доли наручных
часов в общем
производстве.
Таблица
9
Производство
часов по
видам в одном
из регионов
России
за 1985 –
1995 гг.
|
1985
г. |
1995
г. |
|
млн.
шт. |
% |
млн.
шт. |
% |
Часы,
всего
В
том числе
наручные
настенные
будильники
|
52,5
24,4
9,3
18,8
|
100,0
46,5
17,7
35,8
|
60,1
31,6
10,5
18,0
|
100,0
52,6
17,5
29,9
|
Р
ис.
16. Динамика
удельного веса
производства
часов по видам
(1985 – 1995 гг.)
Более
распространенным
способом
графического
изображения
структуры
статистических
совокупностей
является секторная
диаграмма,
которая считается
основной формой
диаграммы
такого назначения.
Это объясняется
тем, что идея
целого очень
хорошо и наглядно
выражается
кругом, который
представляет
всю совокупность.
Удельный вес
каждой части
совокупности
в секторной
диаграмме
характеризуется
величиной
центрального
угла (угол между
радиусами
круга). Сумма
всех углов
круга, равная
360о,
приравнивается
к 100%, а следовательно,
1% принимается
равным 3,6о.
Приведем
пример построения
секторной
диаграммы по
данным таб. 10.
Таблица
10
Динамика
доли негосударственного
сектора экономики
в розничной
торговле
( в % к общему объему
розничного
товарооборота
в России)
|
1992
г. |
1993
г. |
Государственный
сектор
Негосударственный
сектор
В
том числе
предприятия:
частной
и смешанной
форм собственности
потребительской
кооперации
прочих
форм собственности
|
78
22
1,8
20
0,2
|
49
51
31
16
4
|
Построение
секторной
диаграммы
начинается
с определения
центральных
углов секторов.
Для этого процентное
выражение
отдельных
частей совокупностей
умножают на
3,6о.
Например, для
данных:
1992
г.: 78 * 3,6о
= 280,8о
1,8
* 3,6о
= 6,5о
20 * 3,6о
= 72о
0,2
* 3,6о
= 0,7о
1993
г.: 49 * 3,6о
= 176,4о
31 * 3,6о
= 111,6о
16 * 3,6о
= 57,6о
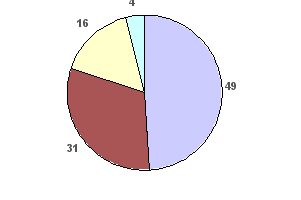
4 * 3,6о
= 14,4о
Р
ис.
17. Динамика
доли негосударственного
сектора экономики
в розничной
торговле (в % к
общему объему
розничного
товарооборота
в России).
По
найденным
значениям углов
круги делятся
на соответствующие
секторы (рис.
17).
Применение
секторных
диаграмм позволяет
не только графически
изобразить
структуру
совокупности
и ее изменение,
но и показать
динамику численности
этой совокупности.
Для этого строятся
круги, пропорциональные
объему изучаемого
признака, а
затем секторами
выделяются
его отдельные
части.
Рассмотренные
способы графического
изображения
структуры
совокупности
имеют как
достоинства,
так и недостатки.
Так,
секторная
диаграмма
сохраняет
наглядность
и выразительность
лишь при небольшом
числе частей
совокупности,
в противном
случае ее применение
малоэффективно.
Кроме того,
наглядность
секторной
диаграммы
снижается при
незначительных
изменениях
структуры
изображаемых
совокупностей:
она выше, если
имеются существенные
различия сравниваемых
структур.
Преимуществом
столбиковых
(ленточных)
структурных
диаграмм по
сравнению с
секторными
являются их
большая емкость,
возможность
отразить более
широкий объем
полезной информации.
5
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
12.
ДИАГРАММЫ
ДИНАМИКИ
Для
изображения
и внесения
суждений о
развитии явления
во времени
строятся диаграммы
динамики.
Для
наглядного
изображения
явлений в рядах
динамики используются
диаграммы:
столбиковые,
ленточные,
квадратные,
круговые, линейные,
радикальные
и др. Выбор вида
диаграммы
зависит в основном
от особенностей
исходных данных,
цели исследования.
Например, если
имеется ряд
динамики с
несколькими
неравноотносящимися
уровнями во
времени (1913, 1940, 1950,
1980, 1985, 1997 гг.), то часто
для наглядности
используют
столбиковые,
квадратные
или круговые
диаграммы. Они
зрительно
впечатляют,
хорошо запоминаются,
н не годны для
изображения
большого числа
уровней, так
как громоздки.
Когда число
уровней в ряду
динамики велико,
целесообразно
применять
линейные диаграммы,
которые воспроизводят
непрерывность
процесса развития
в виде непрерывной
ломанной линии.
Кроме того,
линейные диаграммы
удобно использовать:
если целью
исследования
является изображение
общей тенденции
и характера
развития явления;
когда на одном
графике необходимо
изобразить
несколько
динамических
рядов с целью
их сравнения;
если наиболее
существенным
является
сопоставление
темпов роста,
а не уровней.
Для
построения
линейных графиков
применяют
систему прямоугольных
координат.
Обычно по оси
абсцисс откладывается
время (годы,
месяцы и т.д.),
а по оси ординат
– размеры
изображаемых
явлений или
процессов. На
оси ординат
наносят масштабы.
Особое внимание
следует обратить
на их выбор,
так как от этого
зависит общий
вид графика.
Обеспечение
равновесия,
пропорциональности
между осями
координат
необходимо
в графике в
связи с тем,
что нарушение
равновесия
между осями
координат дает
неправильное
изображение
развития явления.
Если масштаб
для шкалы на
оси абсцисс
очень растянут
по сравнению
с масштабом
на оси ординат,
то колебания
в динамике
явлений мало
выделяются,
и наоборот,
преувеличение
масштаба по
оси ординат
по сравнению
с масштабом
на оси абсцисс
дает резкие
колебания.
Равным периодам
времени и размерам
уровня должны
соответствовать
равные отрезки
масштабной
шкалы.
В
статистической
практике чаще
всего применяются
графические
изображения
с равномерными
шкалами. По оси
абсцисс они
берутся пропорционально
числу периодов
времени, а по
оси ординат
– пропорционально
самим уровням.
Масштабом
равномерной
шкалы будет
длина отрезка,
принятого за
единицу.
Рассмотрим
построение
линейной диаграммы
на основании
следующих
данных (табл.
11).
Таблица
11
Динамика
валового сбора
зерновых культур
в регионе
за
1985 – 1994 гг.
| Год |
1985 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991
|
1992 |
1993 |
1994 |
Млн.т.
|
237,4
|
179,2
|
189,1
|
158,2
|
186,8
|
192,2
|
172,6
|
191,7
|
210,1
|
211,3
|
Изображение
динамики валового
сбора зерновых
культур на
координатной
сетке с неразрывной
шкалой значений,
начинающихся
от нуля, вряд
ли целесообразно,
так как 2/3 поля
диаграммы
остаются
неиспользованными
и ничего не
дают для выразительности
изображения.
Поэтому в данных
условиях
рекомендуется
строить шкалу
без вертикального
нуля, т.е. шкала
значений разрывается
недалеко от
нулевой линии
и на диаграмму
попадает лишь
часть всего
возможного
поля графика.
Это не приводит
к искажениям
в изображении
динамики явления,
и процесс его
изменения
рисуется диаграммой
более четко
(рис. 18).
Нередко
на одном линейном
графике приводится
несколько
кривых, которые
дают сравнительную
характеристику
динамики различных
показателей
или одного и
того же показателя.
Примером
графического
изображения
сразу нескольких
показателей
является рис.
19.
Р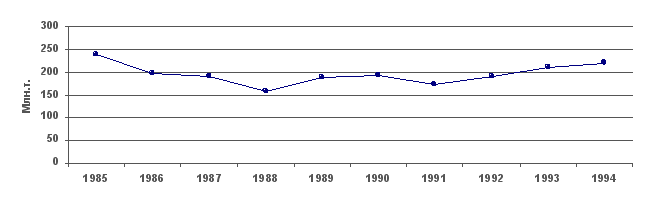
ис.
18. Динамика
валового сбора
зерновых культур
в регионе за
1985 – 1994 гг.
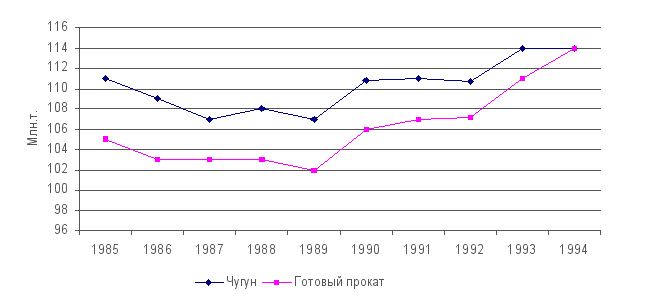
Рис.
19. Динамика
производства
чугуна и готового
проката в регионе
за 1985 – 1994 гг.
Однако
на одном графике
не следует
помещать более
трех – четырех
кривых, так как
большое их
количество
неизбежно
осложняет
чертеж и линейная
диаграмма
теряет наглядность.
В
некоторых
случаях нанесения
на один график
двух кривых
дает возможность
одновременно
изобразить
динамику третьего
показателя,
если он является
разностью
первых двух.
Например, при
изображении
динамики рождаемости
и смертности
площадь между
двумя кривыми
показывает
величину
естественного
прироста или
естественной
убыли населения.
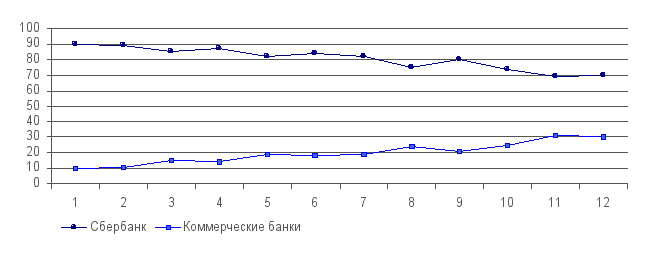
Иногда
необходимо
сравнить на
графике динамику
двух показателей,
имеющих различные
единицы измерения.
В таких случаях
понадобится
не одна, а две
масштабные
шкалы. Одну из
них размещают
справа, другую
– слева.
Однако
такое сравнение
кривых не дает
достаточно
полной картины
динамики этих
показателей,
так как масштабы
произвольны.
Поэтому сравнение
динамики уровня
двух разнородных
показателей
следует осуществлять
на основе
использования
одного масштаба
после преобразования
абсолютных
величин в
относительные.
Примером такой
линейной диаграммы
является рис.
20.
Линейные
диаграммы с
равномерной
шкалой имеют
один недостаток,
снижающий их
познавательную
ценность: равномерная
шкала позволяет
измерять и
сравнивать
только отраженные
на диаграмме
абсолютные
приросты или
уменьшения
показателей
на протяжении
исследуемого
периода. Однако
при изучении
динамики важно
знать относительные
изменения
исследуемых
показателей
по сравнению
с доступным
уровнем или
темпы их изменения.
Именно относительные
изменения
экономических
показателей
в динамике
искажаются
при их изображении
на координатной
диаграмме с
равномерной
вертикальной
шкалой. Кроме
того, в обычных
координатах
теряет всякую
наглядность
и даже становится
невозможным
изображение
для рядов динамики
с резко изменяющимися
уровнями, которые
обычно имеют
место в динамических
рядах за длительный
период времени.
В
этих случаях
следует отказаться
от равномерной
шкалы и положить
в основу графика
полулогарифмическую
систему. Основная
идея полулогарифмической
системы состоит
в том, что в ней
равным линейным
отрезкам
соответствуют
равные значения
логарифмов
чисел. Такой
подход имеет
преимущество:
возможность
уменьшения
размеров больших
чисел через
их логарифмические
эквиваленты.
Однако с масштабной
шкалой в виде
логарифмов
график малодоступен
для понимания.
Необходимо
рядом с логарифмами,
обозначенными
на масштабной
шкале, проставить
сами числа,
характеризующие
уровни изображаемого
ряда динамики,
которые соответствуют
указанным
числам логарифмов.
Такого рода
графики носят
название графиков
на полулогарифмической
сетке.
Полулогарифмическое
сеткой
называется
сетка, в которой
на одной оси
нанесен линейный
масштаб, а на
другой – логарифмический.
В данном случае
логарифмический
масштаб наносится
на ось ординат,
а на оси абсцисс
располагают
равномерную
шкалу для отсчета
времени по
принятым интервалам
(годам, кварталам,
месяцам, дням
и пр.).
Техника
построения
логарифмической
шкалы последующая
(рис. 21).
Логарифмы
чисел Числа
-
Рис.
21. Схема
логарифмического
масштаба
Необходимо
найти логарифмы
исходных чисел,
начертить
ординату и
разделить ее
на несколько
равных частей.
Затем нанести
на ординату
(или равную ей
параллельную
линию) отрезки,
пропорциональные
абсолютным
приростам этих
логарифмов.
Далее записать
соответствующие
логарифмы чисел
и их антилогарифмы,
например (0,000;
0,3010; 0,4771; 0,6021; …; 1,000, что дает
1, 2, 3, 4, …, 10). Полученные
антилогарифмы
окончательно
дают вид искомой
шкалы на ординате.
Приведем
пример логарифмического
масштаба.
Допустим,
что надо изобразить
на графике
динамику производства
электроэнергии
в регионе за
1965 – 1994 гг., за эти
годы оно выросло
в 9,1 раза. С этой
целью находим
логарифмы для
каждого уровня
ряда (табл. 12).
Таблица
12
Динамика
производства
электроэнергии
в регионе
за
1965 – 1994 гг. (млрд.
кВт/ч)
| Год |
Yi
|
LgYi
|
Год |
Yi
|
LgYi
|
1965
|
170
|
2,23
|
1985
|
1039
|
3,02
|
1970
|
292
|
2,46
|
1990
|
1294
|
3,11
|
1975
|
507
|
2,70
|
1994
|
1544
|
3,19
|
1980
|
741
|
2,84
|
|
|
|
Определив
минимальное
и максимальное
значение логарифмов
производства
электроэнергии,
построим масштаб
с таким расчетом,
чтобы все данные
разместились
на графике.
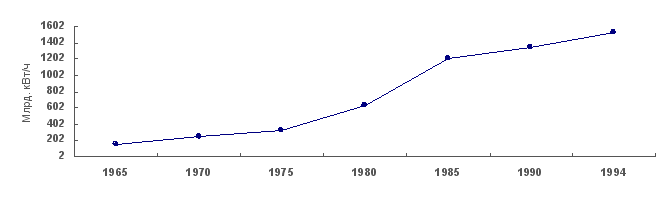
Учитывая
масштаб, находим
соответствующие
точки, которые
соединим прямыми
линиями, в результате
получим график
(рис. 22) с использованием
логарифмического
масштаба на
оси ординат.
Он называется
диаграммой
на полулогарифмической
сетке. Полной
логарифмической
диаграммой
он станет в том
случае, если
по оси абсцисс
будет построен
логарифмический
масштаб. В рядах
динамики это
никогда не
применяется,
так как логарифмирование
времени лишено
всякого смысла.
Рис.
22. Динамика
производства
электроэнергии
в регионе за
1965 – 1994 гг.
Применяя
логарифмический
масштаб, можно
без всяких
вычислений
характеризовать
динамику уровня.
Если кривая
на логарифмическом
масштабе несколько
отклонена от
прямой и становится
вогнутой к оси
абсцисс, значит,
имеет место
прямой – стабильность
темпов; если
она отклоняется
от прямой в
сторону, выпуклую
к оси абсцисс,
изучаемое
явление имеет
тенденцию к
росту с увеличивающимися
темпами.
Динамику
изображают
и радиальные
диаграммы,
строящиеся
в полярных
координатах.
Радиальные
диаграммы
преследуют
цель наглядного
изображения
определенного
ритмического
движения во
времени. Чаще
всего эти диаграммы
применяются
для иллюстрации
сезонных колебаний.
Радиальные
диаграммы
разделяются
на замкнутые
и спиральные.
По технике
построения
радиальные
диаграммы
отличаются
друг от друга
в зависимости
от того, что
взято в качестве
пункта отсчета
– центр круга
или окружность.
Замкнутые
диаграммы
отражают
внутригодичный
цикл динамики
какого – либо
одного года.
Спиральные
диаграммы
показывают
внутригодичный
цикл динамики
за ряд лет.
Построение
замкнутых
диаграмм сводится
к следующему:
вычерчивается
круг, среднемесячный
показатель
приравнивается
к радиусу этого
круга. Затем
весь круг делится
на 12 радиусов,
которые на
графике приводятся
в виде тонких
линий. Каждый
радиус обозначает
месяц, причем
расположение
месяцев аналогично
циферблату
часов: январь
– в том месте,
где на часах
1, февраль – 2, и
т.д. На каждом
радиусе делается
отметка в
определенном
месте согласно
масштабу исходя
из данных за
соответствующий
месяц. Если
данные превышают
среднемесячный
уровень, отметка
делается за
пределами
окружности
на продолжении
радиуса. В
приведенном
примере (рис.
23) R
= 44,8 тыс.т., длина
радиуса – 3,0 см.
Следовательно,
1 см = 44,8 : 3,0
15 тыс.т. Данная
замкнутая
диаграмма
наглядно показывает,
что производство
мяса подвергнуто
сезонным
колебаниям.
Минимум
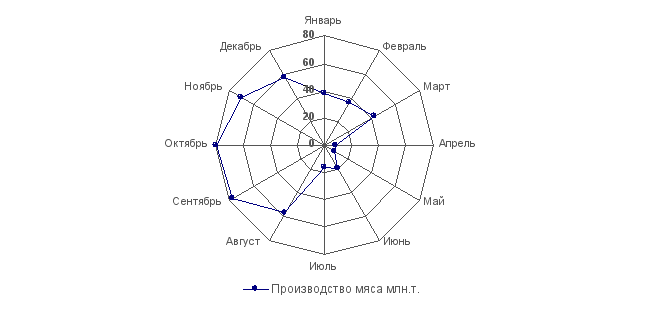
Рис.
23. Сезонные
колебания
производства
мяса в одном
из регионов
России в 1994 г.
производства
мяса приходится
на апрель, май,
затем наблюдается
медленное его
повышение к
августу, резкий
подъем в сентябре,
октябре и опять
спад в декабре,
январе. Если
же в качестве
базы для отсчета
взять не центр
круга, а окружность,
то диаграммы
называются
спиральными.
Построение
спиральных
диаграмм отличается
от замкнутых
тем, что в них
декабрь одного
года соединяется
не с январем
данного же
года, а с январем
следующего
года. Это дает
возможность
изобразить
весь ряд динамики
в виде спирали.
Особенно наглядна
такая диаграмма,
когда наряду
с сезонными
изменениями
происходит
неуклонный
рост из года
в год (рис. 24).
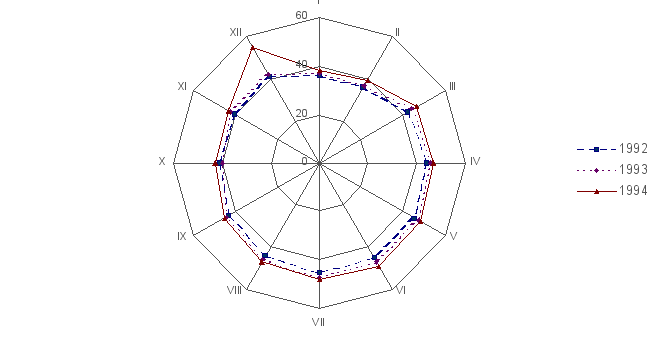
Рис.
24. Продажа
пива в розничной
торговле в
городе за 1992 –
1994 гг.
3
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
2.
ВИДЫ ТАБЛИЦ
ПО ХАРАКТЕРУ
ПОДЛЕЖАЩЕГО
В
практике экономико
– статистического
анализа используются
различные виды
статистических
таблиц, отличающихся
различным
числом и характером
совокупностей,
различным
строением
подлежащего
и сказуемого,
структурой
и соотношением
признаков,
формирующих
их.
В
зависимости
от структуры
подлежащего
и группировки
в нем единиц
различают
статистические
таблицы простые
и сложные, а
последние, в
свою очередь,
подразделяются
на групповые
и комбинационные.
В
простой
таблице
в подлежащем
дается простой
перечень каких
– либо объектов
или территориальных
единиц, т.е. в
подлежащем
нет группировки
единиц совокупности.
Простые таблицы
бывают монографические
и перечневые.
Монографические
таблицы характеризуют
не всю совокупность
единиц изучаемого
объекта, а только
одну какую-либо
группу из него,
выделенную
по определенному,
заранее сформулированному
признаку (табл.
1).
Таблица
1.
Характеристика
выпуска государственных
краткосрочных
облигаций в
РФ в 1996 г.
(цифры
условные)
|
Объем
поданных заявок,
шт.
|
Объем
выпуска,
млн
руб.
|
Доля
ГКО, приобретенная
сторонними
инвесторами
|
| объявленный |
реальный |
Государственные
краткосрочные
облигации
|
476
354
|
295
000
|
230
569
|
34,7
|
Перестроив
подлежащее
табл. 1, чтобы
были показаны
ГКО по нормам,
т.е. показав
единую единицу
совокупности,
получаем перечневую
таблицу (табл.2).
Таблица
2.
Характеристика
выпуска государственных
краткосрочных
облигаций в
РФ в 1996 г.
(цифры
условные)
Номер
ГКО
|
Объем
поданных заявок,
шт.
|
Объем
выпуска,
млн
руб.
|
Доля
ГКО, приобретенная
сторонними
инвесторами
|
| объявленный |
реальный |
21003
RMFS7
21004
RMFS5
21005
RMFS2
|
40
256
164
609
271
489
|
90
000
55
000
150
000
|
37
020
49
848
143
701
|
21,0
37,2
44,7
|
| Всего |
476
354 |
295
000 |
230
569 |
34,5 |
Таким
образом, простыми
перечневыми
таблицами
называются
таблицы, подлежащее
которые содержит
перечень единиц
изучаемого
объекта.
Подлежащее
простой таблицы
может быть
сформировано
по следующим
принципам:
видовому (например,
табл.2); территориальному
(численность
населения по
странам СНГ);
временному
и т.д.
Простые
таблицы не дают
возможности
выявить
социально-экономические
типы изучаемых
явлений, их
структуру, а
также взаимосвязи
и взаимозависимости
между характеризующими
их признаками.
Эти задачи
более полно
решаются с
помощью сложных:
групповых и
особенно
комбинационных
таблиц.
Групповыми
называются
статистические
таблицы, подлежащее
которых содержит
группировку
единиц совокупности
по одному
количественному
или атрибутивному
признаку. Сказуемое
в групповых
таблицах состоит
из числа показателей,
необходимых
для характеристики
подлежащего.
Простейшим
видом групповых
таблиц являются
атрибутивные
и вариационные
ряды распределения.
Групповая
таблица может
быть более
сложной, если
в сказуемом
приводится
не только число
единиц в каждой
группе, но и
ряд других
важных показателей,
количественно
и качественно
характеризующих
группы подлежащего.
Такие таблицы
используются
в целях сопоставления
обобщающих
показателей
по группам, что
позволяет
делать определенные
практические
выводы.
Таблица
3.
Распределение
предприятий,
выставивших
акции
на
чековые аукционы
РФ в 1996 г., по величине
уставного
капитала
(цифры
условные)
| № п.п. |
Группа
предприятий
по величине
уставного
капитала |
Число
предприятий |
Количество
акций, шт. |
1
2
3
4
5
6
|
1215
– 2340
2340
– 3465
3465
– 4590
4590
– 5715
5715
– 6840
6840
– 7965
|
14
4
4
2
5
1
|
7
395
3
402
4
058
3
004
8
587
2
194
|
| Итого |
30 |
28
667 |
Табл.
3 отражает
количественное
распределение
предприятий,
выставивших
акции на чековых
аукционах, по
величине уставного
капитала.
Таким
образом, групповые
таблицы позволяют
выявить и
охарактеризовать
социально –
экономические
типы явлений,
их структуру
в зависимости
только от одного
признака.
Комбинационными
называются
статистические
таблицы, подлежащее
которых содержит
группировку
единиц совокупности
одновременно
по двум и более
признакам:
каждая из групп,
построенная
по одному признаку,
разбивается,
в свою очередь,
на подгруппы
по какому –
либо другому
признаку и т.д.
Подлежащим
в таблице являются
группы предприятий
по величине
уставного
капитала и
числу занятых.
Из табл.4 видно,
что между величиной
уставного
капитала и
числом реализованных
акций имеется
определенная,
не ярко выраженная
зависимость,
которая наиболее
часто проявляется
в зависимости
от числа занятых
на этих предприятиях.
Комбинационные
таблицы позволяют
характеризовать
типические
группы, выделенные
по нескольким
признакам, и
связь между
последними.
Последовательность
разбиения
единиц совокупности
на однородные
группы по признакам
определяется
либо важностью
одного из них
в их комбинации,
либо порядком
их изучения.
Таблица
4.
Группировка
предприятий,
выставивших
акции на чековые
аукционы
РФ в 1996 г., по величине
уставного
капитала и
числу занятых
(цифры
условные)
| № п.п. |
Группы
предприятий
по величине
уставного
капитала, млн
руб. |
Группы
предприятий
по числу занятых,
человек |
Число
предприятий |
Количество
проданных
акций, шт. |
1
|
1235
– 2340
|
14
– 33
33
– 52
52
- 71
|
3
7
4
|
1
206
4
729
1
390
|
| Итого
по группе |
- |
14 |
7
325 |
2
|
2340
– 3465
|
14
– 33
33
– 52
52
- 71
|
3
-
1
|
2
508
-
894
|
| Итого
по группе |
- |
4 |
3
402 |
3
|
3465
– 4590
|
14
– 33
33
– 52
52
- 71
|
1
-
3
|
761
-
3
324
|
| Итого
по группе |
- |
4 |
4
085 |
|
Итого
по подгруппам
|
14
– 33
33
– 52
52
- 71
|
7
7
8
|
4
475
4
729
5
608
|
| Всего |
22 |
14
812 |
Групповые
и комбинационные
таблицы позволяют
глубже раскрыть
сущность и
закономерность
изучаемых
социально –
экономических
явлений и процессов.
1
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
3.
ВИДЫ ТАБЛИЦ
ПО РАЗРАБОТКЕ
СКАЗУЕМОГО
В
сказуемом
статистической
таблицы, как
уже говорилось,
приводятся
показатели,
которые являются
характеристикой
изучаемого
объекта. Эту
характеристику
можно давать
небольшим
числом показателей
или целой системой
показателей.
По
структурному
строению сказуемого
различают
статистические
таблицы с простой
и сложной его
разработкой.
При
простой
разработке
сказуемого
показатель,
определяющий
его, не подразделяется
на подгруппы,
и итоговые
значения получаются
путем простого
суммирования
значений по
каждому признаку
отдельно независимо
друг от друга.
Примером простой
разработки
сказуемого
может служить
следующий
фрагмент
статистической
таблицы.
Распределение
акций среди
работников
приватизированных
предприятий
промышленности
Предприятия
|
Приобретено
акций, всего
|
В
том числе |
|
приватизиро-ванные
типа А
|
обыкновенные |
на
льготных условиях |
по
цене, определенной
Госкомиму-ществом
|
После
заполнения
данного фрагмента
таблицы
получается
подробная
характеристика
приватизированных
предприятий
по структуре
их субъектов
– владельцев.
По каждому
предприятию
можно получить
информацию
о числе и ценовых
условиях продажи
акций.
Сложная
разработка
сказуемого
предполагает
деление признака,
формирующего
его, на подгруппы.
Распределение
акций среди
работников
приватизированных
предприятий
промышленности
Предприятия
|
Приобретено
акций, всего
|
В
том числе |
| на
льготных условиях |
по
цене, определенной
Госкомимуществом |
|
привеилегиро-ванные
типа А
|
обыкновенные |
привилегиро-ванные
типа А |
обыкновенные |
При
сложной разработке
сказуемого
получается
более полная
и подробная
характеристика
объекта.
Комбинированная
разработка
показателей
по условиям
продажи акций
и их видам позволяет
углубить экономико
– статистический
анализ рынка
акций и его
структуры по
приватизированным
предприятиям.
Здесь
оба признака
сказуемого
(ценовой и видовой)
тесно связаны
друг с другом.
Можно проанализировать
не только количество
приобретенных
акций по видам
и условиям
приобретения
их сотрудниками
приватизированных
предприятий,
но и определить
число привилегированных
и обыкновенных
акций, приобретенных
на разных ценовых
условиях. Итак,
при сложной
разработке
сказуемого
каждая группа
предприятий
или каждое
предприятие
в отдельности
могут быть
охарактеризованы
различной
комбинацией
признаков,
формирующих
сказуемое.
Однако
сложная разработка
сказуемого
может привести
к безмерному
увеличению
размерности
статистических
таблиц, что, в
свою очередь,
снижает их
наглядность,
чтение и анализ.
Поэтому
исследователь
при построении
статистических
таблиц должен
руководствоваться
оптимальным
соотношением
показателей
сказуемого
и учитывать
как положительные,
так и отрицательные
моменты сложной
разработки
показателей
сказуемого.
2
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
4.
ОСНОВНЫЕ
ПРАВИЛА ПОСТРОЕНИЯ
ТАБЛИЦ
Статистические
таблицы как
средство наглядного
и компактного
представления
цифровой информации
должны быть
статистически
правильно
оформлены.
Основные
приемы, определяющие
технику формирования
статистических
таблиц, следующие.
1.
Таблица должна
быть компактной
и содержать
только те исходные
данные, которые
непосредственно
отражают исследуемое
социально –
экономическое
явление в статике
и динамике и
необходимы
для познания
его сущности.
Следует
избегать ненужной,
второстепенной,
бессодержательной
к данному объекту
исследования
информации.
Цифровой материал
необходимо
излагать таким
образом, чтобы
при анализе
таблицы сущность
явления раскрывалась
чтением строк
слева направо
и сверху вниз.
2.
Заголовок
таблицы и названия
граф и строк
должны быть
четкими, краткими,
лаконичными,
представлять
собой законченное
целое, органично
вписывающееся
в содержание
текста.
Необходимо
избегать большого
количества
точек и запятых
в названиях
таблицы и граф,
затрудняющих
чтение таблицы.
Если
название таблицы
состоит из двух
и более предложений,
точка ставится
с целью отделения
предложений
друг от друга,
но не после
последнего.
В
заголовках
граф допускаются
точки только
при необходимых
сокращениях.
В
заголовке
таблицы должны
найти отражение
объект, признак,
время и место
совершения
события. Например:
«Курс доллара
США на торгах
ММВБ в 1997 г.» Но
при этом следует
помнить, что
чем более краток
и лаконичен
текст заголовка
таблицы, тем
она яснее и
доходчивее
для чтения и
анализа, естественно,
если это осуществляется
не в ущерб ее
точности и
познавательности.
Заголовки
таблицы, граф
и строк пишутся
полностью, без
сокращений.
3.
Информация,
располагаемая
в столбцах
(графах) таблицы,
завершается
итоговой строкой.
Существуют
различные
способы соединения
слагаемых граф
с их итогом:
В
групповых и
комбинационных
таблицах всегда
необходимо
давать итоговые
графы и строки.
4.
Для того, чтобы
было легче
читать и анализировать
достаточно
большие таблицы
(по количеству
приведенных
строк) целесообразно
оставлять
двойной промежуток
после каждых
пяти (и далее
кратных пяти)
строк.
5.
Если названия
отдельных граф
повторяются
между собой,
содержат
повторяющиеся
термины или
несут единую
смысловую
нагрузку, то
им необходимо
присвоить общий
объединяющий
заголовок.
Данный
прием используется
и для подлежащего,
и для сказуемого
таблиц.
6.
Графы и строки
полезно нумеровать.
Графы, слева
заполненные
названием
строк, принято
обозначать
заглавными
буквами алфавита
(А), (В) и т.д., а все
последующие
графы – номерами
в порядке
возрастания.
7.
Взаимосвязанные
и взаимозависимые
данные, характеризующие
одну из сторон
анализируемого
явления (например,
число предприятий
и удельный вес
заводов (в % к
итогу), абсолютный
прирост и темп
роста и т.д.),
целесообразно
располагать
в соседних друг
с другом графах.
8.
Графы и строки
должны содержать
единицы измерения,
соответствующие
поставленным
в подлежащем
и сказуемом
показателям.
При этом используются
общепринятые
сокращения
единиц измерения
(чел., руб., кВт/ч
и т.д.).
9.
Лучше всего
располагать
в таблицах
сопоставляемую
в ходе анализа
цифровую информацию
в одной и той
же графе, одну
под другой, что
значительно
облегчает
процесс их
сравнения.
Поэтому
в групповых
таблицах, например,
группы по изучаемому
признаку более
грамотно располагать
в порядке убывания
или
возрастания
его значений
при сохранении
логической
связи между
подлежащими
и сказуемыми
таблицы.
10.
Для удобства
работы числа
в таблицах
следует представлять
в середине
граф, одно под
другим: единицы
под единицами,
запятая под
запятой, четко
соблюдая при
этом их разрядность.
11.
По возможности
числа целесообразно
округлять.
Округление
чисел в пределах
одной и той же
графы или строки
следует проводить
с одинаковой
степенью точности
(до целого знака
или до десятого
и т.д.).
Если
все числа одной
и той же графы
или строки даны
с одним десятичным
знаком, а одно
из чисел имеет
два и более
знака после
запятой, то
числа с одним
знаком после
запятой следует
дополнять
нулем, тем самым
подчеркнув
их одинаковую
точность.
12.
Отсутствие
данных об
анализируемом
социально –
экономическом
явлении может
быть обусловлено
различными
причинами, что
по – разному
отмечается
в таблице:
а)
если данная
позиция (на
пересечении
соответствующих
графы и строки)
вообще не подлежит
заполнению,
то ставится
знак «Х»;
б)
когда по какой
– либо
причине отсутствуют
сведения, то
ставится многоточие
«…» или «Нет
свед.», или «Н.
св.»;
Для
отображения
очень малых
чисел используют
обозначения
(0,0) или (0,00), предполагающие
возможность
наличие числа.
13.
В случае необходимости
дополнительной
информации
– разъяснений
– к таблице
могут даваться
примечания.
Соблюдение
приведенных
правил
построения
и оформления
статистических
таблиц делает
их основным
средством
представления,
обработки и
обобщения
статистической
информации
о состоянии
и развитии
анализируемых
социально –
экономических
явлений.
1
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
5.
ЧТЕНИЕ И АНАЛИЗ
ТАБЛИЦЫ
Анализу
статистических
таблиц предшествует
этап ознакомления
– их чтения.
Чтение
и анализ таблиц
должны осуществляться
не хаотично,
а в определенной
последовательности.
Чтение
предполагает,
что исследователь,
прочитав слова
и числа таблицы,
усвоил ее содержание,
сформулировал
первые суждения
об объекте,
уяснил назначение
таблицы, понял
ее содержание
в целом, дал
оценку явлению
или процессу,
описанному
в таблице.
Анализ
таблицы как
метод научного
исследования
путем разбиения
предмета изучения
на части делится
на структурные
и содержательный.
Структурный
анализ предполагает
анализ строения
таблицы, характеристику
представленных
в таблице:
совокупности
и единиц наблюдения,
формирующих
ее;
признаков
и их комбинаций,
формирующих
подлежащее
и сказуемое
таблицы;
признаков:
количественных
или атрибутивных;
соотношения
признаков
подлежащего
с показателями
сказуемого;
вида
таблицы: простая
или сложная,
а последняя
– групповая
или комбинационная;
решаемых
задач –
анализ структуры,
типов явлений
или их взаимосвязей.
Содержательный
анализ
предполагает
изучение внутреннего
содержания
таблицы: анализ
отдельных групп
подлежащего
по соответствующим
признакам
сказуемого;
выявление
соотношения
и пропорций
между группами
явлений по
одному и разным
признакам;
сравнительный
анализ и формулировку
выводов по
отдельным
группам и по
всей совокупности
в целом; установление
закономерностей
и определение
резервов развития
изучаемого
объекта.
Прежде
чем приступать
к анализу числовой
информации,
необходимо
проверить ее
достоверность
и научную
обоснованность.
Исследователь
должен убедиться
в достоверности
и надежности
источника
информации
данных и критически
оценить их
цифровые значения.
Следует произвести
логическую
и счетную проверки
данных. Логическая
проверка
состоит в возможности
определения
конкретных
признаков теми
или иными числовыми
значениями
(например, абсурдно,
если численность
работающих
на фирме составила
106,7 человека).
Счетная
проверка
предполагает
выборочный
расчет отдельных
значений признаков
по группе, либо
итоговых значений
строк или граф
и т.д.
Анализ
данных таблиц
производится
по каждому
признаку в
отдельности,
затем в логико
– экономическом
сочетании всей
совокупности
признаков в
целом.
Анализ
отдельных
признаков и
групп необходимо
начинать с
изучения абсолютных,
затем
- связанных с
ними относительных
величин. При
анализе данных
следует рассматривать
динамику каждого
признака за
весь период,
переходя при
этом от одного
к другому.
Анализ
таблиц может
быть дополнен
расчетными
относительными
и средними
величинами,
если этого
требуют задачи
исследования.
Для
получения более
полного и наглядного
представления
об изучаемых
явлениях и
процессах по
данным статистических
таблиц строятся
графики, диаграммы
и т.д.
Анализ
групповых и
комбинационных
таблиц позволяет
охарактеризовать
типы социально
– экономических
явлений, структуру
совокупности,
соотношения
и пропорции
между отдельными
группами и
единицами
наблюдения;
выявить характер
и направление
взаимосвязей
и взаимозависимостей
между различными,
определенными
логикой экономического
анализа, сочетаниями
признаков и
зависимости
признаков –
следствия от
признаков –
причин.
Соблюдение
правил и последовательности
работы со
статистическими
таблицами
помогает
исследователю
осуществлять
научно обоснованный
экономико –
статистический
анализ объектов
и процессов.
1
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
6.
ТАБЛИЦЫ И МАТРИЦЫ
В
анализе данных
наряду со
статистическими
таблицами
применяются
и другие виды
таблиц, одним
из которых
является матрица.
Матрицей
называется
прямоугольная
таблица числовой
информации,
состоящая из
m
строк и n
столбцов. Таким
образом, матрица
имеет размерность
m x n:
-
А =
|
а11
а12
… а1n
а21
а22
… a2n
… …
… …
аm1
аm2
… amn
|
где
аij
– элемент матрицы,
стоящей на
пересечении
i-й
строки и J-го
столбца
Различают
два вида матриц:
прямоугольная
(размерность
m x
n);
квадратная.
Если число
строк строго
равно
числу столбцов
(m =
n), то
матрица называется
квадратной
порядка n.
Квадратная
матрица порядка
n
называется
диагональной
(Д), если
все элементы,
стоящие вне
главной диагонали
(d1,
d2,
…, dn),
равны нулю.
-
Д =
|
d1
0 …
0
0
d2
… 0
… …
… …
0
0
…
dn
|
Если
в диагональной
матрице Д все
di
= 1, то матрица
называется
единичной,
при di
= 0 –
нулевой.
Матрицы
и анализ явлений
и процессов
на их основе
составляют
базу матричного
моделирования
и позволяют
исследовать
взаимосвязи
между экономическими
объектами.
Таблицы
– матрицы
широко применяются
на практике,
например в
экономике в
виде балансово
– нормативных
моделей, отражающих
соотношение
результатов
производства,
нормативов
производственных
затрат и т.д.
Успешно используют
матрицы и в
межотраслевом
балансе, системе
национального
счетоводства
и т.д.
1
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
7.
ТАБЛИЦЫ СОПРЯЖЕННОСТИ
Таблицей
сопряженности
называется
таблица, которая
содержит сводную
числовую
характеристику
изучаемой
совокупности
по двум и более
атрибутивным
(качественным)
признакам или
комбинации
количественных
и атрибутивных
признаков.
Таблицы
сопряженности
получили наибольшее
распространение
при изучении
социальных
явлений и процессов:
общественного
мнения, уровня
и образа жизни,
общественно
– политического
строя и т.д.
Наиболее
простым видом
таблиц сопряженности
является таблица
частот 2 х 2.
Общая
схема таблицы
частот 2 х 2
|
В1
|
В2
|
Всего
|
А1
|
f11
|
f12
|
f10
|
А2
|
f21
|
f22
|
f20
|
Всего
|
f01
|
f02
|
f00
|
Построение
данной таблицы
исходит из
предложения,
что ответы
респондентов
или анализируемые
атрибутивные
признаки будут
принимать
только два
значения А1
и А2,
В1
и В2.
Внутреннее
цифровое наполнение
таблицы
представляют
частоты (fij),
обладающие
одновременно
i-м
(i
= 1,2) значением
одного (Ai)
и
j-м (j
= 1,2) значением
(Bj)
другого качественного
признака.
Итоговая
графа и срока
содержат информацию
о количественном
распределении
совокупности
соответственно
по А и В атрибутивным
признакам.
Для более
полного описание
и анализа явлений
и процессов,
характеризующихся
атрибутивными
признаками,
используются
таблицы сопряженности
большей разномерности:
i
x j,
где
i
= 1,2, …, к – число
вариантов
значений (например,
ответов респондентов
и т.д.) одного
признака (например,
признака А); j
= 1, 2, …, n
– число вариантов
значений другого
признака (В).
Общая
схема таблицы
сопряженности
большей
размерности
|
В1
|
В2
|
…
|
Bj
|
Всего
|
А1
|
f11
|
f12
|
…
|
f1j
|
f10
|
А2
|
f21
|
f22
|
…
|
f2j
|
f20
|
…
|
…
|
…
|
…
|
…
|
…
|
Аi
|
fi1
|
fi2
|
…
|
fij
|
fi0
|
Всего
|
f01
|
f02
|
…
|
f0j
|
f00
|
Принцип
взаимной
сопряженности
наиболее эффективен
при выявлении
и оценке взаимосвязей
и взаимозависимостей
между социальными
явлениями и
процессами.
2
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
9.
КЛАССИФИКАЦИЯ
ВИДОВ ГРАФИКОВ
Существует
множество видов
графических
изображений
(рис. 5, 6). Их классификация
основана на
ряде признаков:
а) способ построения
графического
образа; б) геометрические
знаки, изображающие
статистические
показатели;
в) задачи, решаемые
с помощью
графического
изображения.
Рис.
5. Классификация
статистических
графиков по
форме графического
образа
По
способу построения
статистические
графики делятся
на диаграммы
и статистические
карты.
Диаграммы
– наиболее
распространенный
способ графических
изображений.
Это графики
количественных
отношений. Виды
и способы их
построения
разнообразны.
Диаграммы
применяются
для наглядного
сопоставления
в различных
аспектах
(пространственном,
временном и
др.) независимых
друг от друга
величин: территорий,
населения и
т.д. При этом
сравнения
исследуемых
совокупностей
производится
по какому –
СТАТИСТИЧЕСКИЕ
ГРАФИКИ ПО
СПОСОБУ ПОСТРОЕНИЯ
И ЗАДАЧИ
ИЗОБРАЖЕНИЯ
  
ДИАГРАММЫ
СТАТИСТИЧЕСКИЕ
КАРТЫ
ДИАГРАММЫ
СРАВНЕНИЯ
ДИАГРАММЫ
ДИНАМИКИ
КАРТОГРАММЫ
КАРТОДИАГРАММЫ
СТРУКТУРНЫЕ
ДИАГРАММЫ
Рис.6.
Классификация
статистических
графиков по
способу построения
и задачам изображения
либо
существующему
варьирующему
признаку.
Статистические
карты – графики
количественного
распределения
по поверхности.
По совей основной
цели они близко
примыкают к
диаграммам
и специфичны
лишь в том отношении,
что представляют
собой условные
изображения
статистических
данных на контурной
географической
карте, т.е. показывают
пространственное
размещение
или пространственную
распространенность
статистических
данных. Геометрические
знаки,
как было сказано
выше, - это либо
точки, либо
линии или плоскости,
либо геометрические
тела. В соответствии
с этим различают
графики точечные,
линейные, плоскостные
и пространственные
(объемные).
При
построении
точечных диаграмм
в качестве
графических
образов применяются
совокупности
точек; при построении
линейных –
линии. Основной
принцип построения
всех плоскостных
диаграмм сводится
к тому, что
статистические
величины изображаются
на столбиковые,
полосовые,
круговые, квадратные
и фигурные.
Статистические
карты по графическому
образу делятся
на картограммы
и картодиаграммы.
В
зависимости
от круга решаемых
задач выделяют
диаграммы
сравнения,
структурные
диаграммы
и диаграммы
динамики.
Особым
видом графиков
являются диаграммы
распределения
величин, представленных
вариационным
рядом. Это
гистограмма
полигон, огива,
кумулята.
3
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
8.
ПОЯНТИЕ О
СТАТИСТИЧЕСКОМ
ГРАФИКЕ.
ЭЛЕМЕНТЫ
СТАТИСТИЧЕСКОГО
ГРАФИКА.
Современную
науку невозможно
представить
без применения
графиков. Они
стали средством
научного обобщения.
Выразительность,
доходчивость
лаконичность,
универсальность,
обозримость
графических
изображений
сделали их
незаменимыми
в исследовательской
работе и в
международных
сравнениях
и сопоставлениях
социально –
экономических
явлений.
Впервые
о технике составления
статистических
графиков упоминается
в работе английского
экономиста
У. Плейфейра
«Коммерческий
и политический
атлас», опубликованной
в 1786 г. и положившей
начало развитию
приемов графического
изображения
статистических
данных.
Трактовка
графического
метода как
особой знаковой
системы –
искусственного
знакового языка
– связана с
развитием
семиотики,
науки о знаках
и знаковых
системах.
Знак
в семиотике
служит символическим
выражением
некоторых
явлений, свойств
или
отношений.
Существующие
в семиотике
знаковые
системы принято
разделять на
неязыковые
и языковые.
Неязыковые
знаковые системы
дают
представление
о явлениях
окружающего
нас мира (например,
шкала измерительного
прибора, высота
столбика ртути
в термометре
и т.д.).
Языковые
знаковые системы
выполняют
сигнальные
функции, а также
задачи сопоставления
совокупностей
явлений и их
анализа. Характерно,
что в этих системах
сочетание
знаков приобретает
смысл только
тогда, когда
их объединение
производится
по определенным
правилам.
В
языковых
знаковых системах
различают
естественные
и искусственные
системы знаков,
или языков.
С
точки зрения
семиотики
человеческая
речь, выраженная
знаками –
буквами, составляет
естественный
язык.
Искусственные
языковые системы
используются
в различных
областях жизни
и техники. К
ним относятся
системы математических,
химических
знаков, алгоритмические
языки, графики
и др.
Не
исключая
естественного
языка, искусственные,
или символические
языки упрощают
изложение
специальных
вопросов определенной
области знаний.
Таким
образом, статистический
график –
это чертеж, на
котором статистические
совокупности,
характеризуемые
определенными
показателями,
описываются
с помощью условных
геометрических
образов или
знаков. Представление
данных таблиц
в виде графика
производит
более сильное
впечатление,
чем цифры, позволяет
лучше осмыслить
результаты
статистического
наблюдения,
правильно их
истолковывать,
значительно
облегчает
понимание
статистического
материала,
делает его
наглядным и
доступным. Это,
однако, вовсе
не означает,
что графики
имеют лишь
иллюстративное
значение. Они
дают новое
знание о предмете
исследования,
являясь методом
обобщения
исходной информации.
Значение
графического
метода в анализе
и обобщении
данных велико.
Графическое
изображение
прежде всего
позволяет
осуществить
контроль
достоверности
статистических
показателей,
так как, представленные
на графике, они
более ярко
показывают
имеющиеся
неточности,
связанные либо
с наличием
ошибок наблюдения,
либо с сущностью
изучаемого
явления. С помощью
графического
изображения
возможны изучение
закономерностей
развития явления,
установление
существующих
взаимосвязей.
Простое сопоставление
данных не всегда
дает возможность
уловить наличие
причинных
зависимостей,
в то же время
их графическое
изображение
способствует
выявлению
причинных
связей, в особенности
в случае установления
первоначальных
гипотез, подлежащих
затем дальнейшей
разработке.
Графики также
широко используются
для изучения
структуры
явлений, их
изменения во
времени и размещения
в пространстве.
В них более
выразительно
проявляются
сравнительные
характеристики
и отчетливо
виды основные
тенденции
развития и
взаимосвязи,
присущие изучаемому
явлению или
процессу.
При
построении
графического
изображения
следует соблюдать
ряд требований.
Прежде всего
график должен
быть достаточно
наглядным, так
как весь смысл
графического
изображения
как метода
анализа в ом
и состоит, чтобы
наглядно изобразить
статистические
показатели.
Кроме того,
график должен
быть выразительным,
доходчивым
и понятным. Для
выполнения
вышеперечисленных
требований
каждый график
должен включать
ряд основных
элементов:
графический
образ; поле
графика; пространственные
ориентиры;
масштабные
ориентиры;
эксплуатацию
графика.
Рассмотрим
подробнее
каждый из указанных
элементов.
Графический
образ (основа
графика) –
это геометрические
знаки, т.е. совокупность
точек, линий,
фигур, с помощью
которых изображаются
статистические
показатели.
Важно правильно
выбрать графический
образ, который
должен соответствовать
цели графика
и способствовать
наибольшей
выразительности
изображаемых
статистических
данных. Графическими
являются лишь
те образы, в
которых свойства
геометрических
знаков – фигура,
размер линий,
расположение
частей – имеют
существенное
значение для
выражения
содержания
изображаемых
статистических
величин, причем
каждому изменению
выражаемого
содержания
соответствует
изменение
графического
образа.
Поле
графика –
это часть плоскости,
где расположены
графические
образы. Поле
графика имеет
определенные
размеры, которые
зависят от его
назначения.
Пространственные
ориентиры
графика
задаются в виде
системы координатных
сеток. Система
координат
необходима
для размещения
геометрических
знаков в поле
графика. Наиболее
распространенной
является система
прямоугольных
координат (рис.
1).
Для
построения
статистических
графиков
используется
обычно только
первый изредка
первый и четвертый
квадраты. В
практике
графического
изображения
применяются
также полярные
координаты.
Они необходимы
для наглядного
изображения
циклического
движения во
времени. В полярной
системе координат
(рис.1) один из
лучей, обычно
правый горизонтальный,
применяется
за ось координат,
относительно
которой определяется
угол луча. Второй
координатой
считается ее
расстояние
от центра сетки,
называемое
радиусом.
В радиальных
графиках лучи
обозначают
моменты времени,
а окружности
– величины
изучаемого
явления. На
статистических
Рис.
1. Полярная
система координат
картах
пространственные
ориентиры
задаются контурной
сеткой (контуры
рек, береговая
линия морей
и океанов, границы
государств)
и определяют
те территории,
к которым относятся
статистические
величины.
Масштабные
ориентиры
статистического
графика определяются
масштабом и
системой масштабных
шкал. Масштаб
статистического
графика – это
мера перевода
числовой величины
в графическую.
Масштабной
шкалой называется
линия, отдельные
точки которой
могут быть
прочитаны как
определенные
числа. Шкала
имеет большое
значение в
графе и включает
три элемента:
линию (или носитель
шкалы), определенное
число помеченных
черточками
точек, которые
расположены
на носителе
шкалы в определенном
порядке, цифровое
обозначение
чисел, соответствующих
отдельным
помеченным
точкам. Как
правило, цифровым
обозначением
снабжаются
не все помеченные
точки, а лишь
некоторые из
них, расположенные
в определенным
порядке. По
правилам числовое
значение необходимо
помещать строго
против соответствующих
точек, а не между
ними (рис. 2).
   5
10 15 20 25
5
10 15 20 25
Графические
интервалы
Длина шкалы
Рис.
2. Числовые
интервалы
Носитель
шкалы может
представлять
собой как прямую,
так и кривую
линии. Поэтому
различают шкалы
прямолинейные
(например,
миллиметровая
линейка) и
криволинейные
– дуговые и
круговые (циферблат
часов).
Графические
и числовые
интервалы
бывают равными
и неравными.
Если на все
протяжении
шкалы равным
графическим
интервалом
соответствуют
равные числовые,
такая шкала
называется
равномерной.
Когда же равным
числовым
интервалам
соответствуют
неравные графические
интервалы и
наоборот, шкала
называется
неравномерной.
Масштабом
равномерной
шкалы называется
длина
отрезка (графический
интервал), принятого
за единицу и
измеренного
в каких – либо
мерах. Чем меньше
масштаб (рис.
3), тем гуще располагаются
на шкале точки,
имеющие одно
и то же значение.
Построить шкалу
– это значит
на заданном
носителе шкалы
разместить
точки и обозначить
их соответствующими
числами согласно
условиям задачи.
0 1 Масштаб
50 мм
0 1 2 3 4 5 Масштаб
10 мм
0 10 20 30 40 50 Масштаб
1 мм
0 100 200 300 400 500 Масштаб
0,1 мм
Рис.
3. Масштабы
Как
правило,
масштаб определяется
примерной
прикидкой
возможной длины
шкалы и ее пределов.
Например, на
поле в 20 клеток
надо построить
шкалу от 0 до
850. Так как не
делится удобно
на 20, то округляем
число 850 до ближайшего
удобного числа,
в данном случае
1000 (1000 : 20 = 50), т.е. в оной
клетке 50, в других
клетках 100; следовательно,
масштаб – 100 в
двух клетках.
Из
неравномерных
наибольшее
распространение
имеет логарифмическая
шкала. Методика
ее построения
несколько иная,
так как на этой
шкале отрезки
пропорциональны
не изображаемым
величинам, а
их логарифмами.
Так, при основании
10 lg1
= 0; lg
= 0 = 1; lg100
= 2 и т.д. (рис. 4).
0 0,5 1,0
0 1 2 3
0 10 100 1000
Числа
0 1 2 3 Логарифмы
чисел
Рис.
4.
Последний
элемент графика
– экспликация.
Каждый график
должен иметь
словесное
описание его
содержания.
Оно включает
его содержание;
подписи вдоль
масштабных
шкал и пояснения
к отдельным
частям графика.
3
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
СОДЕРЖАНИЕ
|
стр. |
1.
Понятие о
статистической
таблице. Элементы
статистической
таблицы. . . . . . . . .
. . . . . . . .
|
3
|
2.
Виды таблиц
по характеру
подлежащего
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
5
|
3.
Виды таблиц
по разработке
сказуемого
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . .
|
8
|
4.
Основные правила
разработки
таблиц . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
|
9
|
5.
Чтение и анализ
таблиц . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . .
|
11
|
6.
Таблицы и матрицы
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . .
|
12
|
7.
Таблицы сопряженности
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . .
|
13
|
8.
Понятие о
статистическом
графике . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . .
|
14
|
9.
Классификация
видов графиков
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .
|
17
|
10.
Диаграммы
сравнения .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . .
|
19
|
11.
Структурные
диаграммы .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . .
|
25
|
12.
Диаграммы
динамики . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . .
|
28
|
|
|
Список
использованной
литературы
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . .
|
36
|
1
Статистические
таблицы и
статистические
графики – основные
способы
наглядного
изображения
статистических
данных
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
СПИСОК
ИСПОЛЬЗУЕМОЙ
ЛИТЕРАТУРЫ
Долгушевский
Ф.Г., Козлов В.С.,
Полушин М.И.,
Эрлих Я.М. Общая
теория статистики.
– М.: Статистика,
1967. – 384 с.
Колмогоров
А. Предисловие
к книге Г. Лебега
«Общие величины».
– М.: Госстатиздат,
1938. – 4 с.
Лившиц Ф.Д.
Статистические
таблицы. – М.:
Госстатиздат,
1958. – 139 с.
Маслов П.П.
Техника работы
с цифрами. –
М.: Статистика,
1969. – 120 с.
Бызов Л.А.
Графические
методы в статистике,
планировании
и учете: Пособие
для экономических
вузов и для
самообразования.
– М.: Госпланиздат,
1940.
Герчук Я.П.
Графические
методы в статистике.
– М.: Статистика,
1968.
Курс лекций
по общей теории
статистики/Под
ред. В.Е. Овсиенко.
– М.: МЭСИ, 1976. – 231 с.
Ланге О.,
Банасиньский
А. Теория статистики.
– М.: Статистика,
1971. – 399 с.
Кан Ю. Описательная
и индивидуальная
статистика.
– М.: Финансы
и статистика,
1981.
АДЫГЕЙСКИЙ
ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ
БЕЛОРЕЧЕНСКИЙ
ФИЛИАЛ
КАФЕДРА
СТАТИСТИКИ
И ПРОГНОЗИРОВАНИЯ
РЕФЕРАТ НА
ТЕМУ:
СТАТИСТИЧЕСКИЕ
ТАБЛИЦЫ И
СТАТИСТИЧЕСКИЕ
ГРАФИКИ –
ОСНОВНЫЕ
СПОСОБЫ НАГЛЯДНОГО
ИЗОБРАЖЕНИЯ
СТАТИСТИЧЕСКИХ
ДАННЫХ
Выполнил:
студентка
группы 4 – Б –
2
4 курса
Арифова Н.А.
Руководитель:
Профессор
Забирова Л.Н.
г. Новороссийск
1999
|