| ЧАСТЬ 2. ФИЗИКА НЕОБХОДИМОГО.
В настоящем и последующем разделах будут рассмотрены понятия и законы классической физики, или, в более общем понимании, физики необходимого. В этих разделах рассматриваются явления, законы теории, в основе которых лежит принцип детерминизма. Идея этого принципа состоит в том, состояние физической системы однозначно определяется ее начальным состоянием и законами ее развития. Под физическими системами подразумеваются структуры, состоящие из вещества или поля.
При наблюдении за каким-либо процессом или явлением относящимся к этим разделам физики, в принципе, всегда можно сказать, как поведет себя система в будущем. Например, упругое тело всегда с необходимостью отскакивает от твердой стенки; вслед за полным оборотом по своей орбите вокруг Солнца Земля с необходимостью сделает следующий.
В разделе «Физика дискретного» рассматриваются законы и явления, связанные с формой материи, существующей в виде вещества, т.е. с материей, локализованной в пространстве. В следующем разделе «Физика непрерывного» будут рассмотрены явления и законы, связанные с другой формой существования материи - полем и волнами. Поля и волны не локализованы в ограниченной части пространства и для их описания требуются другие, отличные от вещества законы.
В следующем разделе настоящего курса - "Физика возможного" мы столкнемся с процессами, которые могут иметь несколько исходов. Например, электрон, сталкиваясь с препятствием (барьером) может либо отскочить от него, либо пройти сквозь него. Последнее возможно лишь для квантовых частиц благодаря так называемому "туннельному эффекту", хорошо известному в квантовой механике. Важнейшим моментом для физики необходимого является строго определенное описание системы , а для физики возможного - вероятностное описание систем. Следствием этого является введение нового детерминизма - вероятностного детерминизма.
6. ЭТАПЫ РАЗВИТИЯ ФИЗИКИ.
Физика - наука, изучающая простейшие и в вместе с тем наиболее общие закономерности явлений природы, свойства и строения материи, законы ее движения. Законы физики лежат в основе всего естествознания. Физика относится к точным наукам и изучает количественные закономерности явлений. Ее законы базируются на фактах, установленных опытным путем. В основе физики лежит научный метод познания.
Слово физика происходит от греческого слова Physic - природа. В эпоху античной культуры наука охватывала всю совокупность знаний человека о природных явлениях. По мере дифференциации знаний и методов исследования из нее выделились различные разделы, в том числе и физика в привычном понимании этого слова. Однако, границы, отделяющие физику от других наук, в значительной мере условны и зависят от общей суммы человеческих знаний.
В истории развития физики обычно выделяют три этапа. Первый из них начинается в античности и заканчивается в 16-ом веке. В это время господствовала метафизики Аристотеля. Второй этап начинается с работ Коперника, Кеплера, Галилея, Декарта, Ньютона и заканчивается в конце 19-го века. На этом этапе идет процесс развития метода научного познания, о котором уже шла речь. И, наконец, третий этап продолжается с начала нашего века по сей день. Это этап развития современной квантовой физики.
Физические явления издавна привлекали внимание людей. В 6-2 веках до н.э. впервые зародились идеи об атомном строении вещества (Демокрит, Эпикур, Лукреций). В это время в работах Птолемея и Аристотеля возникла гелиоцентрическая картина мира и были сформулированы основные законы статики (правило рычага) и гидростатики (закон Архимеда), которые с успехом применялись в строительстве, военном деле и в других областях. Известна легенда об Архимеде, открывшем свой известный закон изменения веса тела в жидкости. Выполняя заказ сиракузского правителя, Архимед должен был определить, какое количество серебра и какое - золота содержалось в сплаве, из которого ювелир должен был сделать корону. В эту эпоху наблюдались и исследовались простейшие проявления электричества и магнетизма.
Итог накопленных знаний подвел Аристотель (384-322 г.г. до н.э.). Из числа дошедших до нас работ наибольший интерес представляют "Первая философия", "Метафизика", "Физика". В этих трудах содержится учение об основных принципах бытия, возможности и осуществлении, форме и материи, действующей причине и цели. Аристотель признавал значение опыта, но не придавал ему решающего значения, считая, что критерием правильности является умозрительное заключение. В средние века учение Аристотеля было канонизировано церковью, что надолго затормозило развитие естественных наук.
Не вдаваясь в сложные рассуждения, рассмотрим основную идею механики Аристотеля, используя современный язык. Как известно из школьного курса физики, согласно второму закону Ньютона ускорение, приобретаемое телом пропорционально сумме действующих на это тело сил: .В основе же механики Аристотеля лежало утверждение, что скорость тела пропорциональна действующей на него силе: . Естественно, что механика Аристотеля и механика Ньютона в корне отличались друг от друга. О втором законе Ньютона речь еще пойдет ниже, а в оправдание Аристотеля отметим, что, если не ставить специальных экспериментов, а только наблюдать за движущимися телами, то видно, как они останавливаются, если к ним не прикладывать дополнительной силы. Сейчас мы, конечно, знаем, что тела останавливаются из-за действия на них сил трения, которые, как правило, бывают пропорциональны скоростям тел. Если же к этим телам приложить некоторою силу, то они станут двигаться с постоянной скоростью, тем большей, чем больше сила тяги. Но легко быть умным, зная ответ на вопрос, и очень непросто самому его найти.
Развитие физики как науки в современном понимании этого слова, т.е. науки в основе которой лежит научный метод познания, началось на рубеже 16-17 веков и связано, в первую очередь, с именем итальянского ученого Галилео Галилея (1564-1642). Галилей понял необходимость математического описания движения материи под которым в его время подразумевалось механическое движение тел - их перемещение в пространстве и времени. Галилей опроверг ошибочные утверждения механики Аристотеля и заложил основы современной механики. Им были сформулированы идеи об относительности движения, установлены законы инерции, свободного падения и движения тел по наклонной плоскости, сложения движений. Галилей показал, что воздействие на тело окружающих тел, определяет не скорость тела, а его ускорение; фактически он открыл два первых закона Ньютона. Столь же велики его заслуги в области астрономии. С помощью построенного своими руками телескопа он открыл горы на Луне, спутники Юпитера, фазы Венеры, темные пятна на Солнце. О Галилее, о его трагической судьбе, о его научных исследованиях и изысканиях написано очень много трудов.
Вряд ли сейчас кто-нибудь вспоминает о том, что Галилей является автором идеи современных маятниковых часов. До него создавалось огромное количество часов, работающих на разных принципах. Все они были недостаточно точны и не позволяли измерять малые интервалы времени - секунды (в то время даже не было понятия о таких малых промежутках времени). Для проведения своих опытов Галилею требовалось измерять время с большой точностью. Он открыл и разработал принцип изохронности колебаний маятника, который положил в основу секундомера. В камне, качающемся на веревке, Аристотель видел лишь сдерживаемое веревкой падение, а Галилей увидел периодический процесс.
Говоря об основоположниках классической физики нельзя пройти мимо Рене Декарта (1596-1650). Французский философ, математик, физик, он заложил основы аналитической геометрии, его имя носит система координат. Он ввел в математике понятие переменной величины и функции, а также ввел множество алгебраических обозначений. В физике он ввел понятие импульса и высказал закон его сохранения. Наибольшую известность получили его работы в области познания.
Основное достижение физики 17-го века - это создание классической механики. Исаак Ньютон (1643-1727) в своем труде "Математические начала натуральной философии" (1687) сформулировал и дал математическую трактовку всем основным законам этой науки, которые дошли практически без изменений до наших дней. Классическая механика лежит в основе многих физических и технических дисциплин, которые изучаются и в наше время специалистами в области науки и техники. Астрономические наблюдения поведения небесных тел в 18-19 веках и открытия новых планет солнечной системы стали блестящими подтверждениями учения Ньютона. Не будем сейчас останавливаться на основных концепциях ньютоновской теории, а вернемся к ним в следующих разделах курса, при изучении законов механического движения.
Благодаря работам Ньютона, основанным на многочисленных экспериментах и наблюдениях, а также на специально разработанных Ньютоном математических методах (методе дифференциального и интегрального исчисления) было окончательно установлено, что задача естественной науки состоит в отыскании наиболее общих количественных формулировок законов природы.
Работы ученых 18-го века продолжили поиски наиболее общих формулировок движения систем, материи. Были заложены основы механики твердого тела, акустики, гидродинамики, теплоты. В 1788 году французский ученый Ж.Л. Лагранж (1736-1813) вывел уравнения механики в наиболее общем виде, получив так называемые уравнения Лагранжа. С их помощью поведение системы описывалось через поведение ее энергии. Эти уравнения до сих пор используются в современных разделах физики - в квантовой механике и электродинамике.
К концу 18-го века была создана единая механистическая картина мира, согласно которой все многообразие мира - результат движения атомов и тел, из которых они состоят и движение которых подчиняется законам Ньютона. Объяснение наблюдаемых физических явлений считалось научным и полным, если их удавалось описать на основе теории Ньютона. Естественно, такие "шоры" не могли устраивать пытливые умы исследователей. Один из интересных эпизодов истории физики относится к теории света. В 17-м веке были выдвинуты две гипотезы. И.Ньютон полагал, что свет - это поток частиц, корпускул, движение которых определяют его свойства и законы. Другой ученый Х.Гюйгенс (1629-1695) считал, что свет - это волны, распространяющиеся в пространстве. Следствием теории Ньютона было то, что скорость света в среде , где - скорость света в вакууме, а - коэффициент преломления света. Из теории Гюйгенса же, следовало, что . Очевидно, что различие этих формул носит принципиальный характер. Однако из-за слабого развития экспериментальной базы вплоть до второй половины 19-го века проверка этих формул была невозможной.
В 1818-м году французский ученый О.Ж.Френель написал работу на конкурс Французской Академии наук. В основе теории распространения света он положил волновые свойства. Один из членов жюри - Пуассон "усомнился" в правильности выводов теории. Из теории Френеля следовало, что в центре тени, отбрасываемой предметом на экран обязательно должно быть светлое пятно. Налицо было даже не количественное, а качественное расхождение с известными фактами. Видимо даже сегодня большинству из нас такое пятно кажется нереальным. Однако, в специально поставленных экспериментах Д.Араго (1786-1853) это пятно было обнаружено и, тем самым, подтверждены выводы теории Френеля. Эти опыты перевернули обыденные представления о свойствах света и перевели почти всех противников волновой теории Френеля, даже самых “маститых” в число ее сторонников. Началось победное шествие волновой теории света. В 50-х годах 19 века были проведены эксперименты по определению скорости света в среде, которые подтвердили справедливость формулы . Однако история физики полна парадоксов. Наблюдаемое пятно теперь называется "Пятном Пуассона", т.е. носит имя человека, усомнившегося в его существовании.
К началу 19-го века были сформулированы простейшие законы в области теплоты, электричества, магнетизма. Уже были накоплены сведения о макроскопических свойствах твердых тел, изучены температурные зависимости поведения твердых тел и газов. Основные достижения физики 19-го века были оформлены в стройных, непротиворечивых теориях электромагнитных волн и теплового движения атомов и молекул. Сейчас эти разделы физики называют классической электродинамикой, термодинамикой и статистической физикой.
Ко второй половине 19-го века благодаря достижениям таких ученых, как А.Вольта (1745-1827), Ш.О.Кулон (1736-1806), Э.К.Эрстед (1777-1862), Ж.Б.Био (1774-1862), П.С.Лаплас (1749-1827), К.Ф.Гаусс (1777-1855), А.М.Ампер (1775-1836), М.Фарадей (1791-1867), Г.Р.Герц (1857-1894) и многих других, электрические и магнитные явления были уже так хорошо изучены, что оказалось возможным построить единую стройную теорию электромагнетизма. Творцом классической электродинамики стал Джеймс Кларк Максвелл (1831-1879). Максвелл написал систему уравнений, описывающих взаимодействие подвижных и неподвижных зарядов, электрических и магнитных полей и процесс распространения переменных электромагнитных полей в пространстве. Следствием уравнений Максвелла стал факт постоянства скорости распространения электромагнитных волн, который не был объяснен в рамках теории Максвелла.
Решающий вклад в становление и развитие термодинамики и статистической физики внесли Д.К.Максвелл, Д.У.Гиббс (1839-1903), Г.Л.Гельмгольц (1821-1894), Л.Больцман (1844-1906), Р.Клаузиус (1822-1888) и ряд других ученых, одно перечисление которых, даже без упоминания работ, заняло бы не одну страницу. Во второй половине 19-го века были сформулированы первое и второе начала термодинамики, сформулированы основные законы молекулярно-кинетической теории газов и твердых тел, развит вероятностный метод подхода к описанию тепловых явлений.
Существенно, что термодинамика и статистическая физика базировались на утверждении, что движение атомов и молекул описывается классической механикой. В основе всех теорий лежал тезис о непрерывности всех процессов в природе. Принципиально новых положений при описании движения на атомно-молекулярном уровне по сравнению с классической механикой не вводилось.
Экспериментальные основы нового этапа развития физики были заложены на рубеже 19-20-х веков. Двадцатые годы нашего столетия принято считать началом нового третьего этапа развития физики - этапа квантовой физики. Перечислим лишь некоторые явления и открытия, которым не было места в рамках старых механистических теорий, и которые перевернули старую физику. Упомянем излучение разреженных газов и нагретых твердых тел, открытие электрона, явления радиоактивности, фотоэффекта, атомного ядра и, наконец создание теории относительности.
Началом атомного века можно считать две даты. Первая - 1942 год, когда под руководством Э.Ферми (1901-1954) был запущен первый ядерный реактор и человечество впервые за свою историю получило не энергию от Солнца, а принципиально новую - атомную. Летом 1945 года было проведено испытание первого атомного оружия, и это тоже веха в развитии человечества - практическое применение нового вида энергии.
Однако этим событиям предшествовал доклад Макса Планка (1848-1947) о полученной им новой формуле излучения в Берлинском университете в 1900 году. Планк открыл элементарный квант действия, новую естественную константу, и это открытие положило начало новой эпохе в развитии физики. Оно показало, что тезис о бесконечной непрерывности всех действий в природе - непрерывности был заблуждением. Выяснилось, что в природе бывают изменения, которые происходят не плавно, а скачком "взрывообразно", как сказал сам Планк. Результатом открытия Планка стал отказ от принципа "Natura non facit saltus" (природа ничего не делает скачком), который владел умами натурфилософов со времен И.Ньютона (1643-1727) и Г.В.Лейбница (1646-1716).
Открытие Планка эпохальное, революционное. Значение его не снижает даже тот факт, что до конца жизни сам Планк считал кванты ни чем иным, как абстракцией, моделью, которая не имеет ничего общего с действительностью. Другие исследователи, менее приверженные к традиции, чем он, вскоре значительно обогнали его и развили новые области и разделы современной физики.
В современной физике возник ряд новых направлений, неведомых классической. Ограничимся перечислением лишь некоторых и очертим круг задач, стоящих перед ними.
Физика элементарных частиц
. Ее основной проблемой было и остается исследование материи на уровне элементарных частиц. Не все теоретические положения этого раздела физики получили прямое подтверждение экспериментами. Обширный экспериментальный материала до сих пор не обобщен. Существуют только попытки построения теории, объединяющей все виды взаимодействий: гравитационное, электромагнитное, слабое и сильное.
Физика ядра
. В 30-х годах была создана протонно-нейтронная модель ядра, был достигнут большой прогресс в понимании структуры ядер и достигнут большой успех в практическом применении ядерных реакций. Одна из важнейших задач в этой области - решение проблемы управляемого термоядерного синтеза. Работы в этом направлении ведутся объединенными усилиями исследователей из ряда стран.
Астрофизика
. Развитие физики элементарных частиц и атомного ядра позволило приблизится к пониманию таких сложных проблем, как эволюция Вселенной на ранних стадиях ее развития, эволюция звезд, образование химических элементов. Однако, несмотря на впечатляющие достижения современной астрофизики, остается неясным, каково строение материи при огромных плотностях внутри нейтронных звезд и "черных дыр". Невыяснена природа квазаров и причина вспышек сверхновых звезд. В целом, можно считать, что положено только начало решению проблемы эволюции Вселенной.
Оптика и квантовая электроника
. На фундаменте квантовой теории излучения, заложенной А.Эйнштейном, возникла новая наука - квантовая электроника. Успехи в этой области связаны, в первую очередь с созданием сверхчувствительных приемных систем и принципиально новых источников света - лазеров или оптических квантовых генераторов. Их уникально по своим параметрам. Создание лазеров дало жизнь новому разделу оптики - нелинейной оптике. Практически строгая монохроматичность лазерного излучения позволяет получить объемное изображение объекта - голограмму. Ведутся работы по использованию лазеров в управляемых термоядерных реакциях. Развитие этой области связано с дальнейшим повышением мощности лазеров и с расширением диапазона рабочих частот. Сейчас стоит задача создания рентгеновских и гамма-лазеров.
Физика плазмы
. Важность изучения плазмы связана с двумя обстоятельствами. Во-первых, в плазменном состоянии находится подавляющая часть вещества Вселенной. Во-вторых, именно в высокотемпературной плазме имеется возможность осуществить управляемую термоядерную реакцию. Получение таких реакций позволит дать человечеству практически вечный экологически чистый источник энергии. Эта проблема очень актуальна, поскольку уже в ближайшее время человечество столкнется с проблемой энергетического голода.
Физика твердого тела
. Пожалуй, ни один из разделов физики не имеет стольких ответвлений в прикладные области, как этот. Прогресс в компьютеростроении целиком базируется на достижениях физики твердого тела. Туннельный эффект
- явление из области квантовой физики, которое заключается в способности элементарных частиц проникать сквозь барьер, который классическая частица не может пройти в принципе. На основе туннельного эффекта созданы специальные приборы - туннельные микроскопы, которые позволяют наблюдать отдельные атомы. Прогресс в этой области зашел так далеко, что коллективу сотрудников фирмы IBM удалось написать название фирмы буквами, размером всего в пять атомов по высоте. По-видимому, это самая эффектная реклама в мире. Размер этих букв во столько же раз меньше букв, написанных Левшой на подкове блохи, во сколько песчинка меньше Эйфелевой башни. Сверхпроводимость
- особое состояние некоторых веществ, открытое достаточно давно. Оно заключается в том, что при температурах порядка 5~200
К электрическое сопротивление совершенно исчезает. Ток может циркулировать в таком проводнике годами. В настоящее время синтезированы материалы, в которых сверхпроводимость возникает при температурах 100~1500
К. Такие материалы могут широко использоваться в науке и технике.
В заключение отметим, что важнейшей особенностью современного физического эксперимента стала неизмеримо возросшая роль измерительной и вычислительной техники. Современные исследования ведутся обычно на больших установках и требуют значительных затрат. Развитые страны идут на это, и не только потому, что естественные науки составляют часть культуры человечества, но и потому, что именно они позволяют увеличивать целостность, независимость и благосостояние государства.
7. ВЕЩЕСТВО И МАССА, ПРИНЦИП ЭКВИВАЛЕНТНОСТИ.
В физике под веществом подразумевают такой вид материи, который обладает массой покоя, т.е. в состоянии неподвижности (хотя бы и относительной) масса системы не равна нулю. В конечном счете, вещество слагается из атомов (или элементарных частиц). В следующих разделах мы узнаем, что существуют частицы, имеющие нулевую или мнимую массу покоя; такие частицы могут существовать только в движении.
Вещество всегда локализовано в ограниченной части пространства. Его положение можно задать с помощью ограниченного числам параметров, которые принято называть степенями свободы. В простейшем случае движения точки, ее положение в пространстве задается 3-мя независимыми координатами (степенями свободы). Даже, когда вещество нельзя моделировать точкой (например, твердое тело), его положение все равно определяется конечным числом независимых координат - степеней свободы. Если вещество состоит из N атомов, то мы можем описать положение каждого атома в отдельности. Всего потребуется задать 3 N параметров. Реально атомы образуют связи; каждая связь превращает одну из независимых координат в зависимую, и число независимых параметров (координат) уменьшается. Положение твердого тела, оказывается, можно задать всего лишь 6 параметрами: тремя координатами - положение центра масс тела и еще тремя углами - его ориентацию (разворот) относительно координатных осей.
В настоящем и в прошлых разделах упоминалось понятие массы, которое требует дополнительного обсуждения. В начале нашего курса говорилось, что масса характеризует количество материи. Это формулировка качественная. Она требует уточнения. Правильнее говорить, что масса - одна из основных характеристик материи, определяющая ее инерционные и гравитационные свойства. Остановимся на этом вопросе подробнее. В теории Ньютона масса рассматривалась, как количество вещества. Понятие массы ввел в механику И.Ньютон, давая определение импульса - . Массой он назвал коэффициент пропорциональности m
, постоянную для тела величину. Эквивалентное определение массы вытекает и из второго закона Ньютона: Здесь масса - это коэффициент пропорциональности между результирующей силой и вызываемым ею ускорением. Определенная таким образом масса характеризует инертность тела. Т.е. чем больше масса тела, тем меньшее ускорение оно приобретает под действием постоянной силы. Определенная таким образом масса называется инертной.
В теории гравитации И. Ньютона масса выступает как источник поля сил тяготения. Каждая масса создает вокруг себя пол сил тяготения (гравитационное поле). На любое тело, помещенное в это поле, действует сила, пропорциональная его собственной массе, массе источника и направленная к источнику. Это значит, что гравитационные силы всегда являются силами притяжения. Закон всемирного тяготения формулируется в следующем виде:, где м3
/(кг×с2
)- гравитационная постоянная, m1
и m2
- массы тел, r
- расстояние между телами.
Из этой формулы можно получить связь между массой тела и его весом Р в поле тяготения Земли, если считать, что m1
- масса тела, m2
= M
- масса Земли, а r
= Rз
- радиус Земли:
т.е. . Определенная таким образом масса называется гравитационной.
В принципе, ниоткуда не следует, что масса, создающая поле тяготения и масса, определяющая инерцию тела - одинаковы. Однако, специальные опыты показали, что инерционная и гравитационная массы при выборе одинаковой системы единиц равны. Этот фундаментальный закон природы называется принципом эквивалентности масс
. Экспериментально этот принцип был проверен в 1971 году с очень высокой точностью - 10-12
.
В классической физике считалось, что масса тела не меняется ни в каких процессах. Это утверждение формулировалось в виде закона сохранения массы. Понятие массы приобрело более глубокий смысл в рамках релятивистской механики или теории относительности, рассматривающей движение тел с большими скоростями. Релятивистская механика показывает, что не существует по отдельности законов сохранения массы и энергии. Они слиты воедино. Это естественно, так как материя (количество которой характеризуется массой) невозможна без движения (количество которой характеризуется энергией). Подробнее рассмотрим этот вопрос после изучения законов сохранения и специальной теории относительности.
Природа массы - важнейший, до сих пор не решенный вопрос физики. Принято считать, что массы элементарных частиц определяется полями, с ними связанными. Однако, до настоящего времени не создана количественная теория массы. Не существует теорий, объясняющих, почему массы элементарных частиц образуют не непрерывный, а дискретный, т.е. прерывный спектр значений, и тем более, позволяющих рассчитать эти значения.
8. ВЗАИМОДЕЙСТВИЕ
.
ПОЛЕ
.
ПРИНЦИПЫ
БЛИЗКОДЕЙСТВИЯ И ДАЛЬНОДЕЙСТВИЯ.
Уже несколько раз упоминалось понятие поле
. Что же следует под ним понимать? В механике Ньютона взаимодействие тел количественно характеризуется силой. Более общей характеристикой взаимодействия тел является потенциальная энергия. Но не для всех сил она может быть введена.
Первоначально в классической механике утвердилась концепция, что взаимодействие между телами происходит через пустое пространство, которое не принимает участия во взаимодействии, передача взаимодействия происходит мгновенно. Так, например, считалось, что перемещение Земли мгновенно приводит к изменению силы тяготения, действующей на Луну. В этом и состояла так называемая концепция
дальнодействия
. По сути дела утверждалась возможность мгновенной передачи какого-либо воздействия от одного тела другому. При этом не оговаривался механизм этой передачи.
Однако, данные представления были откинуты, как не соответствующие реальным, после открытия и исследования электрических и магнитных полей. Понятие поля в применении к электрическому и магнитному полям было введено в 30-х годах 19-го века М. Фарадеем. Концепция поля была возрождением теории близкодействия, основоположником которой был Р.Декарт. Согласно его концепции близкодействия
, взаимодействующие тела создают в каждой точке окружающего их пространства особое состояние - поле, которое проявляется в силовом воздействии на другие тела, в эти поля помещенные. Экспериментально было показано, что взаимодействие электрически заряженных тел осуществляется не мгновенно. Перемещение одной заряженной частицы приводит к изменению сил, действующих на другую заряженную частицу не в тот же момент, а спустя некоторое время. В разделяющем частицы пространстве происходит некоторый процесс, который распространяется с конечной, хотя и очень большой скоростью. Был сделан вывод, что имеется посредник, осуществляющий взаимодействие между заряженными частицами. Этот посредник был назван электромагнитным полем. Каждая заряженная частица создает вокруг себя электромагнитное поле, действующее на другие заряженные частицы. Скорость распространения электромагнитных волн не превышает скорости их распространения в вакууме, равной 3×108
м/с. Таким образом, возникла новая концепция - концепция близкодействия
. Согласно этой концепции, взаимодействие телами осуществляется посредством тех или иных полей, непрерывно распределенных в пространстве. Всемирное тяготение, например, осуществляется за счет гравитационных полей. Взаимодействие тел передается не мгновенно, а через некоторый промежуток времени. Скорость передачи взаимодействия ограничена скоростью света в вакууме.
В современной физике существует квантовая теория поля. Согласно этой теории, любое поле не непрерывно, а дискретно. Дискретность означает наличие некоторых частиц поля - квантов. Каждому полю соответствуют свои частицы. Например, электромагнитному полю соответствуют кванты, называемые фотонами, известными из школьного курса физики. Фотоны - это переносчики электромагнитного взаимодействия.
Как наглядно представить себе процесс взаимодействия посредством квантов электромагнитного поля. Допустим вы стоите в лодке, ваш приятель тоже стоит в другой лодке. Вам надо сдвинуться так, чтобы в лодке ничего не изменилось. Нельзя касаться другой лодки и своего приятеля, нельзя просто выкинуть что-либо из лодки. Проще всего прийти в движение, перекинувшись с приятелем какими-то одинаковыми вещами, например, веслами. Вы как бы оттолкнетесь друг от друга, не касаясь и ничего не выкидывая из лодок. Точно также и тела, обмениваются одинаковыми квантами, ничего не теряя, и таким образом взаимодействуют друг с другом.
Несмотря на великое многообразие взаимодействий тел друг с другом, в природе существует четыре вида взаимодействий и, соответственно, четыре типа полей. Перечислим их все в порядке возрастания величины взаимодействия. Гравитационные
взаимодействия обеспечивают тяготение тел друг к другу. Слабые
взаимодействия ответственны за большинство распадов и превращений элементарных частиц. Электромагнитные
взаимодействия - это взаимодействие заряженных тел. Сильные
взаимодействия связываются протоны и нейтроны (нуклоны) в атомном ядре.
Разные виды взаимодействия различаются на много порядков по величине действующих сил. Приведем такой пример. Силу тяготения двух песчинок, находящихся на расстоянии 20 м друг от друга нельзя измерить с помощью самых точных и современных приборов. Но, если переместить из всех атомов одной песчинки по одному электрону в атомы другой песчинки, то песчинки будут притягиваться друг к другу с силой ~ 1010
ньютонов.
Поскольку поля заданы в каждой точке пространства, т.е. в бесконечном числе точек, для их описания требуется не конечное, а бесконечное число параметров - степеней свободы. Сказанное не означает, что для описания поля надо реально задавать бесконечное число параметров. Достаточно установить закон, позволяющий находить поле в каждой точке пространства. Таковыми являются: закон всемирного тяготения для гравитационных полей, закон Кулона для электрических полей и закон Био-Савара-Лапласа для магнитных полей.
Особой формой существования материи являются волны. Волна представляет из себя процесс распространения возмущения какого-либо физического параметра в пространстве. Также, как и поля, волна не детерминирована в пространстве, поскольку она с необходимостью распространяется в пространстве и существует в каждой точке пространства. Различают волны в упругих средах (примером которых являются звуковые волны в газах или твердых телах), которые локализованы в самой среде, и волны (электромагнитные, гравитационные), не ограниченные средой, т.е. не локализованные в ограниченной части пространства.
9. СОСТОЯНИЕ СИСТЕМЫ, ЕЕ ИЗМЕНЕНИЕ ВО ВРЕМЕНИ.
После введения понятия вещества и поля перейдем к рассмотрению классических подходов в описании физических явлений. В основе ряда теорий естествознания, в том числе классической физики лежит представление о непрерывности процессов или явлений. Изменение состояния любой системы происходит плавно, непрерывно от одной точки к другой.
Простейшей формой движения материи является механическое движение, под которым мы понимаем перемещение тел в пространстве и времени. Наука, изучающая такой вид движения материи, называется механикой. В естествознании для описания систем вводятся модели. Простейшей моделью, на которой удобно изучать механическое движение, является материальная точка, т.е. тело, имеющее массу, но не имеющее геометрических размеров. Материальная точка - это абстракция, модель; таких тел в природе не существует.
Когда же реальную систему можно заменить точкой? Играют ли при этом решающую роль ее размеры? Тело можно заменить материальной точкой, если в рамках поставленной задачи можно пренебречь его размерами и формой, т.е. если перемещение тела много больше размеров самого тела. Одно и тоже тело в одних условиях можно считать материальной точкой, а в других - нет.
Например, наша планета огромна по сравнению с размерами человека, и если человек огибает земной шар, то его движение можно представить как движение точки на огромном глобусе. В свою очередь, размеры земной орбиты во столько же раз больше размеров Земли, во сколько раз сама Земля больше человека. Так что, и Землю можно считать материальной точкой при ее движении вокруг Солнца.
Еще один пример. При измерении пройденного автомобилем расстояния никому не придет в голову вопрос, до какой точки автомобиля это расстояние мерить, однако, когда тот же автомобиль заезжает в гараж необходимо следить, чтобы он никакой своей частью ни за что не зацепился. В первом случае автомобиль можно заменить материальной точкой, а во втором - нельзя, т.к. обязательно нужно учитывать его форму и размеры.
Таким образом, допустимость модели материальной точки, как, впрочем, и любой физической модели, определяется условиями поставленной задачи и требуемой точностью искомого результата.
Раздел механики, в котором описывается движение тела, и не вскрываются причины, его вызывающие, называется кинематикой
.
Для описания движение тела, необходимо ввести систему отсчета, относительно которой задать его координаты, ввести динамические переменные, описывающие изменение положения тела во времени и ввести законы движения тела. Вообще говоря, система отсчета должна в себя включать систему тела, которые мы считаем неподвижными и часы. С системой неподвижных тел необходимо связать систему координат, например декартовых. Положение точки в координатном пространстве задается радиусом-вектором r
(t
), т.е. вектором, проведенным из начала координат в выбранную точку. Начальное положение тела задается радиусом-вектором в начальной момент времени r0
= r
(t
0
), как это показано на рис.9.1. Положение точки в пространстве с течением времени меняется, и конец радиуса-вектора вычерчивает линию, которая называется траекторией движения.
Траекторию можно разбить на бесконечно малые участки - dr
, как это показано на рисунке 9.2. Поскольку перемещение dr,
бесконечно мало, оно лежит на траектории движения. Время dt
, за которое происходит это перемещение, тоже бесконечно мало. Перемещение dr
и время dt
связаны друг с другом при помощи динамического параметра - мгновенной скорости,
определение которой:
u
(t
)=dr
(t
)/dt
(9.
1).
Траекторию можно разбить на бесконечно малые участки - dr
, как это показано на рисунке 9.2. Поскольку перемещение dr,
бесконечно мало, оно лежит на траектории движения. Время dt
, за которое происходит это перемещение, тоже бесконечно мало. Перемещение dr
и время dt
связаны друг с другом при помощи динамического параметра - мгновенной скорости,
определение которой:
u
(t
)=dr
(t
)/dt
(9.
1).
dr
      
 Dr Dr

r(t0
)=
r0
r
(t)
r
(t)
O O
Рис.9.1 Рис. 9.2
Траекторию можно разбить на бесконечно малые участки - dr
, как это показано на рисунке 9.2. Поскольку перемещение dr,
бесконечно мало, оно лежит на траектории движения. Время dt
, за которое происходит это перемещение, тоже бесконечно мало. Перемещение dr
и время dt
связаны друг с другом при помощи динамического параметра - мгновенной скорости,
определение которой:
u
(t
)=dr
(t
)/dt
(9.
1).
Таким образом, dr
= u
dt
, следовательно, направление мгновенной скорости совпадает с направлением элементарного перемещения dr.
Иными словами, мгновенная скорость всегда направлена по касательной к траектории. По правилу сложения векторов сумма всех dr
плюс r0
даст нам вектор r
. Но, операция суммирования по бесконечно малым величинам называется интегрированием. Таким образом, проясняется наглядный смысл интегрирования векторной функции и правило вычисления значения r
(t
), в любой момент времени.
r
(t
)=r0
+u
(t
)dt
(9.2)
Скорость материальной точки, в свою очередь, тоже может меняться со временем. Удобно ввести еще один динамический параметр - ускорение
, которое тоже является векторной величиной и тоже может зависеть от времени и координат:
a
(t
)=d
u
(t
)/dt
(9.3).
Из этого определения следует, что d
u
(t
)=a
(t
)dt.
Если функция a
(t
) известна, то с ее помощью можно найти скорость тела в любой момент времени, а зная ее, при помощи (9.2) можно найти положение тела в любой момент времени.
u
(t
)=u
0
+а
(t
)dt
(9.4),
r
(t
) = r0
+(u
0
+а
(t
)dt
)dt
или
r
(t
)=r0
+u
0
(t-
t)+а
(t
)dtdt
(9.5).
В этих формулах u
0
- начальная скорость тела, т.е. его скорость в момент времени t0
.
Таким образом, если нам известны начальное положение материальной точки - r0
и начальная скорость - u
0
, а также зависимость вектора скорости или вектора ускорения от времени, можно найти координаты системы в любой последующий момент времени - r
(t
).
Только что мы рассмотрели и обозначили путь решения основной задачи кинематики. При решении этой задачи не ставился вопрос, за счет чего меняется ускорение тела, но в рамках кинематики такой вопрос не ставится. Рассматривалось положение тела в произвольные моменты времени.
В ряде случаев требуется найти не только положение тела, но и тот путь, который оно пройдет. Пройденный путь есть скалярная величина, она обозначается S и численно равна длине траектории. Из рисунка очевидно, что путь в общем случае не равен длине (модулю) вектора перемещения r
. Чтобы найти пройденный путь S необходимо просуммировать длины вектора dr,
т.е. провести интегрирование по модулю вектора dr
:
.
Здесь надо помнить, что модуль вектора, т.е. его длина всегда положительна. При выполнении расчета по этой формуле u
(t
) всегда надо брать со знаком плюс.
В случае одномерного движения, когда тело перемещается вдоль прямой, векторную функцию можно заменить ее проекцией на выбранную ось. Проекции вектора на другие оси равны нулю, поэтому можно не пользоваться понятием вектора.
10. КЛАССИЧЕСКАЯ МЕХАНИКА.
10.1. Основные положения механики Галилея.
Классическую механику будем рассматривать в контексте тех принципов, которые использовались при ее становлении вплоть до развития современной физики. Не надо думать, что развитие современной физики перечеркнуло всю классическую механику и заставило использовать при описании какие-то принципиально новые положения. Классическая механика, в сформированном Ньютоном виде, играет большую роль в современной науке и технике. Достаточно сказать, что такая большая область техники, как машиностроение, целиком базируется на законах классической механики. При дальнейшем рассмотрении настоящего раздела нас будет интересовать в основном следующие положения.
Классическая механика развилась как раздел науки (физики) в котором рассматривалось механическое движение макросистем, т.е. систем, размеры которых определяются окружающими нас телами. Диапазон масс и размеров огромен. С одной стороны это и атомы, из которых состоят вещества, и движение которых мы можем с большой точностью описывать классическими понятиями. С другой стороны это и такие большие образования, как планеты и звезды.
Механическое движение рассматриваемых систем определяется скоростью движения системы. Хотя скорость понятие относительное, но всегда можно выбрать какую-то систему отсчета, относительно которой мы и рассматриваем скорость. Такой системой отсчета может быть и наша Земля, и наше Солнце, и центр нашей галактики. Все эти системы отсчета движутся друг относительно друга с небольшими, по сравнению с скоростью света, скоростями. В настоящем разделе будут рассматриваться движения, на скорость которых накладывается условие: u
<<с
, где с @ 3×108
м/с - скорость света в вакууме. Законы движения, которые будут рассмотрены, справедливы с точностью порядка u
/с.
Существуют ограничения и на минимальную скорость. Из школьного курса нам известно, что скорость движения атомов, из которого состоит система определять его температуру. Основные явления и эффекты, рассматриваются в классической механике при температурах тел, далеких от абсолютного 0. Если масса системы мала (например, исследуются отдельные атомы или молекулы), а её температура стремится к абсолютному нулю, то наблюдаются квантовые явления, не описываемые в рамках классической физики.
Все теории, созданные до становления современной физики, базировались на принципе, “Природа не терпит разрывов”. Изменение состояния системы происходит не мгновенно, а плавно. Все процессы и явления развиваются постепенно, плавно переходя из одного состояния в другое. Именно это положение и лежало в основе математического аппарата, разработанного Ньютоном и Лейбницем - дифференциального и интегрального исчислений.
Последнее замечание, которое необходимо сделать. В одном из прошлых разделов рассматривались принципы дальнодействия и близкодействия. На заре развития классической механики подразумевалось, что взаимодействие тел происходит мгновенно. Использовался принцип дальнодействия. В этом случае, коль скоро взаимодействие передается мгновенно, в разных системах отсчета можно было вводить одинаковое время. Например, считалось, что всегда можно синхронизовать часы, находящиеся в любой точке пространства (например, на Земле и в центре Галактики) и считать, что время в разных точках пространства ни от чего не зависит и одинаковое.
Прежде, чем перейти к дальнейшему рассмотрению, вспомним, что такое сила. В механике силой называется мера воздействия на выбранное материальное тело со стороны других тел. Это действие вызывает изменение скоростей точек тела или его деформацию. Воздействие может передаваться как при непосредственном контакте (давление прижатых друг к другу тел, трение и т.д.), так и посредством создаваемых телами полей (гравитационные, электромагнитные силы). Сила - величина векторная, в каждый момент времени она характеризуется численным значением, направлением в пространстве и точкой приложения. Сложение сил осуществляется по правилу сложения векторов- правилу параллелограмма. Прямая, вдоль которой направлена сила назовется линией действия силы. Обычно силу обозначают F
. В общем случае сила может зависеть от координат и времени, т.е. F
= F
(x,y,z,t
).
Законы физики всегда базируются на опытах, экспериментах. Именно в рамках такого подхода Галилей создал основы классической механики. Обратимся к некоторым из опытов Галилея. Напомним, что в основе механики Аристотеля, доминировавшей в тот период, лежало утверждение, что скорость тела пропорциональна приложенной силе: u
~F
. Этот вопрос мы уже обсуждали и пришли к выводу, что кажущееся проявление действие силы связано с наличием в природе сил трения. Именно Галилей доказал неверность положения физики Аристотеля.
В Италии в городе Пизе, в котором проживал Галилей, имеется высокая Пизанская башня. Она интересна тем, что стоит не вертикально, как все здания, а сильно наклонена под углом (рис.10.1). Галилей осуществил эксперимент в ходе которого он определял время, необходимое для падения тел с вершины Пизанской башни.
Попытаемся восстановить ход рассуждений Галилея во время его экспериментов. Возьмем несколько шаров одинакового размера, изготовленных из разного вещества: свинца, меди, чугуна, дерева. Все эти тела при одинаковых размерах и форме имеют разный вес. Вес тела характеризует силу тяготения, действующую на тело со стороны Земли. Сила тяготения, действующая на тело равна его весу. Если справедливо утверждение Аристотеля, то разные тела с разным весом должны обладать разными скоростями падения и, соответственно, достигать поверхности земли при бросании с башни за разные промежутки времени. Однако, эксперименты, проведенные с разными телами показали, что они достигали поверхности земли за практически одинаковые промежутки времени.
    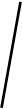 S S
 h h

Рис.10.1 Рис.10.2
Вывод из этих опытов однозначен. Скорость тела не определяется приложенной силой. Приложенной силой определяется какой-то другой динамический параметр. Галилею потребовалось много лет и много усилий, чтобы выяснить, что же это за параметр. В этой области наиболее известны его эксперименты с движением шаров по наклонной плоскости. Схема его опытов приведена на рис.10.2. Шары скатывались по наклонной плоскости, длина которой и высота были заданы. В ходе опыта Галилей определял путь S
, проходимый телом в зависимости от времени t
. Им был установлен закон, являющийся частным случаем второго закона Ньютона. Путь, проходимый телом квадратично зависит от времени: , где константа (сейчас она называется ускорением) прямо пропорциональна высоте h
и обратно пропорциональна длине пути S
, т.е. . Начальная скорость тела - u
0
в его опытах могла меняться. Этот закон сегодня можно легко вывести из 2-го закона Ньютона для равноускоренного движения. В опытах Галилея ускорение определялось ускорением свободного падения: .
Анализируя проводимые эксперименты, Галилей пришел к выводу о существовании закона инерции. Действительно, если устремить длину основание наклонной плоскости к бесконечности, ускорение будет стремиться к нулю, значит, за равные промежутки времени тело будет проходить равные отрезки пути и скорость тела будет постоянной. Тело будет само по себе двигаться по инерции.
Кроме экспериментов Галилей использовал умозрительные заключения. Он рассмотрел поведение тел и живых существ внутри корабля. Их поведение не зависит от того, стоит корабль у причала или двигается по спокойной воде с постоянной скоростью. Анализ этой ситуации привел его к выводу, что если корабль будет двигаться с постоянной скоростью, то находясь внутри корабля невозможно определить, движется он или стоит.
10.2 Принцип относительности Галилея. Преобразования Галилея.
Галилей ввел понятие инерциальной системы отсчета, в которой тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела (силы). Напомним, что понятие системы отсчета включает в себя систему координат и часы. Инерциальных систем отсчета может быть бесконечное множество.
Принцип относительности Галилея
заключается в том, что все физические законы не меняются (инвариантны) в разных инерциальных системах отсчета. Если быть более строгими, то принцип относительности Галилея заключался в том, что все законы механики инвариантны ( т.е. не меняются) при применении к ним преобразований Галилея
.
Для перехода из одной инерциальной системы отсчета в другую Галилей ввел преобразования, которые теперь называют преобразованиями Галилея
. Рассмотрим следующую ситуацию. Пусть у нас имеется инерциальная система отсчета, положение тел в которой задается декартовыми координатами. Например, точка А на рис. 10.3.
Кроме системы координат XYZ
(ее обычно обозначают К
), может быть и другая инерциальная система координат, например, X
’
Y
’
Z
’
(назовем ее К
’). Инерциальная система координат К
’ движется с постоянной скоростью u
относительно системы К
. Пространство изотропное, в нем не существует выделенного направления, поэтому удобно выбрать направление оси OX
совпадающим с направлением скорости u
. Т.е. система К
’ движется вдоль оси OX
системы отсчета К
.
y’
 y y
  v v
  О’ x’ О’ x’
  z’ O x z’ O x
z
x
Рис.10.3
Положение точки А
в системе К
задается вектором r
(x,y,z
) или его проекциями на оси OX
, OY
и OZ
, которые равны, соответственно, x
, y
и z
. Положение той же точки в системе К
’ задаются координатами x
’, y
’ и z
’. Связь между x
, y
, z
и x
’, y
’, z
’ дается преобразованиями Галилея:
Дополнительно к преобразованиям координат введено преобразование времени. Одинаковость хода часов в разных инерциальных системах отсчета соответствует концепции дальнодействия, рассмотренной выше.
Введем понятие инварианта и инвариантности. Инвариантность означает независимость, неизменность относительно каких-либо физических условий. В математике под инвариантностью понимается неизменность величины относительно каких-либо преобразований. Рассмотрим, какие параметры не меняются при преобразованиях Галилея, т.е. являются инвариантами этих преобразований.
Первый из этих параметров - время. При переходе от одной инерциальной системы отсчета к другой не меняется как само время t
=t’,
так и длительность какого-либо события :
.
Помимо времени, неизменным остается расстояние между двумя точками. Обозначим расстояние между точками А
и В
через в системе K
и в системе K
’. Координаты этих точек, соответственно, в системе K
и в системе К
’. Расстояние между точками определяется их координатам по теореме Пифагора:
Продифференцируем по времени соотношения (10.1) и получим преобразования Галилея для скоростей:
Из этих формул видно, что при переходе от системы К
к К
’ изменится лишь проекция скорости на ось OX
, вдоль которой движется система К’
, проекции скорости на направления других осей сохранятся.
Продифференцируем эти выражения по времени еще раз и получим закон преобразования ускорений при переходе из одной инерциальной системы отсчета в другую:
Из этих выражений видно, что все три проекции ускорения на оси координат остаются неизменными при переходе из системы отсчета К
в К’.
Таким образом, ускорение тоже является инвариантом преобразований Галилея.
Закон сохранения массы был сформулирован уже после Галилея и Ньютона. Но, для полноты картины, добавим, что в классической механике масса тела не зависит от выбора системы отсчета и также является инвариантом преобразований Галилея.
10.3. Законы классической механики и их инвариантность относительно преобразований Галилея.
Создание основ классической механики завершается трудами И.Ньютона, сформулировавшего основные законы механики и открывшего закон всемирного тяготения. Классическая механика Ньютона базировалась на работах Галилея, Декарта, Паскаля, Гука и многих других.
Раздел механики, в котором изучаются причины движения тел, т.е. силы, вызывающие их движение, называется динамикой
. Основные законы механики, сформулированные Ньютоном дошли почти без изменений до наших дней. Они известны из школьного курса физики. Напомним их.
Первый закон Ньютона. Всякое тело в инерциальной системе отсчета сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
Второй закон Ньютона. Ускорение тела прямо пропорционально сумме сил, действующих на него и обратно пропорционально его массе. Запишем этот закон в векторной форме с учетом кинематических соотношений
В этих формулировках мы использовали понятие импульса или количества движения P
= m
×
u
, которое было введено Декартом. Закон Ньютона, записанный в виде (10.6.а) или (10.6.б) с математической точки зрения имеет вид дифференциального уравнения, т.е. уравнения в котором значение функции связывается со значением ее производной. Любая из формулировок (10.6.а,б) второго закона Ньютона называется основным уравнением динамики
. Решение этого уравнения является основной задачей динамики
. Основная задача динамики может быть поставлена в форме прямой и обратной задачи. В прямой задаче требуется по известному закону движения тела r
(t)
найти действующие на это тело силы. В обратной задаче по известной зависимости действующих сил от времени SF
(t)
требуется найти закон движения тела r
(t).
Различные формулировки (10.6) могут немного менять постановку основной задачи, как прямой, так и обратной. Однако, прямая задача всегда математически сводится к дифференцированию, а обратная - к интегрированию. Очевидно, что решение обратной задачи динамики должно быть значительно более трудоемким, чем прямой. Отметим также, что для решения обратной задачи требуется знать начальные условия, которых в зависимости от постановки задачи (в форме 10.6.а или 10.6.б) должно быть задано либо столько же, сколько и степеней свободы системы, либо вдвое больше.
Третий закон Ньютона. Силы, с которыми взаимодействуют тела равны по величине, противоположны по направления и направлены вдоль линии взаимодействия. Этот закон утверждает, что силовое воздействие на тело носит характер взаимодействия. Этот же закон утверждает, что взаимодействия всех тел являются центральными.
Закон всемирного тяготения, открытый Ньютоном, иногда называют четвертым законом Ньютона. Его открытие базируется на трудах выдающихся астрономов 16-17-х веков Н.Коперника и И.Кеплера. И.Кеплер на основании учении Коперника о гелиоцентрической системе мира сформулировал три закона движения планет. Эти законы были правильными, но, как показал впоследствии И.Ньютон, являлись частным случаем более общего закона всемирного тяготения. Законы Кеплера позволяли найти орбиты планет, периоды их обращения вокруг солнца и скорость движения планет по орбитам.
С позиций современной механики отметим, что второй закон Кеплера является следствием закона сохранения момента импульса, он справедлив для движения тела в поле любых центральных сил.
С использование введенного нами математического аппарата закон всемирного тяготения можно написать в виде:
, где G
- гравитационная постоянная, m1
и m2
массы тел, единичный вектор, направленный вдоль линии взаимодействия, определяющий направление гравитационной силы .
Тело, двигающееся прямолинейно и равномерно относительно системы отсчета К
, вследствие уравнений (10.4) движется также прямолинейно и равномерно относительно системы отсчета К’.
Это обозначает, что формулировка первого закона Ньютона во всех инерциальных системах отсчета одинакова (правильнее сказать, первый закон Ньютона справедлив во всех инерциальных системах отсчета). Отметим, что, уравнения (10.4) позволяют по одной известной инерциальной системе отсчета построить бесконечное множество других.
В системе координат К
форма записи второго закона Ньютона определяется уравнениями (10.6). Поскольку, ускорение и масса инвариантны относительно преобразований Галилея, уравнение (10.6) одинаково записывается в различных инерциальных системах отсчета.
Поскольку, величина силы не меняется при переходе от одной инерциальной системы отсчета к другой, третий закон Ньютона тоже инвариантен относительно преобразований Галилея.
Четвертый закон не нуждается в доказательстве инвариантности относительно преобразований Галилея, поскольку расстояния, массы и силы не меняются при переходе из одной инерциальной системы отсчета в другую.
Таким образом, все законы Ньютона инвариантны относительно преобразований Галилея. Это значит, что они справедливы и записываются одинаковым образом во всех инерциальных системах отсчета.
10.4. Детерминизм классической механики.
Под детерминизмом понимается философское учение об объективной закономерности, взаимосвязи и причинной обусловленности всех явлений материального и духовного мира. Центральным ядром детерминизма является положение о причинности. Идея детерминизма состоит в том, что все явления и события в мире не произвольны, а подчиняются объективным закономерностям, независимо от наших знаний о природе явлений. Всякое следствие имеет свою причину.
Как и все остальное в физике, понятие детерминизма менялось по мере развития физики и всего естествознания. В 19-м веке теория Ньютона окончательно оформилась и установилась. Существенный вклад в ее становление внес П.С.Лаплас (1749 - 1827). Он был автором классических трудов по небесной механике и теории вероятности. Он же разработал принцип механического детерминизма, который сегодня носит его имя: детерминизм Лапласа.
Согласно классическому механистическому детерминизму
существует строго однозначная связь между физическими величинами, характеризующими состояние системы в какой-то момент времени (координаты и импульсы) и значениями этих величин в любой последующий или предыдущий моменты времени.
Если говорить более простым языком, детерминизм по Лапласу означает, что мы всегда однозначно можем описать поведение тела или любой сколь угодно сложной системы, если знаем начальные координаты и скорости тела, а также знаем законы движения и взаимодействия тел.
Этот принцип совершенно справедлив, если не выходить за рамки классической механики. Действительно, решение основной обратной задачи динамики всегда позволяет по известным силам SF
(x,y,z,t)
, приложенным к телу найти закон его движения r
(x,y,z,t)
и изменения скорости u
(x,y,z,t).
Полученные решения всегда будут однозначными и точными. Сказанное обозначает, что движение тела можно рассчитать сколь угодно далеко вперед. Тоже самое относится и к системе тел. Рассмотренная задача позволила сделать Лапласу сформулировать принцип механического детерминизма. Если известны начальные координаты и скорости тел системы, а также законы взаимодействия тел, то можно определить состояние системы в любой последующий момент времени. Примерами практического воплощения этого принципа еще во времена Лапласа были астрономические таблицы, очень точно описывавшие движения небесных тел на многие годы вперед.
Отметим, что для успешного практического решения подобных задач законы взаимодействия тел нужно знать очень точно, либо нужно смириться с тем, что расчет будет адекватно описывать поведение системы лишь в ограниченном временном интервале. Связано это с тем, что неточности расчета имеют свойство накапливаться и искажать получающуюся картину, - чем дальше, тем больше. Кроме того нужно иметь ввиду, что для решения задачи о движении большого количества взаимодействующих тел нужно задать очень большое количество начальных данных, законов взаимодействия и решать очень громоздкую систему дифференциальных уравнений. Не следует думать, что дело смогут спасти ЭВМ новых поколений; трудности, которые возникнут при решении такой задачи, носят принципиальный характер. За все время существования вселенной невозможно даже задать положения всех молекул воздуха, находящихся в 1-м см3
, не говоря уже о том, что решать эту систему уравнений нужно быстрее, чем в режиме реального времени.
Заметим, однако, что сказанное выше не отменяет принцип детерминизма, поскольку суть его в том, что состояние любой, даже самой сложной механической системы, однозначно определяется начальными условиями и законами взаимодействия. В природе успевают происходить такие движения, которые экспериментатор не может успеть описать, но от этого его расчеты не станут неправильными, они лишь могут стать неактуальными или ненужными.
С позиций сегодняшних знаний о природе можно утверждать, что механистический детерминизм Лапласа не работает в микромере, где процессы взаимодействия частиц по своей природе являются вероятностными. При столкновении двух атомов один из них может возбудиться (перейти в возбужденное состояние), а может и остаться в основном, невозбужденном состоянии. В последнем случае атомы будут сталкиваться как идеально упругие шары, в первом случае как неупругие шары. Результаты столкновения в этих случаях будут сильно различаться, а решить, как будет происходить взаимодействие, до того как оно произойдет, в принципе невозможно. В микромире могут одновременно протекать процессы, которые абсолютно несовместимы в макромире. Например, в опытах по дифракции электронов удавалось одну и туже частицу заставить пролетать одновременно сквозь два разнесенных друг от друга отверстия. Можно говорить лишь о вероятности прохождения данного конкретного электрона через выбранное отверстие. Для таких частиц оказывается неприменимым понятие траектории.
Когда описывается квантовая микросистема, предсказывается ее поведение в рамках вероятностного описания, но не дается однозначного ответа, как конкретно она будет себя вести. При этом всегда остаются в силе причинно-следственные связи.
11. РАБОТА, ЭНЕРГИЯ.
Мы с вами уже обсуждали вопрос, что такое энергия и дали на него следующий ответ. Энергия - это наиболее общая количественная мера движения и взаимодействия материи. Закон сохранения энергии - один из наиболее точных фундаментальных законов. Для изолированной системы энергия остается постоянной, она может переходить из одной формы в другую, но ее количество остается неизменным. Если система не изолирована, то энергия может изменятся при одновременном изменении энергии окружающих тел на такую же величину или за счет энергии взаимодействия тел внутри системы. При переходе системы из одного состояния в другое ее энергия не зависит от того, каким путем произошел этот переход. Энергия системы в общем случае может переходить в другие формы материи. Несколько позднее, при анализе законов общей теории относительности мы установим взаимосвязь энергии массы. С учетом всего вышесказанного можно считать, что закон сохранения энергии является в настоящее время самым точным фундаментальным законом, отступлений от которого не обнаружено.
По сути дела, утверждается, что существует определенная величина, называемая энергией, численное значение которой сохраняется при всех обстоятельствах, и этот закон управляет всеми явлениями в природе.
Поскольку существует многообразие форм движения материи, существует и многообразие видов энергий. Мы рассмотрим наиболее известные в физике виды энергии: кинетическую, потенциальную и полную механическую энергию. Определение этих видов энергии будет дано ниже. Сначала нужно дать определение механической работы. Работа силы - это мера действия силы, которая зависит от численной величины силы и ее направления, от перемещения точки приложения силы. Если сила F
постоянна по величине и направлению, а перемещение происходит вдоль прямой, то работа равна произведению силы на величину перемещения и косинус угла между направлением силы и перемещением (см. рис. 11.1).
,
Если 0£a<900
то работа положительна, если 900
<a£1800
то работа отрицательная. При a=900
механическая работа силы равна нулю, т.е. такая сила работы при перемещении не совершает. Примером последней может служить центростремительная сила при движении тела по окружности. Как видно из определения, работа - величина скалярная. Единицей измерения работы в системе единиц СИ является Джоуль (Дж). Один Джоуль - это работа силы в 1 Ньютон на участке пути в 1 метр. В общем случае для вычисления работы
dr
d
a
     F F
 S F S F

Рис.11.1 Рис.11.2
под действием переменной силы на криволинейном участке траектории вводят элементарную работу d
A
(
или dA)
. Считаем, что на бесконечно малом участке пути dr
сила не меняется и элементарная работа d
A
определяется как:
, так как это показано на рис.11.2. Работа - величина аддитивная; работа силы на конечном участке пути (1)®(2) определяется как сумма элементарных работ. Суммирование по бесконечно малым величинам d
А
есть операция интегрирования:
, где интегрирование ведется вдоль траектории. В векторном анализе такой интеграл называется циркуляцией вектора силы.
Заметим, что в этом выражении легко перейти к другой переменной интегрирования, ко времени.
. Введенная здесь величина N
называется мгновенной механической мощностью или просто мощностью тела.
.
Что будет происходить с системой (в простейшем случае -с материальной точкой) при совершении работы над ней. Запишем элементарную работу и выразим силу в нем при помощи второго закона Ньютона
Слева стоит элементарная работа, а справа дифференциал некоторой функции ,имеющий размерность работы и зависящий от скорости: дифференциал функции скорости, определяемой совершенной работой. Пусть в начальный момент времени t0 скорость тела равнялась u0
. Полную работу за промежуток времени от t0 до t1 получим после интегрирования dA, как это сделано в формуле (11.4). Совершаемая над телом работа привела к увеличению его скорости.
Теперь можно ввести понятие кинетической энергии
:
.
Кинетическая энергия определяется работой, которая совершена над телом. Положительная работа приводит к увеличению скорости тела и к увеличению кинетической энергии, отрицательная - к уменьшению того и другого. Если система состоит из многих тел, то ее кинетическая энергия складывается из кинетических энергий всех тел.
Кроме кинетической энергии есть еще потенциальная энергия
, для которой не существует общей формулы. Это понятие можно ввести лишь для ограниченного класса сил - для консервативных сил
. Это силы, работа которых по замкнутой траектории равна нулю. Существует другое определение консервативных сил. Консервативными силами называются такие силы, работа в поле которых не зависит от траектории и определяется только начальным и конечным положением системы. Нетрудно показать, что эти определения равнозначны. Действительно, если работа не зависит от траектории, то при обратном движении вдоль траектории она будет такая же, но с обратным знаком. Просуммировав движение по замкнутой траектории, состоящей из двух кривых, получаем в сумме 0. Консервативные силы, как правило, зависят только от положения тела, а неконсервативные - от его скорости.
Рассмотрим примеры полей консервативных и неконсервативных сил. Силы трения или сопротивления являются неконсервативными. Их направление определяется скоростью перемещения тел. Силы трения всегда направлены в сторону, противоположную направлению движения, т.е.: . Здесь - единичный вектор, направленный вдоль скорости тела, а значит, по касательной вдоль траектории его движения. Работа силы трения по замкнутой траектории () равна:
. Здесь и в дальнейшем кружок у интеграла означает интегрирование по замкнутой траектории. Последнее подынтегральное выражение скалярное, оно всегда положительно, следовательно, работа силы трения на замкнутой траектории всегда отрицательна. Эта работа тем больше по модулю, чем длиннее путь. Вывод: силы трения - неконсервативные силы.
Заметим, что кроме сил трения движения, есть еще так называемые силы трения покоя, которые, как это ясно из их названия, обеспечивают телу состояние покоя. Поскольку движения тела не происходит, то и работы они не совершают.
Примером поля консервативных сил является поле тяготения вблизи поверхности Земли. Работа, которая затрачивается на перемещение тела из положения r
1
в положение r2
равна: . Из этой формулы видно, что работа силы тяжести зависит от величины этой силы и от разности начальной и конечной высот тела. Никакой зависимости от формы траектории нет, а значит, сила тяжести консервативна.
Также просто можно доказать, что консервативными являются силы, создающие однородное поле. Поле сил называется однородным, если в любой точке этого поля сила, действующая на тело одинакова по величине и направлению.
Консервативными являются также поля центральных сил. Центральными называются силы, направленные вдоль линии взаимодействия тел, величина которых зависит только от расстояния между телами. Такому условию удовлетворяют, например, кулоновские силы и силы тяготения.
В поле консервативных сил можно ввести еще один вид механической энергии - потенциальную энергию.
Прежде чем ее вводить, выбирают точку, в которой она равна нулю. Потенциальная энергия тела в любой точке пространства определяется работой, которую нужно совершить, чтобы переместить тело из этой точки в точку с нулевой потенциальной энергией.
Отметим два существенных момента, вытекающих из этого определения. Во-первых, поскольку рассматривается поле консервативных сил, значение потенциальной энергии тела зависит от положения тела и выбора точки нулевой потенциальной энергии и не зависит от формы пути, по которому тело перемещается. Во-вторых, поскольку выбор нуля потенциальной энергии произволен, значение потенциальной энергии определяется с точностью до аддитивной постоянной, следовательно физический смысл имеет лишь разность потенциальных энергий или приращение потенциальной энергии, но не сама энергия.
На рис.11.3 мы представили три точки в пространстве поля консервативных сил: точку (b), точку (с) и точку (о), потенциальную энергию в которой будем считать равной 0. Обозначим через Abo
работу, которая совершается при переносе тела из точки (b) в точку (o). Если перемещать тело из точки (o) в точку (b), то совершаемая при этом работа будет равна Aob
=-Abo
, поскольку меняется направление движения, но не меняются действующие на тело силы. Работу по перемещению тела из точки (c) в точку (o) будем обозначать, как Асo
. Точно также Асо
=-Аос
. При перемещении тела из точки (b) в точку (c) совершается работа Abc
=-Acb
. Согласно определению потенциальной энергии и формуле (11.3) для вычисления работы имеем:
b E
пот
(b)
  Abo Abo
 А
bc
O А
bc
O
C E
пот
(С)
Aco
Рис. 11.3
Оказалось доказанным следующее утверждение: работа, совершаемая при перемещении тела в поле консервативных сил из точки (b) в точку (c), равна разности потенциальных энергий тела в точках (b) и (c). Однако, эта же работа равна разности кинетических энергий в точке (с) и (b).
Получилось, что сумма кинетической и потенциальной энергии тела, которая называется полной механической энергией тела, оказалась неизменной. Тоже самое справедливо и для системы механических тел. Получившееся утверждение носит название закона сохранения механической энергии
: полная механическая энергия изолированной системы в которой действуют консервативные силы остается неизменной.
Между консервативными силами и потенциальной энергией должна быть связь, поскольку потенциальная энергия вводится только в поле консервативных сил. Найдем эту связь для простейшего случая, когда потенциальная энергия зависит только от одной координаты. Примером может служит потенциальная энергия вблизи поверхности Земли, к нему и обратимся. Пусть ось (oy
) направлена вертикально вверх и имеет ноль на поверхности Земли. Тогда потенциальная энергия зависит только от координаты y и равна: где m
- масса тела, ускорение свободного падения вблизи поверхности Земли. Возьмем частную производную по координате y
от левой и правой частей равенства: . Справа стоит сила тяжести, которая направлена вверх, т.е. против оси (oy
). По-видимому, производной, стоящей в левой части равенства тоже можно приписать направление; ее проекция на ось (oy
) будет равна . В случае, когда действующая сила имеет проекции на все координатные оси, можно записать аналогичные выражения и для проекций на другие оси.
Для силы, таким образом, справедливо выражение:
.
В формуле (11.12) введен вектор градиента
потенциальной энергии. Определение этого понятия дается в разделе математики, который называется теорией поля. Отметим лишь некоторые свойства этого вектора. Особенность его состоит в том, что вдоль координатных осей нужно откладывать не числа, а математические операции дифференцирования по соответствующей координате. За градиентом обязательно должна стоять скалярная функция, к которой он применяется. Градиент потенциальной энергии имеет направление, в котором потенциальная энергия увеличивается быстрее всего, и величину, равную скорости этого увеличения, если двигаться в этом направлении.
Из сказанного следует, что силы поля заставляют тело двигаться в направлении минимума потенциальной энергии. Все естественные процессы стремятся привести систему к минимуму потенциальной энергии. Этот вывод справедлив не только для механики, но и для других разделов физики и естествознания.
Мы рассмотрели взаимопревращение кинетической и потенциальной энергий в поле консервативных сил. Что происходит, если действуют неконсервативные силы. Мы знаем, что, если телу сообщит скорость (сообщить кинетическую энергию)и пустить двигаться, например, по поверхности земли, оно остановиться за счет сил трения. Его потенциальная энергия не изменится, а кинетическая станет равной нулю, когда оно остановиться. Для ответа на вопрос, во что перешла кинетическая энергия, необходимо ввести еще один вид энергии- внутреннюю энергию.
Определим внутреннюю энергию Евн
как сумму кинетических и потенциальных энергий частиц (атомов), составляющих тело:
Евн
= S(Е
i
пот
+Е
i
кин
) (11.13)
Здесь N -число частиц, i -номер частицы. Параметром, характеризующим внутреннюю энергию является температура тела Т0
К, выраженная в градусах Кельвина. Чем больше температура тела, тем с большей скоростью двигаются атомы и тем самым больше внутренняя энергия. Численно внутренняя энергия равна:
Евн
=(М/m)C Т0
(11.14)
М - масса тела, m -молярная масса (численно равная атомному или молекулярному весу составляющих атомов),С -теплоемкость, равная энергии, которую нужно передать одному килограмму-молю, чтобы нагреть его на 1 градус Цельсия или Кельвина. Изменение внутренней энергии при переходе системы из состояния 1 в состояние 2 пропорционально изменению температуры тела : Евн
(2)-Евн
(1)
= DU = (M/m)C DT0
.
Сумму кинетической, потенциальной и внутренней энергий системы принято называть полной энергией Е
. В рассмотренном нами примере с останавливающемся телом кинетическая энергия тела переходит во внутреннюю энергию, т.е. идет на нагревание системы.
С учетом вышесказанного мы можем сформулировать закон сохранения полной энергии системы
: Полная энергия изолированной системы остается постоянной. Мы теперь не конкретизируем, какие силы (консервативные или неконсервативные) действуют в этой системе. Работа в системе, совершаемая за счет потенциальной энергии, может переходить и в кинетическую энергию системы, и во внутреннюю энергию. При увеличении внутренней энергии система нагревается.
12. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ.
12.1 Постулаты теории относительности.
К концу прошлого века Д.К.Максвеллом (1831-1879) были сформулированы основные законы электричества и магнетизма в виде системы дифференциальных уравнений, которые описывали постоянные и переменные электрические и магнитные поля. Решения системы уравнений Максвелла описывали всю гамму поведений электромагнитных полей в пространстве и времени. Из системы уравнений Максвелла следовало, что переменные электрические и магнитные поля могут существовать только в форме единого электромагнитного поля, которое распространяются в пространстве после возникновения с постоянной скоростью, равной скорости света в вакууме - с
.
На вопрос о том, в какой среде распространяется это поле, теория Максвелла ответа не давала. Ключевым моментом теории Максвелла являлось то, что уравнения Максвелла были неинвариантны относительно преобразований Галилея. Это означало, что при переходе с помощью преобразований Галилея из одной инерциальной системы отсчета в другую, уравнения меняли свой вид. Это обозначало, что преобразования Галилея нельзя было применять при описании электрических и магнитных явлений.
Строгое математическое доказательство неинвариантности уравнений Максвелла относительно преобразований Галилея достаточно сложно. Поэтому, проиллюстрируем этот факт на простом и наглядном примере. Для этого потребуется вспомнить, какие силы действуют на движущиеся заряды в электрических и магнитных полях.
Пусть два одноименных заряда летят с одинаковой скоростью u
в направлении оси (ox
), как это показано на рис.12.1. В неподвижной системе отсчета заряды будут создавать электрические и магнитные поля, и, следовательно, будут находиться в полях друг друга. Электрическое поле воздействует на заряд силой Кулона, магнитное - силой Лоренца. Напомним формулы для вычисления этих сил для случая, приведенного на рисунке.
Здесь B1
-
магнитная индукция, создаваемая первым зарядом в точке, где находится второй. Сила Кулона для одноименных зарядов всегда является силой отталкивания, а сила Лоренца в данном случае является силой притяжения. Таким образом, в неподвижной системе отсчета величина силы взаимодействия равна: F
= FK
- FЛ
.
Если перейти к системе отсчета, движущейся вдоль оси (ох
) со скоростью u
вместе с зарядами, то в ней заряды окажутся неподвижными, и сила Лоренца не возникнет. Таким образом, силы взаимодействия зарядов в различных инерциальных системах отсчета окажутся разными. Следовательно и поведение частиц ,их движение во времени, будет разным в зависимости от того, в какой инерциальной системе координат мы рассматриваем это движение. Естественно, что это абсурд и отсюда сделаем вывод, что к движущимся зарядам, законы движения и взаимодействия которых описываются уравнениями Максвелла, нельзя применять принцип относительности Галилея, т.е. преобразования Галилея.
q
 v v
 q v q v
 O X O X
Рис. 12.1
Вторым этапом в становлении специальной теории относительности стал опыт А.А.Майкельсона (1852-1931), проведенный в 1881 году. В опыте определялась скорость света в различных движущихся системах отсчета. Уже говорилось, что по теории Максвелла электромагнитные волны должны распространяться со скоростью в вакууме - с
. Встал вопрос, в какой инерциальной системе отсчета это происходит. Если таковой считать систему отсчета, связанную с неподвижными звездами, то скорость нашей планеты относительно них u
= 30 км/с. Эта скорость большая и сравнимая со скоростью света с.
Майкельсон экспериментально определял скорость света в разных системах отсчета, а именно, он измерял скорость света, идущего в двух противоположных относительно Земли направлениях. В соответствии с преобразованиями Галилея и положениями классической механики, скорости света в этих системах отсчета должны были бы отличатся на величину 2
u
.
Результаты эксперимента Майкельсона однозначно показали, что скорость света не зависит от выбора системы отсчета и всегда равна с
. Т.е. было установлено, что электромагнитные волны во всех инерциальных системах отсчета распространяются с одинаковой скоростью с=3×108
м/с. Эксперименты, подобные опыту Майкельсона повторялись неоднократно со все возрастающей точностью. На сегодняшний день можно утверждать, что скорость в различных системах отсчета одинакова с точностью порядка нескольких мм/с.
В 1904-м году голландский физик Х.А.Лоренц (1853-1928) вывел преобразования для перехода из одной инерциальной системы отсчета в другую, отличные от преобразований Галилея. Система уравнений Максвелла была инвариантна относительно этих преобразований. Преобразования касались и координат, и времени.
Обозначим координаты и время некоторого события (например положения материальной точки в пространстве) в инерциальной системе отсчета К
через x, y, z, t
, а в другой инерциальной системе отсчета К’
через x
’
,y
’
,z
’
,t
’
. Системы отсчета выбраны так, чтобы их координатные сетки начальный момент времени t
=t’
=0
совпадали,
а в дальнейшем система К’
двигалась относительно системы К
со скоростью u
вдоль ее оси (ox
). Преобразования Лоренца имеют вид:
. Сразу можно сказать, что при преобразования Лоренца переходят в преобразования Галилея. Т.е. преобразования Галилея являются частным случаем преобразований Лоренца при малых скоростях движения.
Анализируя сложившееся положение А.Эйнштейн разработал новую механику больших скоростей, называемую сейчас релятивистской механикой или специальной теорией относительности. В основе этой теории лежат два постулата.
Согласно первому постулату скорость распространения света во всех инерциальных системах координат одинакова и равна скорости распространения света в вакууме - с. Этот постулат утверждает эквивалентность инерциальных систем отсчета относительно скорости света.
Второй постулат заключается в том, что все физические законы и явления формулируются и протекают одинаково во всех инерциальных системах отсчета, т.е. инвариантны относительно преобразований Лоренца.
Базируясь на этих постулатах, Эйнштейн разработал теорию движения систем при любых скоростях, вплоть до скоростей света. В рамках теории относительности получены выводы, казалось бы противоречащие законам классической механики. Однако, все выводы этой теории подтверждены экспериментально с высокой точностью.
Согласно принципу соответствия старая теория (классическая механика или механика движения тел при малых скоростях) является частным случаем новой. И наоборот, новая теория относительности переходит в старую классическую механику при скоростях движения v<<c
.
12.2 Релятивистская механика.
Обратимся к преобразованиям Лоренца (12.1). Из них следует, что максимальная скорость движения материальных систем ограничена скоростью света в вакууме с
. Если бы скорость движения тела превысила скорость света, то, как следует из преобразований Лоренца, координаты и время станут мнимыми т.е. потеряют реальный физический смысл.
Теперь рассмотрим некоторые следствия из преобразований Лоренца. В классической механике расстояние между двумя точками и время были одинаковым во всех инерциальных системах отсчета. В релятивистской механике они оказались разными в различных инерциальных системах отсчета, т.е. перестали быть инвариантами. Но инварианты относительно преобразований Лоренца должен быть. Одним из них является скорость света в вакууме - с.
Она действительно одинакова во всех инерциальных системах отсчета. Другим инвариантом этих преобразований является так называемый интервал
между событиями. Его квадрат равен: .
Благодаря инвариантности интервала
пространство и время оказываются взаимосвязанными. Они образуют единое четырехмерное пространство-время
. Вдоль четвертой оси откладывается мнимая величина . Четырехмерное пространство-время было впервые введено Г.Минковским (1864-1909) и сейчас носит его имя. Попробуем представить себе такое пространство. Мы умеем делать проекции трехмерного пространства на двухмерное. Например, таким образом мы рисуем на доске трехмерную систему координат на плоскости - двухмерном пространстве. Представим себе в объемном трехмерном пространстве проекцию четырехмерного куба. Это будут два куба, каждая из вершин одного куба соединена с соответствующей вершиной второго куба линией четвертого измерения. Расстояние между двумя точками в четырехмерном пространстве и будет интервал в соответствии с законами геометрии.
Проанализируем теперь на основе преобразований Лоренца одновременность событий в разных системах отсчета. В классической механике использовался принцип дальнодействия, когда взаимодействие между телами осуществлялись мгновенно через любое расстояние. В этом случае мы могли бы ставить одно и тоже время в разных системах координат. Попросту говоря синхронизовать время и задавать его одним и тем же.
    1
1 2 1
1 2
    
2
Рис.12.2
Рассмотрим эксперимент по синхронизации часов, базируясь на постулатах теории относительности. Представим себе следующую ситуацию (см. рис.12.2). Первый наблюдатель 1
стоит на земле и мимо него двигается вагон, в середине которого стоит второй наблюдатель 2
. В начале и конце вагона расположены часы (1) и (2) которые нужно синхронизовать. Это проще всего сделать следующим образом. Второй наблюдатель в вагоне посылает свет в две стороны и в момент прихода света на часы, они включаются с нуля и идут синхронно. С точки зрения наблюдателя в вагоне часы показывают одинаковое время. Рассмотрим, что покажут часы первому наблюдателю, стоящему на земле.
Скорость распространения света постоянна в любой системе отсчета. Пока свет распространяется в конец вагона, часы 1 переместятся ему навстречу и будут включены раньше. Часы 2 уйдут за время распространения света и будут включены позднее. Таким образом, с точки зрения первого наблюдателя часы будут показывать разное время , а с точки зрения второго наблюдателя - одинаковое. Время будет разное для двух разных наблюдателей, находящихся в различных инерциальных системах отсчета.
К этому же результату можно прийти и чисто формально, при помощи преобразований Лоренца. Покажем это. Пусть в неподвижной системе отсчета К
два события происходят одновременно, т.е. .
Найдем разность в системе отсчета К’
, перемещающейся относительно К вдоль оси x
со скоростью u.
Для этого воспользуемся преобразованием Лоренца для времени.
Не вдаваясь в детальный анализ, укажем, что изменение длительности промежутков времени не касается принципа причинности: если из двух событий, одно является следствием другого и разделены промежутком времени, то в любой инерциальной системе отсчета эти события также разделены промежутком времени, и последовательность событий не нарушается. Т.е. следствие всегда идет после причины.
Рассмотрим парадокс, следующий из преобразований Лоренца. Пусть в одной точке пространства в системе отсчета К
произошли два события (например рождение и смерть человека) в моменты времени t1
и t2
, соответственно. Промежуток времени между этими событиями в системе отсчета К
равен . В движущейся системе отсчета K’
промежуток времени между этими событиями другой, что следует из преобразований Лоренца для времени. Теория относительности позволяет связать длительности промежутков времени в системе отсчета наблюдателя и в системе отсчета, связанной с наблюдаемыми объектами (собственное время).
.
В разных системах отсчета, двигающихся относительно друг друга время течет по разному, причем в системе отсчета, связанной с объектом наблюдения часы идут медленнее всего, т.е. собственное время всегда минимальное. Собственное время
- еще один инвариант преобразований Лоренца, в какой бы инерциальной системе отсчета его ни вычисляли, всегда должен получиться одинаковый результат. Формула (12.3) неоднократно обыгрывалась в фантастических романах, когда отец улетал к звездам на космолете с большой скоростью, возвращался обратно молодым, а его сын, остававшийся на Земле уже успевал состарится.
Обратимся еще раз к примеру, приведенному в параграфе 12.1, в котором рассматривалось взаимодействие двух движущихся зарядов, и ответим на вопрос, почему же все-таки силы взаимодействия окажутся для разных наблюдателей разными. Ответ на него заключается в том, что в движущейся системе отсчета время течет медленнее, и ускорение, а значит, и сила взаимодействия уменьшится.
Кроме изменения хода часов наблюдается изменение размеров (укорочение) быстро движущихся объектов. Этот эффект тоже может быть выведен из преобразований Лоренца. Связь длины отрезка, направленного вдоль скорости движения, в системе К
(наблюдаемая длина ) и в системе K’
(собственная длина ) задается формулой:
.
Таким образом собственная длина всегда максимальна. Отметим, что сокращаются лишь размеры тела вдоль направления скорости системы K’.
Изменение размеров - кажущийся, ненаблюдаемый эффект. Размеры мы определяем, сравнивая длину линейки с размерами тела. Но, и сама линейка в другой системе координат будет менять свои размеры одновременно с телом. Этот эффект напрямую нельзя наблюдать.
Как ни странно, именно сокращение длины и замедление хода времени, предсказанные в теории относительности, удалось наблюдать еще в 30-е годы нашего века. Исследовались нестабильные частицы m-мезоны. Время жизни m-мезонов было измерено, . За это время частица могла пролететь расстояние не превышающее . Однако, m-мезоны могли рождаться лишь на высоте 20-30 км при столкновении космического излучения с ядрами атомов в атмосфере. Казалось бы, все они должны распасться еще в верхних слоях атмосферы, но приборы на земле уверенно регистрировали их. Объясняется это тем, что рождались они с очень большими скоростями, близкими к скорости света. В соответствии с формулой (12.3) течение времени в их их системе отсчета замедлялось и они успевали пройти расстояние в несколько десятков километров. Но как объяснить это же явление, если наблюдать за частицами в их собственной системе отсчета, ведь в этой системе время жизни частиц составляет действительно . А в этом случае для частиц сокращается длина пройденного ими пути. m-мезоны пролетают десятки километров и достигают земли, но для них в полном соответствии в формулой (12.4) длина этого пути сокращается до нескольких сотен метров. Таким образом, наблюдение одного природного явления подтвердило сразу два, казалось бы, абсурдных следствия из преобразований Лоренца.
В настоящее время существуют очень точные часы, которые показали, что время на движущихся искусственных спутниках Земли отстает от земного времени на 1 секунду за 44 года.
В релятивистской механике предсказан еще целый ряд парадоксальных с точки зрения классической механики явлений. В настоящее время большинство из них наблюдались в экспериментах. При этом не наблюдалось отклонений от предсказаний специальной теории относительности.
12.3 Релятивистская динамика, масса покоя, связь массы и энергии
В параграфе 10.3 обсуждалась инвариантность законов классической механики относительно преобразований Галилея. Преобразования Лоренца связывают не только координаты с координатами, но и время с координатами и наоборот. Естественно, что законы классической механики неинвариантны по отношению к преобразованиям Лоренца. При создании релятивистской механики перед Эйнштейном встал вопрос, как записать второй закон Ньютона, чтобы он был инвариантен относительно преобразований Лоренца. Эйнштейном был получен явный вид основного уравнения динамики в релятивистской форме.
Сначала нужно ввести импульс, который сохранялся бы в любой инерциальной системе отсчета. Традиционный классический импульс оказывается неинвариантен по отношению к преобразованиям Лоренца и, как следствие, не сохраняется. Однако, если не меняя формы записи, измерять перемещение в лабораторной системе отсчета К
, а промежуток времени - в системе отсчета K’
, связанной с телом, то импульс будет инвариантен к преобразованиям Лоренца и будет сохраняться. Нужно заменить на . Связь промежутков времени в различных инерциальных системах отсчета задается формулой (12.3). .
Здесь mo
- классическая масса тела, u
- его скорость, измеряемая в лабораторной системе К
, а m
- релятивистская масса: .
Таким образом, импульс тела формально записывается также, как и в классической механике, но понятие массы наполняется новым содержанием. Масса в специальной теории относительности зависит от скорости частицы. Классическую массу частицы mo
можно назвать массой покоя
. Масса покоя равна массе тела, измеренной в той инерциальной системе отсчета, где тело покоится. Ни в какой системе отсчета масса тела не может быть меньше массы покоя. Масса покоя - еще один инвариант преобразований Лоренца.
Основное уравнение динамики движения релятивистской частицы имеет вид, схожий с основным уравнением движения классической динамики: однако, при дифференцировании по времени правой части нужно учесть, что релятивистская масса не есть постоянная величина. Отметим, что классическая формулировка второго закона Ньютона несправедлива даже с релятивистской массой.
Уравнения динамики релятивистской частицы (12.5-12.7) нашли блестящее подтверждение уже в 30-х годах нашего века при разработке первых ускорителей электронов, которые были названы бетатронами. На бетатронах электроны ускорялись в переменных электрических полях и приобретали скорость, сравнимую со скоростью света. Тогда то и было обнаружено, что масса частицы и траектория ее движения зависят от скорости в полном соответствии с формулами (12.5-12.7).
Уравнения релятивистской динамики позволили Эйнштейну найти связь массы и энергии тела. Попробуем вслед за ним найти количественной соотношение между этими величинами. Для этого преобразуем уравнение (12.6):
Если дифференциалы величин равны, то сами величины могут различаться на постоянную величину: . Значение этой константы можно найти из условия, что при , выражение для кинетической энергии должно стремиться к Значение ее окажется равным . Таким образом, получаем релятивистское выражение для кинетической энергии: .
Отметим, что классические выражения для кинетической энергии, как неприменимы, даже если в них подставить релятивистские массы.
Второе слагаемое в этом выражении имеет смысл энергии покоя, внутренней энергии тела, энергии связанной с самим фактом существования тела и наличием у него массы в неподвижном состоянии. Сумма кинетической энергии и энергии покоя называется полной энергией тела. Выражение для полной энергии можно получить из формулы (12.9).
.
Мы получили самую известную формулу 20-го века, которая устанавливает количественную связь между энергией и массой. Ее можно трактовать следующим образом. Между полной энергией системы Е
и ее массой m
существует связь, определяемая формулой (12.10). Энергия при определенных условиях может переходит в массу, а масса - в энергию. Однако, понятие энергии не сводится только к массе и наоборот, масса не сводится только к энергии. Тем самым установлена связь между мерой количества материи - массой и мерой движения материи - энергией. Эта связь является отражением факта, что материя без движения, также, как и движение без материи не существует.
Рассмотрим пример, в котором полученная формула играет определяющую роль. При делении ядра урана образуется два более легких ядра. При этом масса ядра урана больше суммы масс образовавшихся ядер на величину D
m
. Дефект массы
D
m
не исчезает, а переходит в кинетическую энергию осколков - дочерних ядер: D
Е
=D
m
×
c2
. Кинетическая энергия этих осколков - и есть та энергия, которая высвобождается при взрыве атомной бомбы или в атомном реакторе.
13. ЗАКОНЫ СОХРАНЕНИЯ
13.1 Законы сохранения, как отражение симметрии процессов преобразования.
Идея сохранения, следствием которой являются законы сохранения, появилась сначала как чисто философская догадка о наличии стабильного, неизменного в вечно изменяющемся мире. Еще античные философы-материалисты пришли к понятию материи - неучтожимой и несотворимой основы всего существующего. С другой стороны, наблюдения постоянных изменений в природе приводило к представлению о вечном движении материи как важнейшем ее свойстве и, как следствие этого, к изменяемости одних и неизменности других свойств материи.
В этом разделе мы рассмотрим законы сохранения как отражение некоторых операций, вводимых в физике. Напомним, что законами сохранения называются те закономерности, согласно которым численные значения некоторых параметров или величин не меняются со временем в любых процессах или в определенном классе процессов.
Важнейшими законами сохранения, справедливыми для любых изолированных систем, являются законы сохранения энергии, импульса, момента импульса и электрического заряда.
Полное описание физической системы возможно только с использованием динамических законов. Так описание движения материальной точки возможно с использованием законов динамики или законов Ньютона. Однако во многих случаях динамические законы системы либо неизвестны вообще, либо они настолько сложны, что не поддаются анализу. В таких случаях законы сохранения позволяют сделать заключения о характере поведения системы. Причем, зачастую, это можно сделать очень простым образом.
Вспомним школьную задачу о падения тела с высоты h
. Скорость тела в момент удара о землю можно найти с использованием законов динамики: первого и второго законов Ньютона. Но, эту же задачу можно решить, используя закон сохранения механической энергии, как говорится, в одну строку. Приведем это решение.
Энергия тела до падения определялась его потенциальной энергией . После момент ударом о землю его потенциальная энергия полностью перешла в кинетическую и стала равной . Поскольку, значение энергии в процессе падения сохранилось, названные можно приравнять и получить скорость тела в момент падения.
.
Решение задачи оказалось очень простым, благодаря использованию закона сохранения механической энергии. Очень часто решение других, гораздо более сложных задач значительно упрощается с использованием других законов сохранения. Приведенный пример показывает, что чем больше законов сохранения нам известно, тем легче и точнее мы можем описывать поведение сложных систем. Возникает интуитивное понимание того, что законы сохранения являются отображением каких-то более общих закономерностей природы.
Целью настоящего раздела является рассмотрение связи законов сохранения с некоторыми математическими операциями и преобразованиями, которые будут введены ниже.
Любая физическая система может быть подвергнута каким-либо операциям или преобразованиям, не изменяющим ее состояния или ее свойств. Например, можно перейти из одной инерциальной системы отсчета в другую с использованием преобразований Галилея. Если физические законы, устанавливающие связь между физическими величинами или параметрами, не меняются в результате таких операций или преобразований, то говорят, что эти законы инвариантны относительно этих преобразований или обладают симметрией к этим преобразованиям.
Введем некоторые из преобразований пространства и времени. Первое из них - это перенос или сдвиг системы как целого
в пространстве. Такая операция преобразования сводится к переносу начала отсчета, либо всей системы отсчета и задается вектором. Симметрия физических законов относительно сдвигов в пространстве означает эквивалентность всех точек пространства. Не существует какой-то "особой" точки в пространстве, которую можно было бы выделить для введения абсолютной системы отсчета, абсолютной системы координат. Этот важнейший факт принято называть однородностью пространства.
Второе преобразование - это поворот системы отсчета
или системы координат в пространстве. Его можно свести к поворотам системы относительно одной или всех координатных осей. Симметрия физических процессов и законов относительно этого преобразования связана с изотропностью пространства
, т.е. с эквивалентностью всех направлений в пространстве. Нет такого направления, относительно которого мы могли бы задать, например, ось (ох
), и которое имело бы преимущества перед другими направлениями. Все направления в пространстве равноценны.
Третье преобразование - сдвиг во времени
или изменение начала отсчета времени
. Симметрия физических законов относительно сдвига во времени означает, что законы, явления, процессы не меняются со временем, т.е. физический процесс или явление можно повторить или воспроизвести. Безразлично, в каком времени рассматривать физический процесс, в прошлом, в настоящем или в будущем; он всегда будет протекать одинаково. Благодаря этому обстоятельству можно произвольно выбирать начало отсчета времени.
Кроме названных существует еще большое количество специальных преобразований, применимых к конкретным законам. Некоторые из них уже известны, с другими познакомимся позже.
В 1918 году немецкий математик Э.Нетер (1882-1935) сформулировал теорему, названную позднее его именем. Эта теорема играет огромную роль в физике и во всем естествознании. Она устанавливает связь между свойствами симметрии физической системы и законами сохранения. Не вдаваясь в математическую сторону дела, рассмотрим идею теоремы Нетера. Для физической системы, состояние которой описывается системой дифференциальных уравнений, каждому преобразованию, непрерывно зависящему от какого-либо параметра (скорости, времени, координат и т.д.), соответствует свой закон сохранения. При этом на преобразования накладывается условие: при его применении должен остаться инвариантным (т.е. неизменным) некий параметр - действие
(S
). Действие - это физическая величина, имеющая размерность произведения энергии на время или импульса на координату.
Действие - очень важный параметр в физике. Он позволяет сформулировать принцип наименьшего действия. Содержание этого принципа заключается в том, что если система переходит из одного состояния в другое, то этот переход осуществляется таким образом, чтобы изменение действия было бы минимальным. Использование принципа наименьшего действия дает еще одну возможность описать поведение системы, найти уравнения ее движения, изучить ее движение. В общем случае, принцип наименьшего действия указывает, в каком направлении должно изменяться состояние системы. Из этого принципа, например вытекают все законы геометрической оптики как в однородной, так и в неоднородной среде. К сожалению, детальное изучение принципа наименьшего действия требует знание таких разделов высшей математики, как вариационное исчисление, и невозможно в рамках настоящего курса.
13.2. Фундаментальные законы сохранения.
Существует ограниченное число законов сохранения, общих для классической и современной физики. В их числе назовем следующие фундаментальные законы сохранения:
- закон сохранения энергии и массы,
- закон сохранения импульса или количества движения,
- закон сохранения момента импульса или
момента количества движения,
- закон сохранения электрического заряда.
При применении этих законов в первую очередь надо помнить, что они справедливы для изолированных систем. Т.е. систем, которые не взаимодействуют с окружающими системами или телами. Однако, не меняющийся в изолированной системе параметр (импульс, момент импульса, энергия, заряд и др.), может изменяться при взаимодействии этой системы с другими системами или объектами. Например, импульс тела р
=m
u
остается неизменным до тех пор, пока тело не взаимодействует с другими телами. Импульс тела изменяет действующая на него сила. Однако, если расширить систему и включить в нее и второе тело, то суммарный импульс первого и второго тел окажется постоянным.
Рассмотрим подробнее законы сохранения с точки зрения их преобразований симметрии в природе. Начнем с закона сохранения энергии. Его формулировка достаточно проста. Полная энергия изолированной системы остается постоянной и не меняется во времени. Более точную формулировку этого закона дадим в конце раздела. Обратимся снова к уже рассмотренному примеру. Пусть некоторое тело поднято на высоту над поверхностью земли. В таком случае оно обладает потенциальной энергией . Если это тело отпустить, то оно станет падать на землю; при этом его высота, а следовательно, и потенциальная энергия уменьшается. Она переходит в другой вид энергии - в кинетическую энергию. До тех пор, пока тело не упало, сумма потенциальной и кинетической энергии остается постоянной.
Что произойдет с энергией тела в момент, падения на землю. Тело остановится, следовательно, его кинетическая энергия относительно земли станет равной нулю. Куда денется энергия. Она не исчезнет, а перейдет в так называемую внутреннюю энергию. Внутренней энергией тела называется сумма кинетических и потенциальных энергий всех атомов, из которых состоит тело. Внутренняя энергия обычно определяется параметром системы, который называется температурой. Чем больше температура, тем больше внутренняя энергия и тем больше скорости атомов, составляющих эту систему. Таким образом, при падении тела на поверхность земли а его потенциальная энергия сначала переходит в кинетическую, а затем - во внутреннюю энергию системы тело- земля. Поскольку мерой внутренней энергии системы является температура, потенциальная энергия поднятого тела после его падения пойдет на нагрев самого тела и поверхности земли, Или другими словами, на увеличение кинетической энергии атомов тела и поверхности земли. Отметим, что если рассматривать данное тело как изолированную систему, то его полная энергия, не сохранялась бы. Однако, со включением в систему поверхности земли все встало на свои места. Закон сохранения энергии сработал.
Закон сохранения энергии отражает симметрию явлений природы по отношению к переносу во времени, или, иначе, постоянство законов природы во времени. Проще всего доказать это от противного. Покажем, что если бы законы природы менялись во времени, то энергия не сохранялась бы. Пусть, например, меняется во времени закон всемирного тяготения, и даже не сам закон, а только гравитационная постоянная G
(см. формулу 10.7). Поднятое в какой-то момент времени на высоту тело будет обладать потенциальной энергией , где ускорение свободного падения равно: , где М
- масса Земли, а Rз
- ее радиус. Если гравитационная постоянная G
, будет меняться, то вместе с ней будет меняться потенциальная и полная механическая энергия. Налицо нарушение закона сохранения энергии.
Отсюда вывод: если бы законы природы менялись со временем, то это привело бы к нарушению закона сохранения энергии.
Рассмотрим закон сохранения импульса. Импульсом или количеством движения тела называется произведение скорости поступательного движения этого тела на его массу P
=m
u
. Импульсом системы называется векторная сумма импульсов всех тел, образующих эту систему. Если в системе имеются только силы взаимодействия и нет внешних сил, то такая система называется замкнутой. Закон сохранения импульса гласит: полный импульс изолированной системы не меняется, т.е. остается постоянным при любых взаимодействиях внутри этой системы. Отражением какого преобразования пространства или процесса симметрии является этот закон? Он отражает тот факт, что сдвиг начала системы отсчета в произвольном направлении на любое расстояние, не меняет течения явлений природы и никак не отражается на в законах природы. Проще всего это показать следующим образом. Пусть имеется материальная точка массой m
, имеющая скоростью u
в произвольной системе отсчета К
. Импульс материальной точки равен P
=m
u
, где скорость точки u
=
r’(t)
. Пусть мы перешли в другую систему отсчета, начало координат которой сдвинуто на постоянный вектор ro
относительно системы отсчета К
. Как изменится импульс? В системе отсчета K’
он будет равен mu
:
.
Получилось, что импульс тела не меняется при сдвиге начала системы координат на вектор r
o
, т.е. при переходе от одной системы к другой, неподвижной относительно первой.
Таким образом, закон сохранения импульса является отображением однородности пространства, т.е. отсутствием каких-либо выделенных, «особых» точек в пространстве.
Закон сохранения момента импульса или момента количества движения является отображением еще одного фундаментального свойства пространства - его изотропности.
Момент импульса L
равен векторному произведению радиуса вектора тела на импульс тела: L
=[rp
]. Т.е. L
- это вектор, направленный перпендикулярно векторам r
и p
и по модулю равный произведению их длин на синус угла a между ними, т.е. L
=r
×
p
×
sin
a
. Из двух направлений, перпендикулярных векторам r
и p
, направление вектора L
выбирается по правилу буравчика. При вращение ручки буравчика от r
к p
в направлении меньшего угла поступательное движение буравчика укажет направление вектора момента импульса. Полный момент импульса системы равен векторной сумме моментов импульса всех тел системы. Система называется замкнутой, если в ней имеются только силы взаимодействия между телами и нет внешних сил. Закон сохранения момента импульса гласит: полный момент импульса тела или изолированной системы не меняется ни при каких взаимодействиях тел внутри этой системы.
Под изотропностью пространства подразумевают отсутствие каких-либо преимущественных или выделенных направлений в пространстве. Все направления в пространстве равноценны и нет ни одного, которое обладало бы каким-то преимуществом перед другими.
Закон сохранения момента импульса и является отображением изотропности пространства. В терминах предыдущего раздела мы можем сформулировать следующее. При применении операции поворота в пространстве момент количества движения тела не меняется, поскольку его величина и направление зависят лишь от длин и взаимной ориентации векторов r
и p
. Значит, какое бы направление в пространстве мы ни приняли для нашей системы координат, момент импульса тела от этого не изменится. Строгое доказательство этого утверждения требует использование аппарата векторной алгебры и выходит за рамки наших рассмотрений.
Закон сохранения зарядов может быть сформулирован так. Алгебраическая сумма зарядов изолированной системы не меняется ни при каких взаимодействиях внутри этой системы. Понять, отображением каких свойств пространства является этот закон, можно лишь после глубокого знакомства с квантовой механикой. В квантовой механике поведение тела (микрочастицы) описывается волновой функцией - Y, которая в общем случае может быть комплексной. Квадрат модуля этой функции умноженный на элемент объема равен вероятности обнаружить частицу в этом элементе объема. Эта функция тоже может быть подвергнута различным преобразованиям в пространстве и времени. Одно из таких преобразований - записывается как , где - мнимая единица, - некоторое число, - заряд. Наглядного физического смысла это преобразование не имеет. Его называют локальным калибровочным преобразованием. Модуль написанного выражения равен единице,
поэтому, такое преобразование не может изменить волновую функцию по модулю, а физический смысл имеет именно квадрат ее модуля. Значит, поведение частицы не меняется при локальном калибровочном преобразовании. Закон сохранения заряда является отражением симметрии квадрата модуля волновой функции относительно локального калибровочного преобразования.
13.3. Эволюция закона сохранения массы - энергии - материи.
Все многообразие окружающего нас мира нужно рассматривать, как проявление свойств материи. Материя существует вне нас, она отображается и познается нашими органами чувств. Качественная формулировка закона сохранения материи как неучтожимой и несотворимой основы всего существующего была известна еще с античных времен.
Материя не существует вне движения и наоборот, движение не существует без материи. Качественная формулировка этого положения существовала до начала нашей эры.
В настоящем курсе мы рассмотрены и введены меры, характеризующие количество матери - массу и движение материи - энергию.
С появлением математического аппарата в физике появились и математические формулировки законов сохранения массы и энергии. Закон сохранения массы был сформулирован французским химиком А.Л. Лавуазье (1743-1794) в конце 18-го века. Он не требует специальных комментариев. Закон сохранения энергии трансформировался на протяжении полутора веков. Первоначально немецкий ученый Г.В.Лейбниц (1646-1716) сформулировал закон сохранения для механической энергии. В его формулировке утверждалось, что сумма потенциальной и кинетической энергии замкнутой системы остается постоянной во времени.
.
Первоначально теплота и механическая энергия рассматривались независимо друг от друга. Теплоту считали невидимой жидкостью, которая могла перетекать от горячего тела к холодному при контакте. До сих пор сохранились отголоски такого представления; например, говорят о “перетекании” тепла, о “теплоемкостях”. Интересно, что в рамках имеенно такого представления о теплоте Н.Л.С.Карно (1796-1832) удалось разработать теорию тепловых машин.
Первым на эквивалентность теплоты и работы обратил внимание немецкий ученый - естествоиспытатель и врач Ю.Р.Майер (1814-1878). В медицине в то время часто применялось кровопускание. Майер обратил внимание на то, что цвет крови человека меняется при изменении температуры внешней Среды температуры. В тропиках, где температура выше, цвет крови был более алым. Кровь содержала больше кислорода, который необходим для работы мышц тела. Проанализировав эти факты, Ю.Р.Майер пришел к выводу, что чем больше теплоты подводится в систему, тем меньше требуется затрат энергии из самой системы на совершение работы. Он в 1842 году рассчитал механический эквивалент теплоты.
Позднее на основе этих положений был сформулирован закон сохранения энергии, который называется первым началом термодинамики. Этот закон гласит, что теплота Q, подводимая к системе идет на совершение системой работы A и на изменение внутренней энергии системы DU. Математически первое начало термодинамики записывается так:
.
Таким образом, к середине 19-го века были окончательно сформулированы законы сохранения массы и энергии, которые трактовались как законы сохранения материи и движения.
В начале 20-го века оба эти закона подверглись коренному пересмотру в связи с появлением специальной теории относительности. Как уже отмечалось релятивистская масса зависит от скорости, следовательно, характеризует не только количество материи, но и ее движение. В разделе 12.3 выведена самую знаменитую формула 20-го века - формулу (12.10), связывающую массу и энергию тела:
.
В специальной теории относительности естественным образом слились законы сохранения массы и энергии, существовавшие в классической механике порознь. По отдельности эти законы не выполняются. Невозможно охарактеризовать количество материи (ее массу), не учитывая движения (взаимодействия) материи. Это является отражением философской концепции о неразделимости материи и движения.
Формулу иногда ошибочно интерпретируют, как тождественность массы и энергии. Это не правильно. Данная формула означает, что между энергией (мерой движения) и массой (мерой количества матери) существует взаимосвязь. Энергия и масса могут взаимно превращаться друг в друга. Количественное соотношение, определяющее этот переход и дается формулой (13.4).
В настоящее время обобщенный закон сохранения энергии можно сформулировать в следующем виде. Полная энергия замкнутой системы, включающая энергию, эквивалентную массе этой системы, не изменяется во времени.
Естественно, что вплоть до наших дней, до развития такой области физики, как атомная и ядерная физика, нельзя было найти отклонения от законов сохранения массы и энергии в их первоначальных формулировках. Конечно, если мы увеличим скорость тела, то его масса изменится. Но, для реальных тел макроскопического размера никакими весами и сейчас мы не сможем найти изменение этой массы. Например, если скорость движения человека массой 100 кг равна 100 м/с, то его энергия движения равна 1000000 Дж. Эта энергия эквивалентна массе 10-11
кг, которую невозможно определить никакими современными методами на фоне собственной массы в 100 кг. Этот пример показывает, что на современном этапе развития техники как правило можно пользоваться старой формулировкой закона сохранения энергии.
Приведем еще один пример, показывающий, когда нужно применять новую формулировку закона сохранения энергии, и позволяющий дать интерпретацию нового закона сохранения энергии. При делении ядра урана сумма масс дочерних ядер меньше исходного ядра. Разность этих масс в соответствии с формулой (13.4) переходит в кинетическую энергию осколков деления - дочерних ядер. Масса системы (т.е. ядра) уменьшается, но увеличивается кинетическая энергия системы. Энергия при полном делении всего 1 г урана как раз и равна энергии взрыва бомбы над Хиросимой в 1945 году.
Эволюция закона сохранения энергии интересна с двух точек зрения. С одной стороны, законы сохранения, будучи почерпнутыми из опыта, нуждаются в постоянной экспериментальной проверке, в уточнении. Нельзя быть уверенным, что с расширением пределов человеческого опыта данный закон (или его конкретная формулировка) останутся справедливыми и не потребуют уточнения границ, в рамках которых они остаются справедливыми. С другой стороны, в законе сохранения энергии теснейшим образом переплелись физика и философия. Этот закон, все более уточняясь, постепенно превратился из абстрактного и неопределенного философского высказывания в точную количественную формулу.
Другие законы сохранения (импульса, момента импульса, заряда и т.д.) возникли практически сразу в количественной формулировке и не требовали в дальнейшем уточнения.
|