| Негосударственное общеобразовательное учреждение
Высшего профессионального образования
Омский Юридический Институт
Р Е Ф Е Р А Т
По предмету: Концепции современного естествознания.
Тема: Синтез лёгких ядер (дефект массы) и Парадокс моделей вселенной.
Выполнил: студент группы
41-у Рековский В.Р.
Проверил: Гайдамакин А.А.
Омск - 2004
Ядерная энергетика синтеза основана на синтезе легких ядер, протекающего при высоких температурах Т ³ 100 * 106
К, когда реагирующая среда является полностью ионизированным газом – плазмой.
Изучаются различные схемы удержания горючей плазмы.
Первые опытные энергетические ректоры синтеза – термоядерные реакторы, - вероятно, будут построены к концу этого века.
В настоящее мировое производство энергии соответствует сжиганию около 10 млрд. т обычного топлива в год. В следующем веке эта величина, вероятно, возрастет в несколько раз. Ядерная энергетика способна обеспечить длительное развитие человечества без ограничений со стороны топливных ресурсов.
Синтез легких ядер
Если W
> 0, то распад ядра энергетически запрещен. Но в обратном процессе - слиянии ядер X
1
и X
2
- энергия исходной системы должна уменьшится на величину W
. Продукты синтеза приобретут кинетическую энергию W
.
На правой половине Рис. 5 изображена реакция слияния
| 2
H
+ 2
H
--> 3
He
+ n
+ 3,2 МэВ.
|
|
Однако наибольший интерес представляют реакции
| 2
1
H
+ 3
1
H
--> 4
2
He
+ n
+ 17,6 МэВ,
|
|
| 2
1
H
+ 3
2
He
--> 4
2
He
+ 1
1
H
+ 18,3 МэВ.
|
|
Высвобождающаяся энергия, отнесенная к одному нуклону дейтерия, значительно больше энергетического выхода на один нуклон делящегося изотопа урана-235. Для реализации таких реакций необходимо сблизить ядра на расстояние R
~ 10-14
м, затратив энергию k
0
e
2
/R
~ 0,15 ¸0,3 МэВ, поэтому реакции остаются энергетически выгодными. Поскольку тритий очень радиоактивен, то реакция с использованием 3
He
более безопасна.
Надежды на практическую реализацию управляемого термоядерного синтеза продолжают оставаться "умеренно оптимистическими" на протяжении более 40 лет.
Если бы удалось осуществить управляемые термоядерные реакции в промышленных услових, то это дало бы доступ к практически неисчерпаемым источникам энергии и избавило бы человечество от угрозы энергетического кризиса. С другой стороны, если взорвутся те огромные запасы водородных бомб, которые накоплены (и продолжают накапливаться многими странами, несмотря на окончание т.н. холодной войны
), то человечество и большая часть всего живого на Земле будет уничтожено.
Дефект массы – характеристика атомного ядра, энергия связи.
Задача о нецелочисленности атомного веса изотопов долго волновала учёных, но теория относительности, установив связь между массой и энергией тела (E=
mc2
), дала ключ к решению этой задачи, а протон-нейтронная модель атомного ядра оказалась тем замком, к которому этот ключ подошёл. Для решения данной задачи понадобятся некоторые сведения о массах элементарных частиц и атомных ядер (табл. 1.1).
Таблица 1.1
Масса и атомный вес некоторых частиц
Частица
|
Символ
|
Масса, кг
|
Масса в физической шкале[1]
|
| Электрон
|
e
|
(9,1083±0,0003)´10-31
|
(5,48763±0,00006)´10–4
|
| Протон
|

|
(1,67239±0,00004)´10-27
|
1,007593±0,000003
|
| Нейтрон
|
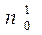
|
(1,67470±0,00004)´10-27
|
1,008982±0,000003
|
| Альфа-частица
|
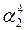
|
(6,6433±0,0001)´10-27
|
4,002780±0,000006
|
(Массы нуклидов и их разности определяют опытным путем с помощью: масс-спектроскопических измерений; измерений энергий различных ядерных реакций; измерений энергий β- и α-распадов; микроволновых измерений, дающих отношение масс или их разностей.)
Сравним массу a-частицы, т.е. ядра гелия, с массой двух протонов и двух нейтронов, из которых оно состоит. Для этого из суммы удвоенной массы протона и удвоенной массы нейтрона вычтем массу a-частицы и полученную таким образом величину назовём дефектом массы
D
m
=2
Mp
+2
Mn
-
M
a
=0,03037 а.е.м.
(1.1)
Атомная единица массы
m
а.е.м.
= (1,6597
±
0,0004)
´
10-27
кг.
(1.2)
Пользуясь формулой связи между массой и энергией, делаемой теорией относительности, можно определить величину энергии, которая соответствует этой массе, и выразить её в джоулях или, что более удобно, в мегаэлектронвольтах (1 Мэв=106
эв
). 1 Мэв соответствует энергии, приобретаемой электроном, прошедшим разность потенциалов в миллион вольт.
Энергия, соответствующая одной атомной единице массы, равна
E
=
m
а.е.м.
×
с2
=1,6597
×
10-27
×
8,99
×
1016
=1,49
×
10-10
дж=931 Мэв.
(1.3)
Наличие у атома гелия дефекта массы (D
m
= 0,03037 а.е.м.
) означает, что при его образовании была излучена энергия (Е=
D
mс2
=
0,03037
× 931=28 Мэв
). Именно эту энергию нужно приложить к ядру атома гелия для того, чтобы разложить его на отдельные частицы. Соответственно на одну частицу приходится энергия, в четыре раза меньшая. Эта энергия характеризует прочность ядра и является важной его характеристикой. Её называют энергией связи, приходящейся на одну частицу или на один нуклон (р
). Для ядра атома гелия р=28/4=7 Мэв
, для других ядер она имеет иную величину.
 |
В сороковые годы ХХ века благодаря работам Астона, Демпстера и других ученых с большой точностью были определены значения дефекта массы и вычислены энергии связи для ряда изотопов. На рис.1.1 эти результаты представлены в виде графика, на котором по оси абсцисс отложен атомный вес изотопов, а по оси ординат – средняя энергия связи частицы в ядре. Анализ этой кривой интересен и важен, т.к. по ней, и очень наглядно, видно, какие ядерные процессы дают большой выход энергии. По существу ядерная энергетика Солнца и звёзд, атомных электростанций и ядерного оружия является реализацией возможностей, заложенных в тех соотношениях, которые показывает эта кривая. Она имеет несколько характерных участков. Для лёгкого водорода 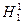 энергия связи равна нулю, т.к. в его ядре всего одна частица. Для гелия энергия связи равна нулю, т.к. в его ядре всего одна частица. Для гелия  энергия связи на одну частицу составляет 7 Мэв. Таким образом, переход от водорода к гелию связан с крупным энергетическим скачком. У изотопов среднего атомного веса: железа, никеля и др. энергия связи частицы в ядре наибольшая (8,6 Мэв) и соответственно ядра этих элементов наиболее прочные. У более тяжёлых элементов энергия связи частицы в ядре меньше и поэтому их ядра относительно менее прочные. К таким ядрам относится и ядро атома урана-235. энергия связи на одну частицу составляет 7 Мэв. Таким образом, переход от водорода к гелию связан с крупным энергетическим скачком. У изотопов среднего атомного веса: железа, никеля и др. энергия связи частицы в ядре наибольшая (8,6 Мэв) и соответственно ядра этих элементов наиболее прочные. У более тяжёлых элементов энергия связи частицы в ядре меньше и поэтому их ядра относительно менее прочные. К таким ядрам относится и ядро атома урана-235.
Чем больше дефект массы ядра, тем большая энергия излучена при его образовании. Следовательно, ядерное превращение, при котором происходит увеличение дефекта массы, сопровождается добавочным излучением энергии. Рисунок 1.1 показывает, что имеются две области, в которых эти условия выполняются: переход от самых лёгких изотопов к более тяжёлым, например, от водорода к гелию, и переход от самых тяжёлых, например урана, к ядрам атомов среднего веса.
Так же есть часто используемая величина, несущая в себе ту же информацию, что и дефект масс – упаковочный коэффициент
(или множитель). Упаковочный коэффициент характеризует стабильность ядра, его график представлен на рисунке 1.2.
Рис. 1.2. Зависимость упаковочного коэффициента от массового числа Современные космологические модели Вселенной.
Как указывалось в предыдущей главе, в классической науке существовала так называемая теория стационарного состояния Вселенной,
согласно которой Вселенная всегда была почти такой же, как сейчас. Астрономия была статичной: изучались движения планет и комет, описывались звезды, создавались их классификации, что было, конечно, очень важно. Но вопрос об эволюции Вселенной не ставился.
Классическая ньютоновская космология явно или неявно принимала следующие постулаты[2]
:
• Вселенная — это всесуществующая, «мир в целом». Космология познает мир таким, как он существует сам по себе, безотносительно к условиям познания.
• Пространство и время Вселенной абсолютны, они не зависят от материальных объектов и процессов»
• Пространство и время метрически бесконечны.
• Пространство и время однородны и изотропны.
• Вселенная стационарна, не претерпевает эволюции. Изменяться могут конкретные космические системы, но не мир в целом.
В ньютоновской космологии возникали два парадокса, связанные с постулатом бесконечности Вселенной.
Первый парадокс получил название гравитационного.
Суть его заключается в том, что если Вселенная бесконечна и в ней существует бесконечное количество небесных тел, то сила тяготения будет бесконечно большая, и Вселенная должна сколлапсировать, а не существовать вечно.
Второй парадокс называется фотометрическим:
если существует бесконечное количество небесных тел, то должна быть бесконечная светимость неба, что не наблюдается.
Эти парадоксы, не разрешимые в рамках ньютоновской космологии, разрешает современная космология, в границах которой было введено представление о расширяющейся и эволюционирующей Вселенной.
Современные космологические модели Вселенной основываются на общей теории относительности А. Эйнштейна, согласно которой метрика пространства и времени определяется распределением гравитационных масс во Вселенной. Ее свойства как целого обусловлены средней плотностью материи и другими конкретно-физическими факторами.
Современная релятивистская космология строит модели Вселенной, отталкиваясь от основного уравнения тяготения, введенного А. Эйнштейном в общей теории относительности. Уравнение тяготения Эйнштейна имеет не одно, а множество решений, чем и обусловлено наличие многих
космологических моделей Вселенной. Первая модель была разработана самим А. Эйнштейном в 1917 г.
Он отбросил постулаты ньютоновской космологии об абсолютности и бесконечности пространства и времени. В соответствии с космологической моделью Вселенной А. Эйнштейна мировое пространство однородно и изотропно, материя в среднем распределена в ней равномерно, гравитационное притяжение масс компенсируется универсальным космологическим отталкиванием. Модель А. Эйнштейна носит стационарный характер, поскольку метрика пространства рассматривается как независимая от времени. Время существования Вселенной бесконечно, т.ё. не имеет ни начала, ни конца, а пространство безгранично, но конечно.
Вселенная в космологической модели А. Эйнштейна стационарна, бесконечна во времени и безгранична в пространстве.
Эта модель казалась в то время вполне удовлетворительной, поскольку она согласовалась со всеми известными фактами.
Но новые идеи, выдвинутые А. Эйнштейном, стимулировали дальнейшие исследования, и вскоре подход к проблеме решительно изменился.
В том же 1917 году голландский астроном Виллем де Ситтер предложил другую модель, представляющую собой также решение уравнений тяготения. Это решение имело то свойство, что оно существовало бы даже в случае “пустой” Вселенной появились массы, то решение переставало быть стационарным: возникало некоторого рода космического отталкивание между массами, стремящееся удалить их друг от друга и растворить всю систему. Тенденция к расширению, по В. де Ситтеру, становилась заметной лишь на очень больших расстояниях.
В 1992г. русский математик и геофизик А.А Фридман отбросил постулат классической космологии о стационарности Вселенной и получил решение уравнения Эйнштейна, описывающее Вселенную с “расширяющимся” пространством.
Решение уравнения А.А. Фридмана допускает три возможности. Если средняя плотность вещества и излучения во Вселенной равна некоторой критической величине, мировое пространство оказывается евклидовым и Вселенная неограниченно расширяется от первоначального точечного состояния. Если плотность меньше критической, пространство обладает геометрией Лобачевского и также неограниченно расширяется. И, наконец, если плотность больше критической, пространство Вселенной оказывается римановым, расширение на некотором этапе сменяется сжатием, которое продолжается вплоть до первоначального точечного состояния.
Поскольку средняя плотность вещества во Вселенной неизвестна, то сегодня мы не знаем, в каком из этих пространств Вселенной мы живем.
В 1927 г. бельгийский аббат и ученый Ж. Леметр связал “расширение” пространства с данными астрономических наблюдений. Леметр ввел понятие начала Вселенной как сингулярности (т.е. сверхплотного состояния) и рождения Вселенной как Большого взрыва.
В 1929 году американский астроном Э.П. Хаббл обнаружил существование странной зависимости между расстоянием и скоростью галактик: все галактики движутся от нас, причем со скоростью, которая возрастает пропорционально расстоянию, - система галактик расширяется.
Расширение Вселенной считается научно установленным фактом
www.wowanium.narod.ru
wowanium@mail.ru
icq 205968979
[1]
В физической шкале атомных весов атомный вес изотопа кислорода  принят равным точно 16,0000. принят равным точно 16,0000.
[2]
См.: Мостепаненко А.М. Методологические и философские проблемы современной физики. — Л.: ЛГУ, 1977. — С. 101.
|