Реферат: Термодинамика

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

ГЛАВА 1

ОСНОВНЫЕ ПОНЯТИЯ И ИСХОДНЫЕ ПОЛОЖЕНИЯ ТЕРМОДИНАМИКИ

1.1. Закрытые и открытые термодинамические системы.

1.2. Нулевое начало термодинамики.

1.3. Первое начало термодинамики.

1.4. Второе начало термодинамики.

1.4.1. Обратимые и необратимые процессы.

1.4.2. Энтропия.

1.5. Третье начало термодинамики.

ГЛАВА 2

ОСНОВНЫЕ ПОНЯТИЯ И ПОЛОЖЕНИЯ СИНЕРГЕТИКИ.

САМООРГАНИЗАЦИЯ РАЗЛИЧНЫХ СИСТЕМ.

2.1. Общая характеристика открытых систем.

2.1.1. Диссипативные структуры.

2.2. Самоорганизация различных систем и синергетики.

2.3. Примеры самоорганизации различных систем.

2.3.1. Физические системы.

2.3.2. Химические системы.

2.3.3. Биологические системы.

2.3.4. Социальные системы.

Постановка задачи.

ГЛАВА 3

АНАЛИТИЧЕСКИЕ И ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ САМООРГАНИЗАЦИИ РАЗЛИЧНЫХ СИСТЕМ.

3.1. Ячейки Бенара.

3.2. Лазер, как самоорганизованная система.

3.3. Биологическая система.

3.3.1. Динамика популяций. Экология.

3.3.2. Система «Жертва - Хищник».

ЗАКЛЮЧЕНИЕ.

ЛИТЕРАТУРА.

ВВЕДЕНИЕ.

Наука зародилась очень давно, на Древнем Востоке, и затем интенсивно развивалась в Европе. В научных традициях долгое время оставался недостаточно изученным вопрос о

взаимоотношениях целого и части. Как стало ясно в середине

20 века часть может преобразовать целое радикальным и неожиданным образом.

Из классической термодинамики известно, что изолированные термодинамические системы в соответствии со вторым началом термодинамики для необратимых процессов энтропия системы S возрастает до тех пор, пока не достигнет своего максимального значения в состоянии термодинамического равновесия. Возрастание энтропии сопровождается потерей информации о системе.

Со временем открытия второго закона термодинамики встал вопрос о том, как можно согласовать возрастание со временем энтропии в замкнутых системах с процессами самоорганизации в живой и не живой природе. Долгое время казалось, что существует противоречие между выводом второго закона термодинамики и выводами эволюционной теории Дарвина, согласно которой в живой природе благодаря принципу отбора непрерывно происходит процесс самоорганизации.

Противоречие между вторым началом термодинамики и примерами высокоорганизованного окружающего нас мира было разрешено с появлением более пятидесяти лет назад и последующим естественным развитием нелинейной неравновесной термодинамики. Ее еще называют термодинамикой открытых систем. Большой вклад в становление этой новой науки внесли И.Р.Пригожин, П.Гленсдорф, Г.Хакен. Бельгийский физик русского происхождения Илья Романович Пригожин за работы в этой области в 1977 году был удостоен Нобелевской премии.

Как итог развития нелинейной неравновесной термодинамики появилась совершенно новая научная дисциплина синергетика - наука о самоорганизации и устойчивости структур различных сложных неравновесных систем : физических, химических, биологических и социальных.

В настоящей работе исследуется самоорганизация различных систем аналитическими и численными методами.

ГЛАВА 1

ОСНОВНЫЕ ПОНЯТИЯ И ИСХОДНЫЕ ПОЛОЖЕНИЯ

ТЕРМОДИНАМИКИ.

ЗАКРЫТЫЕ И ОТКРЫТЫЕ ТЕРМОДИНАМИЧЕСКИЕ

СИСТЕМЫ.

Всякий материальный объект, всякое тело , состоящее из большого числа частиц, называется макроскопической системой . Размеры макроскопических систем значительно больше размеров атомов и молекул. Все макроскопические признаки , характеризующие такую систему и ее отношение к окружающим телам , называются макроскопическими параметрами . К их числу относятся такие , например , как плотность , объем , упругость , концентрация , поляризованность , намогниченность и т.д. Макроскопические параметры разделяются на внешние и внутренние .

Величины , определяемые положением не входящих в нашу систему внешних тел , называются внешними параметрами , например напряженность силового поля ( так как зависят от положения источников поля - зарядов и токов , не входящих в нашу систему ) , объем системы ( так как определяется расположением внешних тел ) и т.д. Следовательно внешние поараметры являются функциями координат внешних тел. Величины, определяемые совокупным движением и распределением в пространстве входящих в систему частиц , называются внутренними параметрами , например энергия , давление , плотность , намогниченность , поляризованность и т.д. ( так как их значения зависят от движения и положения частиц системы и входящих в них зарядов ).

Совокупность независимых макроскопических параметров определяет состояние системы , т.е. форму ее бытия . Величины не зивисящие от предыстории системы и полностью определяемые ее состоянием в данный момент ( т.е. совокупностью независимых параметров ), называются функциями состояния.

Состояние называется стационарным , если параметры системы с течением времени не изменяются.

Если , кроме того , в системе не только все параметры постоянны во времени , но и нет никаких стационарных потоков за счет действия каких-либо внешних источников , то такое состояние системы называется равновесным ( состояние термодинамического равновесия ). Термодинамическими системами обычно называют не всякие , а только те макроскопические системы , которые находятся в термодинамическом равновесии. Аналогично , термодинамическими параметрами называются те параметры , которые характеризуют систему в термодинамическом равновесии.

Внутренние параметры системы разделяются на интенсивные и экстенсивные . Параметры не зависящие от массы и числа частиц в системе , называются интенсивными ( давление , температура и др.) . Параметры пропорциональные массе или числу частиц в системе , называются аддитивными или экстенсивными ( энергия , энтропия и др. ) . Экстенсивные параметры характеризуют систему как целое , в то время как интенсивные могут принимать определенные значения в каждой точке системы .

По способу передачи энергии , вещества и информации между рассматриваемой системы и окружающей средой термодинамические системы классифицируются :

Замкнутая ( изолированная ) система - это система в которой нет обмена с внешними телами ни энергией , ни веществом ( в том числе и излучением ) , ни информацией .

Закрытая система - система в которой есть обмен только с энергией .

Адиабатно изолированная система - это система в которой есть обмен энергией только в форме теплоты .

Открытая система - это система , которая обменивается и энергией , и веществом , и информацией .

НУЛЕВОЕ НАЧАЛО ТЕРМОДИНАМИКИ .

Нулевое начало термодинамики сформулированное всего около 50 лет назад , по существу представляет собой полученное «задним числом» логическое оправдание для введения понятия температуры физических тел . Температура - одно из самых глубоких понятий термодинамики . Температура играет столь же важную роль в термодинамике , как , например процессы. Впервые центральное место в физике занял совершенно абстрактное понятие ; оно пришло на смену введенному еще во времена Ньютона ( 17 век) понятию силы - на первый взгляд более конкретному и «осязаемому» и к тому же успешно « математезированному» Ньютоном.

Первое начало термодинамики устанавливает внутренняя энергия системы является однозначная функция ее состояния и изменяется только под влиянием внешних воздействий.

В термодинамике рассматриваются два типа внешних взаимодействий: воздействие , связанное с изменением внешних параметров системы ( система совершает работу W ), и воздействие не связанные с изменением внешних параметров и обусловленные изменением внутренних параметров или температуры ( системе сообщается некоторое количество теплоты Q ).

Поэтому , согласно первому началу , изменение внутренней энергии U₂ -U₁ системы при ее переходе под влиянием этих воздействий из первого состояния во второе равно алгебраической сумме Q и W , что для конечного процесса запишется в виде уравнения

U₂ - U₁ = Q - W или Q = U₂ - U₁ + W (1.1)

Первое начало формируется как постулат и является обобщением большого количества опытных данных .

Для элементарного процесса уравнение первого начала такого :

dQ = dU + dW (1.2)

dQ и dW не являются полным дифференциалом, так как зависят от пути следования.

Зависимость Q и W от пути видна на простейшем примере расширение газа. Работа совершенная системой при переходе ее из состояния 1 в 2 ( рис. 1) по пути а изображается площадью, ограниченной контуром А1а2ВА :

W_а = p(V,T) dV ;

а работа при переходе по пути в - площадью ограниченную контуром А1в2ВА :

W_b = p(V,T) dV.

Рис. 1

Поскольку давление зависит не только от объема, но и от температуры, то при различных изменениях температуры на пути а и в при переходе одного и того же начального состояния (p₁ ,V₁ ) в одно и тоже конечное (p₂ ,V₂ ) работа получается разной. Отсюда видно , что при замкнутом процессе (цикле) 1а2в1 система совершает работу не равную нулю. На этом основана работа всех тепловых двигателей.

Из первого начала термодинамики следует, что работа может совершаться или за счет изменения внутренней энергии , или за счет сообщения системе количества теплоты . В случае если процесс круговой , начальное и конечное состояние совпадают U₂ - U₁ = 0 и W = Q , то есть работа при круговом процессе может совершаться только за счет получения системой теплоты от внешних тел .

Первое начало можно сформулировать в нескольких видах :

Невозможно возникновение и уничтожение энергии .

Любая форма движения способна и должна превращаться в любую другую форму движения .

Внутренняя энергия является однозначной формой состояния .

Вечный двигатель первого рода невозможен .

Бесконечно малое изменение внутренней энергии является полным дифференциалом.

Сумма количества теплоты и работы не зависит от пути процесса.

Первый закон термодинамики , постулируя закон сохранения

энергии для термодинамической системы. не указывает направление происходящих в природе процессов. Направление термодинамических процессов устанавливает второе начало термодинамики.

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.

Второе начало термодинамики устанавливает наличие в природе фундаментальной асимметрии , т.е. однонаправленности всех происходящих в ней самопроизвольных процессов .

Второй основной постулат термодинамики связан так же с другими свойствами термодинамического равновесия как особого вида теплового движения. Опыт показывает , что если две равновесные системы А и В привести в тепловой контакт , то независимо от различия или равенства у них внешних параметров они или остаются по прежнему в состоянии термодинамического равновесия , или равновесие у них нарушается и спустя некоторое время в процессе теплообмена ( обмена энергией ) обе системы приходят в другое равновесное состояние. Кроме того , если имеются три равновесные системы А,В и С и если системы А и В поразнь находятся в равновесии с системой С, то системы А и В находятся в термодинамическом равновесии и между собой (свойства транзитивности термодинамического равновесия ).

Пусть имеются две системы . Для того , чтобы убедится в том , что они находятся в состоянии термодинамического равновесия надо измерить независимо все внутренние параметры этих систем и убедиться в том , что они постоянны во времени. Эта задача черезвычайно трудная .

Оказывается однако , что имеется такая физическая величина , которая позволяет сравнить термодинамические состояния двух систем и двух частей одной системы без подробного исследования и внутренних параметров. Эта величина , выражающая состояние внутреннего движения равновесной системы , имеющая одно и то же значение у всех частей сложной равновесной системы независимо от числа частиц в них и определяемое внешними параметрами и энергией называется температурой .

Температура является интенсивным параметром и служит мерой интенсивности теплового движения молекул.

Изложенное положение о существовании температуры как особой функции состояния равновесной системы представляет второй постулат термодинамики.

Иначе говоря , состояние термодинамического равновесия определяется совокупностью внешних параметров и температуры.

Р.Фаулер и Э.Гуггенгейм назвали его нулевым началом , так как оно подобно первому и второму началу определяющим существование некоторых функций состояния , устанавливает существование температуры у равновесных систем. Об этом упоминалось выше.

Итак , все внутренние параметры равновесной системы являются функциями внешних параметров и температур . (Второй постулат термодинамики).

Выражая температуру через внешние параметры и энергию , второй постулат можно сформулировать в таком виде : при термодинамическом равновесии все внутренние параметры являются функциями внешних параметров и энергии.

Второй постулат позволяет определить изменение температуры тела по изменению какого либо его параметра , на чем основано устройство различных термометров.

ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ.

Процесс перехода системы из состояния 1 в 2 называется обратимым , если возвращением этой системы в исходное состояние из 2 в 1 можно осуществить без каких бы то ни было изменений окружающих внешних телах.

Процесс же перехода системы из состояния 1 в 2 называется необратимым , если обратный переход системы из 2 в 1 нельзя осуществить без изменения в окружающих телах .

Мерой необратимости процесса в замкнутой системе является изменением новой функции состояния - энтропии , существование которой у равновесной системы устанавливает первое положение второго начала о невозможности вечного двигателя второго рода . Однозначность этой функции состояния приводит к тому , что всякий необратимый процесс является неравновесным.

Из второго начала следует , что S является однозначной функцией состояния. Это означает , что dQ/T для любого кругового равновесного процесса равен нулю. Если бы это не выполнялось , т.е. если бы энтропия была неоднозначной функцией состояния то , можно было бы осуществить вечный двигатель второго рода.

Положение о существовании у всякой термодинамической системы новой однозначной функцией состояния энтропии S , которая при адиабатных равновесных процессах не изменяется и состовляет содержание второго начала термодинамики для равновесных процессов.

Математически второе начало термодинамики для равновесных процессов записывается уравнением:

dQ/T = dS или dQ = TdS (1.3)

Интегральным уравнением второго начала для равновесных круговых процессов является равенство Клаузиуса :

dQ/T = 0 (1.4)

Для неравновесного кругового процесса неравенство Клаузиуса имеет следующий вид :

dQ/T < 0 (1.5)

Теперь можно записать основное уравнение термодинамики для простейшей системы находящейся под всесторонним давлением :

TdS = dU + pdV (1.6)

Обсудим вопрос о физическом смысле энтропии.

1.4.2. ЭНТРОПИЯ.

Второй закон термодинамики постулирует существование функции состояния , называемой «энтропией» ( что означает от греческого «эволюция» ) и обладающей следующими свойствами :

а) Энтропия системы является экстенсивным свойством . Если система состоит из нескольких частей , то полная энтропия системы равна сумме энтропии каждой части .

в) Изменение энтропии в S состоит из двух частей . Обозначим через d_е S поток энтропии, обусловленный взаимодействием с окружающей средой , а через d_i S - часть энтропии , обусловленную изменениями внутри системы , имеем

в S = d_e S + d_i S (1.7)

Приращение энтропии d_i S обусловленное изменением внутри системы , никогда не имеет отрицательное значение . Величина d_i S = 0 , только тогда , когда система претерпевает обратимые изменения , но она всегда положительна , если в системе идут такие же необратимые процессы.

Таким образом

d_i S = 0 (1.8)

( обратимые процессы );

d_i S > 0 (1.9)

( необратимые процессы );

Для изолированной системы поток энтропии равен нулю и выражения (1.8) и (1.9) сводятся к следующему виду :

в S = d_i S > 0 (1.10)

( изолированная система ).

Для изолированной системы это соотношение равноценно классической формулировке , что энтропия никогда не может уменьшаться , так что в этом случае свойства энтропийной функции дают критерий , позволяющий обнаружить наличие необратимых процессов . Подобные критерии существуют и для некоторых других частных случаев .

Предположим , что система , которую мы будем обозначать символом 1 , находится внутри системы 2 большего размера и что общая система , состоящая системы 1 и 2 , является изолированной.

Классическая формулировка второго закона термодинамики тогда имеет вид :

в S = в S¹ + в S² ³ 0 (1.11)

Прилагая уравнения (1.8) и (1.9) в отдельности каждой части этого выражения , постулирует , что d_i S¹ ³ 0 , d_i S² ³ 0

Ситуация при которой d_i S¹ > 0 и d_i S² < 0 , а d( S¹ + S² )>0 , физически неосуществима . Поэтому можно утверждать , что уменьшение энтропии в отдельной части системы , компенсируемое достаточным возрастанием энтропии в другой части системы , является запрещенным процессом . Из такой формулировки вытекает , что в любом макроскопическом участке системы приращение энтропии , обусловленное течением необратимых процессов , является положительным. Под понятием « макроскопический участок » системы подразумевается любой участок системы , в котором содержится достаточное большое число молекул , чтобы можно было принебреч микроскопическими флуктуакциями. Взаимодействие необратимых процессов возможно лишь тогда, когда эти процессы происходят в тех же самых участках системы .

Такую формулировку второго закона можно было бы назвать « локальной » формулировка в противоположность « глобальной » формулировка классической термодинамики . Значение подобной новой формулировке состоит в том ,что на ее основе возможен гораздо более глубокий анализ необратимых процессов .

ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ.

Открытие третьего начала термодинамики связано с нахождением химического средства - величины , характеризующих способность различных веществ химически реагировать друг с другом . Эта величина определяется работой W химических сил при реакции . Первое и второе начало термодинамики позволяют вычислить химическое средство W только с точностью до некоторой неопределенной функции . Чтобы определить эту функцию нужны в дополнении к обоим началам термодинамики новые опытные данные о свойствах тел . Поэтому Нернстоном были предприняты широкие экспериментальные исследования поведение веществ при низкой температуре .

В результате этих исследований и было сформулировано третье начало термодинамики : по мере приближения температуры к 0 К энтропия всякой равновесной системы при изотермических процессах перестает зависить от каких-либо термодинамических параметров состояния и в пределе ( Т= 0 К) принимает одну и туже для всех систем универсальную постоянную величину , которую можно принять равной нулю .

Общность этого утверждения состоит в том , что , во-первых , оно относится к любой равновесной системе и , во-вторых , что при Т стремящемуся к 0 К энтропия не зависит от значения любого параметра системы. Таким образом по третьему началу,

lin [ S (T,X₂ ) - S (T,X₁ ) ] = 0 (1.12)

или

lim [ dS/dX ]_T = 0 при Т ® 0 (1.13)

где Х - любой термодинамический параметр (а_i или А_i ).

Предельно значение энтропии , поскольку оно одно и тоже для всех систем , не имеет никакого физического смысла и поэтому полагается равным нулю (постулат Планка). Как показывает статическое рассмотрение этого вопроса , энтропия по своему существу определена с точностью до некоторой постоянной (подобно, например, электростатическому потенциалу системы зарядов в какой либо точке поля). Таким образом , нет смысла вводить некую «абсолютную энтропию», как это делал Планк и некоторые другие ученые.

ГЛАВА 2

ОСНОВНЫЕ ПОНЯТИЯ И ПОЛОЖЕНИЯ СИНЕРГЕТИКИ.

САМООРГАНИЗАЦИЯ РАЗЛИЧНЫХ СИСТЕМ.

Около 50 лет назад в результате развития термодинамики возникла новая дисциплина - синергетика. Являясь наукой о самоорганизации самых различных систем - физических , химических , биологических и социальных - синергетика показывает возможность хотя бы частичного снятия междисциплинных барьеров не только внутри естественно научной отросли знания , но так же и между естественно научной и гумонитарной культурами .

Синергетика занимается изучением систем , состоящих из многих подсистем самой различной природы , таких , как электроны , атомы , молекулы , клетки , нейтроны , механические элементы , фотоны , органы , животные и даже люди.

При выборе математического аппарата необходимо иметь ввиду , что он должен быть применим к проблемам , с которыми сталкиваются физик , химик , биолог , электротехник и инженер механик. Не менее безотказно он должен действовать и в области экономики , экологии и социологии .

Во всех этих случаях нам придется рассматривать системы , состоящие из очень большого числа подсистем , относительно которых мы можем не располагать всей полной информацией . Для описания таких систем не редко используют подходы , основанные на термодинамики и теории информации.

Во всех системах , представляющих интерес для синергетики , решающую роль играет динамика. Как и какие макроскопические состояния образуются, определяются скоростью роста (или распада) коллективных «мод» . Можно сказать что в определенном смысле мы приходим к своего рода обобщенному дарвенизму , действие которого распознается не только на органический ,но и на неорганический мир : возникновение макроскопических структур обусловленных рождением коллективных мод под воздействием флуктуаций , их конкуренцией и , наконец, отбором «наиболее приспособленной» моды или комбинации таких мод.

Ясно, что решающую роль играет параметр «время» . Следовательно , мы должны исследовать эволюцию систем во времени . Именно поэтому интересующие нас уравнения иногда называют «эволюционными».

ОБЩАЯ ХАРАКТЕРИСТИКА ОТКРЫТЫХ СИСТЕМ.

Открытые системы - это термодинамические системы , которые обмениваются с окружающими телами ( средой ) , веществом , энергией и импульсом . Если отклонение открытой системы от состояния равновесия невелико , то неравновесное состояние можно описать теми же параметрами (температура , химический потенциал и другие) , что и равновесное . Однако отклонение параметров от равновесных значений вызывают потоки вещества и энергии в системе . Такие процессы переноса приводят к производству энтропии . Примерами открытых систем являются : биологические системы , включая клетку , системы обработки информации в кибернетике , системы энергоснабжения и другие . Для поддержания жизни в системах от клетки до человека необходим постоянный обмен энергией и веществом с окружающей средой . Следовательно живые организмы являются системами открытыми , аналогично и с другими приведенными параметрами. Пригожиным в 1945 году был сформулирован расширенный вариант термодинамики.

В открытой системе изменение энтропии можно разбить на сумму двух вкладов :

d S = в S_e + в S_i (2.1)

Здесь в S_e - поток энтропии , обусловленный обменом энергией и веществом с окружающей средой , в S_i - производство энтропии внутри системы (рис. 2.1).

Рис. 2.1. Схематическое представление открытых

систем : производство и поток энтропии.

Х - набор характеристик :

С - состав системы и внешней среды ;

Р - давление ; Т - температура .

Итак , открытая система отличается от изолированной наличием члена в выражении для изменения энтропии , соответствующего обмену . При этом знак члена в S_e может быть любым в отличии от в S_i .

Для неравновесного состояния :

S < S_max

Неравновесное состояние более высокоорганизованно , чем равновесное , для которого

S = S_max

Таким образом эволюцию к более высокому порядку можно представить как процесс , в котором система достигает состояния с более низкой энтропией по сравнению с начальной .

Фундаментальная теорема о производстве энтропии в открытой системе с независимыми от времени краевыми условиями была сформулирована Пригожиным: в линейной области система эволюционирует к стационарному состоянию , характеризуемому минимальным производством энтропии , совместимым с наложенными граничными условиями .

Итак состояние всякой линейной открытой системы с независящими от времени краевыми условиями всегда изменяется в направлении уменьшения производства энтропии P = в S / в t пока не будет достигнуто состояние текущего равновесия , при котором производство энтропии минимально :

d P < 0 (условие эволюции)

P = min , в P = 0 (условие текущего равновесия)

d P/ в t < 0 (2.2)

ДИССИПАТИВНЫЕ СТРУКТУРЫ.

Каждая система состоит из элементов (подсистем) . Эти элементы находятся в определенном порядке и связаны определенными отношениями. Структуру системы можно назвать организацию элементов и характер связи между ними.

В реальных физических системах имеются пространственные и временные структуры .

Формирование структуры - это возникновение новых свойств и отношений в множестве элементов системы . В процессах формирования структур играют важную роль понятия и принципы :

Постоянный отрицательный поток энтропии .

Состояние системы в дали от равновесия .

Нелинейность уравнений описывающих процессы .

Коллективное (кооперативное) поведение подсистем .

Универсальный критерий эволюции Пригожина - Гленсдорфа.

Формирование структур при необратимых процессах должно сопровождаться качественным скачком (фазовым переходом) при достижении в системе критических значений параметров. В открытых системах внешний вклад в энтропию (2.1) в S в принципе можно выбрать произвольно , изменяя соответствующим образом параметры системы и свойства окружающей среды . В частности энтропия может уменьшаться за счет отдачи энтропии во внешнюю среду , т.е. когда в S < 0 . Это может происходить , если изъятие из системы в единицу времени превышает производство энтропии внутри системы , то есть

в S dS_e dS_i

¾ < 0 , если ¾ > ¾ > 0 (2.3)

в t dt dt

Чтобы начать формирование структуры , отдача энтропии должна превысить некоторое критическое значение . В сильно неравновесном расстоянии переменные системы удовлетворяют нелинейным уравнениям .

Таким образом , можно выделить два основных класса необратимых процессов :

Уничтожение структуры вблизи положения равновесия . Это универсальное свойство систем при произвольных условиях .

Рождение структуры вдали от равновесия в открытой системе при особых критических внешних условиях и при нелинейной внутренней динамики . Это свойство не универсально .

Пространственные , временные или пространственно-временные структуры , которые могут возникать вдали от равновесия в нелинейной области при критических значениях параметров системы называются диссипативными структурами.

В этих структурах взаимосвязаны три аспекта :

Функция состояния , выражаемая уравнениями .

Пространственно - временная структура , возникающая из-за неустойчивости .

Флуктуации , ответственные за неустойчивости .

Рис. 1. Три аспекта диссипативных структур.

Взаимодействия между этими аспектами приводит к неожиданным явлениям - к возникновению порядка через флуктуации , формированию высокоорганизованной структуры из хаоса.

Таким образом , в диссипативных структурах происходит становление из бытия , формируется возникающее из существующего.

САМООРГАНИЗАЦИЯ РАЗЛИЧНЫХ СТСТЕМ И

СЕНЕРГЕТИКА.

Переход от хаоса к порядку , происходящий при изменении значений параметров от до критических к сверхкритическим , изменяет симметрию системы . По этому такой переход аналогичен термодинамическим фазовым переходам . Переходы в неравновесных процессах называются кинетическими фазовыми переходами . В близи неравновесных фазовых переходов не существует непротиворечивого макроскопического описания . Флуктуации столь же важны , как и среднее значении . Например , макроскопические флуктуации могут приводить к новым типам не устойчивостей .

Итак , в дали от равновесия между химической , кинетической и пространственно-временной структурой реагирующих систем существует неожиданная связь . Правда , взаимодействие , определяющие взаимодействие констант скоростей и коэффициентов переноса , обусловлены короткодействующими силами ( силами валентности , водородными связями и силами Ван-Дер-Вальса) . Однако решения соответствующих уравнений зависят , кроме того , от глобальных характеристик . Для возникновения диссипативных структур обычно требуется , чтобы размеры системы превышали некоторое критическое значение - сложную функцию параметров , описывающих реакционно-диффузионные процессы . Мы можем по этому утверждать , что химические неустойчивости задают дальнейший порядок , посредством которого система действует как целое .

Если учесть диффузию , то математическая формулировка проблем , связанных с диссипативными структурами , потребует изучении дифференциальных уравнений в частных производных . Действительно , эволюция концентрации компонент Х со временем определяется уравнением вида

(2.4)

где первый член дает вклад химических реакций в изменении концентрации Х_i и обычно имеет простой полиноминальный вид , а второй член означает диффузию вдоль оси r.

По истине поразительно , как много разнообразных явлений описывает реакционно-диффузное уравнение (2.4 ) , по этому интересно рассмотреть ² основное решение ² , которое бы соответствовала термодинамической ветви . Другие решения можно было бы получать при последовательных не устойчивостях , возникающих по мере удаления от состояния равновесия . Неустойчивости такого типа удобно изучать методами теории бифуркации [ Николис и Пригожин , 1977] . В принципе , бифуркация есть нечто иное , как возникновение при некотором критическом значении параметра нового решения уравнений . Предположим , что мы имеем химическую реакцию , соответствующую кинетическому уравнению [ Маклейн и Уолис , 1974] .

в X

¾ = a X (X-R) (2.5)

в t

Ясно что при R < 0 существует только одно решение , независящее от времени , X = 0 . В точке R = 0 происходит бифуркация , и появляется новое решение X = R .

Рис. 2.3. Бифуркационная диограмма для уравнения ( 2.5.) .

Сплошная линия соответствует устойчивой ветви ,

точки - неустойчивой ветви .

Анализ устойчивости в линейном приближении позволяет проверить , что решение X = 0 при переходе через R = 0 становится неустойчивым , а решение X = R - устойчивым . В общем случаи при возрастании некоторого характеристического параметра р происходят последовательные бифуркации . На рисунке 2.4. показано единственное решение при р = р ₁ , но при

р = р ₂ единственность уступает место множественным решения .

Интересно отметить , что бифуркация в некотором смысле вводит в физику и в химию , историю - элемент , который прежде считался прерогативой наук занимающихся изучением биологическим , общественных и культурных явлений .

Рис. 2.4. Последовательные бифуркации :

А и А ¹ - точки первичных бифуркаций из

термодинамической ветви ,

В и В ¹ - точки вторичной бифуркации .

Известно , что при изменении управляющих параметров в системе наблюдаются разнообразные переходные явления . Выделим теперь из этих наблюдений определенные общие черты , характерные для большого числа других переходов в физико химических системах .

С этой целью представим графически (рис. 2.5) зависимость вертикальной компоненты скорости течения жидкости в некоторой определенной точке от внешнего ограничения , или , в более общем виде , зависимость переменной состояние системы Х (или х = Х - Х_s ) от управляющего параметра l . Таким образом мы получим график , известный под названием бифуркационной диаграммы .

Рис. 2.5. Бифуркационная диаграмма :

а - устойчивая часть термодинамической ветви ,

а¹ - не устойчивая часть термодинамической ветви ,

в₁ ,в₂ - диссипативные структуры , рожденные в

сверхкритической области .

При малых значения l возможно лишь одно решение , соответствующее состоянию покоя в бенаровском эксперименте .Оно представляет собой непосредственную экстрополяцию термодинамического равновесия , и подобно равновесно , характеризующейся важным свойством - асимптотической устойчивостью , поскольку в этой области система способна гасить внутренние флуктуации или внешнее возмущения . По этой причине такую ветвь состояний мы будем называть термодинамической ветвью . При переходе критического значения параметра l , обозначенного l_c на рисунке 2.5. , состоящие на этой ветви становится неустойчивыми , так как флуктуации или малые внешние возмущение уже не гасятся . Действуя подобно усилителю , система отклоняется от стационарного состояния и переходит к новому режиму , в случае бенаровского эксперимента соответствующему состоянию стационарной конвекции . Оба этих режима сливаются при l = l_c и различаются при l > l_c . Это явление называется бифуркацией . Легко понять причины , по которым это явление следует ассоциировать с катастрофическими изменениями и конфликтами. В самом деле , в решающий момент перехода система должна совершить критический выбор ( в окрестности l = l_c ) , что в задаче Бенара связано с возникновением право- или левовращательных ячеек в определенной области пространства ( рис. 2.5. , ветви в₁ или в₂ ) .

В близи равновесного состояния стационарное состояние асимптотических устойчивы (по теореме о минимальном производстве энтропии ) , по этому в силу непрерывности эта термодинамическая ветвь простирается во всей докритической области . При достижении критического значения термодинамическая ветвь может стать неустойчивой , так что любое , даже малое возмущение , переводит систему с термодинамической ветви в новое устойчивое состояние , которое может быть упорядоченным . Итак , при критическом значении параметром произошла бифуркация и возникла новая ветвь решений и , соответственно , новое состояние . В критической области , таким образом , событие развивается по такой схеме :

Флуктуация ® Бифуркация ®

неравновесный фазовый переход ®

Рождение упорядоченной структуры .

Бифуркация в широком понимании - приобретении нового качества движениями динамической системы при малом изменении ее параметров ( возникновение при некотором критическом значении параметра нового решения уравнений ) . Отметим , что при бифуркации выбор следующего состояния носит сугубо случайный характер , так что переход от одного необходимого устойчивого состояния к другому необходимому устойчивому состоянию проходит через случайное (диалектика необходимого и случайного) . Любое описание системы , претерпевающей бифуркацию , включает как детерминистический , так и вероятностный элементы , от бифуркации до бифуркации поведении системы детерминировано , а в окрестности точек бифуркации выбор последующего пути случаен . Проводя аналогию с биологической эволюцией можно сказать , что мутации - это флуктуации , а поиск новой устойчивости играет роль естественного отбора . Бифуркация в некотором смысле вводит в физику и химию элемент историзма - анализ состояния в₁ , например , подразумевает знание истории системы , прошедшей бифуркацию .

Общая теория процессов самоорганизации открытых сильно не равновесных системах развивается на основе универсального критерия эволюции Пригожина - Гленсдорфа . Этот критерий является обобщением теоремы Пригожина о минимальном производстве энтропии . Скорость производства энтропии , обусловленная изменением термодинамических сил Х , согласно этому критерию подчиняется условию

d_x P / t £ 0 (2.6)

Это неравенство не зависит не от каких предположений о характере связей между потоками и силами в условиях локального равновесия и носит по этому универсальный характер . В линейной области неравенство (2.6. ) переходит в теорему Пригожина о минимальном производстве энтропии . Итак , в неравновестной системе процессы идут так , т.е. система эволюционирует таким образом, что скорость производства энтропии при изменении термодинамических сил уменьшается ( или равна нулю в стационарном состоянии ).

Упорядоченные структуры , которые рождаются вдали от равновесия , в соответствии с критерием (2.6.) и есть диссипативные структуры .

Эволюция бифуркации и последующей самоорганизации обусловлено , таким образом , соответствующими не равновесными ограничениями .

Эволюция переменных Х будет описываться системой уравнений

(2.7)

где функции F как угодно сложным образом могут зависить от самих переменных Х и их пространственных производных координат r и времени t . Кроме того , эти функции буду зависить от управляющих параметров , т.е. тех изменяющихся характеристик , которые могут сильно изменить систему . На первый взгляд кажется очевидным , что структура функции { F } будет сильно определятся типом соответствующей рассматриваемой системы . Однако , можно выделить некоторые основные универсальные черты , независящие от типа систем.

Решение уравнения (2.7) , если нет внешних ограничений , должны соответствовать равновесию при любом виде функции F . Поскольку равновесное состояние стационарно , то

F_i ({X_рав },l_рав ) = 0 (2.8)

В более общем случае для неравновесного состояния можно аналогично написать условие

F_i ({X},l) = 0 (2.9)

Эти условия налагают определенные ограничения универсального характера , например, законы эволюции системы должны быть такими , чтобы выполнялось требование положительности температуры или химической концентрации, получаемых как решения соответствующих уравнений.

Другой универсальной чертой является нелинейным . Пусть , например некоторая единственная характеристика системы

удовлетворяет уравнению

(2.10)

где k - некоторый параметр , l - внешние управляющие ограничения . Тогда стационарное состояние определяется из следующего алгебраического уравнения

l - kX = 0 (2.11)

откуда

Xs = l / k (2.12)

В стационарном состоянии , таким образом , значении характеристики , например , концентрации , линейно изменяется в зависимости от значений управляющего ограничения l , и имеется для каждого l единственное состояние Х_s . Совершенно однозначно можно предсказать стационарное значение Х при любом l ,если иметь хотя бы два экспериментальных значения Х

(l ) .Управляющий параметр может , в частности , соответствовать степени удаленности системы от равновесия . Поведение в этом случае системы очень похожи на равновесии даже при наличии сильно неравновесных ограничений .

Рис. 2.6. Иллюстрация универсальной черты нелинейности в самоорганизации структур .

Если же стационарное значение характеристики Х не линейно зависит от управляющего ограничения при некоторых значениях , то при одном и том же значении имеется несколько различных решений . Например , при ограничениях система имеет три стационарных решения , рисунок 2.6.в. Такое универсальное отличие от линейного поведения наступает при достижении управляющим параметром некоторого критического значения l - проявляется бифуркация. При этом в нелинейной области небольшое увеличение может привести к неодекватно сильному эффекту - система может совершить скачок на устойчивую ветвь при небольшом изменении вблизи критического значения l , рисунок 2.6.в. Кроме того из состояний на ветви А¹ В могут происходить переходы АВ¹ ( или наоборот ) даже раньше , чем будут достигнуты состояния В или А , если возмущения накладываемые на стационарное состояние , больше значение , соответствующего промежуточной ветви А В . Возмущениями могут служить либо внешнее воздействие либо внутренние флуктуации в самой системе . Таким образом , системе с множественными стационарными состояниями присуще универсально свойствам внутренне возбудимость и изменчивости скачкам .

Выполнение теоремы по минимально производстве энтропии в линейной области , а, как обобщение этой теоремы , выполнение универсального критерия (2.6.) и в линейной , и в нелинейной области гарантируют устойчивость стационарных неравновесных состояний. В области линейности необратимых процессов производство энтропии играет такую же роль , как термодинамические потенциалы в равновесной термодинамике . В нелинейной области величина dP / dt не имеет какого либо общего свойства , однако , величина d_x P/dt удовлетворяет неравенству общего характера (2.6. ) , которая является обобщением теоремы о минимальном производстве энтропии .

2.3 ПРИМЕРЫ САМООРГАНИЗАЦИИ РАЗЛИЧНЫХ

СИСТЕМ.

Рассмотрим в качестве иллюстрации некоторые примеры самоорганизации систем в физике , химии , биологии и социуме.

ФИЗИЧЕСКИЕ СИСТЕМЫ.

В принципе даже в термодинамическом равновесии можно указать примеры самоорганизации , как результаты коллективного поведения . Это , например , все фазовые переходы в физических системах , такие как переход жидкость - газ , ферромагнитный переход или возникновение сверхпроводимости . В неравновесном состоянии можно назвать примеры высокой организации в гидродинамике , в лазерах различных типов , в физике твердого тела - осциллятор Ганна , туннельные диоды , рост кристаллов .

В открытых системах , меняя поток вещества и энергии из вне , можно контролировать процессы и направлять эволюцию систем к состояниям , все более далеким от равновесия . В ходе неравновесных процессов при некотором критическом значении внешнего потока из неупорядоченных и хаотических состояний за счет потери их устойчивости могут возникать упорядоченные состояния , создаваться диссипативные структуры .

2.3.1а. ЯЧЕЙКИ БЕНАРА.

Классическим примером возникновения структуры из полностью хаотической фазы являются конвективные ячейки Бенара . В 1900 году была опубликована статья Х.Бенара с фотографией структуры , по виду напоминавшей пчелиные соты (рис. 2.7).

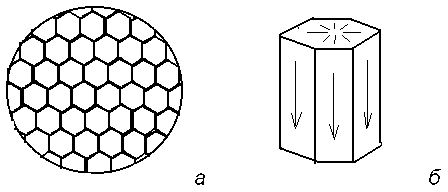
Рис. 2.7. Ячейки Бенара :

а) - общий вид структуры

б) - отдельная ячейка.

Эта структура образовалась в ртути , налитой в плоский широкий сосуд , подогреваемый снизу , после того как температурный градиент превысил некоторое критическое значение . Весь слой ртути (или другой вязкой жидкости) распадался на одинаковые вертикальные шестигранные призмы с определенным соотношением между стороной и высотой (ячейки Бенара). В центральной области призмы жидкость поднимается , а вблизи вертикальных граней - опускается . Возникает разность температур Т между нижней и верхней поверхностью DТ = Т₂ - Т₁ > 0 .Для малых до критических разностей DТ < DТ_kp жидкость остается в покое , тепло снизу вверх передается путем теплопроводности . При достижении температуры подогрева критического значения Т₂ = Т_kp (соответственно DТ = DТ_kp ) начинается конвекция . При достижении критического значения параметра Т , рождается , таким образом , пространственная диссипативная структура . При равновесии температуры равны Т₂ =Т₁ , DТ = 0 . При кратковременном подогреве (подводе тепла) нижней плоскости , то есть при кратковременном внешнем возмущении температура быстро станет однородной и равной ее первоначальному значению . Возмущение затухает , а состояние - асимптотически устойчиво. При длительном , но до критическом подогреве ( DТ < DТ_kp ) в системе снова установится простое и единственное состояние , в котором происходит перенос к верхней поверхности и передачи его во внешнюю среду (теплопроводность) , рис. 2.8 , участок а . Отличие этого состояния от равновесного состояния состоит в том , что температура , плотность , давление станут неоднородными . Они будут приблизительно линейно изменяться от теплой области к холодной .

Рис. 2.8. Поток тепла в тонком слое жидкости.

Увеличение разности температур DТ , то есть дальнейшее отклонение системы от равновесия , приводит к тому , что состояние неподвижной теплопроводящей жидкости становится неустойчивым участок б на рисунке 2.8. Это состояние сменяется устойчивым состоянием (участок в на рис. 2.8) , характеризующимся образованием ячеек . При больших разностях температур покоящаяся жидкость не обеспечивает большой перенос тепла , жидкость ²вынуждена² двигаться , причем кооперативным коллективным согласованном образом.

Далее этот вопрос рассматривается в 3 главе.

2.3.1в. ЛАЗЕР , КАК САМООРГАНИЗУЮЩАЯСЯ

СИСТЕМА.

Итак , в качестве примера физической системы , упорядоченность которой есть следствие внешнего воздействия , рассмотрим лазер.

При самом грубом описании лазер - это некая стеклянная трубка , в которую поступает свет от некогерентного источника (обычной лампы) , а выходит из нее узконаправленный когерентный световой пучок , при этом выделяется некоторое количества тепла.

При малой мощности накачки эти электромагнитные волны , которые испускает лазер , некоррелированные , и излучение подобно излучению обычной лампы. Такое некогерентное излучение - это шум , хаос. При повышении внешнего воздействия в виде накачки до порогового критического значения некогерентный шум преобразуется в ²чистый тон² , то есть испускает число синусоидальная волна - отдельные атомы ведут себя строго коррелированным образом , самоорганизуются.

Лампа ® Лазер

Хаос ® Порядок

Шум ® Когерентное излучение

В сверхкритической области режим ²обычной лампы² оказывается не стабильным , а лазерный режим стабильным , рисунок 2.9.

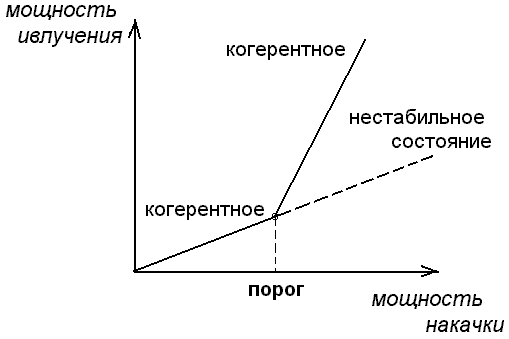
Рис. 2.9. Излучение лазера в до критической (а) и

сверхкритической (б) области.

Видно , что образование структуры в жидкости и в лазере формально описывается весьма сходным образом . Аналогия связана с наличием тех же самых типов бифуркаций в соответствующих динамических уровнях.

Подробнее этот вопрос рассмотрим в практической части , в 3 главе.

ХИМИЧЕСКИЕ СИСТЕМЫ .

В этой области синергетика сосредотачивает свое внимание на тех явлениях , которые сопровождаются образованием макроскопических структур . Обычно если дать реагентам про взаимодействовать, интенсивно перемешивая реакционную смесь, то конечный продукт получается однородный . Но в некоторых реакциях могут возникать временные, пространственные или смешанные ( пространственные - временные) структуры . Наиболее известным примером может служить реакция Белоусова - Жаботинского .

2.3.2а. РЕАКЦИЯ БЕЛАУСОВА - ЖАБОТИНСКОГО.

Рассмотрим реакцию Белоусова -Жаботинского . В колбу сливают в определенных пропорциях Ce₂ (SO₄ ) , KBrO₃ , CH₂ (COOH)₂ , H₂ SO₄ , добавляют несколько капель индикатора окисления - восстановления - ферроина и перемешивают . Более конкретно - исследуются окислительно - восстановительные реакции

Ce ³⁺ _ _ _ Ce ⁴⁺ ; Ce ⁴⁺ _ _ _ Ce ³⁺

в растворе сульфата церия , бромида калия , малоковой кислоты и серной кислоты . Добавление феррогена позволяет следить за ходом реакции по изменению цвета ( по спектральному поглащению ) . При высокой концентрации реагирующих веществ , превышающих критическое значение сродства , наблюдаются необычные явления .

При составе

сульфат церия - 0,12 ммоль/л

бромида калия - 0,60 ммоль/л

малоковой кислоты - 48 ммоль/л

3-нормальная серная кислота ,

немного ферроина

При 60 С изменение концентрации ионов церия приобретает характер релаксационных колебании - цвет раствора со временем периодически изменяется от красного (при избытке Се³⁺ ) до синего ( при избытке Се ⁴⁺ ) , рисунок 2.10а .

Рис. 2.10. Временные (а) и пространственные (б)

периодические структуры в реакции

Белоусова - Жаботинского.

...Такая система и эффект получили название химические часы . Если на реакцию Белоусова - Жаботинского накладывать возмущение - концентрационный или температурный импульс , то есть вводя несколько миллимолей бромата калия или прикасаясь к колбе в течении нескольких секунд , то после некоторого переходного режима будут снова совершаться колебания с такой же амплитудой и периодом , что и до возмущения . Диссипативная

Белоусова - Жаботинского , таким образом , является ассимптотически устойчивой . Рождение и существование незатухающих колебаний в такой системе свидетельствует о том , что отдельные части системы действуют согласованно с поддержанием определенных соотношений между фазами . При составе

сульфата церия - 4,0 ммоль/л,

бромида калия - 0,35 ммоль/л,

малоковой кислоты - 1,20 моль/л,

серной кислоты - 1,50 моль/л,

немного ферроина

при 20 С в системе происходят периодические изменения цвета с периодом около 4 минут . После нескольких таких колебаний спонтанно возникают неоднородности концентрации и образуются на некоторое время ( 30 минут ) , если не подводить новые вещества , устойчивые пространственные структуры , рисунок 2.10б . Если непрерывно подводить реагенты и отводить конечные продукты , то структура сохраняется неограниченно долго .

БИОЛОГИЧЕСКИЕ СИСТЕМЫ .

Животный мир демонстрирует множество высокоупорядоченных структур и великолепно функционирующих . Организм как целое непрерывно получает потоки энергии ( солнечная энергия , например , у растений ) и веществ ( питательных ) и выделяет в окружающую среду отходы жизнедеятельности . Живой организм - это система открытая . Живые системы при этом функционируют определенно в дали от равновесия . В биологических системах , процессы самоорганизации позволяют биологическим системам ²трансформировать² энергию с молекулярного уровня на макроскопический . Такие процессы , например , проявляются в мышечном сокращении , приводящим к всевозможным движениям , в образовании заряда у электрических рыб , в распознавании образов , речи и в других процессах в живых системах. Сложнейшие биологические системы являются одним из главных объектов исследования в синергетике . Возможность полного объяснения особенностей биологических систем , например , их эволюции с помощью понятий открытых термодинамических систем и синергетики в настоящее время окончательно неясна . Однако можно указать несколько примеров явной связи между понятийным и математическим аппаратом открытых систем и биологической упорядоченностью.

Более конкретно биологические системы мы рассмотрим в 3 главе , посмотрим динамику популяций одного вида и систему ²жертва - хищник² .

СОЦИАЛЬНЫЕ СИСТЕМЫ .

Социальная система представляет собой определенное целостное образование , где основными элементами являются люди , их нормы и связи . Как целое система образует новое качество , которое не сводится к сумме качеств ее элементов . В этом наблюдается некоторая аналогия с изменением свойств при переходе от малого к очень большому числу частиц в статической физике - переход от динамических к статическим закономерностям . При этом весьма очевидно , что всякие аналогии с физико - химическими и биологическими системами весьма условны , поэтому проводить аналогию между человеком и молекулой или даже нечто подобное было бы не допустимым заблуждением . Однако , понятийный и математический аппарат нелинейной неравновесной термодинамики и синергетики оказываются полезными в описании и анализе элементов самоорганизации в человеческом обществе.

Социальная самоорганизация - одно из проявлений спонтанных или вынужденных процессов в обществе , направленная на упорядочение жизни социальной системы , на большее саморегулирование. Социальная система является системой открытой способная , даже вынужденная обмениватся с внешним миром информацией , веществом , энергией. Социальная самоорганизация возникает как результат целеноправленных индивидуальных действий ее составляющих.

Рассмотрим самоорганизацию в социальной системы напримере урбанизации зоны . Проводя анализ урбанизации географических зон можно предположить , что рост локальной заселенности данной территории будет обусловлен наличием в этой зоне рабочих мест . Однако , здесь существует некоторая зависимость : состояние рынка , определяющего потребность в товарах и услугах и занятости . Отсюда возникает механизм нелинейной обратной связи в процессе роста плотности населения. Такая задача решается на основе логистического уравнения , где зона характеризуется ростом ее производительности N , новых экономических функций S - функция в локальной области i города. Логистическое уравнение описывает эволюцию численности населения и может быть тогда представлена в виде

dn_i

= Кn_i (N + å R_k S_ik - n_i ) - dn_i ( 2.13 )

dt k

где R_k вес данной к - ой функции , ее значимость . Экономическая функция изменяется с ростом численности : определяется спросом на к - й продукт в i - й области в зависимости от увеличения численности населения и конкуренции предприятий в других зонах города . Появление новой экономической функции играет роль социально экономической флуктуации и нарушает равномерное распределение плотности населения. Такие численные расчеты по логистическим уравнениям могут быть полезны прогнозировании многих проблем.

ПОСТАНОВКА ЗАДАЧИ.

В рассмотренных примерах в литературе имеются лишь общие выводы и заключения , не приведены конкретные аналитические расчеты или численные .

Целью настоящей дипломной работы является аналитические и численные исследования самоорганизации различных систем .

ГЛАВА 3

АНАЛИТИЧЕСКИЕ И ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ

САМООРГАНИЗАЦИИ РАЗЛИЧНЫХ СИСТЕМ.

3.1. ЯЧЕЙКИ БЕНАРА .

Для того , чтобы экспериментально изучить структуры , достаточно иметь сковороду , немного масла и какой ни будь мелкий порошок , чтобы было заметно движение жидкости . Нальем в сковороду масло с размешанным в нем порошком и будем подогревать ее снизу (рис. 3.1)

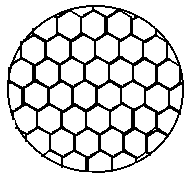
Рис. 3.1. Конвективные ячейки Бенара.

Если дно сковороды плоское и нагреваем мы ее равномерно , то можно считать , что у дна и на поверхности поддерживаются постоянные температуры , снизу - Т₁ , сверху - Т₂ . Пока разность температуры DТ = Т₁ - Т₂ невелика , частички порошка неподвижны , а следовательно , неподвижна и жидкость .

Будем плавно увеличивать температуру Т₁ . С ростом разности температур до значения DТ_c наблюдается все та же картина , но когда DТ > DТ_c , вся среда разбивается на правильные шестигранные ячейки (см. Рис. 3.1) в центре каждой из которых жидкость движется вверх , по кроям вниз . Если взять другую сковороду , то можно убедиться , что величина возникающих ячеек практически не зависит от ее формы и размеров . Этот замечательный опыт впервые был проделан Бенаром в начале нашего века , а сами ячейки получили название ячеек Бенара .

Элементарное качественное объяснения причины движения жидкости заключается в следующем . Из-за теплового расширения жидкость расслаивается , и в более нижнем слое плотность жидкости r₁ меньше , чем в верхнем r₂ . Возникает инверсный градиент плотности , направленный противоположно силе тяжести . Если выделить элементарный объем V , который немного смещается вверх в следствии возмущения , то в соседнем слое архимедова сила станет больше силы тяжести , так как r₂ > r₁ . В верхней части малый объем , смещаясь вниз , поподает в облость пониженной плотности , и архимедова сила будет меньше силы тяжести F_A < F_T , возникает нисходящее движение жидкости . Направление движения нисходящего и восходящего потоков в данной ячейке случайно , движение же потоков в соседних ячейках , после выбора направлений в данной ячейке детерминировано . Полный поток энтропии через границы системы отрицателен , то есть система отдает энтропию , причем в стационарном состоянии отдает столько , сколько энтропии производится внутри системы (за счет потерь на трение).

dS_e q q T₁ - T₂

= ¾ - ¾ = q * ¾¾¾ < 0 (3.1)

dt T₂ T₁ T₁ * T₂

Образование именно сотовой ячеистой структуры объясняется минимальными затратами энергии в системе на создание именно такой формы пространственной структуры . При этом в центральной части ячейки жидкость движется вверх , а на ее периферии - вниз.

Дальнейшее сверхкритическое нагревание жидкости приводит к разрушению пространственной структуры - возникает хаотический турбулентный режим.

Рис. 3.2. Иллюстрация возникновения тепловой

конвекции в жидкости .

К этому вопросу прикладывается наглядная иллюстрация возникновения тепловой конвекции в жидкости .

ЛАЗЕР , КАК САМООРГАНИЗУЮЩАЯСЯ СИСТЕМА.

Во второй главе этот вопрос мы уже рассматривали . Здесь же , рассмотрим простую модель лазера .

Лазер - это устройство , в котором в процессе стимулированного излучения порождаются фотоны .

Изменение со временем числа фотонов n , или другими словами , скорость порождения фотонов , определяется уравнением вида :

dn / dt = «Прирост» - «Потери» (3.2)

Прирост обусловлен так называемым стимулированном излучением . Он пропорционален числу уже имеющихся фотонов и числу возбужденных атомов N . Таким образом :

Прирост = G N n (3.3)

Здесь G - коэффициент усиления , который может быть получен из микроскопической теории . Член , описывающий потери , обусловлен уходом фотонов через торцы лазера . Единственное допущение , которое мы принимаем , - это то , что скорость ухода пропорциональна числу имеющихся фотонов . Следовательно ,

Потери = 2cn (3.4)

2c = 1/ t₀ , где t₀ - время жизни фотона в лазере .

Теперь следует учесть одно важное обстоятельство , которое делает (2.1) нелинейным уравнением вида :

(3.5)

Число возбужденных атомов уменьшается за счет испускания фотонов . Это уменьшение DN пропорционально числу имеющихся в лазере фотонов , поскольку эти фотоны постоянно заставляют атомы возвращаться в основное состояние .

DN = an (3.6)

Таким образом , число возбужденных атомов равно

N = N₀ - DN (3.7)

где N₀ - число возбужденных атомов , поддерживаемое внешней

накачкой , в отсутствии лазерной генерации.

Подставляя (3.3) - (3.7) в (3.2) , получаем основное уравнение нашей упрощенной лазерной модели :

(3.8)

где постоянная k дает выражение :

k₁ = aG

k = 2c - GN₀ >< 0 (3.9)

Если число возбужденных атомов N₀ (создаваемых накачкой) невелико , то k положительно , в то время как при достаточно больших N₀ k - может стать отрицательным . Изменение знака происходит когда

GN₀ = 2c (3.10)

Это условие есть условие порога лазерной генерации .

Из теории бифуркации следует , что при k > 0 лазерной генерации нет , в то время как при k < 0 лазер испускает фотоны.

Ниже или выше порога лазер работает в совершено разных режимах .

Решим уравнение (3.8) и проанализируем его аналитически :

- это уравнение одномодового лазера .

Запишем уравнение (3.8) в следующем виде :

Разделим исходное уравнение на n ² .

и введем новую функцию Z :

1/n = n^-1 = Z Þ Z¹ = - n^-2 следовательно уравнение примет вид :

перепишем его в следующем виде :

разделим обе части данного уравнения на -1 , получим

(3.11)

Уравнение (3.11) - это уравнение Бернулли , поэтому сделаем следующую замену Z = U × V , где U и V неизвестные пока функции n , тогда Z¹ = U¹ V + U V¹ .

Уравнение (3.11) , после замены переменных , принимает вид

U¹ V + UV¹ - k UV = k₁

преобразуем , получим

U¹ V + U(V¹ - k V) = k₁ (3.12)

Решим уравнение (3.12)

V¹ - k V = 0 ® dV/dt = k V

сделаем разделение переменных dV/V =k dt ® ln V = k t

результат V = e^kt (3.13)

Отсюда мы можем уравнение (3.12) переписать в виде :

U¹ e^kt = k₁

- это то же самое , что dU/dt = k₁ e^-kt , dU = k₁ e ^-kt dt выразим отсюда U , получим

(3.14)

По уравнению Бернулли мы делали замену Z = U V подставляя уравнения (3.13) и (3.14) в эту замену , получим

Ранее вводили функцию Z = n^-1 , следовательно

(3.15)

Начальное условие n₀ =1/(c-k₁ /k) , из этого условия мы можем определить константу с следующим образом

Подставляя , найденную нами константу в уравнение (3.15) , получим

(3.16)

Исследуем функцию (3.16) при k = 0 , k < 0 , k > 0 .

При k®0 ; e^kt ® 0 ; (e^kt - 1)®0 , то есть (e^kt - 1)×k₁ /k®0×¥ (неопределенность) , раскроем эту неопределенность по правилу Лопиталя . Эту неопределенность вида 0×¥ следует привести к виду . При этом , как и всегда при применении правила Лопиталя , по ходу вычислений рекомендуется упрощать получившиеся выражения , следующим образом :

n(k)_{при k ® 0} ® 0 , следовательно

Перепишем (3.16) в следующем виде

Линеаризуем нелинейное уравнение , получим

ln n = - kt + c Þ

Построим график для этих условий

Рис. 3.3 К самоорганизации в одномодовом лазере :

кривая 1 : k < 0 , режим лазерной генерации

кривая 2 : k = 0 , точка бифуркации , порог

кривая 3 : k > 0 , режим лампы.

При k = 0 уравнение (3.8) примет вид

решая его , получим

(3.8)

При условии ; n(t) = const , функция (3.8) приближается к стационарному состоянию , не зависимо от начального значения n₀ , но в зависимости от знаков k и k₁ (смотри рисунок 3.3).

Таким образом , функция (3.8) принимает стационарное решение

3.3. ДИНАМИКА ПОПУЛЯЦИИ .

О распространении и численности видов была собрана обширная информация . Макроскопической характеристикой , описывающей популяцию , может быть число особей в популяции . Это число играет роль параметра порядка . Если различные виды поддерживаются общим пищевым ресурсом , то начинается межвидовая борьба , и тогда применим принцип Дарвина : выживает наиболее приспособленный вид . ( Нельзя не отметить сильнейшую аналогию , существующую между конкуренцией лазерных мод и межвидовой борьбой ). Если имеются однотипные пищевые ресурсы , то становится возможным сосуществование видов . Численность видов может быть подвержена временным колебаниям.

ОДИН ВИД.

Рассмотрим сначала одну популяцию с числом особей в ней n . При наличии пищевых ресурсов А особи размножаются со скоростью :

и гибнут со скоростью :

Здесь k и d - некоторые коэффициенты рождаемости и смертности , в общем случае зависящее от параметров внешней среды обитания . Если бы количество пищи было неограниченно , то эволюционное уравнение выглядело бы так :

Введем обозначение a = kA - d

Оно было бы линейным и описывало бы неограниченный экспериментальный рост (при kA > d), либо экспериментальную гибель (при kA < d) популяции.

Рис. 3.4 Кривая 1 : Экспоненциальный рост ; a >0 , kA>d

Кривая 2 : Экспоненциальная гибель ; a >0 , kA>d .

В общем случае , однако , пищевые ресурсы ограничены , так что скорость потребления пищи

Вместе с тем в общем случае возможно восстановление пищевых ресурсов со скоростью :

Здесь , конечно , рассмотрен придельный случай сохранения полного количества органического вещества

A + n = N = const ,

N - способность среды обитания поддерживать популяцию.

Тогда с учетом A = N - n получится следующее уравнение эволюции популяции одного вида (логистическое уравнение Ферхюльста ) :

(3.17)

Решим уравнение (3.17) аналитически , перепишем его следующим образом

, обозначим kN - в = k₁

Получим :

Воспользуемся табличным интегралом , ,полученное уравнение примет вид :

решим это уравнение , преобразуя

сократим полученное выражение на k , и перенесем переменную k₁ в правую часть , получим

отсюда n(t) ®

Начальные условия :

откуда

Подставляя с в решение , получим уравнение в следующем виде

ранее мы обозначали , что , подставляем и преобразуем

сократим на k - коэффициент рождаемости , окончательно получим решение уравнения (3.17)

Итак , получено аналитическое решение логистического уравнения - это решение указывает на то , что рост популяции останавливается на некотором конечном стационарном уровне:

то есть параметр n₁ указывает высоту плато насыщения , к которому стремится n(t) с течением времени .

Параметр n₀ указывает начальное значение численности одного вида популяции : n₀ = n(t₀ ) . Действительно , ,то есть n₁ - предельная численность вида в данной среде обитания . Иначе говоря , параметр n₁ характеризует емкость среды по отношению к данной популяции . И наконец , параметр (kN - d) задает крутизну начального роста .

Отметим , что при малой исходной численности n₀ (начальное число особи) начальный рост популяций будет почти экспоненциальным

Рис. 3.5. Логистическая кривая.

(эволюция популяции одного вида)

Решение уравнения (3.17) можно представить с помощью логистической кривой (рис. 3.5) . Эволюция полностью детерминирована . Популяция перестает расти , когда ресурс среды оказывается исчерпанным .

Самоорганизация - при ограниченном пищевом ресурсе. Система самоорганизованна и взрывоподобный рост популяции (рис. 3.4 Кривая 1) сменяется кривой с насыщением .

Подчеркнем , что при описании данной биологической системы используют понятийный и физико-математический аппарат из нелинейной неравновесной термодинамики.

Может случится , однако, что всегда за событиями , не управляемыми в рамках модели , в той же среде появится , первоначально в малых количествах , новые виды (характеризуемые другими экологическими параметрами k,N и d) . В связи с такой экологической флуктуацией возникает вопрос о структурной устойчивости : новые виды могут либо исчезнуть , либо вытеснить первоначальных обитателей . Пользуясь линейным анализом устойчивости , не трудно показать , что новые виды вытесняют старые только в том случае , если

Последовательность , в которой виды заполняют экологическую нишу , представлена на рисунке 3.6.

Рис. 3.6. Последовательное заполнение экологической

ниши различными видами .

Эта модель позволяет придать точным количественный смысл утверждению о том , что «выживает наиболее приспособленный» , в рамках задачи о заполнении заданной экологической ниши .

СИСТЕМА «ЖЕРТВА - ХИЩНИК».

Рассмотрим систему, состоящую из двух видов - это «жертва» и «хищник» (например , зайцы и лисицы) , то эволюция системы и ее самоорганизация выглядят иначе , чем в предыдущем случае.

Пусть в биологической системе имеются две популяции - «жертв» - кролики (К) , и «хищников» - лисиц (Л), численностью К и Л .

Проведем теперь рассуждение , которое позволит нам объяснить существование диссипативных структур .

Кролики (К) поедают траву (Т) . Предположим , что запас травы постоянен и неисчерпаем . Тогда , одновременное наличие травы и кроликов способствуют неограниченному росту кроличьей популяции . Этот процесс можно символически изобразить так :

Кролики + Трава ® Больше кроликов

К + Т ® 2К

Тот факт , что в стране кроликов всегда имеется в достатке травы , вполне аналогичен непрерывному подводу тепловой энергии в задаче с ячейками Бенара . Вскоре процесс , в целом , будет выглядеть как диссипативный (во многом аналогично процессу Бенара ).

Реакция « Кролики - Трава » происходит спонтанно в направлении увеличения популяции кроликов, что является прямым следствием второго начала термодинамики .

Но вот в нашу картину , где мирно резвятся кролики , прокрались хищные лисицы (Л), для которых кролики являются добычей . Подобно тому , как по мере поедания травы кроликов становится больше , за счет поедания кроликов возрастает число лисиц :

Лисицы + Кролики ® Больше лисиц

Л + К ® 2Л

В свою очередь лисицы , как и кролики являются жертвами - на этот раз человека , точнее говоря происходит процесс

Лисицы ® Меха

Конечный продукт - Меха , не играет непосредственной роли в дальнейшем ходе процесса . Этот конечный продукт можно , однако , рассматривать как носитель энергии, выводимой из системы , к которой она была в начале подведена (например, в виде травы ).

Таким образом , в экологической системе также существует поток энергии - аналогично тому , как это имеет место в химической пробирке или биологической клетке .

Совершенно ясно , что в действительности происходят периодические колебания численности популяции кроликов и лисиц , причем за нарастании численности кроликов следует нарастание численности лисиц , которые сменяются уменьшением численности кроликов , сопровождающимся столь же резким снижением численности лисиц , затем повышенным подъемом численности кроликов и так далее (рис. 3.7).

Рис. 3.7. Изменение численности популяций кроликов и лисиц

со временем. Наличие периодичности означает

возникновение экологической структуры.

С течением времени численность обеих популяций меняется в соответствии с последовательным прохождением точек графика . Через некоторое время (конкретное значение зависит от быстроты поедания лисицами кроликов , а так же от скорости размножения обоих видов) весь цикл начинается вновь.

Поведение популяций при различных степенях плодовитости , а так же различных способностях избегать истребления можно изучить количественно с помощью программы : ПОПУЛЯЦИЯ (в приложении).

Эта программа реализует решение уравнений для диссипативной структуры «кролики - лисицы». Результат решения изображается графически . Решается система дифференциальных уравнений

Здесь буквы К, Л, Т - означают соответственно количество кроликов , лисиц , травы ; коэффициенты k₁ , k₂ , k₃ - обозначают соответственно скорость рождения кроликов , скорость поедания кроликов лисицами и скорость гибели лисиц.

В программе понадобится уточнить значение отношений (примерно равное 1), постоянное количество травы (так же принимаемое обычно равным 1), начальные значения популяции кроликов и лисиц (обычно 0,4), продолжительность цикла (типичное значение 700) и шаг по оси времени (обычно равный 1).

Программа популяции - это график. Он показывает поведение популяций при различных степенях плодовитости , а так же различных способностях избегать истребление.

Совершенно ясно , что в действительности происходят периодические колебания численности популяции кроликов и лисиц , причем за нарастании численности кроликов следует нарастание численности лисиц , которые сменяются уменьшением численности кроликов , сопровождающимся столь же резким снижением численности лисиц , затем повышенным подъемом численности кроликов и так далее, то есть видно , что система самоорганизуется.

Программа прилагается.

ЗАКЛЮЧЕНИЕ.

Мы видели , что необратимость времени тесно связана с неустойчивостями в открытых системах . И.Р. Пригожин определяет два времени . Одно - динамическое , позволяющее задать описание движения точки в классической механике или изменение волновой функции в квантовой механике . Другое время - новое внутренние время , которое существует только для неустойчивых динамических систем . Оно характеризует состояние системы , связанное с энтропией .

Процессы биологического или общественного развития не имеют конечного состояния . Эти процессы неограниченны . Здесь , с одной стороны , как мы видели , нет какого-либо противоречия со вторым началом термодинамики , а с другой стороны - четко виден поступательный характер развития (прогресса) в открытой системе. Развитие связано , вообще говоря , с углублением неравновесности , а значит , в принципе с усовершенствованием структуры . Однако с усложнением структуры возрастает число и глубина неустойчивостей , вероятность бифуркации .

Успехи решения многих задач позволили выделить в них общие закономерности , ввести новые понятия и на этой основе сформулировать новую систему взглядов - синергетику . Она изучает вопросы самоорганизации и поэтому должна давать картину развития и принципы самоорганизации сложных систем , чтобы применять их в управлении . Эта задача имеет огромное значение , и , по нашему мнению , успехи в ее исследовании будут означать продвижение в решении глобальных задач : проблемы управляемого термоядерного синтеза , экологических проблем , задач управления и других .

Мы понимаем , что все приведенные в работе примеры относятся к модельным задачам , и многим профессионалам , работающим в соответствующих областях науки , они могут показаться слишком простыми . В одном они правы : использование идей и представлений синергетики не должно подменять глубокого анализа конкретной ситуации . Выяснить , каким может быть путь от модельных задач и общих принципов к реальной проблеме - дело специалистов. Кратко можно сказать так : если в изучаемой системе можно выделить один самый важный процесс (или небольшое их число) , то проанализировать его поможет синергетика . Она указывает направление , в котором нужно двигаться . И , по-видимому , это уже много.

Исследование большинства реальных нелинейных задач было невозможно без вычислительного эксперимента , без построения приближенных и качественных моделей изучаемых процессов (синергетика играет важную роль в их создании). Оба подхода дополняют друг друга . Эффективность применения одного зачастую определяется успешным использованием другого . Поэтому будущее синергетики тесно связано с развитием и широким использованием вычислительного эксперимента .

Изученные в последние годы простейшие нелинейные среды обладают сложными и интересными свойствами . Структуры в таких средах могут развиваться независимо и быть локализованы, могут размножаться и взаимодействовать . Эти модели могут оказаться полезными при изучении широкого круга явлений .

Известно , что имеется некоторая разобщенность естественно научной и гуманитарной культур . Сближение , а в дальнейшем , возможно , гармоническое взаимообогащение этих культур может быть осуществлено на фундаменте нового диалога с природой на языке термодинамики открытых систем и синергетики .

ЛИТЕРАТУРА :

Базаров И.П. Термодинамика. - М.: Высшая школа, 1991 г.

Гленсдорф П. , Пригожин И. Термодинамическая теория структуры , устойчивости и флуктуаций. - М.: Мир, 1973 г.

Карери Д. Порядок и беспорядок в структуре материи. - М.: Мир, 1995 г.

Курдюшов С.П. , Малинецкий Г.Г. Синергетика - теория самоорганизации. Идеи , методы перспективы. - М.: Знание, 1983 г.

Николис Г. , Пригожин И. Самоорганизация в неравновесных системах. - М.: Мир, 1979 г.

Николис Г. , Пригожин И. Познание сложного. - М.: Мир, 1990 г.

Перовский И.Г. Лекции по теории дифференциальных уравнений. - М.: МГУ, 1980 г.

Попов Д.Е. Междисциплинарные связи и синергетика. - КГПУ, 1996 г.

Пригожин И. Введение в термодинамику необратимых процессов. - М.: Иностранная литература , 1960 г.

Пригожин И. От существующего к возникающему. - М.: Наука, 1985 г.

Синергетика , сборник статей. - М.: Мир, 1984 г.

Хакен Г. Синергетика . - М.: Мир , 1980 г.

Хакен Г. Синергетика . Иерархия неустойчивостей в самоорганизующихся системах и устройствах . - М.: Мир , 1985 г.

Шелепин Л.А. В дали от равновесия. - М.: Знание, 1987 г.

Эйген М. , Шустер П. Гиперцикл . Принципы самоорганизации макромолекул . - М.: Мир , 1982 г.

Эткинс П. Порядок и беспорядок в природе. - М.: Мир , 1987 г