| 1 Понятие о равновесии. Уравновешенная система сил. Равнодействующая системы сил. Силы внешние и внутренние
(в-2.,3.)
Внешние нагрузки:
Р –сосредоточ (а<< h)
q – интенсивность
распределенной нагрузки. Равнодействующая = q*a (площадь эпюры q) Преложена равн-щая в центре тяжести эпюры.
М – пара сил (сосредоточенный момент)
Внутренние силы – это силы взаим-ия м/д отдельными эл-ми конструкции, возник-ие под действием внеш сил т.о. если Fвнеш
отсутствует, то Fвнут
= 0.
R- главный вектор MR
гл векторный момент.
Nя
- продольная сила (раст\сжат)
Qx
или у
поперечная (сдвиг\срез)
Мк (
z
)
крутящий момент (кручение)
Миз (х или у)
изгуб-щий момент (изгиб
чистыйМи
≠0 поперечный Ми
≠0 Q≠0
2 Аксиомы статики. Связи, реакции связей.
1Если на свободное абс. Твёрдое тело действует 2 силы, то тело может нах-ся в равновесии если эти 2 силы= и направлены по 1 прямой в противопол-е стороны. |P1
|=|P2
|
Равнов-е – это состояние
покоя или равномерного
движ-я по отношению к
др. телам.
2.Действие данной системы сил на тело не изменится, если к ней прибавить или от неё отнять уравновешенную систему сил. Две системы сил отличающ-ся на уравнов-ую систему наз-ся эквивалентными.
3.Равнодействующая 2 сил,
сходящихся в 1-ой точке,
изображается диагональю
параллелограмма, построенного на этих силах.
4.III з-н Ньютона: Всякое действие одного тела на др вызывает такое же по вел-не, но противопп-е по направлению противодействие.
5.Любое не свободное тело можно рассматр-ть как своб-ое, если мысленно отбросить связи и заменить их реакциями. (Р-ция связи – это усилие, с которым опора препятствует перемещению тела в опред. направлении. Р-я всегда противоп-на внешним воздействиям.
6.Принцып отвердения: Равновесие деф-ого тела, наход-ся под действием системы сил, не нарушается, если считать тело абсолютно твёрдым. Все ур-я равновесия в статике будем применять к свободному телу поэтому кроме заданных внеш сил необходимо опр и прилож к нему р-ции связи.
Связи:
1)Свободное опирание тела на связь
2)Гибкие связи – это нити,
цепи, тросы, работают на
растяж-е р-ции напр вдоль нити
3)Жесткие стержни,
работают на растяж\сжа
р-ции напр вдоль стержн
4)Шарнирно-подвижная опора(1р-ция)
5)Шарн-неподвиж опора (2 реакции)
6)Жёсткая заделка (3 реакции)
3 Система сходящихся сил. Главный вектор системы сил. Условия равновесия системы сходящихся сил.
Система сходящихся сил
(2 или более сил, сход в
1 точке) может быть заменена 1-й силой, которая наз-ся равнодействующей ‾R∑(‾Pi
). Урав-новешивающая сила R’= по модулю равнодействующей, но напр по той же прямой в противоположную сторону.|R’|=|R|
опред равнодействующей:
1)Графическое суммирование
2) Аналитическое Ry
=∑(Pi
)=P1
sin(a)+P2
sin90+Pn
sin(b)- алгебр сумма проекций на осьОУ. Rz
=∑(Pi
)=P1
cos(a)+P2
cos90+Pn
cos(b)- алгебр сумма проекций на осьОZ. R=√Ry
2
+Rz
2
Любую систему сил произвольно располож в плоскости можно заменить 1-й силой R прилож-й в произвольном центре приведения О и 1-м моментом Мо
. R-гл вектор = векторной сумме сил, вход-х в систему или его проекций.Мо
- гл момент и = алгеб суммемоментов всех сил системы, взятых относительно центра приведения иалгеб сумме пар сил, действующих на тело.
Мо
=mo
(P1
)- mo
(P2
)+M1
-M2
Условие равновесия плоской системы сход-ся сил: необходимо и дост-но, чтобы равнодействующая системыR=0
а)при граф-ом суммировании силовой многоугольник должен быть замкнут.
б)при аналитическом Ry
иRz
должны=0.
Условие равновесия: R=0 (∑(Pi
)z
=0, ∑(Pi
)y
=0); Mo
=0 (∑mo
(Pi
)+∑Mi
=0)
4 Момент силы относительно точки. Пара сил. Момент пары сил. Сложение пар лежащих в одной плоскости.
(в-3)
Пара сил – это 2 силы = по вел-не, параллельные и против-но направ-ные, не леж-щие на1-ой прямой.(при этом равнод-щая R=0). М=Р*h,h-плечо М хар-ся вел-ой и направл вращения.
Св-ва пар сил:
Две пары сил статистически эквивал-
ны(оказывают на плечо одинак действие), если их моменты =
М1
=М2
если P1
*h1
=P2
*h2
5 Пару сил можно переносить в плоскости её действия в любое
6
1)Чистый изгиб Мизг
≠0, Q=0,N=0,Mк
=0
2)Поперечный Мизг
≠0, Q≠0,N=0,Mк
=0
По расположению силовой плос-ти:
1)Прямой или плоскийили простой – это когда силов плос-ть прох-т ч/з одну из главных центр-х осей попер-ого сечения балки. Центр-е оси прох-т ч/з центр тяж-ти, главные оси- оси симметр-ии или оси относ-но которых осевые моменты инерции Jx
Jy
имеют экстремальные знач-я Jx
=∫y2
dF (поF) Jy
=∫x2
dF (по F)
2)Косой изгиб- сложная деф-я. Деф-ции не лежат в силовой плоскости
Внутр усилия опр-ся с помощью метода сечений. Внут ус-я должны уравновеш-ть внеш воздействия.
Q=∑(Pi
)y
Ми
=∑mo
(Pi
)+ ∑Mi
Q-попереч сила в попер-м сечении балки численно= алгеб сумме проекций всех внеш сил действ-х на левую или правую часть балки. Q=f(q,P) M-не влияет на Q
Правило знаков:
Ми
-изгиб-й момент в попер-м сечении балки численно= алгеб сумме моментов внеш сил взятых относит-но центра тяжести сечения и сумме сосредоточенных моментов действующих по 1-у стороны от сеч-я. Ми
=f(q,P,M) Q и Ми
-могут быть с разными знаками. Правило знаков:
Постр-е эпюр Q и Ми:
1)Из условия равновесия балки опр реа-ии опор которые явл такие же как и внеш нагрузки (для консоли р-ии можно не опр-ть, часть с заделкой отбрасывают).
2)Балка разбив-ся на отдельные уч-ки в пределах которых з-н изменения Q и Ми одинаковый. (Границы берутся в точках прилож-я Р, М и в начале и конце q)
3)Сост-ся аналитич-ие выр-я для Q и Ми для каждого из уч-ков.
4)По получ-м выр-ям вычисл-ся ординаты эпюр на границах уч-ов
5)Если есть точки где Q=0 то опр-ся местный экстремум.
При движ-ии слева направо:
1)На уч-ах балки где Q>0 Ми-возрас-т
Где Q<0 Ми-убывает
2)Чем больше по абсол-й вел-не знач-е Q тем круче круче линия огранич-ая
эпюру Ми. |Q|↑ то крут-на Ми↑
если Qi
>Qj
Mи
i
>Ми
j
αi
>αj
3)На уч-ах балки на которых Q=const эпюра Ми- прямая
4)В сеч-ях где Q=0 Ми- достигает экстремального знач-я.
27 Дифференциальные зависимости между внутренними силовыми факторами при изгибе, их использование для проверки правильности эпюр.
QI
=Ra
+P-q*z
Ми
I
=Ra
*z+P*(z-a)-q*z2
/2+M
QII
=Ra
+P-q*(z+dz)
Ми
II
=Ra
*(z+dz)+P*(z+dz-a)-
-q*(z+dz)2
/2+M
QII
-QI
=dQ
dQ=q*dz
q
=
dQ
/
dz
Производная от поперечной силы по абсциссе сеч-я балки z(dQ)= интенсивности распред-ой нагрузки q.
Ми
II
-Ми
I
=dМи
= Ra
*(z+dz)+P*(z+dz-a)-
-q*(z+dz)2
/2+M- Ra
*z-P*(z-a)+q*z2
/2-
-M= Ra
*dz+P*dz-q*z*dz-(q*d2
z)/2
(q*d2
z)/2→0 dМи
= (Ra
+P-q*z)*dz= =QI
*dz Q=d
Ми
/dz
Производная от изгибающего момента Ми по абсциссе сечения балки = поперечной силе Q
28 Напряжения при чистом изгибе. Наиболее экономичные формы поперечных сечений балок.
Ми≠0(чист из-б)
у-расст-е от
нейтрального слоя
до другого.
Справедлива гипотеза плоских сеч-й.
Продольные линии при чистом из-бе искривл-ся по дугам окруж-ти при этом волокна лежащие на оси балки не меняют своей длины.
a'b’-удлинились
c’d’=cd
e’f ‘-укоротились
ρ-радиус изгиба
О-центр тяж-ти.
Совокупность волокон не меняющих своей длины при изгибе наз-ся нейтральным слоем. Нейтр слой-цилиндр поверхность с радиусом ρ. Линия перес-я нейтр слоя с плоскостью попереч сеч-я наз-ся нейтр-ой осью. Линия перес-я силовой плоскости с плос-ю попер-ого сеч-я наз-ся силовой линией и проходит ч/з центр тяж-ти попер-ого сеч-я.
ε(относ удлин-е аb) =Δab/ab=bb’/cd
ac=y ε=(y*dθ)/(ρ*dθ)=y/ρ ρ=const
т.к. γ=0, то τ=0 т.к.ε≠0 σ≠0
ε=σ/Е σ =Е*ε=Е*у/ρ
Предполагая что средние волокна не давят друг на др можно сказать что каждое волокно испытывает одноосное растяж/сжатие. Относит продольная деф-я ε и продольные напряж-я σпри чистом изгибе измен-ся по высоте попереч сечения балки прямо пропорционально расстоянию у от нейтр оси.
Сила действ-ая
на элемен-ую
площадку σ*dF
1)∑(Pi
)x
=0 тожд-
2)∑(Pi
)y
=0 ва
3)∑mz
(Pi
)=0 0=0
|
положение, а также можно переносить в плоскость || плоскости её действия.Результат действия на тело этой пары сил при этом не изменится.
Сложение пар сил, леж в одной плоскости: равнодействующий момент = алгебр сумме моментов.
М=∑Мi
. Условие равновесия системы пар сил: необх и дост-но чтобы алгеб сумма всих моментов =0. МR
=∑Мi
=0
Момент силы относ
точки= mo
(Pi
)=|P|*h
Следствия: 1)момент
силы относ любой точки, располож-ой на линии действия силы =0
mo
(Pi
)=|P|*h т.к. h=0 <= mo
(Pi
)=|P|*h=0
2)Алге сумма моментов сил образующ
пару, относ-но произвольной точки, лежащей в плоскости пары, величина постоянная, равная моменту пары сил.
P=P’
∑mo
(Pi
)=|P|*ОА–Р’*OB=P*(OA-OB)=
P*AB=P*h => mo
=M
5 Теорема о параллельном переносе силы на плоскости. Приведение сил к данному центру.
(в-3, 4)
Силу Р можно ||
переместить в
любую точку О,
добавив при этом
момент присо-единённой пары сил = моменту данной силы относительно точки приведения О. Мпр
= Р*h.
6Условия равновесия произвольной плоской системы сил.
(в-3)
7.Основные гипотезы, лежащие в основе курса сопротивления материалов. Внутренние силовые факторы, метод сечений.
(в-1)
1Материал конструкции однородный и сплошной т.е. его св-ва не зависят от формы и размеров тела и одинак во всех его точках.
2.Мат-л конс-ии изотропен,т.е.его св-ва по всем направлениям одинаковы. (99% мат-ов)
3.Мат-л обладает св-вом идеальной упругости, т.е. способностью полностью восстанав-ть первонач-ю форму и размеры после снятия внеш нагрузок(это справедливо для напр-ий не превыш-их предел упругости).
4.З-н Гука: дефор-ция мат-ла конструк прямо пропорциональна напряжениям
ε = σ / Е γ = τ / G
E-модуль Юнга(модуль упр 1-го рода) G-модуль упругости 2-го рода. (З-н Гука справедлив до предела пропорциональности)
5.Деф-ции констр малы и не влияют на взаимное расположение нагрузок.
6.Принцип независимости действия сил (принцип наложения): результат воздействия на конструкцию системы нагрузок= сумме результатов возд от каждой нагрузки в отдельности
δ = δР
+ δМ
+ δq
(справедлив если выполняются 4и5 предпосылки).
7.Гипотеза плоских сечений (Бернулли): поперечные сеч-я бруса, плоские до приложения, остаются плоскими и после прилож-я нагрузки(справедлив для всех видов деф-ции).
8.Принцип Сен-Венана: если не интересоваться местными деф-ми (в малой части объёма тела), то нагрузку, прилож-ю к малой части объёма тела можно заменить статистически ей эквивалентной или равнодействующей
если а<<L то:
Метод сечений: в интересующем нас месте рассекаем брус; отбрасываем одну из частей бруса(лучше ту, где больше внеш сил); взаимодейс-е частей бруса друг на друга заменяем внутр усилиями, которые уравновешивают внешниесилы.
Σ(Рi
)z
=0
8
Понятия о напряжениях, деформациях, перемещениях.
Напр-ем наз-ся внутр сила, приходя-щаяся на ед-цу площади рассматриваемого сеч-я. Рсреднее
=ΔR/ΔF
Pистинное
= lim ΔR/ΔF(приΔF→0) [H/м2
=Па]
σz
– (нормальное напряж-е) наз-ся составляющая полного напяж-я перпендикулярная плоскости сеч-я.
τ(
zx
или
zy
)
- (касательное напряж-е) наз-ся составляющая полного напяж-я, лежащая в плоскости сечения.
Плоская задача
Р=√σ2
+τ2
N=f(σ)→σmax
<=[ σ]
Q=f(τ)→τmax
<=[ τ] условия
Mк
=f(τ)→ τmax
<=[ τ] прочности
Mи
=f(σ)→ σmax
<=[ σ]
Деф-ции:
1.линейные а)абсолютные Δl=l1
-l Δh=h1
-h[м,см] З-н Гука в абсол вел-х:
Δl=N*l/(E*F) –раст\сжатие
φ = Мк
*l /(G*Jp
) – кручение
k= 1/ρ= Mиз
/(E*Jx
) – изгиб
ΔS= Q*a / (G*F) – сдвиг\срез
В этих 4-х формулах знаменатель= жесткость сечения бруса.
б) относительные ε=Δl/l ε=Δh/h ε=σ/E (E- модуль Юнга)
2.угловые деф-ции γ (угол сдви-га)=α+β, γ=τ/G(G-модуль упр 2 рода)
Деф-я относится к отрезку части бруса – это изменение его первоначальной длины. Перемещение (δ) относится к сечению бруса- это изменение его положения в пространстве относительно какой-либо точки отсчёта. δi
-
I
=Σ(Δli
)
условие жесткости: δmax
<= [δ]
9
Растяжение и сжатие. Определение напряжений и деформаций. Закон Гука. Модуль упругости.
Центральным р\с наз-ся деф-ция при которой в поперечных сечениях бруса возникает только 1-но внут усилие- продольная сила N. Оно вызыв-ся силами действ-ми вдоль оси бруса.
Напряж-е τ =0 γ= 0 σ ≠ 0 = const
σi
=Ni
/Fi
<=[σc
],[σp
]- условие проч-ти.
Деф-ция: ε = σ / Е - з-н Гука Δl/l=N/(F*E) Δl=N*l/(F*E)
Деф-я относится к отрезку части бруса – это изменение его первоначальной длины.
Попереч деф-я:
ε'= - μ*ε ε’-относ
попер деф-я, μ- коэф
Пуассона, ε – относ
Продольная деф-я.
μ хар-ет способность
мат-ла к попер деф-м.
Δ b=ε’ * b
Перемещение (δ) относится к сечению
4)∑(Pi
)z
=0 ∫σdF (поF)=E/ρ∫ydF(поF)=0 ∫ydF- обознач-ся Sx
и наз-ся статисти-ческий момент сечения относ-но оси х
Sx
=yц.т.
*F т.к.Е/ρ≠0, то Sx
=0 Ось х прох-т ч/з центр тяж-ти.
5)∑my
(Pi
)=0 x- плечо σ*dF- сила ∫x*σdF=E/ρ∫xydF ∫xydF= Jxy
наз-ся центробежным моментом инерции сеч-я относ-но х и у. Если он=0 то оси х и у явл-ся главными осями сеч-я.
6)∑mx
(Pi
)=0 ∫yσdF=Ми
Е/ρ∫у2
dF=Ми
∫у2
dF=Jx
- наз-ся осевым моментом инерции сеч-я относ-но оси х
Е/ρ*Jx
=Ми
1/ρ=Ми
/(Е*Jx
) – кривизна нейтр-ого слоя.
σ= Е*у/ρ=Е*у*Ми
/(Е*Jx
)= у*Ми
/*Jx
– справедливо и для чистого и для попер
Наиб эконом формы попер сеч балок:
1)Надо выбирать балки у котор большая часть мат-ла удалена от центра тяж-ти. Выгодно:
2)Расположение балки делают таким чтобы Jx
=max
3)Выбор формы сеч-я зависит от мат-ла. Для пластич мат-ла лучше использ-ть балки с симметр сеч-ми относит-но нейтр оси у которых σmax
p
ас
=σmax
сж
для хрупк ассиметр сеч-я при этом сеч-я располагают так чтобы
σmax
pас
<=σmax сж
т.к. [σсж
]=(3-5)*[σрас
]
29 Условие прочности при изгибе. Подбор размеров поперечных сечений балок.
Усл проч-ти для симметр сеч-й
относ-но оси х:
σmax
p
ас
=σmax
сж
=Ми
*0.5*h/Jx
=Ми
/Wx
Wx
=Jx
/y –наз-ся осевым моментом сопр-я при изгибе.
1)пластич мат-л: σmax
=Ми
/Wx
<=[σ]
2)хруп мат-л: σmax
=Ми
/Wx
<=[σрас
]
Ассиметричные сеч-я:
σmax
рас
=Ми
*ymax
рас
/Jx
<=[σрас
]
σmax
сж
=Ми
*ymax
сж
/Jx
<=[σсж
]
30 Потенциальная энергия деформации при чистом изгибе.
Авнеш
=М1
*θ1
/2 dAвнут
= - Ми
*dθ/2
ρ – радиус крив-ны k –кривизна
dz=ρ*dθ
dθ=dz/ρ
k=1/ρ=Ми
/(Е*Jx
)
dθ= Ми
*dz/(Е*Jx
) dA= - Ми
2
*dz/(2*Е*Jx
) U= -Aвнут
=
= -∫-Ми
2
*dz/(2*Е*Jx
)=∫Ми
2
*dz/(2*Е*Jx
) (от0 до L). – для попер изг-а Ми
≠const.
Для чистого изгиба: Ми
=const
U= Ми
2
*L/(2*Е*Jx
)
31 Напряжение при поперечном изгибе: нормальные и касательные.
Поперечный Мизг
≠0, Q≠0,N=0,Mк
=0
σ= Е*у/ρ=Е*у*Ми
/(Е*Jx
)= у*Ми
/*Jx
– справедливо и для чистого и для попер
Касат напряж в произвольной точке попер сеч-я: τzy
=τ=Qy
*Sx
/(Jx
by
)
Qy
-попер сила в рассматр сеч-и Sx
-статистич момент относит-но нейтр-ой оси той части сеч-я, которая распол-на по одну сторону прямой, провед-ой ч/з данную точку Jx
- момент инерции всего сеч-я относит-но нейтр оси by
-ширина попер сечения на уровне рассматриваемой точки.
32 Дифференциальное уравнение упругой линии балки, его интегрирование.
Перемещения: у- прогиб – это перемещ-е точек оси балки по нормали её недеформированной оси.
max прогиб-это стрела прогиба. Условие жесткости: уmax
<=[y]
[y]=(0.01-0.001)*L
θA
-угол поворота попер сеч-я балки, буде считать его = углу наклона касательной к оси z т.е. углу поворота оси балки. y=f(z) θA
=tg θA
при α<<
θA
=dy/dz=y’ Условие жесткости: θmax
<=[θ] [θ]=(0.5-1)*град.
Изогнутая ось балки y=f(z) наз-ся упругой линией балки. Расчёт балки на жест-ть позволяет опр-ть размеры попереч сечения при которых перемещ-е не превышает установленные нормами пределы.
Правило знаков: y>0-перемещ вверх θ>0- поворот сеч-я против часовой стрелки.
Из матем-ки: k=1/ρ =y’’/(1+(y’)2
)3/2
Из сопромата: k=1/ρ =Mи
/(ЕJx
)
Точное диф ур-е:
y’’/(1+(y’)2
)3/2
= Mи
/(ЕJx
)
y’=θ→min т.к.y’-мал,то (y’)2
-пренебре-
гаем. Получаем: y’’= Mи
/(ЕJx
)
Mи
= y’’ЕJx
- основное диф ур-е упругой линии балки.
y'’=d2
y/dz2
=dy’/dz
аналитическое решение: Mи
= y’’ЕJx
ЕJx
=const ЕJx
d(y’)=Mи
dz
ЕJx
y’= ∫Mи
dz+C y’=θ=(∫Mи
dz+C)/( ЕJx
)
ЕJx
dy/dz= ∫Mи
dz+C
ЕJx
dy= dz(∫Mи
dz+C)
ЕJx
= ∫dz∫Mи
dz+C*z+D
C и D- произвольные const их опр-ют из условия операния балки.
yA
=0 θA
=0
yA
=0 yB
=0
33 Метод начальных параметров вычисления перемещений при изгибе балок.
Для данного
напавления
все знаки +
1) ЕJx
θ= ЕJx
θ0
+∑M(z-a)+(∑P(z-b)2
)/2+ +(∑q(z-c)3
)/6+…
2) ЕJx
y= ЕJx
y0
+ ЕJx
θ0
z+(∑M(z-a)2
)/2+ +(∑P(z-b)3
)/6+ +(∑q(z-c)4
)/24+…
1)справедливы для балок с постоян жёсткостью ЕJx
=const 2)Необходимо иметь только расчётную схему 3)Если q имеет разрыв непрерывности до сечения т.е.
то берутся дополнит слогаемые в 1-е: -(∑q(z-d)3
)/6, во 2-е: -(∑q(z-d)4
)/24
∑-алгеб сумма 4) y0
и θ0
опред-ся из условия операния балки.
34 Понятие о напряжённом состоянии в точке. Главные площадки и главные напряжения.
Объёмная деформация. (
В-12)
Объёмное или 3-х осное напяж сост
σ1
≠0
σ2
≠0
σ3
≠0
Объем деф-я х-ся изменением объёма
υ=(V1
-V0
)/V0
υ-относит изменение объёмаV1
-объем после деф-ииV0
-до
деф-ии
|
бруса- это изменение его положения в пространстве относительно какой-либо точки отсчёта. δi
-
I
=Σ(Δli
)
условие жесткости: δmax
<= [δ]
E- модуль Юнга- модуль упругости 1-го рода (модуль продольной упр-ти) Естали
=2*105
МПа.
10 Потенциальная энергия деформации при растяжении, сжатии.
Элементарная dАвнеш
=P*dδ P=f(δ) Δl=δ=P*l/(E*F) P=E*F*δ/l dA=(E*F*δ/l)*dδ Aвнеш
=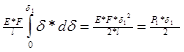
Работа внеш сил выражается площадью диаграммы построенной в коор-х Р*δ и равна половине произведения окончательной силы Р и перемещения δ.
dAвнут
= - N*Δ(dz)/2
Δ(dz)=N*dz/(E*F)
dAвнут
= -N2
*dz/(2*E*F)
Aвнут
= -N2
*dz/(2*E*F) -N2
*dz/(2*E*F)
Aвнут
= -N2
*l/(2*E*F)
Потен эн-я деф-ии наз-ся вел-на = работе внутр сил взятых с противопол знаком:
U= - Aвнут
=N2
*l/(2*E*F), U= N2
*dz/(2*E*F) Aвнут
= -Авнеш
, U=Aвнеш N2
*dz/(2*E*F) Aвнут
= -Авнеш
, U=Aвнеш
11
Эпюры продольных сил, напряжений и перемещения при растяжении, сжатии.
Разбиваем брус на уч-ки границы кот-х нах-ся в точках прилож-я сосред-х сил
0<=z1
<=a a<=z2
<= a+b
Для каждого из уч-ов опр-ем вел-ну продольной силы N (в пределах уч-ка N=const) N1
=P1
N2
= - P2
+P1
строим эпюру прод сил.
Для каждого из уч-ов опр-ем напряж-е: σi
=Ni
/Fi
Для кажд уч-ка опр-ем абсол деф-ю:
Δli
=Ni
*l/(E*Fi
) и опр-ем перемещ-я (Перемещение (δ) относится к сечению бруса- это изменение его положения в пространстве относительно какой-либо точки отсчёта. δi
-
i
=Σ(Δli
)
12
Одноосное напряженное состояние. Определение напряжений в наклонных площадках. Закон парности касательных напряжений.
Напряж-е сост-е в точке хар-ся совокупностью напряж-й возникающ-х на бесконеч-ом множестве произ-но ориентированных площадок произ-но проведённых ч/з эту точку. Напряже сост хар-тся 9 компонентами σx
σy
σz
τxy
τxz
τyx
τyz
τzx
τzy
Главные площ-ки τ=0 х-ся 3 комп-ми: σ1
>σ2
>σ3
(в алгебр смысле). Направлении┴ глав площ наз-ся глав-
ми напр-ми Деф-ии┴ глав площ наз-ся глав-ми деф-ми
Линейное или одноосное напр сост:
σ3или1
≠0,
σ2
=σ1или3
=0
Fα
=F/ cosα
1) ∑(Рi
)площадка
=0 σα
*Fα
–σ1
*F*cosα=0
σα
* F/ cosα –σ1
*F*cosα=0
σα
=σ1
*cos2
α
2) ∑(Рi
)площадка
=0 τα
*Fα
–σ1
*F*cosα=0
τα
* F/ cosα –σ1
*F*cosα=0
τα
=σ1
*cos α * sin α = 0.5* σ1
* sin 2α
τmax
|α
=45
= σ1
/2 τmin
| α
=0,
α
=90
= 0
σα
+π/2
=σ1
*cos2
(α+π/2)=
=σ1
*sin2
α т.о.
σα
+ σα
+π/2
= σ1
*cos2
α +
+ σ1
*sin2
α = σ1
т.о. сумма на 2-х взаимоперпендикуля
площ-ах = σ1
τα+
π
/2
=0.5*σ1
*sin2(α+π/2)=0.5*σ1
sin(2α+ +π)= - 0.5*σ1
sin(2α)
τα
+ τα+
π
/2
=0.5*σ1
sin(2α)- 0.5*σ1
sin(2α)=0
З-н парности кас напряж: на 2-х взаимоперпендик площ-х действуют = по вел-не и обратные по знаку касательные напр-я (τ).
τxy
= - τyx
τzy
= - τyz
τxz
= - τzx
13 Деформации продольные и поперечные. Коэффициент Пуассона.
(в –9)
14
Расчёты на прочность при растяжении/сжатии. Условия прочности.
N=f(σ)→ σi
=Ni
/Fi
<=[σ]–для пластично
σic
<=[ σс
] σi
р
<=[ σр
] –для хрупкого
15
Испытания материалов на растяжение. Диаграмма растяжения пластичного материала механические характеристики.
16
Испытания хрупких материалов на растяжение/сжатие, механические характеристики.
17
Допускаемое напряжение, коэффициент запаса прочности.
Т.к. детали и сооруж-я должны безопасно работать и при неблагоприят условиях, то напряж-я должны быть ниже тех предельных напряж-й при которых может произойти разрушения или возник-ть пластич дефор-ции. Т.о.
[σ]= σu
/n [σ]-допускаемое напяж-е
σu
- предельное напяж-е материала
n – нормативный коэф запаса прочности (коэф безопасности). Коэф запаса проч-ти вводится для того чтобы обеспечить безопасную, надёж работу сооружений и отдельных его частей. Вопрос о “n” решается с учётом имеющегося опыта эксплуатц.
18
Чистый сдвиг. Закон Гука. Модуль сдвига. Напряжения и деформации.
Чистый сдвиг – напряж сост-е если на гранях эл-та действует только τ. Площ-ки на которых действует только τ наз-ся площ-ми чист сдвига. Q≠0 (Qx
или Qy
) Q=f(τ). Практические деф-ции сдвига/среза возник-ет когда брус нагружен 2-мя равными силами действующие на малом раст-ии друг от друга ┴ оси бруса и навстречу друг другу.
Напр-я: Q=P τ = Q/F (т.к равномерно распред-ны по сечению)
Деф-ия: γ – угловая деф-я γ= tgγ ΔS (абсолют деф-я)= γ*a γ =τ/G
V0
=1
l1
=l2
=l3
=1
для ед длины:ε1
=Δl1
/l1
= Δl1
/1= Δl1
=>
V1
= (1+ ε1
)* (1+ ε2
)* (1+ ε3
)=1+ +ε1
ε2
+…+ ε1
ε2
ε3
+…+ ε1
+ ε2
+ ε3
Т.к деф-ии малы то произвед-ями ε1
ε2
+…+ ε1
ε2
ε3
ε2
+…можно пренебречь.=> V1
= 1+ ε1
+ ε2
+ ε3
υ=(V1
-V0
)/V0
=(1+ ε1
+ ε2
+ ε3
-1)/1= ε1
+ +ε2
+ ε3
ε1
= ε11
+ε12
+ε13
=1/Е*(σ1
-μ*(σ2
+σ3
))
ε2
= ε21
+ε22
+ε23
=1/Е*(σ2
-μ*(σ1
+σ3
))
ε3
= ε31
+ε32
+ε33
=1/Е*(σ3
-μ*(σ1
+σ2
))- обобщенный з-н Гука для объем н.с. υ=(1-2μ)*(σ1
+σ2
+σ3
)/E
35 Обобщённый закон Гука.
Обобщ з-н Гука – это зависимость м/д деф-ми и напяж-ми при плоском и объёмном напр сост. Предпосылки для вывода: 1)используем з-н Гука для одноосного н.с.: ε=σ/Е 2)связь м/д продольными и попереч деф-ми:
ε’= -μ*ε 3)принцып наложения (независимости действия сил)
1)Для плоского н.с.:
ε12 1-
направление деф-ии 2-
причина деф
ε11
= σ1
/Е ε22
= σ2
/Е
ε21
= -μ*ε11
= -μ* σ1
/Е ε12
= -μ*ε22
=
= -μ* σ2
/Е =>
ε1
= ε11
+ε12
= σ1
/Е - μ* σ2
/Е=
=1/E *(σ1
-μσ2
)
ε2
= ε22
+ε21
= σ2
/Е - μ* σ1
/Е=
=1/E *(σ2
-μσ1
)
2)Для объёмного н.с.:
ε1
= ε11
+ε12
+ε13
=1/Е*(σ1
-μ*(σ2
+σ3
))
ε2
= ε21
+ε22
+ε23
=1/Е*(σ2
-μ*(σ1
+σ3
))
ε3
= ε31
+ε32
+ε33
=1/Е*(σ3
-μ*(σ1
+σ2
))
(и В-34)
36 Удельная потенциальная энергия деформации, её представление в виде энергий изменения формы и объёма.
ε1
= ε11
+ε12
+ε13
=1/Е*(σ1
-μ*(σ2
+σ3
))
ε2
= ε21
+ε22
+ε23
=1/Е*(σ2
-μ*(σ1
+σ3
))
ε3
= ε31
+ε32
+ε33
=1/Е*(σ3
-μ*(σ1
+σ2
))
удельная потенц энергия ер
=U/V0
Полная энергия U=∫ер
dV(по V)
V0
=1 ер
=U/1=U= - Aвнут
= - (Aвнут 1
+
+ Aвнут 2
+ Aвнут 3
)
Aвнут 1
= - (σ1
* ε1
)/2 Aвнут 2
= - (σ2
* ε2
)/2 Aвнут 3
= - (σ3
* ε3
)/2
ер
=(σ1
* ε1
)/2+(σ2
* ε2
)/2+(σ3
* ε3
)/2
подставив ε1
ε2
ε3
получим:
ер
=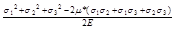
ер
= ер
формоизменения
+ ер
объёмоизменения
ер
ф
зависит от угловых деф-ий
ер
о
зависит от линейных деф-й сторон
ер
ф
=(1+μ)(σ1
2
+σ2
2
+σ3
2
-σ1
σ2
-σ1
σ3
-
-σ2
σ3
)/3Е
ер
о
=(1-2μ)*(σ1
+σ2
+σ3
)2
/6Е
37 Виды напряженных состояний в точке. Плоское напряженное состояние, определение главных напряжений.
(В-12)
1)Прямая задача для плоского н.с.:
σα
=σ1
*сosα+σ2
*sinα
τα
=((σ1
-σ2
)/2)*sinα
τmax
|α
=45
=(σ1
-σ2
)/2
2)Обратная задача для плоск н.с.
по σα
σβ
τ найти σ1
σ2
а) tg2ψ0
=2τ/(σβ
-σα
)-
положение
глав площ-ки
σ1(
max
)/3(
min
)
= (σα
-σβ
)/2±(√((σα
-σβ
)2
+4τ2
))/2 вел-на глав напр-й (+для σ1(
max
)
-для
σ3(
min
)
)
б)для кручения
с изгибом
tg2ψ0
=2τ/σ
σ1/3
=σ/2±(√(σ2
+4τ2
))/2
(+для σ1(
max
)
-для σ3(
min
)
)
38Понятия об эквивалентном напряжении и гипотезах прочности.
1)линейное н.с.(раст\сж, изгиб)
2)простое плоское н.с.(кручение, срез)
3)сложное н.с.
Гипотезы проч стремятся установить критерии проч-ти для мат-ла находящ-ся в сложном н.с. При этом слож н.с. сводится к одноосному линейному н.с. которое обознач-ся σэкв
и явл-ся равноопасным заданным плос или объёмным сост-м. σэкв
выр-ся ч/з напряж-я σ1
σ2
σ3
т.о. σэкв
=f(σ1
σ2
σ3
) и устанавливается гипотезами прочн-и
σэкв
<=[σ]- условие проч при слож н.с.
I)гипотеза наиб-х нормальных напряж
σ1/3
<=[σ] (практикой не подтверждено)
II)гипотеза наиболь линейных деф-й
ε1/3
<=[ε]=σ/E(практикой не подтвержд)
III) Гипотеза max касательн напряж-й
τmax
(для слож н.с.)<=[τ](для линей н.с.) τmax
=(σ1
-σ3
)/2 [τ]=[σ]/2
(σ1
-σ3
)/2<=[σ]/2 σ1
-σ3
<=[σ] =>
σэкв
III
= σ1
-σ3
т.к. не уч-ет σ2
то погрешность сост≈ 15% прошла пров-ку временем но исполь только для пластических мат-ов
IV)Гипотез энергии формоизменения:
Прочность мат-ла при сложном н.с. обеспеч-ся если удельная потенц энергия формоизменения (ер
ф
) не превосходит допустимой ер
ф
установленной для одноосного н.с.
ер
ф
(для слож н.с.)<=[ер
ф
](для линей н.с.
σэкв
IV
=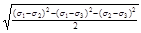 = =
=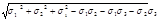 <=<= [σ] –самая применимая более всего оправдавшая себя на практике применима для пластич мат-лов <=<= [σ] –самая применимая более всего оправдавшая себя на практике применима для пластич мат-лов
Мора) σэкв М
= σ1
- ν σ3
<=[σр
] или [σсж
]
ν=[σр
] / [σсж
] подтверж практикой применимо для хрупких мат-ов
Для плоского н.с.(круч с изгибом):
σ1
=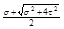 σ3
= σ3
=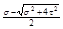
σэкв III
= σ1
- σ3
=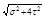 = =
=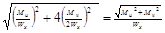 <<=[σ] <<=[σ]
σэкв
IV
=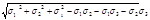 = =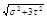 = =
=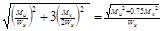
σэкв М
= σ1
- ν σ3
=1/2*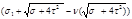 = =
=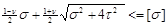 = =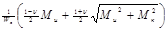
σэкв
=Мприв
/Wx
<=[σ] Wx
=0.1d3
|
ΔS= τ*a/G=Q*a/(G*F) – з-н Гука в абс вел-нах, где G- модуль сдвига (модуль упругости II рода) хар-ет способность мат-ла сопротив-ся деф-ям сдвига.
Авнеш
= -Авнут
U= -Aвнут
= P*ΔS/2=
=Q* ΔS/2= Q2
*a/(2*G*F)
19
Кручение бруса с круглым поперечным сечением. Касательные напряжения при кручении.
Δ l=0 σ =0 γ (угол сдвига)≠0
τ (кас напр)= G*γ
Кручением наз-ся вид деф-ии при кот-м в поперечном сеч-ии возникает только 1-о внутр усилие – крутящий момент (Мкр
)
Внеш скруч
мом-ы: Мскр
Мк
i
= ΣMскр
i
Крутящий момент = алгеб сумме внеш-х скруч моментов действующих по1-ну сторону от сечения. Касатель напр-я: τ = G*γ
Мкр
= f (τ)
Справедлива гипотеза Бернулли (о плоских и жест сеч-ях) Ось вала осталась прямолинейная. Геометр размеры без изм-я.
γ-угол сдвига образующей φ-угол закручивания или угол поворота попереч сечения. r- радиус γmax
=tg γmax
=NN’/dz=r dφ/dz γρ
= tg γρ
=kk’/dz= ρ dφ/dz τρ
=G*dφ/dz* ρ
dφ/dz=const G=const G* dφ/dz=const
S=0 → τ=0 S= r → τmax
При круч-ии деф-ии сдвига γ и кас напр τ пропорц-ны расстоянию от оси вала ρ. dMк
= τρ
*dF *ρ Mк
=∫dMк
(по F) = =∫ ρ *τρ
*dF = ∫ ρ2
*G (
dφ
/
dz
)
dF
=
G
* dφ/dz ∫ ρ2
dF ∫ ρ2
dF=Jp
- полярный момент инерции поперечного сечения.
dφ/dz=Мк
/(G*Jp
)
τρ
= G* ρ* Мк
/(G*Jp
)= Мк
* S/Jp
Jp
(для круга)=0.1*d4
Jp
(пусто-ого вала)=0.1*D4
*(1-c4
) c=d/D
τmax
=Мк
*r /Jp
= Mк
/Wp
<=[τ] –усл проч-и
Wp
=Jp
/r Wp
– полярный момент сопротивления = отнош-ю поляр моменту инер-ии к расст до наиболее удалённых волокон вала (r)
Wp
(круг)= 0.2*d3
Wp
(пустотел вал)= 0.2*D3
*(1-c3
) c=d/D
dφ =Мк
* dz /(G*Jp
) проинтегрируем обе части (правую от0доφ, лев от0доL)
Мк
/(G*Jp
)=const φ= Мк
*l/(G*Jp
) – з-н Гука
Перемещ сеченя: δφ=∑φi
Условие жесткости: δφmax
<=[φ]
Относит угол закр-я: θ=φ/l= Мк
/(G*Jp
)
Услов жесткости: θ <= [θ]
20
Полярный момент инерции, полярный момент сопротивления круглого сечения. Угол закручивания при кручении. (
в-19)
21
Потенциальная энергия деформации при кручении. Условия прочности и жесткости при кручении круглого бруса.
Aвнеш
=Мскр1
*φ1
/2 dАвнут
= - Мк
*φ/2
U= -Авнут
=∫ Мк
2
* dz /(2*G*Jp
(от0 доL) U=Мк
2
* l/(2*G*Jp
)
Перемещ сеченя: δφ=∑φi
Условие жесткости: δφmax
<=[φ]
Относит угол закр-я: θ=φ/l= Мк
/(G*Jp
)
Услов жесткости: θ <= [θ]
τmax
=Мк
*r /Jp
= Mк
/Wp
<=[τ] –усл проч-и
22
Испытание материалов на кручение. Диаграмма кручения пластичного материала, механические характеристики при кручении.
23
Расчёт на прочность заклёпочного и болтового соединений.
d-диаметр отверстия dзак
-диам заклёпк d≈dзак
+(0.5-1)мм
1)Р-равномер распред-но м/д заклёп (болтами) Q1-й зак
=P/n n-число заклёпок
2)По плоскости среза τ распед равном
τ=Q/F
условие проч-ти: τ=Q/F=4P/(nπd2
)<=[τcp
] [τcp
]≈0.8[σ]
n>=4P/(πd2
[τcp
]) n-числ зек из расчёта на прочность.
Расчёт на смятие:
Fсмят
=d*δmin
δmin
-min толщина места. σсмят
=Q/Fсмят
=P/(n’dδmin
)<=[σc
м
]<=2*[σ]
n’-число зак из расчёта на смятие
n’>=P/([σc
м
]*d* δmin
) из n и n’выбир >
24
Расчёт на прочность сварных швов.
Для соед-я встык – расчёт на обычное растяж\сжат: σ=P/Fшва
<=[σ]
Соед-е внахлёст:
Шов хар-ся катетом: АВ=ВС=δ=катет
На биссектрису дейст-ет τмах
. Ширина опасного сечения = 0.7*катет
Площади опасного сечения швов:
Fлоб
=b∑
*0.7*кат-т Fфронт
=l∑
*0.7*кат-т
Допустимая нагрузка:
(l∑
+b∑
)*0.7*кат-т*[τ]>=P
25
Расчёт цилиндрических винтовых пружин малого шага.
α<=10-12град
D-сред диамет
пружины
d-диам проволок
h-шаг
с=D/d-индекс пруж
с=4-12
n-число раб витков
nпол
=n+1.5-2.5
λ-удлинение/осадка
в сечении 2 внутренних усилия:
Q-поперечная сила, Мк
-крутящ момен
Q=P Mк
=P*D/2
Mк
: τmax
=Мк
/Wp
=P*D/2*Wp
Wp
=π*d3
/16 τmax
=8PD/πd3
Q: τ=Q/F=4P/ πd2
Условия проч в опасной точке: τmax
= τmax(
Мк
)
+ τmax(Q)
= 8PD/πd3
+4P/ πd2
= =(8PD+4Pd)/ πd3
= =8PD/πd3
*(1+d/2D)<=[τ]
Если d/2D<=1/6, то τmax
=8PD/πd3
<=[τ]
d>=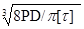 λ=8PD3
n/Gd4 λ=8PD3
n/Gd4
хар-ка пруж-ы график P=f(λ)
k-жёсткост k=P/ λ [H/мм]
26
Изгиб чистый, поперечный. Внутренние силовые факторы при изгибе, построение их эпюр.
Изгибом наз-ся деф-я сопровождающ изменением кривизны оси стержня.
Стержни раб-щие в основном на изгиб наз-ся балками
Виды изгиба по внутр-м усилиям:
dпроч
=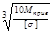
39 Гипотеза
max
касательных напряжений (
III
гипотеза прочности)
(В-38)
40Гипотеза энергии формоизменения (
IV
гипотеза прочности)
(в-38)
41 Критерий Мора.
(в-38)
42 Расчёт на прочность круглого бруса при одновременном действии изгиба и кручения.
(в-38)
1)строим эпюры
Мк1
=0 Мк2
=М
Ми1,2
=Р*z1,2
|0
=0|L
=P*l
2)опасные сечения:
Мк2
=М Ми2
=P*l
3)исследу-ые напр-я:
τmax
(Ми
)=Мк
/Wp
σmax
(Mи
)=Ми
/Wx
τmax
(Q)=Q*Sx
/(b*Jx
)
4)опасная точ на
поверхности вала:
σ=Ми
/Wx
τmax
=Мк
/Wp
= Мк
/2Wх
Wp
=Jp
/r=2*Jx
/r Wx
= Jx
/r= Wp
/2
Jp
=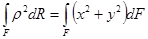
|