Санкт-Петербургский
Государственный
Технический
Университет
Гуманитарный
факультет
Кафедра
социологии
и права
РЕФЕРАТ
На тему :
Методы
алгебраических
и дифференциальных
уравнений
для анализа
и качественного
исследования
социально-экономических
явлений.
По дисциплине:
Математические
методы моделирования
процессов
управления
в социальной
сфере
Выполнил
:
Студент
Кириллова
Н.В.
Группы
5121/1
Проверил:
Руководители
Романов
М.Ф.
Максимов
Ю.Д.
Санкт-Петербург
2000 г.
ВВЕДЕНИЕ
Рынок представляет
собой систему
саморегулирования
экономики по
таким параметрам,
как величина
покупательного
спроса, качество
продукции,
общественно
необходимые
затраты труда,
объем производства
товаров и услуг.
Механизм
саморегулирования
включает в себя
свободные
рыночные цены,
экономическую
конкуренцию
между производителями,
свободный выбор
деловых партнеров.
Регулирование
рынка со стороны
центра осуществляется
с помощью
экономических
рычагов - таких,
как налоговая,
финансовая
и кредитная
политика, цены
на отдельные
группы товаров,
система дотаций
и социальной
защиты человека.
В процессе
регулирования
рынка должны
учитываться
экономические
интересы как
производителей,
так и потребителей.
Естественно,
что для описания
некоторых
элементов
рыночного
механизма
используются
простейшие
математические
модели. Такие
модели отображают
только самые
общие свойства
экономических
систем. В данной
работе приводится
способ исследования
социально-экономических
явлений путем
составления
алгебраических
и дифференциальных
уравнений.
1. Простейшая
модель изменения
зарплаты и
занятости
Характерная
черта рыночной
системы хозяйства
- наличие рынка
труда, на котором
взаимодействуют
работодатели
и наемные рабочие.
Пусть все участники
рынка труда
располагают
на этом рынке
одинаковой
информацией
в одинаковом
объеме и принимают
на основе этой
информации
наилучшие,
оптимальные
для себя решения.
Взаимодействие
спроса и предложения
на этом цивилизованном
рынке приводит
к равновесию,
при котором
за плату' p
> 0 согласны
работать N
> 0 человек.
Если по каким-то
причинам это
равновесие
со временем
нарушается
(например, часть
работников
уходит на пенсию
по возрасту,
либо у работодателя
возникают
финансовые
трудности), то
функции P(t)
и N(t)
отклоняются
от р ,N
.
Функции
P(t)
и N(t)
рассматриваются
как непрерывные
и достаточно
гладкие. Эти
условия принимаются
исключительно
из соображений,
связанных с
математическими
действиями,
основывающимися
на свойствах
достаточно
гладких решений.
Будем
считать, что
число работников
увеличивается
или уменьшается
пропорционально
росту или уменьшению
зарплаты относительно
значения p
.
Тогда
(1)
Предположим,
что работодатели
изменяют зарплату
также пропорционально
отклонению
численности
занятых от
равновесного
значения n
,т. е.
(2)
Дифференцируя
равенство (1)
по t,
получим d
N/dt2
= a
dP/dl.
Из этого равенства
в силу (2) следует
d
N/dt
-= -a
a
(N
- n
), откуда
(3)
Общее решение
уравнения (3),
имеет вид
(4)
где
C
и С - произвольные
постоянные.
Из (1) в силу
(4) получаем
(5)
Умножим
уравнения (4),
(5) соответственно
на и , возведем
затем в квадрат
левые и правые
части получившихся
равенств. После
сложения левых
и правых частей
будем иметь
(P-P
)2+
(N-No)
2=const>0.
(6)
Рассматривая
значения переменных
N,
Р как координаты
точки на плоскости,
можно геометрически
представить
состояние рынка
посредством
точки M(N,P).
Эту точку в
теории дифференциальных
уравнений
называют фазовой
точкой, а
плоскость ONP,
на которой
интерпретируется
решение (6), - фазовой
плоскостью.
Решение (3), (4)
представляет
собой некоторый
закон движения
точки M(N,P)
на фазовой
плоскости.
Из
графика кривой
(6) видно (рис. 1),
что при различных
значениях const
мы будем получать
различные
эллипсы с центром
в точке (n
, P
), отвечающие
соответствующим
начальным
условиям N
и Р.
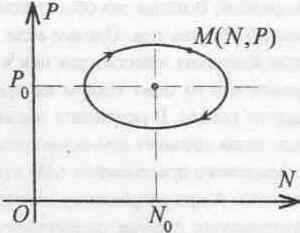
Рис 1.
Соотношение
между зарплатой
(Р) и числом
работников
(N)
при нарушении
равновесия.
Точка
M(N,P),
находящаяся
на эллипсе,
опишет за конечное
время замкнутую
кривую и за
время t=2
/ возвратится
в свое начальное
положение,
возобновив
то же самое
движение.
Следовательно,
имеется периодичность
с периодом 2
/ .
Из
уравнения (6)
видно (см. также
рис. 1), что в некоторые
моменты времени
t,
когда N = N
(т. е. когда число
занятых становится
равным равновесному
значению), имеем
Р>Р ,
т.е. зарплата
превышает
равновесную,
а при Р
= p получаем
N > n
, т. е.
число занятых
больше равновесного.
В эти моменты
фонд заработной
платы, равный
PN,
превышает
равновесное
значение PoNo
или меньше
его). Но в среднем
за период колебаний
величина PN
, равна PoNo
.
Замечание.
Построенная
модель основана
на правдоподобных
представлениях
о характере
взаимодействия
работодателя
и наемных рабочих.
2. Равновесие
в краткосрочном
периоде, в условиях
совершенной
конкуренции
Любой участник
рыночного
экономического
процесса действует
в соответствии
со своими
индивидуальными
интересами
(извлечение
прибыли, улучшение
условий труда,
минимизация
риска, экономия
ресурсов и т.
д.). Миллионы
потребителей
принимают
самостоятельные
решения, какие
товары и в каком
количестве
покупать, а
огромное число
предпринимателей
самостоятельно
решают, что и
как производить.
Координацию
всех независимо
принимаемых
решений осуществляет
рыночный механизм,
важную роль
в котором играет
конкуренция.
Она сдерживает
частные интересы,
направляет
их на производство
общественно
необходимых
товаров. Конкуренция
непременно
приводит к
тому, что ограниченные
ресурсы используются
более полно
и эффективно.
Они устремляются
в те отрасли,
которые производят
необходимую
для потребителя
и рентабельную
для товаропроизводителя
продукцию.
Одной из
главных целей
экономики как
науки является
исследование
того, как взаимодействие
спроса и предложения
приводит к
равновесию
на конкурентном
рынке в условиях,
когда индивидуальные
решения участников
рынка мотивируются
собственным
частным интересом
и вовсе не направлены
на достижение
равновесия
между производством
и потреблением.
В этой главе
исследуется
простейший
вариант рыночной
экономики,
введя понятие
«совершенный
конкурентный
рынок», т. е. рынок,
каждый субъект
которого экономически
ничтожно мал
и не оказывает
непосредственного
влияния на
уровень производства,
цены, зарплату,
и все участники
рыночного
процесса, располагая
одинаковой
информацией,
принимают на
ее основе наилучшие,
оптимальные
для себя решения.
Теория совершенного
конкурентного
рынка может
служить основой
для выявления
закономерностей,
внутренне
присущих другим
рыночным структурам.
Картину
совершенного
конкурентного
рынка можно
сравнить с
идеальной
механической
системой, в
которой совершенно
не учтено трение
между ее деталями
и элементами.
И совершенный
конкурентный
рынок, и упомянутая
идеальная
механическая
система позволяют
определять
главные особенности
изучаемых
явлений, однако
на практике
необходимо
учитывать и
трение в механической
конструкции,
и многие факторы,
действующие
на конкретном
реальном конкурентном
рынке.
При рассмотрении
совершенного
конкурентного
рынка будем
исходить из
того, что разобщенные
действия участников
рыночного
экономического
процесса могут
складываться
через существующую
систему отношений
купли-продажи
в совокупную
согласованную
картину действий
работодателей
и наемных рабочих,
финансистов
и вкладчиков
и т. д. Если в
результате
такого коллективного
взаимодействия
общее производство
товаров и услуг
согласовано
с общим спросом
на них, то такое
состояние
экономики
называется
равновесным,
а устанавливающиеся
при этом цены
- равновесными
рыночными
ценами. Баланс
между спросом
и предложением
имеет место,
не при произвольных,
а именно при
рыночных ценах,
что означает,
в частности,
платежеспособность
спроса.
Наиболее
простые математические
модели экономического
равновесия
в условиях
совершенной
конкуренции
строятся при
следующих
предположениях:
I.
Объемы производства
отдельных
товаропроизводителей
столь незначительны
в сравнении
с выпуском всей
отрасли и изменяются
в таких пределах,
что это не оказывает
никакого влияния
на цену продаваемого
товара.
II.
Производственные
возможности
отрасли, где
функционирует
фирма-товаропроизводитель,
неизменны.
III.
Неизменны во
времени экономические
интересы партнеров:
предприниматели
не пытаются
увеличить свою
прибыль, рабочие
- зарплату,
инвесторов
устраивают
проценты, получаемые
по ценным бумагам,
и т. д.
Отвечающие
таким предположениям
модели описывают
равновесное
состояние
идеальной
рыночной экономики
в краткосрочном
периоде. Этот
весьма частный
случай «застывшей»
во времени
экономики дает
ответ на вопрос
о возможности
существования
экономического
равновесия,
формирующегося
из рыночного
«хаоса», и, кроме
того, связывает
между собой
основные
макропоказатели
экономической
системы.
Рассмотрим
одну из таких
макромоделей
- модель Кейнса.
В этой модели
краеугольным
камнем является
положение о
том, что рыночная
экономика
защищена от
спада, что существуют
определенные
механизмы
саморегулирования,
постоянно
приводящие
объем выпускаемой
продукции к
уровню, соответствующему
полной занятости.
Если под влиянием
каких-то факторов
внешнего
происхождения
(война, неурожай
и т. п.) произойдет
спад производства,
это не будет
длиться долго.
Цены, заработная
плата и процентная
ставка являются
гибкими, и они
вернут экономику
в равновесное
состояние,
когда рабочая
сила будет
полностью
нанята, и все,
что произведено,
- продано. Конкуренция
уравняет спрос
и предложение
на всех рынках.
В этом случае
нет необходимости
государственного
вмешательства
в экономику.
В кейнсианской
модели все
участники
рыночного
экономического
процесса действуют
на рынках рабочей
силы, продуктов
и денег, где
эти товары
(труд, продукты,
деньги) распределяются
и обмениваются
между субъектами
рыночной экономики.
Первый
макропоказатель
экономической
системы - национальный
доход Q,
является
единственным
(для простоты)
продуктом,
производимым
этой системой
в единицу времени.
Этот продукт
вырабатывается
производственным
сектором экономики,
а его величина
дается функцией
F,
зависящей от
количества
и качества
ресурсов, состава
основных фондов
и числа занятых
работников
R
(второй макропоказатель).
В соответствии
с предположением
II в состоянии
равновесия
производственная
функция F,
а с нею и
продукт Q
определяются
лишь занятостью
работников,
т. е.
Q=F{R).
(1)
Относительно
F(R)
обычно считается,
что F(0}=О,
F'(R)>О
при R>0
и F"(R)<О
при R>0
(рис. .2). Функция
F(R)
обладает свойством
«насыщения»:
с ростом R
выпуск растет
все медленнее.
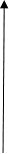
Q Q=F(R)
Р ис
2. Соотношение
между ис
2. Соотношение
между
рынками
труда (R)
и продукта(Q)
O R
R
Такой подход
вполне оправдан,
поскольку при
излишне большом
числе занятых
на производстве
для них попросту
не найдется
соответствующего
фронта работ.
Соотношение,
дополнительное
к соотношению
(1), определяется
с помощью одного
из основных
постулатов
классической
политэкономии:
IV.
Заработная
плата s
работника равна
стоимости
продукта, которая
была бы потеряна
при уменьшении
занятости на
одну единицу.
В этом постулате
не учитываются
(считаются
малыми) другие
издержки, которые
отпали бы в
результате
сокращения
одного рабочего
места (затраты
на ресурсы,
оборудование
и т д.). В рассматриваемой
модели заработная
плата считается
заданной. Она
определяется
в результате
компромисса
между работодателями
и нанимаемыми
(реальная же
зарплата зависит
также от уровня
цен).
Таким
образом, из
постулата IV
получаем
(2)
где
.Q(1)
- количество
продукта, потерянное
при уменьшении
занятости на
одну единицу,
Р - цена
продукта (так
что слева в
равенстве (2)
записана величина
потерянной
стоимости).
Если занятость
изменилась
на величину
R,
то из равенства
(2), очевидно, имеем
P=s
R,
(3)
где
Q
= Q
R
- стоимость,
потерянная
или полученная
при изменении
числа работников
на R. Из равенства
(3) следует
(4)
Считая
R
и Q
малыми в сравнении
с R и Q,
перепишем
равенство (4) в
дифференциальной
форме:
(5)
Из (5), принимая
во внимание
(1), получим
F'(R)=s/P.
(6)
Поскольку
F(R)
задана (а с нею
и производная
F'(R)),
то при известных
макропоказателях
s
и Р из
(6) можно найти
уровень занятости
R, а из
(1) - и величину
продукта Q.
Этот уровень
отвечает числу
работников,
согласных
трудиться за
данную зарплату
при данных
ценах и других
характеристиках
системы, а не
вообще возможному
числу наемных
рабочих. Предполагается,
что для обеспечения
равновесного
уровня занятости
всегда найдется
достаточное
количество
желающих работать
на существующих
условиях, т.
е.:
V.
Предложение
труда не сдерживает
производство,
число занятых
определяется
спросом на труд
со стороны
предпринимателей.
Два уравнения
(1) и (6) содержат
четыре величины.
Для построения
замкнутой
модели необходимо
дальнейшее
рассмотрение
рынка продуктов
и рынка финансов.
Произведенный
на рынке продукт
частично тратится
на потребление,
а частично
сберегается:
Q=S+,
(7)
где
S -
фондообразующий
продукт, т. е.
сберегаемая
часть произведенного
продукта,
возвращаемая
в экономическую
систему, а
- потребляемая
часть продукта,
которая в экономику
не возвращается.

Рис.
3. Соотношение
между потребляемой
частью прдукта
( )
и всем
производимым
продуктом
(Q).
Соотношение
между величинами
S
и
определяется
из следующих
соображений.
Относительно
величины
считается,
что:
VI.
Потребляемая
часть выпуска
зависит от
величины самого
выпуска, т. е.
=(Q).
При этом функция
(Q)
обладает свойством
«насыщения»
так же, как и
функция F(R):
чем больше
выпуск, тем
меньшая доля
дополнительного
выпуска Q
тратится на
потребление
(рис. 3) и тем большая
доля сберегается.
Величина d/dQ=c(Q)
называется
склонностью
к потреблению
и лежит в пределах
0 < с < 1. иначе при
малых выпусках
потреблялось
бы больше продукта,
чем производилось
бы (величина
d
= 1 - с - склонность
к накоплению).
Рис.
4. Зависимость
спроса на инвестиции
(А) от нормы
банковского
процента (r).
Фондообразующий
продукт
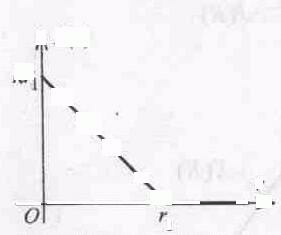
s
= q -
(Q)
(8)
вкладывается
инвесторами
в экономику
с целью
получить в
будущем от
этих инвестиций
доход. В модели
считается, что
инвестиции
эквивалентны
отложенному
(отнесенному
на будущее)
потреблению
и потому определяются
еще одним финансовым
макропоказателем
системы - нормой
банковского
процента r.
Действительно,
cделав
инвестиции
в размере (А)
и получив через
год доход D
= Аr,
инвестор ничего
не теряет (в
данном примере
и не выигрывает)
по сравнению
с вложением
этих средств
в банк под процент
r. В обоих
случаях сегодняшнее
потребление
откладывается
ради возможности
большего потребления
в следующем
году. Спрос на
инвестиции
задается функцией
А(r)
такой, что А'(r)<0
при Q<r<r
и А(r)=0
при r>r
: при большой
норме процента
инвестиции
отсутствуют
(рис. 4).
В условиях
равновесия
предложение
фондообразующего
продукта S(Q)
сбалансировано
со спросом на
инвестиции
А(r),
следовательно,
S(Q)
= A(r).
Из этого равенства
и равенства
(8) следует
Q
- (Q)=A(r).
(9)
Для
окончательного
замыкания
математической
модели рыночного
равновесия
с совершенной
конкуренцией
рассматривается
рынок финансов.
Чтобы произвести
покупки товара
Q (как
фондообразующего,
вкладываемого
в экономику,
так и идущего
на потребление),
нужны деньги.
Относительно
спроса на деньги
делается следующее
предположение:
VII.
Спрос на деньги
представляет
собой сумму
операционного
спроса и спроса
спекулятивного.
Р    ис
5. Зависимость
спекулятивного
спроса (I)
от ис
5. Зависимость
спекулятивного
спроса (I)
от
нормы
процента (r)
Операционный
спрос определяется
количеством
денег, которое
нужно иметь
на руках, чтобы
производить
покупки товара
Q (как
фондообразующего,
так и идущего
на потребление).
Если цена продукта
равна Р,
а время обращения
равно ,
то операционный
спрос равен
величине PQ
Спекулятивный
спрос связан
с величиной
нормы процента
r.
Если норма
процента высока,
то большую
часть денег
их владельцы
предпочитают
хранить в банке,
рассчитывая
на хороший
доход и жертвуя
более высокой
степенью ликвидности
банкнот
(способностью
обмениваться
на продукты)
в сравнении
с банковскими
обязательствами.
При низкой
процентной
ставке спекулятивный
спрос увеличивается:
владельцы
желают иметь
на руках все
больше банкнот,
аккумулируя
в них свои
накопления.
Поэтому спекулятивный
спрос задается
функцией I(r)
(рис. 5), такой, что
I'(r)<O
при г>r
и I(r)
резко возрастает
при r
– r
(I(r)
- при r
– r ; владельцы
денег не приобретают
обязательств
банка). Естественно
считать, что
r <
r,
так как в противном
случае либо
инвестиции
равны нулю, и
говорить об
экономическом-
равновесии
не приходится,
либо функция
I(r)
не определена,
и рассмотрение
не имеет смысла.
Так
как финансовый
рынок находится
в равновесии,
то баланс («закон
сохранения»)
денег дастся
уравнением
'
Z=tPQ+I(r),…………………………………(10)
Где
Z
– количество
денег, являющееся
заданным управляющим
параметром
системы (считается,
что деньги
выпускает
государство).
Из
соединения
в одно уравнений
(1), (6), (9) и (10), возникает
математическая
модель рыночного
равновесия,
полученная
в предположениях
I-VII:
Q
= F(R),
F’(R) = s/P,
Q-
(Q) = A(r), (11)
Z
= PQ
+ I(r).
Р ис.6.
Зависимость
фондообразующего
продукта (S)
от числа занятых
рабочих (R) ис.6.
Зависимость
фондообразующего
продукта (S)
от числа занятых
рабочих (R)
В  модели-(11) задаются
параметры
системы s
(ставка заработной
платы), Z
предложение
денег) и технический
параметр τ
модели-(11) задаются
параметры
системы s
(ставка заработной
платы), Z
предложение
денег) и технический
параметр τ

Функции
F,
F',
ω, А, I -
известные
функции
своих
аргументов
с описанными
выше 
.
 свойствами.
По этим входным
данным из модели
определяются
четыре неизвестные
величины: Q
(величина
выпускаемого
продукта), R
(уровень занятости
), Р (цена
продукта) и r
(норма банковского
процента). свойствами.
По этим входным
данным из модели
определяются
четыре неизвестные
величины: Q
(величина
выпускаемого
продукта), R
(уровень занятости
), Р (цена
продукта) и r
(норма банковского
процента).
Исключая
из (11) величины
Р, r,
Q,
систему уравнений
(11) легко свести
к одному уравнению
(12)
где
А 1 -
функция, обратная
функции А.
Из свойств
строго возрастающей
функции А=
F(R)-ω(F(R))
(рис. 6) легко
установить
качественный
вид функции
А 1 (в
зависимости
от R):
функция А
1
строго убывает
с ростом R.
В свою очередь,
А служит
аргументом
монотонной
функции I:
(13)
Свойства
функции (13) таковы,
что как функция
R она
имеет вид кривой
J{R),
изображенной
на рис. 7 (для
значений R
> R
функция
I
не определена),
где R
- корень уравнения
(14)
Рассмотрим
теперь левую
часть уравнения
(12). Функция
Z-sτF(R)/F'(R)
(15)
равна
Z при R
= 0, т.к. F'(R)
> 0. Первая производная
функции (15)
(16)
в силу
условия F"(R)<
0 (см. рис. 2).
Из (17) тогда следует,
что функция
(15) строго убывает
на промежутке
[О, R
]. Введя
обозначения
(17)
(18)
запишем
уравнение (12)
в виде
J(R)=X(R).
(19)
В силу
отмеченных
выше свойств
функций (17) и (18),
входящих в
левую и правую
части уравнения
(19), графики функций
J(R)
и X(R)
имеют вид кривых,
изображенных
на рис. 7.
Рис.
7. Определение
равновесного
состояния R
в условиях
совершенной
конкуренции.
Следовательно,
модель Кейнса
(11) имеет единственное
решение описывающее
равновесное
состояние
экономики.
Пример.
Используя
равенства (11),
найти уровень
занятости R,
величину
производимого
продукта Q,
цену продукта
Р и норму
прибыли r
для обеспечения
равновесия
на конкурентном
рынке, если
(20)
Приведенные
в формулах (20)
функции удовлетворяют
требуемым
условиям и
выбраны произвольно
из методических
соображении.
Предполагая
заданными
параметры
системы s'=
10, τ=50, Z=100,
произвести
вычисления,
воспользовавшись
программой
1 при следующих
значениях
параметров
функции F,
ω, А, I:
а=10, b=5,
c=0.5,
m=8,
k=2,
r
=5, r
==3, n=1.
В условиях
примера функции
J(R)
и X(R),
определяемые
по формулам
(17) и (18), принимают
вид:
(21)
Графики
функций (21) при
заданных в
примере значениях
параметров
представлены
на рис.8.
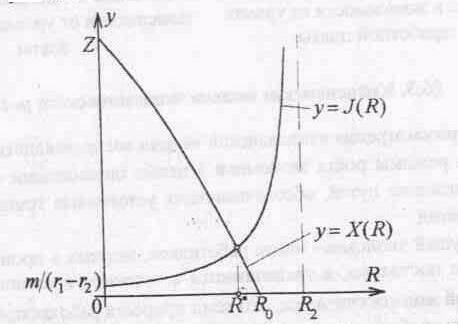
Рис. 8. Графики
функций, определяемых
формулами (21)
Чтобы
найти равновесное
значение R*,
найдем сначала
положительный
корень R
уравнения
соответствующий
вертикальной
асимптоте
функции J(R)
(см. рис. 8), по формуле
или методом
половинного
деления, применяя
программу 2.
Получим
R
=0158.
Равновесное
значение уровня
занятости R
, равное
0.107, находим после
этого в интервале
(0;R
), решая
уравнение
J{R)=X(R),
например,
методом
половинного
деления. Зная
равновесное
значение R
= R , из
системы уравнений
(11) и формул (20) находим
равновесные
значения остальных
трех неизвестных
величин:
(23)
- равновесное
значение выпуска
продукции,
-
равновесное
значение цены
продукта,
- равновесное
значение нормы
прибыли.
Замечание.
В этом анализе
рассматривались
трудовые отношения
в условиях
совершенной
конкуренции,
когда на рынке
труда взаимодействует
неограниченное
количество
работодателей
и не объединенных
в профсоюзы
наемных рабочих,
равновесная
ставка заработной
платы и количество
занятых устанавливаются
под воздействием
спроса и предложения
труда. Предположим,
что в данной
отрасли формируется
профсоюз, надо
определить
специфику его
влияния на
рынок труда.
Как правило,
профсоюз всеми
доступными
средствами
добивается
установления
ставки заработной
платы выше
равновесной.
Допустим, что
профсоюз добился
увеличения
ставки заработной
платы. Как на
такие действия
профсоюза
отреагирует
совершенный
конкурентный
рынок?
Вполне
очевидно, что
предприниматели
сократят спрос
на труд, поскольку
для них выплачиваемая
рабочим заработная
плата является
издержками,
а так как ставка
заработной
платы возросла,
то предприниматели
не могут оставить
число занятых
неизменным.
Модель (11) может
быть использована
для сравнительного
анализа состояния
равновесия
при изменении
величин параметров
s,
τ, Z.
Покажем
на примере
модели (20), рассмотренной
выше, к чему
приведет увеличение
в данной отрасли
заработной
платы вдвое
(с s=10
до s=20):
уровень
занятости
уменьшится
на 36% с R
=0.107 до R
=0.068,
выпуск
продукции
уменьшится
на 27% с Q
= 3.49 до Q
= 2.54,
цена
продукта увеличится
на 52% с Р
=0.472 до Р
=0.719,
значение
нормы прибыли
увеличится
на 13% с r* = 3.45 до r*
= 3.91. Как видим,
увеличение
заработной
платы неминуемо
приводит к
тому, что какая-то
часть рабочих
должна покинуть
отрасль. Аналогичный
по своему воздействию
эффект на рынок
труда производит
законодательно
устанавливаемый
минимум заработной
платы. В западной
экономической
литературе
длительное
время дискутируется
вопрос об
эффективности
законодательства
о минимуме
заработной
платы. В США,
например, минимум
заработной
платы установлен
в размере 40-50% от
среднего уровня
заработной
платы в обрабатывающий
промышленности.
В настоящее
время минимум
заработной
платы в США
составляет
4.75 долл. в час. На
основе многочисленных
исследований
подсчитано,
что повышение
минимума заработной
платы на 10% приводит
к сокращению
занятости
молодежи в
возрасте 16-19 лет
на 1—3%, а среди
лиц наемного
труда в возрасте
от 20 до 24 лет безработица
увеличивается
на 1%. Общепризнанным
считается, что
фиксированный
минимум заработной
платы оказывает
неблагоприятное
воздействие
на занятость,
особенно
низкооплачиваемых
категорий
трудящихся.
Будем
изменять в
модели (20), рассмотренной
в приведенном
выше примере,
величину заработной
платы s.
На рис. .9-12 показано,
как с изменением
s в условиях
совершенной
конкуренции
будут изменяться
R*
,Q*,
P*
и r*.
Из
приведенных
графиков следует,
что с увеличением
заработной
платы в условиях
равновесного
состояния
экономики
наблюдается
уменьшение
уровня занятости
R*
и величины
производимого
продукта Q*.
При этом цена
продукта Р*
и величина
банковского
процента r*
растут.

-
|
Рис.9.
График равновесного
значения R*
в зависимости
от величины
заработной
платы s
|
Рис.
10. График равновесного
значения Q*
величины
производимого
продукта в
зависимости
от уровня
заработной
платы
|
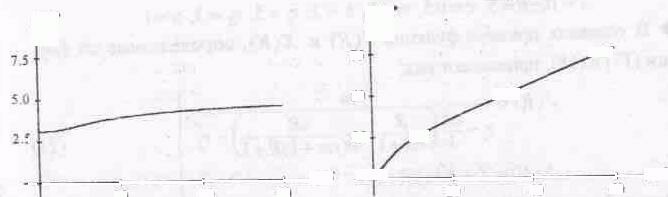
Рис..12.
График равновесного
значения
Р*
цены продукта
в зависимости
от уровня заработной
платы.
Рис.
11. График равновесного
значения
r*
величины банковского
процента
в зависимости
от уровня
заработной
платы
|