Реферат: Расчет стержневых систем и бруса на растяжение, Расчет нагруженной балки, Экзаменационные вопросы по прикладной механике

Название: Расчет стержневых систем и бруса на растяжение, Расчет нагруженной балки, Экзаменационные вопросы по прикладной механике
Раздел: Рефераты по технологии
Тип: реферат

комитет по высшему образованию Российской Федерации

Московская Государственная Академия Тонкой Химической Технологии

им. М.В. Ломоносова

кафедра :

“Прикладная механика и основы конструирования.”

Расчетно-графическая работа № 1 :

“Расчет стержневых систем и бруса на растяжение”

Вариант №: 24

студент: Холин Андрей Юрьевич (группа Е-203)

преподаватель: Грусков Александр Дмитриевич

1998г.

Задание № 1.

1.1 Для заданной стержневой системы определить внутренние усилия в стержнях, поддерживающих абсолютно жесткую балку, нагружаемую внешними силами. Стержни соединяются со стеной, с балкой, между собой посредством шарниров.

1.2 Для рассматриваемой стержневой системы определить по условию прочности диаметр круглых стержней, приняв [s] = 160 н/мм².

Дано: a = l, b = 3l, P = 32 кН.

l = 1,2 м

Определить: N - ?, A_y - ?, A_z - ?

Решение:

1.1

Уравнения равновесия балки: S(P_y) = 0, S(P_z) = 0, S(m_z) = 0

(1). A_y + P – 3P + N • sin 60° = 0

(2). A_z + N • cos 60° = 0

уравнение моментов относительно точки A:

(3). P • a – 3P • (a+b) + N • sin 60° • (a+b) = 0

Из уравнений (1), (2) находим: A_y = 2P – N • sin 60°, A_z = – N • cos 60°

Выражая силу N из уравнения моментов (3), получим:

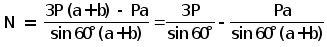
N = 3 • 32 / sin 60° – 32 • 1,2 / (sin 60° • (1,2 + 1,2 • 3)) = 101,61 (кН).

A_y = 2 • 32 – 101,61 • sin 60° = –24 (кН).

A_z = – 101,61 • cos 60° = –50,81

Для проверки посчитаем сумму моментов относительно точки B:

A_y•(a+b) + P•b = 0, –24• (1,2 + 1,2 • 3) + 32•1,2 • 3 = –115,2 + 115,2 = 0.

Обращение левой части уравнения в нуль показывает правильность искомых величин.

1.2

[s] = 160 н/мм², F (мм²), F = N/s, F = pr² = pd²/4,

k - коэффициент запаса прочности. Если принять k = 2, то :

Задание № 2.

2.1 Для ступенчатого бруса определить внутренние усилия и построить эпюру поперечных сил N.

2.2 Используя эпюру N и размеры ступенчатого бруса определить и построить эпюры нормальных напряжений s и перемещений U, считая брус стальным. E = 2•10⁵ н/мм². Проверить прочность бруса в опасном сечении приняв [s] = 160 н/мм².

N_AB = P = 32 кН;

N_BC = P–2P = –P = –32 кН;

N_CD = P–2P–3P = –4P = –128 кН;

N_DE = P–2P–3P+P = –3P = –96 кН

F₁ = pd²/4 = p•20²/4 = 100p » 314,2 (мм²).

F₂ = p(1,4•d)²/4 = p•(1,4•20)²/4 = 196p »

» 615,8 (мм²).

s_AB = N_AB / F₁ = 32000 / 100p »

» 101,9 (н/мм²).

s_BС = N_BС / F₂ = –32000 / 196p »

» –52 (н/мм²).

s_СD = N_СD / F₂ = –128000 / 196p »

»–207,9 (н/мм²).

s_DE = N_DE / F₂ = –96000 / 196p »

» –155,9 (н/мм²).

E = 2•10⁵(н/мм²).

U_E = 0.

U_D = c • s_DE / E = 2l • s_DE / E » –155,9 • 2 • 1,2 • 10³ / (2 • 10⁵) = –1,87 (мм).

U_C = U_D + b • s_CD / E » –1,87 – 207,9 • 3 • 1,2 • 10³ / (2 • 10⁵) = –5,61 (мм).

U_B = U_C + a • s_BC / E » –5,61 – 52 • 1,2 5 10³ / (2 • 10⁵) = –5,93 (мм).

U_A = U_B + a • s_AB / E » –5,93 + 101,9 • 1,2 • 10³ / (2 • 10⁵) = –5,31 (мм).

Проверка прочности бруса в опасном сечении (при ЅsЅ = ЅsЅ_max):

На участке CD ЅsЅ имеет максимальное значение.

Условие прочности s Ј [s] не выполняется: Ѕ–207,9Ѕ> 160.

комитет по высшему образованию Российской Федерации

Московская Государственная Академия

Тонкой Химической Технологии

им. М.В. Ломоносова

кафедра :

“Прикладная механика и основы конструирования.”

Расчетно-графическая работа № 2 :

“Расчет нагруженной балки”

Вариант №: 24

студент: Холин Андрей Юрьевич (группа Е-203)

преподаватель: Сергеев Александр Иванович

1998г.

Задание № 1

1.1 Определить реакции опор

1.2 Построить эпюры поперечных сил и изгибающих моментов

1.3 Подобрать номер двутаврового профиля для Ст. 3 [s] = 160 Мпа

1.4 Начертить в масштабе двутавровый профиль по ГОСТ 8239-72 и построить эпюру нормальных напряжений в опасном сечении балки.

Общая схема нагрузки балки (рис. 1):

Схема нагрузки балки, 24 вариант (рис. 2):

Эквивалентная схема нагрузки свободной балки с правильным направлением данных величин (P,q,M) (рис. 3):

Эквивалентная схема с правильным направлением данных и искомых величин (P,q,M,Y_E,Y_F) (рис. 4):

Дано:

Таблица 1: “Расположение элементов нагрузки”.

A₁	A₂	B₁	B₂	C	D	L [м]
2,5	1,0	1,5	2	0,2	1,2	3,1

Таблица 2: “Величины элементов нагрузки”.

P₁[кН]	P₂[кН]	M₁[кН•м]	M₂[кН•м]	q [кН/м]
-8,0	10,0	16	11	20

Знаки величин принимаются относительно направлений, обозначенных на рисунке.

1.1 Найти: Y_E-? Z_E-? Y_F-? Z_F-?

Решение:

Заменим опоры в точках E и F их реакциями. Таким образом несвободное тело EF становится свободным, и к нему можно применить условия равновесия. Для поперечных сил положительным принято направление по оси y ; положительным моментом - момент, сжимающий верхние волокна балки. Для расчета реакций опор распределенную нагрузку q заменим равнодействующей R, приложенной в середине отрезка CD действия нагрузки q, в точке с координатой (C+D)/2. R = q•Dl; Dl = в – С.

Условия равновесия тела EF :

еQyn = 0 : сумма поперечных сил

еQzn = 0 : сумма продольных сил

еMn = 0 : сумма изгибающих моментов

Силы P₁, P₂, R приложены перпендикулярно к оси z, поэтому их проекции на эту ось будут нулевыми по величине, еQzn = 0.

Уравнение суммы поперечных сил :

Y_E – q • (D – С) + P₂ + P₁ + Y_F = 0

Уравнение суммы изгибающих моментов относительно точки E :

– (D – С) • q • (С +D) / 2 + P₂ • A₂ – M₁ + M₂ + P₁ • A₁ + Y_F • L = 0

Знаки в уравнениях определены исходя из направлений, обозначенных на эквивалентной схеме нагрузки балки (рис.3), поэтому в уравнениях используются модули нагрузочных величин (ЅP₁Ѕ,ЅP₂Ѕ,ЅRЅ,ЅM₁Ѕ,ЅM₂Ѕ) и обозначаются без векторной черты. Возможные отрицательные значения искомых величин Y_E и Y_F будут означать противоположное их направление выбранному на схеме.

Из уравнения моментов вычисляем силу Y_F :

Y_F = [(D – C) • q • (С +D) / 2 – P₂ • A₂ + M₁ – M₂ – P₁ • A₁] / L

Y_F = [(1,2–0,2)•20•(1,2+0,2)/2–10,0•1,0+16–11–8,0•2,5] / 3,1 » –3,6

Из уравнения поперечных сил вычисляем силу Y_E :

Y_E = q • (D – С) – P₂ – P₁ – Y_F

Y_E » 20 • (1,2 – 0,2) – 10,0 – 8,0 – (–3,6) = 5,6 [кН].

Для проверки составим уравнение моментов относительно другой точки. Знаки в уравнении определены исходя из эквивалентной схемы балки (рис.4), где искомые реакции опор Y_E и Y_F имеют правильные направления.

Уравнение суммы изгибающих моментов относительно точки F :

–(D–С)•q• [(L–D)+(L–C)]/2+Y_E•L+P₂•(L–A₂)+P₁•(L–A₁)+M₁–M₂=0

Обращение левой части уравнения в нуль при подстановке данных и найденных величин подтверждает правильность значений найденных реакций опор Y_E и Y_F.

–(1,2–0,2)•20•[(3,1–1,2)+(3,1–0,2)]/2+Y_E•3,1+10,0•(3,1–1,0)+

+8,0•(3,1–2,5)+16–11 = 0; –17,2+5,6•3,1 » 0.

1.2 Найдем зависимость внутренних усилий (поперечных сил Q и изгибающих моментов M) на протяжении балки от координаты z, начиная от точки E (z - расстояние до точки E). Бесконечно близко^¹⁾ слева (со стороны точки E) к точкам приложения сил и моментов проведем сечения. Таким образом, на протяжении балки образуются 7 участков. Рассмотрим, начиная от точки E, изменение внутренних напряжений (Q и M) балки на каждом участке в зависимости от координаты z.

z_n - расстояния от точки E до точек приложения нагрузок, z₀ = 0.

Пусть Q(z) - функция зависимости внутренней поперечной силы (балки) от координаты z; 0 Ј z < z₇.

RQ_n = – lim Q(z) = – е lim Qў_k(x)

^z^®^zⁿ^{слева k=0 x}^®^(z^k^–^z^k^–¹⁾^слева

Пусть Qў_n(x), x = z – z_n_–₁ - функция зависимости внутр. попереч. силы от координаты z на участке n, если z лежит на левой границе участка, то (z – z_n_–₁) = 0. Пусть RQ_n - реакция справа отсеченной части балки, тогда

Изменение внутренней поперечной силы на участке n.

Знаки для сил и моментов определены исходя из схемы балки (рис. 5), в формулах используются модули всех величин.

n	Qў_n(x), x = z – z_n_–₁	пределы z	RQ_n	Rq_n (числ. знач.)
1	Y_E	0 Ј z < z₁	–Y_E	– 5,6
2	– q • (z – z₁)	z₁ Ј z < z₂	–Y_E + q • (z₂ – z₁)	–5,6+20•(10,0–0,2)=10,6
3	P₂ – q • (z – z₂)	z₂ Ј z < z₃	–Y_E + q • (z₂ – z₁) – P₂ + q • (z₃ – z₂)	10,6–10,0+20•(1,2–1,0)=4,6
4	0	z₃ Ј z < z₄		4,6
5	0	z₄ Ј z < z₅		4,6
6	0	z₅ Ј z < z₆		4,6
7	P₁	z₆ Ј z < z₇	–Y_E + q • (z₂ – z₁) – P₂ + q • (z₃ – z₂) – P₁	4,6 – 8,0 » –3,6*

* реакция, действующая на правый край VII участка - есть реакция опоры, совпадение ее численного значения с Y_F означает правильность вычислений.

1⁾ Бесконечно близко для того, чтобы было правомочным утверждение, что найденные зависимости Q(z) и M(z) справедливы на всем рассматриваемом участке, при Z_n_–₁ Ј Z < Z_n.

БИЛЕТ 5 Изгиб. Дифф. зав-ти при изгибе.

dM = Q • dz, Q = dM / dz, dQ / dz = d²M / dz² = q.

производная от изгибающего момента по абсциссе сечения балки равна поперечной силе (теорема Журавского); вторая производная от изгибающего момента по абсциссе сечения балки равна интенсивности распределенной нагрузки.

БИЛЕТ 6 Основные гипотезы при изгибе.

Принцип Бернулли: плоские сечения до и после деформации остаются плоскими, нормальными к продольной оси балки.

БИЛЕТ 12 Косой изгиб. Определение напряж.

БИЛЕТ 14

Напряженное состояние в данной точке - совокупность напряжений на всех елементарных площадках, которые можно провести через какую-либо точку тела. Главные нормальные напряжения - если на грани кубика других нет (касательных напряжений). Тензор напряжения - перемещения при данной нагрузке ???

Закон парности касательных напряжений.

Дан брус произвольного сечения.

A - площадь сечения по нормали

A_a - площадь сечения под углом a к нормали. A_a= A / cos a.

проекция сил на направление s_a :

s_a•A_a – s₁•A•cos a = 0

s_a = s₁ • cos² a

проекция сил на направление t_a :

t_a•A_a – s₁•A•sin a = 0

t_a = 1/2 •s₁ • sin 2a

для BD:

s_b = s₁ • cos² (a+/2)= s₁ • sin² a

t_b = 1/2 •s₁ • sin 2(a+/2) = – 1/2 •s₁ • sin 2a.

s_a+ s_b = s₁; t_a = – t_bз-н парности касат. напряж.).

Из этого закона следует, что :

при a = 90° s_a = 0, t_a= 0; при a = 0 s_a = s_a_max = s₁, t_a= 0; при a = 45° t_a= t_a_max= s₁ / 2.

БИЛЕТ 15 Плоское напряженное состояние.

з-н Гука для одноосного напряженного состояния :

e = s / E; e = Dl / l - относительное удлинение

E [Па, МПа]- модуль продольной упругости (а также : модуль упругости I рода, модуль Юнга).

s [Па, МПа] - напряжение.

eў = –m •e; eў - относит. поперечная деформация.

m - коэфф-нт поперечной деформации (Пуассона).

обобщенный з-н Гука для плоского напряженного состояния :

e₁ = s₁ / E – m•s₂ / E

e₂ = s₂ / E – m•s₁ / E.

находим напряжения s₁ и s₂ :

s₁ = E (e₁ + m•e₂) / (1– m²), s₂ = E (e₂ + m•e₁) / (1– m²).

БИЛЕТ 16 З-н Гука для изотропного материала.

Изотропный материал - материал, свойства которого одинаковы во всех направлениях.

Для объемного напряженного состояния :

e₁ = (1 / E) •[s₁ – m•(s₂ + s₃)],

e₂ = (1 / E) •[s₂ – m•(s₃ + s₁)],

e₃ = (1 / E) •[s₃ – m•(s₁ + s₂)].

Объем кубика 1ґ1ґ1 после деформации :

V = (1+e₁) ґ (1+e₂) ґ (1+e₃) » 1+ e₁+e₂+e₃.

Относительное изменение объема :

u = e₁+e₂+e₃ = (1–2•m) •(s₁+s₂+s₃ ) / E. Отсюда : коэфф-нт Пуассона m не может быть больше 1/2.

з-н Гука при сдвиге : t = G•g

g - угол сдвига [рад]

G [Па]- модуль сдвига (модуль упругости 2 рода).

G = E / [2•(1+m)]

удельная деформация при чистом сдвиге :

u = t² / (2•G)

БИЛЕТ 17 Теории (гипотезы) прочностей.

Эквивалентое напряженное состояние - состояние, равноопасное данному сложному напряженному состоянию, но при одноосном растяжении (сжат.).

I-я гипотеза прочности - гипотеза наибольших нормальных напряжений :

“предельное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшее нормальное напряжение достигает предельного напряжения [s] при одноосном напряженном состоянии”. I-я гипотеза устанавливает критерий хрупкого разрушения (не для пластичных материалов). Если материал имеет различные [s] на растяжение и сжатие, то :

max s_р Ј [s^р], max s_с Ј [s^с].

II-я гипотеза прочности - гипотеза наибольших линейных деформаций :

Опыты не подтверждают эту теорию.

III-я гипотеза прочности - гипотеза наибольших касательных напряжений :

“прочность материала при сложном напряженном состоянии считается обеспеченной, если наибольшее касательное напряжение не превосходит допускаемого касательного напряжения, установленного для одноосного напряженного состояния”. t_max = t_экв Ј [t].

Из закона парности касательных напряжений :

t_max = s /2 при a = 45° a - угол между нормалью и сечением на котором определяем t.

БИЛЕТ 18

Гипотеза теории кручения (гипотеза плоских и жестких сечений): расстояния между нормальными сечениями при кручении не изменяются, не изменяются размеры сечений.

Кручение бруса круглого поперечного сечения.

Касательные напряжения при кручении :

t = M•r / I_p . r - расстояние от центра сечения.

M - приложенный момент. r - радиус сечения.

t_max = M•r / I_p = M / W_p Ј [t].

W_p - полярный момент сопротивления.

Для круглого сплошного сечения радиусом r:

W_p = I_p / r = pd⁴ / (32•d/2) = pd³ /16 » 0,2•d³.

Деформации и перемещения :

dj / dz = M / (G•I_p) - выведено в билете 19

Производная угла закручивания (взаимн. пов.) :

dj = M•dz / (G•I_p). Деформация вала на длине z (взаимный угол поворота сечений) :

j = т!от0доz! [M•dz / (G•I_p)].

Величина G•I_p - жесткость вала при кручении.

Для вала длиной l: j = M•l / (G•I_p).

Относительный угол закручивания - угол закручивания на единицу длины :

g = j / l = M / (G•I_p).

Условие прочности: g Ј [g]; [g] - в ° / на 1м длины.

Зависимость t от угла закручивания :

g = r•dj / dz из рисунка билета 19.

з-н Гука при сдвиге : t = G•g, Ю :t = G•r•dj / dz.

БИЛЕТ 19 Кручение, вывод рассчетн. ф-лы для

касательных напряжений.

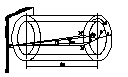
g_maч = r•dj / dz, аналогично g = r•dj / dz.

з-н Гука при сдвиге : t = G•g, отсюда :

t = G•r•dj / dz. При кручении деформации сдвига прямо пропорциональны расстоянию от центра тяжести сечения.

Равнодействующий момент касательных напряжений в сечении : M = _Aт (t•r)•dA; (t•r)•dA - элементарный крутящий момент внутренних сил на площадке dA.

M = G•dj / dz•_Aт (r²)•dA.

Полярный момент инерции сечения : I_p = _Aт (r²)•dA.

dj / dz = M / (G•I_p); t = M•r / I_p .

Условие прочности.

t_max = M•r_max / I_p = M / W_p Ј [t].

W_p - полярный момент сопротивления.

Для круглого сечения радиусом r: W_p = I_p / r.

БИЛЕТ 20 Кручение, вывод ф-лы для

относительного угла закручивания.

переписать билет 19 до ф-лы : dj / dz = M / (G•I_p) и раздел “Деформации и перемещения.” билета 18.

БИЛЕТ 21 Внецентренное растяжение.

В любом поперечном сечении стержня возникает продольная сила N=F и изгибающие моменты :

M_x = F•y_F , M_y = F•x_F . Напряжение в точке (x,y) :

s = N / A + M_x•y / I_x + M_y•x / I_y .

Максимальные напряжения на угловых точках :

s = N / A ± M_x / W_x ± M_y / W_y .

W_x , W_y - моменты сопротивлений .

A - площадь сечения.

По рисунку - наибольшие напряжения - в точке E :

s_E = N / A + M_x / W_x + M_y / W_y .

Алгебраически наименьшие напряж. - в точке D :

s_D = N / A – M_x / W_x – M_y / W_y .

Условие прочности :

N / A + M_x / W_x + M_y / W_y Ј [s].

В плоскости нулевой линии напряжение равно 0.

Уравнение нулевой линии (x,y - координаты) :

N / A + N•y_F•y / I_x + N•x_F•x / I_y = 0; или :

x_F•x / i²_y + y_F•y / i²_x + 1 = 0; или :

x / a + y / b = 1, a = – i²_y / x_F , b = – i²_x / y_F .

a, b - отрезки на осях координат x, y.

Радиус инерции сечения : i_x = Ц(I_x / A), i_y = Ц(I_y / A),

размерность - длина (обычно сантиметр).

В центре тяжести сечения s = N / A = F / A.

Для прямоугольного сечения :

I_x = b•h³ / 12, I_y = b³•h / 12, W_x = 2•I_x/h, W_y = 2•I_y / b

W_x = b•h² / 6, W_y = b²•h / 6; сторона bззоси x, h зз y.

Напряжение в точке (x,y) :

s = N / A + M_x•y / (b•h³ / 12) + M_y•x / (b³•h / 12) =

= N / A + N•y_F •y / (b•h³ / 12) + N•x_F •x / (b³•h / 12).

Максимальные напряжения на угловых точках :

s = N / A ± M_x / (b•h² / 6) ± M_y / (b²•h / 6) =

= N / A ± N•y_F / (b•h² / 6) ± N•x_F / (b²•h / 6).

БИЛЕТ 22 Изгиб с кручением бруса кругл. сеч.

От изгиба в точках C и D: s_max = M / W_X;

от кручения по контуру сечения:

t_max = T/W_P = T / (2•W_X).

Напряженное состояние в точке C :

Главные напряжения: s₁=s_max = (s + Ц(s² + 4•t²)) /2.

s₃=s_min = (s – Ц(s² + 4•t²)) /2.

По 3-й гипотезе прочности : s₁ – s₃ Ј [s];

Ц(s² + 4•t²) Ј [s]; Ц(M² + T²) / W_X Ј [s]; отсюда :

проектный расчет: W_X = Ц(M² + T²) / [s]; если изгиб

в 2-х ^-ных плоскостях, то: M = Ц(M²_X + M²_Y).

БИЛЕТ 23 Ф-ла Эйлера для сжатого стержня

большой гибкости.

Основной случай продольного изгиба

(закрепление на 2-х опорах, неподв. и подв.) :

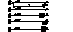
Критическая сила - F_КР : наименьшаяая сила, при которой стержень теряет способность сохранять прямолин. форму.Предел пропорциональности s_пц:

напряжение “до” которого деформация происходит по закону Гука.

Пусть потеря устойчивости происходит при напряжениях, меньших предела пропорцион-ности s_пц материала стержня. Тогда - упругая линия :

1/r » d²u / dz² = M / (EJ); 1/r - кривизна. M = F_КР•u.

Уравнеие изогнутой оси: d²u / dz² = – F_КР•u / (EJ).

заменим: k² = F / (EJ_min) [при потере устойчивости попереч. сечения поворач-ся вокруг главной оси с минимальным моментом инерции J_min ], тогда :

uІ + k²•u = 0; реш.ур.: u = C•cos (k•z) + D•sin(k•z).

Определение C и в из условий опор балки : 1) при z = 0,u = 0;2) при z = l, u = 0. Ю С = 0, D•sin(k•z)=0.

D = 0 не подходит т.к. нет прогиба балки Ю sin(k•z)=0; Ю k = np / l, Ю F_КР = p²•J_min•E•n² / l² .

наи<ее значение F_КР - при n = 1. F_КР = p²•E•J_min / l² .

u = D•sin (p • z / l) - изгиб с одной полуволной.

Для любого способа закрепления концов балки в ф-ле l заменим l_прив = m • l. l_прив - приведенная длина

m - коэффициент приведения длины.

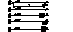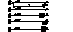
БИЛЕТ 24 Ф-ла Эйлера для критич. напряж.

Нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критическому значению сжимающей силы, наз-ют критическим.

s_кр = F_кр / A, A - площадь сечения.

Формула Эйлера: F_КР = p²•E•J_min / l² .

s_кр = p² • E • J_min / [(m • l)² • A]; J_min / A = i²_min .

Радиус инерции сечения : i_x = Ц(I_x / A), i_y = Ц(I_y / A),

размерность - длина (обычно сантиметр).

s_кр = p² • E • i²_min / [(m • l)²] = p² • E / (m • l / i_min)² .

m • l / i_min = l - гибкость стержня : безразмерная величина,показ-ая сопротивл-ть потере устойч-ти,

зависит от геометрич. характеристик стержня.

s_кр = p² • E / l² . Пределы применимости формулы:

Ф-ла Эйлера справедлива лишь в пределах применимости з-на Гука, т.е. при усл., что критическое напряж. не превыш. предела пропорциональности материала стержня.

s_кр Ј s_пц , p² • E / l² Ј s_пц , l і p • Ц(E / s_пц) = l_пред .

l_пред - предельная гибкость (граничная гибк.): не зависит от размеров,зависит от свой-в материала.

Ф-ла Эйлера применима, когда гибкость стержня і предельн. гибк-ти для материала стержня:l і l_пред .

В случае неприменим-ти ф. Эйлера напряжения опред. по эмпирическим ф-лам s_кр = a – b•l , a и b - коэфф-ты, определяемые опытным путем.

Стержни гибкости : 1. большой (l і l_пред) - по ф. Эйлера 2. средней (l₀ Ј l < l_пред) - по эмпирич. ф-ле. 3. малой (l < l₀)-расчет не на устойчив., а на проч.

БИЛЕТ 25 Напряжение при движении с ускорен.

Груз весом G поднимают вверх с ускорением a.

Определить напряяжение в канате.

s_d - динамическое напряжение, A - площадь сечен.

s_st = G / A - напряжен. при статич. действии груза.

K_d - динамический коэффициент

s_d•A – G•(1+ a / g ) = 0, s_d = G / A•(1+ a/g) = s_st•K_d.

K_d = (1+ a/g).

Экзаменационные вопросы по

прикладной механике (первый семестр II курс).

1. Метод сечений. Определение внутренних усилий.

Задача: эпюры.

2. Растяжение и сжатие бруса. Нормальная сила. Напряжение в поперечном сечении. Усл. прочности при растяжении-сжатии.

Задача: Эпюра нормальных сил и изг. M в балке.

3. Деформация при растяжении-сжатии. Диаграмма деформации стали. Закон Гука.

Задача: построить эпюры изгибающих и крутящих моментов в балке, проверить прочность по 3-й теории прочности.

4. Основные механические характеристики конструкционных материалов. Понятие предельных допускаемых напряжений.

Задача: построить эпюры изгибающих и крутящих моментов ломаного бруса.

5. Изгиб. Дифференциальные зависимости для усилий.

Задача: проверить прочность балки на изгиб.

6. Основные гипотезы при изгибе. Нормальное напряжение при изгибе. Задача: проверить.

7. Изгиб. Определение положения нейтрального слоя.

8. Максимальное напряжение при изгибе. Вывод формулы. Условие прочности. Задача:РГР № 1.

9. Дифференциальное уравнение изогнутой оси бруса. Перемещение при изгибе.

Задача:РГР № 1.

10. Вывод интеграла Мора.

Задача:РГР № 1.

11. Способ перемножения эпюр. Правило Верещагина.

Задача: брус зажат между стенками

12. Косой изгиб. Определение напряжения при косом изгибе.

Задача: определить диаметр ступенчатого бруса.

13. Определение положения нулевой линии при косом изгибе.

Задача: Жестко закрепленная балка, построить эпюру крутящих моментов.

14. Понятие напряженного состояния в точке. Тензор напряжения. З-н парности касательных напряжений.

Задача: Построить эпюру крутящих моментов и определить диаметр вала.

15. Плоское напряженное состояние: вывод формул для напряжений.

Задача: Проверить прочность при заданной нагрузке: Ж, P, l от P до опоры, [s].

16. З-н Гука для изотропного материала.

Задача: угол поворота консольной балки в сечении.

17. Теории прочности. Понятие эквивалентного напряженного состояния. Вывод ф-лы s_экв .

Задача: Проверить прочность балки с квадратным сечением при заданной распределенной нагрузке.

18. Кручение бруса круглого поперечного сечения. Гипотезы теорий кручения. Напряжения и деформации. Зависимость t от производной по углу закручивания.

Задача: Определить перемещение балки на 2-х опорах под действием силы P посередине.

19. Кручение, вывод рассчетной ф-лы для касательных напряжений, условие прочности.

Задача: Определить прогиб консольной балки, в конце балки - момент.

20. Кручение, вывод ф-лы для относительного угла закручивания, условие прочности.

Задача: Из условий прочности найти размеры квадратного поперечного сечения балки.

21. Внецентренное растяжение. Определение напряжения для бруска прямоугольного сечения, условие прочности.

Задача: построить эпюры M, s, перемещения.

22. Изгиб с кручением бруса круглого сечения, напряженное состояние, условие прочности.

Задача: Абсолютно жесткая балка подвешена на стержнях с одинакового сечения и материала.

23. Вывод ф-лы Эйлера для сжатого стержня большой гибкости.

Задача: Из условия прочности найти диаметр балки, нагружена моментом, распред. нагр.

24. Вывод ф-лы Эйлера для критических напряжений. Пределы ... ф-лы Эйлера.

Задача: Эпюры Q и M для балки на 2-х опорах, нагружена моментом, распред. нагр., содержит консольные участки.

25. Общие принципы расчета при динамических нагрузках. Расчет на прочность при движении тел с заданным ускорением.

Задача: Исходя из условий прочности найти размеры сечения прямоугольной консольной балки.