Нижегородский Государственный Технический Университет.
Лабораторная работа по физике №2-27.
Исследование электрических колебаний
.
Выполнил студент
Группы 99 – ЭТУ
Наумов Антон Николаевич
Проверил:
Н. Новгород 2000г.
Цель работы:
экспериментальное исследование собственных и вынужденных колебаний тока и напряжения на элементах в колебательном контуре; измерение параметров контура: индуктивности
L
, сопротивления
R
, добротности
Q
; исследование прохождения синусоидального тока через
LCR
-цепь.
Теоретическая часть.
Рисунок 1.
Уравнение, которому удовлетворяет ток I в колебательном контуре (рис.1) с подключенным к нему генератором синусоидальной ЭДС e
=
e
0
×
cos
w
t
имеет вид: 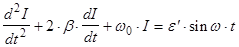 (1) (1)
где:
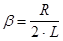 - коэффициент затухания. - коэффициент затухания.
 - собственная круговая частота, R - сопротивление резистора, L - индуктивность катушки, С - емкость конденсатора, - собственная круговая частота, R - сопротивление резистора, L - индуктивность катушки, С - емкость конденсатора, 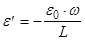 ; e0
, w - амплитуда и круговая частота синусоидальной ЭДС. ; e0
, w - амплитуда и круговая частота синусоидальной ЭДС.
Общее решение неоднородного линейного уравнения (1):
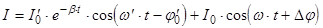 (2) (2)
где: 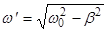 - круговая частота собственных затухающих колебаний тока. - круговая частота собственных затухающих колебаний тока.
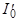 и и 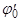 - начальные амплитуда и фаза собственных колебаний. - начальные амплитуда и фаза собственных колебаний.
I
0
- амплитуда вынужденных колебаний тока.
Dj
-
разность фаз между ЭДС и током.
 (3) (3)
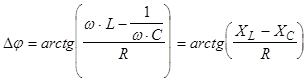 (4) (4)
 - импеданс цепи. - импеданс цепи.
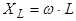 - индуктивное сопротивление, - индуктивное сопротивление, 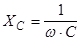 - емкостное сопротивление. - емкостное сопротивление.
Собственные колебания:
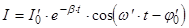
Если b2
<w0
2
, то есть R<2×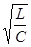 , то w¢ - действительная и собственная частота колебаний представляет собой квазипериодический процесс с круговой частотой w¢, , то w¢ - действительная и собственная частота колебаний представляет собой квазипериодический процесс с круговой частотой w¢, 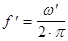 , периодом , периодом 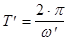 , и затухающей амплитудой , и затухающей амплитудой 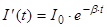 (рис 1). (рис 1).
За характерное время 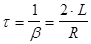 (t - время релаксации) амплитуда тока уменьшается в е
раз, то есть эти колебания практически затухают. (t - время релаксации) амплитуда тока уменьшается в е
раз, то есть эти колебания практически затухают.
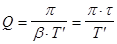 - добротность контура. - добротность контура.
Если b2
³w0
2
, то w¢ - мнимая частота, и колебания представляют собой апериодический процесс.
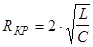 - критическое сопротивление. - критическое сопротивление.
Вынужденные колебания:
c течением времени первый член в формуле (2) обращается в ноль и остается только второй, описывающий вынужденные колебания тока в контуре.
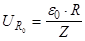 - амплитуда вынужденных колебаний напряжения на резисторе R. - амплитуда вынужденных колебаний напряжения на резисторе R.
При совпадении частоты ЭДС с собственной частотой контура (w=w0
), амплитуды колебаний тока и напряжения UR
0
на резисторе максимальны. Большой селективный отклик колебательной системы на периодическое внешнее воздействие называется резонансом
.
Экспериментальная часть.
Результаты эксперимента:
| №
|
f
, кГц
|
e
ЭФ
, мВ
|
UR
ЭФ
, мВ
|
a
|
b
|
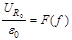 ,
×
10-4
,
×
10-4
|
D
j
,
°
|
| 1
|
180 |
200 |
24 |
4,0 |
3,4 |
1,2 |
58 |
| 2
|
190 |
190 |
32 |
5,2 |
4,0 |
1,7 |
51 |
| 3
|
195 |
185 |
38 |
6,0 |
4,3 |
2,0 |
48 |
| 4
|
200 |
180 |
45 |
2,8 |
2,0 |
2,5 |
46 |
| 5
|
205 |
170 |
54 |
3,2 |
2,0 |
3,2 |
38 |
| 6
|
210 |
155 |
63 |
3,8 |
2,0 |
4,1 |
32 |
| 7
|
215 |
142 |
72 |
4,2 |
1,0 |
5,1 |
14 |
| 8
|
218 |
138 |
75 |
4,4 |
0,0 |
5,4 |
0 |
| 9
|
220 |
135 |
76 |
4,3 |
0,5 |
5,6 |
6 |
| 10
|
225 |
140 |
73 |
4,2 |
1,8 |
5,2 |
25 |
| 11
|
230 |
150 |
65 |
3,8 |
2,6 |
4,3 |
43 |
| 12
|
235 |
165 |
56 |
3,5 |
2,6 |
3,4 |
48 |
| 13
|
240 |
175 |
48 |
3,0 |
2,7 |
2,7 |
64 |
| 14
|
250 |
180 |
36 |
2,2 |
2,1 |
2,0 |
76 |
| 15
|
260 |
195 |
28 |
1,8 |
1,7 |
1,4 |
90 |
| 16
|
270 |
200 |
22 |
1,6 |
1,6 |
1,1 |
90 |
| 17
|
280 |
200 |
18 |
1,3 |
1,3 |
0,9 |
90 |
| 18
|
290 |
200 |
15 |
1,0 |
1,0 |
0,8 |
90 |
| 19
|
300 |
205 |
12 |
1,0 |
1,0 |
0,6 |
90 |
Задание 1.
Исследование зависимости амплитуды вынужденных колебаний от частоты (резонансная кривая).
Исходные данные:Uвых
=200 мВ, eЭФ
=200 мВ. f
Î[180;300] кГц.
Расчеты необходимых величин:
1.  f
0
= 220 кГц - частота резонанса. f
0
= 220 кГц - частота резонанса.
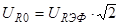 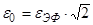
Строим график зависимости 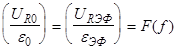
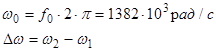
,где w1
и w2
- значения частот на уровне 
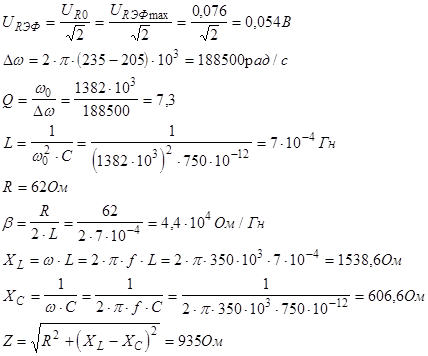
Из экспериментального графика  видно, что он по своей форме совпадает с графиком, полученным теоретически из формулы: видно, что он по своей форме совпадает с графиком, полученным теоретически из формулы: 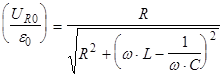
Исследование зависимости разности фаз между ЭДС и током в контуре.
Из экспериментального графика Dj=F(f
) получаем: f
0
=218 кГц.
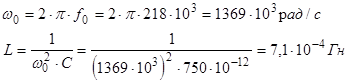
Сравнивая полученные результаты с результатами из предыдущего опыта видно, что различие в величинах w0
и L незначительны.
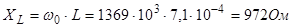
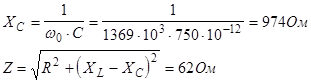
Можно сделать вывод, что при резонансной частоте XL
»XC
и величина импеданса цепи минимальна.
Рисунок 2.
Задание 2.
Исследование собственных электрических колебаний.
На данном рисунке представлена форма затухающих колебаний напряжения UC
на конденсаторе, полученная с помощью осциллографа. Изображение совпадает с теоретическим графиком.
Из графика: Т=2×2,4×10-6
с - период колебаний.
t=2×3,8×10-6
с - время релаксации.
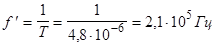 
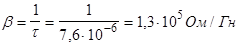 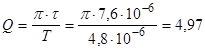
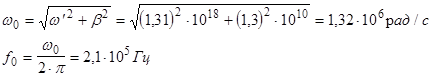
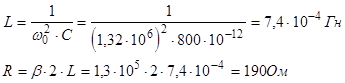 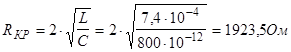
Задание 3.
Исследование прохождения синусоидального тока через
LCR
- цепь
.
| f
,кГц
|
U
ВЫХЭФ
,10-3
В
|
U
0ВЫХ
,
10-3
В
|
| 150 |
41 |
56 |
| 160 |
33 |
46 |
| 170 |
27 |
38 |
| 180 |
22 |
31 |
| 190 |
14 |
19 |
| 200 |
9 |
13 |
| 205 |
6 |
8 |
| 210 |
3 |
4 |
| 215 |
1 |
2 |
| 218 |
0 |
0 |
| 220 |
0 |
0 |
| 225 |
1 |
2 |
| 230 |
2 |
3 |
| 235 |
4 |
6 |
| 240 |
5 |
7 |
| 250 |
9 |
13 |
| 260 |
13 |
18 |
| 270 |
17 |
24 |
| 280 |
22 |
31 |
| 290 |
25 |
35 |
| 300 |
30 |
42 |
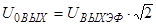
Построим график U0ВЫХ
=F(f
). Резонансная частота из графика равна: f
0
=220 кГц.
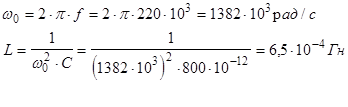 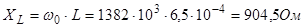
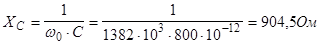
 При этом импеданс цепи является бесконечно большим и ток в цепи не протекает. При этом импеданс цепи является бесконечно большим и ток в цепи не протекает.
R=50 Ом, f
=2 МГц.
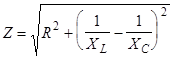
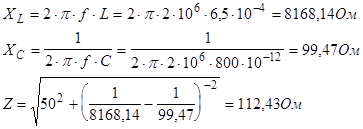
Погрешности измерений.
Задание 1.
1) Погрешностьf
0
:f
определяли на частотомере
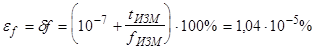 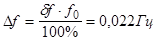
2) Погрешность L:
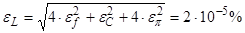 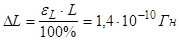 

3) Погрешность Q:
 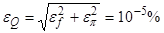 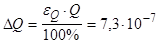
4) Погрешность R:
eR
=5% DR=3,1Ом
5) Погрешность XL
: 
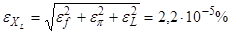 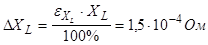
6) Погрешность XC
:
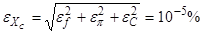 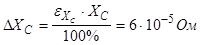
7) Погрешность b
:
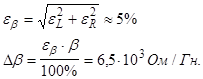
Вывод:
на этой работе мы экспериментально исследовали собственные и вынужденные колебания тока и напряжения на элементах в колебательном контуре; измерили параметры контура: индуктивности
L
, сопротивления
R
, добротности
Q
; исследовали прохождение синусоидального тока через
LCR
-цепь.
|