И. Волков, М. Грачева
В данном разделе исследуется один из наиболее сложных инструментов анализа рисков инвестиционного проекта, базирующийся на использовании вероятностного подхода. Одним из наглядных примеров, основанном на вероятностной оценке конкретного события, является так называемое дерево решений.
Метод анализа индивидуального проектного риска с помощью построения дерева решений проекта
.
Как правило, производимые во время реализации проекта затраты, требуют осуществления финансовых вложений не единовременно, а в течение определенного, достаточно длительного промежутка времени. Такое положение вещей дает менеджеру возможность проводить переоценку своих вложений и оперативно реагировать на изменение конъюктуры реализации проекта.
Риск по проектам, при реализации которых инвестирование средств происходит в течение длительного периода времени, часто оценивается с помощью дерева решений.
Пример. Некая компания собирается инвестировать средства в производство роботов для использования в космических исследованиях. Инвестиции в данный проект производятся в три этапа.
1этап. В начальный момент времени t=0 необходимо потратить $500 тыс. долл. на проведение маркетингового исследования рынка.
2 этап. Если в результате исследования будет выяснено, что потенциал рынка достаточно высок, то компания инвестирует еще $1,000 тыс. долл. на разработку и создание опытных образцов робота. Опытные образцы должны быть предложены к рассмотрению инженерам в центре космических исследований, которые решают вопрос о размещении заказа у данной компании.
3 этап. Если реакция инженеров благоприятная, то в момент времени t=2 компания начинает строительство нового предприятия по производству данного робота. Строительство такого предприятия требует затрат в $10,000 тыс. долл. Если данная стадия будет реализована, то по оценкам менеджеров проект будет генерировать притоки наличности в течение четырех лет. Величина этих потоков наличности будет зависеть от того, насколько хорошо этот робот будет принят на рынке.
Для анализа именно таких многостадийных решений чаще всего используется метод дерева решений (см. рисунок).
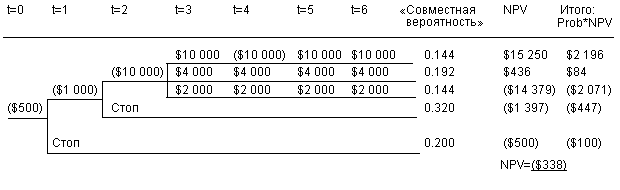
В этом примере мы предполагаем, что очередное решение об инвестировании принимается компанией в конце каждого года. Каждое “разветвление” обозначает точку принятия решения, либо очередной этап. Число в круглых скобках, записанное слева от точки принятия решения, представляет собой чистые инвестиции. В интервале с третьего по шестой годы (с t=3 по t=6) показаны притоки наличности, которые генерируются проектом. Например, если компания решает реализовывать проект в точке t=0, то она должна потратить 500 тыс. долл на проведение маркетингового исследования. Менеджеры компании оценивают вероятность получения благоприятного результата в 80%, и вероятность получения неблагоприятного результата в 20%. Если проект будет остановлен на этой стадии, то издержки компании составят 500 тыс. долл.
Если по результатам маркетингового исследования компания приходит к оптимистическому заключению о потенциале рынка, то в момент времени t=1 необходимо потратить еще 1,000 тыс.долл. на изготовление экспериментального варианта робота. Менеджеры компании оценивают вероятность положительного исхода в 60%, а вероятность отрицательного исхода в 40%.
Если инженеров центра космических исследований устраивает данная модель робота, тогда компания в момент времени t=2 должна инвестировать 10 000 тыс. долл. для постройки завода и начала производства. Менеджеры компании оценивают вероятность того, что в центре космических исследований воспримут такую модель благожелательно в 60% и вероятность противоположного исхода в 40% (что приведет к прекращению рализации проекта).
Если компания приступает к производству робота, то операционные потоки наличности в течение четырехлетнего срока жизни проекта будут зависеть от того, насколько хорошо продукт будет “принят” рынком. Вероятность того, что продукт будет хорошо “принят” рынком составляет 30% и в этом случае чистые притоки наличности должны составлять около 10 000 тыс. долл. в год. Вероятность того, что притоки наличности будут составлять около 4 000 тыс. долл. и 2 000 тыс. долл. в год, равна 40% и 30% соответственно. Эти ожидаемые потоки наличности показаны на нашем рисунке с третьего года по шестой.
Совместная вероятность, подсчитанная на выходе данной схемы, характеризует ожидаемую вероятность получения каждого результата.
Предположим, что ставка цены капитала компании при реализации данного проекта составляет 11,5%, и по оценкам финансовых менеджеров компании реализация данного проекта имеет риск, равный риску реализации типичного “среднего” проекта компании. Затем, умножая полученные значения чистой приведенной стоимости на соответствующие значения совместной вероятности, мы получим ожидаемую чистую приведенную стоимость инвестиционного проекта.
Поскольку ожидаемая чистая приведенная стоимость проекта получилась отрицательной, то компания должна отвергнуть этот инвестиционный проект. Однако на самом деле, вывод не так однозначен. Необходимо также учесть возможность отказа компании от реализации данного проекта на определенном этапе или стадии, что приводит к существенному изменению одной из ветвей дерева решений.
Издержки отказа от реализации проекта значительно сокращаются, если компания имеет альтернативу для использования активов проекта. Если бы в нашем примере, компания могла бы использовать оборудование для производства принципиально иного вида роботов, тогда бы проект по производству роботов для космических нужд мог быть ликвидирован с большей легкостью, следовательно, риск реализации проекта был бы меньше.
Наконец, отметим, что финансирование инвестиционных проектов — это динамичный процесс. В каждой узловой точке дерева решений условия реализации проекта могут измениться, что приводит к автоматическому изменению чистой приведенной стоимости.
|