И.Я. Лукасевич
Купонные облигации, наряду с возвращением основной суммы долга, предусматривают периодические денежные выплаты. Размер этих выплат определяется ставкой купона k, выраженной в процентах к номиналу. Купонные выплаты осуществляются 1, 2 или 4 раза в год.
Классическим примером подобных ценных бумаг, обращающихся на отечественных и мировых фондовых рынках, являются облигации внутреннего валютного займа (ОВВЗ) министерства финансов России (так называемые "вэбовки") с номиналом в 1000, 10000 и 100000 долларов США. Купонная ставка по этим облигациям равна 3%, выплачиваемых раз в год. Срок погашения зависит от серии выпуска. Первая серия была выпущена в 1993 году и погашалась, начиная с 14.05.1994 г. В настоящее время в обращении находятся 4-я (срок обращения 6 лет, погашение с 14.05.99), 5-я (срок обращения 10 лет, погашение с 14.05.2003), 6-я (срок обращения 15 лет, погашение с 14.05.2008) и 7-я (срок обращения 15 лет, погашение с 14.05.2011) серии этих облигаций.
В ноябре 1996 года был осуществлен выпуск пятилетних еврооблигаций РФ первого транша на общую сумму в 1 млрд. долларов США с погашением 21 ноября 2001 г. Ставка купона по еврооблигациям первого транша – 9,25%. Выплата дохода осуществляется раз в полгода (27 мая и 27 ноября). С 25 марта 1997 года в обращение были выпущены еврооблигации РФ второго транша на общую сумму в 2 млрд. немецких марок с погашением в 2004 году. Ставка купона по этим бумагам установлена в размере 9% годовых. Выплата периодического дохода осуществляется раз в году – 25 марта.
Выпуск третьего транша еврооблигаций на сумму в 1 млрд. долларов США состоялся в июне 1997 года. Срок обращения облигаций – 10 лет, ставка купона – 10%, выплачиваемых 2 раза в год.
Эмиссию подобных обязательств осуществили и ряд субъектов РФ. В частности с мая 1997 года в обращение выпущены еврооблигации Правительства Москвы с погашением в 2000 г. Ставка купона установлена в размере 9,5%, выплачиваемых два раза в год.
С 24 февраля 1997 года в обращение на внутренних рынках страны выпущена первая серия облигаций федерального займа с фиксированным (постоянным) купонным доходом – ОФЗ-ПД, на сумму 500 млрд руб. Дата погашения серии – 06.06.1999, срок обращения – 3 года. Выплата купонного дохода осуществляется 1 раз в год (6 июня). Ставка купона определена в размере 20% годовых. Весь объем выпуска был первоначально приобретен Банком России.
На внутренних рынках большой популярностью среди юридических и физических лиц также пользуются серии облигаций федерального займа (ОФЗ-ПК) с номиналом в 1 млн. руб. и государственного сберегательного займа (ОГСЗ) с номиналами 100000 и 500000 рублей. Срок погашения таких облигаций составляет один или два года. Купонные выплаты по ним осуществляются по плавающей ставке. При этом величина ставки каждого последующего купона объявляется МФ России за несколько дней до даты погашения предыдущего.
Далее при рассмотрении методов анализа купонных облигаций мы будем полагать, что периодические выплаты производятся по фиксированной ставке.
Доходность операций с купонными облигациями
В общем случае, доход по купонным облигациям имеет две составляющие: периодические выплаты и курсовая разница между рыночной ценой и номиналом. Поэтому такие облигации характеризуются несколькими показателями доходности: купонной, текущей (на момент приобретения) и полной (доходность к погашению).
Купонная доходность задается при выпуске облигации и определяется соответствующей процентной ставкой. Ее величина зависит от двух факторов: срока займа и надежности эмитента.
Чем больше срок погашения облигации, тем выше ее риск, следовательно тем больше должна быть норма доходности, требуемая инвестором в качестве компенсации. Не менее важным фактором является надежность эмитента, определяющая "качество" (рейтинг) облигации. Как правило, наиболее надежным заемщиком считается государство. Соответственно ставка купона у государственных облигаций обычно ниже, чем у муниципальных или корпоративных. Последние считаются наиболее рискованными.
Поскольку купонная доходность при фиксированной ставке известна заранее и остается неизменной на протяжении всего срока обращения, ее роль в анализе эффективности операций с ценными бумагами невелика.
Однако если облигация покупается (продается) в момент времени между двумя купонными выплатами, важнейшее значение при анализе сделки, как для продавца, так и для покупателя, приобретает производный от купонной ставки показатель – величина накопленного к дате операции процентного (купонного) дохода (accrued interest).
Накопленный купонный доход – НКД
В отечественных биржевых сводках и аналитических обзорах для обозначения этого показателя используется аббревиатура НКД (накопленный купонный доход). Механизм формирования доходов продавца и покупателя для сделки, заключаемой в момент времени между двумя купонными выплатами, продемонстрируем на реальном примере, взятом из практики российского рынка ОГСЗ.
Пример 2.3
ОГСЗ пятой серии с номиналом в 100000, выпущенной 10/04/96 была продана 18/03/97. Дата предыдущей выплаты купона – 10/01/97. Дата ближайшей выплаты купона – 10/04/97. Текущая купонная ставка установлена в размере 33,33% годовых. Число выплат – 4 раза в год.
Поскольку облигация продается 18/03/97, т.е. за 23 дня до следующей выплаты, купонный доход, равный 33,33% годовых от номинала, будет получен 10/04/97 новым хозяином бумаги – покупателем. Определим его абсолютную величину:
CF = 100000 (0,3333/4) = 8332,50.
Для того, чтобы эта операция была выгодной для продавца, величина купонного дохода должна быть поделена между участниками сделки, пропорционально периоду хранения облигации между двумя выплатами.
Причитающаяся участникам сделки часть купонного дохода может быть определена по формуле обыкновенных, либо точных процентов. Накопленный купонный доход на дату сделки можно определить по формуле:
 , (2.2) , (2.2)
где CF – купонный платеж; t – число дней от начала периода купона до даты продажи (покупки); N – номинал; k – ставка купона; m – число выплат в год; В = {360, 365 или 366} – используемая временная база (360 для обыкновенных процентов; 365 или 366 для точных процентов).
В рассматриваемом примере с момента предыдущей выплаты 10/01/97 до даты заключения сделки 18/03/97 прошло 67 дней.
Определим величину НКД по облигации на дату заключения сделки:
НКД = (100000 ´ (0,3333 / 4) ´ 67) / 90 = 6203,08
НКДточн. = (100000 ´ (0,3333 / 4) ´ 67) / 91,25 = 6118,10.
Рассчитанное значение представляет собой часть купонного дохода, на которую будет претендовать в данном случае продавец. Свое право на получение части купонного дохода (т.е. за 67 дней хранения) он может реализовать путем включения величины НКД в цену облигации. Для упрощения предположим, что облигация была приобретена продавцом по номиналу.
Определим курс продажи облигации, обеспечивающий получение пропорциональной сроку хранения части купонного дохода:
К = (N + НКД) / 100 = (100000 + 6203,08) / 100 = 106,20308 » 106,2.
Таким образом, курс продажи облигации для продавца, должен быть не менее 106,20. Превышение этого курса принесет продавцу дополнительный доход. В случае, если курсовая цена будет меньше 106,20, продавец понесет убытки, связанные с недополучением своей части купонного дохода.
Соответственно часть купонного дохода, причитающаяся покупателю за оставшиеся 23 дня хранения облигации, может быть определена двумя способами.
1. Исходя из величины НКД на момент сделки:
CF - НКД = 8332,50 - 6203,08 = 2129,42 или
N + CF - P = 100000 + 8332,50 - 106203,08 = 2129,42.
2. Путем определения НКД с момента приобретения до даты платежа:
(100000 ´ (0,3333 / 4) ´ 23) / 360 = 2129,42.
Нетрудно заметить, что курс в 106,2 соответствует ситуации равновесия, когда и покупатель, и продавец, получают свою долю купонного дохода, распределенную пропорционально сроку хранения облигации. Любое отклонение курсовой цены приведет к выигрышу одной стороны и, соответственно, к проигрышу другой.
На практике, минимальный курс продажи данной облигации на бирже 18/03/97 был равен 108,00, средний – 108,17. Средний курс покупки по итогам торгов составил 107,43, а максимальный – 108,20 . Таким образом, в целом, ситуация на рынке в тот день складывалась в пользу продавцов ОГСЗ этой серии.
В процессе анализа эффективности операций с ценными бумагами, для инвестора существенный интерес представляют более общие показатели – текущая доходность (current yield – Y) и доходность облигации к погашению (yield to maturity – YTM). Оба показателя определяются в виде процентной ставки.
Текущая доходность (current yield – Y)
Текущая доходность облигации с фиксированной ставкой купона определяется как отношение периодического платежа к цене приобретения:
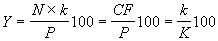 , (2.3) , (2.3)
где N – номинал; P – цена покупки; k – годовая ставка купона; K –
курсовая цена облигации.
Текущая доходность продаваемых облигаций меняется в соответствии с изменениями их цен на рынке. Однако с момента покупки она становится постоянной (зафиксированной) величиной, так как ставка купона остается неизменной. Нетрудно заметить, что текущая доходность облигации приобретенной с дисконтом будет выше купонной, а приобретенной с премией – ниже.
Определим текущую доходность операции из предыдущего примера при условии, что ОГСЗ была приобретена по цене 106,20.
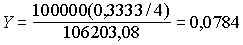 или 7,84%. или 7,84%.
Как и следовало ожидать, текущая доходность Y ниже ставки купона k (8,33%), поскольку облигация продана с премией, равной НКД.
Показатель текущей доходности не учитывает вторую составляющую поступлений от облигации – курсовую разницу между ценой покупки и погашения (как правило – номиналом). Поэтому он не пригоден для сравнения эффективности операций с различными исходными условиями.
В качестве меры общей эффективности инвестиций в облигации используется показатель доходности к погашению.
Доходность к погашению (yield to maturity – YTM)
Доходность к погашению представляет собой процентную ставку (норму дисконта), устанавливающую равенство между текущей стоимостью потока платежей по облигации PV и ее рыночной ценой P.
Для облигаций с фиксированным купоном, выплачиваемым раз в году, она определяется путем решения следующего уравнения:
 , (2.4) , (2.4)
где F – цена погашения (как правило F = N).
Уравнение (2.4) решается относительно YTM каким-либо итерационным методом. Приблизительное значение этой величины можно определить из соотношения (2.5):
 . (2.5) . (2.5)
Поскольку применение ППП EXCEL освобождает нас от подобных забот, рассмотрим более подробно некоторые важнейшие свойства этого показателя.
Доходность к погашению YTM – это процентная ставка в норме дисконта, которая приравнивает величину объявленного потока платежей к текущей рыночной стоимости облигации. По сути, она представляет собой внутреннюю норму доходности инвестиции (internal rate of return – IRR). Подробное обсуждение недостатков этого показателя можно найти в [9, 16]. Здесь же мы рассмотрим лишь один из них – нереалистичность предположения о реинвестировании периодических платежей.
Применительно к рассматриваемой теме это означает, что реальная доходность облигации к погашению будет равна YTM только при выполнении следующих условий.
Облигация хранится до срока погашения.
Полученные купонные доходы немедленно реинвестируются по ставке r = YTM.
Очевидно, что независимо от желаний инвестора, второе условие достаточно трудно выполнить на практике. В табл. 2.1 приведены результаты расчета доходности к погашению облигации, приобретенной в момент выпуска по номиналу в 1000 с погашением через 20 лет и ставкой купона 8%, выплачиваемого раз в год, при различных ставках реинвестирования.
Таблица 2.1
Зависимость доходности к погашению от ставки реинвестирования
Ставка
реинвестирования
r
|
Купонный доход
за 20 лет
|
Общий доход
по облигации
за 20 лет
|
Доходность
к
погашению
|
| 0% |
1600,00 |
1600,00 |
4,84% |
| 6% |
1600,00 |
3016,00 |
7,07% |
| 8% |
1600,00 |
3801,00 |
8,00% |
| 10% |
1600,00 |
4832,00 |
9,01% |
Из приведенных расчетов следует, что между доходностью к погашению YTM и ставкой реинвестирования купонного дохода r существует прямая зависимость. С уменьшением r будет уменьшаться и величина YTM; с ростом r величина YTM будет также расти.
На величину показателя YTM оказывает влияние и цена облигации. Зависимость доходности к погашению YTM облигации со сроком погашения 25 лет и ставкой купона 6% годовых от ее цены Р показана на рис. 2.1.

Рис. 2.1. Зависимость YTM от цены P
Нетрудно заметить, что зависимость здесь обратная. Сформулируем общие правила, отражающие взаимосвязи между ставкой купона k, текущей доходностью Y, доходностью к погашению YTM и ценой облигации Р:
если P > N, k > Y > YTM;
если P < N, k < Y < YTM;
если P = N, k = Y = YTM.
Руководствуясь данными правилами, не следует забывать о зависимости YTM от ставки реинвестирования купонных платежей, рассмотренной выше. В целом, показатель YTM более правильно трактовать как ожидаемую доходность к погашению.
Несмотря на присущие ему недостатки, показатель YTM является одним из наиболее популярных измерителей доходности облигаций, применяемых на практике. Его значения приводятся во всех публикуемых финансовых сводках и аналитических обзорах. В дальнейшем, говоря о доходности облигации, мы будем подразумевать ее доходность к погашению.
|