| Научная работа
Автор Бирюков Павел Вячеславович.
Гимназия №1 города Полярные Зори
Январь-май 2004 г.
Производная функция
Поставим своей задачей определить скорость, с которой изменяется величина у в зависимости от изменения величины х. Так как нас интересуют всевозможные случаи, то мы не будем придавать определенного физического смысла зависимости y=f(x), т.е. будем рассматривать величины х и у как математические.
Рассмотрим функцию y=f(x), непрерывную на отрезке [а, b]. Возьмем два числа на этом отрезке: х и х+∆x; первое, х, в ходе всего рассуждения считаем неизменным, ∆x — его приращением. Приращение ∆x; аргумента обусловливает приращение ∆у функции, причем:
∆y=f(x+∆x)-f(x). (I)
Найдем отношение приращения ∆у функции к приращению ∆x аргумента:
∆у/∆x=(f(x+∆x)-f(x))/ ∆x. (II)
По предыдущему, это отношение представляет собой среднюю скорость изменения у относительно х на отрезке
[x, x+∆x].
Будем теперь неограниченно приближать ∆x к нулю.
Для непрерывной функции f(x) стремление ∆x к нулю вызывает стремление к нулю ∆у, отношение (II) становится при этом отношением бесконечно малых, вообще величиной переменной. Пусть это переменное отношение (II) имеет вполне определенный предел(утверждать, что определенный предел отношения ∆x/∆у всегда существует нельзя), обозначим его символом f '(х).
| lim((f(x+∆x)-f(x))/ ∆x)=f’(x)
∆
x→0
|
|
(III)
С физической точки зрения этот предел есть значение скорости изменения функции f(x) относительно ее аргумента при данном значении х этого аргумента. В анализе этот предел называют производной данной функции в точке х.
Определение. Производной данной функции в точки х называется предел отношения приращения этой функции к приращению аргумента в точке х, когда приращение аргумента стремится к нулю.
2°. Пусть каждому значению аргумента х соответствует определенное значение скорости изменения функции f(x). Тогда скорость f '(х) есть новая функция аргумента х, она называется производной функцией от данной функции f(x).
Например, производная функция от квадратной функции Q=bt+at2 есть линейная функция Q' = b + 2at.
3°. Производная функция обозначается так: 1) у данной функции ставится штрих на том месте, где обычно помещается показатель степени, или 2) перед обозначением
данной функции ставится символ d/dx.
Если данная функция обозначена буквой у, то ее производная может быть обозначена:
1) у', читать: «производная функции у»,
или
2) dy/dx, читать: «дэ игрек по дэ икс».
Если данная функция обозначена символом f(x), то ее производная может быть обозначена:
1) f '(х), читать: «производная функции f(x)»,
или же
2) df(x)/dx, читать: «дэ эф от икс по дэ икс».
4°. Нахождение производной от данной функции называется дифференцированием данной функции.
Общее правило дифференцирования (нахождения производной) следующее:
1) найти приращение ∆y функции, т. е. разность значений функции при значениях аргумента x + ∆x и x;
2) найти отношение ∆y/∆x, для этого полученное выше равенство разделить на ∆x;
3) найти предел отношения ∆y/∆x при ∆x →0.
Пример. Найти производную функции у = х3 + 1 в любой точке x.
Решение. 1) ∆y = (x + ∆x)3 + 1 — (х3 + 1).
По выполнении действий:
∆y = Зx2*∆x+Зx*∆x 2+∆x 3;
2) ∆y/∆x=3x2 + Зx*∆x+∆x 2;
3) dy/dx = lim(3x2+3x*∆x+∆x 2 = 3x2+3x*0+0 = 3x2.
∆x→0
5°. Заметим, что производная линейной функции у= =kx+b есть величина постоянная, равная k.
Действительно, для линейной функции y = kx+b
∆у = k*∆x;
∆y/∆x=k;
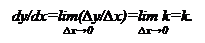
6°. Производные часто встречаются в технике и естествознании. Примеры производных: 1) при движении тела пройденный путь s есть функция от времени t скорость движения в данный момент времени t есть производная от пути s по времени t, т. е.
υ=ds/dt;
2) при вращательном движении твердого тела (например, маховика) (черт) вoкруг оси Ох, угол поворота его φ есть функция времени t:
φ=f(t);
угловая скорость (омега) в данный момент времени t есть производная от угла поворота по времени, т. е.

ω=dφ/dt;
3) при охлаждении тела температура Т тела есть функция времени t,
T=f(t);
скорость охлаждения в момент времени t есть производная от температуры Т по времени с, т. е. dT/dt;
4) теплоемкость С для данной температуры t есть производная от количества теплоты Q по температуре t,
C=dQ/dt;
5) при нагревании стержня его удлинение ∆l, как показывают тщательные опыты, лишь приближенно можно считать пропорциональным изменению температуры Дt. Поэтому функция l=f(t) является не линейной, а отношение ∆l/∆t лишь средним коэффициентом линейного расширения на отрезке [t, t+Дt]. Коэффициент линейного расширения а при данном значении температуры t есть производная от длины l по температуре t,
α=dl/dt
Касательная к кривой
1°. Возьмем на прямой АВ (черт) точку С и проведем через нее прямую СМ, не совпадающую с АВ. Вообразим, что прямая СМ вращается вокруг точки С так, что угол γ между прямыми стремится к нулю. Неподвижная прямая АВ называется в этом случае предельным положением подвижной прямой СМ.
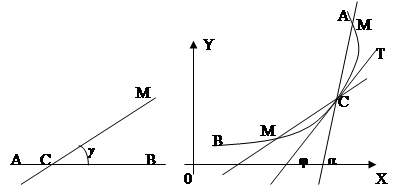 2°, Вообразим, что на кривой АВ (черт. 93) точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ. 2°, Вообразим, что на кривой АВ (черт. 93) точка М неограниченно приближается к неподвижной точке С, секущая СМ при этом вращается вокруг точки С. Может случиться, что, независимо от того, будет ли точка М приближаться к С в направлении от A к С или от В к С (на черт точка M'), существует одна и та же прямая СТ — предельное положение секущей СМ.
Определение. Прямая СТ, предельное положение секущей СМ, называется касательной к кривой в точке С.
Точка С называется точкой прикосновения или касания.
3°. Следствие. Угол φ (черт.), образуемым касательной СТ с осью Ох, есть предел угла α, образуемого с осью Ох секущей СМ, для которой данная касательная служит предельным положением.
Действительно, угол γ между касательной СТ и секущей СМ равен разности α — φ:
α — φ = γ.
По определению касательной, угол γ — бесконечно малая величина, а поэтому
φ — limα. (I)
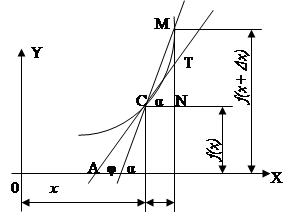 4°. Теорема. Если к линии y=f(x) в точке х имеется касательная, непараллельная Оу, то угловой коэффициент касательной равен значению производной f '(х), в точке х. 4°. Теорема. Если к линии y=f(x) в точке х имеется касательная, непараллельная Оу, то угловой коэффициент касательной равен значению производной f '(х), в точке х.
Доказательство. Угловой коэффициент касательной:
tgφ = tg(limα),
так как, по предыдущему, φ = limα.
Исключая случай φ = π/2,
в силу непрерывности тангенса имеем: tg(limα) = lim tgα.
Поэтому tgφ = lim tgα.
По формуле (VI) для СМ (черт.) имеем:
tgα=(f(x+Δx) -f (x))/Δx
Переходя к пределу при Δx→0 (точка М при Δx→ 0 неограниченно приближается к С, а угол α→φ), имеем:
| lim tg α =lim((f(x+Δ
x)-f(x))/Δ
x)=f '(x).
Δ
x→0 Δ
x→0
|
|
Следовательно, (IV)
Геометрический смысл производной
1°. Справедлива обратная теорема, выражающая геометрический смысл производной: если функция y=f(x) имеет определенную производную в точке х, то:
1) в этой точке имеется касательная к графику функции,
2) угловой коэффициент ее равен значению производной f '(x) в точке х.
Д о к а з а т е л ь с т в о. По условию, существует предел отношения Δy/Δx. Но отношение Δу/Δx есть тангенс угла секущей СМ (черт.).
| lim tgα = tg(limα)
Δ x→0 Δ x→0
|
|
Δy/Δx=tgx (1) Значит, согласно условию, существует
Из равенства (1) следует:
α=arctg(Δy/Δx).
Вследствие непрерывности арктангенса, имеем:
Но, по условию, существует и равен числу f '(х). Поэтому
| lim α = arctg f’(x).
Δ x→0
|
|
Полагая arctg f '(x)=φ, получаем:
Следовательно, существует предел α. Значит, существует прямая, проходящая через точку С, угол которой с Ох равен Такая прямая есть касательная в данной точке С[х, f(x)] и ее угловой коэффициент tgφ = f '(x). 2°. Замечания. 1. Угловой коэффициент k прямой y=kx+b называется наклоном прямой к оси Ох. Наклоном кривой y=f(x) в точке (х1, у1) называется угловой коэффициент касательной к кривой, он равен значению производной в этой точке, т. е. tgφ = f '(х1).
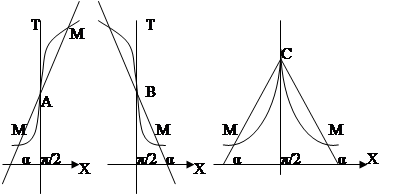
2. Если касательная в точке (х1, y1) кривой y=f(x) образует с Ох: а) острый угол φ, то производная f '(x)>0, так как tgφ >0 (черт.); б) тупой угол φ, то производная f '(х1)<0, так как tgφ<0 (черт.). Если касательная параллельна оси Оx (черт.), то угол φ=0, tgφ=0 и f '(х1) = 0.
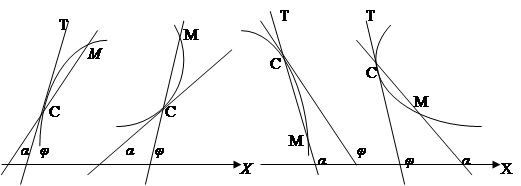
Когда касательная перпендикулярна оси Ох, то стремление α к π/2 может дать один и тот же бесконечный предел как «справа», так и «слева»: tgφ= + ∞ (черт.) пли tgφ=- ∞(черт.), или давать «слева» и «справа» бесконечные пределы разного знака (на черт. в точке С «слева» tgφ = +∞, а «справа» tgφ= - ∞). В первом случае, в точках А и В, функция f(x), говорят, имеет бесконечную производную; во втором случае, в точке С, не существует ни конечной, ни бесконечной производной.
 Заметим, что бесконечные производные рассматриваются лишь в точках непрерывности функции f(x). Заметим, что бесконечные производные рассматриваются лишь в точках непрерывности функции f(x).
3. Функция называется дифференцируемой в точке х, если ее производная в этой точке конечна. Функция f(x) дифференцируема в промежутке а<х<b, если ее производная f '(х) конечна в каждой точке промежутка.
4. Кривая, имеющая касательную, иногда расположена по обе стороны касательной (черт.). В этом случае говорят, что касательная пересекает кривую.
 4°. Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к кривой. Согласно условию взаимной перпендикулярности прямых, угловой коэффициент нормали есть -1/f '(x1). 4°. Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к кривой. Согласно условию взаимной перпендикулярности прямых, угловой коэффициент нормали есть -1/f '(x1).
Зависимость между дифференцируемостью и непрерывностью функции
1°. Теорема. Если функция y=f(x) имеет в точке х определенную производную, то она непрерывна в этой точке.
Доказательство. Напишем тождество:
Δy=(Δy/Δx)*Δx
так как всегда считаем Δx ≠ 0. При стремлении Δx к нулю отношение Δy/Δx имеет определенный предел (по условию) и, следовательно, есть величина ограниченная, Δx; есть бесконечно малая. Поэтому произведение (Δy/Δx)*Δx есть бесконечно малая величина, предел ее равен нулю, т. е.
 Следовательно, данная функция y=f(x) непрерывна. Следовательно, данная функция y=f(x) непрерывна.
2°, Обратная теорема неверна: непрерывная функция может не иметь производной. Например, функция:
y = |х|
(черт.) в точке x = 0 непрерывна. В то же время в точке х = 0 определенной касательной не существует, функция не дифференцируема.
3°. Следствие. В точке разрыва функция не имеет производной.
Впервые отчетливое различие между понятием непрерывности и дифференцируемости было дано гениальным русским ученым Н. И. Лобачевским.
Производные от элементарных функций
Производная постоянной
Теорема Постоянная функция имеет в любой точке x производную, равную нулю.
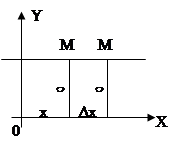 Дано: y=c (черт.). Дано: y=c (черт.).
Требуется доказать: с’=0.
| lim (Δ
x/Δ
y)=0,
т. е.
Δ
x→0
|
|
Доказательство: Для любого значения x и для всякого приращения Δx приращение функции Δy равно нулю, также равно нулю и отношение Δx/Δy. Отсюда
Таблица элементарных производных
| Функция
|
Ее производная
|
| Xp
|
px p-1, pÎR
|
| c (c-const)
|
0
|
| 1/x
|
-1/x2
|
| ____
√x
|
____
1/2√x
|
| Ex
|
ex
|
| sin x
|
cos x
|
| cos x
|
-sin x
|
| tg x
|
1/cos2x
|
| ctg x
|
-1/sin2x
|
| y = up
|
pu’up-1
|
| ln x
|
1/x
|
| ax
|
ax lna, a>0
|
| log a x
|
1/(x lna), a>0, a¹0
|
| arcsinx
|
___________
1/Ö1-x2
|
| arccosx
|
____________
-1/Ö1-x2
|
| arctg x
|
1/(1+x2)
|
| arcctg x
|
-1/(1+x2)
|
Правила дифференцирования
Пусть c – постоянная, f(x) и g(x) – дифференцируемые функции, тогда
c = 0;
(c * f(x))’ = c * (f(x))’;
(f(x) + g(x))’ = f ‘(x) + g ‘(x);
(f(x) * g(x))’ = f ‘(x) * g(x) + f(x) * g ‘(x);
(f(x)/g(x))’ = (f ‘(x) * g(x) – f(x) * g ‘(x))/g2(x);
Изучение функций с помощью производной
Признаки постоянства, возрастания и убывания функций
Будем считать, что рассматриваемая функция y=f(x) определена и дифференцируема в каждой точке отрезка a ≤ x ≤ b.
1°. Известно, что постоянная функция имеет в каждой точке отрезка производную, равную нулю. В полных курсах анализа доказывается обратное, что функция f(x) постоянна на отрезке [а, b], если в каждой точке отрезка ее производная f '(х) равна нулю.
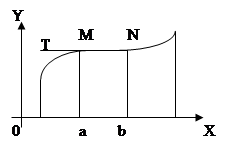 Иллюстрируем это геометрически. Если f ' (x) = 0 в каждой из точек отрезка [а, b], то касательная к графику функции y=f(x) в каждой из точек х (а ≤ х ≤ b) параллельна оси Ох. При переходе х от одного значения к его последующим значениям точка М. графика функции, являющаяся точкой прикосновения касательной, сдвигается вправо, но остается на направлении касательной, проведенной вточке М, так как касательная при этом переходе не меняет своего направления. Вследствие этого на отрезке [а, b] Иллюстрируем это геометрически. Если f ' (x) = 0 в каждой из точек отрезка [а, b], то касательная к графику функции y=f(x) в каждой из точек х (а ≤ х ≤ b) параллельна оси Ох. При переходе х от одного значения к его последующим значениям точка М. графика функции, являющаяся точкой прикосновения касательной, сдвигается вправо, но остается на направлении касательной, проведенной вточке М, так как касательная при этом переходе не меняет своего направления. Вследствие этого на отрезке [а, b]
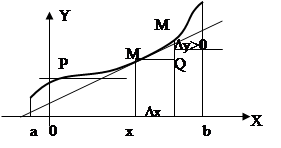 график функции y=f(x) обращается в прямую MN, параллельную оси Ох, а значение функции, равное f(а), остается неизменным (черт.). график функции y=f(x) обращается в прямую MN, параллельную оси Ох, а значение функции, равное f(а), остается неизменным (черт.).
2°. Если в промежутке a<x<b функция y=f(x) возрастающая (черт.), то при увеличении х каждое последующее ее значение более предыдущего и потому для каждого данного значения х приращения Δx и Δу положительны, отношение Δy/Δx положительно и при стремлении Δx к нулю принимает только положительные значения. Вследствие этого его предел — производная f '(х) — положительна или равна нулю
f '(x) ≥ 0
Если в промежутке а<х<b функция y=f(x) убывающая (черт.), то при увеличении х каждое последующее значение функции менее предыдущего. Поэтому для каждого данного значения x в то время, когда приращение Δx положительно, приращение Δy отрицательно, отношение Δy/Δx принимает только отрицательные значения и при стремлении Δx к нулю имеет своим пределом отрицательное число или нуль, т. е.
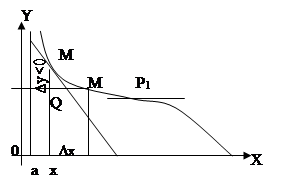 f '(x) ≤ 0. f '(x) ≤ 0.
Так как значение производной f '(х) равно угловому коэффициенту касательной к графику функции y = f(x):
f '(x) = tgφ,
и у возрастающей функции f '(x) = tgφ ≥ 0, то касательная к графику возрастающей функции образует с осью Ох острый угол или параллельна оси Ох (черт. 106). У убывающей функции f '(х) = tgφ ≤ 0, касательная к графику образует с осью Ох тупой угол или параллельна оси Ох (черт.).
В промежутке a<x<b возрастания (или убывания) функции не существует никакого отрезка а ≤ х ≤ b1 (a<a1<b1<b), во всех точках которого производная равна нулю, так как если бы f '(x) = 0 на отрезке a1 ≤ х ≤ b1 то функция f(x) имела бы одно и то же значение во всех точках этого отрезка, т. е. не была бы возрастающей (или убывающей).
Точки графика возрастающей (или убывающей) функции, в которых касательная параллельна оси Ox, являются отдельными точками в том смысле, что абсциссы их не составляют отрезка. На черт. и черт. такими точками являются Р и Р1.
3°. В полных курсах анализа доказываются следующие достаточные признаки возрастания и убывания функции:
функция f(x) возрастает (или убывает) в промежутке a<x<b, если:
1) производная f '(х) не отрицательна (или не положительна) в промежутке а<х<b,
f '(x) ≥ 0 (или f '(x) ≤ 0)
и
2) в этом промежутке не существует отрезка a1 ≤ x ≤ b1 (а<а1<b1<b), во всех точках которого производная f '(х) = 0.
4°. Пример. Определить промежутки возрастания и убывания функции: у = х3 — х2 — 8х + 2.
Решение. Чтобы применить признаки возрастания и убывания функции, найдем производную данной функции и определим значения х, при которых она положительна или отрицательна:
у' = Зх2 — 2х — 8.
Разложим трехчлен второй степени на множители, так как гораздо легче судить о знаке произведения по знакам множителей, чем о знаке суммы по знакам слагаемых.
Корни трехчлена:
| _______________
x=(1+
√1+24)/3=(1+
5)/3; x1
= - 4/3, x2
=2
.
|
|
Отсюда:
у' =3(х+4/3)(х-2).
Множитель x + 4/3 отрицателен при х < - 4/3 и положителен при х > - 4/3. Множитель х - 2 отрицателен при х < 2 и положителен при х > 2. Знак произведения будет тот или иной в зависимости от расположения точки х на оси Ох относительно точек -4/3 и 2.
Точки -4/3 и 2 разделяют всю ось на три промежутка;
1) — ∞ <x<-4/3, 2) -4/3<x<2, 3)2<x< + ∞.
Чтобы определить знак производной в каждом из промежутков, составим таблицу:
| № про-межутка
|
Характеристика промежутка
|
Знак x+4/3
|
Знак x-2
|
Знак f ’(x)
|
Данная
функция
|
| 1
|
- ∞ < x< - 4/3
|
—
|
—
|
+
|
возрастает
|
| 2
|
-4/3 < x < 2
|
+
|
—
|
—
|
убывает
|
| 3
|
2 < х < + ∞
|
+
|
+
|
+
|
возрастает
|
 Следовательно, данная функция возрастает в промежутках Следовательно, данная функция возрастает в промежутках
- ∞ <x < -4/3 и 2 <x < + ∞ и убывает в промежутке — 4/3 < х <2.
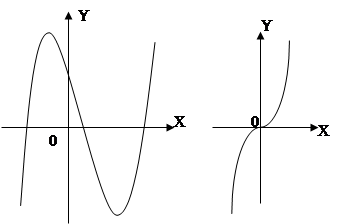
График данной функции представлен на черт.
5°.Функция у = х3 (черт.) имеет производную у = 3х2, которая положительна при всяком значении х, отличном от нуля. При х = 0 производная у' = 0. Функция у = х3 возрастает в промежутке — ∞<x<+∞; x= 0 есть отдельная единственная точка, в которой производная равна нулю, в ней функция возрастает. Действительно, при х = 0 х3 = 0, а при х < 0 х3 < 0 и при х > 0 х3 > 0.
Задачи на отыскание наибольших и наименьших значений величин
 1°. Требуется огородить проволочной сеткой длиной 60 м прямоугольный участок, прилегающий к стене дома ( черт.). Каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь? 1°. Требуется огородить проволочной сеткой длиной 60 м прямоугольный участок, прилегающий к стене дома ( черт.). Каковы должны быть длина и ширина участка, чтобы он имел наибольшую площадь?
Решение. Пусть ширина участка x м, а площадь у м2, тогда:
y = (60-2x)x = 60x - 2х2
Значения x и y не могут быть отрицательными, поэтому множитель 60 - 2x > 0, а 0<x<30.
Площадь y есть функция x, определим промежутки ее возрастания и убывания:
y' = 60 - 4x.
y'>0, и функция возрастает, когда x<15; y<0, и функция убывает, когда x>15.
| Если ширина х =
|
0
|
5
|
10
|
15
|
20
|
25
|
30
|
| то площадь y =
|
0
|
250
|
400
|
450
|
400
|
250
|
0
|
Кривая (черт.) поднимается от начала 0 до точки М(х= 15), а затем начинает падать. В точке х= 15 функция имеет наибольшее значение.
 Следовательно, площадь участка наибольшая (максимум), если ширина х =15м, а длина 60 — 2x = 60 -- 30=30 (м) Следовательно, площадь участка наибольшая (максимум), если ширина х =15м, а длина 60 — 2x = 60 -- 30=30 (м)
2°. Каковы должны быть размеры прямоугольной комнаты, площадь которой 36 x2, чтобы периметр ее был наименьший?
Решение. Пусть длина равна х м, тогда ширина прямоугольника 36/x м, а периметр:
Y=2(x+36/x)=2x+72/x.
Периметр у есть функция длины x, определенная для всех положительных значений x:
0<x<+∞
Определим промежутки ее возрастания и убывания:
y’=2-72/x2=2(x2-36)/x2=2(x-6)(x+6)/x2.
 Знак производной определяется знаком разности x-6. В промежутке Знак производной определяется знаком разности x-6. В промежутке
0<x<6 y'<0, а в промежутке 6<x<+∞ y'>0.
Периметр убывает в промежутке 0<x<6 и возрастает в промежутке 6<x<+∞. График (черт.) построим по таблице:
| Если х =
|
→0
|
3
|
4
|
5
|
6
|
7
|
8
|
→∞
|
| То у =
|
→∞
|
30
|
26
|
24,4
|
24
|
24,3
|
25
|
→∞
|
Следовательно, периметр прямоугольника имеет наименьшее значение (минимум), если длина его 6 м и ширина 36/6 м = 6 м, т. е. когда он квадрат.
Максимум и минимум функции
Задачи на отыскание наибольших и наименьших значений величин имеют важное значение в технике и, как это ясно из примеров, сводятся к отысканию максимума и минимума функции.
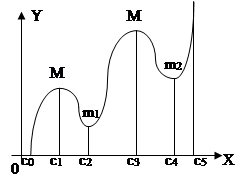 Определение. 1. Функция f(x) имеет при х=с максимум, если ее значение при х=с больше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с. Определение. 1. Функция f(x) имеет при х=с максимум, если ее значение при х=с больше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с.
2. Функция f(x) имеет при x= с минимум, если ее значение при х=с меньше, чем при любом другом значении х, взятом в некоторой окрестности точки х=с.
Термины "максимум" и "минимум" объединяются в один общий для них термин "экстремум".
Значение аргумента, которое дает максимум (или минимум) функции, называется точкой максимума (минимума), или точкой экстремума.
Функция может иметь только максимум, например функция y = 60x— 2х2 (черт. 111), или только минимум, например функция у = 2х+72/x (черт. 112), или иметь
максимум и минимум, как, например, функция у = х3— — х2 — 8х+2 (черт. 108). Функция может иметь несколько максимумов и минимумов (черт. 113), причем в этом случае максимумы и минимумы чередуются. Функция может не иметь ни максимума, ни минимума. Например, функции у = х3, y = ctgx, y = ax не имеют ни максимума, ни минимума, так как при возрастании х от — ∞ до +∞ первая и третья функции возрастают, а вторая только убывает.
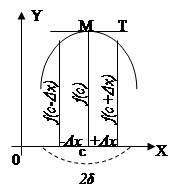 Максимум (минимум) функции может не быть наибольшим (наименьшим) значением ее. Так, изображенная на черт. 113 функция имеет в точке с. значение, большее максимумов с1М1 и с3М2, а в точке с0 значение, меньшее минимума c2m1, и c4m2, минимум c4m2 больше максимума с1М1. Максимум (минимум) функции в данной точке вообще есть наибольшее (наименьшее) значение функции по сравнению с ее значениями в точках, лежащих слева и справа от точки экстремума лишь в достаточной близости к ней. Максимум (минимум) функции может не быть наибольшим (наименьшим) значением ее. Так, изображенная на черт. 113 функция имеет в точке с. значение, большее максимумов с1М1 и с3М2, а в точке с0 значение, меньшее минимума c2m1, и c4m2, минимум c4m2 больше максимума с1М1. Максимум (минимум) функции в данной точке вообще есть наибольшее (наименьшее) значение функции по сравнению с ее значениями в точках, лежащих слева и справа от точки экстремума лишь в достаточной близости к ней.
Признаки существования экстремума
1°. Теорема (необходимый признак). Если в окрестности 2δ точки х=с:
1) функция f(х) дифференцируема, 2) значение х=с есть точка экстремума функции f(x), то ее производная в точке с равна нулю, m. e. f '(c) = 0.
Доказательство. Пусть для определенности х=c есть точка максимума (черт. 111). Представим значения независимого переменного х левой полуокрестности точки с в виде с — Δx:, а правой в виде с+ Δx, где 0< Δx < δ. Значение функции f(x) в точке с есть f(c), в левой полуокрестности оно равно f(с — Δx), а в правой f(c + Δx). Значения f(x) в окрестности 2δ точки с поставлены, таким образом, в зависимость от значений Δx, причем значение х = с -/+ Δx неограниченно приближается к числу с, если Δx стремится к нулю.
По определению максимума функции:
f(c- Δx)<f(c) и f(c + Δx)<f(c).
Отсюда:
f(c-Δx)-f(c)<0 и f(c + Δx)-f(с)<0.
Левые части неравенств выражают приращение функции в точке х = с при изменении аргумента соответственно на — Δx и + Δx. Составив отношение приращения функции к приращению аргумента, получаем:
| lim ((f(c - Δx
)-f(c))/(—Δx
)) = f‘(c)
и lim ((f(c + Δx
)-f(c))/(+Δx
)) = f‘(c)
.
- Δx
→0 +
Δx
→0
|
|
(f(c —Δx)—f(с))/(-Δx))>0 (1); (f(с + Δx)—f(с)/(+Δx))<0 (2) Оба отношения (1) и (2) имеют один и тот же предел при Δx → 0, так как по условно функция f(x) имеет в точке с определенную произвольную: Из неравенства (1) следует, что f '(с) либо положительна, либо равна нулю, а неравенство (2) показывает, что f '(с) не может быть положительной. Следовательно,
f‘(c) = 0,
что и требовалось доказать.
2°. Теорема (достаточный признак). Если в окрестности 2δ точки x = с:
1) функция f(x) непрерывна,
2) ее производная, f '(х), слева от точки х = с положительна, а справа отрицательна, то значение х = с есть точка максимума функции.
| lim f(c - Δ
x) = f(c)
и lim f(c +
Δ
x) = f(c).
- Δx
→0 +
Δx
→0
|
|
Доказательство. Данная функция непрерывна в точке c, поэтому число f(с) есть общий предел для f(c — Δx) и f(c+Δx) при Δx → 0 (как и в предыдущей теореме, здесь и в последующем 0 < Δx< δ): Данная функция f(x) в левой полуокрестности точки с — возрастающая, так как ее производная слева от точки с положительна, а в правой полуокрестности — убывающая, так как ее производная справа от точки с отрицательна (черт.), и вследствие этого ее значения
f(c —Δx) и f(c+Δx)
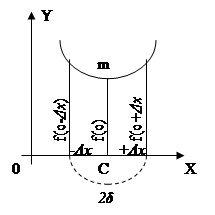 возрастают при стремлении Δx к нулю (по определению убывающей функции, меньшему значению аргумента отвечает большее значение функции, т. е. при x1>x2 f(x1)<f(x2)). возрастают при стремлении Δx к нулю (по определению убывающей функции, меньшему значению аргумента отвечает большее значение функции, т. е. при x1>x2 f(x1)<f(x2)).
Другими словами, как f(c — Δx), так и f(c+Δx) приближаются к своему пределу f(с) так, что для каждого значения Δx ≠ 0:
f(c - Δx) < f(c) и f(c + Δx) < f(c).
Но в таком случае f(c) есть максимум функции f(x) в точке х = с.
3°. Так же можно доказать, что если в окрестности 2δ точки х = с:
1) функция f(x) непрерывна, 2) производная f '(x) слева от точки х = с отрицательна, а справа положительна, то значение х = с есть точка минимума функции (черт.).
4°. Как в точке максимума, так и в точке минимума производная равна нулю (1°). Обратное неверно. Функция может не иметь ни максимума, ни минимума в точке, в которой производная равна нулю.
Например, функция у = х3 имеет в точке x =0 производную, равную нулю. Однако в точке х = 0 нет ни максимума, ни минимума, функция у = х3 при всех значениях х, в том числе и при x = 0, возрастает. Отсюда, в точке х=с функция f(x) не имеет на максимума, ни минимума, если при х = с ее производная равна нулю и имеет один и тот же знак как слева, так и справа от точки х = с.
5°. Определение. Значения аргумента х, при которых производная f '(х) равна нулю, называются стационарными точками.
Касательная в стационарных точках параллельна оси Ох. В окрестности точки максимума касательная составляет с осью абсцисс острый угол, если точка лежит слева от точки максимума, и тупой угол, если справа от нее (черт.). В случае минимума, напротив, касательная составляет с осью абсцисс тупой угол, если точка находится слева от точки минимума, и острый, если справа от нее (черт.).
Правило нахождения экстремума
1°. Чтобы найти экстремум функции, надо:
1) найти производную данной функции;
2) приравнять производную нулю и решить полученное уравнение; из полученных корней отобрать действительные и расположить их (для удобства) по их величине от меньшего к большему; в том случае, когда все корни оказываются мнимыми, данная функция не имеет экстремума;
3) определить знак производной в каждом из промежутков, отграниченных стационарными точками;
4) если производная положительна в промежутке, лежащем слева от данной стационарной точки, и отрицательна в промежутке, лежащем справа от нес, то данная точка есть точка максимума функции, если же производная отрицательна слева и положительна справа от данной стационарной точки, то данная точка есть точка минимума функции; если производная имеет один и тот же знак как слева, так и справа от стационарной тонки, то в этой точке нет ни максимума, ни минимума, функции;
5) затенить в данном выражении функции аргумент значением, которое дает максимум или минимум функции; получим значение соответственно максимума или минимума функции.
Если функция имеет точки разрыва, то эти точки должны быть включены в число стационарных точек, разбивающих Ох на промежутки, в которых определяется знак производной.
Нахождение экстремума при помощи второй производной
1°. Лемма. Если при х = с производная положительна (или отрицательна), то в достаточно малой окрестности точки х = с приращение функции и приращение аргумента в точке с имеют одинаковые (или разные) знаки.
Доказательство от противного. Пусть для определенности f '(c)>0, т. е. Предположим, что при стремлении ∆x к нулю приращения ∆y и ∆x имеют разные знаки. Тогда отношение ∆y/∆x отрицательно и его предел
f '(c) ≤ 0,
что противоречит условию.
Так же доказывается и вторая часть леммы.
2°. Теорема. Если при х = с первая производная функции f(x) равна нулю, f '(c)=0, а вторая производная положительна, f "(c)>0, то в точке х = с функция f(x) имеет минимум;
если же вторая производная отрицательна, f "(с) < 0, то в точке х = с функция f(x) имеет максимум.
| f ’’(c) = lim ((f’(c + ∆x)-f ’(c))/∆x)>0.
∆x→0
|
|
Доказательство. Вторая производная по отношению к первой производной является тем же, чем первая производная по отношению к данной функции, т. е. Согласно лемме, если при х = с производная (в данном случае вторая) положительна, то в достаточно малой окрестности 2δ точки с приращение функции (в данном случае первой производной) имеет тот же знак, что и приращение аргумента. Слева от точки с приращение аргумента отрицательно, значит, и приращение функции отрицательно, т.е.
f '(c — ∆x)—f(c)<0, (0 < ∆x < δ).
Отсюда:
f '(c-∆x)<f '(c) = 0. (1).
Справа от точки с приращение аргумента положительно, т. е.
f '(c +∆x)-f '(c)>0.
Отсюда:
f '(c + ∆x)>f '(c) = 0. (2)
Получили: первая производная функции f(x) слева от точки с отрицательна (1), а справа положительна (2). Значит, в точке х = с функция f(x) имеет минимум, как это и требовалось доказать.
Так же доказывается теорема и в случае f "(с)<0.
3°. Доказанная теорема определяет второй способ нахождения экстремума. Он отличается от первого тем, что третья и четвертая операции первого способа заменяются: а) нахождением второй производной и б) определением ее знака в стационарной точке. Результат исследования можно выразить так:
| Если знак числа f "(с),
|
то при х = с f(x) имеет
|
| плюс
минус
|
минимум
максимум
|
Если f '(с) = 0, то исследование функции на максимум и минимум надо провести первым способом.
4°. Пример 1. Исследовать вторым способом на максимум и минимум функцию: у = 5 — х2 — х3 — x4/4.
Решение. 1. Находим первую производную:
y ' = - 2х - Зx2 — x3
2. Приравниваем первую производную нулю и решаем полученное уравнение:
— 2x — Зx2 — x3 = 0, или x(x2+3х+2) = 0,
отсюда x = 0 или x2+ 3х + 2 = 0.
Решая квадратное уравнение x2 + 3х + 2 = 0, получаем:
x = (-3 + 1)/2.
Стационарных точек три: x1 = — 2, x2 = — 1 и х3 = 0.
3. Находим вторую производную:
у" = — 2 - бx — Зx2.
4. Определяем знак второй производной, заменяя х его значением сначала в первой, затем во второй и потом в третьей стационарной
точке:
при х = — 2 у'' = — 2 — 6(— 2) — 3(— 2)2 = — 2, при х = — 1 у" = — 2 — 6(— 1) — 3(— l)2 = + 1, при x = 0 у" = — 2.
Следовательно, данная функция имеет минимум при х = —1 и максимум при х = — 2 и при х =0,
Пример 2, Исследовать на максимум и минимум функцию: у = х4.
Решение: 1) y' = 4x3;
2) 4х3 = 0; х = 0;
3) y" = 12x2;
4) при х = 0 y" = 0.
Так как оказалось, что вторая производная равна нулю, то исследование ведем первым способом: при х < 0 у' = 4x3 < 0, а при х > 0 у' = 4x3 > 0. Следовательно, функция у = х4 имеет минимум в точке x = 0.
5°. Второй способ нахождения экстремума имеет смысл применять в том случае, когда вторая производная отыскивается просто; если же дифференцирование сопровождается трудными преобразованиями и не упрощает выражение первой производной, то первый способ может быстрее привести к цели.
Направление вогнутости кривой
Пусть две точки M1 и M2 имеют одну и ту же абсциссу. Если при этом ордината точки M1 более (менее) ординаты точки M2, то говорят, что точка M1 лежит выше (ниже) точки M2. Говорят также, что в промежутке а<х<b линия y = f(x) лежит выше (ниже) линии у=φ(х), если в этом промежутке каждая точка первой линии лежит выше (ниже) соответствующей ей точки второй линии, т. е. если
f(x)> φ(x) [или f(x)< φ(x)].
Определение. В промежутке а < х < b кривая— график дифференцируемой функции y=f(x) — называется вогнутой вверх (вниз), если она лежит выше (ниже) касательной в любой точке данного промежутка.
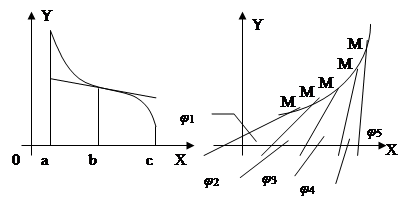 Кривая, изображенная на черт., является вогнутой, вверх в промежутке а < х < b и вогнутой вниз в промежутке b < х < с. Кривая, изображенная на черт., является вогнутой, вверх в промежутке а < х < b и вогнутой вниз в промежутке b < х < с.
2°. В более подробных курсах анализа доказывается, что если производная f '(х) — возрастающая (убывающая) функция в промежутке а < х < b, то кривая y=f(х) является вогнутой вверх (вниз) в этом промежутке.
Чтобы уяснить эту теорему, наметим на оси Ох (черт.)
произвольно ряд точек и проведем через каждую из них
прямую так, чтоб и угловом коэффициент прямой возрастал с возрастанием абсциссы намеченных точек; затем, приняв эти прямые за касательные к некоторой кривой линии [tgφ = f '(x)], построим эту кривую линию. Мы видим, что она может лежать только выше каждой из проведенных касательных.
3°. Достаточный признак вогнутости вверх (вниз). Если в промежутке а<х<b вторая производная f ''(x) положительна (отрицательна), за исключением отдельных точек, в которых она равна нулю, то кривая у=f(х) в этом промежутке вогнута вверх (вниз).
Действительно, если в промежутке а<х<b вторая производная f "(x), например, положительна, за исключением отдельных точек, в которых она равна нулю, то первая производная f '(х)—возрастающая функция, а кривая y = f(x), согласно предыдущему, является вогнутой вверх.
Если f "(x) = 0 не в отдельных точках, а в некотором промежутке, то в этом промежутке f '(x) — постоянная функция, a f(x) — линейная функция, график ее — прямая линия, и говорить о вогнутости не имеет смысла.
Точки перегиба
1°. Определение, Если в некоторой окрестности точки х = с кривая —график дифференцируемой функции y = f(x) — имеет слева и справа от точки х = с вогнутости противоположного направления, то значение х = с называется точкой перегиба.
 Точку М кривой (черт.), абсцисса которой х = с, называют также точкой перегиба, она отделяет дугу кривой, вогнутую вверх, от дуги, вогнутой вниз. Точкой перегиба может быть только та точка, в которой к кривой имеется касательная. В окрестности точки перегиба кривая лежит по обе стороны от касательной: выше и ниже ее. Заметим, что она расположена также по обе стороны от нормали. Но такая точка, как Р (черт.), в которой единственной касательной не имеется, точкой перегиба не является. Точку М кривой (черт.), абсцисса которой х = с, называют также точкой перегиба, она отделяет дугу кривой, вогнутую вверх, от дуги, вогнутой вниз. Точкой перегиба может быть только та точка, в которой к кривой имеется касательная. В окрестности точки перегиба кривая лежит по обе стороны от касательной: выше и ниже ее. Заметим, что она расположена также по обе стороны от нормали. Но такая точка, как Р (черт.), в которой единственной касательной не имеется, точкой перегиба не является.
2°. Так как слева и справа от точки перегиба х = с вогнутости кривой y=f(x) разного направления, то вторая производная f "(x) имеет слева и справа от точки х = с разные знаки или равна нулю. Полагая вторую производную непрерывной и окрестности точки х = с, заключаем, что в точке перегиба она равна нулю, т. е.
f(c) = 0.
3°. Отсюда следует правило нахождения точек перегиба:
1) найти вторую производную данной функции;
2) приравнять ее нулю и решить полученное уравнение (или найти те значения х, при которых производная теряет числовой смысл), из полученных корней отобрать действительные и расположить их no величине от меньшего к большему;
3) определить знак второй производной в каждом, из промежутков, отграниченных полученными корнями;
4) если при этом в двух промежутках, отграниченных исследуемой точкой, знаки второй производной окажутся разными, то имеется точка перегиба, если одинаковыми, то точки перегиба нет.
4°. Примеры. Найти точки перегиба и определить промежутки вогнутости вверх и вниз кривых:
1) у = lп х.
Р е ш е н и е. Находим вторую производную:
y '=1/x; y ''= -1/x2.
При всяком значении x = (0 < х <+∞) у" отрицательна. Значит, логарифмика точек перегиба не имеет и обращена вогнутостью вниз.
2) у = sin x.
Решение. Находим вторую производную:
y' =cos x, y'' = -sin x.
Полагая - sin x = 0, находим, что x = kπ, где k - целое число.
Если 0 < x< π, то sin x положителен и y '' отрицательна, если же π < x< 2π, то sin x отрицателен и y'' положительна и т. д. Значит, синусоида имеет точки перегиба 0, π, 2π,...
В первом промежутке 0 < x< π она обращена вогнутостью вниз, во втором - вогнутостью вверх и т. д.
Механическое значение второй производной
Предположим, что точка движется прямолинейно и пройденный ею путь определяется уравнением s = f(t), где t время. Скорость v в момент времени t есть производная от пути по времени, т. е.
v=ds/dt.
Скорость изменения скорости в момент времени t есть ускорение а,
a=(v)' = (ds/dt)' = (d2s/dt2).
Вторая производная от пути по времени есть ускорение прямолинейного движения в данный момент времени.
Пример. Прямолинейное движение точки совершается по закону:
s = (t3 — 2) м.
Определить ускорение в момент t = 10 сек.
Решение. Ускорение а = d2s/dt2.
Дифференцируя функцию s=t3 — 2, находим d2s/dt2 =6t
Следовательно,
a = 6t = 6*10 = 60; a = 60 м\сек2.
2°. Если движение неравномерное, то сила F, производящая его, непостоянна, каждому моменту времени t соответствует определенное значение действующей силы F, и сила, таким образом, есть функция времени t, F=f(t).
По закону Ньютона, в каждый момент времени действующая сила F равна произведению массы т на ускорение а, т. е.
F=ma, или f(t) = ma.
При прямолинейном движении a =d2s/dt2, поэтому
f(t) = m*d2s/dt2.
Зная уравнение прямолинейного движения, можно дифференцированием найти значение действующей силы в каждый момент времени.
Пример. Определить силу, под действием которой материальная точка совершает прямолинейные колебания по закону
s = А*sin(ωt + ω0).
Решение. f(f) = m*d2s/dt2, поэтому находим вторую производную функции:
s = А*sin(ωt + ω0), ds/dt = А*cos(ωt+ω0)* ω,
d2s/dt2=— А*sin (ωt + ω0)* ω2 = — s*ω2 = — ω2s; f(t) = — mω2s,
т. е. рассматриваемые колебания совершаются под действием силы, пропорциональной перемещению s и направленной в противоположную сторону.
Дифференциал
Сравнение бесконечно малых
1°. Составим отношение бесконечно малых, приближающихся к нулю по различным законам, так что каждому рассматриваемому моменту приближения к нулю одной из бесконечно малых отвечает определенное значение каждой из рассматриваемых бесконечно малых. Например, пусть в те моменты приближения к нулю, когда значения α = 10;1; 0.1; 0,01 и т.д.;
значения β =1000; 1; 0,001; 0,000001 и т.д.
Отношение β/α =100; 1; 0, 01; 0, 0001 и т.д., т.е.
значение отношения бесконечно малых не остается неизменным в процессе приближения их к нулю. Отношение бесконечно малых, таким образом,—величина переменная, и у нее может существовать предел, конечный (равный нулю, как в примере, или отличный от нуля) или бесконечный, а может предела и не существовать.
2°. Определения: 1) β называется бесконечно малой высшего порядка малости, чем α, если предел отношения β/α равен нулю, т. е. если
limβ/α =0;
2) β называется бесконечно малой низшего порядка малости, чем α, если
limβ/α = ∞;
3) β и α называются бесконечно малыми одинакового порядка малости, если предел их отношения есть число k, отличное от нуля, т. е. если
limβ/α = k, где k ≠ 0 и k ≠ ∞
4) β и α называются несравнимыми бесконечно малыми, если предела их отношения не существует.
3°. Примеры. 1. В рассмотренном выше примере limβ/α = 0, β высшего порядка малости, чем α, a limα/β = ∞ и α низшего порядка, чем β.
| lim (
β
/α
) = lim (1+x) =2
.
х→1
|
|
2. α =1—х и β=1— x2 —бесконечно малые, если х→1. Отношение β/α=(1- x2)/(1-x) = 1+x. Значит, 1—х и 1—x2 —бесконечно малые одинакового порядка малости при х→1.
3. Сравним 1 —cosx с х при x→ 0.
| lim((1-cosx)/x) = lim((2sin2
(x/2))/x) = lim((sin(x/2))*sin(x/2)/(x/2))=
x→0 x→0 x/2→0
=lim((sin(x/2))/(x/2))*lim(sin(x/2)) = 1*0 = 0
x/2
→
0 x/2
→
0
|
|
т. е. 1—cos x при х → 0 есть бесконечно малая высшего порядка малости, чем х.
Дифференциал функции
1°. Определение. Дифференциалом (dy) функции y=f(x) называется произведение значения производной f '(х) на произвольное приращение ∆x аргумента х, т. е.
(I)
2°. Для получения значения дифференциала функции необходимо знать два числа: начальное значение аргумента, х, и его приращение, ∆x.
Пример. Вычислить дифференциал функции у = x2 при изменении значения аргумента х от 3 до 3,1.
Решение. dy=f '(х)* ∆х. Найдем dy сначала для произвольных значений х и ∆x.
f '(x) = (x2)' =2x.
Поэтому
dy=2x*∆x.
Начальное значение аргумента х=3, приращение его ∆x = 3,1 — 3 = 0,1. Подставляя эти значения в выражение dy находим:
dy =2*3*0,1=0,6.
 Для данного значения независимого переменного х дифференциал функции f(x) есть линейная функция приращения независимого переменного ∆х. Для данного значения независимого переменного х дифференциал функции f(x) есть линейная функция приращения независимого переменного ∆х.
3°. Рассмотрим геометрический смысл дифференциала функции. На черт. в точке х проведена касательная к графику функции y=f(x). Из ∆MPT следует, что
PT = MP*tgφ = ∆x*f '(x).
Но по определению f '(х) *∆x = dy, поэтому PT = dy.
Дифференциал функции f(x) при данном значении х геометрически выражается приращением ординаты касательной к графику функции y=f(x) в точке х.
4°. Дифференциал dy и приращение ∆у вообще не равны между собой. На черт. dy = PT менее ∆y=PQ.
Очевидно, dy может быть и более ∆y. Это будет, например, если поднимающаяся кривая MN будет вогнута вниз.
5°. Пример. Для функции у=x2 при изменении х от 3 до 3,1 приращение ∆y = 2x*∆x + + ∆x2 = 2*3*0,1 + 0, 12 = 0, 61 Дифференциал dy = 2х *∆x = 2*3 * 0, 1 = 0,6. Принимая dy за приближенное значение ∆у, имеем: абсолютная погрешность приближения равна разности ∆у—dy=0,01, а относительная погрешность приближения есть отношение:
(∆y—dy)/dy=00,1/0,60=1,7%
6°. Разность между приращением и дифференциалом функции, ∆у—dy, высшего порядка малости, чем приращение аргумента, ∆x.
Действительно, отношение ∆y/∆x отличается от своего предела f '(x) на бесконечно малую α, причем α → 0 при стремлении ∆x к нулю,
∆y/∆x — f '(x)= α.
Производя вычитание в левой части равенства, получаем:
(∆y-f '(x)*∆x)/∆x = α, или (∆у - dy) ∆x= α,
| lim((∆y-dy)/ ∆x) = lim α
= 0.
∆x → 0 ∆x → 0
|
|
7°. Из сказанного следует: дифференциал функции есть приближенное значение ее приращения с относительной погрешностью, стремящейся к нулю вместе с приращением аргумента.
8°. Из изложенного следует, что дифференциал dy функции y=f(x) обладает двумя свойствами:
1) dy пропорционален ∆x (dy = k∆x, где k=y');
2) отношение (∆y—dy)/∆x стремится к нулю при стремлении ∆x к нулю.
Обратно. Если величина z обладает двумя свойствами:
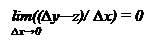 1) z=k∆x и 2) то z есть дифференциал функции у. 1) z=k∆x и 2) то z есть дифференциал функции у.
 Доказательство. Внося из (1) значение z во (2), имеем: Доказательство. Внося из (1) значение z во (2), имеем:
т. е. k = y',
а следовательно,
z = k∆x = y’∆x,
т. е. z есть дифференциал функции у.
Таким образом, эти два условия полностью определяют дифференциал.
Дифференциал аргумента. Производная как отношение дифференциалов
1°. Определение. Дифференциалом (dx) аргумента х называется, его приращение, ∆x:
dx = ∆х (II)
Может быть, некоторым основанием к этому служит то, что дифференциал функции у=х и приращение ее аргумента совпадают. Действительно,
dy = (x)' ∆x, или dy = ∆x.
Но так как
dy = dx, то dx = ∆x,
т.е. дифференциал функции у =х и приращение ее аргумента совпадают.
2°. Внеся в формулу (I) значение ∆x=dx, получаем:
(III)
т. е. дифференциал функции есть произведение ее производной на дифференциал аргумента.
3°. Формула (III) обладает замечательным свойством, именно: формула dy = f '(x)dx справедлива и в том случае, если x не является независимой переменной величиной, а является функцией другого аргумента, например и.
Действительно, если х есть функция от и, то f(x) есть сложная функция от u приращение dx обусловлено приращением ∆u, и dy надо вычислять по формуле;
dy = f 'u (x)* ∆u.
Но
f 'u (x)= f’x (x)* x’u
Значит,
dy = f’(x)—x'u * ∆u.
Но так как, по определению,
x'u ∆u = dx,
то, следовательно,
dy = f '(x)dx.
4°. Пример. Найти дифференциал функции:
_____________________
у = √ (e2x—1).
Решение. По формуле (III)
dy = у'*dx.
Находим у': ________ ________
y’ = e2x*2/( 2√ (e2x—1)) = e2x/ √ (e2x—1).
Значит _______
dy = e2x*dx/ √ (e2x—1)
5°. Из формулы (III) следует;
f’(x)=dy/dx,
т. е. производная функции равна отношению дифференциала функции к дифференциалу аргумента. Это иллюстрирует черт., где
dy/dx = PT/MP = tgφ=f '(x)
для произвольного значения dx = MP.
Приложения понятия дифференциала к приближенным вычислениям
1°. Разность ∆y—dy—бесконечно малая высшего порядка малости, чем ∆x, поэтому при достаточно малом ∆x
(IV)
Это означает, что при малых изменениях аргумента (от начального значения х) величину изменения функции y=f(x) можно приближенно считать пропорциональной величине изменения аргумента с коэффициентом пропорциональности, равным значению производной f '(x); кривую y=f (x) при этом можно приближенно заменить касательной к ней в точке х.
Так как ∆у = f(х + ∆x)—f (x), то, заменяя в формуле (IV) ∆у его выражением, имеем: f(x+∆x) - f(x) ≈ f '(x)* ∆x
| f(x+∆x) ≈ f(x) + f '(x)* ∆x
|
|
(V)
В математике производную применяют для:
Исследования функции на монотонность, экстремумы.
Нахождения касательной к графику.
Нахождения наибольших, наименьших значений функций.
Нахождения дифференциала для приближенных вычислений.
Для доказательства неравенств.
Рассмотрю некоторые примеры применения производной в алгебре, геометрии и физике.
Задача 1. Найти сумму 1+2*1/3+3(1/3)2+…+100(1/3)99;
Решение.
Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее x=1/3.
Для этого потребуется вспомогательная функция f(x)=x+x2+…+x100.
Ясно, что f ’(x)=g(x).
f(x) — сумма геометрической прогрессии.
Легко подсчитать, что f(x)=(x—x101)/(1—x). Значит,
g(x) = f ’(x) = ((1—101x100)(1—x)—(x—x100)(-1))/(1—x)2=(1—102x100+101x101)(1—x)2.
Подставлю x = 1/3.
Ответ: 0,25(9—205*3-99)
Задача 2. Найти сумму 1+2*3+3*32+…+100*399;
Решение.
Найду сумму g(x)=1+2x+3x2+…+100x99 и подставлю в нее x=1/3.
Для этого потребуется вспомогательная функция f(x)=x+x2+…+x100.
Ясно, что f ’(x)=g(x).
f(x) — сумма геометрической прогрессии.
Легко подсчитать, что f(x)=(x—x101)/(1—x). Значит,
g(x) = f ’(x) = ((1—101x100)(1—x)—(x—x100)(-1))/(1—x)2=(1—102x100+101x101)(1—x)2.
Подставлю x = 3.
Ответ: ≈ 2,078176333426855507665737416578*1050.
Задача 3. Найдите площадь треугольника AMB, если A и B — точки пересечения с осью OX касательных, проведенных к графику y = (9—x2)/6 из точки M(4;3).
Решение.
 т. A = укас1∩OX Решение: т. A = укас1∩OX Решение:
т. B = укас2∩OX укас =y(x0)+у’(x0)(x—x0);
y = (9—x2)/6 y’(x0) = -2x*1/6 = -x/3;
M(4;3)________ т.к. укас проходит через M(4;3), то
SAMB —? 3 = (9—x02) — (4—x0)* x0/3 | *3
18 = 9—x02—2x0(4—x0);
x02—8 x0—9 = 0;
Д/4 = 16 + 9;
x0 = 4+5 = 9;
x0 = 4—5 = -1
укас1 = -12 — (x—9)*9/3 = -3x+15;
укас1 = 4/3 + (x+1)*1/3 = x/3+5/3;
A(5;0); B(-5;0);
AM = √10 (ед.);
AB = 10 (ед.);
BM = 3√10 (ед.);
p — полупериметр; __
p = (4√10 + 10)/2 = 2√10 + 5;
__ __ __ __ __ __
S = √(2√10 + 5) (2√10 + 5—√10) (2√10 + 5—3√10) (2√10 + 5—10) =
= √(2√10 + 5)(√10 + 5)(5—3√10)(2√10—5) =
= √(40—25)(25—10) = 15 (ед2);
Ответ: 15 (ед2).
 Задача 4. Какая наименьшая плоскость может быть у треугольника OAB, если его стороны OA и OB лежат на графике функции y = (|x|—x)/2, а прямая AB проходит через точку M(0;1). Задача 4. Какая наименьшая плоскость может быть у треугольника OAB, если его стороны OA и OB лежат на графике функции y = (|x|—x)/2, а прямая AB проходит через точку M(0;1).
Решение:
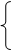 -x, x<0 -x, x<0
y =
0, x>0
A(a;-a); B(b;0);_
AO = |a|√2 = -a√2 (т.к. a<0);
BO = b;
Для т. B:
у1 = kx +z;
т.к. у1—график линейной пропорциональности, проходящий через т M(0;1), то z = 1.
0=kx+1;
k=-1/b;
Для т. A:
у1=kx+1;
-a=kx+1;
k=(-1-1a)/a;
у1A= у1B
(-a—a)/a = -1/b;
b+ab=a;
a(1—b)=b;
a = b/(1-b);
S∆AOB=0,5*AO*OB*sin/_AOB
ÐAOB =180o—45o = 135o
S∆AOB=0,5*(√2/2)* (-a)b√2 = -ab/2;
S∆AOB = -b2/(2(1—b)) = b2/(2(1—b)); D(y): b>1(т.к. при b<1 не образует ∆AOB.);
т.к. функция непрерывна и дифференцируема на b>1, то найду ее производную:
S’ = (4b(b—1)—b2)/(4(b—1)2) = (4b2—4b—2b2)/(4(b—1)2) = 2b(b—2)/(4(b—1)2) =
= b(b—2)/(2(b—1)2);
S’ = 0;
точки экстремума:
 b=0; b=0;
b=1;
b=2;
но b>1, значит
Sнаим =S(2) = 4/(2(2—1))=2(ед2);
Ответ: 2 ед2.
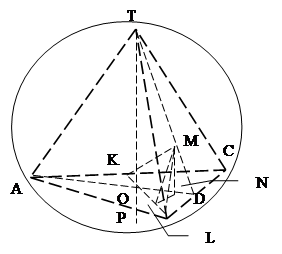
Задача 5. В прямоугольном параллелепипеде ABCDA1B1C1D1 с ребрами CD = 24, AD= 6 и DD1 =4 проведена плоскость через центр симметрии грани A1B1C1D1 , вершину А и точку Р, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью? На какие части делит точка P ребро DC в этом случае?
Решение. Проведем плоскость и построим сечение (рис.). АО Î АA1C1С - линия, принадлежащая данной плоскости. Продолжим АО до пересечения с CC1 в точке S. Тогда SP - линия пересечения грани DD1C1C и данной плоскости, а сечение ANMP - параллелограмм. Sсеч = SAMNP = SK*AP/2 , потому что SK/2— высота параллелограмма ANMP. Это видно из следующего рассуждения.
 В ΔASC ОC1 - средняя линия (значит SC1 = 4), в ΔPSC также средняя линия МC1, а плоскость A1B1C1D1 делит пополам любую линию между S и плоскостью ABCD, а значит и SK. В ΔASC ОC1 - средняя линия (значит SC1 = 4), в ΔPSC также средняя линия МC1, а плоскость A1B1C1D1 делит пополам любую линию между S и плоскостью ABCD, а значит и SK.
Пусть PC = x; ΔCLP подобен ΔDAP,
LC/AD = x/(24—x), LC = 6x/(24—x);_____________ ____________
Из ΔCLP: KC = (6x*x/(24—x))/(√(36x2/(24—x)2)+x2) = 6x/(√(36+ (24—x)2);
________ ___________________ __________________
Из ΔSCK: SK = √SC2+ KC2 = √64+36x2/(36+(24—x)2) = 2√16+9x2/(36+(24—x)2) ;
Из ΔADP: AP = √36+(24—x)2;_____ _________________ __________________
Sсеч = AP*SK/2 = 0,5*(√36+(24—x)2) 2√16+9x2/(36+(24—x)2) = √16(36+(24—x)2)+9x2;
Если S’(x) = 0, то 18x+16*2(24—x)(-1) = 0;
50x—32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min);
Sсеч = 312;
DP = 24—16*24/25 = 216/25;
Ответ: 312 кв. ед.; DC: 384/25; 216/25.
 Задача 6. Высота пирамиды TABC с основанием ABC проходит через середину ребра AC. Выберите на AC точку М так, чтобы площадь сечения пирамиды плоскостью, проходящей через точку M, середину ребра TC и вершину B, была наименьшей, если AB=BC=AC=TC=2. Задача 6. Высота пирамиды TABC с основанием ABC проходит через середину ребра AC. Выберите на AC точку М так, чтобы площадь сечения пирамиды плоскостью, проходящей через точку M, середину ребра TC и вершину B, была наименьшей, если AB=BC=AC=TC=2.
Решение. HF=FC=1/2;
S∆BME = BM*EK*1/2;___ _
Из ∆TCH => TH = √4—1=√3;
EF = TH/2=√3/2;
Пусть MC = x.
Из ∆BMC по теореме косинусов MB2= x2+4—2*2*x*1/2;
MB = √x2—2x+4; _ _
S∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2;
S∆BMC = 0,5*BM*PC, _ ________
PC = (2S∆BMC)/BM, PC = x√3/√x2—2x+4 ;
∆KMF подобен ∆PMC(по двум углам):
KF/PC = MF/MC(рис 2),_____ _ _________
KF = x√3(x—1/2)/(x√x2—2x+4) = √3(x—1/2)/(√x2—2x+4);
________ ______________________
Из ∆KEF => KE = √ KF2+EF2 = √3(x—1/2)2/(x2—2x+4)+3/4; _
S∆BME = 0,5√x2—2x+4 *√3(x—1/2)2/(x2—2x+4)+3/4 = 0,5√3(x—1/2)2+(x2—2x+4)*3/4;
Если S’(x) = 0, то
6(x—1/2)+(2x—2)*3/4 = 0;
15x—9 = 0;
x = 3/5; __
S(3/5) = √15/5 кв.ед.
Ответ: √15/5 кв.ед.
Задача 7. В сферу радиусом R вписана правильная треугольная пирамида, у которой боковое ребро образует с высотой пирамиды угол 60o. Какую наименьшую площадь может иметь треугольник MBK, если точка M лежит на апофеме пирамиды, а BK — высота основания пирамиды, не пересекающая апофему?
Решение. TP = 2R, ÐATO = 60o.
Пусть AB = BC = CA = a(рис.)
Тогда AO = a√3/3,
AD = BK = a√3/2, _ _
TO = AO*ctg60o= a√3/3*1/√3 = a/3,
OD = a√3 /6,
 AO2 = TO*OP = TO(2R - TO), AO2 = TO*OP = TO(2R - TO),
a2/3 = a(2R – a/3)/3, a = 3R/2.
S∆MBK = BK*LM*1/2, BK = const,
S∆MBK = f(LM),__
LM = √MN2+NL2
Пусть MD = x, тогда MN = x cos / NMD; _
cos Ð NMD = TO/TD = a/(3√a2/9+a2/12 = 2/√7, MN = 2x/√7 .
Из ∆ONL: LN = ON cos30o (ÐONL = 30o);
ON = OD – ND, _ _ _ _ _
ND = x sin ÐNMD = x √3/√7, ON = a√3/6 - x√3/√7,
LN = (a√3/6 - x√3/7)√3/2 = (a/4 – 3x/(2√7)),
LM = √4x2/7+(a/4 – 3x/(2√7))2. _ _
Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0,
8x/7 – 3a/4√7 + 9x/14 = 0,
25x/14 = 3a/4√7,
x = 21a/50√7. __ __
MN = (21a/50√7)*(2/√7) = 3a/25,
LN = a/4 – (3/2√7)*(21a/50√7) = 4a/25,
LM = √a2/625 + 9a2/625 = a√10/25. _
S∆MBK = a√3/2*a/5*1/2 = a√3/20 = 9√3 R2/80.
Ответ: 9√3 R2/80.
Задача 8. В сферу радиусом R вписана правильная треугольная пирамида, высота которой в 1,5 раза меньше высоты основания. Между боковой гранью пирамиды и сферой расположена правильная четырехугольная призма, одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем.
Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу радиусом R,
SO*1,5 = AD,
LMN – правильная четырехугольная призма.
Найти. Vпр = f(LM).
Пусть SO = H, тогда AD = 1,5H;
SO1 = R – радиус сферы; LM = x –высота призмы.
∆SKO1 подобен ∆SOD => O1K/OD = SO1/SD => OK1 = OD*SO1/SD.
Из ∆AO1O: R2 = AO2 + O1O2 = (2AD/3)2 + (AD*2/3 - R)2,
R2 = 4AD2/9 + 4AD2/9 –AD*R*4/3,
8AD2/9 = AD*R*4/3 => AD = 3R/2.
Отсюда OD = R/2;
AO1 = R и SO1 = R; _
SD = √R2 + R2/4 = R√5/2, _
OK1 = 2*R*R/(2R√5) = R√5/5;
O1K = R√5/5.
Из ∆O1FN => R2 = (O1K + x)2 + NF2,
NF = √R2 – R2/5 – 2x(√5)2/5 – x2 , Sосн = 2NF2. _
Vпр = Sосн*x = 2(R2 – R2/5 – 2x√5 R/5 - x2)*x;
Vпр = 2(4R2x/5 – 2x2√5 R/5 - x3);
V’пр(x) = 2(4R2/5 – 2x√5 R/5 - 3x2) = 0; _
x 1,2 = (2R√5/5 + √4R2/5 + 12R2/5)/(-3) = (2R√5/5 + 4R/√5)/(-3);
x = 2√5 R/15 _ _
Vпр.max = 2(4R2*2√5R/(5*15) – 2√5R*4R2/(45*5) - _ 40√5R3/(225*15)) = 16R3√5(1 – 1/3 – 5/45)/75 = 16√5R3/135.
Ответ: 16√5R3/135 м3 при H = 2√5R/15.
 Задача 9. В конус вписан цилиндр, одно из оснований которого лежит в плоскости основания конуса, а окружность другого основания принадлежит боковой поверхности конуса. Правильная четырехугольная призма расположена так, что ее нижнее основание лежит в плоскости верхнего основания цилиндра, вершины верхнего основания принадлежат боковой поверхности конуса. Отношение длины диагонали основания призмы к ее высоте равно отношению длины диаметра цилиндра к его высоте. При какой высоте цилиндра объем призмы будет наибольшим? Найти этот объем призмы, если высота конуса – H и радиус основания – R. Задача 9. В конус вписан цилиндр, одно из оснований которого лежит в плоскости основания конуса, а окружность другого основания принадлежит боковой поверхности конуса. Правильная четырехугольная призма расположена так, что ее нижнее основание лежит в плоскости верхнего основания цилиндра, вершины верхнего основания принадлежат боковой поверхности конуса. Отношение длины диагонали основания призмы к ее высоте равно отношению длины диаметра цилиндра к его высоте. При какой высоте цилиндра объем призмы будет наибольшим? Найти этот объем призмы, если высота конуса – H и радиус основания – R.
Дано. ASO – конус;
SO = H;
AO = R;
CL/CM = BK/BN;
Найти. BN, чтобы Vпр = max
Решение. BN = x, CM = h, Vпр = Sосн CM = CL2h/2.
∆CSD подобен ∆ASO: CD/AO = SD/SO;
CD/R = (H – x - h)/H;
CD = R(H – x -h)/H.
∆BSE подобен ∆ASO: BE/AO = SE/SO;
BE/R = (H - h)/H;
BE = R(H - h)/H.
Находим отношение CD/BE = (H – x - h)/(H - x).
Исходя из условия (CL/CM = BK/BN) задачи делаем вывод,
что CD/BE = h/x, т. е. (H – x - h)/(H - x) = h/x => h = (Hx – x2)/H
Тогда CD = R(H – x – (Hx – x2)/H)/H = R(H2 – Hx – Hx +x2)/H2 = R(H - x)2/H2,
CL = 2CD = 2R(H - x)2/H2.
V = 4R2(H - x)4(H - x)x/(2H*H4) = 2R2(H - x)5x/H5;
 V’(x) = 2R2((H - x)5 – 5(H - x)4 x)/H5 = 0, V’(x) = 2R2((H - x)5 – 5(H - x)4 x)/H5 = 0,
(H – x) – 5x = 0, x = H/6.
V = 2HR2(5H/6)5/(6H5) = 2R2H*55/66.
Ответ: при H/6, Vmax = 2R2H*55/66.
В физике производная применяется в основном для вычисления наибольших или наименьших значений для каких-либо величин.
Задача 1.Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: U = a/r2 – b/r, где a и b — положительные постоянные, r — расстояние между частицами.
Найти:
а) значение r0 соответствующее равновесному положению частицы;
б) выяснить устойчиво ли это положение;
в) Fmax значение силы притяжения;
г) изобразить примерные графики зависимости U(r) и F(r).
 U = a/r2 – b/r; Решение: U = a/r2 – b/r; Решение:
a и b — counts; Для определения r0 соответствующего равновесному
 r0 — ? положению частицы исследуем f = U(r) на экстремум. r0 — ? положению частицы исследуем f = U(r) на экстремум.
Fmax — ? Используя связь между потенциальной энергией поля
U и F, тогда F = -dU/dr, получим F = -dU/dr = - (-2a/r3+b/r2) = 0;
при этом r = r0; 2a/r3 = b/r2 => r0 = 2a/b;
Устойчивое или неустойчивое равновесие определим по знаку второй производной:
d2U/dr02= dF/dr0=-6a/r04 + 2b/r03 = -6a/(2a/b)4+2b/(2a/b)3=(-b4/8a3)<0;
равновесие устойчивое.
Для определения Fmax притяжения исследую на экстремумы функцию:
F = 2a/r3— b/r2;
dF/dr = -6a/r4 + 2b/ r3 = 0;
при r = r1 = 3a/b;
подставляя, получу Fmax = 2a/r31 — b/r31 = - b3/27a2;
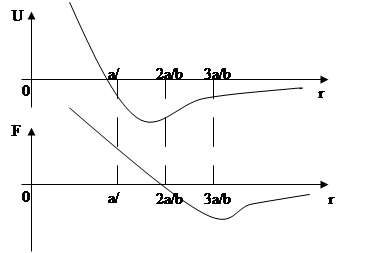 U(r) = 0; при r = a/b; U(r)min при r = 2, a/b = r0; U(r) = 0; при r = a/b; U(r)min при r = 2, a/b = r0;
F = 0; F(r)max при r = r1 = 3a/b;
Задача 2. Три резистора сопротивлениями R1, R2, R3 соединены параллельно. Сопротивление R1 в 9 раз больше сопротивления R2. Если все три резистора соединить последовательно, то сопротивление цепи равно R.
Определить сопротивления резисторов при которых сопротивление исходной цепи будет наибольшим.
 R1 = 9 R2 Решение: R1 = 9 R2 Решение:
При параллельном соединении резисторов эквивалентное
R1, R2, R3 сопротивление по формуле:
 1/Rэкв = 1/R1+1/R2+1/R3; 1/Rэкв = 1/R1+1/R2+1/R3;
Rэкв max— ? выражу R3 через R2:
R3 = R— R1—R2=R—10R2;
тогда 1/Rэкв = (10R—91R2)/(9R2(R—10R2));
Задача сведена к определению наименьшего значения функции в интервале [0;R/10].
Возьмем производную от f(1/Rэкв) по R2 и преобразуем ее:
(1/Rэкв)’ = -910(R2—R/7)(R2—R/13)/(9R22 (R-10R2)2);
В интересующем нас интервале только одна точка R2 = R/13 в которой эта производная меняет знак с “—” слева на ”+”справа. Поэтому в точке R2 = R/13 достигается минимум функции 1/Rэкв и максимум функции Rэкв, при этом
R1 = 9R/13; R2 = 1R/13; R3 = 3R/13;
Rэкв max = 9R/169;
Задача 4. В магнитном поле с большой высоты падает кольцо, имеющее диаметр в и сопротивление R. Плоскость кольца все время горизонтальна. Найти установившуюся скорость падения кольца, если вертикальная составляющая индукции магнитного поля изменяется с высотой H по закону B = B0(1 + αH), где α = const (черт.).
Решение. Пусть n – нормаль к плоскости кольца, тогда магнитный поток, созданный вертикальной составляющей магнитного поля.,
Ф = BS = B0(1 + αH)S, где S = πd2/4 – площадь контура.
ЭДС индукции, возникающая в кольце,
E = - Ф’(t) = - (B0(1 + αH)S)’ = - B0SαH’(t).
 Производная H’(t) = νн – это проекция скорости кольца на ось H. Таким образом, Производная H’(t) = νн – это проекция скорости кольца на ось H. Таким образом,
Ei = - B0Sα( - νн).
Так как скорость кольца направлена против оси H, то νн = - ν, где ν – модуль скорости кольца и Ei = B0Sαν.
По кольцу протекает индукционный ток
J = Ei /R = B0Sαν/R.
В результате в кольце за промежуток времени Δt выделяется количество теплоты
Q = J2RΔt.
На высоте H1 кольцо обладает механической энергией
W1 = mgH1 + mν2/2,
на высоте H2
W2 = mgH2 = mgH2 + mν2/2
(ν = const, т. е. скорость кольца не меняется). По закону сохранения энергии
W1 = W2 + Q => mgH1 = mgH2 + J2RΔt => mg(H1 - H2) = (B0Sαν/R)2RΔt =>
mg(H1 - H2) = (B0Sαν)2Δt/R (*)
Разность (H1 - H2) есть расстояние, пройденное кольцом при равномерном движении, поэтому H1 - H2 = νΔt, и уравнение (*) примет вид:
mgνΔt = (B0Sαν)2Δt/R => mg = (B0Sα)2ν/R =>
ν = mgR/(B0Sα)2 = 16mgR/(B0πd2α)2.
Ответ: ν = mgR/(B0Sα)2 = 16mgR/(B0πd2α)2.
Задача 6. Цепь с внешним сопротивлением R = 0,9 Ом питается от батареи из k=36 одинаковых источников, каждый из которых имеет ЭДС E=2 В и внутреннее сопротивление r0 = 0,4 Ом. Батарея включает n групп, соединенных параллельно, а в каждой из них содержится m последовательно соединенных аккумуляторов. При каких значениях m, n будет получена максимальная J во внешнем R(см. рис.).
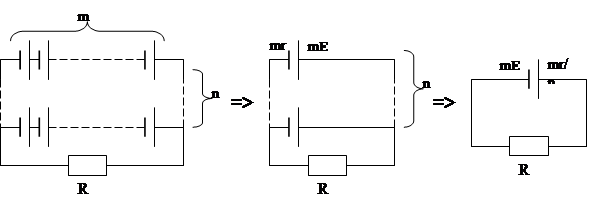
Решение:
При последовательном соединении аккумуляторов Eгр = m*E; rгр = r0*m;
а при параллельном соединении одинаковых rбат = r0m/n; Eбат = m*E,
По закону Ома J = mE/(R+ r0m/n) = mEn/(nR + r0m)
Т.к. k – общее число аккумуляторов, то k = mn;
J = kE/(nR + r0m) = kE/(nR + kr0/n);
Для нахождения условия при котором J тока в цепи максимальная исследую функцию J = J(n) на экстремум взяв производную по n и приравняв ее к нулю.
J’n-(kE(R—kr0/n2))/ (nR + kr0/n)2 = 0;
n2 = kr/R; .
n = √kr/R = √3,6*0,4/0,9 = 4;
m = k/n = 36/4 = 9;
при этом Jmax = kE/(nR + mr0) = 36*2/(4*0,9 + 9*0,4) = 10 А;
Ответ: n = 4, m = 9.
Задача 7. Платформа массой М начинает двигаться вправо под действием постоянной силы F. Из неподвижного бункера на нее высыпается песок. Скорость погрузки постоянна и равна m кг/с. Пренебрегая трением, найти зависимость от времени ускорения а платформы в процессе погрузки. Определить ускорение а1 платформы в случае, если песок не насыпается на платформу, а из наполненной высыпается через отверстие в ее дне с постоянной скоростью m кг/с.
Решение.
Рассмотрим сначала случай, когда песок насыпается на платформу
 Движение системы платформа-песок можно описать с помощью второго закона Ньютона: Движение системы платформа-песок можно описать с помощью второго закона Ньютона:
dP/dt = FS
P – импульс системы платформа-песок, FS – сила, действующая на систему платформа-песок.
Если через p обозначить импульс платформы, то можно написать:
dp/dt = F
Найдем изменение импульса платформы за бесконечно малый промежуток времени Dt:
Dp = (M+m(t+Dt))(u+Du) – (M+mt)u =FDt
где u – скорость платформы
Раскрыв скобки и, проведя сокращения получаем:
Dp = muDt + MDu+mDut+ mDuDt =FDt
Разделим на Dt и перейдем к пределу Dt ®0
Mdu/dt+mtdu/dt+mu=F
или
d[(M+mt)u]/dt = F
Это уравнение можно проинтегрировать, считая начальную скорость платформы равной нулю:
(M+mt)u = Ft
Следовательно:
u = Ft/(M+mt)
Тогда, ускорение платформы:
a = du/dt = (F(M+mt)-Ftm)/(M+mt)2 = FM / (M+mt)2
Рассмотрим случай, когда песок высыпается из наполненной платформы.
Изменение импульса за малый промежуток времени:
Dp = (M-m(t+Dt))(u+Du) +mDtu – (M-mt)u = FDt
Слагаемое mDtu есть импульс количества песка, которое высыпалось из платформы за время Dt
Тогда:
Dp = MDu - mtDu - mDtDu = FDt
Разделим на Dt и перейдем к пределу Dt ®0
(M-mt)du/dt = F
или
a1=du/dt= F/(M-mt)
Ответ: a = FM / (M+mt)2 , a1= F/(M-mt)
Список литературы
И. Ф. Суворов “Курс высшей математики для техникумов”. М.: Просвещение, 1964.
В. В. Ткачук “Математика—абитуриенту”. М.: Просвещение, 1980.
Д. Е. Родионов, Е. М. Родионов “Стереометрия в задачах”. М.: Учебный центр “Ориентир” – “Светоч”, 1998.
В. А. Колесников. “Физика. Теория и методы решения конкурсных задач. Часть II”. М.: Учебный центр “Ориентир” – “Светоч”, 2000.
Л. М. Лоповок “1000 проблемных задач по математике”. М.: Просвещение, 1995.
Д. Т. Письменный “Математика для старшеклассников. Теория\задачи”. М.: “Айрис”, “Рольф”, 1996.
М. Я. Выгодский “Справочник по элементарной математике”. Спб.: Союз, 1997.
В. И. Васюков, И. С. Григорьян, А. Б. Зимин, В. П. Карасева “Три подсказки – и любая задача решена! Часть III”. М.: Учебный центр “Ориентир” при МГТУ им. Н. Э. Баумана, 2000.
В. А. Чуянов “Энциклопедический словарь юного физика”. М.: Педагогическа-Пресс, 1999.
А. Б. Басков, О. Б. Баскова, Н. В. Мирошин “Математика. Часть 2. Алгебра и начала анализа”. М.: МИФИ, 1997.
|