А. С. Чуев, к.т.н. доцент Государственного университета управления, г. Москва.
В физике ... нет места для путанных мыслей ...
Действительно понимающие природу того или иного явления должны получать основные законы из соображений размерности.
Э. Ферми
В работе рассмотрены некоторые физические величины и закономерности квантовой механики с позиций логики строения дифференциальных уравнений, описывающих волновые процессы, а также системности физических величин, расположенных в LT- или MLT- размерностных элементах, имеющих планарное и упорядоченное размещение.
Приводится логический вывод уравнений Шредингера и объясняется происхождение так называемых операторов физических величин. Анализируются известные соотношения неопределенностей и системно обнаруживаемое расширение их числа и качественного вида. Исходя из системных представлений, предлагаются и рассматриваются известные и некоторые новые физические величины. С помощью представления о изоэнергетических электронных поверхностях атома дается физическое объяснение численного заполнения атомных электронных оболочек, которое получено без привлечения математического аппарата операторов физических величин.
Сделан вывод о том, что истинно (первоначально) квантуемыми величинами в составе водородоподобного атома являются длина волны, частота и скорость орбитального движения электрона, которые, в отличие от энергии, упорядоченно и целочисленно кратно (или дольно) изменяются с изменением порядкового номера орбиты.
В работе помещен раздел, касающийся плотности распределения квантовых состояний и физических представлений об этом, рассмотрены также и некоторые другие квантово механические представления.
Начало становления квантовой механики
Возникновение и начало становления квантовой механики связывают с открытием германским физиком Максом Планком (1900 г.) некой константы, связывающей энергию фотона с его частотой.
 или или 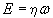 (1.1) (1.1)
В честь первооткрывателя эту константу назвали постоянной Планка. Значение h = (6,62618± 0,0004)× 10–34 Дж× с. Значение этой постоянной в 2π раз меньшее называют рационализированной постоянной Планка и обозначают той же буквой с чертой - 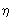 . Позднее физическую величину, равную по размерности произведению энергии на время, американский физик Р. Фейнман назвал действием. В системе СИ размерность действия ML2T–1. Таким образом, постоянная Планка является элементарным квантом физической величины действия. . Позднее физическую величину, равную по размерности произведению энергии на время, американский физик Р. Фейнман назвал действием. В системе СИ размерность действия ML2T–1. Таким образом, постоянная Планка является элементарным квантом физической величины действия.
Следует остановиться на используемом здесь понятии кванта и квантуемой физической величины (в дальнейшем, ФВ). Например, почему-то часто говорят о дискретных уровнях и квантах энергии, но совсем не говорят о квантуемости масс элементарных частиц или атомов. Хотя неравномерная дискретность (прерывистость) величин в том и другом случаях очень похожи.
По нашему мнению, настоящей (истинно) квантуемой (или упорядоченно-квантуемой) величиной следует называть ФВ, изменение которой происходит отдельными порциями целочисленно кратными некой элементарной доле, меньше которой она и не бывает. К таким упорядоченно-квантуемым ФВ относится рассматриваемый здесь квант действия (постоянная Планка, точнее, половина ее величины). К таким же истинно квантуемым величинам можно отнести элементарный электрический заряд, квант магнитного потока и некоторые другие величины. Эти кванты ФВ являются фундаментальными физическими постоянными (ФФП), связанными между собой закономерными взаимосвязями. А взаимосвязи ФФП наиболее ярко выражают единство и целостность всей природы.
Открытие М. Планка было связано с решением проблемы правильного описания энергетики равновесного теплового излучения, которое к механике вроде бы и не имеет прямого отношения. Некоторая связь излучения с механическим движением появилась лишь после выдвижения А. Эйнштейном (в 1905 г.) корпускулярной теории электромагнитного излучения, объяснявшей явления фотоэффекта.
Самым заметным вкладом в начальное зарождение квантовой механики можно считать разработку датчанином Нильсом Бором (в 1913 г.) теории, объяснившей планетарную модель строения атома - ранее созданную известным физиком новозеландского происхождения Эрнстом Резерфордом.
Теория Н. Бора для атома водорода была сформулирована в виде трех постулатов [1]:
1. Электрон в атоме может двигаться только по определенным стационарным орбитам, каждой из которых можно приписать определенный номер n = 1, 2, 3, … Такое движение соответствует стационарному состоянию атома, обладающему неизменной полной энергией En. Это означает, что электрон, движущийся по стационарной замкнутой орбите, вопреки законам классической электродинамики, не излучает энергию.
2. Разрешенными стационарными орбитами являются только те, для которых угловой момент импульса L электрона равен целому кратному значению постоянной Планка 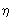 . Поэтому для n-й стационарной орбиты выполняется условие квантования . Поэтому для n-й стационарной орбиты выполняется условие квантования
 n = 1, 2, 3,… (1.2) n = 1, 2, 3,… (1.2)
3. Испускание или поглощение кванта излучения происходит при переходе атома из одного стационарного состояния в другое, при этом частота w излучения атома определяется разностью энергий атома в двух стационарных состояниях:
w nk = (Ek – En)/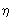 , k > n. (1.3) , k > n. (1.3)
Большой вклад в разработку основ квантовой механики внес французский физик Луи де Бройль, выдвинувший (в 1924 г.) идею о наличии волновых свойств у любых движущихся материальных частиц. Согласно гипотезе де Бройля свободно движущейся частице, обладающей энергией E и импульсом p, соответствует волновой процесс, частота которого
w =  , (1.4) , (1.4)
а длина волны
l Б =  . (1.5) . (1.5)
Как известно плоская волна частотой w , распространяющаяся вдоль оси x, представляется в комплексной форме выражением [1]:
x (x, t) = A exp[– i(w t – kx)], (1.6)
где A – амплитуда волны, а k =  – волновое число. – волновое число.
Поэтому согласно гипотезе де Бройля, свободной частице (с энергией E и импульсом p), движущейся вдоль оси x соответствует плоская волна
Y (x, t) = A exp[– 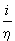 (Et – px)], (1.7) (Et – px)], (1.7)
распространяющаяся в том же направлении и описывающая волновые свойства частицы. Эту волну называют волной де Бройля. Связь параметров, как в волновом, так и в корпускулярном представлении микрочастиц осуществляется выражениями, включающими в себя постоянную Планка
E = 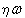 , , 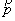 = =  , (1.8) , (1.8)
где 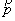 – импульс частицы, а – импульс частицы, а 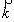 – волновой вектор. Эти выражения получили название уравнений де Бройля. – волновой вектор. Эти выражения получили название уравнений де Бройля.
Глядя на уравнения (1.8) можно предположить что, если бы не было размерностных различий между энергией и частотой, а также между импульсом и величиной, обратной длине волны, то постоянная Планка в этих уравнениях вовсе была бы не нужна. Но данная мысль является уж слишком необычной, поэтому она требует отдельного обсуждения. Рассмотрим здесь вещи более привычные.
Из условия постоянства фазы волны (1.7)
(Et – px) = const (1.9)
определяется фазовая скорость волны де Бройля, которая равна
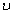 фаз = фаз = 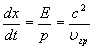 . (1.10) . (1.10)
Фазовая скорость всегда превышает скорость света в вакууме – с, поэтому ее принято считать фиктивной. Групповая скорость волн де Бройля 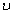 гр, совпадающая со скоростью движения частицы определяется, с учетом соотношений (1.8), выражением гр, совпадающая со скоростью движения частицы определяется, с учетом соотношений (1.8), выражением
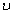 гр = гр =  . (1.11) . (1.11)
Дальнейшее развитие идей квантовой механики и ее становление в первую очередь обязано работам таких известных ученых физиков как Эрвин Шредингер, Вернер Гейзенберг, Макс Борн, Поль Дирак, Иордан, а также работам многих и многих других.
2. ВОЛНОВЫЕ УРАВНЕНИЯ КВАНТОВОЙ МЕХАНИКИ
Физическая теория, описывающая движение частиц, обладающих волновыми свойствами, первоначально получила название волновой механики. Однако это название вскоре было заменено другим – квантовая механика, так как оказалось, что волновая механика способна предсказывать дискретный характер или квантование различных параметров (ФВ) у движущихся микрочастиц.
Движение микрочастиц в квантовой механике описывается волновой функцией Y (x, y, z, t), подобной (1.7), но характеризующей поведение микрочастиц в трехмерном пространстве и времени. Иногда волновую функцию называют пси-функцией, по наименованию используемой для ее обозначения буквы.
Одним из постулатов квантовой механики является постулат о представлении волновой функции периодически меняющейся во времени и пространстве. Для стационарного случая волна принимается периодически меняющейся, но с неизменной плотностью распределения вероятности пространственного расположения микрочастицы.
Поскольку любая периодически меняющаяся функция может быть разложена в ряд Фурье, то волновую функцию принято описывать в суперпозиционном полигармоническом виде, приписывая каждой составляющей синусоидальный характер.
Общее временное уравнение Шредингера имеет вид
  . (2.1) . (2.1)
Здесь  – мнимая единица, а – мнимая единица, а 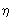 – рационализированная постоянная Планка. Стандартным символом в в (2.1) обозначен дифференциальный оператор Лапласа, который в декартовой прямоугольной системе координат определяется следующим образом: – рационализированная постоянная Планка. Стандартным символом в в (2.1) обозначен дифференциальный оператор Лапласа, который в декартовой прямоугольной системе координат определяется следующим образом:
D º 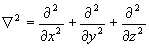 . (2.2) . (2.2)
Уравнение Шредингера для стационарных состояний, образуемое из (2.1) при допущении, что Ψ- функция может быть представлена в виде произведения двух частей, зависящих: одна от пространственных координат, а другая от времени, имеет следующий вид
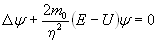 . (2.3) . (2.3)
Здесь малая буква ψ, в отличие от используемой в (2.1) большой буквы Ψ, обозначает лишь одну часть волновой функции, которая зависит только от пространственных координат. Вторая часть волновой функции, считающаяся находящейся в произведении с первой и здесь отсутствующая, зависит только от времени.
Почти все традиционные учебники физики, например [1, 2], говорят о невозможности выведения уравнений (2.1) и (2.3), приводя объяснение, что данные уравнения “сконструированы” или угаданы автором, точно также как в свое время были сконструированы или угаданы знаменитые уравнения Максвелла. Отдельные авторы считают, что вообще все природные закономерности устанавливаются лишь на основе опытных данных [1, стр.125].
С позиций системной взаимосвязи ФВ и системной обусловленности всех физических закономерностей, что изложено в работах автора [3-6], с таким заключением согласиться никак нельзя. Во-первых, системное и целостное представление природных закономерностей помогает формированию действительно научного мировоззрения [5, 6]. Во вторых, возможно выведение отдельных природных закономерностей привычным логическим путем. Оба эти направления необходимо раскрывать и показывать при обучении студентов физике, которую многие готовы признать - чуть ли не постулативной.
Система ФВ, варианты исполнения отдельных частей которой, применительно к рассматриваемой задаче, приведены на рис.1- рис.6, строится на упорядоченно расположенных LT- или MLT- размерностных элементах. ФВ непосредственно или с дополнительными размерностными коэффициентами многоуровнево входят в элементы системы. Закономерные взаимосвязи ФВ обнаруживаются в системе как их ближайшие системные связи или как попарное равенство произведений размерностей ФВ, располагаемых в элементах системы на противоположных вершинах выделенных параллелограммов. Более подробно эти моменты раскрыты в работе [4].
Применительно к рассматриваемой проблеме вывода волновых уравнений Шредингера следует уяснить ближайшие системные размерностные взаимосвязи ФВ действие. В системе по рис.3 и в последующих вариантах она названа действием актуальным, поскольку в квантовой механике (да и не только в ней) выявляется существование еще одного действия – это действие потенциальное, которое рассматривается чуть ниже.
Действие актуальное, квантом которого является постоянная Планка, связано через время с энергией и через длину с импульсом. В системном представлении ФВ по рис.1 - рис.4 эти связи хорошо видны.
Известна также и системно обнаруживается взаимосвязь кинетической энергии и импульса через массу микрочастицы (рассматриваем нерелятивистский случай):
 . (2.4) . (2.4)
Далее можно идти чисто логическим путем.
Если волновая функция описывается синусоидой (или суммой синусоид), то первая производная этой функции будет косинус, который отстает по фазе от синусоиды на p /2.
Не принимая пока во внимание амплитудных и размерностных различий, мы можем установить фазовое равенство первой производной Ψ- функции по времени и ее самой, умножив эту первую производную на  и приписав противоположный знак одной из сравниваемых величин. и приписав противоположный знак одной из сравниваемых величин.
Теперь ликвидируем размерностные отличия. Поскольку Ψ- функция от своей первой производной по времени отличается на размерность времени, то для получения размерностного равенства умножим Ψ- функцию на отношение энергии и постоянной Планка, являющейся квантом действия актуального.
Таким образом, получаем примерное размерностное соотношение:
 , (2.5) , (2.5)
в котором W – представляет собой полную энергию, а коэффициент пропорциональности n - безразмерная числовая величина. С учетом соотношения (2.4) выражение (2.5) можно переписать в виде
 , (2.6) , (2.6)
где в скобках фигурирует сумма кинетической и потенциальной энергий, называемая функцией Гамильтона.
Из представленной на рисунках системы (или просто из размерностных соображений) можно определить, что в выражении (2.6) импульс p можно представить - как отношение актуального действия (постоянной Планка) к длине. Коэффициент n возможно изменится, что непринципиально, а длина в минус второй степени в дифференциальных уравнениях, описывающих динамические волновые процессы, обычно представлена второй производной по направлению в пространстве (D ). Таким образом, мы логически приходим к уравнению (2.1). При этом размерность самой Ψ- функции может быть любой.
В общем случае числовой коэффициент n имеет не единственное, а множество значений, определяющих амплитуды различных гармоник Ψ- функции. Эти значения устанавливаются решением дифференциального уравнения с учетом начальных условий.
Заметим, что отношение квадрата постоянной Планка к удвоенному значению массы, представляющее по размерности произведение энергии на площадь, присутствует в правой части уравнения (2.1) вполне логично. Системные соотношения этой ФВ рассмотрены в разделе 4. В атомной физике эта величина характеризует изоэнергетическую поверхность, называемую поверхностью Ферми.
Однако использование временного уравнения Шредингера в форме выражения (2.1) не всегда может быть оправданным. Дело в том, что постоянная Планка сама представляет собой соотношение энергии с частотой (а также произведение импульса на длину волны), поэтому ее использование в формулах одновременно с указанными величинами ведет, как правило, к сильному затуманиванию в этих формулах физической сути явлений.
Если разделить обе части уравнения (2.1) на 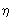 , то ситуация становится несколько яснее. Временное уравнение Шредингера принимает вид: , то ситуация становится несколько яснее. Временное уравнение Шредингера принимает вид:
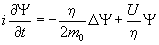 . (2.7) . (2.7)
Отношение потенциальной энергии U к постоянной Планка 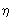 есть частота, а отношение постоянной Планка есть частота, а отношение постоянной Планка 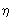 к массе, является физической величиной, называемой кинематической вязкостью (в термодинамике это коэффициент диффузии). Вот такие физические параметры, скорее всего, и определяют изменение пси-функции во времени. к массе, является физической величиной, называемой кинематической вязкостью (в термодинамике это коэффициент диффузии). Вот такие физические параметры, скорее всего, и определяют изменение пси-функции во времени.
Используя выражение (2.7) возможно осуществить простейший переход к волновому описанию стационарного состояния, что достигается приравниванием этого выражения нулю (поскольку изменения во времени принимаются отсутствующими). Сменив обозначение пси-функции на стационарное и сгруппировав одноименные величины, из (2.7) можно получить:
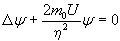 (2.8) (2.8)
В сравнении с выражением (2.3), называемым уравнением Шредингера для стационарных состояний, здесь отсутствует (не учтена) только кинетическая энергия Е.
Если вышерассмотренным способом анализировать с самого начала выражение (2.3), то оно легко выводится из следующих логических соображений. Синусоидальная y - функция будет равна своей собственной второй пространственной производной с обратным знаком (без учета амплитудных различий), если ее умножить на квадрат отношения импульса к действию актуальному.
В действительности мы это и наблюдаем, если выражение (2.3) переписать несколько иначе:
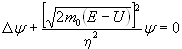 . (2.9) . (2.9)
Подкоренное выражение в этой формуле представляет собой квадрат импульса, а общий коэффициент при втором члене слева (при ψ) представляет собой квадрат волнового вектора k, так что в итоге мы приходим к выводу о том, что уравнение Шредингера для стационарных состояний это обычное волновое уравнение гармонических стационарных колебаний:
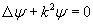 . (2.10) . (2.10)
Если взять не вторую, как в выражении (2.10), а первую пространственную производную пси-функции, представленной в общем виде, и построить дифференциальное уравнение на сравнении этой производной с самой Ψ- функцией, то мы получим уравнение с известным в квантовой физике оператором проекции импульса (формула 3.61 учебника [1]):
 . (2.11) . (2.11)
Из этого уравнения определяются возможные значения px. Запись последнего выражения становится более понятной с использование в уравнении волнового вектора
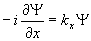 . (2.12) . (2.12)
Решением уравнения (2.12) является гармоническая функция вида
 . (2.13) . (2.13)
Считается, что собственные значения оператора проекции импульса px образуют непрерывный спектр значений от -  до + до +  . Однако, при ограничении пси-функции по координате спектр значений волнового вектора обязательно становится дискретным. Причем получаемые дискретные значения будут целочисленно кратны основному значению, определяемому максимально возможной длиной волны (вернее . Однако, при ограничении пси-функции по координате спектр значений волнового вектора обязательно становится дискретным. Причем получаемые дискретные значения будут целочисленно кратны основному значению, определяемому максимально возможной длиной волны (вернее  ). ).
Исходя из представленных и ряда иных соображений, можно предположить, что используемые в квантовой механике так называемые операторы ФВ, по сути, есть искусственные образования. Они представляют собой комбинации ограниченного числа ФВ (действия актуального, энергии и импульса) с операторами дифференцирования, изымаемыми (совместно с указанными ФВ) из начальных дифференциальных уравнений, описывающих волновое представление микрочастиц.
В этой связи можно поставить под сомнение оправданность применения в квантовой механике операторов ФВ, как не имеющих физического смысла. Тем более что используются еще и операторы квадратов ФВ.
По крайней мере, с системных позиций никак не подтверждается постулат квантовой механики о том, что в ней каждой ФВ ставится в соответствие определенный оператор, а соотношения между операторами имеют ту же структуру, что и соотношения между ФВ. Построить или изобразить систему операторов ФВ, структура которой была бы подобна структуре размерностной системы самих ФВ (или имела хотя бы какой-то свой смысл), никак не получается.
Можно отметить, что применение операторного метода в квантовой механике, раз он так широко используется, видимо в какой-то мере и оправдано, например, при вычислении средних значений ФВ, хотя эти вычисления возможны и без операторов, а на основе объемной плотности распределений ФВ (раздел 8).
3. КВАНТОВОМЕХАНИЧЕСКИЕ ПОТЕНЦИАЛЬНЫЕ ЯМЫ, ПОРОГИ И БАРЬЕРЫ ДЛЯ МИКРОЧАСТИЦ
В учебниках по квантовой механике обычно принято рассматривать примеры, описывающие поведение микрочастиц, находящихся в энергетических ямах или проходящих над (или под) энергетическими барьерами и порогами. При описании этих явлений, как правило, используются достаточно громоздкие математические формулы, из-за которых теряется физический смысл явлений.
Как пояснялось ранее, волновое уравнение Шредингера для стационарных состояний можно записать в форме (2.10) или в виде:
 . (3.1) . (3.1)
Решением (3.1) в общем виде является функция:
 . (3.2) . (3.2)
Для одномерной потенциальной ямы шириной а с бесконечно высокими (непроницаемыми) стенками, при использовании граничных условий  и и 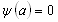 , получаем В = 0. Тогда уравнение (3.2) преобразуется в , получаем В = 0. Тогда уравнение (3.2) преобразуется в
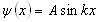 , (3.3) , (3.3)
которое для А ≠ 0 формально выполняется при
 , n = 0,1,2,3,… (3.4) , n = 0,1,2,3,… (3.4)
Последнее условие можно представить в виде
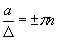 , n = 1,2,3,… (3.5) , n = 1,2,3,… (3.5)
где  - длина волны де Бройля с чертой ( - длина волны де Бройля с чертой (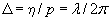 ). ).
Выражение (3.5) имеет физический смысл – это отношение ширины потенциальной ямы к модам длин стоячих волн де Бройля, способных к существованию в этой потенциальной яме и характеризующих микрочастицу, находящуюся в яме. Это выражение показывает, что в потенциальной яме с бесконечно высокими стенками присутствуют (отбираются или резонируют) лишь моды волны, с длиной волны целочисленно дольной основной длине волны  . Реально – половине этого значения. . Реально – половине этого значения.
Последнее выражение говорит о первоначальном квантовании в потенциальной яме длин волн или волновых векторов. Квантование уровней энергии для микрочастицы, находящейся в потенциальной яме, - это уже следствие отмеченного первоначального квантования дебройлевских длин волн.
Значит линейный или частотный спектр стоячих волн, описывающих состояние микрочастицы, находящейся в одномерной потенциальной яме с абсолютно непроницаемыми стенками, представляет собой основную длину волны (основную частоту) и бесконечно большой набор других волн, целочисленно дольных половине основной. Если же брать частоту волн де Бройля, то это основная частота и бесчисленное множество других частот, целочисленно кратных основной частоте.
Известное выражение, определяющее дискретный спектр уровней энергии микрочастицы, находящейся в одномерной потенциальной яме с бесконечно высокими стенками
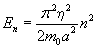 , n = 1, 2, 3, … (3.6) , n = 1, 2, 3, … (3.6)
для понимания, лучше преобразовать и представлять в виде:
 , n = 1, 2, 3, … (3.7) , n = 1, 2, 3, … (3.7)
Еще более понятным будет представление этого выражение в виде:
 , n = 1, 2, 3, … , (3.8) , n = 1, 2, 3, … , (3.8)
откуда вытекает равенство
 , n = 1, 2, 3, … , (3.9) , n = 1, 2, 3, … , (3.9)
Последнее выражение показывает, что на ширине одномерной потенциальной ямы обязательно укладывается целое чисто дебройлевских полуволн (их гармоник), каждая из которых по частоте выше, а по длине волны меньше основной моды в целое число раз. В потенциальной яме с бесконечно высокими стенками число этих волн бесконечно большое множество. То есть, начиная с граничной частоты, имеется частотный спектр волн де Бройля. Этот спектр линейчатый и он расположен в сторону увеличения частоты до бесконечности.
Выше мы рассмотрели параметры микрочастицы, помещенной в одномерную потенциальную яму с непроницаемыми стенками. Теперь рассмотрим волновые и другие параметры для микрочастиц, находящихся в многомерных потенциальных ямах, а также в ямах, ограниченных по высоте.
Нормированная волновая функция, получаемая решением уравнения Шредингера для микрочастицы, находящейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками, имеет вид:
 , (3.10) , (3.10)
0 < x <a1, 0 < y < a2, n1, n2 = 1, 2, 3, …
Энергия микрочастицы описывается выражением
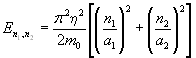 , n1, n2 = 1, 2, 3, … (3.11) , n1, n2 = 1, 2, 3, … (3.11)
Последнее выражение можно упростить и представить по аналогии с (3.8) в виде
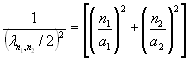 , n1, n2 = 1, 2, 3, … (3.12) , n1, n2 = 1, 2, 3, … (3.12)
Однако из последнего выражения нельзя получить простого соотношения, подобного (3.9). Выражение (3.12) говорит о том, что сложение волн происходит по правилу сложения векторных величин.
Аналогичное выражение для трехмерной потенциальной ямы имеет вид:
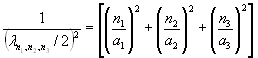 , n1, n2, n3 = 1, 2, 3, … (3.13) , n1, n2, n3 = 1, 2, 3, … (3.13)
Таким образом, можно заключить, что частица, находящаяся в многомерной потенциальной яме с бесконечно высокими стенками, описывается набором стационарных волн, длины которых целочисленно дольны величинам сторон этой потенциальной ямы.
Уравнение Шредингера для частицы, находящейся в сферической потенциальной яме с непроницаемой стенкой радиуса а, имеет решение идентичное (3.3) – (3.5) [1]. Это означает, что в такой потенциальной яме стационарные волны де Бройля состоят из основной волны, половина длины которой равна длине окружности сферы, и бесконечно большого набора других волн, целочисленно дольных основной.
Волновое представление микрочастиц позволяет описывать их проникновение в стенки потенциальных ям и прохождение сквозь потенциальные барьеры конечной высоты. Свободное движение частицы в области, где уровень потенциальной энергии меньше уровня кинетической энергии, описывается уравнением (3.1). Его решение, записанное в показательной форме, имеет вид:
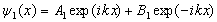 . (3.14) . (3.14)
В области потенциального порога или стенки потенциальной ямы, где потенциальная энергия превышает уровень кинетической энергии (U-E) > 0 волновое уравнение имеет другой вид:
 . (3.15) . (3.15)
Решением этого уравнения является сумма двух экспонент с действительными показателями степеней
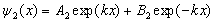 (3.16) (3.16)
В результате сшивки двух функций (3.14) и (3.16) с учетом требований конечности и гладкости, предъявляемых к пси-функции, коэффициент А2 принимается равным нулю, коэффициент А1 принимается равным единице и определяются значения коэффициентов В1 и В2.
При прохождении микрочастицы над низким потенциальным порогом (E – U) >0 тоже наблюдается отражение. При этом уравнение Шредингера в любой зоне имеет вид (3.1), решения уравнения предстают в виде (3.14), а коэффициенты получают значения:
А1 = 1, В2 = 0, 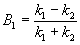 и и 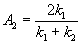 . (3.17) . (3.17)
Квадрат коэффициента В1 представляет собой коэффициент отражения R частицы от высокого потенциального порога, а квадрат коэффициента А2, представляет собой коэффициент прозрачности D, причем в = 1 – R.
Думается, что коэффициент прозрачности прямоугольного потенциального барьера, обычно представляемый в виде
 (3.18) (3.18)
лучше записывать по иному, в виде:
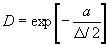 . (3.19) . (3.19)
Такая форма представления не только понятнее, но и проще для запоминания. Выражение (3.19) говорит и о том, что высокочастотные составляющие волновой функции проходят потенциальные барьеры с большими потерями. То есть волновые свойства микрочастицы, попадающей внутрь потенциальной стенки или потенциального барьера, становятся качественно иными. По-видимому, имеет место также и качественно иное изменение микрочастиц, при преодолении ими потенциального порога и освобождении из связанного состояния, например для электронов, покидающих атом.
4. СООТНОШЕНИЯ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА, ИХ СИСТЕМНОЕ ПРЕДСТАВЛЕНИЕ И РАЗВИТИЕ
Известные соотношения неопределенностей, сформулированные Вернером Гейзенбергом,
 (4.1) (4.1)
и
 (4.2) (4.2)
не только безупречны с точки зрения их системного представления, но и вполне могут быть расширены на соотношения неопределенностей иных пар ФВ.
Системная иллюстрация приведенных соотношений показана на рис.1. Другие возможные закономерные соотношения неопределенностей иных пар ФВ показаны на рис.2. Все эти соотношения представляют собой системные соотношения ФВ, называемой действием актуальным, элементарным квантом которой является постоянная Планка или ее половина.
Ниже приведены не только показанные на рисунках, но и другие возможные системные соотношения неопределенностей, проистекающие из действия актуального. Соотношения приведены в наименованиях пар ФВ, участвующих в соотношении неопределенностей данного типа. Эти пары ФВ в микромире дополнительны друг другу и их невозможно одновременно точно измерить, вот они:
Энергия – Время;
Импульс – Длина;
Момент инерции – Угловая скорость;
Вязкость динамическая – Объем пространства;
Масса – Вязкость кинематическая;
Ток (расход) массы – Площадь;
Гравитационный потенциал – Изменение (вращение) объема;
Действие потенциальное – Градиент времени;
Сила – Кинематическая физическая величина с размерностью LT;
Динамическая физическая величина с размерностью МL – скорость.
Можно привести и иные соотношения данного типа, в том числе с участием электромагнитных величин.
При обсуждении этих новых соотношений обычно возникает возражение – какой смысл в квантовой механике имеет момент инерции или угловая скорость? На эти возражения можно дать такой ответ: эти соотношения следуют из системы и, вероятнее всего, каждое из этих соотношений имеет свой определенный смысл, но мы эти смыслы пока не улавливаем.
Надо отметить, что традиционное в квантовой механике определение возможных и невозможных для одновременного и точного измерения пар ФВ, что обычно выполняется при помощи определения коммутируемости их операторов, обладает несравненно большей сложностью и количественной ограниченностью.
5. СИСТЕМНЫЕ СООТНОШЕНИЯ ПОТЕНЦИАЛЬНОГО ДЕЙСТВИЯ И АНАЛИЗ СТРОЕНИЯ ВОДОРОДОПОДОБНЫХ АТОМОВ
В системе ФВ по рис.3 - рис.6 потенциальным действием названа величина, представляющая собой произведение силы на площадь или энергии на длину. В микромире, судя по всему, данная величина относится к сохраняющимся и квантуемым (вернее, дискретным). Рассмотрим этот вопрос подробнее.
На рис.3 представлены возможные системные соотношения ФВ действие потенциальное, выполненные аналогично рассмотренным выше соотношениям неопределенностей с участием действия актуального.
Проследим происхождение ФВ потенциальное действие и рассмотрим ее свойства на примере боровской теории строения водородоподобного атома (иона атома, имеющего Z протонов в ядре и один орбитальный электрон с зарядом – e).
Приведем уравнение, описывающее условие вращения в атоме электрона массой me по круговой орбите радиуса r под действием кулоновской силы со стороны ядра, а также формулу Бора для квантования момента импульса электрона [1]:
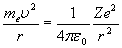 (5.1) (5.1)
 . (5.2) . (5.2)
Обычно совместным решением этих двух уравнений, определяют радиусы допустимых (стационарных) орбит электрона в водородоподобном атоме:
 , n = 1, 2, 3… (5.3) , n = 1, 2, 3… (5.3)
Здесь буквой а обозначен радиус первой стационарной орбиты в атоме водорода, так называемый боровский радиус.
Из выражений (5.1) и (5.2) можно определить не радиус орбит, а скорость электрона, находящегося на n - ой орбите:
 . (5.4) . (5.4)
Если применить известное соотношение между ФФП: постоянной Планка, зарядом электрона и электрической постоянной
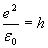 × 2a с , (5.5) × 2a с , (5.5)
то выражение (5.4) становится совсем простым
 (5.6) (5.6)
Учитывая, что последнее соотношение определяется только скоростью света – с, поскольку 2 и α (постоянная тонкой структуры) представляют собой числовые константы, то можно констатировать, что с изменением номера орбиты именно скорость электрона меняется упорядоченно и целочисленно кратно относительно некого значения, связанного со скоростью света. Поэтому истинно квантуемой величиной (в смысле первичности и упорядоченности квантования) для электрона, находящегося в составе атома, скорее всего, является его скорость.
Если при этом масса остается неизменной, то это означает квантование импульса. А если квантуется импульс, то это значит целочисленно дольно изменяются длины волн. Вернее целочисленно кратно изменяется количество дебройлевских полуволн, укладывающихся на данной орбите.
Отметим, что радиус электронной орбиты изменяется (в теории) более сложным образом - по квадратичной зависимости и, судя по всему, не может быть первоначально квантуемой величиной.
Обычно принято анализировать не скорости, а энергии электрона, находящегося на n – ой орбите атома. Полная энергия электрона складывается из его кинетической энергии
  (5.7) (5.7)
и потенциальной энергии кулоновского взаимодействия электрона с ядром
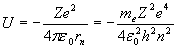 . (5.8) . (5.8)
Суммарная энергия электрона составляет:
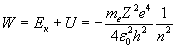 . (5.9) . (5.9)
С использованием соотношения (5.5) последняя формула тоже упрощается, принимая более простой и понятный вид:
 . (5.10) . (5.10)
Таким образом, заключаем, что энергия электрона, находящегося в составе атома на разных энергетических орбитах, почти полностью определяется зарядом ядра, порядковым номером орбиты (зависимость квадратична) и величиной внутренней энергии электрона.
Используя известное выражение для рационализированной постоянной Планка,
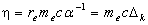 , (5.11) , (5.11)
выражение (5.10), без учета знака, можно преобразовать в следующее:
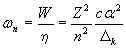 . (5.12) . (5.12)
Выражение (5.12) аналогично (1.4). Оно определяет дебройлевскую частоту обращения электрона, находящегося на орбите водородоподобного атома. Эта частота также как и энергия электрона, имеет квадратичную зависимость от n. Нетрудно заметить, что для электрона водородоподобного атома указанное соотношение (энергии и частоты) остается неизменным.
Действительно, при любых изменениях энергии и частоты электрона, находящегося на определенной орбите атома, их соотношение всегда остается неизменным, и это соотношение мы называем постоянной Планка. При переходах электрона с одной орбиты на другую указанное соотношение если и изменяется, то это изменение обязательно целочисленно кратно минимальной величине.
Поскольку дебройлевская частота электрона связана с его дебройлевской длиной волны, а последняя с импульсом, то постоянная Планка есть также и соотношение орбитального импульса электрона с его длиной волны. Соотношение, которое для определенного энергетического уровня тоже является неизменным, а с изменением номера орбиты изменяется целочисленно кратно.
Из вышеприведенных формул можно сделать и другие важные выводы:
- при ограничении максимальной орбитальной скорости электрона величиной скорости света, числовое значение Z (формулы 5.6 – 5.10) не может превышать величину 137 @ a –1. Таким образом, водородоподобный атом (с одним электроном) в основном состоянии (n = 1) не может иметь число протонов, превышающее это число. Значит, постоянная тонкой структуры a своим значением в определенной степени ограничивает количество химических элементов, потенциально возможных к существованию в природе (здесь надо отметить возможность поправки на релятивистский эффект изменения массы);
- произведение кинетической (потенциальной, а также полной) энергии электрона на радиус его орбиты есть величина постоянная для любой стационарной орбиты атома, имеющего определенное значение Z.
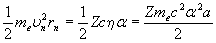 . (5.13) . (5.13)
Последнее выражение можно записать по иному:
 . (5.14) . (5.14)
Как видим в соотношении (5.14) имеется соотношение (5.5), которое представляет собой элементарный квант так называемого потенциального действия (не исключено, что 4p входит в состав этого кванта). Отметим, что ФВ потенциальное действие по размерности равна произведению силы на площадь и эта величина, похоже, является константой, общей и единой для любой электронной орбиты водородоподобного атома.
Из выражения (5.13) следует также постоянство произведения квадрата орбитальной скорости электрона на его орбитальный радиус. Это означает, что в потенциальном действии имеется (сопряженной или дополнительной к массе) еще одна сохраняющаяся ФВ, имеющая размерность L3T–2. Это соотношение характеризует вихреподобное строение электронных оболочек атома (если в нем есть движение, а оно есть). Отсюда следует, что третий закон Кеплера как бы соблюдается и в микромире.
Если рассмотреть более сложные уравнения, описывающие поведение электрона в составе водородоподобного атома с привлечением оператора квадрата момента импульса, например, уравнение (5.20) в учебнике [1], то с учетом выше изложенного, такие уравнения тоже можно попытаться упростить.
Итак, стационарное уравнение Шредингера в сферической системе координат (без привлечения обозначения оператора квадрата импульса) запишется в виде:
 , (5.15) , (5.15)
где:
 (5.16) (5.16)
представляет собой радиальную часть, а
 (5.17) (5.17)
угловую часть оператора Лапласа, представляемого в полном виде так:
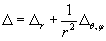 . (5.18) . (5.18)
С учетом (5.5) и других известных соотношений, выражение (5.15) преобразуемо к виду:
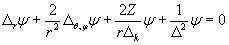 . (5.19) . (5.19)
В последнем выражении, кроме оператора Лапласа, представленного в сферических координатах, присутствуют: дебройлевская длина волны -  конкретного электрона, его комптоновская длина волны - конкретного электрона, его комптоновская длина волны -  и расстояние от центра атома – r. Пси-функция в этом выражении будет зависеть как от радиуса, так и от угловых координат. Все возможные решения этого уравнения, по всей видимости, определимы и без привлечения так называемого оператора квадрата импульса, а исходя из более ясных представлений о дебройлевской длине волны электрона и целочисленной укладке половинок волн (включая моды) на различных электронных орбитах атома. и расстояние от центра атома – r. Пси-функция в этом выражении будет зависеть как от радиуса, так и от угловых координат. Все возможные решения этого уравнения, по всей видимости, определимы и без привлечения так называемого оператора квадрата импульса, а исходя из более ясных представлений о дебройлевской длине волны электрона и целочисленной укладке половинок волн (включая моды) на различных электронных орбитах атома.
Системные соотношения потенциального действия, которые представлены на рис.4, скорее всего, подобны ранее рассмотренным системным соотношениям действия актуального. Из этого следует дополнительность друг другу и невозможность одновременного измерения в микромире следующие пар ФВ:
Действие актуальное – Скорость;
Энергия – Длина;
Сила – Площадь;
Натяжение – Пространственный объем;
Импульс – Вязкость кинематическая;
Вязкость динамическая – Поток объема;
Момент инерции – Ускорение.
Смысл некоторых из приведенных соотношений можно попытаться объяснить:
- ограничение на скорость перемещения автоматически означает и ограничение на минимальную величину кванта действия актуального. То есть, скорость света и постоянная Планка – взаимообусловленные ФВ;
- чем больше энергия микрочастицы, тем более компактно ее размещение в атоме или тем меньше ее собственный размер, если частица находится в свободном состоянии;
- чем меньший пространственный объем наблюдается, тем большие внутренние натяжения в нем обнаруживаются.
6. ИЗОЭНЕРГЕТИЧЕСКИЕ И ОЗОИМПУЛЬСНЫЕ ПОВЕРХНОСТИ АТОМОВ И МОЛЕКУЛ
В разделе 2 отмечалось наличие в уравнениях квантовой механики соотношения, характеризующегося отношением квадрата рационализированной постоянной Планка к удвоенному значению массы электрона. По размерности это отношение равно произведению энергии на площадь. В системе ФВ этой величине, а также величине, равной произведению импульса на площадь соответствующие места находятся (см. рис.3 – рис.6).
Попробуем разобраться, что могут означать эти величины и существуют ли они в действительности. Исследуем опять область микромира, поскольку в макромире такие величины, вроде бы, не встречаются.
В разделе 5 мы изучили ФВ микромира действие потенциальное, которая является сохраняющейся величиной для любой n – ой электронной орбиты водородоподобного атома. Определим на примере той же модели водородоподобного атома, что собой будет представлять ФВ, равная произведению энергии электрона, находящегося на n – ой орбите, на площадь сферы, имеющей радиус, равный радиусу этой электронной орбиты.
Необходимые расчетные формулы и результаты вычислений сведены в таблицу.
Как видно из таблицы, ФВ, равная произведению энергии электрона на площадь сферы с радиусом, равным орбитальному радиусу электрона, имеет вполне ясный физический смысл. Эта величина определяет максимальное количество электронов, которые могут быть размещены на том или ином энергетическом уровне. Как известно это количество равно 2n2, где n – номер энергетического уровня электронной орбиты.
Однако от общепринятого представления об увеличении радиуса электронных орбит, соответствующих большим энергетическим уровням, скорее всего, надо отказаться. Из опытных данных известно, что размеры атомов не позволяют электронам находиться на столь отдаленных расстояниях от ядра.
На основе данных приводимой выше таблицы, можно сделать предположение, что константной величиной, единой для всех электронных энергетических уровней, является произведение энергии одного электрона на их максимальное число, соответствующее определенному энергетическому уровню. Таким образом, мы выходим на представление о существовании в каждом атоме одной или нескольких изоэнергетических поверхностей, которые следует отнести к наиболее сохраняющимся физическим величинам.
По всей видимости, эта новая не совсем привычная величина определяет те внешние пространственные поверхности атома или молекулы (не обязательно сферические по форме), на которых размещаются электроны всех или отдельных энергетических уровней. Тогда изоэнергетическая поверхность атома, если она одна (или, лучше сказать, едина) вероятнее всего должна выступать в роли константы, определяющей свои собственные соотношения неопределенностей, наподобие ранее рассмотренных. Часть системных соотношений, иллюстрирующих эту мысль, можно видеть на рис. 5.
Подобные поверхности в атомных структурах для электронов с минимальной энергией (при температуре, равной абсолютному нулю) предсказаны и рассматриваются в квантовой механике уже давно. Этот энергетический уровень назван уровнем Ферми, а сама поверхность - поверхностью Ферми.
Из экспериментов известно, что с увеличением количества электронов на внешней электронной оболочке происходит уменьшение ее площади (своеобразное сжатие), а с ростом порядковых номеров атомов наблюдается периодическое изменение их в размерах. При этом, судя по всему, произведение суммарной энергии электронов на площадь электронной оболочки, в определенных пределах, остается величиной сохраняющейся. Поэтому, вполне возможно, что изоэнергетическая поверхность является также и квантуемой величиной в обозначенном нами понимании.
Очень возможно, что так называемые электроны атома, с физической точки зрения, представляют собой своеобразные моды колебательных движений, существующие всего лишь на одной или нескольких (немногих) пузыреподобных изоэнергетических электронных оболочках атома. По-видимому, эти изоэнергетические электронные оболочки могут иметь многолепестковый вид или размещаться одна в другой - наподобие матрешек. Во всяком случае, компьютерные модели, основанные на решении уравнений Шредингера, дают примерно такие картины.
Аналогично изоэнергетическим поверхностным величинам в микромире вполне возможно существование и изоимпульсных поверхностных величин. По крайней мере, на возможность существования таких величин указывает система ФВ.
Теперь от представлений об изоэнергетических и изоимпульсных поверхностных величинах вернемся к более привычным ФВ, в том числе к волне де Бройля.
В квантовой механике используются представления об энергии Ферми, а также об импульсе, скорости и температуре Ферми. Однако совсем не употребляется термин “длина волны Ферми”. Хотя этот термин, по нашим представлениям, должен быть первичен среди других понятий. По сути, мы говорим о той же волне де Бройля.
Энергия Ферми при абсолютном нуле температуры определяется известным выражением:
 . (6.1) . (6.1)
Привычным способом преобразуем это выражение с выявлением длины волны де Бройля, соответствующей этой энергии:


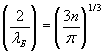
 . (6.2) . (6.2)
Если энергия Ферми представляет собой максимальную энергию электронов, то соответствующая этой энергии длина волны де Бройля (которую можно называть длиной волны Ферми), представляет собой минимально возможную из всех волн, присущих данной совокупности электронов. Эта минимальная длина волны (вернее ее половина) полностью определяется лишь объемной плотностью электронов.
Этот факт весьма примечательный – оказывается, минимальная длина волны не зависит ни от массы, ни от скорости, ни от чего-либо иного, кроме пространственной плотности ансамбля микрочастиц.
Хорошо, а что мы можем сказать о максимальной длине волны де Бройля? Распределение Ферми-Дирака обозначает наличие меньших и совсем малых, даже нулевого значения, энергии электронов. Такие же меньшие значения, по сравнению с импульсом Ферми, будут значения других импульсов и волновых векторов.
Тогда, исходя из соотношения неопределенностей, можно говорить о возможности существования для электронной или иной совокупности микрочастиц, очень больших и даже бесконечно больших длин волн де Бройля. Применительно к электронному газу в проводниках это находит подтверждение практикой – когда маленькая антенна радиоприемника реагирует на длинные радиоволны километровой длины.
Однако с привычной точки зрения, как-то трудно воспринимается существование вокруг атомов или электронов стоячих волн больших размеров. Заметим, что для приема радиосигналов антенной используется не только пространственный (в полуволновом вибраторе), но и частотный (в LC – контуре) резонанс.
Обычно поверхность Ферми трактуется как граница, разделяющая электроны, находящиеся в вырожденном состоянии, и свободные электроны, приобретшие тепловую кинетическую энергию, превышающую уровень, называемый энергией Ферми.
Одновременно мы знаем, что свободными становятся внешние электроны атома, но более глубоко расположенные электроны атома, характеризуются еще большей кинетической энергией и, значит, еще меньшей длиной волны. Это означает, что привычное распределение Ферми-Дирака с энергией от нулевого значения до уровня Ферми соответствует лишь свободным электронам, не входящим в состав атомов. Это их скорости лежат в диапазоне от нулевой скорости до скорости Ферми. А электроны, входящие в состав атомов и подчиняющимися тому же распределению Ферми-Дирака, скорее всего, образуют свои внутриатомные изоэнергетические поверхности, расположенные внутри общей (для всех атомов) изоэнергетической поверхности Ферми.
Тогда поверхность Ферми, в традиционном ее понимании, это наименее энергоемкая (в удельном значении) поверхность, находящаяся внутри проводящего или полупроводящего материального образования. Другие изоэнергетические поверхности, располагаются внутри данной поверхности Ферми и они, в сравнении с ней, более энергоемки.
Может быть, свободные электроны, находящиеся внутри проводящих тел, следует воспринимать - как своеобразные колебания изоэнергетической поверхности Ферми. А связанные электроны, входящие в составе атомов и молекул, воспринимать в виде колебаний внутренних пузыреподобных изоэнергетических поверхностей. Указанные колебания не следует отождествлять с чисто механическими. Это могут быть особые параметрические колебания натяжения, плотности или иных параметров.
На рис.5 показаны некоторые очень интересные системные связи прогнозируемых в существовании изоэнергетических и изоимпульсных поверхностей с электромагнитными величинами. Эти системные связи способны помочь в уяснении физического смысла как новых, так и уже известных ФВ. Кроме того, вновь обнаруживаемые системные взаимосвязи ФВ представляют собой еще неизученные природные закономерности.
Общее примечание к дальнейшему изложению:
Далее необходимо обратить внимание обучающихся пользованию системой (и просто читателей) на то, что в системе по рис.5 (и рис.6) совершен отход от ранее применявшегося показа в ячейках с ФВ не размерности самих ФВ, а размерности системных элементов, имеющих строго упорядоченное расположение.
Конечно, строго упорядоченное расположение системных элементов удобно для общего восприятия, однако неоднозначность размерности этих элементов, зачастую вызывает смущение. Кто-то трудно идентифицирует привычные ФВ с непонятными системными элементами, а у кого-то, при взгляде на систему, просто возникает отторжение из-за необходимости вникать в что-то непривычное.
С целью возможного преодоления этих трудностей, система по рис.5 и рис.6 специально выполнена с использование различных систем размерности для системных элементов. Но в ячейках системы показывается не размерность элементов, а размерность ФВ в СИ. Сравнение этих двух вариантов и прошлых наших обозначений системных элементов позволяет лучше понять - как изменяются дополнительные размерностные коэффициенты в ячейках с ФВ, при изменении типа размерности системных элементов.
Например, сравнение LT- вариантов системы по рис.2-рис.4 и рис.6 (или MLT- вариантов по рис.1 и рис.5) позволяет понять достаточную условность и инвариантность представления дополнительных размерностных коэффициентов при ФВ. Во всех вариантах в системе действует правило выделенного параллелограмма, с помощью которого обнаруживаются системные (и закономерные) соотношения (между ФВ). Варианты по рис 1, рис.5 и рис.6 лучше тем, что дополнительные размерностные коэффициенты, стоящие при ФВ, помогают выявлению действительно закономерных взаимосвязей.
Следует отметить еще два преимущества представления системы по рис.5 и рис.6. Во-первых, данное представление системы постоянно иллюстрирует нам неуклюжесть и даже дикость размерностной системы СИ в части электромагнитных величин. Размерности полевых и структуро-средовые электромагнитные ФВ в системе СИ столь нелепы, что о выражении физической сущности этих ФВ их размерностью, не стоит даже и говорить.
Во вторых, данный вариант системы лучше подходит для электронного (компьютерного) представления. В электронном варианте легко решается вопрос показа многоуровневой системы ФВ. Кроме того, логика обнаружения системных (а значит и природных) закономерностей автоматически может заводиться в программу компьютера.
О возможности не только сознательного, но и автоматического поиска природных закономерностей, до появления подобной системы ФВ, можно было только мечтать.
7. О ФИЗИЧЕСКОЙ СУТИ ПОНЯТИЙ: ПОДВИЖНОСТЬ НОСИТЕЛЕЙ ТОКА И ПОСТОЯННАЯ ХОЛЛА
На рис.6 в системе физических величин показаны физические величины подвижность носителей тока и постоянная Холла, используемые при квантовом рассмотрении токовых явлений в физике твердого тела. Эти величины, с размерностной точки зрения, хотя и помещены на самостоятельные системные уровни, скорее всего, не являются самостоятельными ФВ. Подвижность - это величина, обратная индукции магнитного поля, а постоянная Холла – является величиной, обратной объемной плотности электрического заряда.
С физической сущностью постоянной Холла все вполне ясно. А вот уяснение обратно пропорциональной зависимости достаточно понятной величины подвижности носителей электрического тока и магнитной индукции не столь очевидно. Попробуем разобраться в этом.
Подвижность электрических зарядов (u0) в проводниках и полупроводниках определяется как отношение скорости перемещения носителей зарядов (электронов и дырок) к напряженности E0 электрического поля, вызывающего их движение.
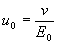 . (7.1) . (7.1)
Движение электрических зарядов (величиной q) в стороннем магнитном поле с индукцией В сопровождается действием на них известной силы Лоренца:
 , (7.2) , (7.2)
где α – угол между направлениями скорости v и индукции В.
Произведение vB sin α в этом выражении представляет собой поперечную (к основному направлению движения зарядов) составляющую напряженности электрического поля (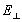 ), обеспечивающую как раз действие на заряды поперечной силы Лоренца. ), обеспечивающую как раз действие на заряды поперечной силы Лоренца.
Отношение поперечной скорости перемещения электрических зарядов к указанной поперечной напряженности электрического поля (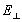 ) будет определять ту же подвижность электрических зарядов, поскольку подвижности как поперечная, так и продольная, вроде бы, должны быть одинаковы. ) будет определять ту же подвижность электрических зарядов, поскольку подвижности как поперечная, так и продольная, вроде бы, должны быть одинаковы.
Известно, что чем больше скорость движения электрического заряда, тем больше величина индукции магнитного поля, возникающего при движении этого заряда. В нашем случае: чем больше индукция В, тем больше сила Лоренца и тем большей должна быть поперечная скорость перемещения электрических зарядов. В этом случае большее значение имеется и у поперечной составляющей электрического поля.
Поперечная составляющая электрического поля вызывает появление поперечной составляющей скорости в движении электрического заряда. Указанное движение заряда в поперечном направлении в том же магнитном поле с индукцией В вызовет (по правилу левой руки) появление как бы вторичной силы Лоренца, действующей уже прямо против основного движения заряда под действием первичного поля Е0. Таким образом, магнитное поле, внешне созданное или от собственного тока, обязательно тормозит направленное перемещение и, соответственно, ограничивает подвижность носителей электрического тока.
Не случайно, что внутри сверхпроводников, имеющих по определению бесконечно большую подвижность носителей тока, магнитного поле обязательно выталкивается вовне. Как магнитное поле связано с проводимостью обычных проводников и подвижностью носителей тока в этих проводниках - требуется еще изучать.
По всей видимости, до прояснения этого вопроса, физическую величину подвижность электрических зарядов целесообразно применять и использовать, несмотря на совершенно одинокое ее расположение в системе физических величин.
8. О ФИЗИЧНОСТИ ПРЕДСТАВЛЕНИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ КВАНТОВЫХ СОСТОЯНИЙ
Устоявшиеся в квантовой механике представления о плотности распределения квантовых состояний в шестимерном фазовом пространстве с взаимно перпендикулярными осями x, y, z, px, py, pz, где полный объем состоит из произведения двух объемов - объема в пространстве координат и объема в пространстве импульсов, не очень-то понятны с физической точки зрения.
Попробуем внести ясность в эти представления на традиционном примере рассмотрения нерелятивистских электронов, находящихся в свободном состоянии.
Плотность квантовых состояний по энергии (без учета дискретности ее уровней), для единичного объема, обычно записывается в виде:
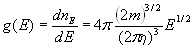 . (8.1) . (8.1)
В этом выражении dnE трактуется как число состояний, приходящееся в единичном объеме на интервал энергии от Е до Е + dE ([2] стр.178).
Полное число состояний, различных по энергии и находящихся в единичном объеме, равно:
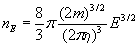 . (8.2) . (8.2)
Последнее уравнение можно преобразовать к более простому и понятному виду:
 . (8.3) . (8.3)
Выражение (8.3) показывает нам число полуволн де Бройля, содержащихся в единичном объеме. Это число, конечно же, равно числу дискретных уровней энергии или дискретных частот, содержащихся в единичном объеме. Только выражение для них будет не столь прозрачным и ясным для понимания. Прояснению ситуации несколько помогает только размерность, принимающая всегда одно и то же значение, обратное пространственному объему.
Число полуволн в единичном объеме, приходящихся на единичный интервал длины волны, определяется дифференцированием выражения (8.3)
 . (8.4) . (8.4)
Знак минус здесь показывает увеличение плотности размещения волн с уменьшением их длины.
Формулы (8.3) и (8.4) достаточно просты для запоминания. Кроме того, с их помощью легко выводятся формулы, определяющие плотности состояний, приходящиеся на единичное значение того или иного параметра.
Для определения плотности распределений числа полуволн (частот, скоростей, импульсов и др.), приходящихся в единичном объеме на единичное значение соответствующей физической величины, требуется лишь знание взаимосвязи этих параметров с длиной волны и умение дифференцировать.
Таким путем легко выводятся следующие соотношения:
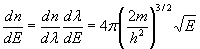 , (8.5) , (8.5)
 , (8.6) , (8.6)
 , (8.7) , (8.7)
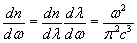 . (8.8) . (8.8)
Количество отдельных уровней энергии, импульса и частот, приходящихся на единичный объем, совпадает с подобным количеством для длин волн. Это значение, выраженное через соответствующие параметры, имеет различный вид, но всегда идентично числу для длин полуволн.
 , (8.9) , (8.9)
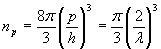 , (8.10) , (8.10)
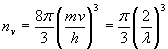 , (8.11) , (8.11)
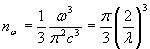 , (8.12) , (8.12)
В квантовой механике и статистической физике чаще всего рассматриваются энергетические распределения (8.5), объемная плотность которых, как известно, различна для классического газа и квантовых распределений из бозонов или фермионов.
Список литературы
1. Мартинсон Л.К., Смирнов Е.В. Квантовая физика: Учебное пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
2. Савельев И.В. Курс общей физики: Учеб. пособие. В 3-х томах. Т. 3. Квантовая оптика. Атомная физика. Физика твердого тела Физика атомного ядра и элементарных частиц. – 3-е изд., испр. – М.: Наука, Гл. ред. физ.-мат. лит., 1987.
3. Чуев А.С. Физическая картина мира в размерности “длина-время”. Серия “Информатизация России на пороге XXI века”. – М.: СИНТЕГ, 1999 – 96 с. (Текст книги имеется на сайте автора: http://www.chuev.narod.ru/).
4. Чуев А.С. О многоуровневой системе физических величин, выражающей законы природы, в частности, структуру и взаимосвязи электромагнитных величин. www.sciteclibrary.ru/rus/catalog/pages/7335.html . 2004.
5. Чуев А.С. О целостном подходе в преподавании естественно-научных закономерностей с использованием системы физических величин//Материалы международной научно-практической конференции "Актуальные проблемы управления - 2004". 10-11 ноября 2004 г. Выпуск 4. Москва. ГУУ-2004.
6. Чуев А.С. Преподавание и изучение природных закономерностей с использованием системы физических величин (целостный подход).//Сборник тезисов докладов Третьей Всероссийской конференции “Необратимые процессы в природе и технике”, 24-26 января 2005 г. М: МГТУ им. Н.Э. Баумана, 2005.
|