МЕТОД ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.
1. Основная идея метода.
Может оказаться, что система
Ax=f
(1)
имеет единственное решение, хотя какой-либо из угловых миноров матрицы А
равен нулю. В этом случае обычный метод Гаусса оказывается непригодным, но может быть применен метод Гаусса с выбором главного элемента.
Основная идея метода состоит в том, чтобы на очередном шаге исключать не следующее по номеру неизвестное, а тонеизвестное, коэффициент при котором является наибольшим по модулю. Таким образом, в качестве ведущего элемента здесь выбирается главный
, т.е. наибольший по модулю элемент.
Тем самым, если  , то в процессе вычислений не будет происходить деление на нуль.
, то в процессе вычислений не будет происходить деление на нуль.
Различные варианты метода Гаусса с выбором главного элемента проиллюстрируем на примере системы из двух уравнений
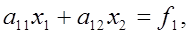 (2) (2)
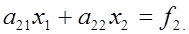
   Предположим, что Предположим, что  . Тогда на первом шаге будем исключать переменное . Тогда на первом шаге будем исключать переменное 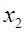 . Такой прием эквивалентен тому, что система (2) переписывается в виде . Такой прием эквивалентен тому, что система (2) переписывается в виде
 (3) (3)

и к (3) применяется первый шаг обычного метода Гаусса. Указанный способ исключения называется методом Гаусса с выбором главного элемента по строке
. Он эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация переменных.
Применяется также метод Гаусса с выбором главного элемента по столбцу. Предположим, что  . Перепишем систему (2) ввиде . Перепишем систему (2) ввиде
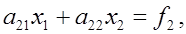

и к новой системе применим на первом шаге обычный метод Гаусса. Таким образом, метод Гаусса с выбором главного элемента по столбцу
эквивалентен применению обычного метода Гаусса к системе, в которой на каждом шаге исключения проводится соответствующая перенумерация уравнений.
Иногда применяется и метод Гаусса с выбором главного
элемента по
всей матрице,
когда в качестве ведущего выбирается максимальный по модулю элемент среди всех элементов матрицы системы.
2. Матрицы перестановок.
Ранее было показано, что обычный метод Гаусса можно записать в виде
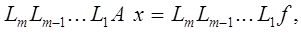 
где 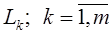 -элементарные нижние треугольные матрицы. Чтобы получить аналогичную запись метода Гаусса с выбором главного элемента, необходимо рассмотреть матрицы перестановок. -элементарные нижние треугольные матрицы. Чтобы получить аналогичную запись метода Гаусса с выбором главного элемента, необходимо рассмотреть матрицы перестановок.
ОПРЕДЕЛЕНИЕ 1.
Матрицей перестановок Р
называется квадратная матрица, у которой в каждой строке и в каждом столбце только один элемент отличен от нуля и равен единице.
ОПРЕДЕЛЕНИЕ 2.
Элементарной матрицей перестановок
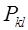 называется матрица, полученная из единичной матрицы перестановкой называется матрица, полученная из единичной матрицы перестановкой  к
-й и l
-й строк. к
-й и l
-й строк.
Например, элементарными матрицами перестановок третьего порядка являются матрицы
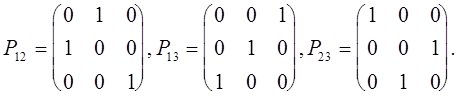
Можно отметить следующие свойства элементарных матриц перестановок, вытекающие непосредственно из их определения.
1) Произведение двух (а следовательно, и любого числа) элементарных матриц перестановок является матрицей перестановок (не обязательно элементарной).
2) Для любой квадратной матрицы А
матрица  отличается от А
перестановкой к
-й иl
-é ñòðîê. отличается от А
перестановкой к
-й иl
-é ñòðîê.
3) Для любой квадратной матрицы А
матрица 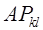 отличается от А
перестановкой к
-го и l
-го столбцов. отличается от А
перестановкой к
-го и l
-го столбцов.
Применение элементарных матриц перестановок для описания метода Гаусса с выбором главного элемента по столбцу можно пояснить на следующем примере системы третьего порядка:
 (4) (4)
Система имеет вид (1), где
 (5) (5)
Максимальный элемент первого столбца матрицы А
находится во второй строке. Поэтому надо поменять местами вторую и первую строки и перейти к эквивалентной системе
 (6) (6)
Систему (6) можно записать в виде
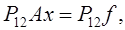 (7) (7)
т.е. она получается из системы (4) путем умножения на матрицу
перестановок

Далее, к системе (6) надо применить первый шаг обычного метода исключения Гаусса. Этот шаг эквивалентен умножению системы (7) на элементарную нижнюю треугольную матрицу
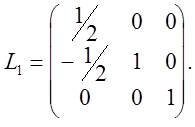
В результате от системы (7) перейдем к эквивалентной системе
 (8) (8)
или в развернутом виде
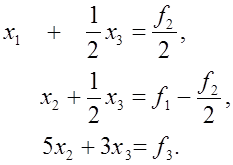 (9) (9)
Из последних двух уравнений системы (9) надо теперь исключить переменное 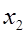 . Поскольку максимальным элементом первого столбца укороченной системы . Поскольку максимальным элементом первого столбца укороченной системы
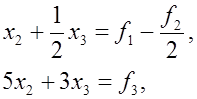 (10) (10)
является элемент второй строки, делаем в (10) перестановку строк и тем самым от системы (9) переходим к эквивалентной системе
 (11) (11)
которую можно записать в матричном виде как
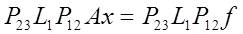 . (12) . (12)
Таким образом система (12) получена из (8) применением элемен-тарной матрицы перестановок
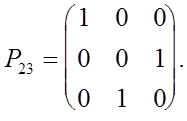
Далее к системе (11) надо применить второй шаг исключения обычного метода Гаусса. Это эквивалентно умножению системы (11) на элементарную нижнюю треугольную матрицу

В результате получим систему
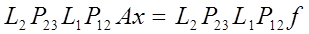 (13) (13)
или
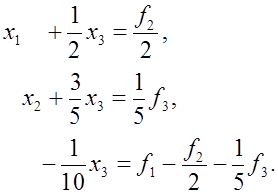 (14) (14)
Заключительный шаг прямого хода метода Гаусса состоит в замене последнего уравнения системы (14) уравнением

что эквивалентно умножению (13) на элементарную нижнюю треугольную матрицу
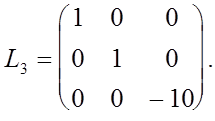
Таким образом, для рассмотренного примера процесс исключения Гаусса с выбором главного элемента по столбцу записывается в
виде
 (15) (15)
По построению матрица
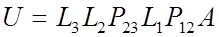 (16) (16)
является верхней треугольной матрицей с единичной главной диагональю.
Отличие от обычного метода Гаусса состоит в том, что в качестве сомножителей в (16) наряду с элементарными треугольными матрицами  могут присутствовать элементарные матрицы перестановок могут присутствовать элементарные матрицы перестановок 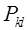 . .
Покажем еще, что из (16) следует разложение
PA=LU
, (17)
где L
-
нижняя треугольная матрица, имеющая обратную, P
-
матрица перестановок.
Для этого найдем матрицу
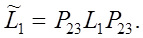 (18) (18)
По свойству 2) матрица  получается из матрицы получается из матрицы 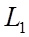 перестановкой второй и третьей строк, перестановкой второй и третьей строк,
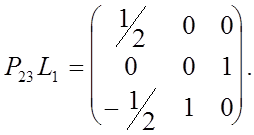
Матрица 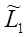 согласно свойству 3) получается из согласно свойству 3) получается из  перестановкой второго и третьего столбцов перестановкой второго и третьего столбцов

т.е. 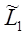 -нижняя треугольная матрица, имеющая обратную. -нижняя треугольная матрица, имеющая обратную.
Из (18), учитывая равенство 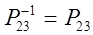 , получим , получим
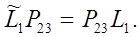 (19) (19)
Отсюда и из (16) видно, что
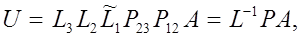
где обозначено 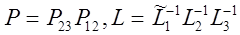 . Поскольку Р
-матрица перестановок и L
-нижняя треугольная матрица, свойство (17) доказано. Оно означает, что метод Гаусса с выбором главного элемента по столбцу эквивалентен обычному методу Гаусса, примененному к матрице РА
, т.е. к системе, полученной из исходной системы перестановкой некоторых уравнений. . Поскольку Р
-матрица перестановок и L
-нижняя треугольная матрица, свойство (17) доказано. Оно означает, что метод Гаусса с выбором главного элемента по столбцу эквивалентен обычному методу Гаусса, примененному к матрице РА
, т.е. к системе, полученной из исходной системы перестановкой некоторых уравнений.
3. Общий вывод.
Результат, полученный ранее для очень частного примера, справедлив и в случае общей системы уравнений (1).
А именно, метод Гаусса с выбором главного элемента по столбцу можно записать в виде
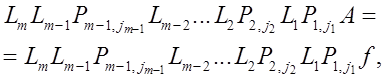 (20) (20)
где  - элементарные матрицы перестановок такие, что - элементарные матрицы перестановок такие, что
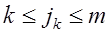 и и 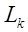 -элементарные нижние треугольные матрицы. -элементарные нижние треугольные матрицы.
Отсюда, используя соотношения перестановочности, аналогичные (19), можно показать, что метод Гаусса с выбором главного элемента эквивалентен обычному методу Гаусса, примененному к системе
PAx=Pf,
(21)
где Р - некоторая матрица перестановок.
Теоретическое обоснование метода Гаусса с выбором главного элемента содержится в следующей теореме.
ТЕОРЕМА 1.
Если 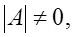 то существует матрица перестано- то существует матрица перестано-
вок Р
такая, что матрица РА
имеет отличные от нуля угловые ми-
норы.
Доказательство в п.4.
СЛЕДСТВИЕ.
Если 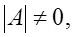 то существует матрица престана- то существует матрица престана-
вок Р
такая, что справедливо разложение
РА=LU,
(22)
где L
-
нижняя треугольная матрица с отличными от нуля диагональными элементами и U-
верхняя треугольная матрица с единичной главной диагональю. В этом случае для решения системы (1) можно применять метод Гаусса с выбором главного элемента.
4. Доказательство теоремы 1.
Докажем теорему индукцией по числу m
-порядку матрицы А
.
Пусть m=2
, т.е.
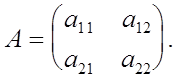
Если  то утверждение теоремы выполняется при Р=Е
, где Е
- единичная матрица второго порядка. Если то утверждение теоремы выполняется при Р=Е
, где Е
- единичная матрица второго порядка. Если 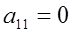 , то , то  , т.к. , т.к.  При этом у матрицы При этом у матрицы
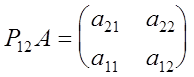
все угловые миноры отличны от нуля.
Пусть утверждение теоремы верно для любых квадратных матриц порядка m
-1
. Покажем, что оно верно и .для матриц порядка m. Ра
зобьем матрицу А
порядка m на блоки

где
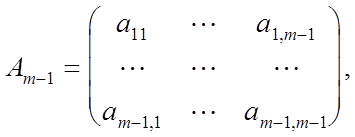 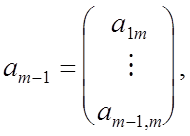

Достаточно рассмотреть два случая : и и 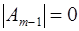 . В первом случае по предположению индукции существует матрица перестановок . В первом случае по предположению индукции существует матрица перестановок 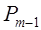 порядка m-1
такая, что порядка m-1
такая, что  имеет отличные от нуля угловые миноры. Тогда для матрицы перестановок имеет отличные от нуля угловые миноры. Тогда для матрицы перестановок
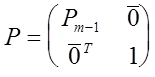
имеем
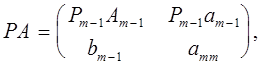
причем 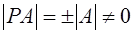 . Тем самым все угловые миноры матрицы РА
отличны от нуля. . Тем самым все угловые миноры матрицы РА
отличны от нуля.
Рассмотрим второй случай, когда . Т.к. . Т.к.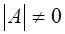 , найдется хотя бы один отличный от нуля минор порядка m-1
матрицы А,
полученный вычеркиванием последнего столбца и какой-либо строки. Пусть, например, , найдется хотя бы один отличный от нуля минор порядка m-1
матрицы А,
полученный вычеркиванием последнего столбца и какой-либо строки. Пусть, например,
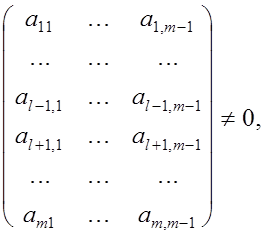
где 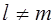 . .
Переставляя в матрице А
строки с номерами l
и m,
получим матрицу 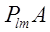 ,
у которой угловой минор порядка m-1
имеет вид ,
у которой угловой минор порядка m-1
имеет вид

и отличается от (23) только перестановкой строк. Следовательно, этот минор не равен нулю и мы приходим к рассмотренному выше случаю.
Теорема доказана.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МЕТОДОМ ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.
Одновременно с решением системы линейных алгебраических уравнений

можно вычислить определитель матрицы А.
Пусть в процессе исключения найдено распожение
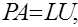
т.е. построены матрицы L èU . Тогда
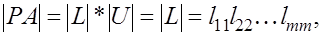
и, таким образом, произведение диагональных елементов матрицы L (ведущих, главных елементов метода исключения) равно определителю матрицы РА. Поскольку матрицы РА и А отличаются только перестановкой строк, определитель матрицы РА может отличаться от определителей матрицы А только знаком.
А именно, 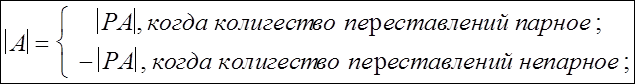
Таким образом, для вычисления определителя необходимо знать, сколько перестановок было осуществлено в процессе сключения.
Если матрица А выроджена, то при использовании метод Гаусса с выбором главного элемента по столбцу на некотором шаге исключения К все элементы которого столбца, находящиеся ниже главной диагонали и на ней, окажутся равными нулю.При этом дальнейшее исключение становится невозможным и программа должна выдать информацию о том, что определитель матрицы равен нулю.
ОБРАЩЕНИЕ МАТРИЦ.
Нахождение матрицы, обратной матрице А , еквивалентно решению матричного уравнения
 (1) (1)
где Е - единичная матрица, X - искомая квадратная матрица.
Уравнение (1) можно записать в виде системы 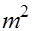 уравнений уравнений
 (2) (2)
где 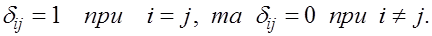
Можно заметить, что система (2) распадается на m независимых систем уравнений с одной и той же матрицей А , но с различными правыми частями. Эти системы имеют
вид ( фиксируем j ) :
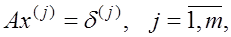 (3) (3)
где 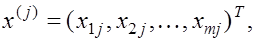 у вектора - столбца у вектора - столбца 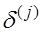 равна единице j-та компонента и равны нулю остальные компоненты. равна единице j-та компонента и равны нулю остальные компоненты.
Например, для матрицы второго порядка система (2) распадается на две независимые системы:

Äëÿ ðåøåíèÿ систем (3) используется метод Гаусса ( обычный или с выбором главного элемента).
Рассмотрим применение метода Гаусса без выбора главного элемента. Поскольку все системы (3) имеют одну и ту же матрицу А , достаточно один раз совершить прямой ход метода Гаусса, т.е. получить разложение A=LU и запомнить матрицы L i U .
Обратный ход осуществляется путем решения систем уравнений 
с треугольными матрицами L è U.
При осуществлении обратного хода можно сократить число действий, принимая во внимание специальный вид правых частей системы (4).
Запишем подробнее первые j-1 уравнений системы (4):

Учитывая невырожденность матрицы L ( т.е. 
отсюда получаем
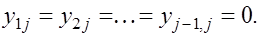
При этом оставшиеся уравнения системы (4) имеют вид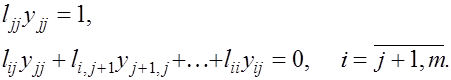
Отсюда последовательно находятся неизвестные  по формулам: по формулам: 
Можно показать, что общее число действий умножения и деления, необходимое для обращения матрицы указанным способом, порядка 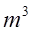 . Тем самым обращение матрицы требует не намного больше времени, чем решение системы уравнений. . Тем самым обращение матрицы требует не намного больше времени, чем решение системы уравнений.
МЕТОД ПРОГОНКИ.
Система уравнений для определения коэффициентов сплайна представляет собой частный случай систем линейных алгебраических уравнений
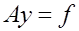
с трехдиагональной матрицей  , т.е. с матрицей, все элементы которой,не лежащие на главной и двух побочных диагоналях, равны нулю , т.е. с матрицей, все элементы которой,не лежащие на главной и двух побочных диагоналях, равны нулю 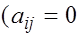 при при 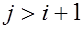 та та 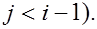
В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид
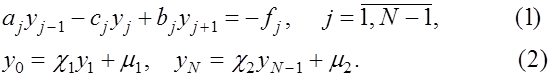
Для численного решения систем трехдиагональными матрицами применяется метод прогонки
, который представляет собой вариант метода последовательного исключения неизвестных.
Т.е. матрицу А
можно записать
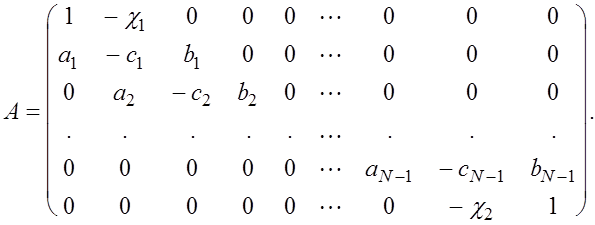
(1) Идея метода прогонки состоит в следующем. Решение системы (1) ищется в виде

где 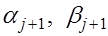 -неизвестные коэффициенты, которые последовательно находятся от -неизвестные коэффициенты, которые последовательно находятся от  до до 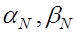 (прямая прогонка ), а затем последовательно вычисляются (прямая прогонка ), а затем последовательно вычисляются 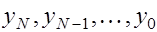 (обратная прогонка) . (обратная прогонка) .
Выведем формулы для вычисления  Из (3) можно получить Из (3) можно получить

Подставляя имеющиеся выражения для 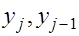 в уравнение (1),приходим при в уравнение (1),приходим при 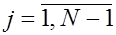 к уравнению к уравнению 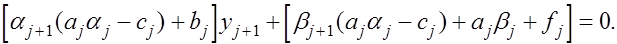 Последнее уравнение будет выполнено если коэффициенты Последнее уравнение будет выполнено если коэффициенты 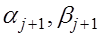 выбрать такими, чтобы выражения в квадратных скобках обращались в нуль. выбрать такими, чтобы выражения в квадратных скобках обращались в нуль.
А именно, достаточно положить  Для отыскания всех Для отыскания всех 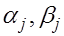 достаточно задать достаточно задать 
Эти начальные значения находим из требования эквивалентности условия (3) при  т.е. условия т.е. условия 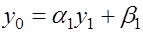 , первому из уравнений (2). , первому из уравнений (2).
Таким образом, получаем
 (5) (5)
Нахождение коэффициентов 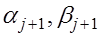 по формулам (4), (5) называется прямой прогонкой
. После того, как прогоночные коэффициенты по формулам (4), (5) называется прямой прогонкой
. После того, как прогоночные коэффициенты  найдены, решение системи (1), (2) находится по рекуррентной формуле (3), начиная с найдены, решение системи (1), (2) находится по рекуррентной формуле (3), начиная с 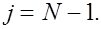 Для начала счета по этой формуле требуется знать Для начала счета по этой формуле требуется знать  , которое определяется из уравнений , которое определяется из уравнений
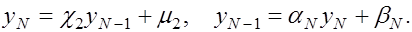
И равно
 . .
Нахождение 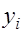 по формулам по формулам
 (6) (6)
называется обратной прогонкой.
Алгоритм решения системы (1), (2) определяемый формулами (4)-(6) называется методом прогонки
.
Метод прогонки можно пременять, если знаменатели выражений (4), (6) не обрщаются в нуль.
Покажем, что для возможности применения метод прогонки достаточно потребовать, чтобы коэффициенты системы (1), (2) удовлетворяли условиям
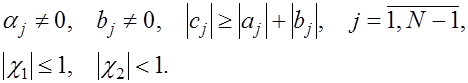 (8) (8)
Сначала докажем по индукции, что при условиях (7), (8) модули прогоночных коэффициентов  не превосходят единицы. Согласно (5), (8) имеем не превосходят единицы. Согласно (5), (8) имеем 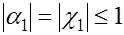 . Предположим,что . Предположим,что 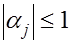 для некоторого для некоторого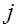 и докажем, что и докажем, что 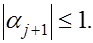
Прежде всего для любых двух комплексных чисел  и и  докажем неравенство докажем неравенство
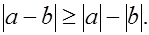
Из неравенства треугольника имеем
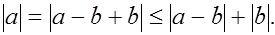
Откуда
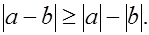
Вернемся теперь к доказательству  , если , если 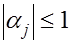 . Согласно имеем оценку . Согласно имеем оценку

а, используя (7) , получаем
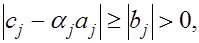  
т.е. знаменатели выражений (4) не обращаются в нуль.
Более того
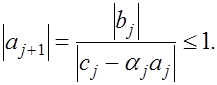
Следовательно, 
Далее, учитывая второе из условий (8) и только что доказанное неравенство  , имеем , имеем
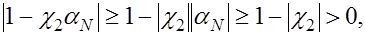
т.е. не обращается в нуль и знаменатель в выражении для  . .
К аналогичному выводу можно прийти и в том случае, когда условия (7), (8) заменяются условиями
 Таким образом при выполнении условий (7), (8) (так же как и условий (9), (10)) система (1), (2) эквивалентна системе (4)-(6). Поэтому эти условия гарантируют существование и единственность решения системы (1), (2) и возможность нахождения этого решения методом прогонки. Таким образом при выполнении условий (7), (8) (так же как и условий (9), (10)) система (1), (2) эквивалентна системе (4)-(6). Поэтому эти условия гарантируют существование и единственность решения системы (1), (2) и возможность нахождения этого решения методом прогонки.
Кроме того, доказанные неравенства 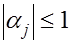 , , обеспечивают устойчивость счета по рекуррентным формулам (6). Последнее означает, что погрешность,внесенная на каком-либо шаге вычислений, не будет возрастать при переходе к следующим шагам. обеспечивают устойчивость счета по рекуррентным формулам (6). Последнее означает, что погрешность,внесенная на каком-либо шаге вычислений, не будет возрастать при переходе к следующим шагам.
Действительно, пусть в формуле (6) при  вместо вместо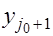 вычислена величина вычислена величина 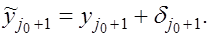
Тогда на следующем шаге вычислений, т.е. при 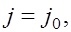
вместо
 получим величину получим величину 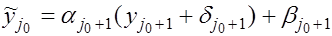 и погрешность окажется равной и погрешность окажется равной
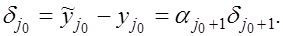
Отсюда получаем, что 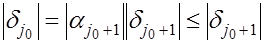 ,т.е. погрешность не возрастает. ,т.е. погрешность не возрастает.
Подсчитаем число арифметических действий, выполняемых при решении задачи (1), (2) методом прогонки.
По формулам (4), что реализуемые с помощью шести арифметических действий, вычисления производятся  раз, по формуле (6) выполняется 5 арифметических действий, наконец по формуле (3), требующей всего два действия, вычисления осуществляются раз, по формуле (6) выполняется 5 арифметических действий, наконец по формуле (3), требующей всего два действия, вычисления осуществляются 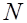 раз. Итак в методе прогонки всего затрачивается раз. Итак в методе прогонки всего затрачивается

арифметических действий, т.е. число действий растет линейно относительно числа неизвестных 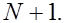
При решении же произвольной системы линейных алгебраических уравнений методом Гаусcа число действий пропорционально кубу числа неизвестных.
ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ.
Большое число задач математики и физики требует отыскания собственных значений и собственных векторов матриц, т.е. отыскания таких значений +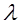 , для которых существуют нетривиальные решения однородной системы линейных алгебраических уравнений , для которых существуют нетривиальные решения однородной системы линейных алгебраических уравнений
 , (1) , (1)
и отыскания этих нетривиальных решений.
Здесь 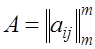 -квадратная матрица порядка m
, -квадратная матрица порядка m
,
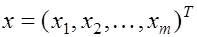 - неизвестный вектор - столбец. - неизвестный вектор - столбец.
Из курса алгебры известно, что нетривиальное решение системы (1) существует тогда и только тогда, когда
 , (2) , (2)
где Е
- единичная матрица. Если раскрыть определитель 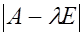 , ïîëó÷àåòñÿ алгебраическое уравнение степени m
относительно , ïîëó÷àåòñÿ алгебраическое уравнение степени m
относительно .Таким образом задача отыскания собственных значений сводится к проблеме раскрытия определителя .Таким образом задача отыскания собственных значений сводится к проблеме раскрытия определителя 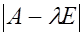 по степеням по степеням  и последующему решению алгебраического уравнения m
- й степени. и последующему решению алгебраического уравнения m
- й степени.
Определитель 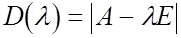 называется характеристическим
(или вековым
) определителем
, а уравнение (2) называется характеристическим
(или вековым
) уравнением
. называется характеристическим
(или вековым
) определителем
, а уравнение (2) называется характеристическим
(или вековым
) уравнением
.
Различают полную проблему собственных значений
, когда необходимо отыскать все собственные значения матрицы А
и соответствующие собственные векторы, и частичную проблему собственных значений
, когда необходимо отыскать только некоторые собственные значения, например, максимальное по модулю собственное значение .
Метод Данилевского развертывание векового определителя.
Определение.
Квадратная матрица Р
порядка m
называетсяподобной
матрице А
, если она представлена в виде
 , ,
где S
- невыродженная квадратная матрица порядка m
.
ТЕОРЕМА
. Характеристический определитель исходной и подобной матрицы совпадают .
Доказательство
.

Идея метода Данилевского состоит в том, что матрица А
подобным преобразованиям приводится, к так называемой нормальной форме Фробениуса
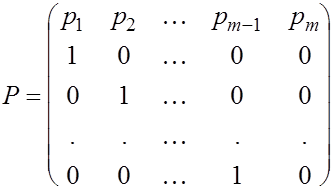 . .
Характеристическое уравнение для матрицы Р
имеет простой вид
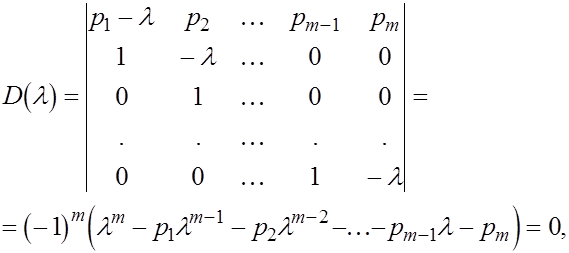 т.е. коэффициенты при степенях т.е. коэффициенты при степенях 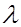 характеристического полинома непосредственно выражаются через элементы первой строки матрицы Р. характеристического полинома непосредственно выражаются через элементы первой строки матрицы Р.
Приведение матрицы А
к нормальной форме Фробениуса Р
осуществляется последовательно построкам, начиная с последеней строки.
Приведем матрицу А

подобным преобразование к виду

Пусть 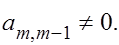 Можн проверить,что такой вид имеет матрица Можн проверить,что такой вид имеет матрица 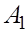 , которая равна , которая равна
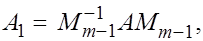
где


Слудующий шаг - приведение матрицы 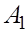 подобным преобразованием к виду подобным преобразованием к виду  , где и вторая снизу строка имеет единицу в , где и вторая снизу строка имеет единицу в 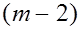 -ом столбце, а все остальные элементы строки равны нулю: -ом столбце, а все остальные элементы строки равны нулю:
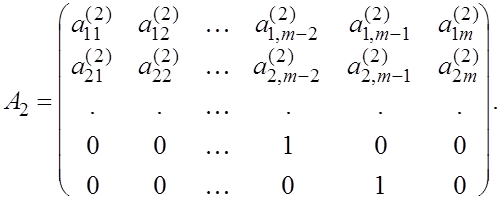
Если 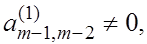 то можно проверить, что такой вид имеет матрица то можно проверить, что такой вид имеет матрица  : :
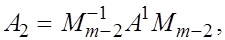
где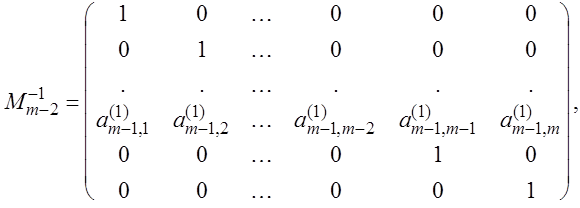

Таким образом
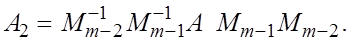
Далее процедура аналогичная, если на кождом шаге в очередной строке, на месте которого подобным преобразованием нужно получить единицу, не равную нулю.
В этом случае ( будем называт его регулярным
) нормальная формула Фробениуса будет получена за ( m
-1 ) шагов и будет иметь вид

Рассмотрим нерегулярный
случай, когда матрица, полученная в результате подобных преобразований приведена уже к виду
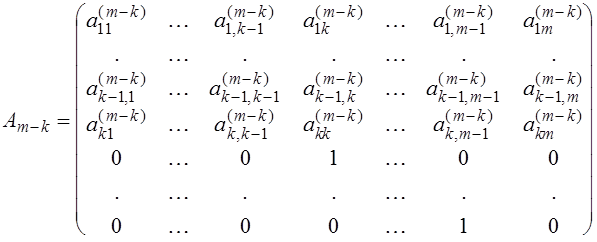 и элемент и элемент  . Таким образом обычная процедура метода Данилевского не подходит из-за необходимости деления на ноль. . Таким образом обычная процедура метода Данилевского не подходит из-за необходимости деления на ноль.
В этой ситуации возможно два случая. В первом случае к-й
строке левее элемента 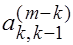 есть элемент есть элемент 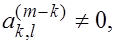
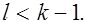 Тогда домножая матрицу Тогда домножая матрицу 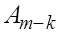 слева и справа на элементарную матрицу перестановок слева и справа на элементарную матрицу перестановок  , получаем матрицу , получаем матрицу
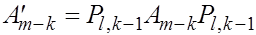 , ,
у которой по сравнению с матрицей 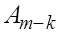 переставлены l
-я и (k
-1 )-
я строка l
-
й и ( k
-1)-
й стодбец. В результате на необходимом нам месте оказывается ненулевой элемент переставлены l
-я и (k
-1 )-
я строка l
-
й и ( k
-1)-
й стодбец. В результате на необходимом нам месте оказывается ненулевой элемент 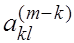 , уже преобразованная часть матрицы не меняется, можно применять обычный шаг метода Данилевского к матрице , уже преобразованная часть матрицы не меняется, можно применять обычный шаг метода Данилевского к матрице  . Она подбна матрице . Она подбна матрице 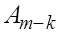 (и, следовательно, исходной матрице А
), т.к. елементарная матрица перестановок совпадает со своей обратной, т.е. (и, следовательно, исходной матрице А
), т.к. елементарная матрица перестановок совпадает со своей обратной, т.е. 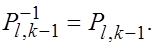
Рассмотрим второй нерегулярный случай, когда в матрице 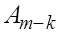 ýлемент ýлемент 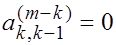 и все элементы этой строки, которые тоже находятся левее его, тоже равны нулю. В этом случае характеристический определитель матрицы и все элементы этой строки, которые тоже находятся левее его, тоже равны нулю. В этом случае характеристический определитель матрицы 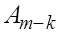 можно представить в виде можно представить в виде

где  і і 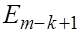 - единичные матрицы соответствующей размерности, а квадратные матрицы - единичные матрицы соответствующей размерности, а квадратные матрицы 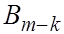 и и 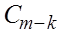 имееют вид: имееют вид:
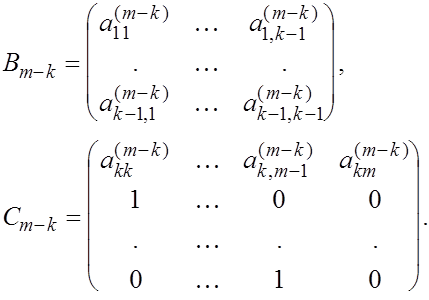
Обративм внимание на то, что матрица 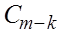 уже нормальную форму Фробениуса, и поэтому сомножитель уже нормальную форму Фробениуса, и поэтому сомножитель  просто развертывается в виде многочлена с коэффциентами, равными элементам первой строки. просто развертывается в виде многочлена с коэффциентами, равными элементам первой строки.
Сомножитель 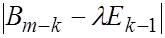 , åñòü характеристический определитель матрицы , åñòü характеристический определитель матрицы 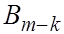 . Для развертывания можн опять применять метод Данилевского, приводя матрицу . Для развертывания можн опять применять метод Данилевского, приводя матрицу 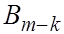 подобными преобразованиями к нормальной форме Фробениуса. подобными преобразованиями к нормальной форме Фробениуса.
Предположим теперь, что матрица А
подобным преобразованиям
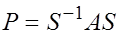 уже приведена к нормальной форме Фробениуса. Решая характеристическое уравнение уже приведена к нормальной форме Фробениуса. Решая характеристическое уравнение
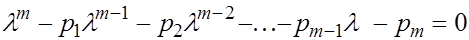 , ,
находим одним из известных методов его корни 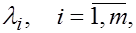 которые являются собственными значениями матрицы Р
и исходной матрицы А
. которые являются собственными значениями матрицы Р
и исходной матрицы А
.
Теперь стоит задача отыскать собственные векторы, соответствующие этим собственным значениям, т.е. векторы 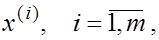 такие, что такие, что
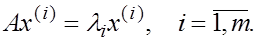
Решим ее следующим образом: найдем собственные векторы матрицы Р
, а затем по определенному соотношению я пересчитаем собственные векторы матрицы А
. Это соотношение дает следующая теорема.
ТЕОРЕМА
. Пусть 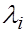 є есть собственное значение , а є есть собственное значение , а  есть соответствующий собственный вектор матрицы Р ,
которая подобна матрице А ,
т.е. есть соответствующий собственный вектор матрицы Р ,
которая подобна матрице А ,
т.е.

Тогда  есть собственный вектор матрицы А
, соответствующий собственному значению есть собственный вектор матрицы А
, соответствующий собственному значению 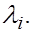
Доказательство.
Тривиально следует из того, что

Домножая левую и правую часть этого равенства слева на S
,
имеем
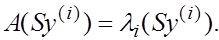
А это и означает, что 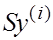 -собственный вектор матрицы А , -собственный вектор матрицы А ,
отвечающий собственному значению 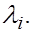
Íàéäåì ñîáñòâåííûé вектор матрицы Р ,
которая имеет нормальную форму Фробениуса и подобна матрице А.
Записывая 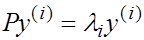 в развернутой форме, имеем в развернутой форме, имеем

или

В этой системе одна из переменных может быть сделана свободной и ей может быть придано произвольное значение. В качестве таковой возьмем 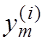 и положим и положим 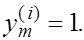
Тогда последовательно находим
 , ,
т.е. искомый собственный вектор матрицы Р
имеет вид
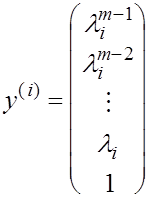 . .
Если процесс приведения матрицы А
к форме Р
был регулярным, то
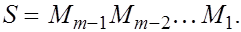
 ñîîòâåòñòâèè ñ òåîðåìîé ñîáñòâåííûì âåêòîðîì ìàòðèöû А
для собственного значения 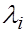 будет вектор будет вектор
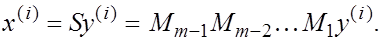
Таким образом, задача вычисления собственных векторов матрицы А
решена.
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
.
Пусть имеется функция 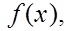 которую необходимо продифференцировать несколько раз и найти эту производную в некоторой точке. которую необходимо продифференцировать несколько раз и найти эту производную в некоторой точке.
Если задан явный вид функции, то выражение для производной часто оказывается достаточно сложным и желательно его заменить более простым. Если же функция задана только в некоторых точках (таблично), то получить явный вид ее производных ввобще невозможно. В этих ситуациях возникает необходимость приближенного (численного) дифференцирования.
Простейшая идея численного дифференцирования состоит в том, что функция заменяется интерполяционным многочленом (Лагранжа, Ньютона) и производная функции приближенного заменяется соответствующей производной интерполяционного многочлена
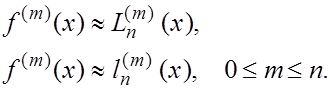
Рассмотрим простейшие формулы численного дифференцирования, которые получаются указанным способом.
Будем предполагать, что функция задана в равностоящих узлах
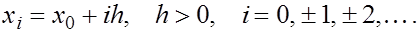
Ее значения и значения производных в узлах будем обозначать
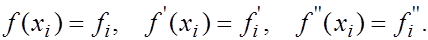
Пусть функция задана в двух точках  и и  ее значения ее значения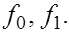
Посстроим интерполяционный многочлен первой степени
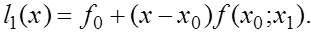
Производная  равна равна
 
Производную функцию  в точке в точке  приближенно заменяем производной интерполяционного многочлена приближенно заменяем производной интерполяционного многочлена
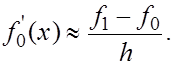 (1) (1)
Величина 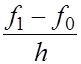 называется первой разностной производной
. называется первой разностной производной
.
Пусть  задана в трех точках задана в трех точках 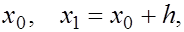 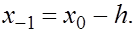
Интерполяционный многочлен Ньютона второй степени имеет вид

Берем производную

В точке  она равна она равна
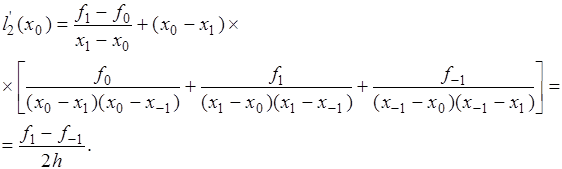
Получаем приближенную формулу
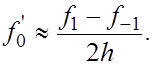 (2) (2)
Величина  называется центральной разностной производной
. называется центральной разностной производной
.
Наконец, если взять вторую производную
 получаем приближенную формулу. получаем приближенную формулу.
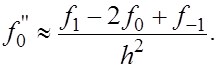 (3) (3)
Величина 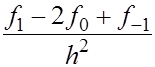 называется второй разностной производной. называется второй разностной производной.
Формулы (1)-(3) называются формулами численного дифференцирования
.
Предполагая функцию  достаточное число раз непрерывно дифференцируемой, получим погрешности приближенных формул (1)-(3). достаточное число раз непрерывно дифференцируемой, получим погрешности приближенных формул (1)-(3).
В дальнейшем нам понадобится следующая лемма.
Лемма 1.
Пусть 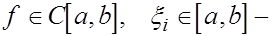 произвольные точки, произвольные точки,  Тогда существует такая точка Тогда существует такая точка 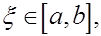 что что

Доказательство
.
Очевидно неравенство
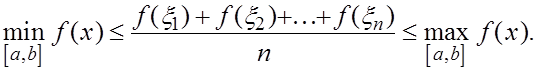
По теореме Больцано-Коши о промежуточных значениях непрерывной функции на замкнутом отрезке она принимает все значения между 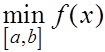 и и 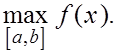 Значит существует такая точка Значит существует такая точка 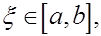 что выполняет указанное в лемме равенство. что выполняет указанное в лемме равенство.
Погрешности формул численного дифференцирования дает следующая лемма.
Лемма 2.
1.Предположим, что  Тогда существует такая точка Тогда существует такая точка  , что , что
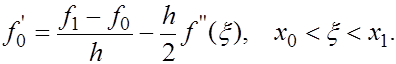 (4) (4)
2. Если  то существует такая точка то существует такая точка  , что , что
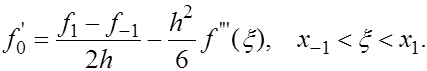 (5) (5)
3. Когда 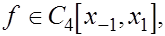 то существует то существует  такая, что такая, что
 (6) Доказательство.
По формуле Тейлора (6) Доказательство.
По формуле Тейлора
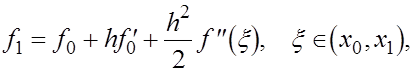
откуда следует (4).
Если 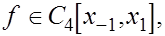 то по формуле Тейлора то по формуле Тейлора
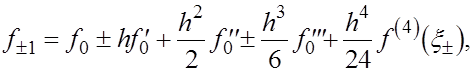 (7) (7)
где 
Подставим (7) в 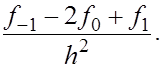 Получаем Получаем
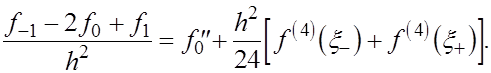
Заменяя в соответствии с леммою 1
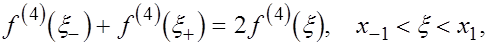
получаем
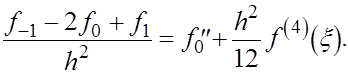
Откуда и следует (6).
Равенство (5) доказывается аналогично ( доказательство провести самостоятельно).
Формулы (4)-(6) называются формулами численного дифференцирования с остаточными членами.
Погрешности формул (1)-(3) оцениваются с помощью следующих неравенств, которые вытекают из соотношений (4)-(6):
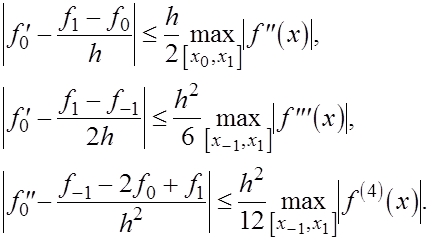
Говорят, что погрешность формулы (1) имеет первый порядок относительно
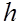 (или порядка (или порядка
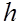 ), а погрешность формул (2) и (3) имеет второй порядок относительно ), а погрешность формул (2) и (3) имеет второй порядок относительно
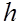 (или порядка (или порядка
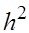 ). Также говорят, что формула численного дифференцирования (1) первого порядка точности
(относительно ). Также говорят, что формула численного дифференцирования (1) первого порядка точности
(относительно 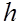 ), а формулы (2) и (3) имеют второй порядок точности
. ), а формулы (2) и (3) имеют второй порядок точности
.
Указанным способом можно получать формулы численного дифференцирования для более старших производных и для большего количества узлов интерполирования.
Выбор оптимального шага
. Допустим, что граница абсолютной погрешности при вычислении функции  в каждой точке удовлетворяет неравенству в каждой точке удовлетворяет неравенству
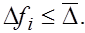 (8) (8)
Пусть в некоторой окрестности точки 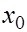 производные, через которые выражаются остаточные члены в формулах (5), (6), непрерывны и удовлетворяют неравенствам производные, через которые выражаются остаточные члены в формулах (5), (6), непрерывны и удовлетворяют неравенствам
 (9) (9)
где  - некоторые числа. Тогда полная погрешность формул (2), (3) (без учета погрешностей округления) в соответствии с (5), (6), (8), (9)не превосходит соответственно величин - некоторые числа. Тогда полная погрешность формул (2), (3) (без учета погрешностей округления) в соответствии с (5), (6), (8), (9)не превосходит соответственно величин 
Минимизация по 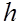 этих величин приводит к следующим значениям этих величин приводит к следующим значениям 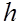 : :
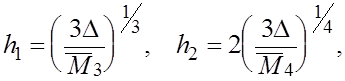 (12) (12)
при этом
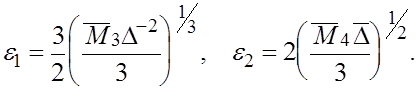 (13) (13)
Если при выбранном для какой-либо из формул (2), (3) значении 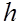 отрезок отрезок  не выходит за пределы окрестности точки не выходит за пределы окрестности точки 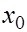 , в которой выполняется соответствующее неравенство (9), то найденное , в которой выполняется соответствующее неравенство (9), то найденное 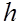 есть оптимальным
и полная погрешность численного дифференцирования оценивается соответствующей величиной (13). есть оптимальным
и полная погрешность численного дифференцирования оценивается соответствующей величиной (13).
ИНТЕРПОЛИРОВАНИЕ СПЛАЙНАМИ.
Интерполирование многочленом Лагранжа или Ньютона на отрезке 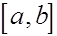 с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того, чтобы избежать больших погрешностей, весь отрезок с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того, чтобы избежать больших погрешностей, весь отрезок 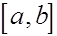 разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию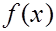 многочленом невысокой степени ( так называемая кусочно-полиномиальная интерполяция
). многочленом невысокой степени ( так называемая кусочно-полиномиальная интерполяция
).
Одним из способов интерполяции на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном
называют кусочно-полиномиальную функцию, определенную на отрезке 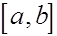 и имеющую на этом отрезке некоторое число непрерывных производных. и имеющую на этом отрезке некоторое число непрерывных производных.
Слово ,,сплайн’’ (английское spline) означает гибкую линейку, используемую для проведения гладких кривых через заданные точки плоскости.
Преимущество сплайнов перед обычной интерполяцией является, во-первых, их сходимость, и, во-вторых, устойчивость процесса вычислений.
Рассмотрим частный, но распространенный в вычислительной практике случай, когда сплайн определяется с помощью многочленов третьей степени ( кубический сплайн).
Пусть на 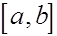 задана непрерывная функция задана непрерывная функция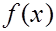 . Введем узлы ( сетку): . Введем узлы ( сетку):

и обозначим 
Интерполяционным кубическим сплайном
, соответствующим данной функции 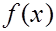 и данным узлам, называеться функция и данным узлам, называеться функция 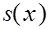 , удовлетворяющая следующим усовиям: , удовлетворяющая следующим усовиям:
а) на кождом сегменте 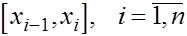 функция функция 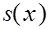 является многочленом третьей степени; является многочленом третьей степени;
б) функция 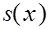 , а так же ее первая и вторая производные непрерывны на , а так же ее первая и вторая производные непрерывны на 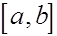 ; ;
в) 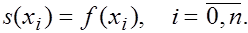
Последнее условие называется условием интерполирования
.
Докажем существование и единственность сплайна, определяемого перечисленными условиями (плюс некоторые граничные условия, которые будут введены в процессе доказательства). Приводимое ниже доказательство содержит также способ построения сплайна.
На каждом из отрезков 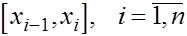 будем искать функцию будем искать функцию 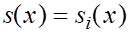 в виде многочлена третьей степени в виде многочлена третьей степени
 (1) (1)
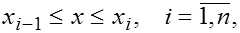
где 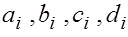 - коэффициенты, подлежащие определению. Выясним смысл введенных коэффициентов. Имеем - коэффициенты, подлежащие определению. Выясним смысл введенных коэффициентов. Имеем
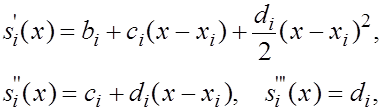
поэтому 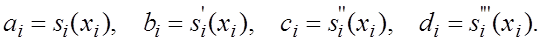
Из условий интерполирования  получаем, что получаем, что

Доопределим , кроме того ,  . .
Далее , требование непрерывности функции 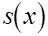 приводит к условиям приводит к условиям
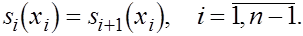
Отсюда,учитывая выражения для функций  получаем при получаем при 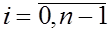 уравнения уравнения
 Обозначая Обозначая  перепишем эти уравнения в виде перепишем эти уравнения в виде
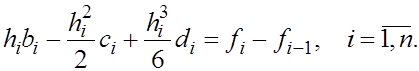 (2) (2)
Условия непрерывности первой производной

приводят к уравнениям
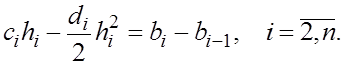 (3) (3)
Из условий непрерывности второй производной получаем уравнения
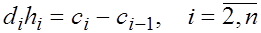 . (4) . (4)
Объединяя (2) -(4) , получим систему 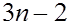 уравнений относительно уравнений относительно 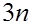 неизвестных неизвестных 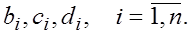
Два недостающих условия получают, задавая те или иные граничные условия для 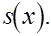 Предположим, например, что функция Предположим, например, что функция  удовлетворяет условиям удовлетворяет условиям 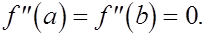 Тогда естественно требовать, чтобы Тогда естественно требовать, чтобы 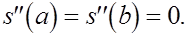 Отсюда получаем Отсюда получаем 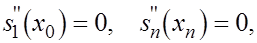
т.е. 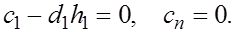
Заметим, что условие  совпадает с уравнением (4) при совпадает с уравнением (4) при 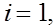 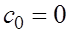 . Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна: . Таким образом, приходим к замкнутой системе уравнений для определения коэффициентов кубического сплайна:
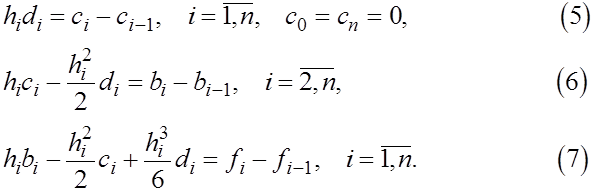 Убедимся в том, что эта система имеет единственное решение. Исключим из (5)- (7) переменные Убедимся в том, что эта система имеет единственное решение. Исключим из (5)- (7) переменные 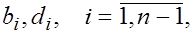 и получим систему, содержащую только и получим систему, содержащую только  Для этого рассмотрим два соседних уравнения (7) : Для этого рассмотрим два соседних уравнения (7) :
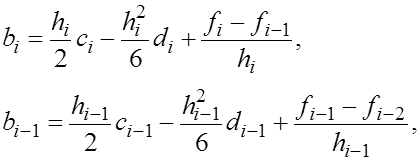
и вычтем второе уравнение из первого.Тогда получим
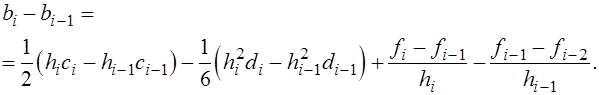
Подставляя найденное выражение для 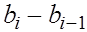 в правую часть уравнения (6), получим в правую часть уравнения (6), получим
 (8) (8)
Далее, из уравнения (5) получаем
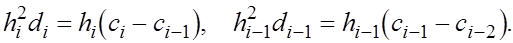
И подставляя эти выражения в (8) , приходим к уравнению

Окончательно для определения коэффициентов 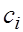 получаем систему уравнений получаем систему уравнений
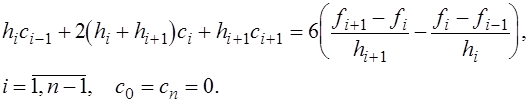 (9) (9)
В силу диагонального преобладания система (9) имеет единственное решение. Так как матрица системы трехдиагональная, решение можно найти методом прогонки. По найденным коэффициентам 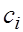 коэффициенты коэффициенты  і і  определяются с помощь явных формул определяются с помощь явных формул
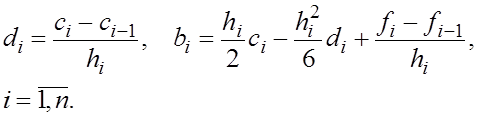 (10) (10)
Таким образом, доказано, что существует единственный кубический сплайн, определяемый условиями а)-в) и граничными условиями 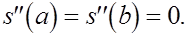 Заметим , что можно рассматривать и другие граничные условия. Заметим , что можно рассматривать и другие граничные условия.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
.
На практике редко удается вычислить точно определенный интеграл. Например, в элементарных функциях не вычисляется функция Лапласа

широко используемая в теории вероятностей для вычисления вероятностей, связанных с нормально распределенными случайными величинами.
Рассмотрим некотрые широко используемые приемы приближенного вычисления определенных интегралов.
Квадратурные формулы.
Введем понятие квадратурные формулы. Пусть дан определенный интеграл
 (1) (1)
от непрерывной на отрезке 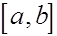 функции функции  . Приближенное неравенство . Приближенное неравенство
 (2) (2)
где  - некоторые числа, - некоторые числа,  - некотрые точки отрезка - некотрые точки отрезка 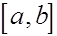 , называется квадратурной формулой
, определяемой весами , называется квадратурной формулой
, определяемой весами
 и уз
л
ами и уз
л
ами
 . .
Говорят, что квадратурная формула точна
для многочленов степени  , если при замене , если при замене  на произвольный алгебраический многочлен степени на произвольный алгебраический многочлен степени  приближенное равенство (2) становится точным. приближенное равенство (2) становится точным.
Рассмотрим наиболее простые квадратурные формулы.
Формула прямоугольников
. Допустим, что   . Положим приближенно . Положим приближенно
 (3) (3)
где 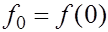 , т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции , т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции  , аппроксимируется площадью прямоугольника, высота которого равна значению , аппроксимируется площадью прямоугольника, высота которого равна значению  в средней точке основания трапеции . в средней точке основания трапеции .

Найдем остаточный член , т.е. погрешность формулы (3) .
Пусть
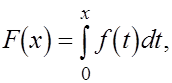 (4) (4)
 Так как Так как 
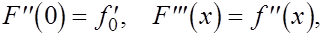 то согласно формуле Тейлора с остаточным членом в форме Лагранжа имеем то согласно формуле Тейлора с остаточным членом в форме Лагранжа имеем
 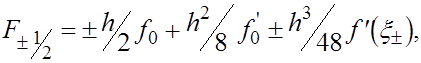 (5) (5)
где 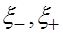 -некоторые точки , -некоторые точки , 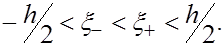
Функция 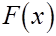 является первообразной для является первообразной для 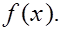 Поэтому для интеграла, стоящего в левой части приближенного равенства (3), из формулы Ньтона - Лейбница с расчетом (5) вытекает следующее соотношеие Поэтому для интеграла, стоящего в левой части приближенного равенства (3), из формулы Ньтона - Лейбница с расчетом (5) вытекает следующее соотношеие

Отсюда с помощью ранее доказанной леммы получаем формулу прямоугольников с остаточным членом
:
 (6) (6)
Формула трапеций
. Пусть 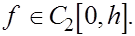 Полагаем Полагаем
 (7) (7)
где 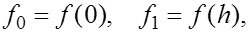 т.е. интеграл т.е. интеграл  приближенно заменяется площадью заштрихованной трапеции, показанной на рисунке. приближенно заменяется площадью заштрихованной трапеции, показанной на рисунке.

Найдем остаточный член, т.е. погрешность формулы (7). Выразим 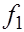 і і 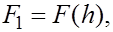 где где 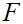 - функция (4), по формуле Тейлора с остаточным членом в интегральной форме - функция (4), по формуле Тейлора с остаточным членом в интегральной форме  : :
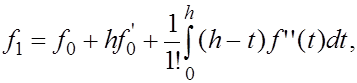 (8) (8)
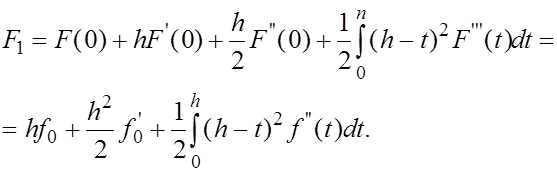 (9) (9)
Согласно (8) имеем
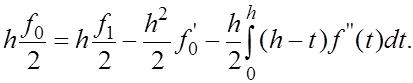 (10) (10)
Отделив в правой части (9) слагаемое 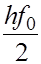 и заменив его выражением (10), с учетом того, что и заменив его выражением (10), с учетом того, что 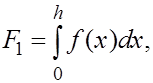 находим находим
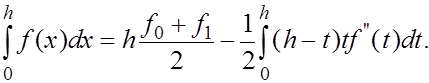 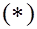
Преобразуем теперь второе слагаемое в правой части, используя обобщенную теорему о среднем.
* Формула Тейлора с остаточным членом в интегральной форме

Теорема 1
(обобщенная теорема о среднем). Пусть  причем причем  на на 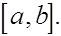 Тогда существует такая точка Тогда существует такая точка 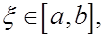 что что

Доказательство
. Положим
 (11) (11)
Тогд, так как  то то

и, следовательно,
 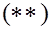
Если 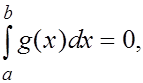 то то  и в качестве и в качестве  можн взять любую точку из можн взять любую точку из 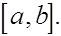
Если 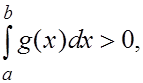 то вытекает существование такого числа с
, удовлетворяющего неравенствам ( для этого делим все части то вытекает существование такого числа с
, удовлетворяющего неравенствам ( для этого делим все части 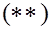 на на  ): ):
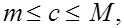 (12) (12)
что
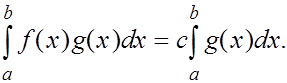 (13) (13)
По теореме о промежуточных значениях непрерывной функции в силу (11) , (12) найдется точка  , в которой , в которой  что вместе с равенством (13) доказывает теорему . что вместе с равенством (13) доказывает теорему .
Теперь, так как  то по доказанной теоремою то по доказанной теоремою
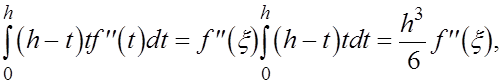
где 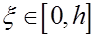 - некоторая точка . Подставляя полученное в - некоторая точка . Подставляя полученное в 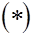 , приходим к формуле трапеций с остаточным членом
: , приходим к формуле трапеций с остаточным членом
:
 (14) (14)
Формула Симпсона .
Предположим, что 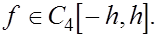 Интеграл Интеграл  приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки  де де 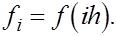

Указанная парабола задается уравнением
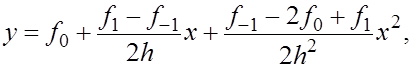
в чем нетрудно убедиться, положив поочередно 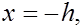 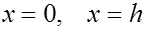 (ее можно также получить, построив интерполяционный многочлен второй степени и приводя подобные ) Отсюда находи ( проверить самостоятельно) (ее можно также получить, построив интерполяционный многочлен второй степени и приводя подобные ) Отсюда находи ( проверить самостоятельно)
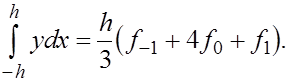
Таким образом , формула Симпсона
, называемая также формулой парабол
, имеет вид
 (15) (15)
Положим  где где 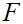 -функция (4). Поскольку -функция (4). Поскольку
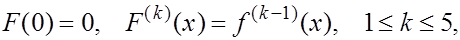
то согласно формул Тейлора с остаточным членом в интегральной форме имеем
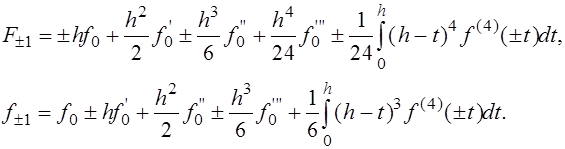 Отсюда получаем Отсюда получаем
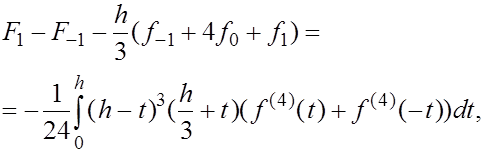 (16) (16)
т.к. остальные члены взаимно уничтожаются.
Поскольку  то применяя к интегралу (16) теорему 1 , а затем к полученному результату лемму, находим то применяя к интегралу (16) теорему 1 , а затем к полученному результату лемму, находим
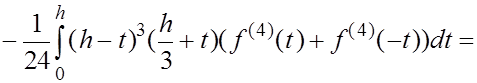
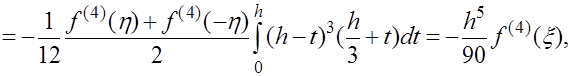 (17) (17)
где  нектрые точки. нектрые точки.
Принимая во внимание, что 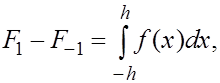 из (16), (17) приходим к формуле из (16), (17) приходим к формуле
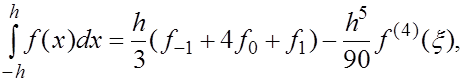 (18) т.е. к формуле Симпсона с остаточным членом. (18) т.е. к формуле Симпсона с остаточным членом.
Рассмотрим квадратурные формулы прямоугольников (3), трапеций (7) и Симпсона (15) называются каноничными
.
Усложненные квадратурные формулы
.
На практике, если требуется вычислить приближенно интеграл (1) , обычно делят заданный отрезок 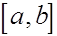 на на  равных частей и на кождом частичном отрезке применяют какую-либо одну каноничную квадратурную формулу, а затем суммируют полученные результаты. Построенная таким путем квадратурная формула на отрезке равных частей и на кождом частичном отрезке применяют какую-либо одну каноничную квадратурную формулу, а затем суммируют полученные результаты. Построенная таким путем квадратурная формула на отрезке 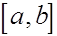 называется усложненной
. При применении формул прямугольников и трапеций длину частичных отрезков удобно применять за называется усложненной
. При применении формул прямугольников и трапеций длину частичных отрезков удобно применять за 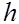 , а при использовании формулы Симпсона - за , а при использовании формулы Симпсона - за  . .
Остановимся сначала на применении формулы прямоугольников. Пусть 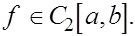 Обозначим частичные отрезки через Обозначим частичные отрезки через 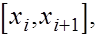
где 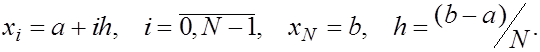
В соответствии с (3) полагаем
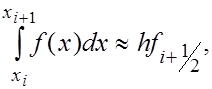 (19) (19)
где 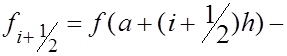 значение значение  в середине частичного отрезка в середине частичного отрезка  . При этом справедливо аналогичное (6) равенство . При этом справедливо аналогичное (6) равенство
 (20) где (20) где 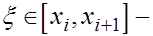 некоторая точка. некоторая точка.
Суммирование по всем частичным отрезкам приближенного равенства (19) приводит к усложненной квадратурной формуле прямоугольников
:
 (21) (21)
а суммирование равенств (20) с учетом того,что по лемме
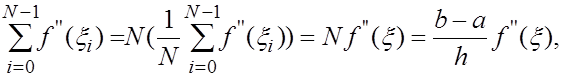
где  -некоторая точка отрезка -некоторая точка отрезка 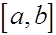 , дает усложненную формулу прямоугольников с остаточным членом: , дает усложненную формулу прямоугольников с остаточным членом:
 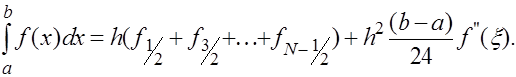 (22) (22)  Совершенно àíàëîãè÷íî при услвии, что Совершенно àíàëîãè÷íî при услвии, что  с использованием формул (7), (14) получается усложненная квадратурная формула трапеций с использованием формул (7), (14) получается усложненная квадратурная формула трапеций
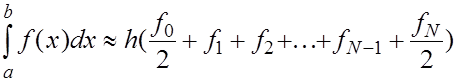 (23) (23)
и отвечающая ей формула с остаточным членом
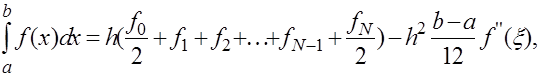 (24) (24)
где 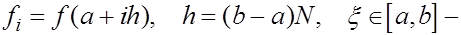 некоторая точка.
некоторая точка.
Пусть теперь  и, как обычно, и, как обычно, 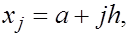 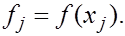 Перепишем каноническую квадратурную формулу Симпсона (15) применительно к отрезку Перепишем каноническую квадратурную формулу Симпсона (15) применительно к отрезку  длины длины 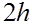 : :
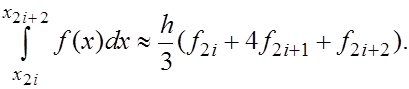
Суммируя левую и правую части этого соотношения от 0 до
N-1, получаем усложненную квадратурную формулу Симпсона
(25)
Сответствующая ей формула с остаточным членом, полученная суммированием по частичным отрезкам  равенств вида (18), при условии, что равенств вида (18), при условии, что 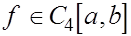 , такова : , такова :
 (26) (26)
где 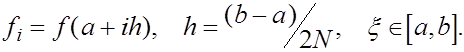
Введем краткие обозначения
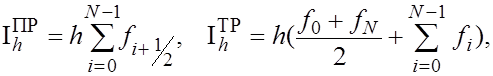 (27) (27)
где 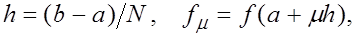 а также положим а также положим
 (28) (28)
где 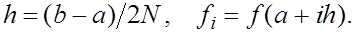
Приближенные равенства
 (29) (29)
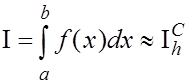 (30) (30)
назовем сответственно формулами прямоугольников, трапеций и формулой Симпсона, опуская слова ‘’усложненная квадратурная’’.
Из виражений остаточных членов в (22), (24), (26) видно, что формулы (29) прямоугольников трапеций точны для многочленов первой степени, т.е. для линейных функций, а формула (30) Симпсона точна для многочленов третьей степени (для них остаточный член равен нулю ). Погрешность формул (29) имеет второй порядок относительно 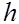 (заведомо не лучше, если (заведомо не лучше, если 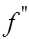 непрерывна на непрерывна на 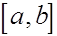 и не обращается в нуль), а формула Симпсона при соответствующей гладкости и не обращается в нуль), а формула Симпсона при соответствующей гладкости  является формулой четвертого порядка точности. Поэтму для функций класса является формулой четвертого порядка точности. Поэтму для функций класса 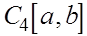 при малом при малом 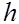 формула Симпсона обычно дает более высокую точность, чем формула (29). формула Симпсона обычно дает более высокую точность, чем формула (29).
Погрешность формулы прямугольников и формулы Симпсона при вычислении интеграла (1) в силу (22), (26) удовлетворяет неравенствам
 (31) (31)
 (32) (32)
Аналогичное неравенство имеет место и для погрешности формули трапеций.
Наряду с оценками погрешноси сверху полезны оценки снизу. В частности, для погрешности формулы прямоугольников оценка снизу, вытекающая из (22), такова:
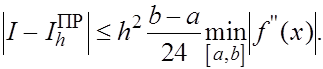 (33) (33)
Пример.
Исследовать погрешность квадратурных формул для интеграла
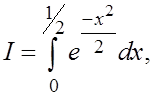 при при 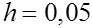 . .
Имеем
о 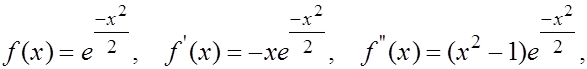
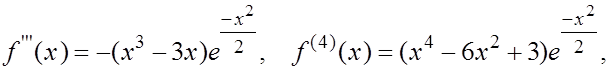
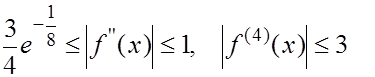 на на 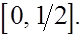
Согласно (31)-(33) получаем
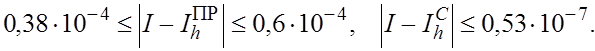
Формулы прямоугольников трапеций в отдельности уступают при интегрировании гладких функций формуле Симпсона. Однако в паре они обладают ценным качеством, а именно, если 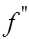 не изменяет знака на не изменяет знака на  то формулы (29) дают двусторонние приближения для интеграла (1), так как согласно (22), (24) их остаточные члены имеют противоположные знаки. то формулы (29) дают двусторонние приближения для интеграла (1), так как согласно (22), (24) их остаточные члены имеют противоположные знаки.
В рассмотренном примере  Поэтому Поэтому 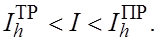
В данной ситуации естественно положить 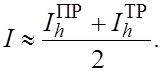
Тогда  т.е. погрешность оценивается через самые приближенные значения интеграла. т.е. погрешность оценивается через самые приближенные значения интеграла.
|