ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ

Раздел: ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ

1. Статистический и термодинамический методы исследования.

Молекулярная физика и термодинамика — разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в телах атомов и молекул. Для исследования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: статистический (молекулярно-кинетический) и термодинамический. Первый лежит в основе молекулярной физики, второй — термодинамики.

Молекулярная физика — раздел физики, изучающий строение и свойства вещества исходя из того, что все тела состоят из атомов или молекул, находящихся в непрерывном хаотическом движении.

Этапы развития атомно-молекулярного строения вещества:

Идея об атомном строении вещества высказана древнегреческим философом Демокритом (460—370 до н. э.).
Атомистика возрождается вновь лишь в XVII в. и развивается в работах М. В. Ломоносова
Строгое развитие молекулярной теории относится к середине XIX в. и связано с работами немецкого физика Р. Клаузиуса (1822—1888), Дж. Максвелла и Л. Больцмана.

Законы поведения огромного числа молекул изучаются с помощью статистического метода. Этот метод определяется св-ами частиц системы, особенностями их движения и усредненными значениями динамических характеристик частиц (скорости , энергии E и т.д.). Например, температура T тела определяется скоростью хаотического движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул.

Термодинамика — раздел физики, изучающий общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями.

Термодинамика не рассматривает микропроцессы, которые лежат в основе этих превращений. Этим термодинамический метод отличается от статистического. Термодинамика базируется на двух началах — фундаментальных законах, установленных в результате обобщения опытных данных.

Область применения термодинамики значительно шире, чем молекулярно-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термодинамическим методом. Однако, с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явлений, а лишь устанавливает связи между макроскопическими свойствами вещества. Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различными методами исследования.

2. Термодинамическая система — совокупность макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Задача термодинамического метода — определение состояния термодинамической системы.

Состояние системы задается термодинамическими параметрами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодинамической системы: температурой Т, давлением р и объемом V.

Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом.

Температура — физ. величина, характеризующая состояние термодинамического равновесия макроскопической системы.

В соответствии с решением XI Генеральной конференции по мерам и весам (1960) в настоящее время можно применять только две температурные шкалы:

1. термодинамическую, градуированную в кельвинах (К)

2. Международную практическую, градуированную в градусах Цельсия (°С) (система СИ).

В Международной практической шкале реперными точками являются температуры:

замерзания воды 0°С при давлении 1,013105 Па (нормальное атмосферное давление на уровне моря – 760 мм рт.ст.)

кипения воды 100°С при давлении 1,013105 Па.

Термодинамическая температурная шкала определяется по одной реперной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии).

Рис. 1.

Температура этой точки по термодинамической шкале равна 273,16 К (точно).

Градус Цельсия равен кельвину.

В термодинамической шкале температура замерзания воды равна 273,15 К (при том же давлении, что и в Международной практической шкале), поэтому, по определению, термодинамическая температура и температура по Международной практической шкале связаны соотношением

Т = 273,15 + t.

Температура Т=0 К называется нулем кельвин. Анализ различных процессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно.

Удельный объем v — это объем единицы массы. Когда тело однородно, т.е. его плотность = const, то v = V/m = l/. Так как при постоянной массе удельный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризовать объемом тела.

Параметры состояния системы могут изменяться. Изменение хотя бы одного из ее термодинамических параметров называется термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что внешние условия рассматриваемой системы при этом не изменяются).

3. Экспериментальное обоснование молекулярно-кинетической теории

- Возможность прямого наблюдения индивидуальных молекул и атомов в микроскоп

- Изменяемость объема газа, например его сжимаемость

- Наличие сил притяжения и отталкивания между молекулами отчетливо обнаруживается в свойстве твердых тел сохранять свою форму. Даже для небольшой деформации твердого тела необходимо приложить значительное усилие. Понятно, что растяжению тела препятствуют силы притяжения, а сжатию — силы отталкивания между молекулами.

- Непрерывное хаотическое движение молекул наиболее наглядно обнаруживается в явлениях диффузии и броуновского движения.

Если поместить капельку брома на дно высокого стеклянного сосуда, то в результате ее испарения через несколько минут около дна суда образуется слой пара брома, имеющий темно-бурый цвет. Этот пар довольно быстро распространяется кверху, перемешиваясь с воздухом, так что через час бурый столбик смеси газов в сосуде достигнет 30см. Очевидно, что перемешивание воздуха с паром брома произошло не под влиянием силы тяжести, а наоборот, вопреки действию силы тяжести, так как первоначально бром располагался ниже воздуха, а плотность пара брома приблизительно в 4 раза больше, чем воздуха.

В данном случае перемешивание могло быть вызвано только хаотическим движением молекул, в процессе которого молекулы брома распространялись между молекулами воздуха, а молекулы воздуха — между молекулами пара брома. Рассмотренное явление называется диффузией.

В 1827 г. английский ботаник Броун, исследуя под микроскопом жидкие препараты, случайно обнаружил следующее интересное явление. Взвешенные в жидкости мельчайшие твердые частички совершали быстрые беспорядочные движения, как бы перескакивая с места на место. В результате таких скачков частички описывали зигзагообразные траектории самой причудливой формы. В дальнейшем это явление неоднократно наблюдалось как самим Броуном, так и другими исследователями в различных жидкостях и с различными твердыми частичками. Чем меньше был размер частичек, тем интенсивнее они двигались. Описанное явление получило название броуновского движения.

Броуновское движение можно наблюдать, например, в капле воды, слегка подчерненной тушью или подбеленной молоком, пользуясь микроскопом с пятисоткратным увеличением. Диаметр броуновской частицы составляет в среднем 0,0001 мм, наибольший же допустимый ее диаметр — 0,005 мм.

Рис. 2.

На рис. 2 представлена зарисовка траектории одной из броуновских частиц. Местоположение этой частицы отмечалось через каждые 30 с черными точками.

4. Экспериментальные законы идеального газа:

а) закон Бойля-Мариотта

б) закон Гей-Люссака

в) закон Шарля

В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой считают, что:

собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
между молекулами газа отсутствуют силы взаимодействия;
столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу. Кроме того, внеся поправки, учитывающие собственный объем молекул газа и действующие молекулярные силы, можно перейти к теории реальных газов.

Рассмотрим законы, описывающие поведение идеальных газов.

а) Закон Бойля — Мариотта:

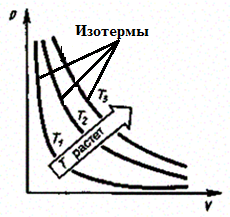
pV = const при Т = const, т = const. (1)

Процесс изотермический.

Рис. 3

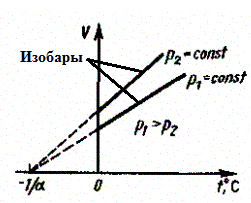
б) Закон Гей-Люссака:

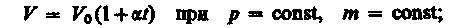(2)

Процесс изобарный.

Рис. 4

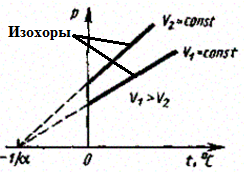
в) Закон Шарля:

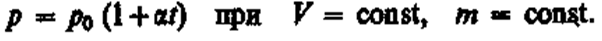(3)

Процесс изохорный.

Рис. 5.

В этих уравнениях t — температура по шкале Цельсия, р0 и V0 — давление и объем при 0°С, коэффициент = 1/273,15 К-1.

Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных условиях этот объем равен 22,4110-3 м3/моль.

По определению, в одном моле различных веществ содержится одно и то же число молекул, называемое постоянной Авогадро:

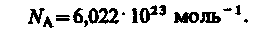
1 моль – количество вещества, содержащее столько же структурных элементов (атомов, молекул, ионов, электронов и др. частиц или группы частиц), сколько содержится атомов в изотопе 12С массой 0,012 кг.

5. Уравнение Клапейрона — Менделеева

Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением

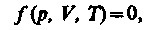
где каждая из переменных является функцией двух других.

Французский физик и инженер Б. Клапейрон (1799—1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть: V1, p1 и T1;

р2, V2, Т2 при одинаковой массе (рис. 6).

Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1 — 1, 2) изохорного (изохора 1 - 2).

Рис. 6

В соответствии с законами Бойля — Мариотта (1) и Шарля (3) запишем:

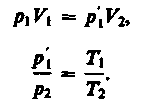
(4)

(5)

Исключив из уравнений (4) и (5) p1, получим

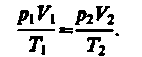
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.

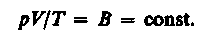(6)

Выражение (6) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов.

Русский ученый Д. И. Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (6) к одному молю, использовав молярный объем Vm. Согласно закону Авогадро, при одинаковых р и Т моли всех газов занимают одинаковый молярный объем Vm, поэтому постоянная B будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению

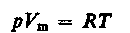(7)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона — Менделеева.

Числовое значение молярной газовой постоянной определим из формулы (7), полагая, что моль газа находится при нормальных условиях (р0= 1,013105 Па, T0 = 273,15 К, Vm = 22,4110-3 м3/моль): R = 8,31 Дж/(мольК).

От уравнения (7) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем Vm, то при тех же условиях масса m газа займет объем V= (т/М) Vm, где М — молярная масса (масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы т газа

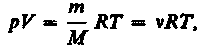(8)

где v=m/M — количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана:

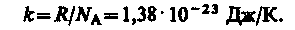
Исходя из этого уравнение состояния (7) запишем в виде

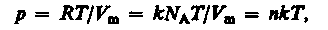
где NA/Vm = n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

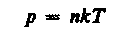(9)

следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м3 газа при нормальных условиях, называется числом Лошмидта:

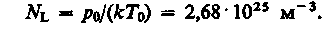
6. Основное уравнение молекулярно-кинетической теории идеальных газов

Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одноатомный идеальный газ, т.е.:

1. молекулы газа движутся хаотически

2. число столкновений nстолк м/у молекулами << числа ударов о стенки сосуда

3. соударения молекул со стенками сосуда абсолютно упругие.

Выделим на стенке сосуда некоторую элементарную площадку S (рис. 7) и вычислим давление, оказываемое на эту площадку.

Импульс, получаемый стенкой, m0 - (- т0 ) = 2т0 , где m0 — масса молекулы, — ее скорость.

За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой t (рис. 7). Число этих молекул равно nS t (n — концентрация молекул).

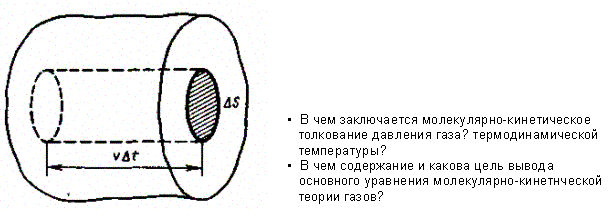
Рис. 7.

Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул, причем половина молекул - 1/6 - движется вдоль данного направления в одну сторону, половина — в противоположную.

При столкновении с площадкой эти молекулы передадут ей импульс

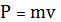l/6 nS t - число ударов молекул о площадку S, движущихся в заданном направлении.

Тогда давление газа, оказываемое им на стенку сосуда,

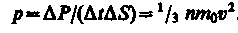(10)

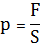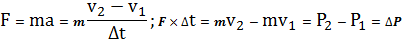
Если газ в объеме V содержит N молекул, движущихся со скоростями 1, 2, ..., n, то целесообразно рассматривать среднюю квадратичную скорость

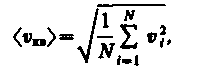(11)

характеризующую всю совокупность молекул таза. Уравнение (10) с учетом (11) примет вид

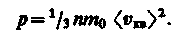(12)

Выражение (12) называется основным уравнением молекулярно-кинетической теории идеальных газов. Точный расчет с учетом движения молекул по всевозможным направлениям дает ту же формулу.

Учитывая, что n=N/V, получим

Разделим и умножим на 2

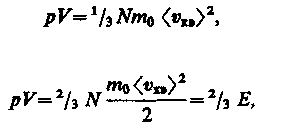(13)

где Е — суммарная кинетическая энергия поступательного движения всех молекул газа.

Так как масса газа m=Nm0, то уравнение (13) можно переписать в виде

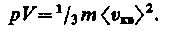
Для одного моля газа т = М (М — молярная масса), поэтому

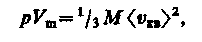
где Vm — молярный объем. С другой стороны, по уравнению Клапейрона — Менделеева, pVm = RT. Таким образом,

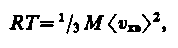
откуда

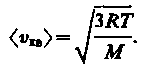(14)

Так как M = m0NA — масса одной молекулы, а NА — постоянная Авогадро, то из уравнения (43.6) следует, что

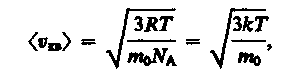(15)

где k=R/NA — постоянная Больцмана. Отсюда найдем, что при комнатной температуре молекулы кислорода имеют среднюю квадратичную скорость 480 м/с, водорода — 1900 м/с. При температуре жидкого гелия те же скорости будут соответственно 40 и 160 м/с.

Приравняв левые части формул (9) и (12), находим среднюю кинетическую энергию поступательного движения одной молекулы идеального газа

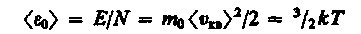(16)

Она пропорциональна термодинамической температуре и зависит только от нее. Из этого уравнения следует, что при Т=0 <0> = 0, т. е. при 0 К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Таким образом, термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула (16) раскрывает молекулярно-кинетическое толкование температуры.

Элементы статистики:

а) распределение Максвелла

Из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое число молекул.

В состоянии равновесия при Т = const скорость молекул остается постоянной и равной .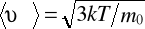

Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.

При выводе закона Максвелл предположил, что:

1. газ состоит из очень большого числа N тождественных молекул

2. они находятся в хаотическом тепловом движении

3. температура газа по всему объему одинакова

4. силовые поля на газ не действуют.

Закон Максвелла предполагает разбиение диапазона скоростей молекул на малые интервалы d, на каждый из которых приходится некоторое число молекул dN(). Такой подход приводит к появлению функции распределения молекул по скоростям f(), позволяющей определить относительное число молекул dN()/N, скорости которых лежат в интервале от до + d, т. е.

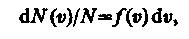
откуда

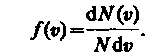
Применяя методы теории вероятностей, Максвелл нашел явный вид функции f() — закон о распределении молекул идеального газа по скоростям:

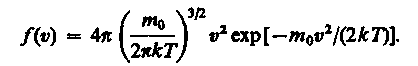(17)

Из (17) видно, что конкретный вид функции зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т).

Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно найти, продифференцировав выражение (17) по аргументу , приравняв результат нулю и используя условие для максимума выражения f():

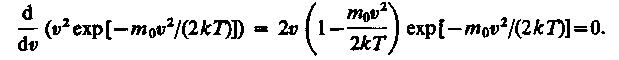
Значения = 0 и = соответствуют минимумам выражения (17), а значение , при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость b:

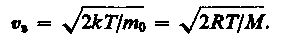(18)

Из формулы (18) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 8) сместится вправо (значение наиболее вероятной скорости становится больше). Однако площадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

Средняя скорость молекулы < > (средняя арифметическая скорость) определяется по формуле

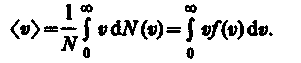
Подставляя сюда f() и интегрируя, получаем

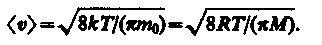(19)

Скорости, характеризующие состояние газа: 1) наиболее вероятная

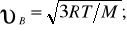2) средняя 3) средняя квадратичная 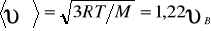(рис. 8). Исходя из распределения молекул по скоростям

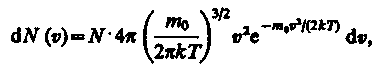(20)

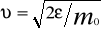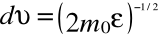можно найти распределение молекул газа по значениям кинетической энергии . Для этого перейдем от переменной к переменной = m02/2. Подставив в (20) и , получим

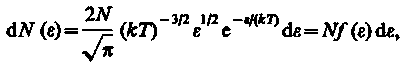
где dN() — число молекул, имеющих кинетическую энергию поступательного движения, заключенную в интервале от до + d.

Таким образом, функция распределения молекул по энергиям теплового движения

Средняя кинетическая энергия <> молекулы идеального газа

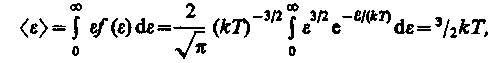
т. е. получили результат, совпадающий с формулой (16).

Вставить из Открытой физики.

8. Первое начало термодинамики

Для характеристики состояния и свойств Газа – (Г) мы ввели ряд параметров (характеристик): T,P,V, нашли связь между ними:

а) PV= const m=const , T=const - изотермический

б) V=V0(1+t) m=const, P=const –изобарический

в) P=P0(1+t) m=const, V=const- изохорический

Написали основное уравнение МКТ газов

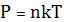
Ввели постоянные: -

NA=6,022 1023 1/моль – число Авагадро

R=8,31 дж/моль К – универсальная газовая постоянная

k=R/NA=8,31/60221023 1/моль – постоянная Больцмана

Vm=22,41 10-3 м3/моль – объем 1 моля любого газа

=V\m =1\ – удельный объем

NL=2,681025 1\м3 – число Лошмидта (кол-во частиц в 1 м3)

Введем еще одну важную характеристику терм-ской системы: внутреннюю энергию. Обозначим –U. Она состоит из:

U=Uхаот.движ +Uвз(потенц.энерг.)

В U не учитывается:

Uk- энергия движения системы в целом
Uпот – энергия системы во внешних полях (напр. поле тяготения)

U это хар-тика каждого отдельного состояния. Это однозначная функция. Она не зависит как она пришла в данное состояние какой путь при этом она прошла.

Это означает что U=U1-U2, т.е. значениями U в начальном U1 и конечном U2 состояниях.

В предыдущей лекции отмечалось, что положение системы в пространстве определяется числом независимых переменных (координат): матер. (), например, имеет 3 степени свободы поступательного движения x,y,z. Если газ одноатомный и атомы в нем приняты за материальную точку, то данному атому можно приписать также 3 степени свободы поступательного движения. При этом энергия вращения движения равна нулю, т.к. r 0, J = mr2 0, т.е. момент инерции равен нулю. Поэтому

Екин вращ=J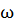2\2, J=0 Екин.вращ=0

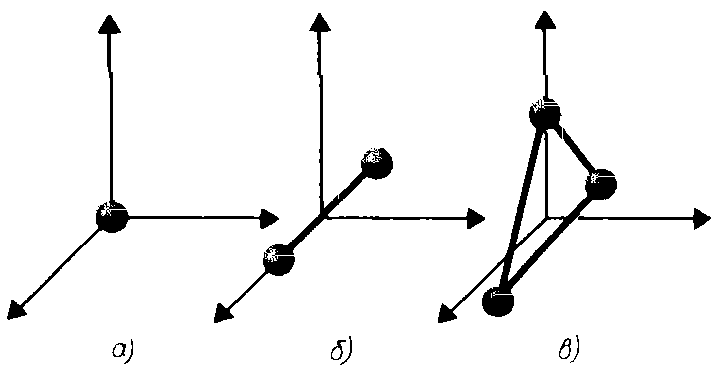
Рис. 1.

Обозначим степени свободы через i . По аналогии, если газ двухатомный, т.е. две материальные точки, то i=5 степеней свободы, т.к. требуется 2 степени свободы на вращательное движение

Если газ трехатомный, т.е. три материальные точки, то требуется 3 степени свободы на три вращательных движения.

Понятно, что атомы участвуют еще и в других видах движения, а именно в колебательных. Т.е. они тоже имеют степень свободы. Об этом чуть позже.

3 поступательных степени свободы имеются всегда независимо от числа степеней свободы. Поэтому на одну степень свободы поступательного движения приходится:

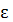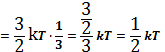1 (2)

Согласно закону Больцмана о равномерном распределении энергии по степеням свободы молекул, находящихся в термодинамическом равновесии, на каждую поступательную и вращательную степень свободы приходится энергия равная:

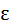пост.вращ.=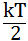

а на каждую колебательную степень свободы в среднем

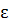кол=kT,

т.е. в два раза больше, т.к. колебательная степень свободы iкол не только 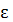кин, но и 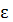потенц. Причем 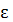кин и 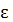потенц. равны между собой.

Таким образом, средняя энергия молекулы равна:

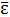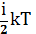= (3)

где i=iпост+iвращ+2iколеб (4)

С учетом выше сказанного внутренняя энергия 1 моля идеального газа Um равна:

Um=(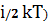NA=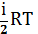, (kNA=R) (5)

Для произвольной массы

PV=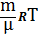 (ур-е Клапейрона-Менделеева)

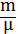
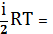
U= 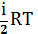(6)

Значение U можно менять 2-мя способами:

Совершая работу над системой (сжимать газ) (Поршень, цилиндр)
Сообщая тепло газу (нагревая) в процессе обмена внутренними энергиями соприкасаемых тел с разными Т.

Т.е. есть две формы передачи энергии от одних тел другим:

- работа

- теплопередача

В первом случае механическая работа (энергия) превращается в тепловую.

Во втором случае наоборот, тепловая энергия превращается в механическую работу. Т.е. наблюдается взаимное превращение энергии одного вида в энергию другого вида. При этом превращении соблюдается закон сохранения и превращения энергии.

Первый закон термодинамики указывает на то, что при любом способе перехода системы из первого состояния во второе, изменение внутренней энергии U=U2-U1 будет одинаковым и равным разности между теплом Q, переданным системе, и работой A, совершаемой системой против внешних сил:

U=Q-A (6)

Q=U+A (7)

– первое начало термодинамики.

Дифференциальная форма:

dQ=dU+dA (8)

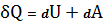(9)

dU - малое изменение внутренней энергии

A – элементарная работа

- бесконечно малое количество теплоты

3. Работа газа при изменении его объема

Вспомним, что:

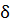A=Fdl cos. При =0 cos=1.

С другой стороны,

P=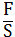; F=PS

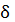A=PSdl=PdV (10)

Полная работа:

A=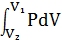 (11)

Формула (11) справедлива при любых изменениях V твердых, жидких и газообразных молекул.

Работу, произведенную при любом процессе, можно изобразить графически:

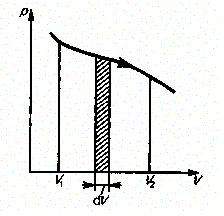
Рис. 2.

Рис. 2 характерен только для равновесных процессов. Равновесными называются процессы, состоящие из последовательности равновесных состояний. Медленные процессы близки к равновесным.

9. Теплоемкость. Уравнение Майера.

Введем еще одну характеристику вещества – теплоемкость.

1). Удельная теплоемкость:

С=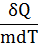 [Дж/(кгК)] (12)

При m=1кг, Т=1К C=Q.

2). Молярная теплоемкость:

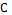m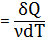 [Дж\мольК] (13)

где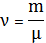

Связь С и Cm:

Сm=СM (14)

Введем в уравнение первого начало термодинамики 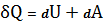для одного моля газа (v=1)значение теплоемкости

CmdT=dUm+PdV (15)

Если процесс изохорический (V=const), то PdVm=0, т.е. работа А внешних сил равна нулю, то Q идет только на увеличение U. Тогда:

(16)

т.е Сv- молярная теплоемкость, равная изменению dU одного моля газа при Т=1К.

С учетом формулы dUm=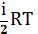

Cv=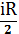 (17)

Если процесс изобарический, т.е P=const, с учетом первого начала термодинамики, записанного в форме (15), получим:

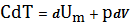
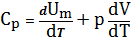
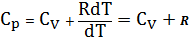
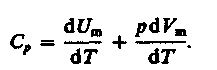
Запишем уравнение Клайперона –Менделеева одного моля газа:

PVm=RT

Продифференцируем его с учетом того, что:

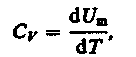
Которая не зависит от вида процесса, потому что внутренняя энергия U идеального газа не зависит ни от P, ни от V, а зависит только от T:

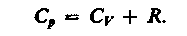(18)

(18) – Уравнение Майера.

Из (18) видно, что Cp>Cv. Это связано с тем, что, при нагревании газа при P=const, требуется дополнительное количество Q на совершение работы А расширения газа, т.к. постоянство Р обеспечивается увеличением объема газа.

В (18) подставим значение (17), получим:

Сp=Cv+R== 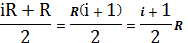(19)

Найдем отношение 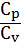с учетом выше написанных формул. Получаем:

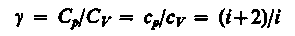(20)

Как видно из (17) и (20), молярная теплоемкость Cm определяется лишь значением i (см. степени свободы), т.е. Cp, Cv=f(i) от Т не зависят.

Однако это утверждение справедливо только для одноатомных газов (i=3) в только широком интервале температур.

Для многоатомных газов i=f(T). Так, экспериментально установлено что, Cv принимает значения (см. рис):

Такой ход зависимости Cv=f(i) можно объяснить предположив, что:

-при низких температурах наблюдается только поступательное движение (i=3)

-при комнатных температурах поступательное + вращательное движения

-при высоких температурах поступательное + вращательное + колебательное движения молекул.

10. Применение 1-го начала термодинамики к изопроцессам

Дело имеем с равновесными процессами. Есть состояние, есть процесс.

Изопроцессы могут протекать в равновесных условиях. Их мы и рассмотрим.

а. Изохорный процесс. V=const, m=const,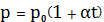

поршень в цилиндре неподвижен, Т растет.

1 – 2 – изохора нагревания;

3 – 4 – изохора охлаждения.

При изохорном процессе

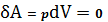тогда, согласно 1-му закону термодинамики,

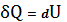(21)

С учетом того, что

(21) примет вид

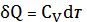(22)

Для произвольной массы газа (22) перепишется

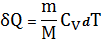(23)

б. изобарный процесс (p=const).

В данном случае совершается работа

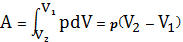, (24)

равная площади S под прямой.

Запишем ур-е К-М для состояний 1 и 2.

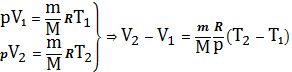(24`)

Подставим (24`) в (24)

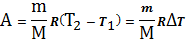(25)

Из (25) вытекает физический смысл R

R=A при T=1K 1моля газа.

Работа при изобарном расширении 1 моля идеального газа при нагревании его на 1К.

Если при изобарном процессе газу массой m сообщить тепло, равное

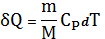то

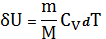и будет совершена работа

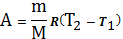в. Изотермический процесс. Т = const, т.е. выполняется закон Бойля – Мариотта:

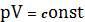
С учетом того, что

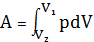
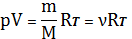
получим

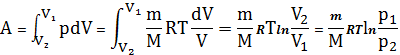T=const, тогда . Первое начало термодинамики запишется:

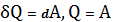Все тепло идет на совершение работы. Следовательно,

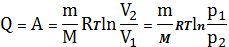(26)

Требуется восполнение энергии системы.

11. Адиабатический процесс и уравнение Пуассона. Политропический процесс. Работа при адиабатическом процессе

Процесс, сопровождающийся без теплообмена (Q=0), называется адиабатическим. К адиабатическим процессам близки:

- быстропротекающие процессы (поршень – цилиндр, звук в среде, холодильник)

- либо, наоборот, медленно протекающие процессы (теплообмен над озером).

В этом случае 1-е нач. термо-ки примет вид

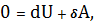
или

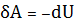, (27)

т.е. работа совершается за счет изменения внутренней энергии. С учетом (10) и (16) ур-е (27) примет вид:

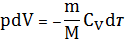(28)

Используем ур-е состояния идеального газа в дифференциальной форме

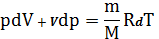. (29)

Разделим почленно (28) на (29). После преобразований получим

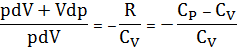Учитывая, что

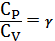
получим

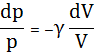Проинтегрируем

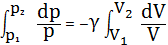Затем, потенцируя, получим

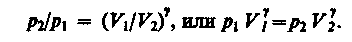
Так как состояния 1 и 2 выбраны произвольно, то можно записать

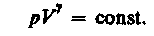(30)

(30) – уравнение адиабатического процесса, называемое также уравнением Пуассона.

В (30) отсутствует параметр Т. его можно ввести, воспользовавшись ур-ем К-М

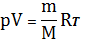Получим

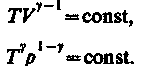(31)

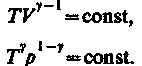(32)

–

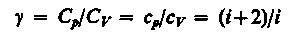называется показателем адиабаты. Для идеальных газов = 1,67.

Работа, совершаемая в адиабатическом процессе, равна

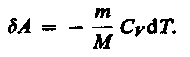
Если газ адиабатически расширяется от объема V\ до V2, то его температура уменьшается от T1 до T2 и работа расширения идеального газа

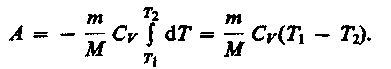(33)

Преобразуем (33), воспользовавшись ур-ем К-М

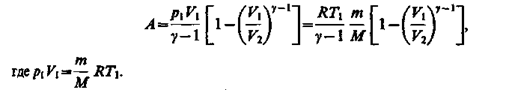
Аад < Aизотер, потому что при адиабатическом процессе Т уменьшается, а при изотермическом Т = const за счет притока тепла извне.

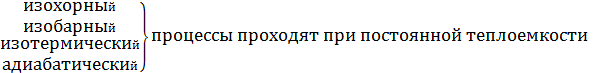
При изохорном С=СV

При изобарном С=Сp

При изотермическом (dT=0) C=±

При адиабатическом (Q=0) C=0.

Процесс, в котором теплоемкость остается постоянной, называется политропным. Уравнение политропы:

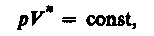(34)

где n=(C—Cp)/(C—CV) — показатель политропы. Из (34) вытекает, что

при С=0, n = 0, (34) принимает вид 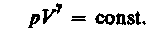- уравнение адиабаты

при С = , n = 1 — уравнение изотермы pV=const

при С = Сp, n = 0 — уравнение изобары (p=const) V=V0(1+t)

при С = СV, n = ± — уравнение изохоры (V=const) p=p0(1+t).

Т.е. рассмотренные 4 процесса являются частным случаем политропного процесса.

12.Круговой процесс. Обратимые и необратимые процессы.

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.

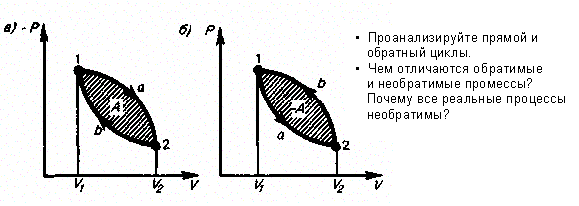
Работа положительна;

A = pdV > 0--- прямой цикл по часовой стрелке (1-а-2). Используется в двигателях внутреннего сгорания, работа совершается за счет полученной из вне теплоты (сгорает бензин).

Работа отрицательна:

A = pdV < 0---обратный цикл против часовой стрелки (2-b-1). Используется в холодильных машинах, работа совершается за счет внешних сил (электроэнергия), тепло отнимается у рабочего тела (газа) и передается телу с более высокой Т т.е холодильник греет окружающую среду.

В результате кругового процесса 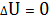, системам приходит в исходное состояние. Тогда 1 нач. термо-ки можно записать

Q=0+A Q = A, (35)

Т.е А за цикл = к-ву полученной из вне теплу.

В результате круг. процесса система может как получить теплоту так и отдать ее, поэтому

Q=Q1- Q2

Q1 – кол-во теплоты полученная системой

Q2 – кол-во теплоты отданное системой

Поэтому КПД круг. цикла

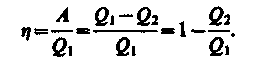(36)

Обратимы процесс - процесс(прямой обратный), когда в окр. среде и в самой системе не происходит никаких изменений (пройти по снегу туда и обратно, и чтобы при этом не остался след).

Процесс не удовлетворяющий этим условиям - необратимый процесс.

Обратимые процессы это идеализация реальных процессов.

С чем связана необратимость?- С диссепацией энергии (из-за трения, теплопроводности и.т.д.).

Однако в природе есть процессы близкие к обратимым. Их рассмотрение важно в силу:

Они более экономичны
Их КПД максимален, что позволяет указать пути повышения КПД реальных тепловых двигателей.

ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ