Взаимное расположение плоскостей, прямой и плоскости

Лекция 6

6.1 Параллельность прямой и плоскости

При решении вопроса параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости.

Оценим взаимное положение прямой АВ и плоскости, представленных на рис. 6.1.

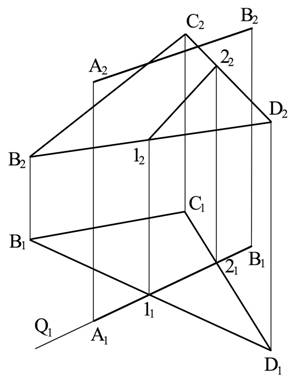
Рис.6.1

Для этого проведем через прямую АВ вспомогательную плоскость Q (Q^П1).

В данном случае через прямую проведена горизонтально-проецирующая плоскость, горизонтальный след которой сливается с одноименной проекцией прямой А1В1. Далее построены проекции линии пересечения плоскостей 1-2 сравнение которых с проекциями прямой показывает, что прямая АВ не параллельна плоскости треугольника ВСD.

На рис. 6.2 показано построение прямой параллельной заданной плоскости треугольника АВС и проходящей через точку К. Через заданную точку в пространстве можно провести бесчисленное множество прямых линий параллельных заданной плоскости. Для получения единственного решения требуется какое-нибудь дополнительное условие. Например, искомая прямая должна быть параллельна плоскости треугольника АВС и параллельна плоскости проекций П1 (дополнительное условие).

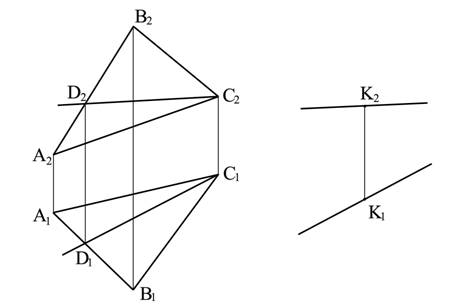
Рис. 6.2

Для решения задачи в плоскости треугольника АВС проведена одна из горизонталей и затем через точку К проведена прямая, параллельная этой горизонтали.

6.2 Перпендикулярность прямой и плоскости

Из стереометрии известна теорема об условии перпендикулярности прямой к плоскости: прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости. Известно также, что прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, лежащим в этой плоскости, в том числе к её линиям уровня.

Рис. 6.3

При построении проекций прямой перпендикулярной к плоскости, в качестве пересекающихся прямых этой плоскости берутся её линии уровня или следы плоскости, а не случайные прямые.

Пусть прямая К^Р (рис. 6.3). Проведем через точку А горизонталь h (АС) плоскости Р. Эти прямые образуют прямой угол (КА^АС), одна сторона которого АС параллельна плоскости П1. Такой угол спроецируется на плоскость П1 без искажения А1К1^h1(А1С1). Но так как h1||Р1, то А1К1^Р1. Проведем фронталь f(АВ) плоскости Р: АК^f(АВ) и А2К2^f2(А2В2), так как f||П2. Но f2 (А2В2) || Р2, поэтому А2К2^Р2.

Итак условие построения модели взаимно перпендикулярных прямых и плоскости: если АК^Р и (h, f)Р, то А1К1^h1 и А2К2^f2.

Выводы: если прямая перпендикулярна к плоскости, то горизонтальная проекция её перпендикулярна к горизонтальным проекциям горизонталей, а фронтальная проекция перпендикулярна к фронтальным проекциям фронталей этой плоскости.

Приведенное положение дает возможность решать ряд задач и, в частности, опустить или восстановить перпендикуляр к плоскости, решить обратную задачу – провести плоскость перпендикулярно прямой, определить расстояние от точки до плоскости (см. пример 7.8)

6.3 Параллельность плоскостей

Рассмотрим случай взаимной параллельности плоскостей. Если плоскости параллельны, то всегда в каждой из них можно построить по две пересекающиеся между собой прямые линии так, чтобы прямые одной плоскости были соответственно параллельны двум прямым другой плоскости (рис. 6.4,а).

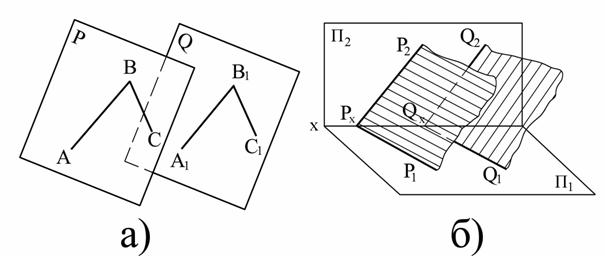
Рис. 6.4

Это служит основным признаком для определения, параллельны плоскости между собой или не параллельны. Такими прямыми могут служить, например, следы обеих плоскостей: если два пересекающихся между собой следа одной плоскости параллельны одноименным с ними следам другой плоскости, то обе плоскости параллельны между собой (3.17, б, где Р1||Q1, P2||Q2).

На рис. 6.5 показано построение плоскости, параллельной заданной плоскости Р.

В первом случае (рис. 6.5,а) искомая плоскость задана двумя пересекающимися прямыми, проходящими через точку А и являющимися главными линиями плоскости – горизонталью и фронталью. На рис. 6.5 б показано построение следов искомой плоскости Т, проходящей через заданную точку А.

Решение начато с построения горизонтали искомой плоскости и её фронтального следа N, через который проведен фронтальный след плоскости Т(Т1,Т2). Через точку схода следов Тх прошел горизонтальный след искомой плоскости Т1||Р1.

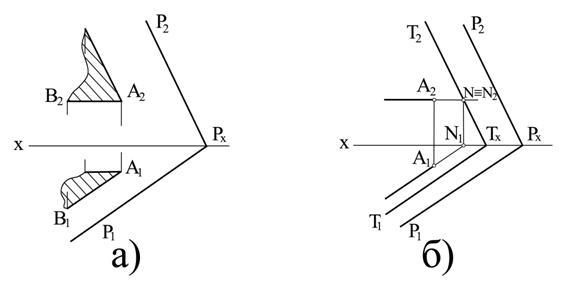
Рис. 6.5

6.4 Перпендикулярность плоскостей

Из стереометрии известно условие перпендикулярности двух плоскостей: если плоскость проходит через перпендикуляр к данной плоскости (или параллельна этому перпендикуляру), то она перпендикулярна к данной плоскости.

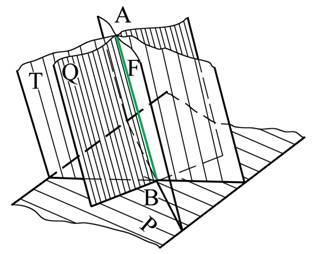
Рис. 6.6

Через данную точку А можно провести бесчисленное множество плоскостей перпендикулярных данной плоскости Р (рис. 6.6). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр АВ, опущенный из точки А на плоскость Р.

На эпюре (рис. 6.7) показано построение одной из плоскостей этого пучка. Прежде всего через проекции точки А проведены проекции перпендикуляра АК к данной плоскости. Построение А1К1 и А2К2 не вызывает затруднений, так как плоскость Р задана главными линиями. Затем через проекции той же точки А проведены проекции произвольной линии АD. Эти две пересекающиеся линии АК и АD и определяют искомую плоскость Р.

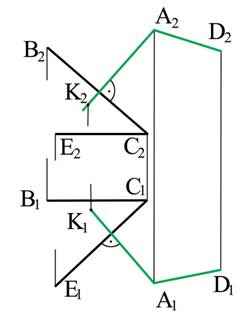
Рис. 6.7

Примеры позиционных и метрических задач на плоскость

Пример 1. В плоскости, заданной треугольником АВС, построить точку D (рис. 3.21).

Решение.

1. Необходимо в данной плоскости провести прямую. Зададим для этого две точки, заведомо лежащие в данной плоскости. Одной из таких точек может быть вершина А(А1;А2) треугольника. Вторую точку Е(Е1;Е2) зададим на стороне ВС. Через одноименные проекции А1 и Е1, А2 и Е2 проведем прямые. Эти прямые являются проекциями прямой, лежащей в данной плоскости.

2. На построенной прямой АЕ зададим точку D. Для этого построим D1А1Е1 и D2А2Е2. Точка D лежит в заданной плоскости, т.к. она принадлежит прямой АЕ, лежащей в этой плоскости

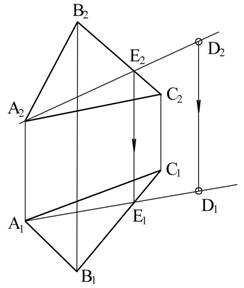
Рис. 3.21

Пример 2. Построить линию наибольшего уклона плоскости, заданной параллельными прямыми а(а1; а2) и b(b1; b2) и определить угол a между этой плоскостью и горизонтальной плоскостью проекций (рис. 3.22)

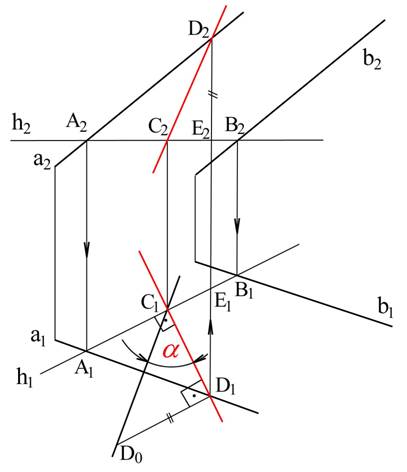
Рис. 3.22

Решение

Проведем горизонталь h данной плоскости (см. гл.3 рис. 3.3, в). Проекциями этой горизонтали будут прямые h1 и h2.
Проведем прямую, перпендикулярную к горизонтальной проекции горизонтали, и отметим точки С1 - пересечения её с h1 D1 – са1. Прямая С1D1 является горизонтальной проекцией линии наибольшего ската.
Построим фронтальные проекции С2 и D2. Для этого из С1 и D1 проведем вертикальные линии связи до пересечения соответственно с h2 и а2.
Прямая, соединяющая точки С2 и D2, является фронтальной проекцией линии наибольшего уклона.
Угол a определяем из прямоугольного треугольника D1C1E0, построенного на С 1D1 как на катете. Второй катет D0D1 = E2D2. Искомый угол a=D0C1D1

Пример 3. Задана плоскость пересекающимися прямыми АВ и CD. Определить, лежит ли прямая KL в этой плоскости.

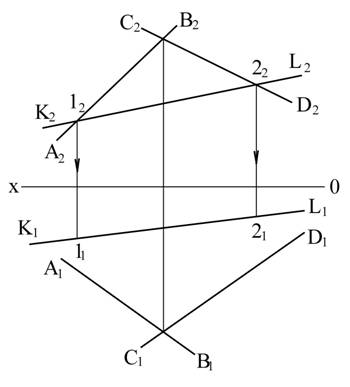
Рис. 3.23

Решение.

1. Обозначим точки пересечения фронтальных проекций прямых АВ и KL через 12 и прямых CD и KL через 22.

2. Строим их горизонтальные проекции – точки 11 и 22 на горизонтальной проекции (K1L1) прямой KL. Из построения видно, что точки 1(1112) и 2(2122) прямая KL на заданной плоскости не лежат. Следовательно, прямая KL в плоскости не лежит. Решение этой задачи можно начать и с пересечения горизонтальных проекций.

Пример 4. В плоскости, заданной двумя параллельными прямыми АВ и CD, провести фронталь на расстоянии 15 мм от фронтальной плоскости проекций (рис. 3.24)

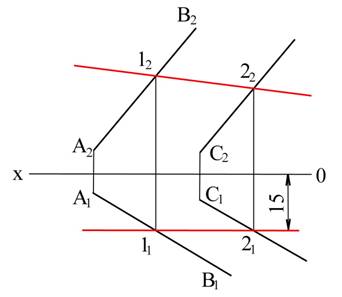
Рис. 3.24

Решение. Проводим на расстоянии 15 мм от оси проекций параллельную ей горизонтальную проекцию (11-22) фронтали, которая пересекает прямые А1В1 и C1D1 в точках 11 и 22.

Затем находим точки 11 и 22 на прямых А2В2 и C2D2 и проводим через них фронтальную проекцию (1222) фронтали.

Пример 5. Найти прямую пересечения плоскостей Р и Q.

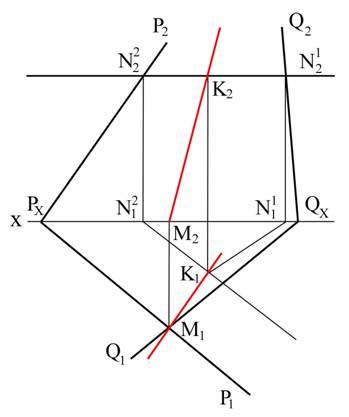
Рис. 3.25

Решение. Плоскость Р и Q пересекаются по прямой общего положения, проходящей через точку-след (М1;М2) пересечения горизонтальных следов плоскостей. Точка-след (N1;N2) пересечения фронтальных следов плоскостей недоступна, т.к. эти следы плоскостей по заданию, в пределах чертежа не пересекаются.

Вместо точки (N1;N2) необходимо найти другую произвольную точку прямой пересечения, общую для заданных плоскостей. Для этого вводим вспомогательную плоскость R, например параллельную П которая, как известно, пересекает каждую из данных плоскостей по горизонтали. На их пересечении получаем вспомогательную точку (К1;К2), общую для данных плоскостей. Найдя эту вторую точку (К1;К2) прямой, проводим её проекцию: горизонтальную – через точки М1 и К1 и фронтальную через точки М2 и К2.

Пример 6. Найти точку пересечения прямой АВ с плоскостью Р (рис. 3.26)

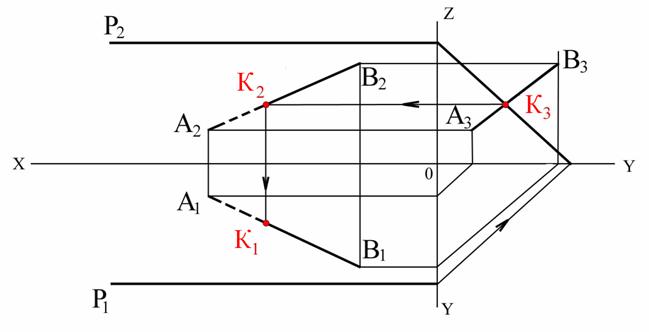
Рис. 3.26

Решение. Обозначим искомую точку через точку К. Так как точка К (К1;К2) лежит на профильно-проецирующей плоскости. То её профильная проекция (К3) должна лежать на профильном следе (Р3) плоскости. Вместе с тем, так как эта же точка лежит и на прямой АВ, то её профильная проекция (К3) должна лежать так же где-то на профильной проекции (А3В3) прямой. Следовательно искомая точка должна лежать на их пересечении. Найдя профильный след плоскости и профильную проекцию прямой, получаем на их пересечении профильную проекцию (К3) искомой точки. Зная профильную проекцию (К3) искомой точки, находим две другие её проекции на одноименных проекциях прямой.

Пример 7. Даны плоскость Р и точка А. Определить расстояние то точки до плоскости (рис. 3.27)

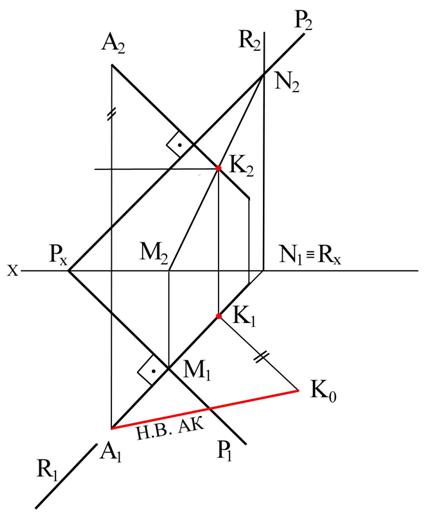
Рис. 3.27

Решение. Опускаем из точки А (А1;А2) перпендикуляр на плоскость Р и находим его основание на этой плоскости, для чего ищем точку К (К1;К2) пересечения перпендикуляра с плоскостью. Имея проекции (А1К1;А2К2) отрезка перпендикуляра, определим его действительную величину методом прямоугольного треугольника.

Пример 8. Даны треугольник АВС и точка К. Определить расстояние между ними. (рис. 3.28)

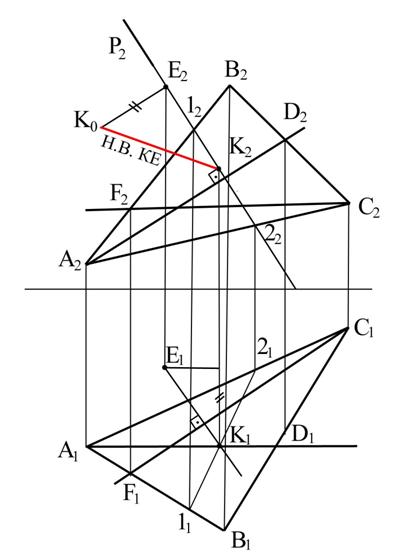
Рис. 3.28

Решение. Опускаем из заданной точки Е (Е1;Е2) перпендикуляр на плоскость треугольника: К1Е1 перпендикулярно горизонтальной проекции горизонтали (К1Е1^С1F1), К2Е2 перпендикулярно фронтальной проекции фронтали (К2Е2^А2 D2). Находим точку пересечения перпендикуляра с плоскостью треугольника (К1;К2) , определяем натуральную величину отрезка перпендикуляра (К1Е1;К2Е2) методом прямоугольного треугольника.

Взаимное расположение плоскостей, прямой и плоскости