НЕЛИНЕЙНЫЕ СИСТЕМЫ

5. НЕЛИНЕЙНЫЕ СИСТЕМЫ

Физические законы движения окружающего нас мира таковы, что все объекты управления нелинейны. Одни нелинейности (люфт, насыщение, сухое трение, гистерезис) являются сопутствующими. Они не включены в систему преднамеренно, а оказываются следствием несовершенства физических элементов или зависят от свойств материалов. Такие нелинейности, как правило, нежелательны. Другие нелинейности, называемые структурными, вводятся в систему преднамеренно для получения требуемых характеристик системы. Они имеют обычно чётко выраженный характер, являются существенными. Некоторые нелинейности можно представить графически плавными однозначными кривыми, их называют аналитическими. На статических характеристиках неаналитических нелинейностей имеются точки резких изменений координат. Эти характеристики представляются на графиках ломаными или многозначными линиями. Если нелинейности выражены слабо, то поведение нелинейной системы незначительно отличается от поведения линейной системы. В таких случаях для исследования нелинейных систем прибегают к линеаризации нелинейностей либо с помощью метода малых отклонений, либо путём осреднения. Создать точную модель реальной системы невозможно. Обычно увеличение точности модели связано с увеличением её порядка. Однако наступает момент, когда увеличение порядка не вносит существенного улучшения в модель системы.

При исследовании систем управления технологическими объектами с несущественными нелинейностями придерживаются классической концепции Вышнеградского-Максвелла, в соответствии с которой исследование систем управления проводится методами линейной теории путём перехода к приближённым линейным моделям. Это в значительной степени предопределило и выбор алгоритмов функционирования управляющих устройств (регуляторов, блоков компенсации, командных блоков) в классе линейных алгоритмов.

Все системы, которые считаются линейными, являются таковыми лишь в определённых диапазонах сигналов и всегда могут стать нелинейными. Кроме того, некоторые реальные системы изначально являются существенно нелинейными. Поэтому в тех случаях, когда линеаризованная модель даёт очень плохую аппроксимацию характеристик реальной системы, при анализе системы необходимо использовать её нелинейную модель и специальные методики расчёта.

Если нелинейность является существенной, то получение линейной модели становится затруднительной, а сама модель утрачивает ряд важных свойств оригинала.

Когда исследуемая линейная система устойчива, то выходная функция системы будет оставаться ограниченной при любом ограниченном входном воздействии и любых ограниченных начальных условиях. Нелинейные же системы при одних входных воздействиях могут быть устойчивы, но при других становятся неустойчивыми. Разработаны лишь частные методы исследования нелинейных систем, каждый из которых не может быть применён к любой из нелинейных систем. Наиболее важными и распространёнными методами исследования систем с существенными нелинейностями являются методы фазовых траекторий, гармонического баланса, абсолютной устойчивости, второй метод Ляпунова и имитационного компьютерного моделирования. Выбор метода определяется классом решаемой задачи и целями исследования. Достоверность результатов анализа зависит от точности математических моделей систем.

В большинстве случаев устойчивость систем высокого порядка, содержащих нелинейности, поддаётся исследованию только путём имитационного моделирования. Для некоторых систем вообще невозможно подобрать адекватный метод анализа и единственное, что остаётся сделать – это прибегнуть к имитационному моделированию. Учитывая специфику нелинейных систем, даже если применение какого-то метода анализа является оправданным, полученные результаты должны быть проверены путём моделирования в интерактивных компьютерных средах.

Управление крупными, сложными и дорогостоящими объектами, как правило, многоуровневое.

Первый (нижний) уровень составляют локальные нелинейные системы автоматического управления объектом. Задача управления состоит в устранении недетерминизма систем, обусловленного действием неконтролируемых случайных возмущений и неполнотой априорной информации о модели объекта. Приемлемая реакция нелинейной системы на ступенчатое возмущение может сопровождаться автоколебаниями в установившемся режиме, что может быть недопустимо для объекта по технологическим показателям функционирования. Изменениям динамических свойств объекта, обусловленных изменением режимных факторов, доступных для контроля, соответствует коррекция, вводимая в регулятор соответствующим модулем.

Второй уровень управления объектом предназначен для формирования нелинейных командных воздействий с учётом ограничений на управляющие воздействия и их производные (задача оптимального управления). Обычно управляющие воздействия – заранее известные функции времени (часто ступенчатые) с целью быстрого перевода объекта управления с одного режима функционирования на другой.

На третьем уровне управления решаются нелинейные задачи оптимизации режима работы объекта по технико-экономическим критериям и оптимизации параметров нижних уровней системы управления с целью адаптации к меняющимся свойствам объекта и среды функционирования.

5.1. Определение нелинейных систем и их технические характеристики

Нелинейной называется такая система, для которой не применим принцип суперпозиции из-за наличия в дифференциальном уравнении степеней, тригонометрических функций, произведений переменных, звеньев с нелинейными статическими характеристиками и других нелинейных членов.

Реальные САУ нелинейны. Нелинейности подразделяют на линеаризуемые (несущественные) и нелинеаризуемые (существенные). Использование аппарата линейной теории для целей анализа и синтеза систем автоматического управления следует считать целесообразным, если при этом не допускается принципиальных качественных ошибок, а также если количественные погрешности не выходят за рамки допустимых пределов.

Различают статические и динамические нелинейности. Первые описываются нелинейными алгебраическими уравнениями, а вторые представляются в виде нелинейных дифференциальных уравнений.

Нелинейным автоматическим системам присущи принципиально новые свойства в динамике, которые отсутствуют у линейных:

К нелинейным системам не применим принцип суперпозиции;
Устойчивость и качество переходных процессов в нелинейных системах зависят от степени возмущения и начальных условий;
Возможность возникновения в них автоколебаний (предельных циклов) в общем случае несинусоидальных, амплитуда которых не зависит от внешних воздействий и начальных условий;
Частота вынужденных колебаний на выходе системы может быть либо субгармоникой, либо гармоникой входного периодического сигнала;
Явление скачкообразного резонанса (рис. 5.1);

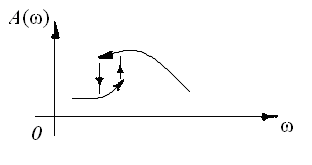
Рис. 5.1. АЧХ системы с явлением скачкообразного резонанса

Множество состояний равновесия;
Конечная длительность процессов, чему способствуют зоны нечувствительности элементов, сухое трение и люфты (зазоры кинематических сочленений);
Ограниченность уровней переменных энергетическими, материальными, прочностными ресурсами.

В нелинейных системах следует исследовать не устойчивость вообще, а устойчивость определённого их режима.

Чтобы судить о свойствах нелинейных систем, кроме математических и физических характеристик элементов необходимо знать вид и величины входных воздействий и область начальных условий.

Появление нелинейности в системе с линейной структурой обычно приводит к снижению качества работы последней.

5.2. Математическое описание нелинейных элементов

5.2.1. Безынерционные нелинейные элементы

В теории и практике управления объекты управления рассматривают как преобразователи сигналов-носителей информации о цели функционирования объекта, его состоянии и воздействиях окружающей среды.

Если безынерционный элемент линейный, то он описывается полностью значением передаточного коэффициента.

Нелинейные зависимости между постоянными значениями входных и выходных сигналов

(5.1)

задаются аналитически, графически или таблично.

В том случае, когда нелинейный элемент имеет один вход и один выход (рис. 5.2) особенно наглядны графики статических характеристик (рис. 5.3).

Рис. 5.2. Элемент системы как преобразователь сигналов

Рис. 5.3. Пример статической характеристики нелинейного элемента

Условия преобразования сигналов безынерционными нелинейными элементами зависят от уровней сигналов и не зависят от их частоты.

Примеры наиболее распространённых (типовых) нелинеаризуемых по методу малых отклонений нелинейных характеристик безынерционных элементов:

Двухпозиционное реле (звено с релейной характеристикой). Описать линейной зависимостью элемент с такой рабочей характеристикой невозможно, так как в рабочей точке имеется разрыв (рис. 5.4).

Уравнение элемента:

(5.2)

Рис. 5.4. Статическая характеристика двухпозиционного реле

Трёхпозиционное реле (звено с релейной характеристикой и зоной нечувствительности) (рис. 5.5).

Уравнение звена имеет вид

(5.3)

Рис. 5.5. Статическая характеристика

трехпозиционного реле

Ограничение (звено с характеристикой типа «насыщение») (рис. 5.6).

Необходимость исследования поведения системы «в большом» заставляет рассматривать характеристики элементов при больших значениях входных воздействий. В этом случае элемент может оказаться нелинейным, хотя и является линеаризуемым «в малом».

Уравнение элемента:

(5.4)

Рис.5.6. Статическая характеристика типа «ограничение»

4. Зона нечувствительности (элемент с зоной нечувствительности) (рис. 5.7).

Уравнение элемента:

(5.5)

Рис.5.7. Статическая характеристика элемента с зоной нечувствительности

5. Ограничение с зоной нечувствительности (рис. 5.8).

Уравнение звена:

(5.6)

Рис.5.8. Статическая характеристика элемен-

та с зоной нечувствительности и ог-

раничением

6. Двухпозиционное реле с зоной возврата (элемент с петлей гистерезиса) (рис. 5.9).

Уравнение элемента:

(5.7)

Рис.5.9. Статическая характеристика двухпозиционного реле с зоной возврата

7. Трехпозиционное реле с зоной нечувствительности и зоной возврата (элемент с зонами нечувствительности и неоднозначности) (рис. 5.10).

Уравнение элемента:

(5.8)

Рис.5.10. Статическая характеристика трёхпозиционного реле с зоной

нечувствительности и зоной возврата

5.2.2. Динамические нелинейные звенья САУ

В общем случае дифференциальные уравнения, описывающие элементы систем, являются нелинейными

. (5.9)

Иногда они разрешаются относительно старшей производной переменной выхода

(5.10)

Часто дифференциальные уравнения представляются в форме Коши:

(5.11)

где х – вектор переменных состояния; -вектор-функция; - функция выхода. В уравнениях (5.9-5.11) предполагается, что нелинейные функции заданы аналитически.

Преобразование сигналов динамическими нелинейными элементами в значительной степени зависит как от уровней сигналов, так и от их частотных спектров.

Во многих случаях нелинейное динамическое звено представляется в форме линейной модели и дополнительного нелинейного элемента, учитывающего такие естественные факторы, как ограниченность управляющих воздействий, наличие зоны нечувствительности в измерительных и исполнительных элементах, люфтов в кинематических сочленениях или искусственное введение нелинейностей в алгоритмы управления для получения свойств, не достижимых в линейных системах.

Простейший пример такой модели – нелинейный интегратор

(5.12)

структурно изображается как последовательное соединение безынерционного нелинейного элемента и линейного интегрирующего звена (рис. 5.11).

Рис. 5.11. Нелинейный интегратор

В этом примере нелинейные эффекты сосредоточены в безынерционном элементе, а динамические – в линейном элементе.

5.3. Определение статических характеристик систем

с типовой структурой

Структуры систем называют типовыми, если они образованы последовательным или параллельным соединением звеньев, а также одноконтурные системы со встречно-параллельным соединением двух звеньев.

1. Эквивалентные статические характеристики последовательно соединенных звеньев.

Последовательное соединение нелинейных элементов (рис. 5.12) эквивалентно одному нелинейному элементу со статической характеристикой

, (5.13)

являющейся композицией статических характеристик составляющих звеньев:

. (5.14)

Рис. 5.12. Последовательное соединение нелинейных элементов

В общем случае перестановка нелинейных элементов дает другой результат (нелинейные операторы не коммутативны), т.е.

. (5.15)

Например, при последовательном соединении идеального реле и линейного безынерционного звена с передаточным коэффициентом k>0 (линейный усилитель предшествует реле) статическая характеристика последовательного соединения звеньев повторяет в точности статическую характеристику реле:

, (5.16)

если же звенья переставить, то

. (5.17)

Бывают исключения, когда нелинейные преобразования коммутативны. Так, в случае взаимно обратных НЭ, когда графики статических характеристик симметричны относительно биссектрисы первого и третьего квадрантов при одинаковом масштабе по осям абсцисс и ординат, имеем:

(5.18)

Если статические характеристики последовательно соединенных нелинейных элементов заданы графически, то достаточно просто строится статическая характеристика эквивалентного нелинейного элемента (рис. 5.13).

Рис. 5.13. Процедура построения статической характеристики последовательного соединения нелинейных звеньев

2. Эквивалентные статические характеристики параллельно соединенных звеньев.

Параллельно соединенные нелинейные элементы эквивалентны одному нелинейному элементу со статической характеристикой

. (5.19)

Перестановка нелинейных элементов дает тот же результат.

Графическая процедура построения статической характеристики сводится к покоординатному сложению статических характеристик и .

Если

, (5.20)

то такие нелинейные элементы называются взаимно дополнительными. Компенсация нелинейного звена достигается параллельным подключением взаимно дополнительной нелинейности. Например, зона нечувствительности компенсируется параллельным включением нелинейного элемента типа «насыщение» (рис. 5.14).

Рис.5.14. Компенсация зоны нечувствитель-

ности элемента подключением взаимно дополнительного звена

3. Эквивалентные статические характеристики систем с обратной связью.

Если два нелинейных элемента образуют контур с отрицательной обратной связью, то для получения эквивалентной статической характеристики необходимо исключить переменные и z в системе уравнений:

(5.21)

Отсюда выражение для выхода системы

(5.22)

Получена требуемая зависимость в неявной форме.

Пусть существует обратная нелинейность . Применим это преобразование к последнему выражению

(5.23)

т.е. получили статическую характеристику, обратную искомой,

отсюда

. (5.24)

Алгоритм графического построения требуемой статической характеристики системы (в предположении о её обратимости) следующий:

строится обратная статическая характеристика ;
характеристики и суммируются;
определяется статическая характеристика, обратная суммарной:

а) б)

Рис. 5.15. Эквивалентные структурные схемы системы

Если существуют обратные нелинейности , то исходная структура преобразуема к эквивалентной, как показано на рис. 5.15.

Покажем справедливость этого преобразования.

Из выражения (5.23) находим

(5.25)

Пусть существует обратная нелинейность . Тогда, применив соответствующее преобразование к выражению (5.25), получим

(5.26)

Этому выражению соответствует соединение с обратной связью двух нелинейных элементов (рис. 5.15,б), эквивалентное исходному соединению (рис. 5.15,а) в смысле статической характеристики .

Сравнивая преобразованную структуру с исходной, замечаем, что нелинейные элементы поменялись местами, а их характеристики заменены на обратные. На практике такой прием иногда используется для упрощения реализации нелинейных элементов.

Эквивалентность структур, показанных на рис. 5.15 , имеет место и для динамических звеньев. В случае линейных звеньев с передаточными функциями и обратными будут операторы и соответственно.

Пример 5.1. Пусть нелинейный элемент типа «насыщение» со статической характеристикой охвачен отрицательной обратной связью в виде динамического звена с передаточной функцией (гибкая обратная связь)

(5.27)

Эквивалентное преобразование структуры показано на рис. 5.16.

а) б)

Рис. 5.16. Эквивалентные структуры системы с охватом нелинейного элемента

линейным динамическим звеном

В случае большого усиления нелинейного элемента в линейной зоне , когда , в схеме рис. 5.16,б можно игнорировать обратную связь с передаточным коэффициентом . В результате приближенно получим:

(5.28)

т.е. передаточную функцию пропорционально-интегрального звена.

Такой способ применим для реализации аналоговых регуляторов, реализующих ПИ-закон управления объектами.

5.4. Расчетные структурные схемы нелинейных систем

Класс нелинейных моделей очень широк, что чрезвычайно затрудняет их единообразное описание и возможность использования универсальных методов анализа и синтеза. Поэтому при разработке методик исследования автоматических систем управления по нелинейным моделям выбираются расчетные формы моделей, к которым, по возможности, приводят исходные модели. Основными критериями при выборе расчетных форм нелинейных моделей являются:

широта класса автоматических систем, моделируемых принятыми типами моделей;
удобство последующего анализа и простота эквивалентного приведения к этому виду других нетиповых исходных моделей.

Рис. 5.17. Расчетная структурная схема нелинейной системы

Большая группа точных и приближенных методов исследования автоматических систем на основе нелинейного подхода использует типовую структурную схему, приведенную на рис. 5.17.

В качестве дополнительного ограничения этого расчетного вида математических моделей обычно принимают безынерционность единственного нелинейного элемента с одним входом и одним выходом.

Динамические свойства системы сосредоточены в линейной части с передаточной функцией

(5.29)

По структурной схеме запишем систему уравнений:

(5.30)

где - оператор дифференцирования.

Для автономной системы воздействие тождественно равно нулю, тогда уравнения (5.30) приводятся к виду

Уравнения линейной части в форме пространства состояний при условии m<n имеют вид

(5.31)

С учетом нелинейного элемента для автономной системы получим следующие уравнения:

(5.32)

Если структурная схема исследуемой системы отличается от расчетной, то в некоторых случаях ее можно преобразовать в расчетную форму. Проблема заключается в том, что в случае нелинейных моделей не всегда применимы правила структурных преобразований линейных систем.

5.5. Устойчивость нелинейных систем

Нелинейные системы в отличие от линейных могут быть устойчивы в одних режимах работы и неустойчивы в других. Различают устойчивость в малом, в большом, в целом.

Движение устойчиво в малом, если условия устойчивости выполняются лишь в малой окрестности равновесия, то есть при малых начальных отклонениях.

Устойчивость “в малом” – понятие качественное, поскольку не оговариваются размеры области притяжения невозмущённого движения. Применение первой теоремы Ляпунова ограничено лишь малой окрестностью точки равновесия.

Если же движение устойчиво при конечных отклонениях, возможных в данной системе по условиям её работы, то его принято называть устойчивым в большом.

Устойчивость “в большом” – понятие количественное (практическое), когда указываются границы переменных относительно равновесного режима (в большой области пространства состояний, прилегающей к точке равновесия).

Движение устойчиво в целом (глобальная устойчивость), если оно устойчиво при любых начальных отклонениях, то есть не зависит от них.

В этом случае область притяжения совпадает со всем пространством состояния. Асимптотическую устойчивость “в целом” для класса нелинейностей называют абсолютной устойчивостью.

5.6. Линеаризация нелинейных систем, описываемых дифференциальными уравнениями

n-го порядка

Без потери общности рассмотрим процедуру линеаризации уравнения движения относительно опорной траектории на примере системы, описываемой дифференциальным уравнением второго порядка:

, (5.33)

где F- нелинейная функция своих аргументов.

Предположим, что задана опорная траектория , которая получается в результате решения уравнения (5.33) с начальными условиями и известным входным сигналом , т.е.

. (5.34)

Обозначим

(5.35)

отклонения от опорного режима,

где y(t) – решение уравнения (5.33) с начальными условиями и входным сигналом r(t). Графики функций приведены на рис. 5.18.

Рис. 5.18. Графики опорной траектории и реакции системы на входной

сигнал

Разложим функцию F в ряд Тейлора в окрестности опорной траектории, ограничиваясь членами только первого порядка (линейными членами):

, (5.36)

где индекс «оn» означает, что все частные производные рассчитываются на опорной траектории.

Первый член уравнения обращается в нуль, так как опорная траектория удовлетворяет уравнению (5.34).

Введем обозначения:

,, , , . (5.37)

Тогда уравнение (5.36) переписывается в форме

(5.38)

с начальными условиями

Его решение определяет отклонение от опорной траектории (см. рис. 5.18).

Пример 5.2. Пусть требуется провести линеаризацию системы, описываемой дифференциальным уравнением

с начальными условиями относительно опорной траектории .

Определим коэффициенты разложения функции F в ряд Тейлора:

Отсюда получим дифференциальное уравнение линеаризованной системы:

Структурная схема, соответствующая линеаризованному дифференциальному уравнению (знак условно опущен), приведена на рис. 5.19.

Рис. 5.19. Структурная схема САУ, соответствующая линеаризованному

дифференциальному уравнению

Алгоритм построения схемы:

Выражается член со старшей производной из дифференциального уравнения и представляется полученное соотношение с помощью сумматора, интегрирующих и усилительных звеньев;
Все низшие производные получаются как сигналы на соответствующих выходах последовательно соединенных интегрирующих звеньев;
Начальные условия представляются как постоянные во времени воздействия, приложенные на выходах интегрирующих звеньев.

Необходимое условие устойчивости Рауса (положительность всех коэффициентов характеристического уравнения системы

)

не выполняется, так как . По критерию Гурвица должно выполняться неравенство условие Гурвица не выполнено, поэтому делаем вывод, что система неустойчива.

Корни характеристического полинома ,

- имеют положительную вещественную часть, поэтому согласно теоремам первого метода Ляпунова система неустойчива.

5.7. Линеаризация нелинейных систем, описываемых дифференциальными

уравнениями в форме Коши

Метод применяется для исследования устойчивости нелинейных систем по линеаризованным уравнениям для малых вариаций переменных.

Применим первый метод Ляпунова к дифференциальным уравнениям в пространстве состояний нелинейных систем.

Пусть динамическая система описывается уравнением

(5.39)

где x - вектор состояния, - вектор-функция.

Обозначим через x* вектор координат исследуемого положения равновесия, т.е. решение системы уравнений , и положим, что функция допускает разложение в ряд Тейлора в точке x*. Пренебрегая малыми высшего порядка по сравнению с малыми вариациями x, получим вместо уравнения (5.39) линеаризованную систему

, (5.40)

где -

- матрица первых производных нелинейной функции (матрица Якоби), вычисляемых в точке равновесия x=x* (рис.5.20).

Рис.5.20. Линеаризация в окрестности положения равновесия

Согласно первому методу Ляпунова об устойчивости “в малом” положения равновесия нелинейной системы можно судить по результатам анализа линеаризованной системы:

если все собственные значения матрицы А имеют отрицательные действительные части, т.е. линеаризованная система устойчива асимптотически, то положение равновесия устойчивое;
если линеаризованная система неустойчива, то положение равновесия неустойчивое.

Первый метод Ляпунова имеет следующие недостатки:

исследуется только устойчивость «в малом»;
применим только для систем, линеаризуемых в окрестности положения равновесия.

Если требуется провести линеаризацию уравнения движения системы относительно опорной траектории , являющейся решением уравнения

(5.41)

при некотором входном сигнале и начальных условиях ,

т.е. (5.42)

то поведение x(t) нелинейной системы в окрестности опорной траектории может быть представлено с помощью отклонений (вариаций) x(t) от опорной траектории: (5.43)

Подставляя (5.43) в (5.41), имеем

, (5.44)

где - вариация внешних воздействий,

Разложим функцию F в ряд Тейлора в окрестности опорной траектории, ограничимся членами только первого порядка (линейными членами) и вычтем (5.42) из (5.44), получим, что вариации x(t) описываются системой линейных уравнений:

, (5.45)

где и - матрицы частных производных вектор-функции F(t,x,r) по соответствующим аргументам,

Дальнейший анализ нелинейной системы в окрестности опорного режима проводится методами анализа линейных систем, применяемыми к уравнениям в вариациях (5.45).

Пример 5. 3.

Проведем исследование устойчивости положения равновесия

системы с нелинейным демпфированием с помощью первого

метода Ляпунова.

Математическое описание системы в форме Коши имеет вид

Положение равновесия

Так как

то согласно (5.40) матрица

Линеаризация дает систему уравнений для малых отклонений, которую представим в векторно-матричной форме:

Собственные значения (характеристические числа) квадратной матрицы - корни уравнения

т.е. линеаризованная система находится на границе устойчивости. Согласно теоремам Ляпунова первого метода в этом критическом случае об устойчивости положения равновесия исходной нелинейной системы нельзя судить по линеаризованным уравнениям.

5.8. Теорема Ляпунова (второй метод) об устойчивости нелинейных

систем

Формулировка теоремы:

“Если при заданных в форме Коши уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова , чтобы ее производная во времени тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива”.

При знакоопределенной функции W будет иметь место асимптотическая устойчивость. Пусть заданы дифференциальные уравнения автоматической системы в форме системы уравнений первого порядка (форме Коши, уравнений состояния), полагая, что они записаны для переходного процесса в отклонениях всех переменных от их значений в установившемся процессе:

(5.46)

где функции произвольны и содержат любого вида нелинейности, но всегда удовлетворяющие условию

при

так как в установившемся состоянии все отклонения переменных и их производные равны нулю по самому определению понятия этих отклонений, и пусть имеется функция нескольких переменных (функция Ляпунова)

, (5.47)

которая обращается в нуль в начале координат, т.е. при , и непрерывна в некоторой области вокруг него.

Функция V называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только начала координат.

Пример 5.4. Пусть и Это будет знакоопределенная (положительная) функция, так как V=0 только тогда, когда одновременно и , и V > 0 при всех вещественных значениях и .

Функция - знакоопределенная отрицательная.

Функция V называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Пример 5.5. Функция при - знакопостоянная (положительная) функция, так как она обращается в нуль при любом значении , если

Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Пример 5.6. Функция - знакопеременная, так как она положительна для всех точек плоскости справа от прямой и отрицательна слева от прямой (рис. 5.21).

Рис.5.21. Плоскость переменных ()

Проиллюстрируем справедливость этой теоремы на примере системы третьего порядка (). Возьмем знакоопределенную положительную функцию Ляпунова в виде

, (5.48)

где a,b,c - произвольно заданные вещественные числа.

Будем придавать величине V возрастающие постоянные значения что означает

(5.49)

Первое из этих выражений соответствует одной точке (началу координат фазового пространства), а остальные - поверхностям эллипсоидов в фазовом пространстве, причём каждый последующий эллипсоид содержит внутри себя целиком предыдущий. Возьмем теперь производную от функции Ляпунова по времени:

(5.50)

и подставим сюда значения из заданных уравнений системы (5.46)

при n=3:

(5.51)

Если полученная таким путем функция окажется знакоопределенной отрицательной, т.е. если

(5.52)

во всех точках исследуемого фазового пространства, кроме одного только начала координат, где

при ,

то при любых начальных условиях изображающая точка М (рис.5.22), вследствие (5.52), будет двигаться в сторону уменьшения значений V , т.е. будет пересекать эллипсоиды извне внутрь.

Рис.5.22.Движение изображающей точки М относительно замкнутых

поверхностей, окружающих начало координат

В результате с течением времени изображающая точка М будет стремиться к началу координат фазового пространства (асимптотическая устойчивость) и уже никак не сможет выйти за пределы тех эллипсоидов, в которые она проникла. Это и означает затухание всех отклонений в переходном процессе с течением времени, тем самым установлена устойчивость данной системы.

Теорема справедлива для исследования устойчивости систем управления не только при малых, но и при больших отклонениях, если для них имеют место исходные уравнения исследуемой системы управления.

Теорема Ляпунова обеспечивает получение достаточных условий устойчивости, которые не всегда будут и необходимыми, т.е. при выполнении условий теоремы система будет устойчива, но эти условия могут не охватить всей области устойчивости системы по параметрам, так как выбор функции V произволен и нет уверенности в том, что нельзя подобрать другой вариант функции V, который бы еще более полно охватывал область устойчивости данной системы.

Понятие устойчивости по Ляпунову допускает, чтобы при знакоопределенной функции V производная от нее W была не обязательно знакоопределенной или знакопостоянной, а могла быть и тождественно равна нулю во всем рассматриваемом фазовом пространстве. В этом случае изображающая точка М будет оставаться все время на какой-нибудь одной из поверхностей V=const, куда ее забросили начальные условия. В результате система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.

Если же функция W будет не знакоопределенной, а знакопостоянной, то траектория изображающей точки М не везде будет пересекать поверхности V=C, а может их касаться в тех точках, где W обращается в нуль (помимо начала координат). При решении задачи остается только проверить, не останется ли изображающая точка М там, где W=0.

Теорема Ляпунова (второй метод) о неустойчивости нелинейных систем.

Поскольку кроме области устойчивости нелинейная система может иметь целый ряд особых областей, то возникает потребность в отдельном определении области неустойчивости путем использования теоремы Ляпунова, которая дает достаточные условия неустойчивости систем.

Формулировка теоремы:

“Если при заданных в форме Коши уравнениях системы n-ого порядка производная от какой-нибудь функции Ляпунова окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива”.

Справедливость этой теоремы может быть проиллюстрирована так же, как и в предыдущем случае.

Второй метод Ляпунова универсален, так как не связан с линеаризацией уравнений движения и не накладывает особых ограничений на их правые части. Однако применение этого метода осложняется двумя причинами:

достаточным характером утверждений, то есть если условия метода не выполнены, то об устойчивости положения равновесия ничего сказать нельзя, можно только порекомендовать подобрать другую функцию V(х);
отсутствием общих рекомендаций по выбору функций Ляпунова.

Обычно функцию V(x) выбирают квадратичной формы

(5.53)

где Н - положительно-определенная матрица. Это выражение для n=2 раскрывается так:

(5.54)

Для установления положительной определенности матрицы Н можно воспользоваться критерием Сильвестра, сводящимся к проверке положительности диагональных определителей матрицы. Например, для n=2 условия записываются так:

(5.55)

Недостатком функции V(x) является то, что она не учитывает особенностей нелинейных систем.

Если статическая характеристика F() безынерционного нелинейного элемента в структурной схеме расчетного вида удовлетворяет следующим условиям:

функция однозначна и непрерывна;
F(0)=0;
F()>0, 0, т.е. график статической характеристики проходит через начало координат и располагается в первом и третьем квадрантах, то для этого практически важного случая А.И. Лурье и В.Н. Постников предложили следующую форму функции Ляпунова (квадратичная форма плюс интеграл от нелинейности):

(5.56)

Пример 5.7. Пусть линейная часть системы, приведенной к расчетному виду, имеет передаточную функцию

а нелинейный элемент удовлетворяет приведенным выше требованиям.

При отсутствии воздействия (r=0) положению равновесия системы соответствует x=0. Дифференциальное уравнение системы первого порядка в форме Коши запишется так (примем =x):

Выберем функцию Ляпунова в следующем виде

(5.57)

Продифференцируем эту функцию по времени в силу дифференциального уравнения системы:

Получили отрицательно-определенную функцию W(x), что позволяет сделать вывод об асимптотической устойчивости положения равновесия.

Так как функция (5.57) определена для всех x и при имеем V(x), положение равновесия асимптотически устойчиво в целом. Наконец, примем во внимание, что полученный результат справедлив для целого класса нелинейных функций F(x), удовлетворяющих введенным выше ограничениям, а это значит, что система абсолютно устойчива.

Пример 5.8.

В примере 5.3 заключение об устойчивости нелинейной системы по теоремам Ляпунова первого метода не принято. Воспользуемся вторым методом Ляпунова. Выберем скалярную функцию переменных состояния в виде квадратичной формы:

и продифференцируем по времени в силу дифференциальных уравнений системы:

Получили отрицательно-определенную функцию, что означает асимптотическую устойчивость положения равновесия. Поскольку при имеем W(x) , положение равновесия устойчиво в целом.

5.9. Критерий абсолютной устойчивости В.М. Попова

Рассматривается замкнутая система с одним нелинейным звеном.

Система называется асимптотически устойчивой, если при ненулевых ограниченных начальных условиях свободное движение y(t) ограничено при t є [0,) и lim y(t)=0 (t).

Если окажется, что это свойство выполняется для любых нелинейных элементов из некоторого класса, то устойчивость называется абсолютной.

Теорема В.М. Попова.

Пусть выполняются условия:

все полюсы передаточной функции линейной части системы имеют отрицательные действительные части;
характеристика нелинейного элемента принадлежит сектору [0,k],

т.е. F(0)=0, 0 F() / k при всех 0 (рис.5.23);

3) существует действительное число q такое, что при всех є [0,)

выполняется неравенство

Re [(1+jq)W(j)]+1/k = u()-q()+1/k >0,

q-произвольное действительное число.

Тогда при любых ограниченных начальных отклонениях от нулевого значения система будет абсолютно устойчивой.

Алгоритм анализа абсолютной устойчивости:

Построим годограф модифицированной

частотной характеристики

W(j) = Re W(j) + jImW(j).

Находим параметр k (наименьший из возможных), удовлетворяющий условию п.2 теоремы.
Анализ геометрической интерпретации условий абсолютной устойчивости:

Рис.5.23. Характеристика

нелинейного элемента, принадле-

жащая сектору [0,k]

3.1. Абсолютной устойчивости нет (рис.5.24).

Рис.5.24. Годограф модифицированной частотной характеристики, когда абсолютной

устойчивости нет

3.2. Система абсолютно устойчива (рис.5.25).

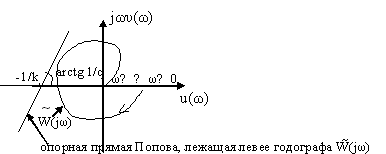
Рис.5.25. Годограф модифицированной частотной характеристики,

когда система абсолютно устойчива

3.3. Заключение об абсолютной устойчивости сделать не представляется возможным (рис.5.26).

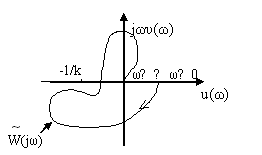
Рис.5.26. Годограф модифицированной частотной характеристики,

когда требуются дополнительные исследования для заключения

об абсолютной устойчивости

Приведем утверждение об абсолютной устойчивости часто встречающихся систем, в которых передаточная функция линейной части W(р) имеет один нулевой полюс, а нелинейный элемент F() имеет зону нечувствительности:

“Пусть все полюсы передаточной функции W(р) линейной части системы лежат в левой полуплоскости (Rep<0), за исключением одного, равного нулю, причем . Пусть, кроме того, характеристика F() нелинейного элемента удовлетворяет условиям: F()=0 при 0<F() k(-) при при ; причем , (т.е. график функции u=F() не приближается “плотно” к границе секторов, изображенных на рис. 5.27).

Тогда, если существует такое действительное число q>0, что не является полюсом W(p), и для всех выполняется неравенство

, (5.58) то при любых ограниченных начальных условиях процессы в системе останутся ограниченными и (t) при t стремится к одной из точек отрезка покоя ”.

Рис.5.27. График функции u=F() в границах секторов

Пример 5.9. Требуется исследовать абсолютную устойчивость системы, структурная схема которой (рис.5.28,а) включает релейный элемент с зоной нечувствительности (рис.5.28,в) или элемент с зонами нечувствительности, линейности и насыщения (рис.5.28,б).

Рис.5.28. Структурная схема нелинейной системы и статические

характеристики нелинейного элемента

Передаточная функция линейной части системы удовлетворяет условиям утверждения об абсолютной устойчивости, так как один полюс равен нулю (=0), а второй лежит в левой полуплоскости (=-1), причем =1>0. Сравнивая характеристики нелинейных элементов с характеристикой изображенной на рис.5.27, определяем значения величин: =-1, =1, k=1 для элемента рис.5.28, б и k=+ для элемента рис.5.28, в.

Запишем неравенство (5.58):

Выделяя действительную часть, получаем

Очевидно, что при q>1 последнее неравенство выполняется при всех и любых k>0. Таким образом, точки отрезка покоя =[-1;1] являются устойчивыми положениями равновесия для системы (рис.5.28, а) с любым из рассматриваемых нелинейных элементов.

5.10. Анализ устойчивости нелинейных систем по модели в форме

структурной схемы

Если модель нелинейной системы представлена в форме структурной схемы, то можно записать систему дифференциальных уравнений в форме Коши или одно дифференциальное уравнение n-го порядка, тогда устойчивость исследуется по соответствующим схемам методов Ляпунова.

Однако устойчивость положения равновесия нелинейной системы можно исследовать и непосредственно по структурной схеме.

Пусть имеется модель в форме структурной схемы. Положим, что все нелинейные элементы безынерционные, тогда методика исследования устойчивости системы следующая:

Определяются равновесные режимы (если они существуют), устойчивость которых необходимо исследовать.
Производится расчет соответствующих этим состояниям значений переменных на входах всех нелинейных элементов системы.

Для определения значений переменных на входах нелинейных элементов можно применить аналитические, графические или численные методы. Анализ проводится по частной модели для равновесных режимов – динамические звенья заменяются безынерционными. Если звено интегрирующего типа (астатическое звено) с передаточной функцией:

, (5.59)

то в равновесном режиме переменная входа равняется нулю. Если в системе есть дифференцирующее звено

; , (5.60)

то в равновесном режиме его выход равен нулю.

Производим линеаризацию нелинейного элемента.

После того как найдено значение переменной на входе нелинейного элемента, заданного аналитически , линеаризация означает его замену безынерционным звеном

(5.61)

с передаточным коэффициентом ,

равным значению производной в точке равновесия. Статическая характеристика нелинейного элемента в точке линеаризации должна быть гладкой (дифференцируемой).

Если статическая характеристика нелинейного элемента задана графически (рис. 5.29), линеаризация сводится к определению тангенса угла наклона касательной к статической характеристике в точке равновесия. Практически коэффициент усиления определяется как отношение приращений:

Рис. 5.29. Линеаризация графически заданной статической характеристики

нелинейного звена

Если нелинейный элемент имеет несколько входов

то в результате линеаризации получим:

, (5.62)

где передаточные коэффициенты по различным входам равны значениям частных производных функции F в точке равновесия.

Например, линеаризация элемента перемножения двух переменных

(5.63)

в точке даёт . (5.64)

Составляется линейная модель системы.

В результате линеаризации всех нелинейных элементов для конкретного положения равновесия получается линейная модель для малых отклонений переменных на входах нелинейных элементов.

5. Исследование устойчивости нелинейной системы.

Анализ устойчивости системы «в малом» по линеаризованной модели в соответствии с первым методом Ляпунова даёт возможность судить об устойчивости выбранного положения равновесия нелинейной системы.

Анализ устойчивости системы «в большом» и «в целом» по нелинейной модели.

Пример 5.10. Проведём исследование устойчивости нелинейной системы, структурная схема которой изображена на рис. 5.30.

Рис. 5.30. Модель нелинейной системы

Рис. 5.31. Модель системы для установившегося режима работы

По модели системы для установившегося режима работы (рис. 5.31) определим положения равновесия (равновесные режимы) этой системы. Если её параметры медленно изменяются, то положения равновесия также будут изменяться. В том случае, когда при некоторых значениях параметров рассматриваемое положение равновесия перестанет существовать, система будет вынуждена перескочить в другое устойчивое равновесное состояние, которое может быть весьма далёким от первоначального. Эволюция системы завершается скачкообразным изменением или, как говорят, катастрофой (например, разрушение экономики или строительного сооружения). В линейных системах положение равновесия единственно. Нелинейные системы могут иметь несколько положений равновесия. Можно ожидать, что при исследовании эволюций нелинейных систем окажется много вариантов возникновения устойчивых и неустойчивых положений равновесия.

Пусть нелинейный элемент системы расчётной структуры является квадратором:

. (5.65)

На вход системы подано постоянное воздействие , передаточный коэффициент линейной части равен k. Переменные системы определяются двумя параметрами – уровнем воздействия r и передаточным коэффициентом k, которые могут медленно изменяться.

Найдем значения переменной на входе нелинейного элемента в равновесных состояниях и изучим, как влияют на эти значения изменения параметров k и r.

Для решения задачи запишем уравнения статики:

. (5.66)

Рис. 5.32. Пример катастрофы типа «складка»

Графическое определение положений равновесия иллюстрирует рис. 5.32. В зависимости от соотношения параметров k и r система имеет два положения равновесия (прямая 1), одно (прямая 2) или ни одного (прямая 3). Соотношение параметров k и r, отвечающее касанию прямой и параболы, является критическим – сколь угодно малое изменение параметров приводит к качественному изменению ситуации. Множество значений (k,r), когда два положения равновесия сливаются в одно, называется множеством катастроф K.

Для аналитического определения множества K вместо системы (5.66) запишем одно уравнение для положения равновесия:

. (5.67)

Формула определения координат для положения равновесия

(5.68)

даёт действительное значение при условии

, ,

причём равенству отвечает критическая ситуация, когда два положения равновесия сливаются в одно. Множество катастроф К на плоскости (k,r) описывается уравнением

. (5.69)

Данный тип катастроф получил название «складка».

Если изменяется только один из параметров, например r, а k>0, то график зависимости положений равновесия имеет вид параболы (рис. 5.33). Ветви параболы при r>-k/4 соответствуют двум положениям равновесия. При r=-k/4 они сливаются в одно (точка катастрофы), а при дальнейшем уменьшении значения r положение равновесия исчезает.

Исследуемая система имеет два положения равновесия при уровнях постоянного воздействия r(t)>-0,25 и k=1.

Рис. 5.33. График зависимости положения равновесия от параметра

Значение r =- 0,25 соответствует катастрофе – малейшее уменьшение r(t) приводит к исчезновению положения равновесия, а малейшее увеличение – к появлению двух положений равновесия. Если r(t)>-0,25 ,то положениям равновесия отвечают следующие значения переменной на входе нелинейного элемента:

Графическая процедура определения координат точек равновесия, показанная на рис. 5.34, соответствует решению системы двух уравнений (5.66) при k=1 или уравнения

при r>-0,25. (5.70)

Рис. 5.34. Линеаризация нелинейного элемента

Линеаризуем статическую характеристику нелинейного элемента в этих точках; получим

Характеристические полиномы замкнутых линеаризованных систем имеют вид

.(5.71)

Один из полиномов этого выражения не удовлетворяет необходимому условию устойчивости Рауса (знак «минус» при свободном члене). Для устойчивости системы с другим полиномом в соответствии с критерием Гурвица необходимо и достаточно выполнение условия

, т.е. r<20 .

Таким образом, делаем вывод о том, что из двух положений равновесия, в которых может находиться система при постоянном значении воздействия r>-0,25 , устойчивым является одно

и только при ограничении сверху уровня воздействия r(t)<20. При рассчитанных ограничениях входного воздействия нелинейная система устойчива «в малом» и «в большом».

F(x)

Z=F()

Z=k

j()

u()

-1/k

W(j)

Положение равновесия

исчезнет

k>0

arctg k1

arctg k2

НЕЛИНЕЙНЫЕ СИСТЕМЫ