ОСНОВЫ ТЕХНИЧЕСКОЙ ТЕРМОДИНАМИКИ
Лекция 2
ОСНОВЫ ТЕХНИЧЕСКОЙ ТЕРМОДИНАМИКИ
1. Понятие о термодинамическом процессе
1.1. Рабочее тело и параметры его состояния
1.2. Законы идеальных газов
1.3. Уравнение состояния идеальных газов
2. Второй закон термодинамики
2.1 Физическая основа второго закона термодинамики
2.2 Цикл теплового двигателя
2.3 Цикл Карно
1. Понятие о термодинамическом процессе
1.1. Рабочее тело и параметры его состояния
Всякая тепловая машина приводится в действие вследствие происходящего в ней изменения состояния вещества, называемого рабочим телом или рабочим агентом.
Совокупность тел, находящихся в тепловом и механическом взаимодействии друг с другом и окружающей средой, называется термодинамической системой.
Рабочее тело определяет тип и назначение тепловой машины. Так у паровой машины рабочим телом является водяной пар, у поршневых двигателей внутреннего сгорания и газотурбинных двигателей — продукты сгорания топлива, у компрессоров холодильных машин рабочим агентом является пар аммиака, фреона и т. д. Для расчета термодинамического анализа работы тепловой машины необходимо знать термодинамические свойства рабочего тела.
Наиболее эффективными рабочими телами для тепловых машин являются газы и пары, обладающие наибольшим коэффициентом объемного расширения.
В технической термодинамике в качестве рабочего тела принимается идеальный газ — условное газообразное вещество, силами взаимодействия, между молекулами которого пренебрегают.
В реальных же газах учитываются силы притяжения между молекулами, а молекулы имеют объем. Если реальные газы сильно разряжены, их свойства близки к свойствам идеального газа.
В качестве идеальных газов могут рассматривать такие газы, как азот, гелий, водород.
В общем случае для теплотехнических расчетов вполне допустимо распространение свойств идеального газа на все рассматриваемые газы. Это позволяет упростить математические выражения законов термодинамики.
Очевидно, что одно и то же вещество при различных условиях может находиться в различных состояниях.
Для того чтобы определить конкретные физические условия, при которых рассматривается данное вещество и тем самым однозначно определить его состояние, вводятся параметры состояния вещества.
Параметрами состояния газа называются величины, характеризующие данное состояние газа.
К параметрам состояния газа относятся абсолютная температура, абсолютное давление, удельный объем, внутренняя энергия, энтропия, энтальпия и др. Абсолютная температура, абсолютное давление и удельный объем являются основными параметрами газообразного вещества.
Абсолютная температура
Температура газа служит мерой кинетической энергии поступательного движения молекул газа и характеризует степень его нагрева. Температуру газа измеряют приборами, основанными на тех или иных свойствах вещества, меняющихся с изменением температуры. Эти приборы имеют градуировку, т. е. температурную шкалу.
Создателем первого такого прибора — термометра был немецкий ученый Фаренгейт, который за начало шкалы принял уровень, соответствующий температуре таяния смеси, состоящей из равных мacc нашатыря и тающего льда. Верхней точкой был уровень, соответствующий температуре кипения воды при нормальном атмосферном давлении. Расстояние между этими двумя уровнями он разделил на 180 частей и, таким образом, получил один градус.
В 1723 г. французский физик Реомюр предложил шкалу, основанную на двух опорных точках, соответствующих температурам таяния льда и кипения воды при нормальном атмосферном давлении. Расстояние между двумя точками он разделил на 80 равных частей.
В 1742 г. шведский астроном Цельсий предложил температурную шкалу с теми же опорными точками, на которых построена шкала Реомюра, но расстояние между ними он разделил на 100 частей. Обозначается градус Цельсия — °С.
В настоящее время в термодинамике в качестве основной принята термодинамическая температурная шкала, где нижней границей шкалы является температура абсолютного нуля (практически недостижимая), когда прекращается тепловое движение молекул.
Единица температуры по термодинамической температурной шкале получила название Кельвин по имени ученого У. Томпсона, лорда Кельвина, предложившего начало отсчета вести от абсолютного нуля.
Тройной точке воды, т. е. когда в равновесии находятся три фазы воды: лед, жидкость и пар, присвоена температура 273,15 К. Она находится на 0,01 °С выше точки плавления льда.
На рис. 1 показано соотношение между шкалой Цельсия и шкалой Кельвина, т. е.
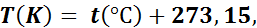
где Т — температура по термодинамической шкале, К;
t — температура по шкале Цельсия, °С.

Рис. 1. Сопоставление шкалы Цельсия и термодинамической шкалы
К преимуществам термодинамической температурной шкалы можно отнести следующее:
- во-первых, значения температур по этой шкале не зависят от физических свойств термометрических тел;
- во-вторых, температура по этой шкале может быть воспроизведена с большой точностью, так как она строится по одной опорной точке;
- в-третьих, все температуры — величины положительные, что упрощает расчеты.
Абсолютное давление
Давление — физическая величина, характеризующая интенсивность сил, действующих по нормали к поверхности тела и отнесенных к единице площади этой поверхности.
Различают следующие виды давлений: барометрическое (атмосферное), нормальное, абсолютное, манометрическое (избыточное) и вакууметрическое (разряжения).
Для измерения давления применяются различные единицы: Паскаль (Па), бар, техническая атмосфера или просто атмосфера, миллиметр ртутного или водяного столба, которые находятся в следую�щих соотношениях:
1 Па = 10-5 бар = 1,02 • 10-5 кгс/см2 = 7,5024 • 10-3 мм рт. ст.
Барометрическое давление зависит от массы слоя воздуха. Самое большое барометрическое давление было зарегистрировано на уровне моря и составило 809 мм рт. ст., а самое низкое — 684 мм рт. ст. Барометрическое давление выражается высотой столба ртути в мм, приведенного к 0 °С.
Нормальное давление — это среднее значение давления воздуха за год на уровне моря, которое определяется ртутным барометром при температуре ртути 273 К. Оно равно примерно 101,3 кПа (750 мм рт. ст.). То есть нормальным давлением называется барометрическое давление, равное одной физической атмосфере и является частным случаем барометрического давления.
Абсолютным давлением называется давление газов и жидкостей в закрытых объемах. Оно не зависит от состояния окружающей среды.
Манометрическим давлением называется разность между абсолютным давлением и барометрическим давлением, если первое больше второго.
Манометр — прибор, с помощью которого измеряют давление в закрытом сосуде, находясь вне этого сосуда, испытывает давление, как со стороны окружающей среды, так и со стороны сосуда. Поэтому полное или абсолютное давление газа в сосуде равно сумме манометрического давления и барометрического.
Вакуумметрическим давлением называется разность между баро�метрическим давлением и абсолютным давлением, если последнее меньше первого.
Удельный объем
Удельный объем вещества — это величина, равная отношению его объема к его массе:
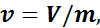
где m — масса вещества;
V — объем вещества.
Величина, обратная удельному объему, есть плотность вещества:
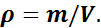
1.2. Законы идеальных газов
В XVII—XIX-x столетиях исследователями, изучавшими поведение газов при давлениях, близких к атмосферному, опытным путем были установлены важнейшие закономерности.
В 1662 г. Р. Бойлем, а в 1676 г. независимо от него Э. Мариоттом было доказано, что при постоянной температуре произведение давления газа на его объем постоянно, т. е. в изотермическом процессе расширения или сжатия газа
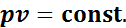
Иначе говоря, при постоянной температуре удельные объемы газа обратно пропорциональны его давлениям:
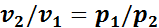
и
(при Т = const),
где v1 и v2 — удельные объемы в начальном и конечном состояниях газа;
р1 и р2 — соответствующие им давления.
В 1802 г. французский ученый Гей-Люссак открыл закон, согласно которому объем данной массы газа при постоянном давлении меняется линейно с температурой, т. е. для начального и конечного состояний газа
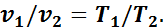
За 15 лет до того, как Гей-Люссак открыл свой закон, французский физик Шарль доказал, что при постоянном удельном объеме изменение давления газа прямо пропорционально его абсолютным температурам:
(при v = const),
или
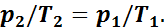
1.3. Уравнение состояния идеальных газов
Законы Бойля—Мариотта, Гей-Люссака и Шарля устанавливают связь только между двумя из трех основных параметров газа р, v и Т при условии, что значение третьего параметра остается постоянным. Уравнение состояния идеального газа устанавливает связь между всеми тремя основными его параметрами.
Допустим, что идеальный газ, заключенный в цилиндре с поршнем имеет параметры p1, v1 и T1, (рис. 2, а). Если уменьшить давление газа в цилиндре и подвести к нему некоторое количество теплоты, то газ перейдет в новое состояние, где будут иметь место параметры р2, v 2 и Т2 (рис. 2, б).
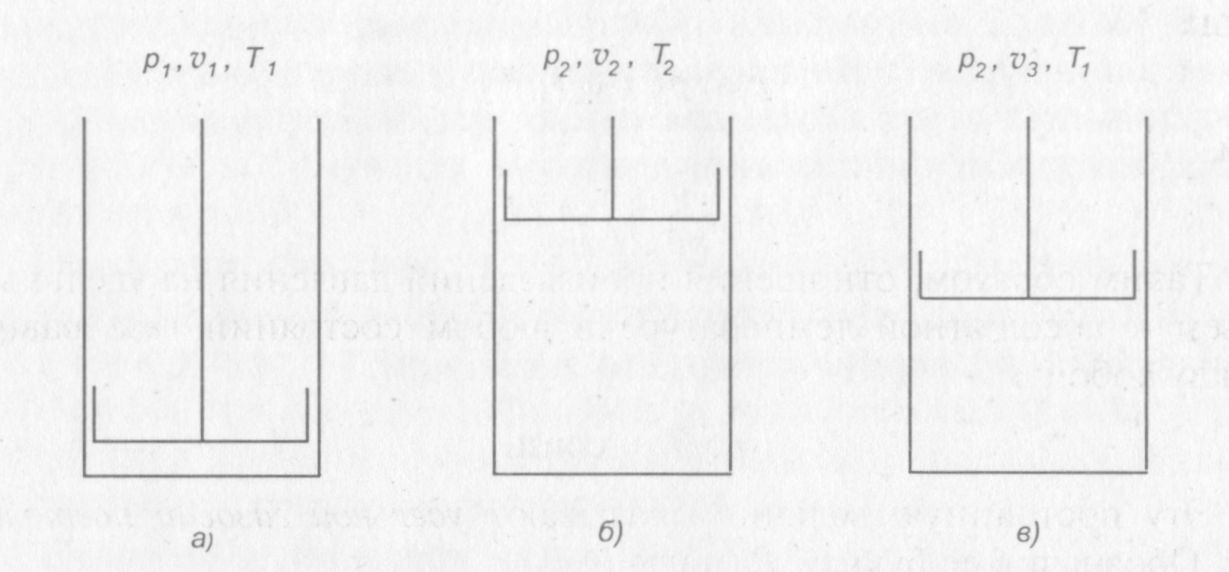
Рис. 2. Иллюстрация уравнения состояния идеального газа
Чтобы установить связь между начальным и конечным состояниями газа, осуществим переход из первого состояния в последнее двумя промежуточными операциями. Сначала уменьшим давление газа от р1 до р2, поддерживая температуру T1 постоянной путем подвода теплоты к газу. Тогда газ окажется в промежуточном состоянии (рис. 2, в) и будет иметь параметры р2, v3 и T1. Затем будем подогревать газ так, чтобы он продолжал расширяться, сохраняя свое давление неизменным, его температура при этом повысится до Т2 (рис. 2, б).
Сопоставим эти три состояния газа. Так как в первом состоянии и третьем температуры одинаковы, то между удельными объемами и давлением газа в этих состояниях должна по закону Бойля—Мариотта существовать следующая связь:
,
тогда
.
Так как в третьем и втором состояниях давления одинаковы, то по закону Гей-Люссака
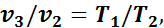
откуда
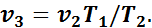
Тогда
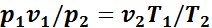
или
.
Таким образом, отношения произведений давления на удельный объем к абсолютной температуре в любом состоянии газа равны между собой:
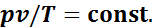
Эту постоянную величину называют удельной газовой постоянной. Обозначив ее буквой R, получим
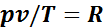
или
. (1.1)
Уравнение (1.1) называется уравнением идеального газа, или уравнением Клайперона.
Для использования уравнения Клайперона необходимо определить численное значение газовой постоянной для данного газа по справочным материалам. Газовая постоянная становится универсальной, т. е. одинаковой для всех газов, если количество газа выразить в киломолях. Умножив левую и правую часть уравнения (1.1) на мыссу 1 кмоля, получим:
,
где — молекулярная масса газа.
На основании закона А. Авогадро, который устанавливает, что при одинаковых температурах и одинаковых давлениях равные объемы различных идеальных газов содержат одинаковое число молекул, было установлено значение универсальной газовой постоянной:
.
Для 1 кмоля газа уравнение состояния можно представить как
(1.2)
где V — объем 1 кмоль газа.
Уравнение (1.2) носит название уравнения Клайперона— Менделеева. Зная значение относительной молекулярной массы , можно определить газовую постоянную любого газа:
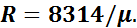
Теплоемкость газов
Теплоемкостью газа, как и любого другого тела, называется количество теплоты, необходимое для нагрева тела на один градус.
Теплоемкость единицы количества вещества называется удельной теплоемкостью. Так как в термодинамике рассматривается главным образом удельная теплоемкость, то ее можно называть просто теплоемкостью.
Если единице количества вещества сообщить (или отвести от нее) какое-то количество теплоты (q) и если при этом происходит изменение температуры данного вещества от Т1 до Т2, то отношение теплоты q к разности данных температур представляет собой среднюю теплоемкость (с) газа в пределах от Т1 до Т2:
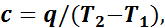
следовательно,
(1.3)
Теплоемкость вещества и в частности газа зависит от его природных свойств, а также от условий, в которых происходит процесс изменения его состояния, от температуры, а для реальных газов и от давления.
Теплоту можно подводить к рабочему телу различными способами. В термодинамике широко используется два способа подведения теплоты:
1) при постоянном удельном объеме (изохорный способ);
2) при постоянном давлении рабочего тела (изобарный способ).
Изохорный подвод теплоты происходит в цилиндре с неподвижным поршнем, изобарный — в цилиндре с подвижным поршнем при увеличении объема, давление при этом остается постоянным.
Величина q в соответствии с формулой (1.3) зависит не только от соотношения температур, но и от способа подвода теплоты. Поэтому различают теплоемкость при постоянном объеме сv (изохорная теплоемкость) и теплоемкость при постоянном давлении ср (изобарная теплоемкость).
Первый закон термодинамики
Первый закон термодинамики: теплота может превращаться в механическую работу, а работа в теплоту лишь в строго эквивалентных количествах, причем количество теплоты, полученное рабочим телом от какого-либо источника тепла, равно сумме приращения внутренней энергии этого тела и количества совершенной им работы, т. е.
(1.4)
где Q — подведенная к рабочему телу теплота;
А — коэффициент пропорциональности;
L — работа, произведенная рабочим телом в результате подвода теплоты;
U1 — внутренняя энергия рабочего тела в начале подвода теплоты;
U2 — внутренняя энергия рабочего тела в конце подвода теплоты.
В 1843—1860 гг. английский физик Джоуль провел опыт по установлению соотношения между работой, затраченной при выделении теплоты и количеством выделенной теплоты. Ему удалось вычислить величину
A = 0,002345 ккал (кгс • м), которая называется тепловым эквивалентом работы. Также он вычислил и механический эквивалент теплоты I:
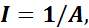
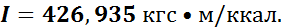
В настоящее время для измерения количества теплоты и работы используются различные единицы, соотношения между которыми приведены в табл. 1.
В дальнейшем для упрощения в термодинамических уравнениях коэффициенты А и I будут опускаться, а работа и теплота будут выражаться в одинаковых единицах.
Таблица 1. Соотношения между единицами измерения теплоты и работы
|
Единица
|
Дж
|
энг
|
кгс•м
|
ккал
|
кВт•ч
|
|
Дж
|
-
|
107
|
0,101972
|
2,4•10-4
|
2,7778•10-7
|
|
эрг
|
10-7
|
-
|
10,1972•10-9
|
24•10-12
|
27,778•10-15
|
|
кгс•м
|
9,80665
|
98,0665•106
|
-
|
2,3•10-3
|
2,7207•10-6
|
|
ккал
|
4186,8
|
41,868•109
|
426,935
|
-
|
1,163•10-3
|
|
кВт•ч
|
3,6•106
|
36•1012
|
367 098
|
859,862
|
-
|
Для рабочего тела массой 1 кг уравнение первого закона термо�динамики примет вид:
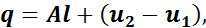
где q — удельная теплота, подводимая к рабочему телу или отводимая от него;
l — удельная работа изменения объема рабочего тела;
u1 и u2 — удельная внутренняя энергия в начале и конце подвода теплоты соответственно.
В термодинамике принято следующее:
• теплоту Q считать положительной, если она подводится к газу и отрицательной, если она отводится;
• изменение внутренней энергии U считать положительным, если температура газа растет, и отрицательным, если она падает;
• работу L считать положительной, если газ расширяется и от�рицательной, если газ сжимается под действием внешних сил.
Внутренняя энергия
Внутренняя энергия состоит из внутренней кинетической и внутренней потенциальной энергий. Первая — результат хаотического движения частиц тела, с увеличением скорости которых возрастает и внутренняя кинетическая энергия.
Так как температура тела определяется скоростью движения его частиц (молекул), то увеличение температуры тела означает увеличение его внутренней кинетической энергии.
Внутренняя потенциальная энергия связана с силами взаимо�действия между частицами вещества.
Изменение удельной внутренней энергии в процессе подвода или отвода теплоты может быть выражено уравнением
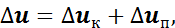
где uк — изменение кинетической энергии газа,
uп — изменение потенциальной энергии газа.
Так как силы взаимодействия между молекулами идеального газа отсутствуют, то и его потенциальная энергия равна нулю. Поэтому внутренняя энергия идеального газа зависит только от его температуры.
Поскольку температура идеального газа определяется внутренней кинетической энергией, а температура тела является параметром его состояния, то и внутренняя энергия является параметром его состояния.
Если в результате подвода теплоты рабочее тело переходит из первого состояния во второе, то подводимая теплота q1,2 будет равна u2-u1.
На основании формулы (3) можно записать
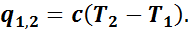
Обратимые и необратимые процессы
Термодинамическим процессом называется последовательное изменение состояния рабочего тела, при котором параметры его состояния (все или некоторые) изменяются, а масса рабочего тела, совершающего процесс, остается неизменной.
В термодинамике широко используется диаграмма, в которой по оси абсцисс откладываются значения удельных объемов v, а по оси ординат — значения давлений р.
По координатам р и v можно определить состояние рабочего тела.
Если тело перешло из состояния 1 в состояние 2 через ряд состояний а, b, с и др., то это означает, что тело совершило термодинамический процесс. Проведя через эти точки кривую, получим линию процесса на р—v диаграмме (рис. 3).
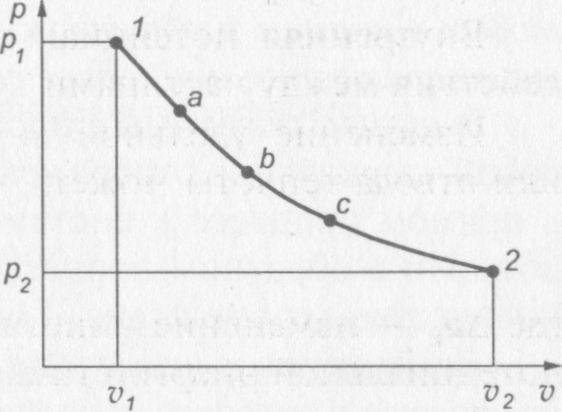
Рис. 3. р—v диаграмма
При изменении своего состояния газ совершает работу против внешних сил (процесс расширения) или воспринимает работу этих внешних сил (процесс сжатия).
Если подводить к газу теплоту, то поршень (рис. 4) в результате расширения газа переместится слева направо, и газ совершит работу при постоянном давлении:
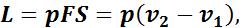
где р — постоянное давление газа;
F — площадь поршня;
S — ход поршня,
v1, v2 — начальный и конечный объемы газа.
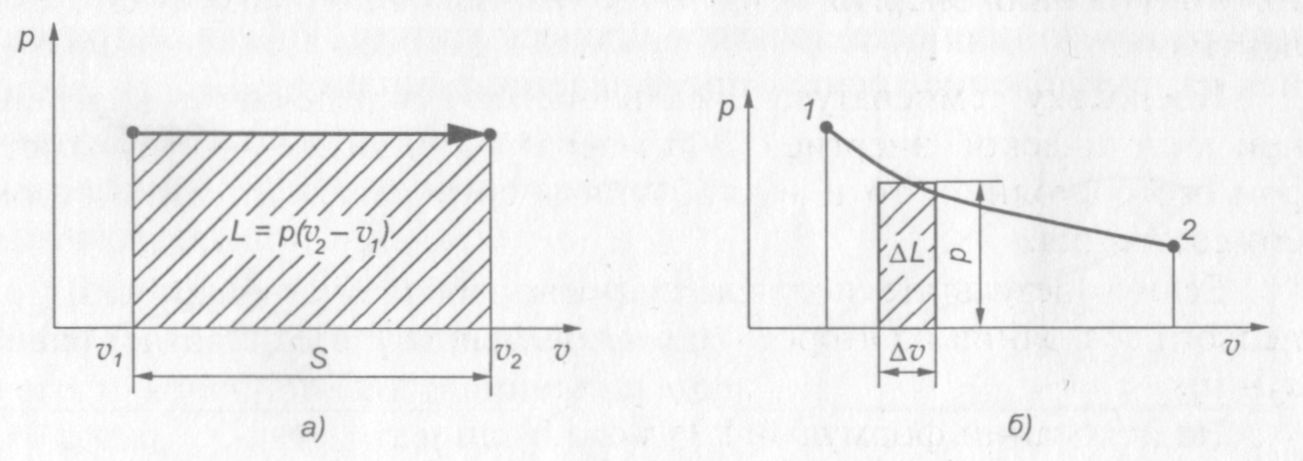
Рис. 4. Работа расширения газа: а — при р = const;
б — при переменном давлении, L = p v
В p—v диаграмме эта работа изображается площадью заштрихо�ванного прямоугольника.
Если рассмотреть произвольный процесс, то очевидно элементарную работу расширения L можно подсчитать как площадь элементарного прямоугольника с основанием v и высотой р, а вся работа будет равна сумме площадей таких прямоугольников.
Таким образом, работа расширения газа будет равна площади, ограниченной сверху кривой процесса, снизу — осью абсцисс, а слева и справа двумя крайними ординатами процесса, соответствующими начальному и конечному состояниям газа.
Работа не является только функцией состояния газа, так как она зависит и от характера процесса.
На рис. 5 показаны два различных процесса перехода газа из со�стояния 1 в состояние 2. Работы этих процессов не равны при одинаковых начальных и конечных состояниях газа: L1 = sm1а2п > L2 = sm1b2n (s — площадь).
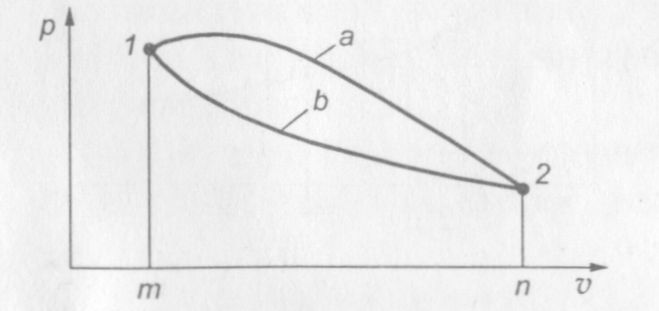
Рис. 5. Два различных процесса расширения газа
Это свойство работы как функции процесса и позволило создать периодически действующие тепловые машины. В тепловом двигателе работа расширения всегда больше работы, затраченной на сжатие. Полученная таким образом разность работ (согласно первому закону термодинамики эквивалентна применяемой в двигателе теплоте) используется для различных целей.
Обратимыми называются процессы, в результате совершения которых в прямом и обратном направлениях термодинамическая система возвращается в исходное состояние.
В случае обратимых процессов обратный процесс представляет собой «зеркальное отображение» прямого процесса: если, например, в прямом процессе к системе подводится какое-то количество теплоты, то в обратном процессе от системы отводится точно такое же количество теплоты (рис. 6).
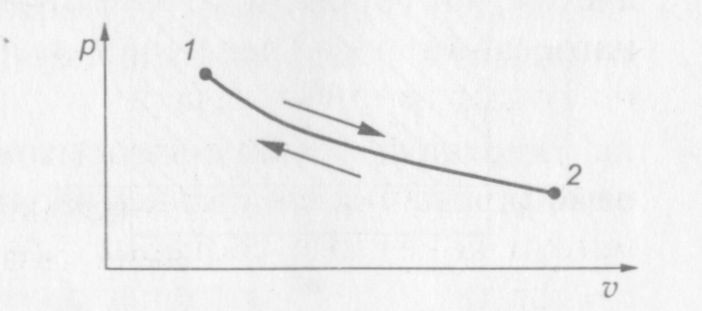
Рис. 1.6. p—v диаграмма обратимого процесса
Необратимым называется процесс, при котором система не возвращается в исходное состояние.
Все естественные самопроизвольные процессы необратимы. Обратимых процессов в природе не существует. Типичным примером необратимого процесса является процесс трения. Работа, затраченная на преодоление трения, превращается в теплоту.
Рабочее тело может произвести работу только при переходе из неравновесного состояния в равновесное. На рис. 7, а представлена схема перехода газа из неравновесного состояния в равновесное. Предварительно сжатый газ находится в цилиндре под застопоренным поршнем в неравновесном состоянии под давлением р1. Давление окружающей среды р значительно меньше, чем давление газа. При удалении стопора G поршень начнет перемещаться вправо из-за разности давлений.
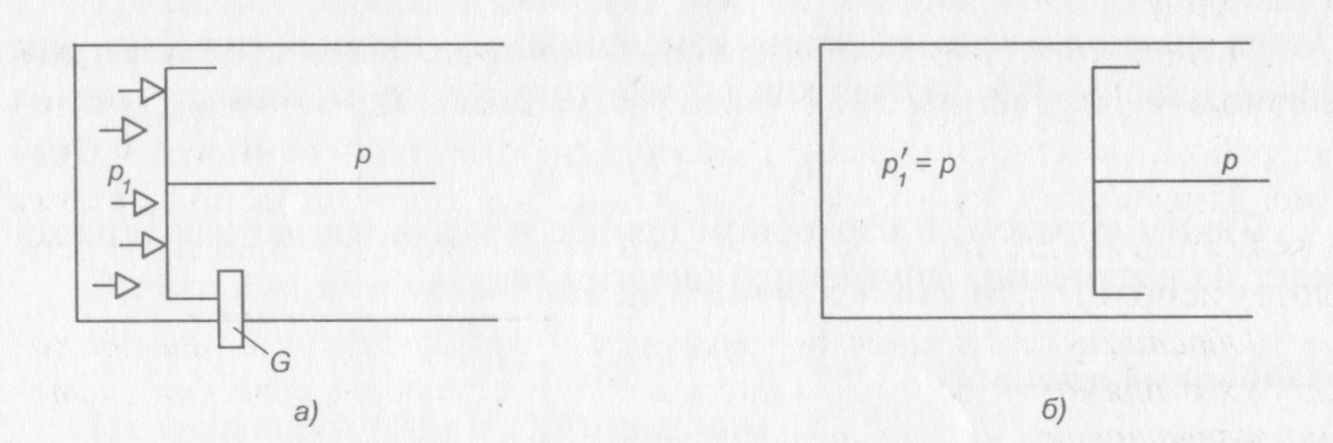
Рис. 7. Схема перехода газа из неравновесного состояния (а) в равновесное (б)
Поршень будет перемещаться только до тех пор, пока давление под поршнем не станет равно давлению окружающей среды (рис. 7, б), т. е. работа будет совершаться до тех пор, пока система не придет в состояние равновесия.
Изохорный процесс
Изохорными называются процессы, протекающие при постоянном объеме. К таким процессам относятся нагревание или охлаждение газа в сосуде постоянного объема: v = const.
На рис. 8 показана p—v диаграмма изохорного процесса.
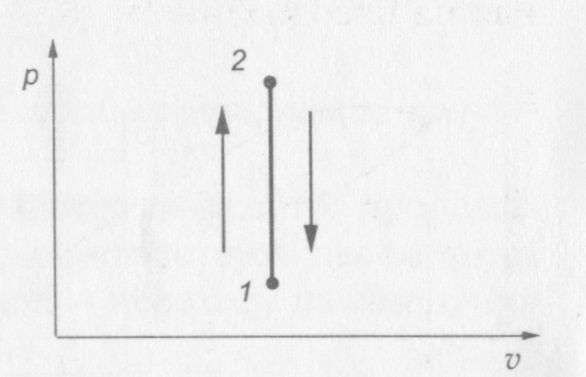
Рис. 8. р—v диаграмма изохорного процесса
Переход газа из состояния 1 в состояние 2 сопровождается нагреванием газа, а переход из состояния 2 в состояние 1 — охлаждением. Направление процесса определяется по изменению давления: при нагревании газа давление растет, а при охлаждении — падает.
Для определения соотношения параметров напишем уравнения начального и конечного состояния газа при v = const:
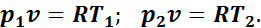
Разделим почленно второе уравнение на первое, получим
(1.5)
Выражение (1.5) показывает, что в изохорном процессе давление газа прямо пропорционально абсолютной температуре.
Изменение удельной внутренней энергии в изохорном процессе (как и во всех процессах) определяется по формуле
(1.6)
В процессе при постоянном объеме внешняя работа не совершается, т. е. удельная работа изменения равна нулю:
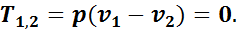
Тогда внешняя теплота равна изменению внутренней энергии, так как q1,2 = u + Al1,2, но так как l1,2 = 0, то q1,2 = u2 - u1, или
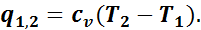
Таким образом, в изохорном процессе вся подведенная теплота идет на увеличение внутренней энергии газа.
Изобарный процесс
Изобарными процессами называются процессы, протекающие при постоянном давлении: р = const.
На рис. 9 показана p—v диаграмма изобарного процесса.
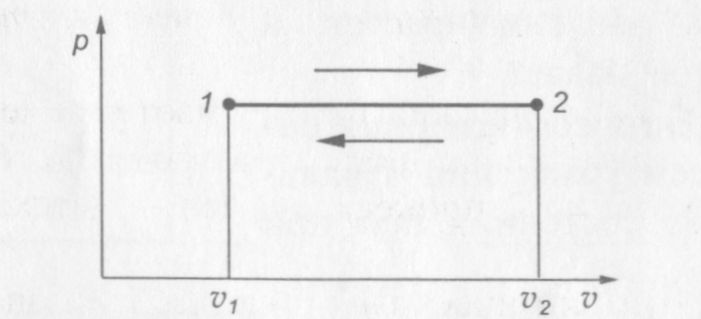
Рис. 9. p—v диаграмма изобарного процесса
Процесс расширения газа на диаграмме соответствует переходу из состояния 1 в состояние 2, а процесс сжатия — переходу из состояния 2 в состояние 1.
Для определения соотношения параметров напишем уравнение начального и конечного состояний газа при р = const:
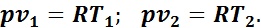
Разделив почленно второе уравнение на первое, получим
(1.7)
Выражение (1.7) показывает, что в изобарном процессе объемы газа пропорциональны абсолютным температурам.
Изменение внутренней энергии, как известно, не зависит от вида процесса и поэтому для изобарного процесса определяется так же, как и для всех процессов:
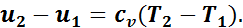
Удельная работа газа в этом случае будет равна площади прямоугольника, основанием которого служит отрезок абсциссы v2—v1, а высотой — отрезок ординаты р:
(1.8)
Уравнение работы изменения объема идеального газа в изобарном процессе можно представить и в другом виде, написав для этого два уравнения состояния газа (одно для конечного состояния, другое — для начального):
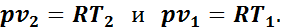
Вычитая второе уравнение из первого, получим
(1.9)
Из уравнений (1.8) и (1.9) получим
(1.10)
Теплота, которая сообщается газу в изобарном процессе, на основании первого закона термодинамики может быть найдена по формуле
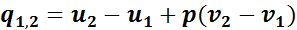
или по общей формуле
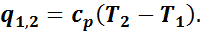
Изотермический процесс
Изотермическим процессом называется процесс, протекающий при постоянной температуре: Т= const.
На рис. 10 показана диаграмма изотермического процесса. Процесс расширения газа на диаграмме соответствует переходу из состояния 1 в состояние 2, процесс сжатия — переходу из состояния 2 в состояние 1.
Поскольку в изотермическом процессе Т = const, то уравнение состояния газа pv = RT= const.
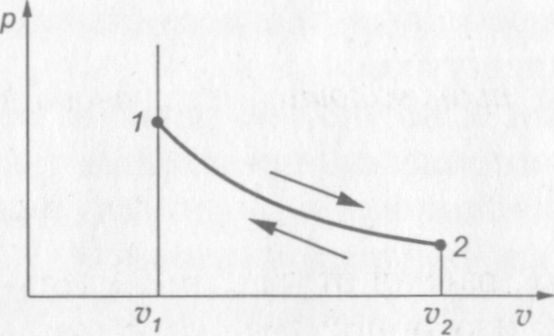
Рис. 10. р— v диаграмма изотермического процесса
В изотермическом процессе в соответствии с законом Бойля—Мариотта справедливо следующее соотношение:
(1.11)
или
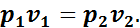
Соотношение (1.11) показывает, что в изотермическом процессе объемы при различных состояниях газа обратно пропорциональны давлениям, соответствующим этим состояниям.
При вычислении внутренней энергии, используя общую формулу (1.6), получим
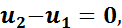
так как
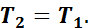
Следовательно, в изотермическом процессе изменение внутренней энергии равно нулю, т. е. внутренняя энергия в течение всего процесса остается постоянной.
Удельная работа изменения объема в изотермическом процессе определяется уравнением
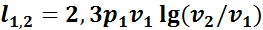
или
(1.12)
На основании первого закона термодинамики
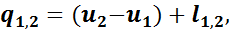
а так как u2 - u1 = 0, то
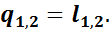
Таким образом, в изотермическом процессе расширения вся подведенная теплота расходуется на внешнюю работу, а при изотермическом процессе сжатия внешняя работа полностью превращается в теплоту.
Адиабатный процесс
Адиабатным процессом называют процесс, протекающий без подвода и отвода теплоты:
(1.13)
где k — показатель адиабаты — величина, равная отношению удельной изобарной теплоемкости к удельной изохорной теплоемкости:
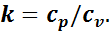
Для идеальных газов k есть величина постоянная, зависящая от природы газа, т. е. от числа атомов в молекуле газа. В табл. 2 приведены значения теплоемкостей ср и сv согласно молекулярно-кинетической теории.
Таблица 2. Значения удельной изобарной и удельной изохорной теплоемкостей и показателя адиабаты в зависимости от числа атомов в молекуле
|
Число атомов
|
сv
|
ср
|
k = ср / сv
|
|
1
|
2,98
|
4,36
|
1,67
|
|
2
|
4,97
|
6,97
|
1,4
|
|
3
|
5,96
|
7,96
|
1,53
|
Протекание адиабатного процесса без теплообмена с окружающей средой может осуществляться в цилиндре, который имеет идеально теплоизолированные стенки. Однако в природе не существует такой изоляции. Поэтому адиабатный процесс есть идеальный процесс и на практике осуществить его невозможно. Реально можно получить процесс с некоторым приближением к идеальному адиабатному процессу. Например, если процессы протекают очень быстро, т. е. в такое короткое время, что газ не успевает принять или передать теплоту стенкам цилиндра.
На рис. 11 представлена р—v диаграмма адиабатного процесса.
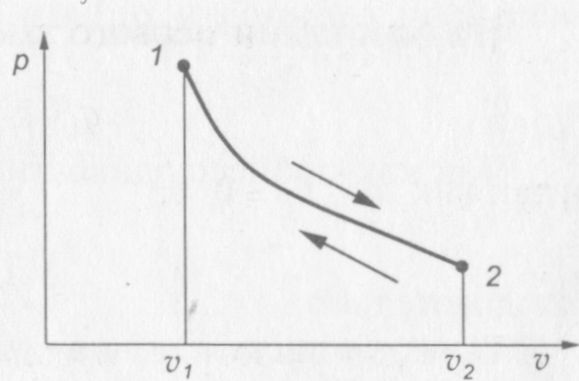
Рис. 11. р— v диаграмма адиабатного процесса
Кривая адиабатного процесса называется адиабатой. Она представляет собой неравнобокую гиперболу.
Зависимость между давлением и объемом для двух точек адиабатного процесса имеет вид
(1.14)
При сравнении формулы (1.14) с формулой (1.13) видно, что при адиабатном расширении газа давление уменьшается интенсивнее, чем при расширении в изотермическом процессе, отсюда следует, что р—v диаграмма адиабаты круче p—v диаграммы изотермы.
Для начального и конечного состояний газа в адиабатном процессе
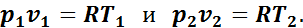
Разделив почленно второе уравнение на первое, получим
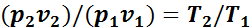
Или
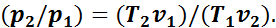
Подставив это выражение в формулу (12), получим
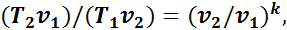
(1.15)
Из уравнения (1.14) следует, что
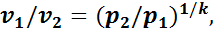
а из уравнения (1.15)
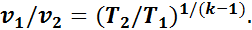
Следовательно,
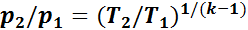
или
(1.16)
Изменение внутренней энергии определяется формулой
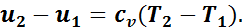
На основании первого закона термодинамики
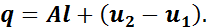
Так как процесс адиабатный, то
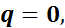
следовательно,
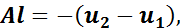
откуда
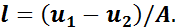
Учитывая, что А — величина постоянная, можно сделать вывод о том, что удельная работа в адиабатном процессе получается только за счет изменения внутренней энергии рабочего тела.
Политропный процесс
Политропным процессом называют процесс, в котором могут изме�няться одновременно все параметры газа (р, v, Т), и между газом и окружающей средой осуществляется теплообмен.
Процессы в тепловых машинах, как правило, являются политропными.
Уравнение политропного процесса:
(1.17)
где n — показатель политропы.
Если выразить теплоемкость газа в политропном процессе через cn, то показатель n будет иметь вид
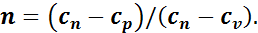
Учитывая, что ср/сv = k, получим
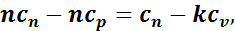
откуда
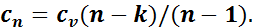
Количество теплоты определяется из уравнения первого закона термодинамики
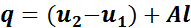
или из уравнения (3):
(1.18)
Учитывая уравнения (1.13)—(1.17) для политропного процесса можно написать
(1.19)
(1.20)
(1.21)
Уравнение политропного процесса является общим для всех основных рассматриваемых процессов. Так уравнения изохорного, изобарного, изотермического и адиабатного процессов можно получить из уравнения политропного процесса, если показателю политропы n давать соответствующие значения. Например, если n = ±, то уравнение (1.17) примет вид v = const, что соответствует изохорному процессу, если п = 0, то vn = v0 = 1, и уравнение (1.17) примет вид р = const, что соответствует изобарному процессу, если п = 1, то уравнение политропного процесса преобразуется в уравнение адиабатного процесса pvk = const. Таким образом:
- для изохорного процесса n = ±,
- для изобарного процесса п = 0,
- для изотермического процесса п = 1,
- для адиабатного процесса п = k.
Кроме перечисленных процессов, являющимися частными случаями политропного процесса, уравнение (1.17) может выражать бесконечное число процессов, в каждом из которых показатель п будет иметь свое определенное значение, находящееся в пределе от - до +.
2. Второй Закон Термодинамики
2.1. Физическая основа второго закона термодинамики
Первый закон термодинамики устанавливает количественное соотношение между различными видами энергии при их взаимном превращении. Однако он не дает ответа на вопрос о возможном направлении таких превращений и условиях, при которых преобразование энергии может быть реализовано.
В то же время было установлено, что не все процессы, связанные с передачей и преобразованием различных видов энергии, равновозможны. Так например, распространение тепловой энергии от горячих тел или участков системы к холодным протекает самопроизвольно, но обратные процессы в природе никогда не наблюдаются. Для того чтобы охладить тело до температуры ниже окружающей среды, необходимо затратить энергию.
Таким же необратимым является процесс расширения сжатого газа в вакуум. Известно, что газ, сконцентрированный в одной части какого-либо резервуара и изолированный в нем перегородкой, самопроизвольно распространяется по всему объему, если в этой перегородке проделать отверстие. Однако молекулы газа никогда без постороннего вмешательства не соберутся вновь в ограниченной части пространства.
Особое значение для практики имеет необратимость взаимного преобразования теплоты и механической работы.
Опыт показывает, что преобразование механической энергии в тепловую, всегда происходит полностью и самопроизвольно без каких-либо дополнительных условий или процессов.
Так, работа трения или удара целиком преобразуется в теплоту и нагревает систему, в которой эти процессы происходят. Подобным же образом в результате молекулярного трения повышается температура жидкости или газа из-за превращения кинетической энергии потока в теплоту. Однако обратное преобразование тепловой энергии, рассеянной в окружающей среде, в механическую работу самопроизвольно происходить не может. Переход этот возможен не полностью и лишь при соблюдении определенных условий.
Наблюдения характерных особенностей тепловой энергии привели к определению второго закона или второго начала термодинамики. Существует несколько эмпирических формулировок этого закона, каждая из которых описывает определенные внешние проявления рассмотренных особенностей теплоты и устанавливает, так или иначе, необратимость самопроизвольных термодинамических процессов.
Одна из таких формулировок утверждает, что теплота не может самопроизвольно перейти от более холодного тела к более теплому.
По другой формулировке самопроизвольный выход термодинамической системы из равновесного состояния практически невозможен.
Таким образом, можно утверждать следующее:
• теплота только тогда может быть преобразована в механическую работу, когда в термодинамической системе имеется перепад температур;
• совершаемая работа зависит от уровня этих температур;
• полный переход теплоты в работу невозможен.
2.2 Цикл теплового двигателя
Принцип преобразования тепловой энергии в механическую работу состоит в использовании эффекта значительного объемного расширения газообразных рабочих тел при их нагревании.
Чтобы реализовать этот принцип необходимо иметь машину с рабочей полостью переменного объема, который должен быть заполнен рабочим телом. Один их вариантов такой машины — цилиндр с поршнем, перемещение которого позволяет изменять рабочий объем. При подводе теплоты к газу, последний расширяется и, оказывая силовое воздействие на поршень, перемещает его и производит внешнюю работу:
. (1.22)
Из выражения (1.22) видно, что работа будет производиться только при увеличении объема рабочего тела, и как только возможности его расширения будут исчерпаны, преобразование прекратится. Для возобновления полезного действия машины, рабочее тело надо вернуть в исходное состояние, т. е. переместить поршень, уменьшив объем рабочего тела.
Таким образом, для непрерывного получения механической работы необходимо осуществить круговой процесс, т. е. цикл.
Циклом называется совокупность процессов, происходящих в опре�деленной последовательности, в результате осуществления которых рабочее тело возвращается в первоначальное состояние.
На рис. 12 представлены р— v диаграммы циклов работы тепловых машин.
В реальных тепловых двигателях после осуществления каждого цикла происходит смена рабочего тела. Однако возможны и замкнутые циклы, совершаемые с одним и тем же рабочим телом путем изменения параметров его состояния. С точки зрения термодинамики эти две схемы совершенно эквивалентны.
При уменьшении объема рабочего тела будет происходить его сжатие с изменением параметров состояния. При этом, чем больше повышается давление и температура газа, тем выше поднимается кривая сжатия, и тем больше затраты работы на его осуществление. Возможны случаи, когда линия сжатия располагается выше или ниже линии расширения (см. рис. 12).
Очевидно, что при необходимости получения полезной работы имеют смысл только такие циклы, в которых работа сжатия lсж меньше работы расширения lp. Эти циклы называются прямыми (рис. 12, а). Они лежат в основе работы тепловых двигателей.
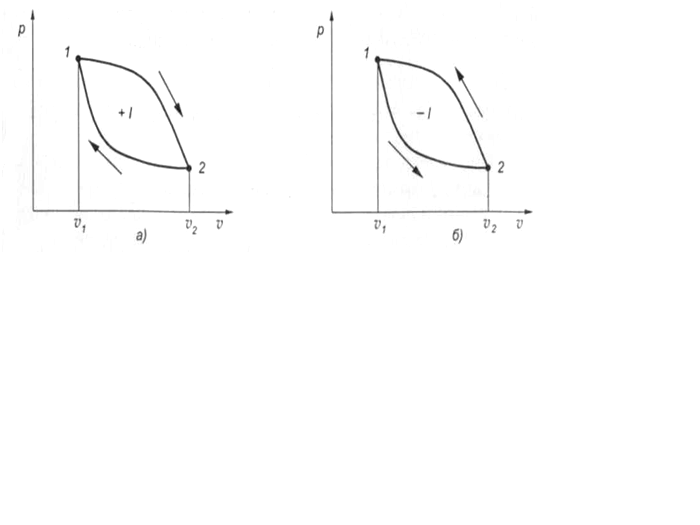
Рис. 12. Прямой (а) и обратный (б) циклы работы тепловых машин
Полезная работа прямого цикла равна разности работ расширения lр и сжатия lсж.
.
В обратных циклах
.
Работа обратного цикла отрицательна и используется в холодильных машинах.
Таким образом, в непрерывно действующем тепловом двигателе необходимо периодическое повторение прямых циклов, в которых процесс сжатия должен характеризоваться минимальной затратой работы.
Для выполнения последнего условия требуется, чтобы сжатие происходило при наименьшем повышении текущих значений температуры и давления, что может быть достигнуто только в случае отвода теплоты в период возвращения рабочего тела в состояние минимального объема.
Если теплоту не отводить, то работа затраченная на сжатие будет, по крайней мере, равна работе расширения и эффективность такой машины окажется равна нулю.
Таким образом, в любом случае непременным условием преобразования тепловой энергии в механическую, является прямой или косвенный расход теплоты, подведенной в цикле на возвращение рабочего тела в состояние минимального объема. Основным показателем эффективности циклов тепловых двигателей является их термический или термодинамический коэффициент полезного действия (КПД) t.
Термодинамический КПД определяет степень преобразования тепловой энергии в механическую в прямом цикле. Он представляет собой отношение величины тепловой энергии, преобразованной в механическую работу Аl, ко всей подведенной теплоте q1:
. (1.23)
В соответствии с законом сохранения энергии [формула (1.4)]
,
где q2 — количество теплоты, отведенной холодильником.
Тогда
. (1.24)
2.3. Цикл Карно
Одна из формулировок второго закона термодинамики звучит так: непременным условием преобразования теплоты в механическую работу является процесс передачи теплоты холодильнику. Поэтому важным вопросом является определение максимального КПД тепловых двигателей, работающих на идеальных газах.
Изучая эту проблему, французский инженер Карно в 1824 г. предложил цикл, который состоит только из обратимых процессов, совершаемый с идеальным газом. При этом Карно использовал такие процессы, которые наилучшим образом удовлетворяют своему назначению в цикле.
Знание данного цикла важно потому, что ни один из обратимых циклов не может иметь термический КПД выше термического КПД цикла Карно, осуществляемого при тех же перепадах температур.
Подвод и отвод теплоты в цикле Карно осуществляется изотермически, процессы сжатия и расширения протекают адиабатно, т. е. наиболее экономичным способом без тепловых потерь.
Двигатель, работающий по циклу Карно, представляет собой поршневую машину, цилиндр которой заполнен идеальным газом. Газ периодически контактирует с источником тепла, имеющим температуру Т1, или с холодильником, имеющим температуру Т2 (рис. 13).
Пусть газ имеет первоначальную температуру Т1 и давление р1 (точка 1). При нагревании газа от источника тепла происходит медленное изотермическое расширение (кривая 1—2) с подводом теплоты q1. После этого источник тепла удаляется и газ самопроизвольно расширяется без внешнего теплообмена (кривая 2—3) до температуры Т2 (точка 3). В процессе адиабатного расширения работа совершается за счет уменьшения внутренней энергии рабочего тела.
При осуществлении процесса расширения двигатель производит работу.
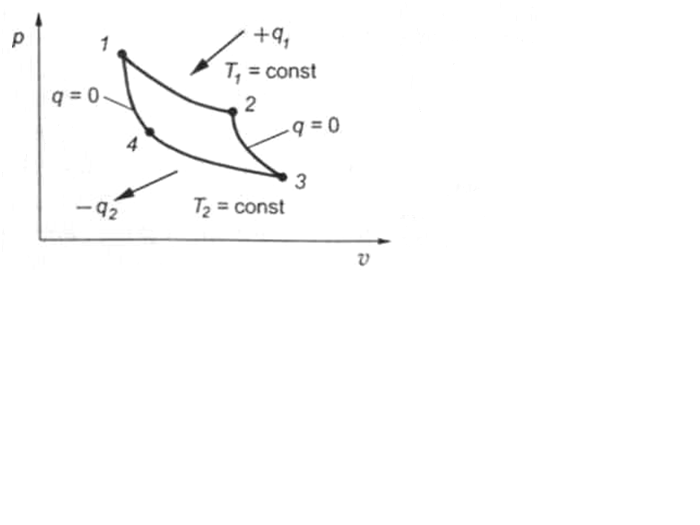
Рис. 13. р—v диаграмма цикла Карно
По окончании расширения цилиндр соприкасается с холодильником и осуществляется отвод тепла q2 в холодильник (кривая 3—4), при этом рабочее тело меняет значения своих параметров, уменьшаясь в объеме, а его давление увеличивается. Затем рабочее тело возвращается в исходное состояние путем адиабатного сжатия (кривая 4—1).
В результате цикла Карно рабочее тело совершает полезную работу, соответствующую площади, заключенной внутри контура 1—2—3—4.
Эта работа эквивалентна разности между подведенной (q1) и отведенной (q2) теплотой, т. е.
.
Тогда термический КПД цикла Карно на основании формул (2) и (3) можно представить как
.
Для изотермических процессов
,
.
Отсюда
.
Здесь отношения объемов v3/v4 и v2/v1 равны. Тогда
. (1.25)
Анализируя последнее выражение, можно сделать следующие выводы.
1. Термический КПД обратимого цикла, осуществляемого между двумя источниками теплоты, не зависит от свойств рабочего тела, так как в выражении (1.25) нет каких-либо величин, отражающих свойства рабочего тела.
2. Термический КПД цикла Карно не может быть равен единице, поэтому не возможен полный переход теплоты в работу и неизбежна отдача неиспользованной части этой теплоты холодильнику. Теоретически КПД цикла Карно мог бы быть равен единице при T1 = или Т2 = 0, однако, такие условия практически не достижимы. Его величина зависит от интервала температур T1 и Т2, в котором осуществляется цикл: чем выше температура T1, тем в большем удалении от равновесного состояния находится рабочее тело, и тем большая работа может быть получена при самопроизвольном процессе расширения.
3. Цикл Карно, составленный из оптимальных термодинамических процессов, обладает максимальным КПД из всех возможных циклов, осуществляемых в том же интервале температур. Для любого цикла, отличного от цикла Карно,
.
Практически цикл Карно осуществить трудно и даже не целесообразно по причине чрезвычайно малой удельной работы и необходимости значительного увеличения габаритных размеров двигателя. Тем не менее, теоретическое значение цикла Карно огромно, так как он является неким эталоном при определении максимальной возможности полезного использования теплоты при данных температурных условиях. Сравнение термических КПД цикла Карно и любого другого цикла дает возможность судить о степени совершенства последнего.
Контрольные вопросы
1. Что такое рабочее тело?
2. Почему в тепловых машинах в качестве рабочего тела используются газы и пары?
3. Что такое параметры состояния рабочего тела? Назовите их.
4. В чем заключается преимущество термодинамической температур�ной шкалы?
5. Чем отличается абсолютное давление от манометрического?
6. Что такое удельный объем вещества?
7. Напишите уравнение состояния идеального газа.
8. Что называется теплоемкостью газа?
9. Дайте формулировку первого закона термодинамики?
10. Что такое термодинамический процесс?
11. Как графически на р—v-диаграмме определяется работа процесса?
12. Что такое изохорный, изобарный, изотермический и адиабатный про�цессы? Напишите их уравнения.
13. Что такое политропный процесс? Чему равен показатель политропы для изохорного, изобарного, изотермического и адиабатного про�цессов?
14. В чем заключается физическая основа второго закона термодина�мики?
15. Что называется циклом теплового двигателя?
16. Что такое термодинамический КПД? Что он определяет?
17. Значение и особенности цикла Карно.
18. Что является основным при работе компрессора? Как вычисляется ра�бота компрессора?
PAGE \* MERGEFORMAT 1
ОСНОВЫ ТЕХНИЧЕСКОЙ ТЕРМОДИНАМИКИ