Элементы теории множеств

Лекция 2 ММ ТП в маш.

Множество – совокупность объектов, объединенных каким-либо общим признаком. Отдельные объекты, из которых состоит множество, называются элементами множества. О множестве элементов можно говорить только тогда, когда эти элементы различимы между собой.

Общим обозначением множества служат фигурные скобки , внутри которых перечисляются элементы множества. Для обозначения конкретных множеств используются прописные буквы латинского алфавита , для обозначения элементов множества используется строчные буквы , или строчные буквы с индексами

Для указания того, что некоторый элемент, а принадлежит множеству S используется знак « ». Запись означает, что элемент а принадлежит S, а запись означает. что элемент а не принадлежит множеству S. Записью пользуются для сокращения записи

Множества бывают конечными и бесконечными. Множество называется конечным, если число его элементов конечно, т.е. если существует такое натуральное число N, являющееся числом элементов множества и бесконечным, если оно содержит бесконечное число элементов.

Чтобы оперировать с конкретными множествами нужно их задавать. Существует два способа задания множеств:

а) задание множества способом перечисления всех элементов, составляющих множество;

б) задание множества описанием общего признака, которым обладают элементы множества.

Способом перечисления обычно задаются конечные множества. Так, например, множество отличников в группе можно задать, перечислив пофамильно всех студентов, учащихся на отлично. Для сокращения записи иногда пишут , или вводят множество индексов и пишут . Задание множества способом задания общего признака элементов состоит в том, что указывается этот признак. Например, множество отличников группы в виде . В тех случаях, когда не вызывает сомнений, из какого множества берутся элементы х, указание о принадлежности элемента х к множеству М можно не делать: . Примеры задания множеств способом указания общего признака:

- множество четных чисел; - множество .

Пусть С – множество целых чисел. Тогда есть множество .

Пустым множеством называется множество , не содержащее ни одного элемента и обозначается через . Например, . Пустое множество относится к конечным множествам. Понятие пустого множества играет важную роль при задании множеств способом описания. Так, например, без понятия пустого множества мы не могли бы говорить о множестве отличников группы, не убедившись предварительно, есть ли вообще в группе отличники. Введение пустого множества позволяет совершенно спокойно оперировать со множеством отличников в группе, не заботясь о том, есть ли вообще в рассматриваемой группе отличники.

Два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют одно и тоже множество. Множества не равны , если либо в множестве есть элементы, не принадлежащие , либо в есть элементы, не принадлежащие . Символ равенства обладает свойствами

рефлексивность;
если симметричность;
если - транзитивность.

Из определения множества вытекает, что порядок элементов в множестве несущественен, то есть, например, . Из определения же следует, что в множестве не должно быть неразличимых элементов, то есть запись некорректна и ее следует заменить на .

Понятие подмножества

Множество Х является подмножеством множества У, если любой элемент множества Х является элементом множества У.

В теории множеств применяются специальные символы. Для определения подмножества применяются два таких символа :

символ, называемый «квантор» и означающий любой, какой бы ни был, «для всех»;

символ следствия (импликации), означающий «влечет за собой».

Определение подмножества, которое может быть сформулировано в виде: для любого х утверждение «х принадлежит Х» влечет за собой утверждение «х принадлежит У» запишется так:

Более краткой записью выражения «Х является подмножеством У» будет запись

что читается как «Y содержит Х». Символ означает включение, а строгое включение, которое применяется тогда, когда хотят подчеркнуть, что множество содержит и другие элементы, кроме элементов из Х, т.е. . Связь между символами и дается выражением

и .

Здесь использован знак , означающий эквивалентность, т.е. «то же самое, что».

Свойства подмножества:

рефлексивность – «множество Х является подмножеством самого себя»;
транзитивность – «если Х есть подмножество Y, а Y есть подмножество Z, то Х есть подмножество Z ».
для любого множества М.

Взаимно однозначное соответствие между множествами

Зачастую приходится сопоставлять элементы множеств. Если каждому элементу множества Х поставлен в соответствие элемент множества Y , то такое попарное соответствие между элементами двух множеств называется взаимно однозначным соответствием.

Пусть Х и Y два конечных множества, соответственно т- и п- элементные.

Между ними можно установить взаимно однозначное соответствие только в том случае, когда т = п. Для двух п – элементных множеств число взаимно однозначных соответствий будет

Множество можно разбить на подмножества различными способами. Общее число к-элементных подмножеств п-элементного множества М равно

, (2.1)

т.е. равно числу сочетаний из п элементов по к.

Общее число L всевозможных подмножеств п-элементного множества М равно

(2.2)

Счетные и несчетные множества

Если бесконечное множество возможно привести во взаимно однозначное соответствие с натуральным рядом, то такое множество называется счетным множеством. Если такое соответствие привести нельзя, то множество называется несчетныим.

Примеры счетных множеств.

Множество М квадратов целых чисел: 1, 4, 9, 16, … представляет собой лишь подмножество множества натуральных чисел, Однако множество М является счетным множеством, так как приводиться во взаимно однозначное соответствие с натуральным рядом, квадратом которого он является.
Счетным является множество С всех целых чисел – положительных и отрицательных, хотя натуральный ряд представляет собой только положительное подмножество этого множества

Из которого следует, что

Счетным является множество всех рациональных чисел где любые целые числа. Чтобы убедиться в этом, представим все множество рациональных чисел в виде таблицы, в которую заносим несократимые дроби

Обходя таблицу по направлению стрелок, приходим к последовательности

позволяющей занумеровать эти числа.

Теорема. (Г.Кантор) Множество всех действительных чисел интервала 0 < x 1

несчетно. Равносильное утверждение: множество всех точек интервала (0,1] несчетно. Рассмотренный интервал (0,1] может быть приведен во взаимно однозначное соответствие с любым интервалом (a, b] (например, с помощью центральной проекции). Отсюда, множество всех действительных чисел любого интервала (a, b] несчетно.

Верхняя и нижняя границы множества

Имея дело со множеством действительных чисел, можно сравнивать элементы этого множества по их значению и, в частности находить их наибольшее и наименьшее элементы этого множества. Для конечных множеств, заданных перечислением, эта задача не представляет труда. Например, для множества

Если множество задано описательным способом, например, указано лишь правило вычисления числовых значений его элементов, то задача определения наибольшего и наименьшего элементов становится весьма трудоемкой. Несколько более легкой задачей является нахождение области, внутри которого лежат все элементы множества. При решении этой задачи очень полезными оказываются понятия верхней и нижней границ множества.

S- множество вещественных чисел. Верхней границей S является число С такое, что для имеет место . Точной верхней границей или супермумом множества S, обозначаемой sup S, называют верхнюю границу, которая не превосходит любую другу верхнюю границу. Множество может иметь только одну верхнюю границу.

Нижней границей множества S является число с такое, что имеет место . Точной нижней границей или инфинумом множества S, обозначаемой inf S, называют нижнюю границу, не меньшую любой другой нижней границы.

Теорема. Если , то

. (2.3)

Операции над множествами

Над множествами можно производить действия, которые во многом напоминают действия сложения и умножения в обычной алгебре. Напомним свойства этих действий.

Пусть a и b некоторые числа. Сумма и произведение этих чисел обладают следующими свойствами:

коммутативный или переместительный закон;
ассоциативный или сочетательный закон;
дистрибутативный или распределительный закон.

В коммутативном и ассоциативном законах можно действие сложения заменить действием умножения и наоборот, при этом получим другие законы, которые также справедливы как и первые. Но в дистрибутативном законе такая замена приводит к неверному результату:

В отличии от обычной алгебры, в алгебре множеств все три закона симметричны относительно операций сложения и умножения.

Объединение множеств

Объединением множеств X и Y называют множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X,Y,тол есть принадлежат множеству Х или множеству Y.

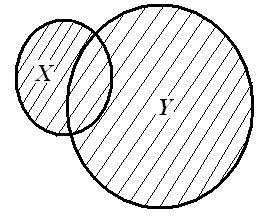
Рисунок 2.1

Объединение обозначается знаком «» или знаком «+»:

(2.4)

Формальное определение объединения

. (2.5)

Пример. Если , а , то .

Если задано п множеств Xi , , то объединение этих множеств

. (2.6)

Для объединения множеств справедливы коммутативный и ассоциативный законы

(2.7)

Пересечение множеств

Пересечением множеств X и Y называется множество, состоящее из всех тех элементов и только тех, которые принадлежат как множеству Х, так и множеству Y,

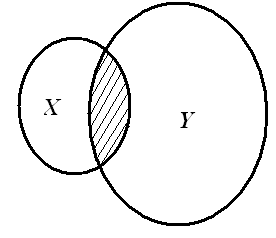
Рисунок 2.2

то есть пересечение множеств, есть множество состоящее из элементов, общих для обеих множеств X, Y.

Пересечение множеств обозначается знаком «». Формальное определение пересечения множеств

(2.8)

Пересечение множеств иногда называют произведением множеств и обозначают.

Множества X и Y называются непересекающимися, если они не имеют общих элементов (рисунок 3), т. е.

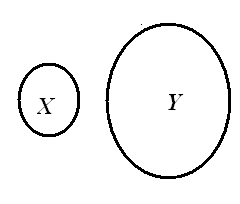
Рисунок 2.3

Если задано множество М множеств Хi , т.е. , пересечение этих множеств записывается так

. (2.9)

и представляет собой множество элементов, общих для всех множеств Хi.. Имее5т место также соотношение

Разность множеств

Разностью множеств X и Y называется множество, состоящее из всех тех и только тех элементов, которые принадлежат Х и не принадлежат Y (рисунок 4)

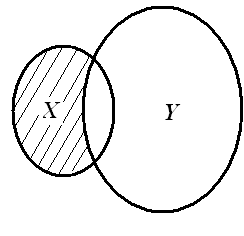
Рисунок 2.4

Разность множеств обозначается знаком «\»:

. (2.10)

Универсальное множество

. (2.11)

Соотношение (11) означает, что пересечение или «общая часть» множества I и множества Х для любого множества Х совпадает с самим этим множеством. Но это возможно лишь в том случае, если множество I содержит все элементы, из которых может состоять множество Х, так что любое множество Х полностью содержится в множестве I. Множество I играет роль единицы (как в обычной алгебре ).

Множество I, удовлетворяющее этому условию называется универсальным или полным.

Универсальное множество удобно графически представлять в виде прямоугольника

Рисунок 2.5

Различные области внутри этого прямоугольника будут представлять различные подмножества универсального множества.

Универсальное множество обладает свойством, не имеющем аналогов в обычной алгебре

. (2.12)

Дополнение множества

Множество , определяемое из соотношения

, (2.14)

называется дополнением множества Х (до полного множества I )

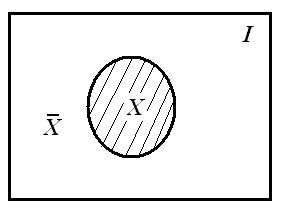
Рисунок 2.6

Из (14) следует, что если и не имеют общих элементов

(2.15)

Кроме того, не имеется элементов I, которые не принадлежали бы ни , ни , так как те элементы, которые не принадлежат , принадлежат

(2.16)

Из (15) и (16) следует, что

. (2.17)

Разбиение множества

Одной из наиболее часто встречающихся операций над множествами является разбиение множества на систему подмножеств.

Пусть задано множество М и система множеств . Систему множеств Т называют разбиением М, если удовлетворяются следующие условия:

любое множество Х из Т является подмножеством множества М:

;

любые два множества X и Y из Т являются непересекающимися:

объединение всех множеств, входящих в разбиение, дает множество М:

Упорядоченные множества

Кортежом или упорядоченным множеством называется последовательность элементов, т.е. совокупность элементов, в которой каждый элемент занимает определенное положение. Сами элементы при этом называются компонентами кортежа (первый компонент, второй компонент и т.д.), Примеры кортежей: множество людей, стоящих в очереди; множество слов в фразе; долгота и широта точки на местности; множество солдат, идущих строем и т.п. Во всех этих приметах место каждого элемента вполне определенно и не может быть произвольно изменено. Часто в технических задачах часто эта определенность является предметом договоренностей.

Число элементов кортежа называют его длиной. Для определения кортежа используются круглые скобки

Кортежи длиной в 2 элемента называются парами или упорядоченными парами; длиной 3 – тройками и т.д. В общем случае кортежи длиной п называют п-картами. Частным случаем кортежа является кортеж (а) длиной 1 и пустой кортеж длиной 0, обозначаемый ( ) или . В отличии от обычного множества в кортеже могут быть и одинаковые элементы.

Для нас большое значение имеют упорядоченные множества, элементами которых являются действительные числа. Такие упорядоченные множества называются точками пространства или векторами. Так, кортеж (а1, а2) может рассматриваться как точка плоскости или вектор, проведенный из начала координат в точку с координатами (а1, а2). Тогда компоненты кортежа а1 и а2 будут проекциями вектора на оси 1 и 2

или в общем виде

Кортеж (а1, а2, а3) может рассматриваться как трехмерный вектор. Тогда

Обобщая понятие вектора, можно рассматривать упорядоченное п-элементное множество вещественных чисел

как точку в воображаемом п-мерном пространстве или п-мерным вектором. При этом компоненты п-элементного кортежа будем рассматривать как проекции этого кортежа на соответствующие оси

(2.18)

Ели множество конечно, то

Если множество упорядоченно, то вводится прямое произведение множеств. Прямым произведением множеств Х и Y называется множество, обозначаемое XY и состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству Х, а вторая – множеству Y. Прямое произведение обозначается

. (2.19)

Прямое произведение не обладает свойством коммутативности

Прямое произведение двух множеств может быть легко обобщено на случай большего числа множество. Прямым произведением множеств называется множество, обозначаемое и состоящее из всех тех и только тех кортежей длины п, первый элемент которых принадлежит Х1, вторая – Х2 и т.д. Частным случаем прямого произведения является понятие степени множества. Пусть М произвольное множество. s-ой степенью множества М называется прямое произведение s одинаковых множеств М.

Проекция множества

Операция проектирования множества тесно связана с операцией проектирования кортежа и может применяться только к тем множествам, элементами которых являются кортежи одинаковой длины.

Пусть М – множество, состоящее из кортежей одинаковой длины s. Тогда проекцией множества М называется множество проекций кортежей из М.

Если , то

Пр1М=Х, Пр2 М=Y, (2.20)

а если то

. (2.21)

Соответствия

Рассмотрим два множества X и Y. Элементы этих множеств могут каким либо образом сопоставляться друг и другом , образуя пары (х,y). Если способ такого сопоставления определен, то есть для каждого элемента указан элемент , с которым сопоставляется элемент х, то говорят, что между множествами X и Y установлено соответствие. При совершенно необязательно, чтобы в сопоставлении участвовали все элементы множеств X и Y, важно указать закон, в соответствии с которым осуществляется соответствие, т.е. перечисляющее все пары (х,y), участвующие в сопоставлении. Соответствие обозначается буквой «q», представляет собой тройку множеств

в которой В этом выражении первую компоненту Х называют областью отправления соответствия, вторую компоненту Y – областью прибытия соответствия, третью компоненту Q – графиком соответствия. Кроме этих множеств, с каждым соответствием неразрывно связаны еще два множества:1) множество , называемое областью определения соответствия, в которую входят элементы множества , участвующие в сопоставлении; 2) множество называемое областью значений соответствия, в которую входят элементы множества, участвующие в сопоставлении.

Если , то говорят, что элемент у соответствует элементу х.

Для каждого соответствия существует обратное соответствие

(2.22)

Последовательное применение двух соответствий называется композицией соответствий

(2.23)

Причем область значений первого соответствия совпадает с областью значений второго соответствия:

Композицию соответствий q и p обозначается q(p), а график композиции - . При этом композиция соответствий (23) запишется в виде

Отображения

Пусть X и Y некоторые множества и , причем . Тройка множеств определяет некоторое соответствие, обладающее, однако, тем свойством, что его область определения совпадает с областью отправления, т.е. Х и следовательно, это соответствие определено всюду на Х. Другими словами, для каждого существует , так что . Такое всюду определенное соответствие называется отображением Х в Y и записывается так

Под термином «отображение» часто понимают однозначное соответствие. Но под более полные понятием отображения понимается соответствие, когда каждому элементу х Х отображение Г ставит в соответствие некоторое подмножество Y

которое называется образом элемента х. Закон, по которому осуществляется соответствие, определяется множеством Г.

Пусть . Тогда образом будет множество . Совокупность всех элементов Y, являющихся образами Гх для называется образом А и обозначается ГА

Если А1 и А2 - подмножества Х, то

Но соотношение

справедливо только для однозначных отображений. В общем же случае

Важным частным случаем отображения является случай когда множества и совпадают. При этом отображение будет представлять отображение множества Х самого на себя и будет определяться парой

, где .

Подробным изучением таких отображений занимается теория графов. Здесь отметим несколько соотношений.

и т.д.,

обратное отображение.

Тогда

и т.д.

Пример. Пусть Х-множество людей. Для каждого человека обозначим через множество его детей. Тогда есть множество его внуков, - множество правнуков; множество родителей и т.д.

Отношения

Отображение множества самого на себя называют отношениями.

Пусть отображение является отношением. Рассмотрим элемент . Говорят, что элемент у находится в отношении Г к элементу х и пишется в виде

Так символ Г в рассмотренном ранее примере означает «быть детьми данного человека».

Таким образом, отношение есть пара множеств (Х, Г) в которой . Поскольку элементами множества Х2 , то можно сказать что отношения есть множество упорядоченных пар. Так как каждая пата связывает между собой только два элемента множества Х2 , то такое отношение называют бинарным. В дальнейшем под отношениями будем иметь ввиду бинарные отношения.

Можно ввести более общее понятие отношения, называя отношением пару множеств (Х, Г), где , то есть элементами множества Г будут упорядоченные пары (п=2), упорядоченные тройки (п=3) , упорядоченные четверки (п=4) и т.д. В частности, множество упорядоченных троек называется тернарным отношением.

Отношения делятся на различные виды в зависимости от того, обладают или нет некоторыми свойствами: рефлексивность: хГх истинно; антирефлексивность хГх ложно: симметричность хГууГх; антисимметричность: хГу и уГхх = у; несимметричность: если хГу истинно, то уГх ложно; транзитивность: хГу и уГzхГz. При описании этих свойств будем считать, что - любые элементы из множества Х.

Отношение эквивалентности

Некоторые элементы множества можно рассматривать как эквивалентные в том случае, когда любой из этих элементов при некотором рассмотрении может быть заменен другим. В этом случае говорят, что данные элементы находятся в отношении эквивалентности.

Будем считать, что термин « отношение эквивалентности» применяется только в лучае, если выполняются следующие три условия:

Каждый элемент эквивалентен самому себе (рефлексивность).
Не имеет значения, какой элемент рассматривается первым, а какой вторым – (симметричность).
Два элемента, эквивалентные третьему, эквивалентны между собой – (транзитивность)

Для обозначения эквивалентности применяется знак . Тогда для обозначения условий эквивалентности применяются соотношения:

1. - рефлексивность;

2. - симметричность;

3. - транзитивность.

Иногда для обозначения эквивалентности применяют знак «» . Однако для отдельных частных отношений эквивалентности применяют и другие знаки :

= - для обозначения равенства;

|| - параллельности;

- логической эквивалентности.

Отношения порядка

Часто приходится сталкиваться с отношениями, которые определяют некоторый порядок расположения элементов множества. Так, мы различаем понятия «раньше» и «позже»; «больше» «меньше» и т.п. Во всех этих случаях можно расположить элементы в некотором порядке. Различают отношения нестрого порядка, для которого используется знак и строгого порядка <.

Отношением нестрого порядка называется отношение, обладающее тремя свойствами:

истинно (рефлексивность);
(антисимметричность);
(транзитивность).

Отношением строгого порядка называется отношение, обладающее свойствами:

ложно (антирефлексивность);
взаимоискбчаются (несимметричность);

PAGE \* MERGEFORMAT 1

Элементы теории множеств