Элементы теории графов

Лекция 4 ММ ТП в маш.

Наглядное представление о графе можно получить, если представить себе некоторое множество точек плоскости Х, называемых вершинами, и множество направленных отрезков U, соединяющих все или некоторые из вершин и называемых дугами (ребрами). Математически граф G можно определить как пару множеств X и U:

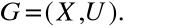(4.1)

Рисунок 4.1 Общий вид графа

На рисунке 1 изображен граф, вершинами которого являются точки a, b, c, d, t, g, h, а дугами – отрезки (а, а), (с, b), (c, e), (d, c), (d, d), (e, d), (g, h).

Иногда удобно дать графу другое определение. Можно считать, что множество направленных дуг U, соединяющих элементы множества Х, отображает это множество само на себя. Поэтому можно считать граф заданным, если дано множество его вершин Х и способ отражения Г множества Х в Х. Тогда граф G есть пара (Х,Г), состоящая из множества Х и отображения Г, заданного на этом множестве

(4.2)

Для графа, изображенного на рисунке 1, отображение осуществляется следующим образом:

Данное определение графа полностью совпадает с определение отношения на множестве. Граф, соответствующий данному определению, называют также ориентированным графом или орграфом.

Подграфом G графа называется граф, в который входит лишь часть вершин графа G, образующих множество А, вместе с дугами, соединяющими эти вершины. Например, на рисунке 1 это область, очерченная пунктиром. Математически подграф

где

Частичным графом G по отношению к графу называется граф, содержащий только часть дуг графа G,, то есть определяемый условием

, где .

На рисунке 1 граф, образованный жирными дугами образует частичный граф.

Пример. Пусть - карта дорог РФ. Тогда карта дорог Оренбургской области есть подграф, а карта дорог федерального значения есть частичный граф.

Дуга, соединяющая вершины a и b и направленная от а к b, обозначается .

Путем в графе называют такую последовательность дуг , в которой конец каждой предыдущей дуги совпадает с началом следующей. Путь , последовательными вершинами которого являются вершины a, b, …m, обозначается через .

Длиной пути называется число равное числу дуг, составляющих путь . Иногда каждой дуге ui приписывается некоторое число , называемое длиной дуги. Тогда длина пути определяется как суммы длин дуг, составляющих путь

Путь, в котором никакая дуга не встречается дважды, называется простым, а путь, в котором никакая вершина не встречается дважды, называется элементарным.

Контур - это конечный путь , у которого начальная вершина х1 совпадает с конечной вершиной хк. При этом контур называется элементарным, если все его вершины различны ( кроме первой и конечной, которые совпадают). Контур единичной длины, образованный дугой вида (а, а), называется петлей.

При решении задач с помощью компьютеров наглядные представления графов в виде изображений на плоскости совершенно бесполезны. Поэтому для этих случаев удобнее представление графов в математическом виде, а именно в виде матриц.

Вершины х и y являются смежными, если они различны и если существует дуга, идущая из х в у.

Дугу называют инцидентной вершине х, если она заходит в эту вершину или выходит из нее.

Обозначим через х1,х2, …, хп вершины графа, а через и1, и2, … ит его дуги. Введем числа

Квадратная матрица порядка называется матрицей смежности графа.

Введем числа

Матрица порядка называется матрицей инциденций для дуг графа. Матрицы инциденций применимы только для графов без петель. В случае наличия в графе петель эту матрицу следует расчленить на две полуматрицы:

положительную и отрицательную. На рисунке 2 приведен6 граф без петель и матрицы смежности и инциденций для него.

Неориентированные графы

Иногда граф рассматривают без учета ориентации дуг. Тогда его называют неориентированным графом. Для неориентированного графа понятия «дуга».«путь», «контур» заменяются понятиями «ребро», «цепь», «цикл» соответственно.

Матрицы смежности и инциденций строятся аналогично ориентированным графам, только не делается различия между заходящей в вершину и исходящей из нее дугами. При этом две вершины называются смежными, если есть ребро, которое их соединяет, а само ребро называется инцидентным этим вершинам.

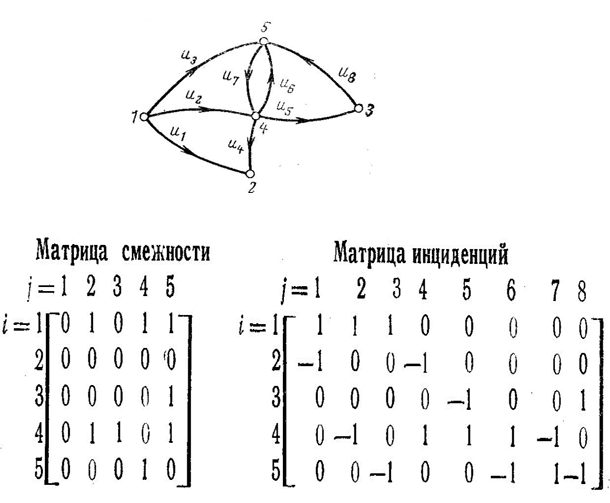
Рисунок 4.2

На рисунке 2 приведен граф без петель и матрицы смежности и инциденций.

Ребро – это отрезок, соединяющий две вершины; цепь - последовательность ребер; цикл – цепь, у которой начальная и конечная вершины совпадают.

Описать неориентированный граф можно путем задания пары множеств 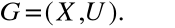(Х – множество вершин, G – множество ребер). Однако более удобно задавать неориентированный граф с помощью матриц смежности и инциденций, которые строятся также как и для ориентированных, с той разницей, что не делается различия между дугами, заходящими в вершину и выходящими из нее.

Степенью вершины х, обозначаемой deg(x) или dx , называют число ребер инцидентных вершине х. Так, для графа, изображенного на рисунке 3 имеем:

Если то вершину называют тупиковой, если то изолированной.

Теорема. Пусть G – неориентированный граф с п вершинами и т ребрами dj – степень j-ой вершины. Тогда

(4.3)

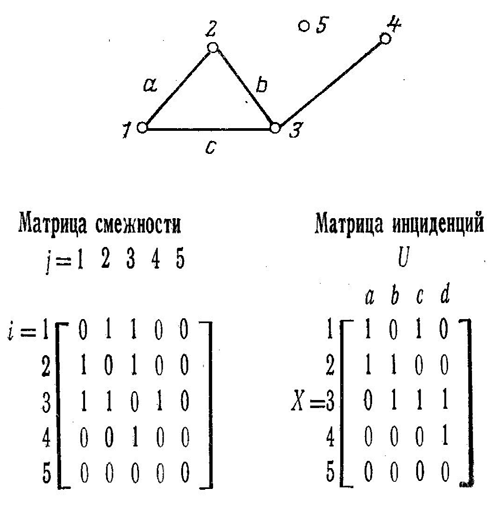
Рисунок 4.3

Следствие. В каждом графе число вершин нечетной степени четно.

Для неориентированного графа понятия «подграф» и «частичный граф» имеют аналогичный смысл.

С понятием неориентированного графа связана важная характеристика, называемая связностью графа. Граф связен, если любые две его вершины можно соединить цепью. Если граф G не связен, то его можно разбить на такие подграфы Gi ,что все вершины в каждом подграфе связны, а вершины из различных подграфов не связны. Такие подграфы называются компонентами связности графа G.

Если из графа на рисунке 3 исключить изолированную вершину 5, то полученный граф будет связным.

Изоморфизм графов

Один и тот же граф можно изобразить различными способами. Так, на рисунке 4 при ведены три изображения одного и того же графа

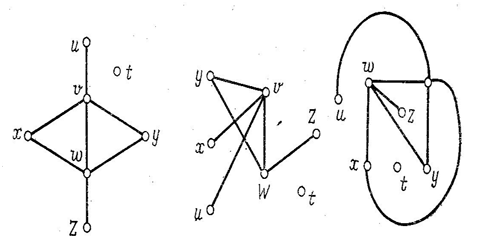
Рисунок 4.4

Такие графы называются изоморфными. Установить, являются ли два графа изоморфными достаточно трудно. На практике обычно определяют некоторые параметры графов, такие как число вершин, число роббер, число компонент связности, последовательность степеней вершин в убывающем порядке. Если какие-то параметры у графов различны, то эти графы различны. Но бывают случаи, когда все параметры совпадают, но тем не менее графы различны (рисунок 5)

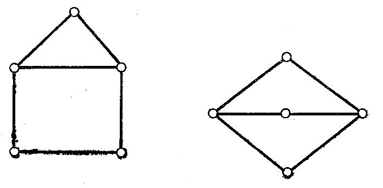
Рисунок 4.5

Отношения порядка и отношения эквивалентности

на графе

Будем считать, что на графе введено отношение порядка, если для ,любых двух вершин (х и у), удовлетворяющих условию , существует путь из х в у. В этом случае говорят, что вершина х предшествует вершине у, или вершина у следует за вершиной х . Это определение отражает на графе все свойства отношения порядка.

Рефлексивность. Условие

истинно (4.4)

означает эквивалентность вершины самой себе, т.е. условие . В то же время это условие можно рассматривать как наличие пути из х в х, т.е. как петлю в вершине х. (рисунок 6)

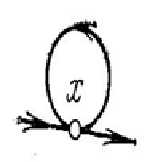Рисунок 4.6

Транзитивность. Условие

(4.5)

означает, что вершины последовательно встречаются на одном и том же пути (рисунок 7).

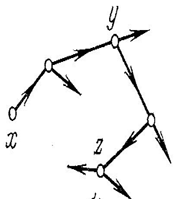
Рисунок 4.7

Антисимметричность. Условие

(4.6)

означает, что в графе имеется контур, на котором лежат вершины х и у (рисунок 8)

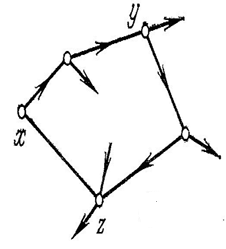Рисунок 4.8

Левая часть этого выражения (слева от стрелки) говорит о том, что существует путь из х в у, а также существует путь из у в х, а это означает, что в графе имеется контур,

на котором лежат вершины х и у. Из правой части этого условия вытекает, что вершины, лежащие на одном и том же контуре, являются эквивалентными.

Иногда этот вывод рассматривают как определение эквивалентности на графе, так как удовлетворяются все три условия: рефлексивности, симметричности, транзитивности.

Таким образом, отношение порядка и эквивалентности определяют некоторый граф.

На графе может быть введено отношение строго порядка. В этом случае для любых двух вершин (х и у), удовлетворяющих условию x < y, существует путь, идущий из х в у. Условие транзитивности x < y < z x < z, означает, что вершины x, y, z встречаются последовательно на одном и том же пути. Условие антирефлексивности (х<x ложно) говорит об отсутствии петель на графе, а условие несимметрии (x<y, y<x взаимоисключаются) говорит об отсутствии контуров. Таким образом отношения строго порядка определяют граф без контуров.

Характеристики графов

Решение многих технических задач методами теории графов сводятся к определению тех или иных характеристик графов. К важнейшим характеристикам графов относятся: цикломатическое число, хроматическое число, множество внутренней устойчивости, множество внешней устойчивости.

Цикломатическое число. Пусть G – неориентированный граф, имеющий п вершин, т ребер и r компонент связности. Цикломатическим числом графа G называется число:

(4.7)

Это число имеет следующий смысл: оно равно наибольшему числу независимых циклов в графе.

Хроматическое число. Пусть р – натуральное число. Граф G называют р –хроматическим, если его вершины можно раскрасить р различными цветами так, чтобы никакие две смежные вершины не были раскрашены одинаково. Наименьшее число р, при котором граф является р – хроматическим, называется хроматическим числом и обозначают (G).

Если (G) = 2, то граф называется бихроматическим. Необходимым и достаточным условием того, чтобы граф был бихроматическим, является отсутствие в нем циклов нечетной длины. Хроматическое число, например, играет важную роль при решении задачи наиболее экономичного использования памяти при программировании. Однако его определение, за исключением случая бихроматического графа, представляет собой трудную задачу, требующую для своего решения компьютер.

Множество внутренней устойчивости. Множество графа называется внутренне устойчивым, если никакие две вершины из S не смежны, т.е. для 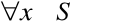имеет место

Множество внутренней устойчивости, содержащее наибольшее число элементов, называется наибольшим внутренним устойчивым множеством, а число элементов этого множества – числом внутренней устойчивости графа G.

Множество внешней устойчивости. Множество графа называется внешне устойчивым, если любая вершина, не принадлежащая Т, соединена дугами с вершинами из Т, т.е. имеет место .

Множество внешней устойчивости, содержащее наименьшее число элементов, называется наименьшим внешние устойчивым множеством, , а число элементов этого множества - числом внешней устойчивости графа G.

Задача о кратчайшем пути

В практических приложениях имеет большое значение задача нахождения кратчайшего пути между двумя вершинами связного неориентированного графа. К такой задаче сводятся многие задачи выбора наиболее экономичного ( с точки зрения расстояния или времени или стоимости) маршрута на имеющейся карте дорог; многие задачи выбора наиболее экономичного перевода динамической системы из одного состояния в другое и т.п. В математике разработан ряд методов решения подобных задач, однако методы, основанные на использовании графов, оказываются наименее трудоемкими.

Задача о кратчайшем пути на графе в общем виде может быть сформулирована следующим образом. Дан неориентированный граф 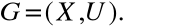Каждому ребру этого графа приписано некоторое число l(u) 0, называемое длиной ребра. В частных случаях l(u) может между вершинами, соединяемыми ребром и, временем или стоимостью проезда по этому ребру и т.п. При этом любая цепь будет характеризоваться длиной, определяемой формулой

Требуется для произвольных вершин а и b графа G такой путь ab, который был бы наименьшим.

Прежде чем найти общий метод решения этой задачи, рассмотрим решение задачи частного вида, когда длина каждого ребра равна единице.

Нахождение кратчайшего пути на графе с ребрами единичной длины

Общее правило для нахождения кратчайшего пути в графе состоит в том, чтобы каждой вершине xi приписать индекс i , равный длине кратчайшего пути из данной вершины в конечную. Приписывание индексов вершинам в случае графа с ребрами единичной длины производится в следующем порядке:

конечной вершине приписывается индекс 0;
всем вершинам, из которых идет ребро в конечную вершину, приписывается индекс 1
всем вершинам, еще не имеющим индексов, из которых идет ребро в вершину с индексом i , приписывается индекс i+1. Этот процесс продолжается до тех пор, пока не будет помечена начальная вершина. По окончании разметки индекс у начальной вершины будет равен длине кратчайшего пути. Сам кратчайший путь найдем, если будем двигаться из начальной вершины в направлении убывания индексов.

PAGE \* MERGEFORMAT 1

Элементы теории графов