Элементы математической логики

Лекция 3 ММ ТП в маш.

Исходным понятием математической логики является понятие высказывания.

Высказыванием называется предложение, которое может быть либо истинным, либо ложным и не иметь никакого третьего значения.

Не всякое предложение является высказыванием. В частности все вопросительные и восклицательные предложения не являются высказываниями, а также предложения, являющиеся определением чего-то («Который час?»; «Мойте руки перед едой!»; «Точка есть объект, не имеющий размеров»). Существуют предложения, которые, безусловно, являются истинными или ложными, но не можем в данный момент сказать точно истинны они или ложны (« Земля – единственная обитаемая планета в о Вселенной» или «Всякое четное число есть сумма двух простых»).

Из всех свойств высказываний нас будет интересовать в дальнейшем только одно: истинно оно или ложно. Все прочие свойства высказывания: особенности грамматической формы, смысловые значения отдельных слов и всего высказывания в целом будем полагать несущественными.

Высказывания будем обозначать прогписн67ыми буквами латинского алфавита: P, Q, R,… и т.д.

Условимся каждому истинному высказыванию сопоставлять число 1, а ложному – число 0, то есть введем на множестве всех высказываний функцию (Р), которая может принимать значения 1 или 0 в зависимости от того истинно высказывание Р или ложно

Число называется значением истинности высказывания Р.

Операции над высказываниями

В алгебре логики имеется много различных операций. Наиболее употребительными из них являются инверсия, конъюнкция, дизъюнкция.

Отрицание высказывания или инверсия ( НЕ)

Отрицанием высказывания называется новое высказывание, обозначаемое (читается «Не Р» или «Неверно, что Р») которое считается истинным, если высказывание Р ложно, и ложным, если Р истинно.

Например, для высказывания Р: «Снег – белый», высказывание выглядит так: « Не снег – белый» или « Неверно, что снег – белый». В смысловом выражении оба высказывания имеют различное содержание. Поэтому в первом варианте частицу не переводят в другое место, обычно перед сказуемым: «Снег – не белый».

Конъюнкция высказываний ( «И»)

Конъюнкцией высказываний Р и Q называется новое высказывание, обозначаемое (читается « » которое считается истинным, если оба высказывания истинны и ложными во всех остальных случаях.

Таким образом, значение истинности высказывания связано со значениями истинности .

Примеры.

Высказывание «Число 2 четное и простое» является конъюнкцией высказываний «Число 2 четное» и «Число» простое». Так оба последних высказывания истинны, то истинна и их конъюнкция.
Высказывания «2 меньше 5» и « 5 меньше 10» истинны, поэтому истинна и их конъюнкция.

Таблица истинности для конъюнкций

Дизъюнкция высказываний ( «ИЛИ»)

Дизъюнкций высказываний Р и Q называется новое высказывание, обозначаемое (читается «» ), которое истинно в тех случаях, когда истинно хотя бы одно из высказываний , и ложно, когда ложны оба высказывания.

Таблица истинности для дизъюнкций

Примеры.

Высказывание «В неделе 10 дней или в годе 12 месяцев» является дизъюнкцией двух высказываний: «В неделе 10 дней» и «В году 12 месяцев». По таблице (третья строка) исходное высказывание является дизъюнкцией.
Высказывание «» является дизъюнкцией высказываний «» и «» из которых первое высказывание истинно, а второе ложно. Следовательно, истинна сама дизъюнкция (вторая строка таблицы).

Импликация высказываний

Импликацией высказываний Р и Q называется высказывание, обозначаемое

(читается «Если Р, то Q», или «Из Р следует Q», или «Из Р следует Q», или «Р влечет Q», которое ложно лишь в том случае, если Р истинно, а Q ложно.

Таблица истинности для импликаций

При рассмотрении импликации высказывание Р называют условием (посылкой) импликации, а Q – следствием (заключением) импликации.

Примеры.

Высказывание «Если Земля круглая, 22=4» является импликацией высказываний «Земля круглая» и «22=4» Оно истинно, так как истинны оба последних высказывания (первая строка таблицы).

Эквивалентность высказываний

Эквивалентностью (или эквиваленцией) высказываний Р и Q называется новое высказывание, обозначаемое (читается «Р эквивалентно Q» или «Р тоuда и только тогда, когда Q», которое истинно в том и только в том случае, если Р и Q одновременно истины или ложны

Таблица истинности для эквивалентности

Примеры.

Высказывание «22=4 тогда и только тогда, когда Земля – круглая» представляет собой эквиваленцию двух высказываний «22=4» и «Земля – круглая» и оно истинно, такт как оба последних высказываний истинны.

Нормальные формы для формул алгебры высказываний

Операции импликации и эквиваленции можно выразить через остальные операции (конъюнкции, дизъюнкции и отрицание). Это значит, что для любой формулы алгебры высказываний можно указать равносильную ей формулу, содержащую только операции отрицания, конъюнкции, дизъюнкции, причем сделать это можно бесчисленным множеством способов. Однако среди этого множества выражений данной формулы лишь через операции , существуют некоторые особые, играющие важную ролью Они называются совершенными нормальными формами.

Совершенная дизъюнктивная нормальная форма

Введем обозначение

Теорема. Для всякой формулы алгебры высказываний справедливо соотношение:

Совершенным конъюнктивным одночленом от переменных Х1, Х2, … Хп называется выражение вида

где каждое есть либо 1, либо 0.

Совершенной дезъюнктивной нормальной формой (СДНФ) называется формула вида

где каждая из формул К1… Кs представляет собой совершенный конъюнктивный одночлен.

Примером СДНФ от двух переменных Х1, Х2 может служить выражение

Совершенная конъюнктивная нормальная форма

Теорема. Для любой формулы алгебры высказываний справедливо соотношение:

Совершенным дизъюнктивным одночленом от переменных называется выражение вида

где каждое есть либо 1, либо 0.

Совершенной конъюнктивной нормальной формой (СКНФ) называется формула вида

где каждая из формул представляет собой совершенный дизъюнктивный одночлен.

Логические операции как операции на множестве {0,1}

Рассматривая любую из рассмотренных логических операций, можно

оперировать не с высказываниями, а с числами 1 и 0 таким образом, что каждой логической операции над высказываниями соответствует некоторая функция, определенная на двухэлементном множестве {0,1} и принимающей значения в том же множестве определив конъюнкцию над ними в виде таблицы

Аналогичные замечания можно сделать и по отношению к остальным логическим операциям. Например,

и т. д.

Формулы алгебры высказываний

Определение и примеры формул.

С помощью логических операций, рассмотренных ранее, можно, исходя из простейших высказываний, строить более сложные. Например, исходя из высказываний Р: «Пушкин – русский поэт», Q: «Гаусс – немецкий математик», R; «», можно построить новое высказывание: «Если Пушкин – русский поэт и Гаусс – немецкий математик, то ». Это новое высказывание имеет вид .

Полученное выражение, если отвлечься от конкретного смысла высказываний , можно рассматривать как некоторую схему, позволяющую, исходя из любых высказываний , строить новые высказывания. Такие схемы называются формулами алгебры высказываний.

Прежде чем дать общее определение формулы алгебры высказываний, дадим следующее определение.

Высказывательными переменными называются такие переменные, которые могут принимать в качестве своих значений любые конкретные высказывания. Такие переменные обозначаются заглавными латинскими буквами: , или теми же буквами с индексами: . Кроме того, введем еще две специфические высказывательные переменные И и Л: вместо первой можно подставлять любое истинное высказывание, вместо второй – любое ложное высказывание.

Полное описание понятия формулы алгебры высказываний дают соглашения:

Каждая отдельно взятая высказывательная переменная есть формула;
Если F1 и F2 - две формулы, то выражения

так же являются формулами;

Не существует никаких других формул, кроме тех, которые получаются в результате применения конечного числа раз п.п 1 и 2.

Так, например, формулами являются следующие выражения:

ит .д., а выражения

формулами не являются (в последнем выражении не хватает скобок).

Формулы алгебры высказываний обозначаются . Значения истинности формулы полностью определяются значениями истинности переменных , что позволяет для каждой формулы алгебры высказываний можно составить таблицу истинности.

Тавтологии

Формула алгебры высказываний называется тождественно истинной или тавтологией, если ее значение истинности равно 1 при любых значениях истинности Xi.

Наиболее важные тавтологии:

Законы коммутативности конъюнкции и дизъюнкции

Законы ассоциативности конъюнкции и дизъюнкции:

Законы дистрибутативности:

Законы де Моргана:

Закон исключения третьего:

Закон композиции:

Правило цепного заключения (закон силлогизма):

Правило «модус поненс»:

Схема доказательства «от противного»:

Равносильность формул

Две формулы алгебры высказываний называются равносильными, если при любых логических значениях переменных логические значения высказываний F и H совпадают и обозначается так .

Существует связь между понятиями равносильности и тавтологии: формулы F и Н равносильны тогда и только тогда, когда формула является тавтологией.

Предикаты

Рассмотрим предложение «». Ясно, что это предложение не является высказыванием, потому что о его истинности или ложности можно судить только тогда, когда будет указано, какое число подразумевается под х. При значении оно истинно и ложно при других .

Предложение, в которое входят переменные и которое при замене переменных возможными для них значениями становится высказыванием, называется предикатом или высказывательной формой.

При задании предиката должно указываться множество Х тех значений, которые могут принимать переменные; оно называется областью определения предиката.

Если предикат содержит лишь одну переменную, то он называется одноместным; пр наличии п переменных предикат называется п – местным. Например, предложение « Река х впадает в Каспийское море» - одноместный предикат, а предложение « Река х впадает в море у» - двухместный. Предикат «» - одноместный, а «» - двухместный.

Подмножество множества Х, состоящее из тех значений переменных, при которых данный предикат превращается в истинное высказывание, называется областью или множеством истинности предиката.

Одноместные предикаты обозначаются 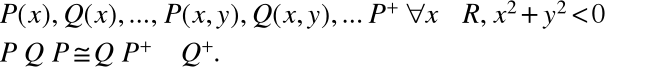а двухместные и т.д. или просто . Множество истинности предиката обозначается тоже буквой, что и сам предикат но с верхним индексом «+»: .

Тождественно истинные и тождественно ложные предикаты.

Равносильность и следование предикатов

Предикат с областью определения Х называется тождественно истинным, если при любых значениях переменных из Х он превращается в истинное высказывание; тождественно ложным, если при любых значениях переменных из Х он превращается в ложное высказывание. Например, предикат «» истинный для где R – множество действительных чисел, истинно ложный для

Два предиката с одной и той же областью определения Х называются равносильными, если они имеют одинаковые множества истинности.

Равносильность предикатов и обозначается так: .

Переход от некоторого предиката к равносильному ему предикату называется равносильным преобразованием предиката .

Пусть Р и Q – два предиката с общей областью определения Х. Говорят, что Q есть следствие Р, если область истинности предиката Р является частью области истинности предиката Q (или совпадает с ней) т.е. если

Примеры.

Предикат «» с областью определения есть следствие предиката «» с той же областью определения.
Предикат : «Углы треугольника х равны в некотором порядке углам треугольника у» есть следствие предиката : «Стороны треугольника х параллельны в некотором порядке сторонам треугольника у 2». В то же время эти предикаты не равносильны, поскольку существуют треугольники с соответственно равными углами, расположенные так, что стороны одного не параллельны сторонам другого ни в каком порядке.

Из определения равносильности и следования вытекает следующее положение: предикат Р равносилен предикату тогда и только тогда, когда есть следствие , а есть следствие .

Логические операции над предикатами

Отрицанием предиката с областью определения называется предикат с той же областью определения и обозначаемый (читается «Неверно, что »), который превращается в истинное высказывание для тех и только для тех значений , при которых есть ложное высказывание .

Множество истинности предиката представляет собой дополнение множества 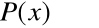(до Х).

Примеры.

Отрицанием предиката «» с областью определения служит предикат «» с той же областью определения.

PAGE \* MERGEFORMAT 1

Элементы математической логики